Energy Recuperation in a Spiral Reactor for Lean Methane Combustion: Heat Transfer Efficiency and Design Guidelines
Abstract
1. Introduction
2. Materials and Methods
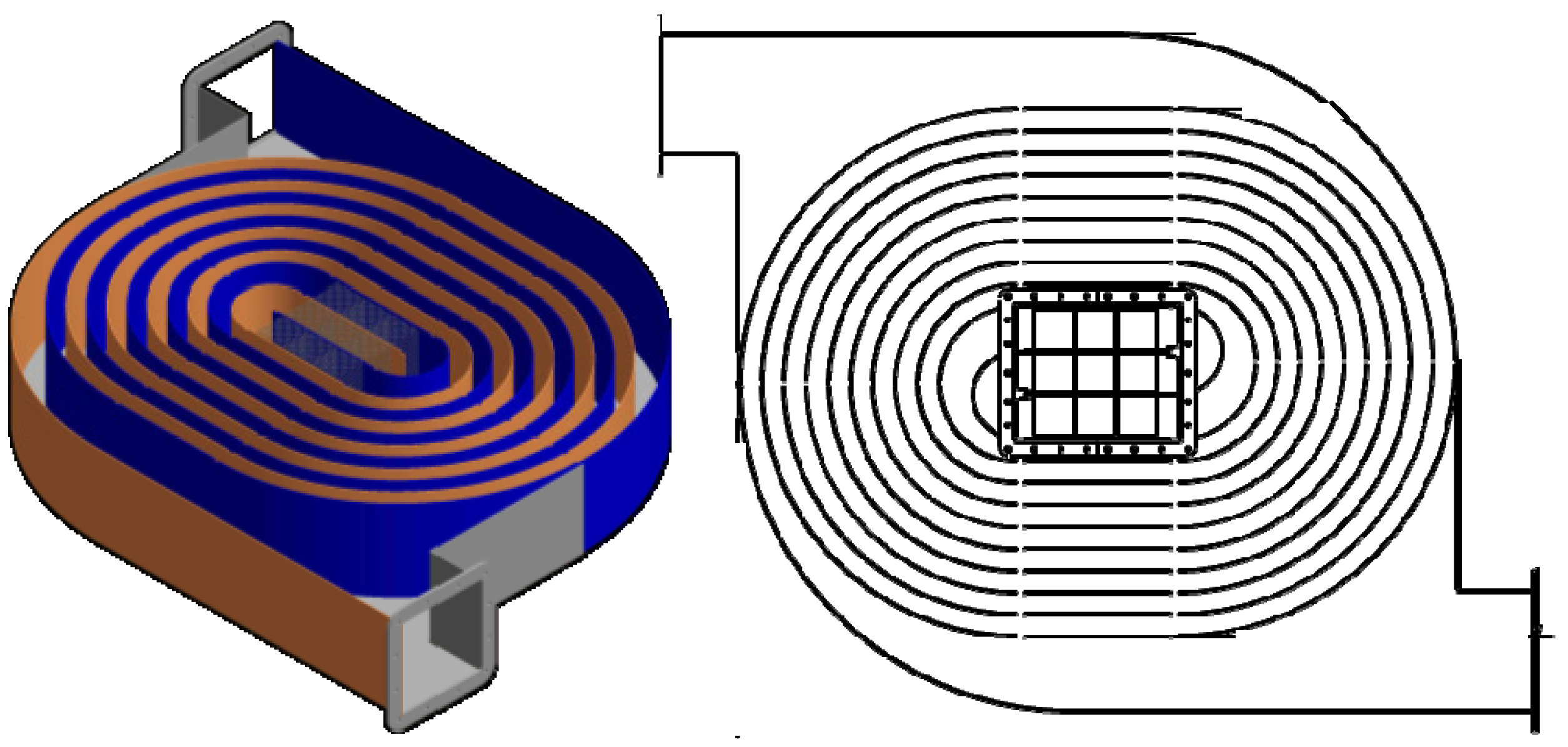
2.1. A Description of the Catalyst Used as a Basis for This Study
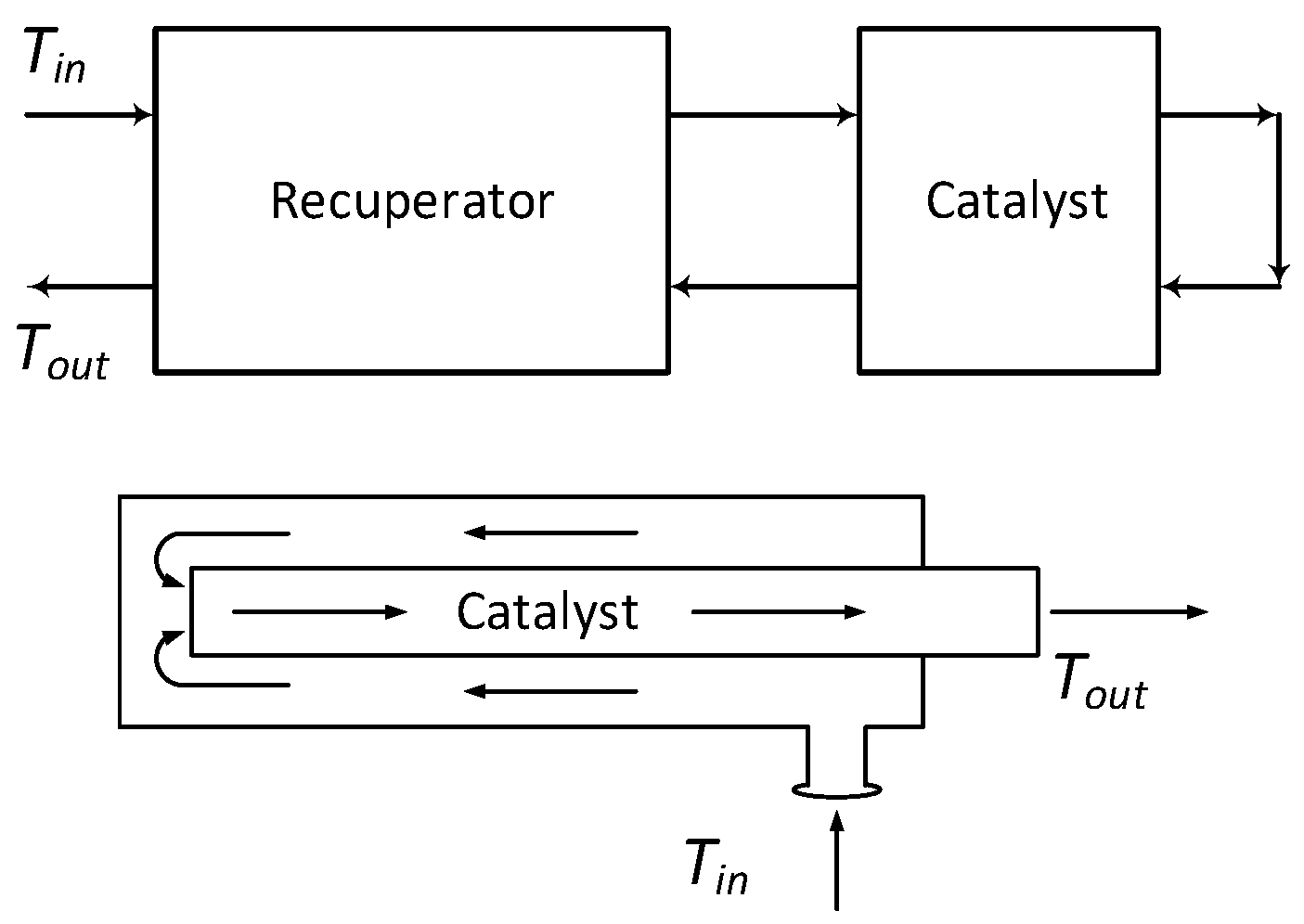
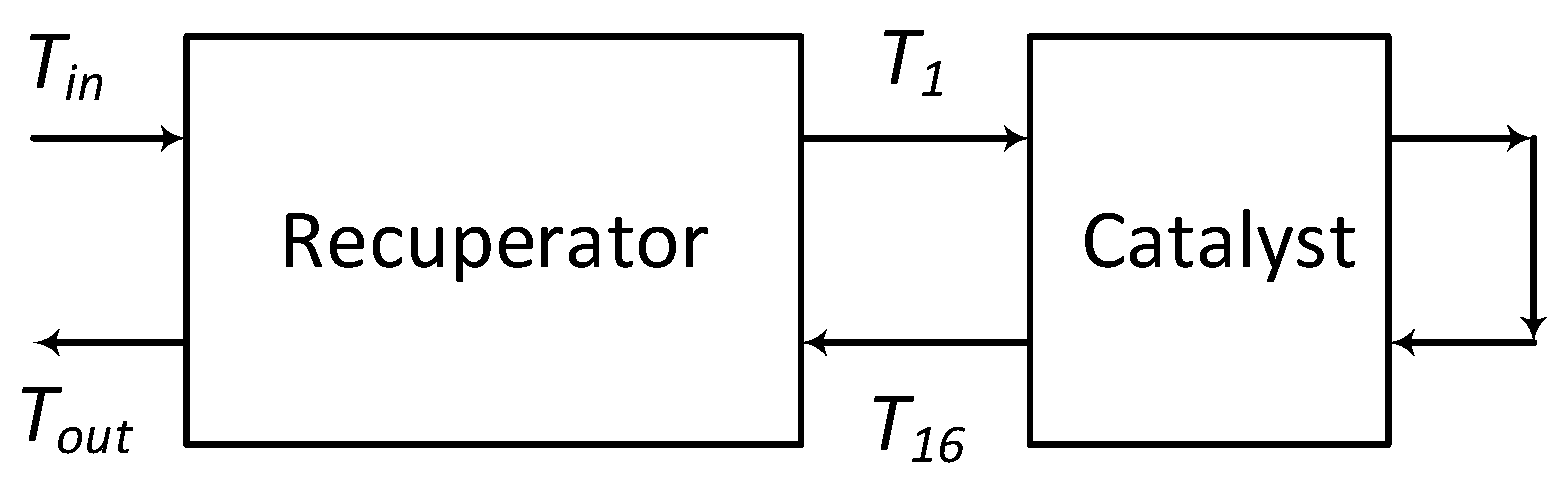
2.2. The Basic Design Concept for the Recuperative Systems: Factors Influencing the Design
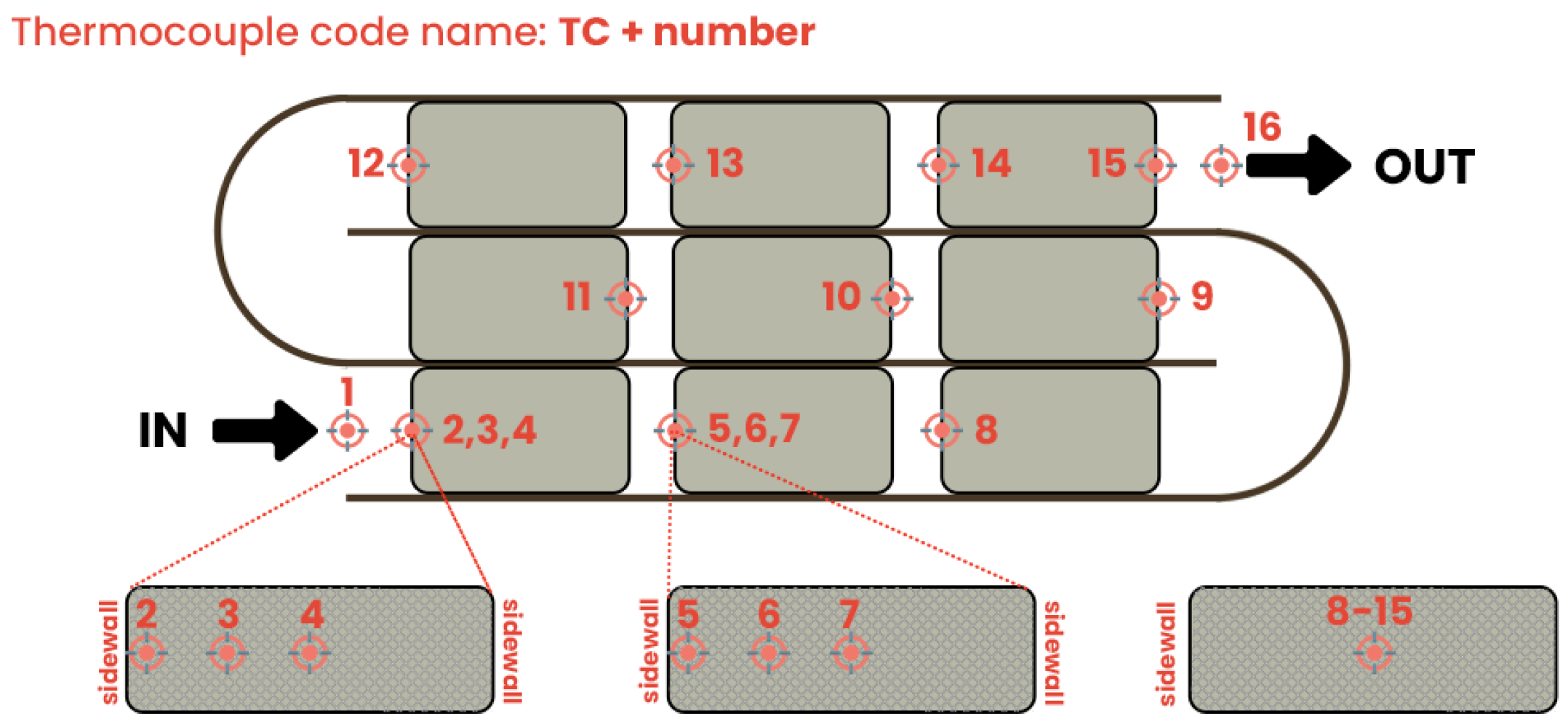
2.3. Experimental Methodology
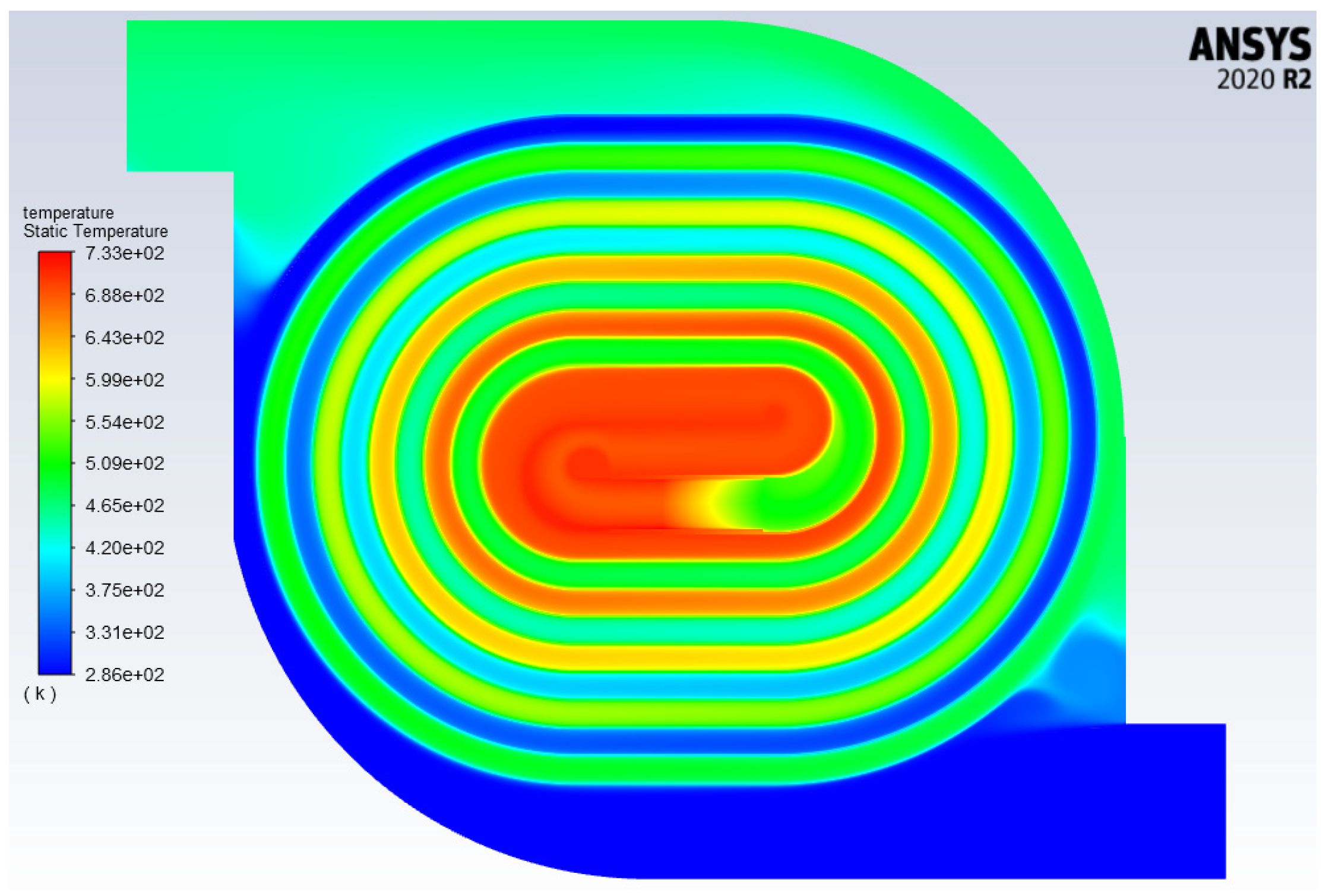
2.4. Computational Model
3. Results and Discussion
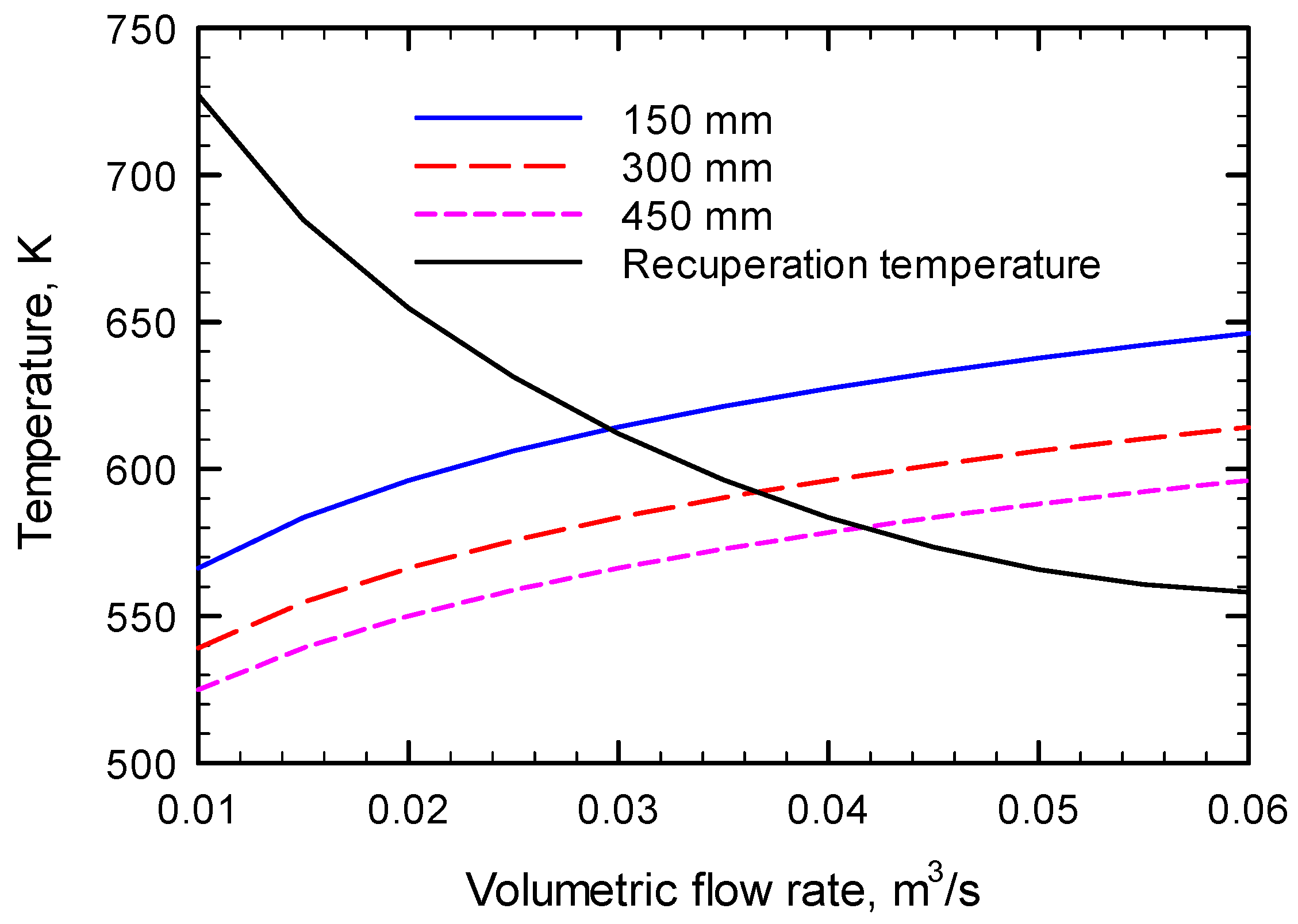
3.1. Determining the Catalyst Operating Window
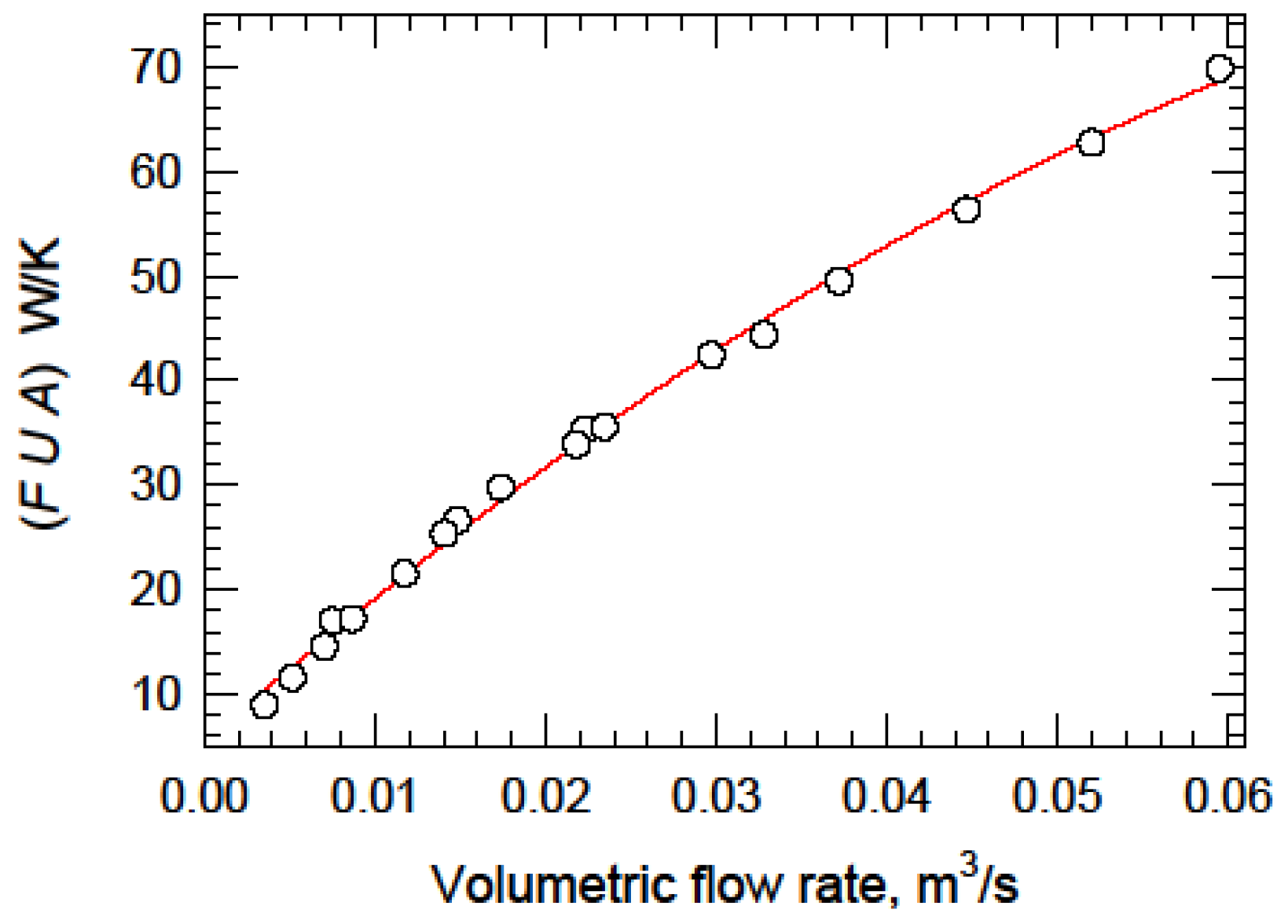
3.2. Determining the Recuperation Ability
3.3. Experimnetal Validation
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Harvey, L.D.D. A guide to global warming potentials (GWPs). Energy Policy 1993, 21, 24–34. [Google Scholar] [CrossRef]
- O’Connor, F.M. Why Methane Matters. Front. Sci. 2024, 2, 1462198. [Google Scholar] [CrossRef]
- IEA Global Methane Tracker 2024, Paris. Available online: https://www.iea.org/reports/global-methane-tracker-2024 (accessed on 7 March 2025).
- Hayes, R.E. Catalytic solutions for fugitive methane emissions in the oil and gas sector. Chem. Eng. Sci. 2004, 59, 4073–4080. [Google Scholar] [CrossRef]
- Wang, W.; Ren, J.; Li, X.; Li, H.; Li, D.; Li, H.; Song, Y. Enrichment experiment of ventilation air methane (0.5%) by the mechanical tower. Sci. Rep. 2020, 10, 808. [Google Scholar] [CrossRef]
- Schatzel, S.J.; Krog, R.B.; Dougherty, H. Methane emissions and airflow patterns on a longwall face: Potential influences from longwall gob permeability distributions on a bleederless longwall panel. Trans. Soc. Min. Metall. Explor. 2017, 342, 51–61. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Swolkien, J.; Fix, A.; Gałkowski, M. Factors influencing the temporal variability of atmospheric methane emissions from Upper Silesian coal mines. Atmos. Chem. Phys. 2022, 22, 16031–16052. [Google Scholar] [CrossRef]
- Kesselring, J. Catalytic combustion. In Advanced Combustion Methods; Weinberg, J., Ed.; Academic Press: London, UK, 1986; pp. 237–275. [Google Scholar]
- Prasad, R.; Kennedy, L.; Ruckenstein, E. Catalytic combustion. Catal. Rev. Sci. Eng. 1984, 29, 219–267. [Google Scholar] [CrossRef]
- Hayes, R.E.; Kolaczkowski, S.T. Introduction to Catalytic Combustion; Gordon and Breach Science Publishers: Reading, UK, 1997. [Google Scholar]
- Chen, J.; Arandiyan, H.; Gao, X.; Li, J. Recent advances in catalysts for methane combustion. Catal. Surv. Asia 2015, 19, 140–171. [Google Scholar] [CrossRef]
- Forzatti, P.; Groppi, G. Catalytic combustion for the production of energy. Catal. Today 1999, 54, 165–180. [Google Scholar] [CrossRef]
- Cullis, C.F.; Willatt, B.M. Oxidation of methane over supported precious metal catalysts. J. Catal. 1983, 83, 267–285. [Google Scholar] [CrossRef]
- Choudhary, T.; Banerjee, S.; Choudhary, V. Catalysts for combustion of methane and lower alkanes. Appl. Catal. A Gen. 2002, 234, 1–23. [Google Scholar] [CrossRef]
- Gélin, P.; Primet, M. Complete oxidation of methane at low temperature over noble metal based catalysts: A review. Appl. Catal. B Environ. 2002, 39, 1–37. [Google Scholar] [CrossRef]
- Ciuparu, D.; Lyubovsky, M.; Altman, E.; Pfefferle, L.; Datye, A. Catalytic combustion of methane over palladium-based catalysts. Catal. Rev. Sci. Eng. 2002, 44, 593–649. [Google Scholar] [CrossRef]
- Monai, M.; Montini, T.; Gorte, R.; Fornasiero, P. Catalytic Oxidation of Methane: Pd and Beyond. Eur. J. Inorg. Chem. 2018, 25, 2884–2893. [Google Scholar] [CrossRef]
- Kumar, R.S.; Mmbaga, J.P.; Semagina, N.; Hayes, R.E. Methane Combustion Kinetics over Palladium Based Catalysts: Review and Modelling Guidelines. Catalysts 2024, 14, 319. [Google Scholar] [CrossRef]
- Istratescu, G.M.; Hayes, R.E. Ageing studies of Pt and Pd based catalysts for the combustion of lean methane mixtures. Processes 2023, 11, 1373. [Google Scholar] [CrossRef]
- Kolios, G.; Frauhammer, J.; Eigenberger, G. Autothermal fixed-bed reactor concepts. Chem. Eng. Sci. 2000, 55, 5945–5967. [Google Scholar] [CrossRef]
- Churchill, S.W. The Interaction of Reactions and Transport Part II: Combined Reactors and Exchangers. Int. J. Chem. React. Eng. 2007, 5, A55. [Google Scholar] [CrossRef]
- Salomons, S.; Hayes, R.E.; Poirier, M.; Sapoundjiev, H. Modelling a reverse flow reactor for the catalytic combustion of fugitive methane emissions. Comput. Chem. Eng. 2004, 28, 1599–1610. [Google Scholar] [CrossRef]
- Kushwaha, A.; Poirier, K.; Hayes, R.E.; Sapoundjiev, H. Heat Extraction from a Flow Reversal Reactor in Lean Methane Combustion. Chem. Eng. Res. Des. 2005, 83, 205–213. [Google Scholar] [CrossRef]
- Kushwaha, A.; Hayes, R.E.; Poirier, M.; Sapoundjiev, H. Effect of reactor internal properties on the performance of a flow reversal catalytic reactor for methane combustion. Chem. Eng. Sci. 2004, 59, 4081–4093. [Google Scholar] [CrossRef]
- Liu, B.; Checkel, M.D.; Hayes, R.E. Experimental study of a reverse flow catalytic converter for a dual fuel engine. Can. J. Chem. Eng. 2001, 79, 491–506. [Google Scholar] [CrossRef]
- Liu, B.; Hayes, R.E.; Mmbaga, J.P.; Yi, Y.; Checkel, M.D.; Zheng, M. Three-dimensional modelling of methane ignition in a reverse flow catalytic converter. Comput. Chem. Eng. 2007, 31, 292–306. [Google Scholar] [CrossRef]
- Kolios, G.; Gritsch, A.; Morillo, A.; Tuttlies, U.; Bernnat, J.; Opferkuch, F.; Eigenberger, G. Heat-integrated reactor concepts for catalytic reforming and automotive exhaust purification. Appl. Catal. B Environ. 2007, 70, 16–30. [Google Scholar] [CrossRef]
- Bernnat, J.; Rink, M.; Tuttlies, U.; Danner, T.; Nieken, U.; Eigenberger, G. Heat-integrated concepts for automotive exhaust purification. Top. Catal. 2009, 52, 2052–2057. [Google Scholar]
- Salamon, E.; Cornejo, I.; Mmbaga, J.P.; Kołodziej, A.; Lojewska, J.; Hayes, R.E. Investigations of a three-channel autogenous reactor for lean methane combustion. Chem. Eng. Process. Process Intensif. 2020, 153, 107956. [Google Scholar] [CrossRef]
- Litto, R.; Nien, T.; Hayes, R.E.; Mmbaga, J.P.; Votsmeier, M. Parametric Study of a Recuperative Catalytic Converter. Catal. Today 2012, 188, 106–112. [Google Scholar] [CrossRef]
- Hayes, R.E.; Fadic, A.; Mmbaga, J.P.; Najafi, A. CFD Modelling of the Automotive Catalytic Converter. Catal. Today 2012, 188, 94–105. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys Fluent Ansys 18.2 Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Poling, B.E.; Prausnitz, J.M.; O’connell, J.P. The Properties of Gases and Liquids; McGraw-Hill: New York, NY, USA, 2001; Volume 5. [Google Scholar]



| Cell density | 400 CPSI |
| Substrate density | 1650 kg/m3 |
| Substrate volume fraction | 0.243 |
| Washcoat density | 1100 kg/m3 |
| Washcoat volume fraction | 0.12 |
| Palladium loading in monolith (est) | 100–150 g/ft3 |
| GHSV h−1 | Catalyst Entrance Temperature Required, Kelvin | |||||
|---|---|---|---|---|---|---|
| Fresh Catalyst | Aged Catalyst | |||||
| 1% | 0.7% t | 0.4% | 1% | 0.7% | 0.4% | |
| 180,000 | 646 | 678 | 715 | 704 | 739 | 775 |
| 120,000 | 625 | 658 | 692 | 677 | 712 | 748 |
| 90,000 | 610 | 643 | 677 | 660 | 694 | 730 |
| 72,000 | 600 | 630 | 667 | 647 | 680 | 717 |
| 60,000 | 592 | 620 | 658 | 638 | 670 | 707 |
| 48,000 | 582 | 610 | 648 | 626 | 657 | 695 |
| 36,000 | 570 | 597 | 633 | 612 | 642 | 678 |
| 24,000 | 555 | 580 | 615 | 593 | 622 | 659 |
| 18,000 | 544 | 568 | 603 | 580 | 608 | 645 |
| 12,000 | 531 | 553 | 587 | 564 | 590 | 627 |
| 9000 | 521 | 542 | 577 | 553 | 578 | 613 |
| 6000 | 509 | 528 | 561 | 539 | 562 | 597 |
| 4500 | 501 | 519 | 551 | 529 | 551 | 585 |
| 3000 | 490 | 507 | 538 | 517 | 537 | 571 |
| Exp. # | Inlet Flow Rate, m3/s | Mole Fraction Methane | Thermal Energy Generation Rate W/m3 | Monolith Inlet Temperature, K |
|---|---|---|---|---|
| 1 | 1.48 × 10−2 | 0.01 | 4.312 × 106 | 693 |
| 2 | 2.23 × 10−2 | 0.01 | 6.528 × 106 | 646 |
| 3 | 2.97 × 10−2 | 0.01 | 8.704 × 106 | 613 |
| 4 | 3.72 × 10−2 | 0.01 | 1.088 × 107 | 592 |
| 5 | 4.47 × 10−2 | 0.01 | 1.306 × 107 | 576 |
| 6 | 5.20 × 10−2 | 0.01 | 1.523 × 107 | 564 |
| 7 | 5.95 × 10−2 | 0.01 | 1.741 × 107 | 557 |
| 8 | 1.48 × 10−2 | 0.007 | 3.046 × 106 | 575 |
| 9 | 2.23 × 10−2 | 0.007 | 4.569 × 106 | 542 |
| 10 | 2.97 × 10−2 | 0.007 | 6.092 × 106 | 519 |
| 11 | 3.72 × 10−2 | 0.007 | 7.515 × 106 | 504 |
| 12 | 7.50 × 10−3 | 0.004 | 8.75 × 105 | 499 |
| 13 | 1.48 × 10−2 | 0.004 | 1.74 × 106 | 457 |
| 14 | 2.23 × 10−2 | 0.004 | 2.61 × 106 | 438 |
| 15 | 2.97 × 10−2 | 0.004 | 3.48 × 106 | 425 |
| 16 | 3.72 × 10−2 | 0.004 | 4.35 × 106 | 417 |
| Exp. # | Inlet Flow Rate, m3/s | Mole Fraction CH4 | Average Temperature at Monolith Inlet, K (T1) | Energy Transfer kW | FUA W/K | |
|---|---|---|---|---|---|---|
| 1 | 1.48 × 10−2 | 0.01 | 693 | 393 | 7.1 | 26.6 |
| 2 | 2.23 × 10−2 | 0.01 | 646 | 346 | 9.4 | 35.3 |
| 3 | 2.97 × 10−2 | 0.01 | 613 | 313 | 11.3 | 42.4 |
| 4 | 3.72 × 10−2 | 0.01 | 592 | 292 | 13.2 | 49.5 |
| 5 | 4.47 × 10−2 | 0.01 | 576 | 276 | 15.0 | 56.3 |
| 6 | 5.20 × 10−2 | 0.01 | 564 | 264 | 16.7 | 62.7 |
| 7 | 5.95 × 10−2 | 0.01 | 557 | 257 | 18.6 | 69.8 |
| 8 | 1.48 × 10−2 | 0.007 | 575 | 275 | 4.97 | 26.6 |
| 9 | 2.23 × 10−2 | 0.007 | 542 | 242 | 6.59 | 35.3 |
| 10 | 2.97 × 10−2 | 0.007 | 519 | 219 | 7.92 | 42.4 |
| 11 | 3.72 × 10−2 | 0.007 | 504 | 204 | 9.24 | 49.5 |
| 12 | 7.50 × 10−3 | 0.004 | 499 | 199 | 1.82 | 17.0 |
| 13 | 1.48 × 10−2 | 0.004 | 457 | 157 | 2.84 | 26.6 |
| 14 | 2.23 × 10−2 | 0.004 | 438 | 138 | 3.76 | 35.3 |
| 15 | 2.97 × 10−2 | 0.004 | 425 | 125 | 4.23 | 42.4 |
| 16 | 3.72 × 10−2 | 0.004 | 417 | 117 | 5.30 | 49.5 |
| 17 | 3.52 × 10−3 | 0.0096 | 837 | 537 | 2.30 | 8.95 |
| 18 | 5.16 × 10−3 | 0.0096 | 774 | 474 | 2.98 | 11.59 |
| 19 | 7.03 × 10−3 | 0.0096 | 737 | 437 | 3.74 | 14.57 |
| 20 | 8.67 × 10−3 | 0.0096 | 718 | 418 | 4.42 | 17.19 |
| 21 | 1.17 × 10−2 | 0.0096 | 687 | 387 | 5.53 | 21.51 |
| 22 | 1.41 × 10−2 | 0.0096 | 680 | 380 | 6.51 | 25.34 |
| 23 | 1.73 × 10−2 | 0.0096 | 662 | 362 | 7.65 | 29.77 |
| 24 | 2.18 × 10−2 | 0.0096 | 628 | 328 | 8.71 | 33.90 |
| 25 | 2.34 × 10−2 | 0.0096 | 620 | 320 | 9.14 | 35.57 |
| 26 | 3.28 × 10−2 | 0.0096 | 585 | 285 | 11.40 | 44.35 |
| Inlet Flow Rate, m3/s | Mole Fraction CH4 | Temperature at Catalyst Inlet, K (T1), CFD | Temperature at Catalyst Inlet, K (T1), Correlation |
|---|---|---|---|
| 1.48 × 10−2 | 0.01 | 693 | 686 |
| 2.23 × 10−2 | 0.01 | 646 | 643 |
| 2.97 × 10−2 | 0.01 | 613 | 613 |
| 3.72 × 10−2 | 0.01 | 592 | 590 |
| 4.47 × 10−2 | 0.01 | 576 | 574 |
| 5.20 × 10−2 | 0.01 | 564 | 563 |
| 5.95 × 10−2 | 0.01 | 557 | 558 |
| 1.48 × 10−2 | 0.007 | 575 | 570 |
| 2.23 × 10−2 | 0.007 | 542 | 540 |
| 2.97 × 10−2 | 0.007 | 519 | 519 |
| 3.72 × 10−2 | 0.007 | 504 | 503 |
| 7.50 × 10−3 | 0.004 | 499 | 484 |
| 1.48 × 10−2 | 0.004 | 457 | 454 |
| 2.23 × 10−2 | 0.004 | 438 | 437 |
| 2.97 × 10−2 | 0.004 | 425 | 425 |
| 3.72 × 10−2 | 0.004 | 417 | 416 |
| 3.52 × 10−3 | 0.0096 | 837 | 850 |
| 5.16 × 10−3 | 0.0096 | 774 | 788 |
| 7.03 × 10−3 | 0.0096 | 737 | 749 |
| 8.67 × 10−3 | 0.0096 | 718 | 725 |
| 1.17 × 10−2 | 0.0096 | 687 | 694 |
| 1.41 × 10−2 | 0.0096 | 680 | 675 |
| 1.73 × 10−2 | 0.0096 | 662 | 655 |
| 2.18 × 10−2 | 0.0096 | 628 | 632 |
| 2.34 × 10−2 | 0.0096 | 620 | 625 |
| 3.28 × 10−2 | 0.0096 | 585 | 591 |
| Methane Fraction | a | b | c |
|---|---|---|---|
| Fresh | |||
| 0.01 | 394.4 | 47.67 | 4.807 |
| 0.007 | 407.8 | 51.58 | 4.104 |
| 0.004 | 449.2 | 50.54 | 2.977 |
| Aged | |||
| 0.01 | 394.9 | 58.45 | 5.447 |
| 0.007 | 417.8 | 60.93 | 4.392 |
| 0.004 | 461.6 | 59.44 | 3.510 |
| Catalyst State | Methane Mole Fraction | Catalyst Length, mm | Maximum Flow Rate, m3/s |
|---|---|---|---|
| Fresh | 0.01 | 150 | 0.0296 |
| 300 | 0.0365 | ||
| 450 | 0.0416 | ||
| Aged | 0.01 | 150 | 0.0216 |
| 300 | 0.0272 | ||
| 450 | 0.0311 | ||
| Fresh | 0.007 | 150 | 0.0105 |
| 300 | 0.0137 | ||
| 450 | 0.0159 | ||
| Aged | 0.007 | 150 | 0.0075 |
| 300 | 0.0098 | ||
| 450 | 0.0114 |
| Data Point | Time, h | Mole % Methane | Flow Rate m3/s | T in K | T out K | T1 K | T16 K |
|---|---|---|---|---|---|---|---|
| Experiment 1 | |||||||
| 1 | 10 | 0.40 | 0.0082 | 576 | 648 | 728 | 827 |
| 2 | 13 | 0.40 | 0.0096 | 475 | 563 | 633 | 739 |
| 3 | 21 | 0.60 | 0.0072 | 447 | 580 | 691 | 833 |
| 4 | 24 | 0.60 | 0.0070 | 395 | 536 | 644 | 796 |
| 5 | 26 | 0.62 | 0.0076 | 368 | 515 | 620 | 778 |
| 6 | 31 | 0.70 | 0.0070 | 368 | 539 | 672 | 844 |
| 7 | 36 | 0.70 | 0.0036 | 326 | 505 | 631 | 810 |
| Experiment 2 | |||||||
| 1 | 5.5 | 0.40 | 0.0031 | 579 | 653 | 743 | 843 |
| 2 | 8.8 | 0.40 | 0.0045 | 440 | 539 | 614 | 728 |
| 3 | 11.6 | 0.60 | 0.0076 | 449 | 588 | 713 | 860 |
| 4 | 16 | 0.60 | 0.0083 | 366 | 519 | 633 | 793 |
| 5 | 18.5 | 0.70 | 0.0064 | 370 | 543 | 684 | 856 |
| 6 | 23 | 0.70 | 0.0044 | 327 | 512 | 647 | 829 |
| Experiment 3 | |||||||
| 1 | 14 | 0.41 | 0.0126 | 567 | 637 | 721 | 810 |
| 2 | 16 | 0.40 | 0.0130 | 526 | 601 | 679 | 772 |
| 3 | 18 | 0.60 | 0.0102 | 518 | 626 | 748 | 868 |
| 4 | 20 | 0.60 | 0.0118 | 446 | 568 | 679 | 809 |
| 5 | 23 | 0.70 | 0.0113 | 438 | 586 | 724 | 868 |
| 6 | 27 | 0.70 | 0.0160 | 314 | 479 | 588 | 767 |
| Experiment 4 | |||||||
| 1 | 6 | 0.43 | 0.0087 | 602 | 664 | 764 | 839 |
| 2 | 9.5 | 0.70 | 0.0087 | 474 | 586 | 746 | 869 |
| 3 | 13.5 | 0.70 | 0.0097 | 374 | 517 | 666 | 807 |
| 4 | 16 | 0.90 | 0.0077 | 383 | 547 | 756 | 905 |
| 5 | 18.5 | 0.90 | 0.0083 | 315 | 508 | 710 | 873 |
| Experiment 5 | |||||||
| 1 | 8 | 0.70 | 0.0116 | 381 | 551 | 693 | 841 |
| 2 | 11.9 | 0.70 | 0.0124 | 311 | 473 | 608 | 772 |
| 3 | 12.4 | 0.70 | 0.0142 | 311 | 477 | 604 | 776 |
| 4 | 13 | 0.70 | 0.0169 | 312 | 480 | 596 | 776 |
| 5 | 13.4 | 0.70 | 0.0209 | 313 | 485 | 589 | 787 |
| Experiment 6 | |||||||
| 1 | 23 | 0.40 | 0.0132 | 477 | 560 | 636 | 722 |
| 2 | 28 | 0.60 | 0.0097 | 437 | 591 | 725 | 832 |
| 3 | 34 | 0.80 | 0.0091 | 438 | 579 | 757 | 885 |
| 4 | 43 | 0.80 | 0.0125 | 309 | 478 | 626 | 790 |
| Experiment 7 | |||||||
| 1 | 13 | 0.40 | 0.0071 | 525 | 557 | 647 | 719 |
| 2 | 22 | 0.60 | 0.0073 | 392 | 489 | 625 | 731 |
| 3 | 29 | 0.70 | 0.0067 | 399 | 498 | 660 | 769 |
| 4 | 35 | 0.70 | 0.0084 | 307 | 442 | 586 | 736 |
| 5 | 39 | 0.90 | 0.0058 | 315 | 471 | 687 | 813 |
| Data Point | Flow Rate m3/s | Mole % Methane | Combustion Energy, W | ΔT Obs. | ΔT Adi. | Heat Loss, W | % Loss |
|---|---|---|---|---|---|---|---|
| Experiment 1 | |||||||
| 1 | 0.0082 | 0.40 | 1073 | 73 | 107 | 340 | 32 |
| 2 | 0.0096 | 0.40 | 1249 | 88 | 107 | 221 | 18 |
| 3 | 0.0072 | 0.60 | 1414 | 132 | 160 | 250 | 18 |
| 4 | 0.0070 | 0.60 | 1368 | 141 | 160 | 166 | 12 |
| 5 | 0.0076 | 0.62 | 1525 | 147 | 166 | 172 | 11 |
| 6 | 0.0070 | 0.70 | 1600 | 171 | 187 | 138 | 9 |
| 7 | 0.0036 | 0.70 | 821 | 179 | 187 | 36 | 4 |
| Experiment 2 | |||||||
| 1 | 0.0031 | 0.40 | 397 | 74 | 107 | 122 | 31 |
| 2 | 0.0045 | 0.40 | 591 | 98 | 107 | 49 | 8 |
| 3 | 0.0076 | 0.60 | 1489 | 139 | 160 | 199 | 13 |
| 4 | 0.0083 | 0.60 | 1626 | 153 | 160 | 75 | 5 |
| 5 | 0.0064 | 0.70 | 1467 | 173 | 187 | 111 | 8 |
| 6 | 0.0044 | 0.70 | 1000 | 185 | 187 | 11 | 1 |
| Experiment 3 | |||||||
| 1 | 0.0126 | 0.41 | 1685 | 70 | 110 | 609 | 36 |
| 2 | 0.0130 | 0.40 | 1699 | 75 | 107 | 507 | 30 |
| 3 | 0.0102 | 0.60 | 1991 | 108 | 160 | 650 | 33 |
| 4 | 0.0118 | 0.60 | 2303 | 122 | 160 | 551 | 24 |
| 5 | 0.0113 | 0.70 | 2570 | 148 | 187 | 537 | 21 |
| 6 | 0.0160 | 0.70 | 3649 | 165 | 187 | 432 | 12 |
| Experiment 4 | |||||||
| 1 | 0.0087 | 0.43 | 1224 | 62 | 115 | 564 | 46 |
| 2 | 0.0087 | 0.70 | 1980 | 93 | 187 | 996 | 50 |
| 3 | 0.0097 | 0.70 | 2216 | 143 | 187 | 523 | 24 |
| 4 | 0.0077 | 0.90 | 2273 | 164 | 241 | 723 | 32 |
| 5 | 0.0083 | 0.90 | 2444 | 193 | 241 | 483 | 20 |
| Experiment 5 | |||||||
| 1 | 0.0116 | 0.70 | 2642 | 169 | 187 | 256 | 10 |
| 2 | 0.0124 | 0.70 | 2832 | 162 | 187 | 380 | 13 |
| 3 | 0.0142 | 0.70 | 3227 | 166 | 187 | 364 | 11 |
| 4 | 0.0169 | 0.70 | 3866 | 168 | 187 | 395 | 10 |
| 5 | 0.0209 | 0.70 | 4763 | 172 | 187 | 385 | 8 |
| Experiment 6 | |||||||
| 1 | 0.0132 | 0.40 | 1725 | 83 | 107 | 386 | 22 |
| 2 | 0.0097 | 0.60 | 1893 | 154 | 160 | 76 | 4 |
| 3 | 0.0091 | 0.80 | 2372 | 140 | 214 | 819 | 35 |
| 4 | 0.0125 | 0.80 | 3254 | 169 | 214 | 683 | 21 |
| Experiment 7 | |||||||
| 1 | 0.0071 | 0.40 | 925 | 32 | 107 | 648 | 70 |
| 2 | 0.0073 | 0.60 | 1427 | 97 | 160 | 564 | 40 |
| 3 | 0.0067 | 0.70 | 1536 | 99 | 187 | 723 | 47 |
| 4 | 0.0084 | 0.70 | 1912 | 135 | 187 | 533 | 28 |
| Data Point | LMTD K | Flow Rate m3/s | q Inlet W | q Outlet W | q Mean W | FUA Exp | FUA Model |
|---|---|---|---|---|---|---|---|
| Experiment 1 | |||||||
| 1 | 85.1 | 0.0082 | 1527 | 1803 | 1665 | 19.6 | 16.8 |
| 2 | 96.6 | 0.0096 | 1842 | 2053 | 1947 | 20.2 | 18.9 |
| 3 | 137.2 | 0.0072 | 2150 | 2235 | 2193 | 16.0 | 15.3 |
| 4 | 146.4 | 0.0070 | 2123 | 2212 | 2168 | 14.8 | 14.9 |
| 5 | 152.4 | 0.0076 | 2319 | 2420 | 2370 | 15.5 | 15.8 |
| 6 | 171.4 | 0.0070 | 2599 | 2607 | 2603 | 15.2 | 15.0 |
| 7 | 179.1 | 0.0036 | 1340 | 1338 | 1339 | 7.5 | 9.3 |
| Experiment 2 | |||||||
| 1 | 86.1 | 0.0031 | 610 | 707 | 658 | 7.6 | 8.4 |
| 2 | 105.9 | 0.0045 | 962 | 1049 | 1006 | 9.5 | 10.9 |
| 3 | 142.3 | 0.0076 | 2449 | 2521 | 2485 | 17.5 | 15.9 |
| 4 | 156.6 | 0.0083 | 2705 | 2773 | 2739 | 17.5 | 17.0 |
| 5 | 172.5 | 0.0064 | 2455 | 2455 | 2455 | 14.2 | 14.0 |
| 6 | 183.0 | 0.0044 | 1709 | 1696 | 1703 | 9.3 | 10.7 |
| Experiment 3 | |||||||
| 1 | 79.0 | 0.0126 | 2375 | 2649 | 2512 | 31.8 | 23.2 |
| 2 | 83.4 | 0.0130 | 2430 | 2714 | 2572 | 30.8 | 23.7 |
| 3 | 114.2 | 0.0102 | 2853 | 3007 | 2930 | 25.7 | 19.8 |
| 4 | 125.8 | 0.0118 | 3346 | 3460 | 3403 | 27.1 | 22.0 |
| 5 | 146.2 | 0.0113 | 3917 | 3868 | 3893 | 26.6 | 21.3 |
| 6 | 172.0 | 0.0160 | 5353 | 5612 | 5483 | 31.9 | 27.6 |
| Experiment 4 | |||||||
| 1 | 68.2 | 0.0087 | 1720 | 1863 | 1791 | 26.3 | 17.6 |
| 2 | 117.5 | 0.0087 | 2882 | 2996 | 2939 | 25.0 | 17.5 |
| 3 | 141.7 | 0.0097 | 3456 | 3439 | 3448 | 24.3 | 19.1 |
| 4 | 156.2 | 0.0077 | 3524 | 3372 | 3448 | 22.1 | 16.1 |
| 5 | 177.0 | 0.0083 | 4017 | 3707 | 3862 | 21.8 | 17.0 |
| Experiment 5 | |||||||
| 1 | 158.4 | 0.0116 | 4404 | 4107 | 4255 | 26.9 | 21.7 |
| 2 | 163.4 | 0.0124 | 4499 | 4529 | 4514 | 27.6 | 22.9 |
| 3 | 168.5 | 0.0142 | 5051 | 5156 | 5103 | 30.3 | 25.2 |
| 4 | 174.2 | 0.0169 | 5857 | 6107 | 5982 | 34.3 | 28.7 |
| 5 | 184.9 | 0.0209 | 7029 | 7678 | 7353 | 39.8 | 33.4 |
| Experiment 6 | |||||||
| 1 | 85.0 | 0.0132 | 2573 | 2615 | 2594 | 30.5 | 24.0 |
| 2 | 129.1 | 0.0097 | 3403 | 2845 | 3124 | 24.2 | 19.0 |
| 3 | 134.1 | 0.0091 | 3537 | 3394 | 3465 | 25.8 | 18.1 |
| 4 | 166.3 | 0.0125 | 4817 | 4738 | 4777 | 28.7 | 23.0 |
| Experiment 7 | |||||||
| 1 | 48.9 | 0.0071 | 1057 | 1401 | 1229 | 25.1 | 15.1 |
| 2 | 101.9 | 0.0073 | 2072 | 2149 | 2111 | 20.7 | 15.4 |
| 3 | 103.8 | 0.0067 | 2136 | 2220 | 2178 | 21.0 | 14.5 |
| 4 | 142.0 | 0.0084 | 2854 | 3006 | 2930 | 20.6 | 17.1 |
| 5 | 140.7 | 0.0058 | 2647 | 2431 | 2539 | 18.0 | 13.1 |
| Data Point | Flow Rate m3/s | Mole % Methane | System Inlet T, K | Catalyst Inlet T, K, Exp | Catalyst Inlet T K, CFD |
|---|---|---|---|---|---|
| Experiment 1 | |||||
| 1 | 8.23 × 10−3 | 0.4 | 575 | 728 | 743 |
| 2 | 9.58 × 10−3 | 0.4 | 475 | 633 | 635 |
| 3 | 7.23 × 10−3 | 0.6 | 447 | 691 | 706 |
| 4 | 7.00 × 10−3 | 0.6 | 395 | 644 | 656 |
| 5 | 7.55 × 10−3 | 0.62 | 368 | 620 | 635 |
| 6 | 7.02 × 10−3 | 0.7 | 368 | 672 | 670 |
| 7 | 3.60 × 10−3 | 0.7 | 326 | 631 | 695 |
| Experiment 5 | |||||
| 1 | 1.16 × 10−2 | 0.70 | 381 | 693 | 655 |
| 2 | 1.24 × 10−2 | 0.70 | 311 | 608 | 580 |
| 3 | 1.42 × 10−2 | 0.70 | 311 | 604 | 575 |
| 4 | 1.70 × 10−2 | 0.70 | 312 | 595 | 563 |
| 5 | 2.09 × 10−2 | 0.70 | 313 | 589 | 545 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mmbaga, J.P.; Hayes, R.E.; Profic-Paczkowska, J.; Jędrzejczyk, R.; Chlebda, D.K.; Dańczak, J.; Hildebrandt, R. Energy Recuperation in a Spiral Reactor for Lean Methane Combustion: Heat Transfer Efficiency and Design Guidelines. Processes 2025, 13, 1168. https://doi.org/10.3390/pr13041168
Mmbaga JP, Hayes RE, Profic-Paczkowska J, Jędrzejczyk R, Chlebda DK, Dańczak J, Hildebrandt R. Energy Recuperation in a Spiral Reactor for Lean Methane Combustion: Heat Transfer Efficiency and Design Guidelines. Processes. 2025; 13(4):1168. https://doi.org/10.3390/pr13041168
Chicago/Turabian StyleMmbaga, Joseph P., Robert E. Hayes, Joanna Profic-Paczkowska, Roman Jędrzejczyk, Damian K. Chlebda, Jacek Dańczak, and Robert Hildebrandt. 2025. "Energy Recuperation in a Spiral Reactor for Lean Methane Combustion: Heat Transfer Efficiency and Design Guidelines" Processes 13, no. 4: 1168. https://doi.org/10.3390/pr13041168
APA StyleMmbaga, J. P., Hayes, R. E., Profic-Paczkowska, J., Jędrzejczyk, R., Chlebda, D. K., Dańczak, J., & Hildebrandt, R. (2025). Energy Recuperation in a Spiral Reactor for Lean Methane Combustion: Heat Transfer Efficiency and Design Guidelines. Processes, 13(4), 1168. https://doi.org/10.3390/pr13041168







