Mechanism of Enhanced Control and Technological Application of Surrounding Rock Anchoring in Fully Mechanized Caving Face of Extra-Thick Coal Seams
Abstract
1. Introduction
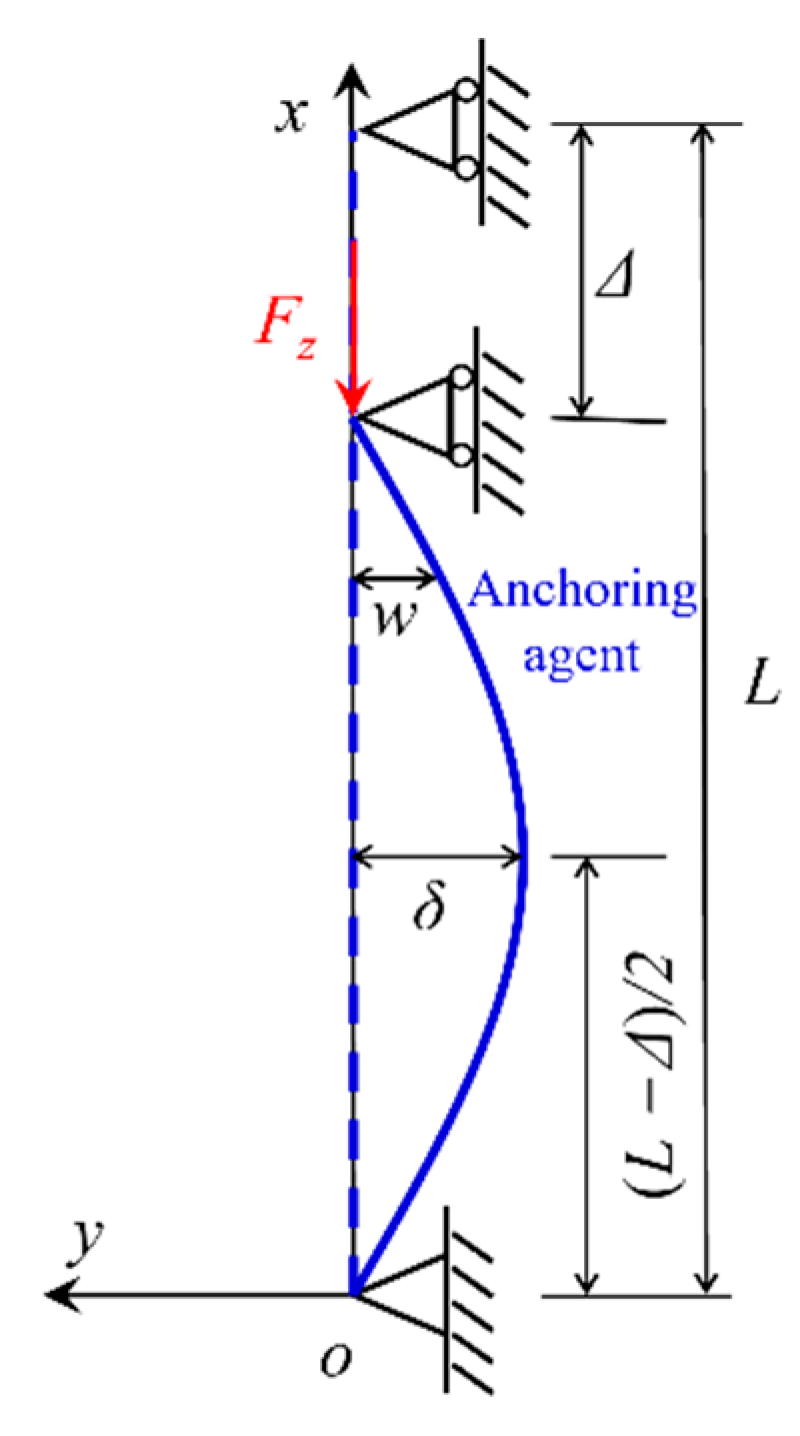
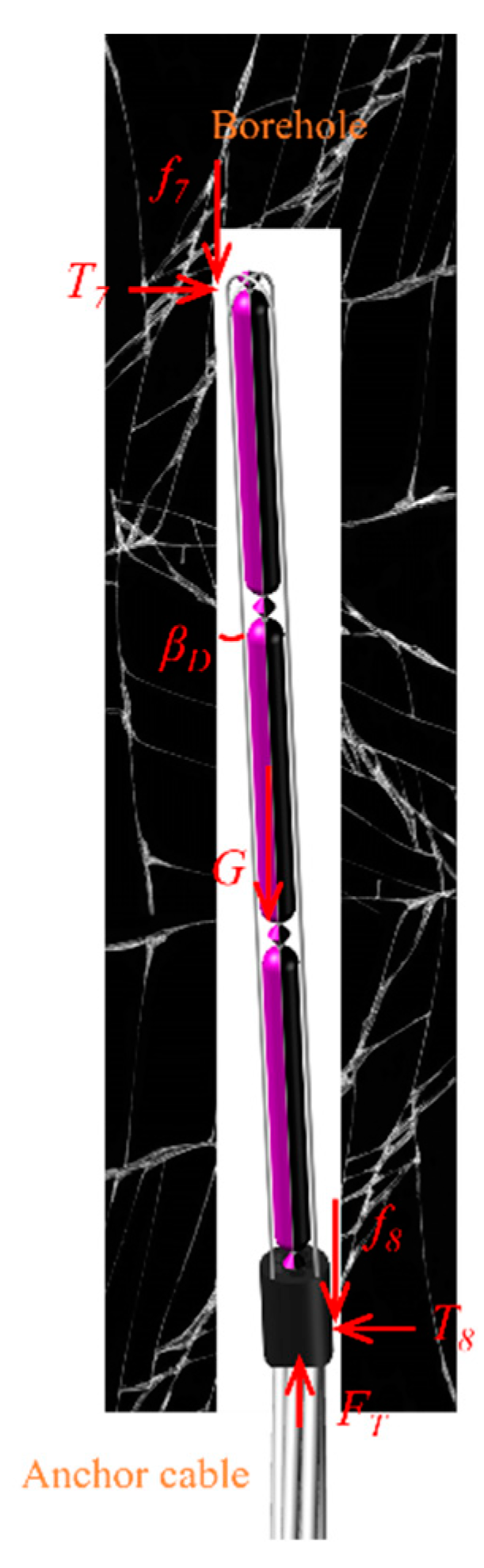
2. Unconstrained Pushing and Integrated Pushing Force Analysis of Anchoring Agent
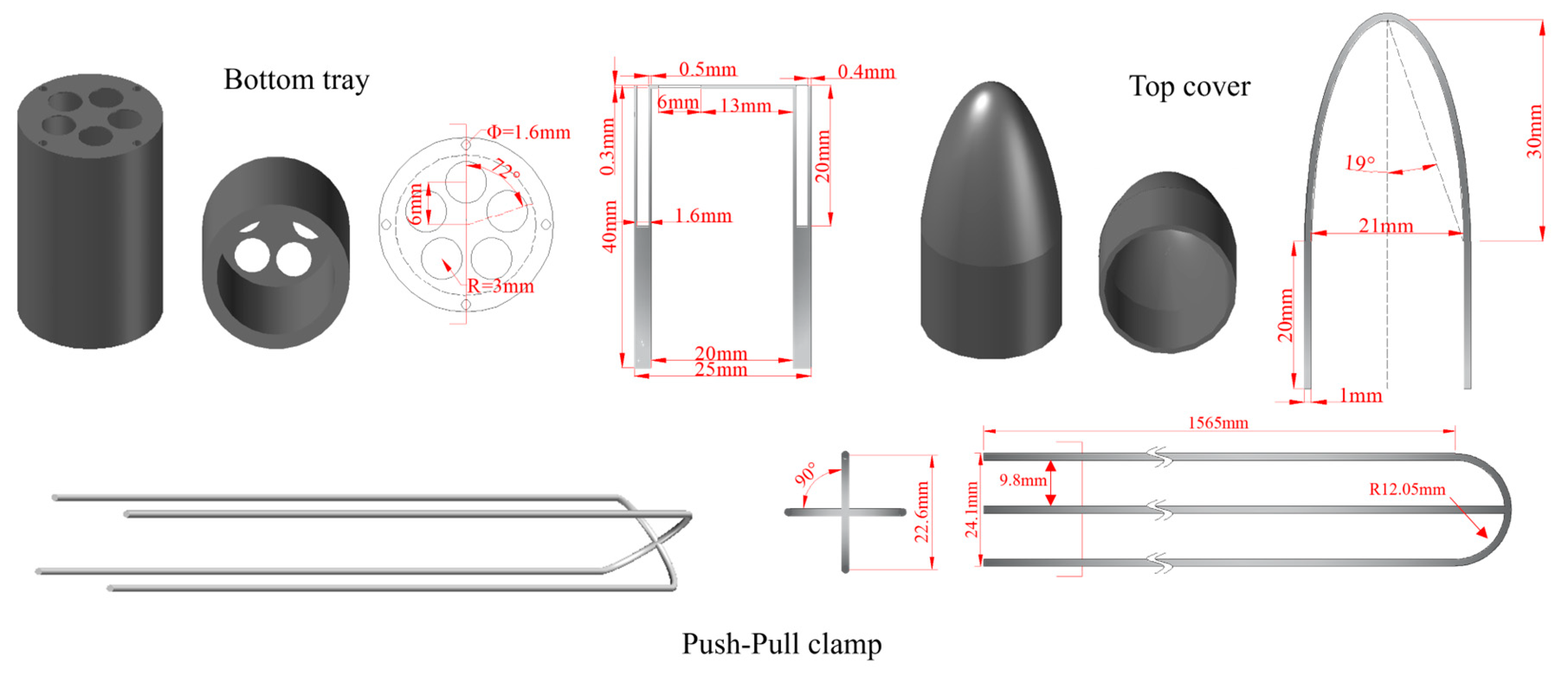
3. Development of the Push–Pull Device
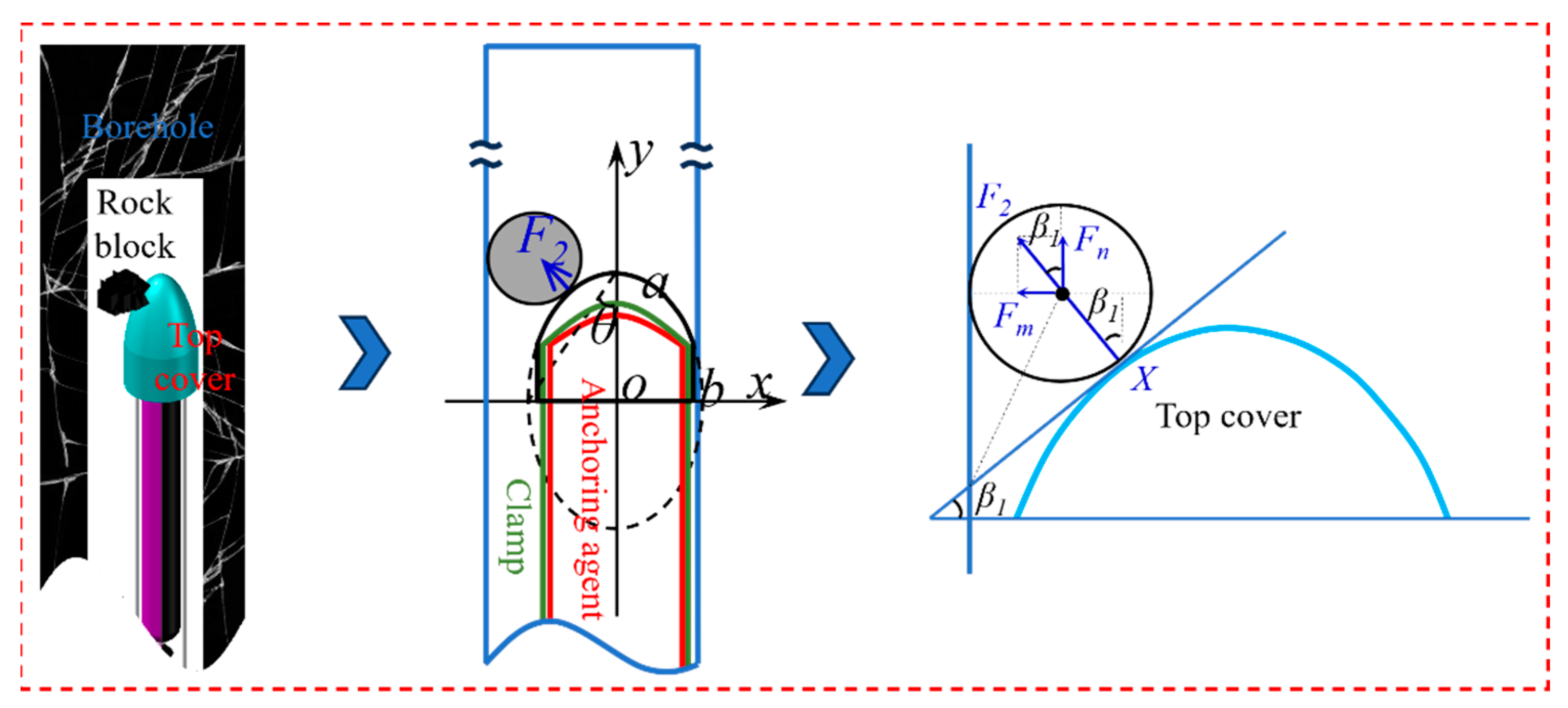
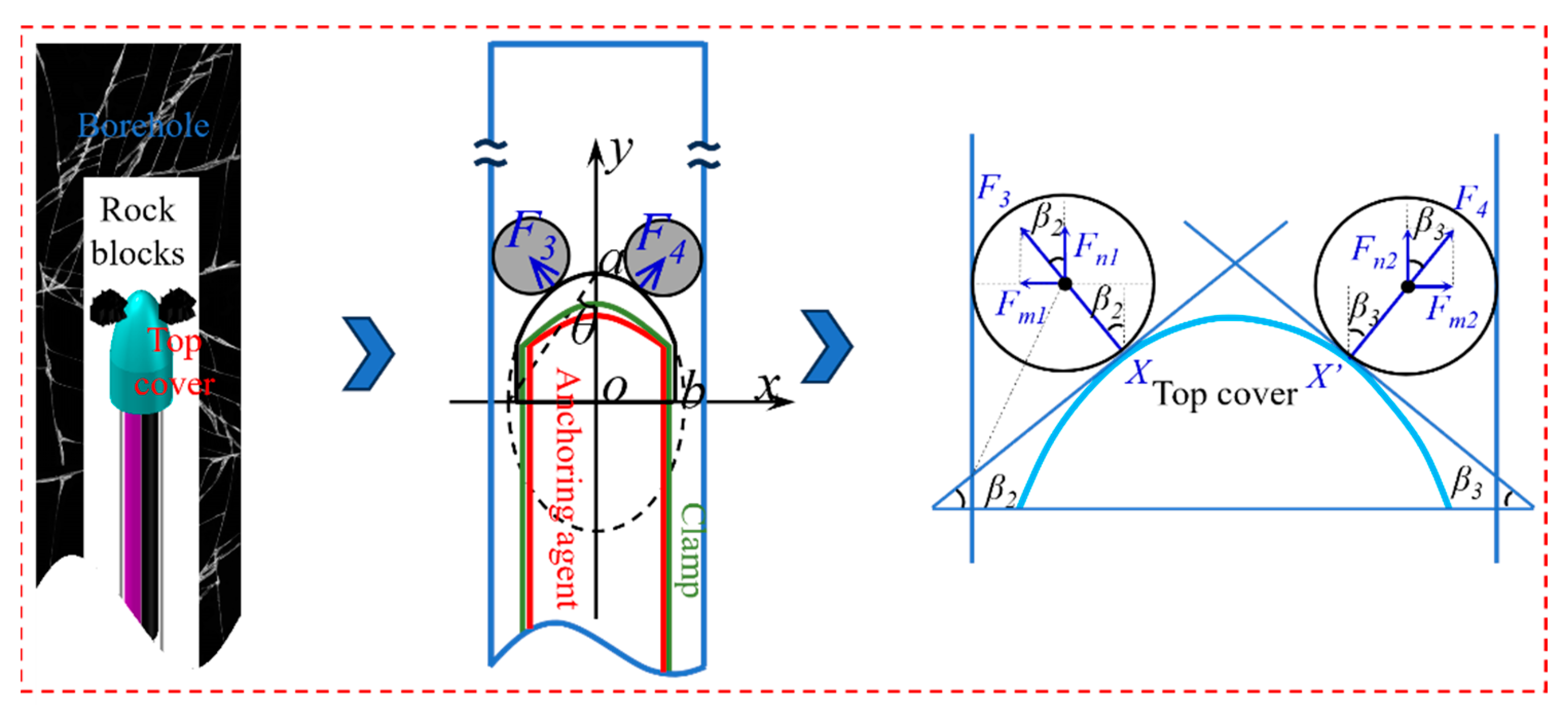
3.1. Top Cover Design
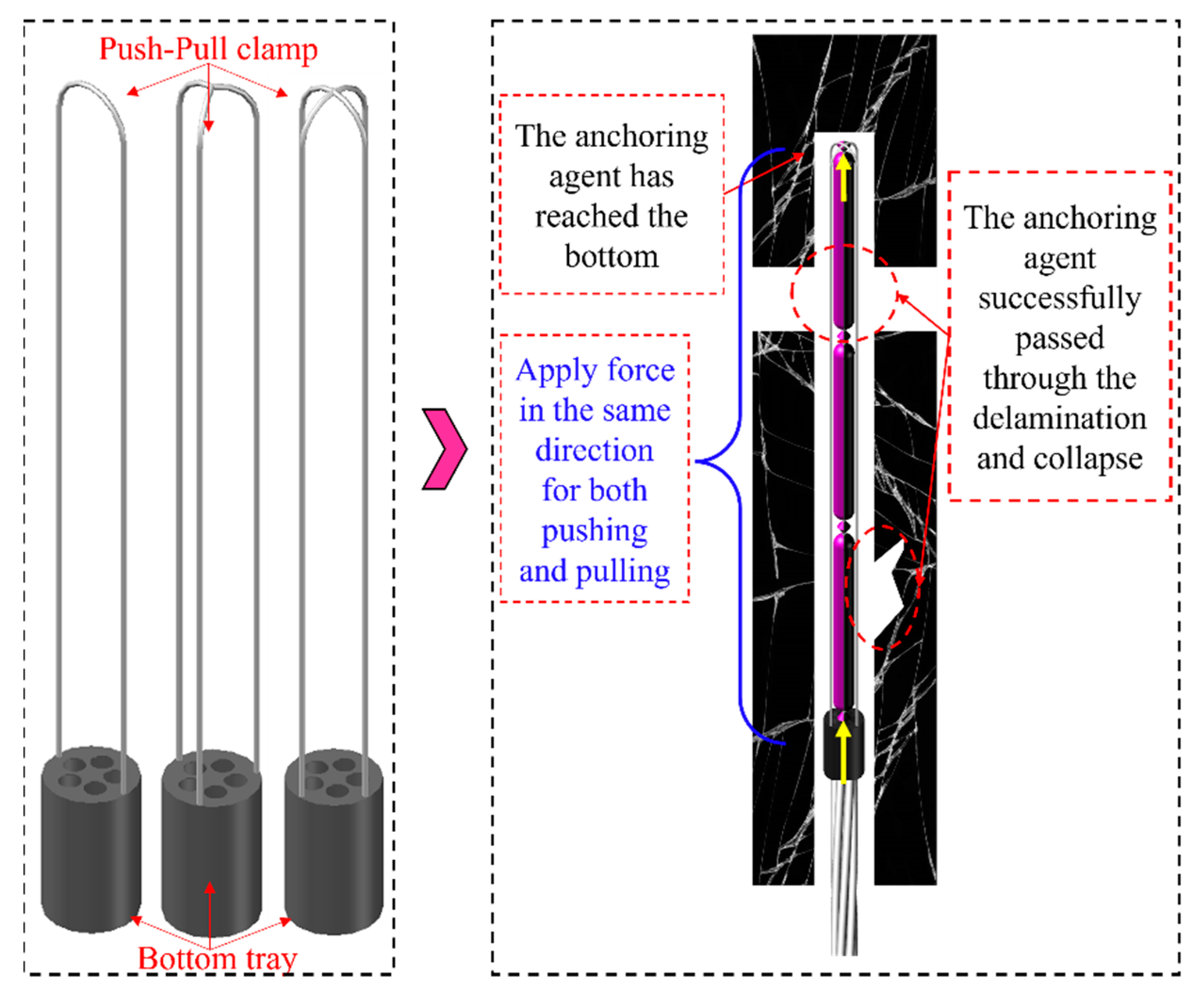
3.2. Bottom Tray Design
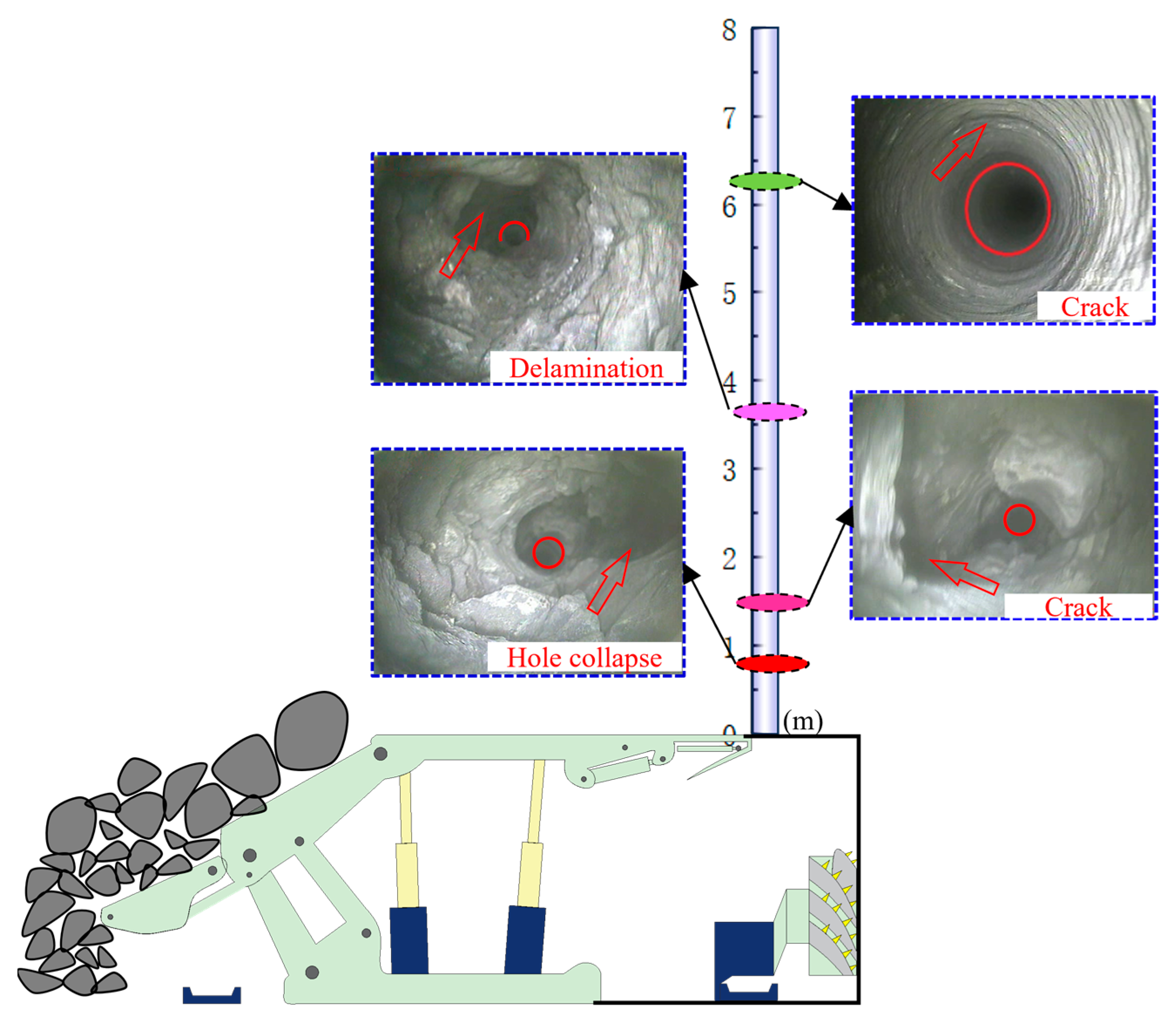
4. Similar Simulation Test for Anchoring Agent Pushing in Borehole
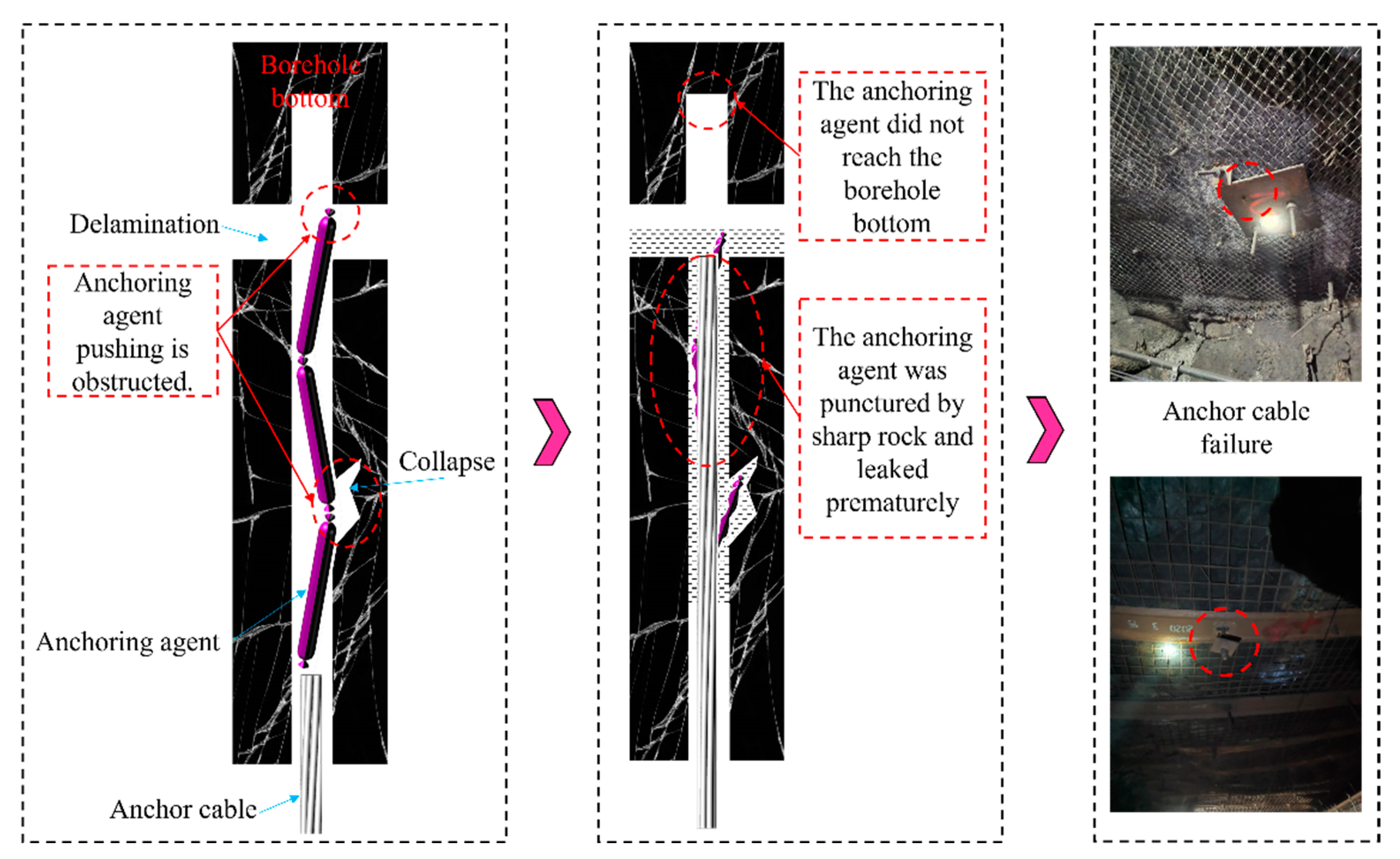
4.1. Push-Through Capability Test for Anchoring Agent in Borehole Delamination and Collapse Zones
4.2. Push-Through Capability Test for Anchoring Agent with Push–Pull Device in Clogged Borehole
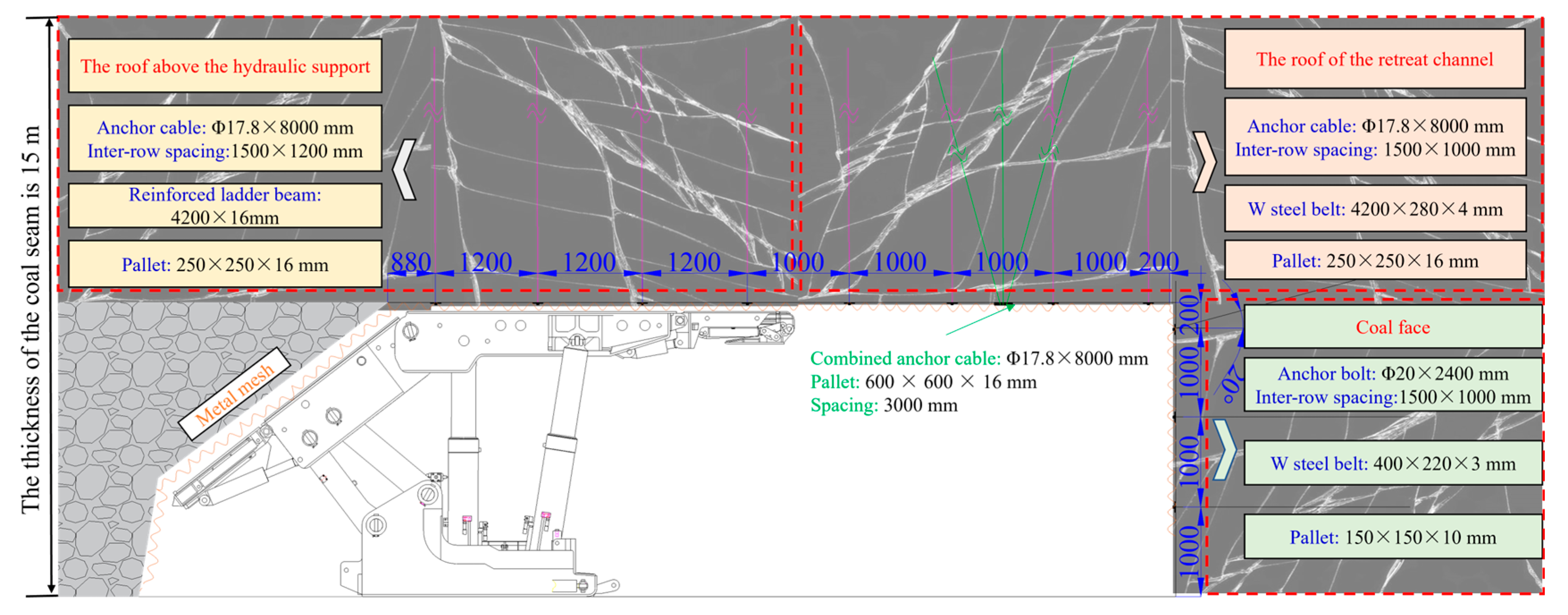
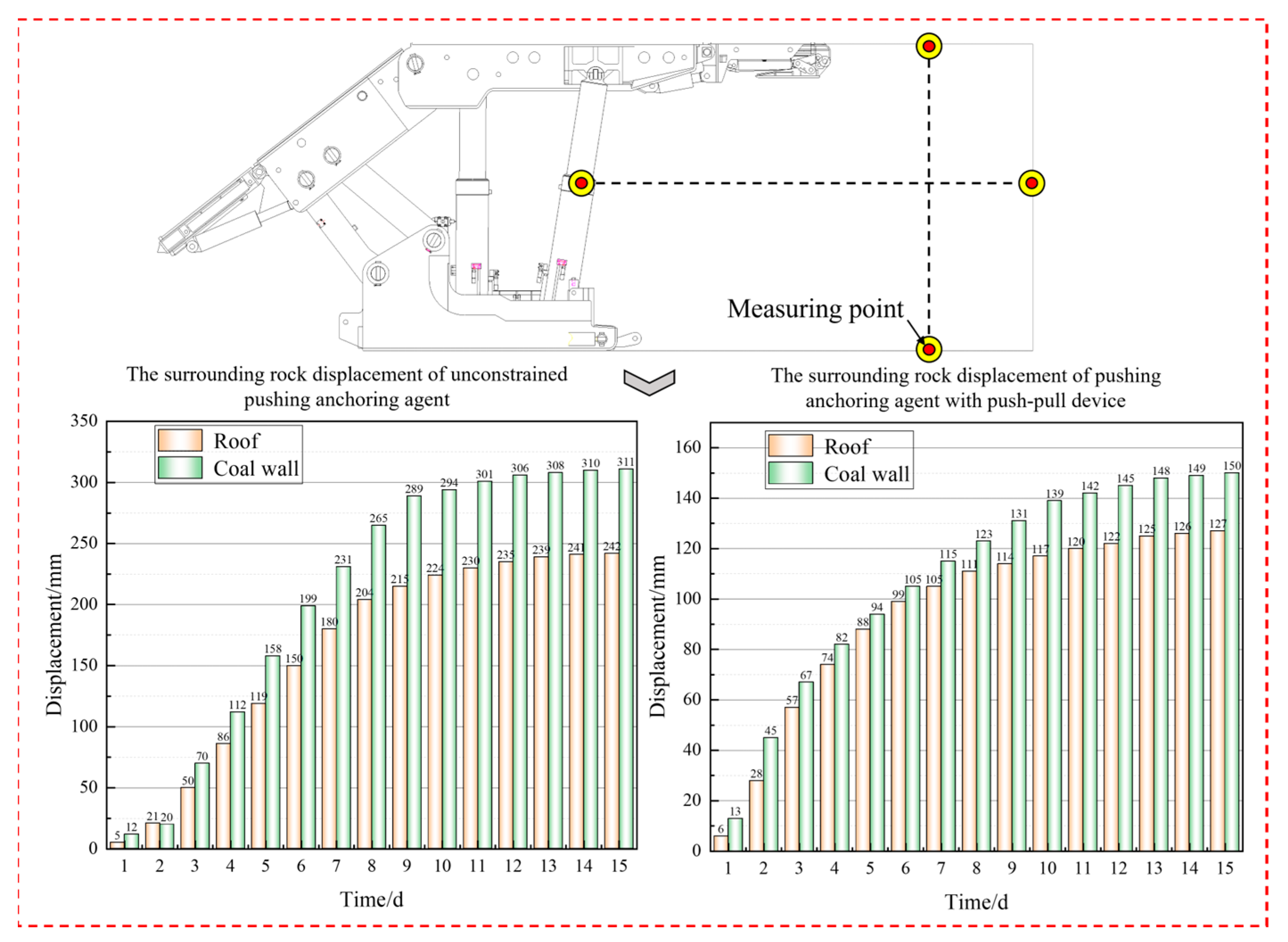
5. Field Application
6. Conclusions
- (1)
- An ideal elastic compression rod model for the anchoring agent was established. The state of the anchoring agent inside the borehole during unrestrained pushing was categorized into two types: bending equilibrium and bending instability. The pushing force for the anchoring agent in the bending equilibrium state was 15.01 N. The bending instability of the anchoring agent was categorized into three types: the bending instability of the lower anchoring agent, the bending instability of the middle-lower anchoring agent, and the bending instability of the upper-middle-lower anchoring agent. The pushing force for these three instability types was 15.58 N, 16.02 N, and 16.32 N, respectively. The pushing force for the anchoring agent installed using the integrated push–pull method was calculated to be 13.52 N.
- (2)
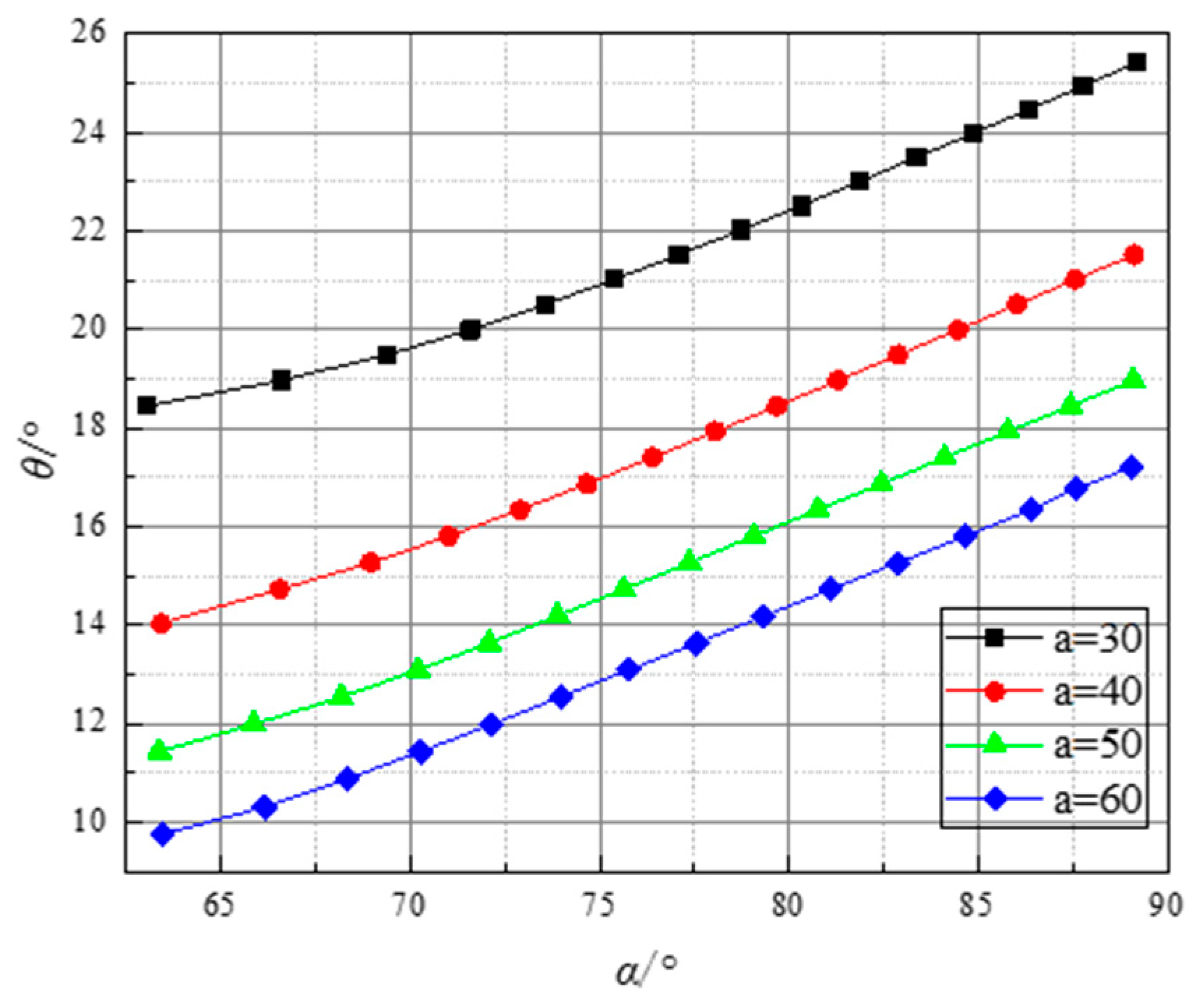
- Borehole blockages were classified into three types: protruding rock blocks on one side of the borehole, fallen rock blocks on one side of the borehole, and fallen rock blocks on both sides of the borehole. Through force analysis, the optimal value of the angle θ on the elliptical cross-section of the top cover was determined to be 19°. When fallen rock blocks are present on one side of the borehole, the maximum pushing force is 14.79 N. When fallen rock blocks are present on both sides, the maximum pushing force is 13.61 N.
- (3)
- Mechanical loading tests were conducted on different types of bottom trays, and it was determined that the optimal thickness of the roof is 0.3 mm. Additionally, indoor physical simulation tests were performed to model the pushing of anchoring agents through the borehole. The results indicated that unrestrained pushing could not smoothly pass through borehole delamination and collapse zones, while pushing with the push–pull device was able to smoothly pass through these areas. When using a push–pull device without a top cover, it could not successfully pass through the borehole if protruding or fallen coal blocks were present. However, it was able to pass through the borehole smoothly with a top cover on the push–pull device.
- (4)
- The results of on-site anchor cable pull-out tests showed that, when the pull-out force reached 160 kN and 180 kN, the actual elongation of the anchor cables installed using the integrated push–pull technology was almost identical to the theoretical elongation. No significant slip or failure was observed in the anchored section of the cable. Monitoring of the surrounding rock deformation in the retreat channel indicated that the support system with the push–pull device for installing the anchoring agent reduced rock deformation by nearly 50%. This demonstrated that the technology significantly enhances the control of surrounding rock deformation.
7. Prospect
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, M.C.; Guo, A.P.; Meng, Z.G.; Pan, Y.F.; Tao, Z.G. Impact and explosion resistance of NPR anchor cable: Field test and numerical simulation. Undergr. Space 2023, 10, 76–90. [Google Scholar] [CrossRef]
- Zhou, C.; Huang, C.; Chen, Y.D.; Dong, Q.H.; Sui, W.H. Development of a novel resilient anchor cable and its large shear deformation performance. Int. J. Rock Mech. Min. Sci. 2023, 163, 105293. [Google Scholar] [CrossRef]
- Li, G.; Zhu, C.; Hongliang, L.; Tang, S.B.; Du, K.; Wu, C.Z. Energy balance support method in soft rock tunnel with energy absorbing anchor cable. Tunn. Undergr. Space Technol. 2023, 141, 105380. [Google Scholar] [CrossRef]
- Chen, D.D.; Jiang, Z.S.; Xie, S.R. Mechanism and key parameters of stress load-off by innovative asymmetric hole-constructing on the two sides of deep roadway. Int. J. Coal Sci. Technol. 2023, 10, 82. [Google Scholar] [CrossRef]
- Luo, J.W.; Zhang, D.L.; Sun, Z.Y.; Fang, Q.; Liu, D.P.; Xu, T.; Li, R. Numerical modelling and field monitoring study on large-span tunnelling using pretensioned bolt–cable combined support system. Tunn. Undergr. Space Technol. 2023, 132, 104911. [Google Scholar] [CrossRef]
- Wang, D.Q.; He, F.L.; Wu, Y.H.; Lv, K.; Zhang, J.L.; Shi, S.H.; Guo, J.; Xu, X.H.; Tao, K.; Zhang, Y.J.; et al. Study on stability and control of surrounding rock in the large section stopping space with extra-thick coal seam. Alexandria Eng. J. 2025, 117, 205–220. [Google Scholar] [CrossRef]
- Zheng, S.N.; Chen, H.X.; Xiao, Y.; Liu, Y.M.; Kuang, D.L.; Wu, Y.C.; Qiu, H.P. Influence mechanism of mineral composition ratios on the early anchorage properties for cement anchoring agents. Constr. Build Mater. 2024, 414, 135031. [Google Scholar] [CrossRef]
- Chen, D.D.; Jiang, Z.S.; Ma, X.; Xie, S.R.; Wang, E.; Li, H. Evolution law and engineering application on main stress difference for a novel stress relief technology in two ribs on deep coal roadway. J. Cent. South. Univ. 2023, 30, 2266–2283. [Google Scholar] [CrossRef]
- Hyett, A.J.; Bawden, W.F.; Macsporran, G.R.; Moosavi, M. A constitutive law for bond failure of fully-grouted cable bolts using a modified hoek cell. Int. J. Rock Mech. Min. Sci. 1995, 32, 11–36. [Google Scholar] [CrossRef]
- Li, D.L.; Masoumi, H.; Saydam, S.; Hagan, P.C. A constitutive model for load-displacement performance of modified cable bolts. Tunn. Undergr. Space Technol. 2017, 68, 95–105. [Google Scholar] [CrossRef]
- Chen, J.H.; Zeng, B.Q.; Liu, L.; Tao, K.M.; Zhao, H.B.; Zhang, C.; Zhang, J.W.; Li, D.Q. Investigating the anchorage performance of full-grouted anchor bolts with a modified numerical simulation method. Eng. Failure Anal. 2022, 141, 106640. [Google Scholar] [CrossRef]
- Shi, H.; Song, L.; Zhang, H.Q.; Chen, W.L.; Lin, H.S.; Li, D.Q.; Wang, G.Z.; Zhao, H.Y. Experimental and numerical studies on progressive debonding of grouted rock bolts. Int J Min. Sci. Technol. 2022, 32, 63–74. [Google Scholar] [CrossRef]
- He, D.Y.; Liu, S.W.; Jia, H.S.; Fu, M.W.; Jia, L.X.; Zhang, Y. Analysis of eccentric resin anchoring characteristics for cable bolts and the design of pushing and limiting device for resin cartridges. China J. Rock Mech. Eng. 2023, 42, 708–723. [Google Scholar] [CrossRef]
- Li, H.Z.; Li, X.H.; Zhong, Z.H.; Long, J.K. Experimental research on slippage mode and analysis on mechanical properties of coal rock anchorage system. J. Min. Saf. Eng. 2017, 34, 1088–1093. [Google Scholar] [CrossRef]
- Cao, C.; Ren, T.; Zhang, Y.D.; Zhang, L.; Wang, F.T. Experimental investigation of the effect of grout with additive in improving ground support. Int. J. Rock Mech. Min. Sci. 2016, 85, 52–59. [Google Scholar] [CrossRef]
- Zhang, M.; Han, J.; Cao, C.; Ma, S.W. Experimental study on anchorage performance of rockbolts by adding steel aggregates into resin anchoring agents. PLoS ONE 2021, 16, e0255046. [Google Scholar] [CrossRef]
- Chen, D.D.; Wu, Y.Y.; Xie, S.R.; Guo, F.F.; He, F.L.; Liu, R.P. Reasonable location of stopping line in close-distance underlying coal seam and partition support of large cross-section roadway. Int. J. Coal Sci. Technol. 2022, 9, 55. [Google Scholar] [CrossRef]
- Song, W.H.; Yu, S.Q.; Rong, H.; Jiao, H.C.; Xu, X.T. Study on the characteristic of overburden rock structure and support system of the retraction channel in layered fully mechanized caving face. Sci. Rep. 2024, 14, 1360. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, O.M.; Peters, D.M. On stability analyses of three classical buckling problems for the elastic strut. J. Elast. 2011, 105, 117–136. [Google Scholar] [CrossRef]
- Murphy, J.G. The stability of thin, stretched and twisted elastic rods. Int. J. Non-Lin. Mech. 2015, 68, 96–100. [Google Scholar] [CrossRef]
- Patel, A.; Basu, S. Numerical study of the compression of tightly constrained slender rods. Int. J. Solids Struct. 2023, 265, 112107. [Google Scholar] [CrossRef]
- Feng, C.; Liu, S.W.; Fu, M.X.; Yao, B.G.; Jia, H.S.; He, D.Y. Failure mechanism and strengthening countermeasures of end-anchored cable free section under combined tension and shear. Eng. Failure Anal. 2024, 157, 107949. [Google Scholar] [CrossRef]
- Dong, Z.Z.; Peng, H.D.; Liu, T.; Wang, K.; Zheng, J.G.; Li, H.F.; Qiu, X.Y. Study on the mechanism of prestress loss caused by friction in the free segment of anchor cables. Constr. Build Mater. 2024, 413, 134927. [Google Scholar] [CrossRef]
- Guo, F.X.; Tu, M.; Dang, J.X. Analysis and Design of Protection Device for Anchor Cable Pull-Out in High-Stress Roadways. Appl. Sci. 2023, 13, 12023. [Google Scholar] [CrossRef]






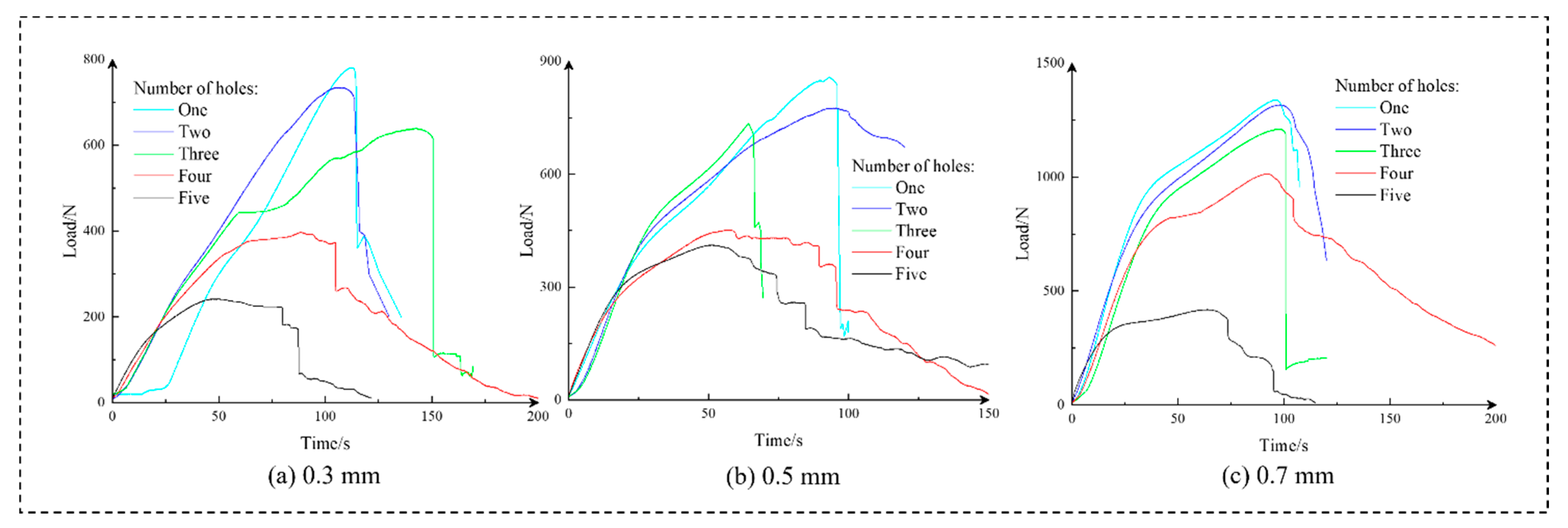




| Thickness of Tray Roof | One Hole | Two Holes | Three Holes | Four Holes | Five Holes |
|---|---|---|---|---|---|
| 0.3 mm | 781 N | 734 N | 639 N | 268 N | 241 N |
| 0.5 mm | 858 N | 775 N | 734 N | 451 N | 412 N |
| 0.7 mm | 1338 N | 1317 N | 12,111 N | 1013 N | 418 N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; He, F.; Chen, D.; Bascompta, M.; Wang, X.; Xu, C.; Liu, B.; Tian, W. Mechanism of Enhanced Control and Technological Application of Surrounding Rock Anchoring in Fully Mechanized Caving Face of Extra-Thick Coal Seams. Processes 2025, 13, 1216. https://doi.org/10.3390/pr13041216
Wang D, He F, Chen D, Bascompta M, Wang X, Xu C, Liu B, Tian W. Mechanism of Enhanced Control and Technological Application of Surrounding Rock Anchoring in Fully Mechanized Caving Face of Extra-Thick Coal Seams. Processes. 2025; 13(4):1216. https://doi.org/10.3390/pr13041216
Chicago/Turabian StyleWang, Deqiu, Fulian He, Dongdong Chen, Marc Bascompta, Xiao Wang, Chenyu Xu, Bingquan Liu, and Wang Tian. 2025. "Mechanism of Enhanced Control and Technological Application of Surrounding Rock Anchoring in Fully Mechanized Caving Face of Extra-Thick Coal Seams" Processes 13, no. 4: 1216. https://doi.org/10.3390/pr13041216
APA StyleWang, D., He, F., Chen, D., Bascompta, M., Wang, X., Xu, C., Liu, B., & Tian, W. (2025). Mechanism of Enhanced Control and Technological Application of Surrounding Rock Anchoring in Fully Mechanized Caving Face of Extra-Thick Coal Seams. Processes, 13(4), 1216. https://doi.org/10.3390/pr13041216







