Modeling the Temperature and Pressure Variations of Supercritical Carbon Dioxide in Coiled Tubing
Abstract
:1. Introduction
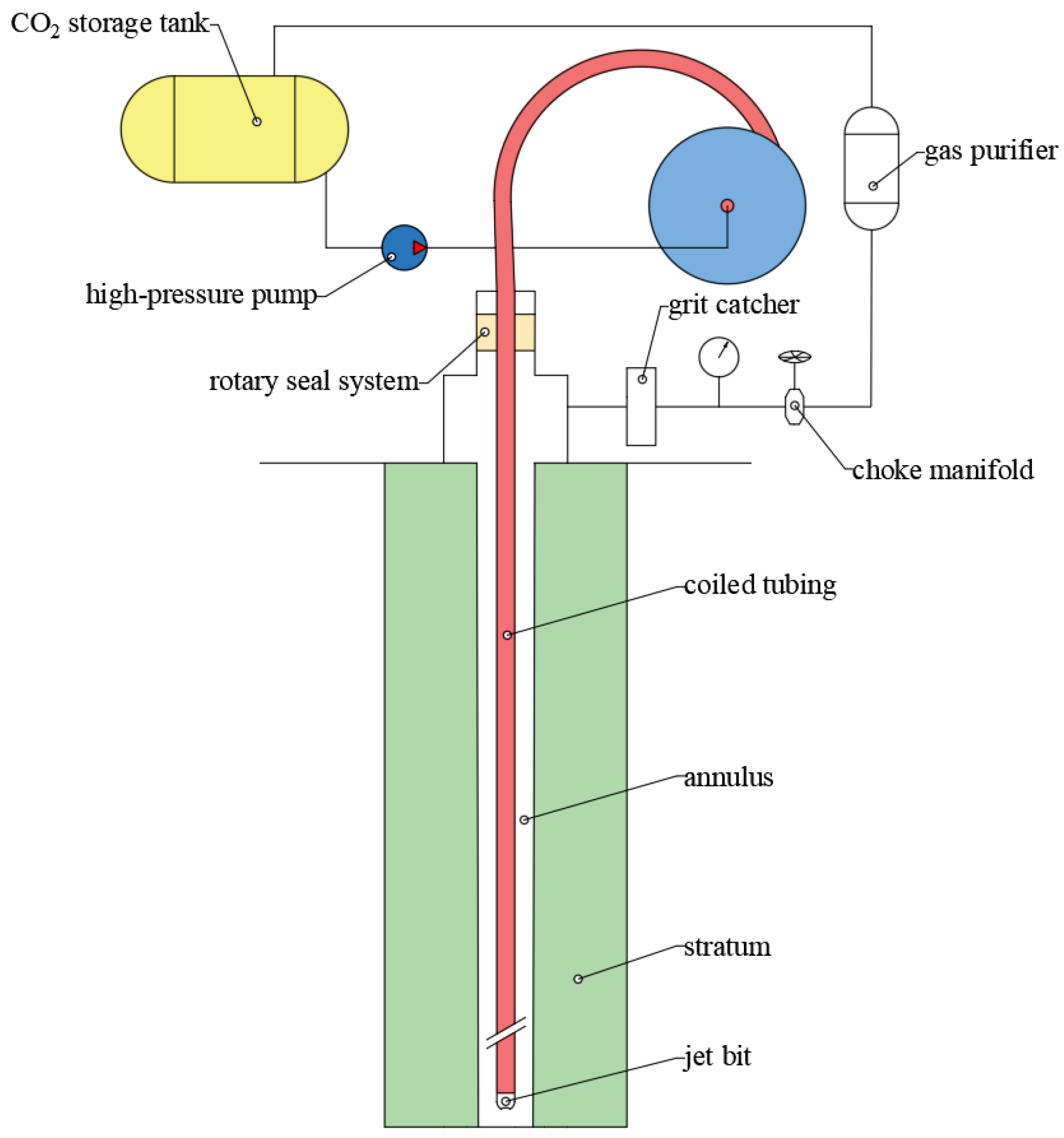
2. Modeling
2.1. Heat Transfer in the Helical Coiled Tube
2.1.1. Heat Transfer of the First Layer of Helical Coiled Tube
2.1.2. Heat Transfer of the nth Layer of Helical Coiled Tube
2.2. Pressure Drop in the Helical Coiled Tube
2.3. Solution Algorithm
3. Results and Discussion
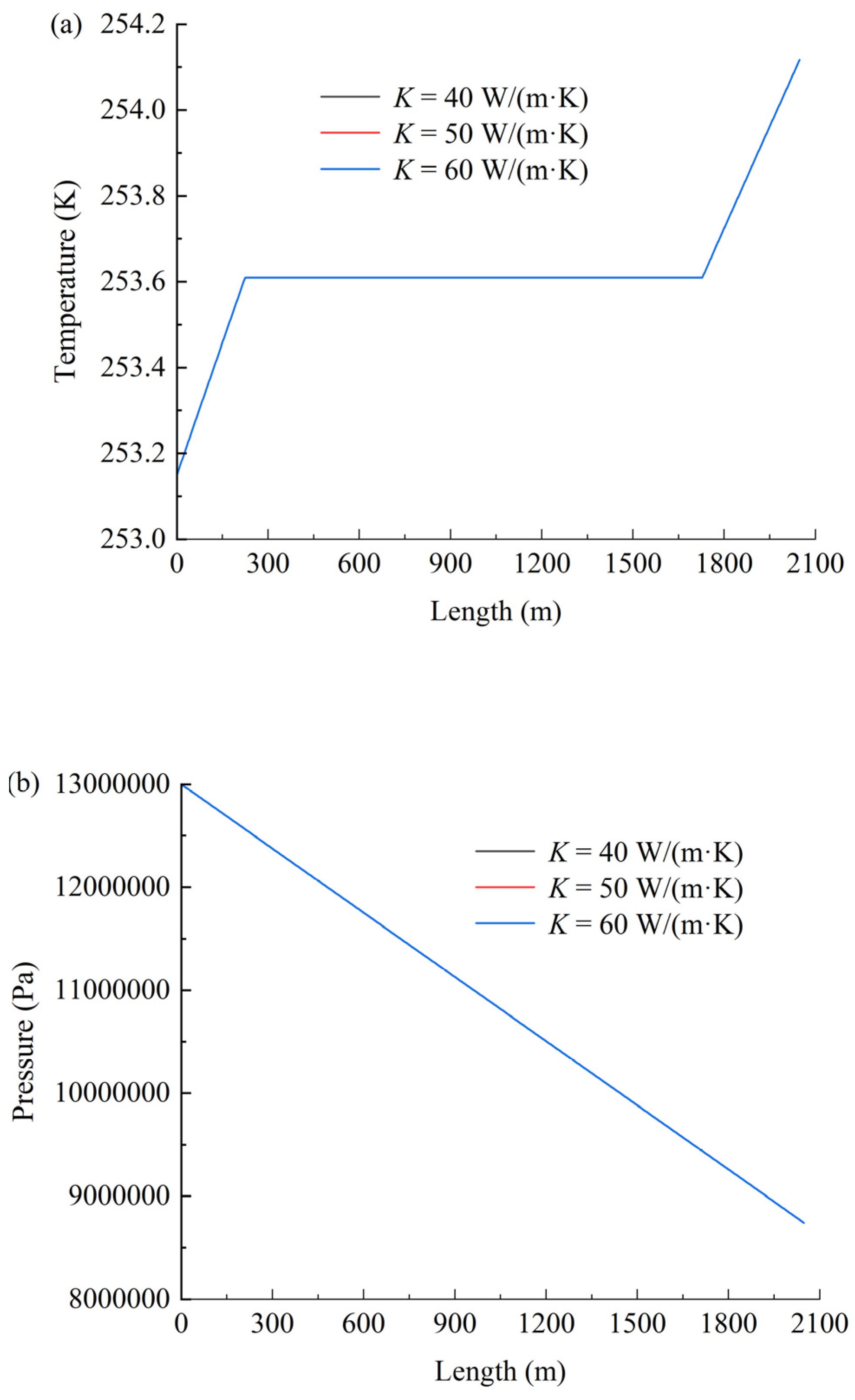
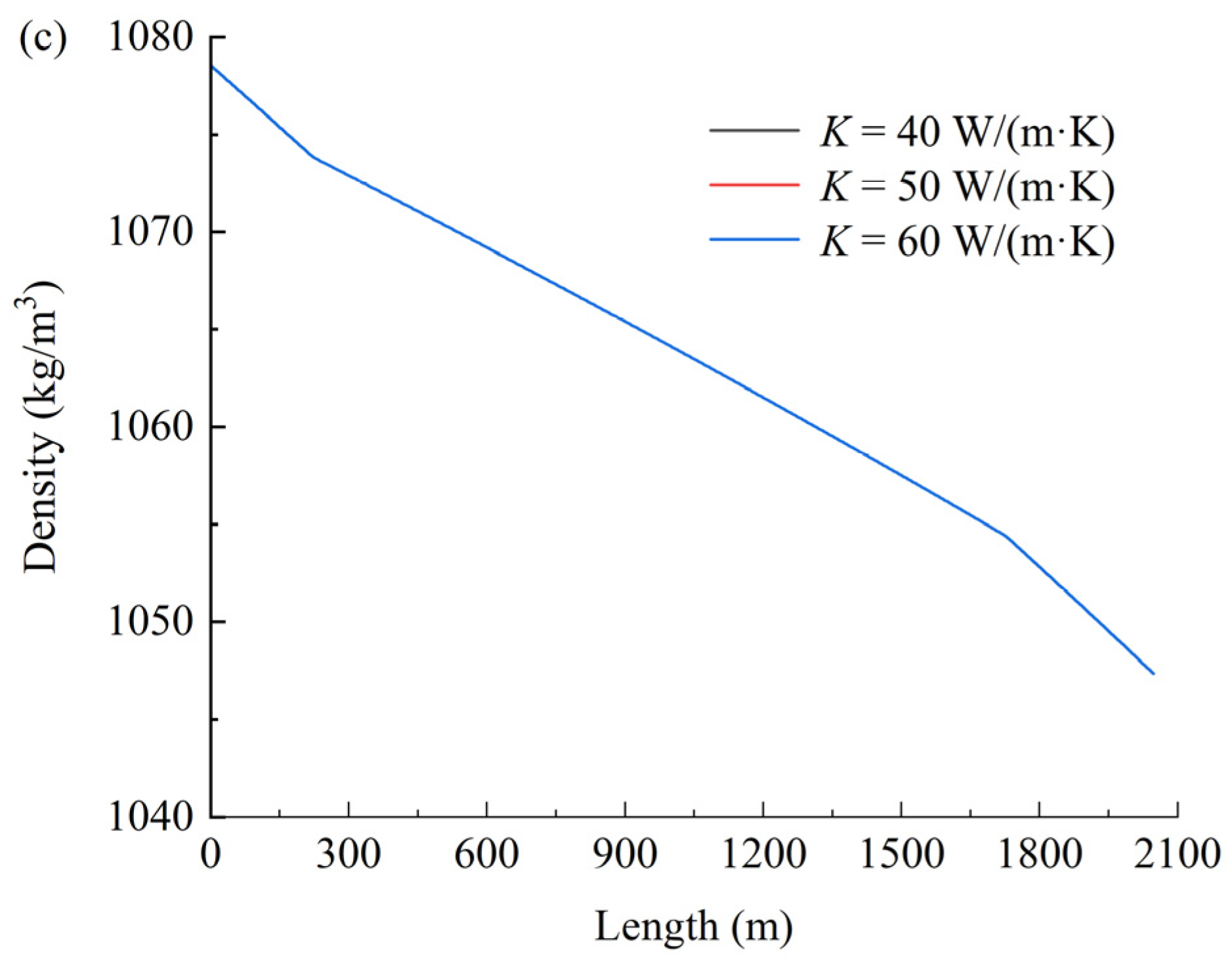
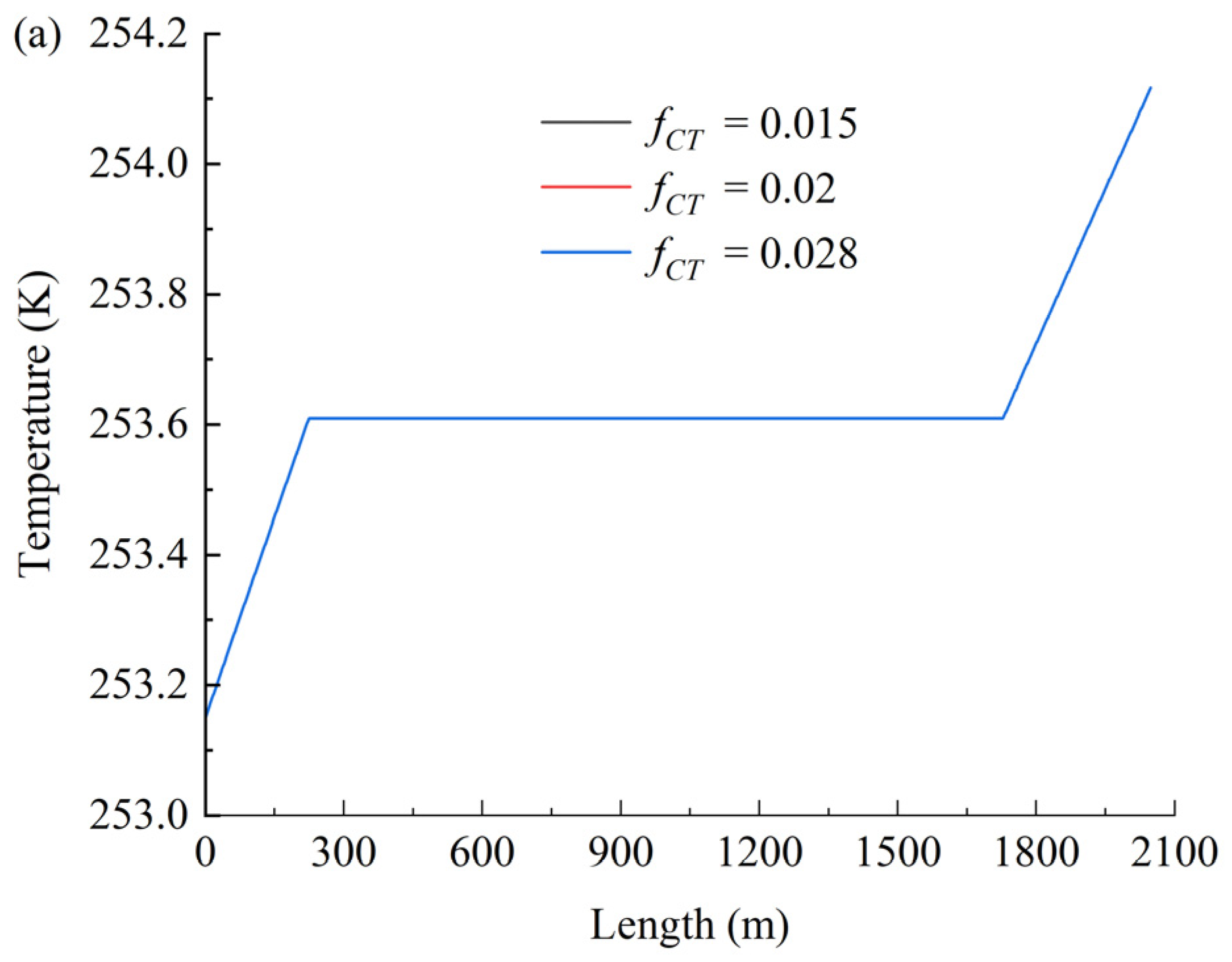
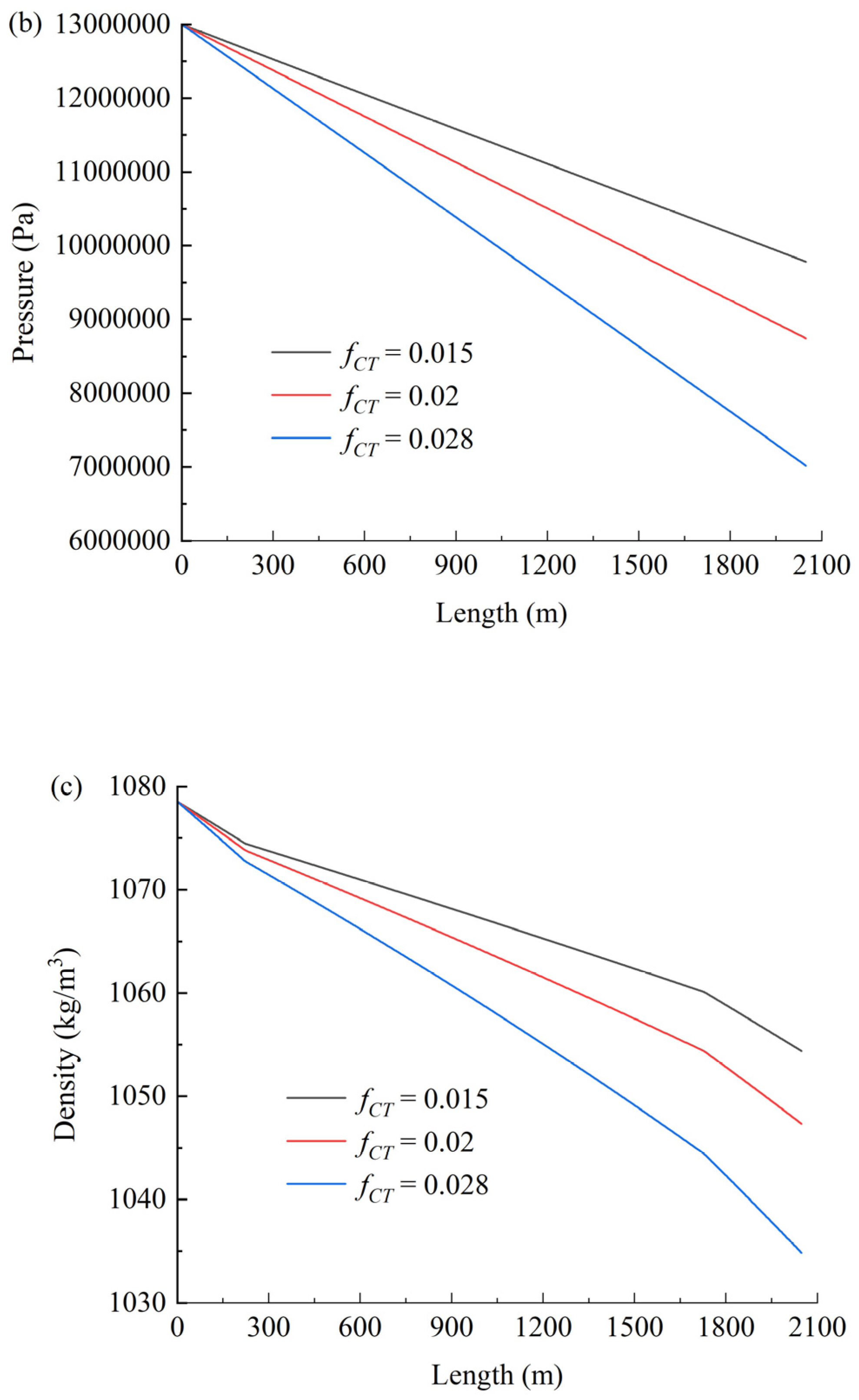
4. Sensitivity Analysis on Uncertain Parameters
4.1. Thermal Conductivity Coefficient K
4.2. Friction Coefficient fCT
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Adwani, F.; Langlinais, J.; Hughes, R. Modeling of an Underbalanced-Drilling Operation Using Supercritical Carbon Dioxide. SPE Drill. Complet. 2009, 24, 599–610. [Google Scholar] [CrossRef]
- Song, J.; Kim, H.Y.; Kim, H.; Bae, Y.Y. Heat transfer characteristics of a supercritical fluid flow in a vertical pipe. J. Supercrit. Fluids 2008, 44, 164–171. [Google Scholar] [CrossRef]
- Bruch, A.; Bontemps, A.; Colasson, S. Experimental investigation of heat transfer of supercritical carbon dioxide flowing in a cooled vertical tube. Int. J. Heat Mass Transf. 2009, 52, 2589–2598. [Google Scholar] [CrossRef]
- Schuler, M.J.; Rothenfluh, T.; von Rohr, R. Simulation of the thermal field of submerged supercritical water jets at near-critical pressures. J. Supercrit. Fluids 2013, 75, 128–137. [Google Scholar] [CrossRef]
- Ničeno, B.; Sharabi, M. Large eddy simulation of turbulent heat transfer at supercritical pressures. Nucl. Eng. Des. 2013, 261, 44–55. [Google Scholar] [CrossRef]
- Jiang, P.-X.; Shi, R.-F.; Xu, Y.-J.; He, S.; Jackson, J. Experimental investigation of flow resistance and convection heat transfer of CO2 at supercritical pressures in a vertical porous tube. J. Supercrit. Fluids 2006, 38, 339–346. [Google Scholar] [CrossRef]
- Cao, X.L.; Rao, Z.H.; Liao, S.M. Laminar convective heat transfer of supercritical CO2 in horizontal miniature circular and triangular tubes. Appl. Therm. Eng. 2011, 31, 2374–2384. [Google Scholar] [CrossRef]
- Withag, J.A.; Sallevelt, J.L.; Brilman, D.W.; Bramer, E.A.; Brem, G. Heat transfer characteristics of supercritical water in a tube: Application for 2D and an experimental validation. J. Supercrit. Fluids 2012, 70, 156–170. [Google Scholar] [CrossRef]
- Oh, H.-K.; Son, C.-H. New correlation to predict the heat transfer coefficient in-tube cooling of supercritical CO2 in horizontal macro-tubes. Exp. Therm. Fluid Sci. 2010, 34, 1230–1241. [Google Scholar] [CrossRef]
- Lee, H.-S.; Kim, H.-J.; Yoon, J.-I.; Choi, K.-H.; Son, C.-H. The cooling heat transfer characteristics of the supercritical CO2 in micro-fin tube. Heat Mass Transf. 2013, 49, 173–184. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Bhuvaneswari, M. Numerical study on influence of water based hybrid nanofluid and porous media on heat transfer and pressure loss. Case Stud. Therm. Eng. 2022, 34, 102022. [Google Scholar] [CrossRef]
- Thomson, J.V. On the Origin of Windings of Rivers in Alluvial Plains, with Remarks on the Flow of Water round Bends in Pipes. Proc. R. Soc. Lond. 1877, 25, 5–8. [Google Scholar]
- Dean, W.R. Fluid Motion in a Curved Channel. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1928, 121, 402–420. [Google Scholar]
- Janssen, L.A.M.; Hoogendoorn, C.J. Laminar convective heat transfer in helical coiled tubes. Int. J. Heat Mass Transf. 1978, 21, 1197–1206. [Google Scholar] [CrossRef]
- Cioncolini, A.; Santini, L. An experimental investigation regarding the laminar to turbulent flow transition in helically coiled pipes. Exp. Therm. Fluid Sci. 2006, 30, 367–380. [Google Scholar] [CrossRef]
- Cioncolini, A.; Santini, L. On the laminar to turbulent flow transition in diabatic helically coiled pipe flow. Exp. Therm. Fluid Sci. 2006, 30, 653–661. [Google Scholar] [CrossRef]
- White, C.M. Streamline Flow through Curved Pipes. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1929, 123, 645–663. [Google Scholar]
- Zhou, Y.; Shah, S. Fluid Flow in Coiled Tubing: A Literature Review and Experimental Investigation. J. Can. Pet. Technol. 2004, 43, 52–61. [Google Scholar] [CrossRef]
- Moawed, M. Experimental study of forced convection from helical coiled tubes with different parameters. Energy Convers. Manag. 2011, 52, 1150–1156. [Google Scholar] [CrossRef]
- Ito, H. Friction factors for turbulent flow in curved pipes. J. Basic Eng. 1959, 81, 123–124. [Google Scholar] [CrossRef]
- Srinivasan, P.S.; Nandapurkar, S.S.; Holland, F.A.J.C.E. Pressure drop and heat transfer in coils. Chem. Eng. 1968, 218, 113–119. [Google Scholar]
- Ferng, Y.M.; Lin, W.C.; Chieng, C.C. Numerically investigated effects of different Dean number and pitch size on flow and heat transfer characteristics in a helically coil-tube heat exchanger. Appl. Therm. Eng. 2012, 36, 378–385. [Google Scholar] [CrossRef]
- Jayakumar, J.S.; Mahajani, S.M.; Mandal, J.C.; Iyer, K.N.; Vijayan, P.K. CFD analysis of single-phase flows inside helically coiled tubes. Comput. Chem. Eng. 2010, 34, 430–446. [Google Scholar] [CrossRef]
- Chen, C.-N.; Han, J.-T.; Jen, T.-C.; Shao, L. Thermo-chemical characteristics of R134a flow boiling in helically coiled tubes at low mass flux and low pressure. Thermochim. Acta 2011, 512, 163–169. [Google Scholar] [CrossRef]
- Owhadi, A.; Bell, K.J. Forced convection boiling inside helically-coiled tubes. Int. J. Heat Mass Transf. 1967, 10, 397–401. [Google Scholar] [CrossRef]
- Jamshidi, N.; Farhadi, M.; Sedighi, K.; Ganji, D.D. Optimization of design parameters for nanofluids flowing inside helical coils. Int. Commun. Heat Mass Transf. 2012, 39, 311–317. [Google Scholar] [CrossRef]
- Akbaridoust, F.; Rakhsha, M.; Abbassi, A.; Saffar-Avval, M. Experimental and numerical investigation of nanofluid heat transfer in helically coiled tubes at constant wall temperature using dispersion model. Int. J. Heat Mass Transf. 2013, 58, 480–491. [Google Scholar] [CrossRef]
- Haruki, N.; Horibe, A. Flow and heat transfer characteristics of ice slurries in a helically-coiled pipe. Int. J. Refrig. 2013, 36, 1285–1293. [Google Scholar] [CrossRef]
- Di Piazza, I.; Ciofalo, M. Numerical prediction of turbulent flow and heat transfer in helically coiled pipes. Int. J. Therm. Sci. 2010, 49, 653–663. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; De Witt, D.P. Fundamentals of Heat and Mass Transfer, 8th ed.; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Rao, B. Coiled Tubing Hydraulics Modeling; Tech Note; CTES, L.C.: Conroe, TX, USA, 1999; Available online: https://ctes.nov.com/Documentation/technotes/Tech%20Note%20Basic%20Hydraulics.pdf (accessed on 12 April 2025).
- Hasan, A.R.; Kabir, C.S. Aspects of Wellbore Heat Transfer During Two-Phase Flow. SPE Prod. Facil. 1994, 9, 211–216. [Google Scholar] [CrossRef]
- Ramey, H.J. Wellbore Heat Transmission. J. Pet. Technol. 1962, 14, 427–435. [Google Scholar] [CrossRef]
- Holmes, C.S.; Swift, S.C. Calculation of Circulating Mud Temperatures. J. Pet. Technol. 1970, 22, 670–674. [Google Scholar] [CrossRef]
- McCann, R.C.; Islas, C.G. Frictional Pressure Loss During Turbulent Flow in Coiled Tubing. In Proceedings of the SPE Gulf Coast Section/ICoTA North American Coiled Tubing Roundtable, Conroe, TX, USA, 26 February 1996. [Google Scholar]
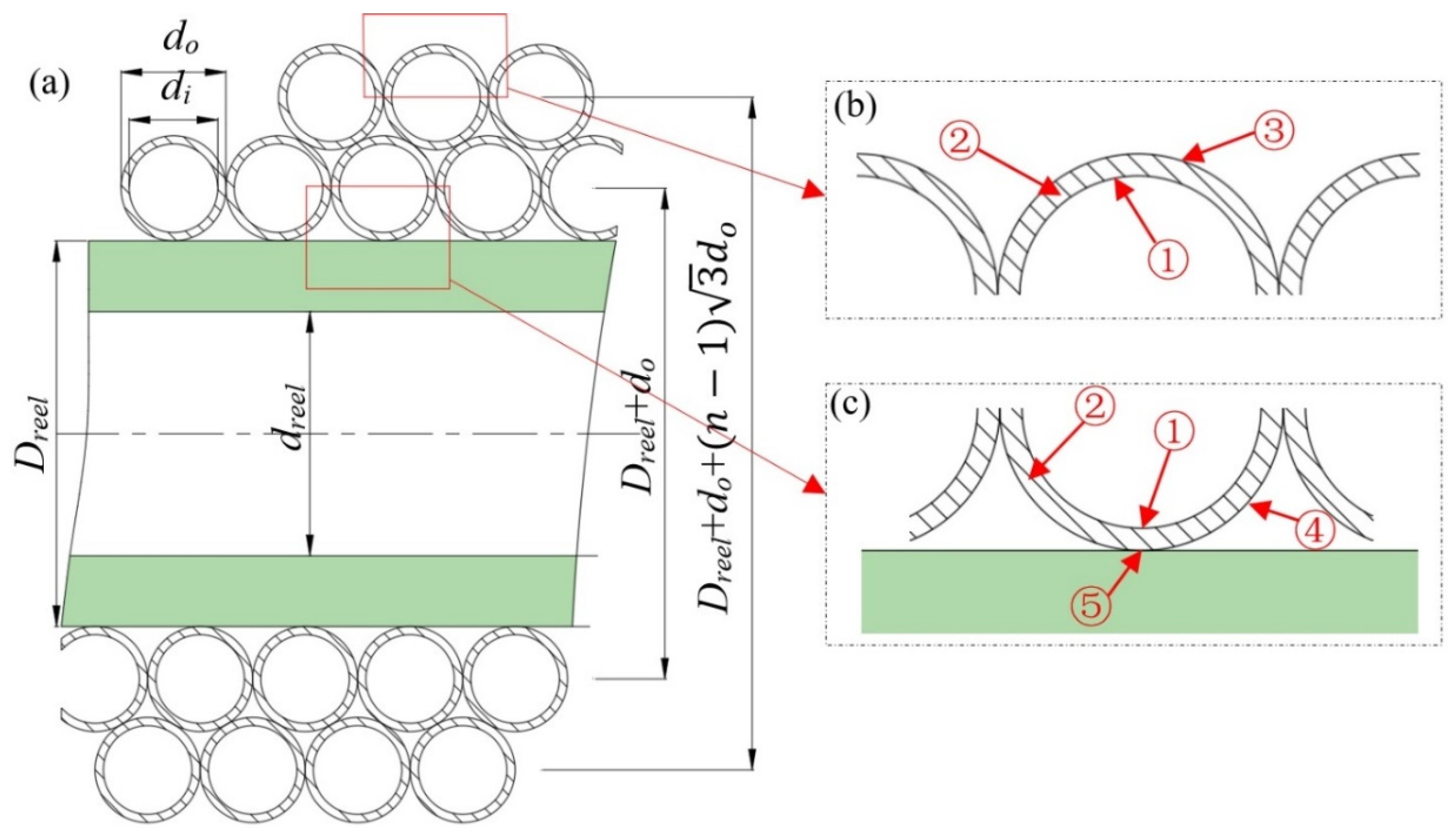

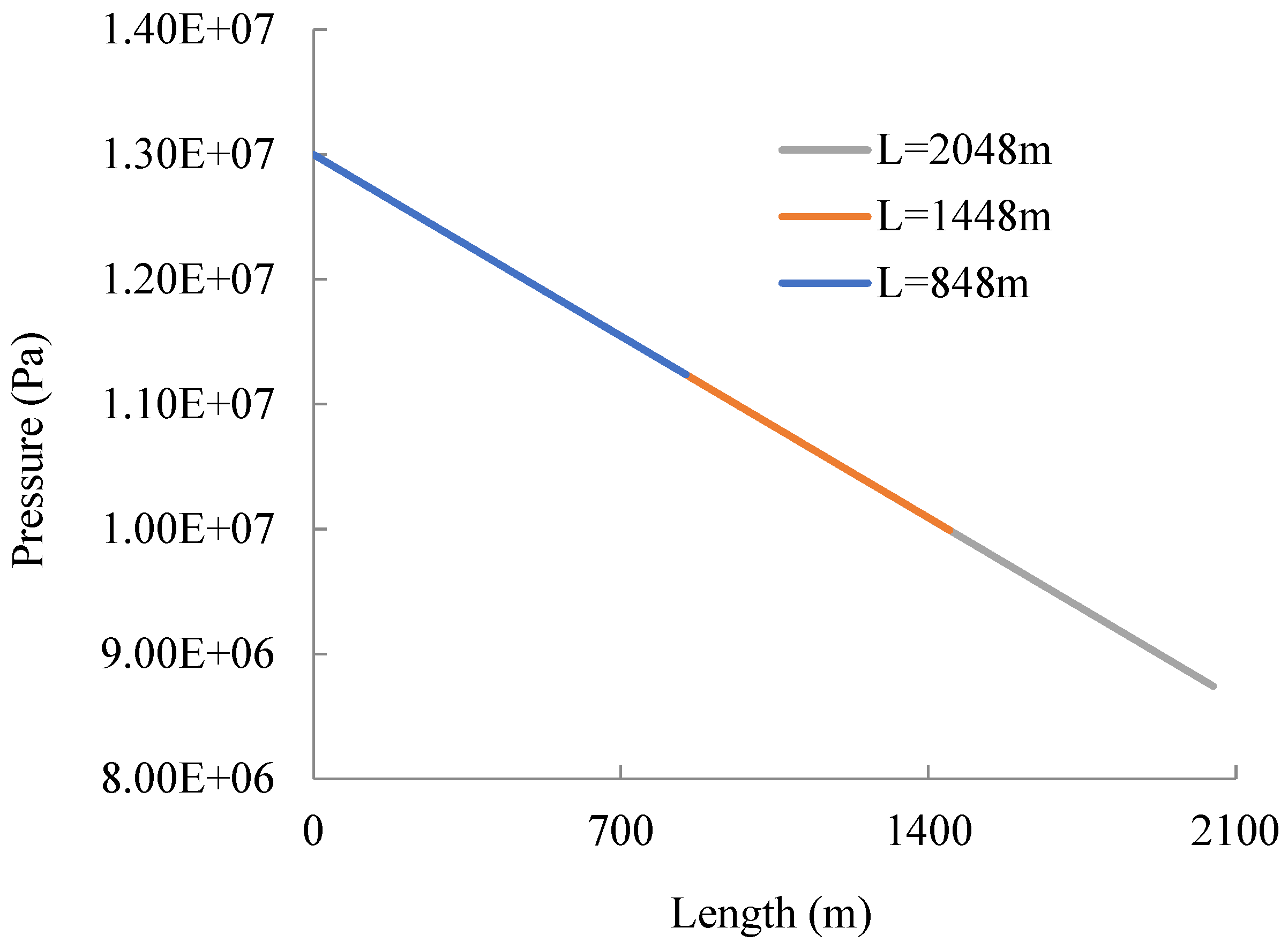

| Length of Coiled Tubing (m) | Layer Number | Length of Each Layer (m) | Curvature Ratio of Each Layer d/D |
|---|---|---|---|
| L = 848 m | 1 | 222.5006 | 0.0206 |
| 2 | 231.9357 | 0.0198 | |
| 3 | 241.3709 | 0.0190 | |
| 4 | 152.1928 | 0.0176 | |
| L = 1448 m | 1 | 222.5006 | 0.0206 |
| 2 | 231.9357 | 0.0198 | |
| 3 | 241.3709 | 0.0190 | |
| 4 | 250.8060 | 0.0183 | |
| 5 | 260.2412 | 0.0176 | |
| 6 | 241.1455 | 0.0165 | |
| L = 2048 m | 1 | 222.5006 | 0.0206 |
| 2 | 231.9357 | 0.0198 | |
| 3 | 241.3709 | 0.0190 | |
| 4 | 250.8060 | 0.0183 | |
| 5 | 260.2412 | 0.0176 | |
| 6 | 269.6764 | 0.0170 | |
| 7 | 279.1116 | 0.0165 | |
| 8 | 288.5468 | 0.0159 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, Z.; Wang, P. Modeling the Temperature and Pressure Variations of Supercritical Carbon Dioxide in Coiled Tubing. Processes 2025, 13, 1230. https://doi.org/10.3390/pr13041230
Luan Z, Wang P. Modeling the Temperature and Pressure Variations of Supercritical Carbon Dioxide in Coiled Tubing. Processes. 2025; 13(4):1230. https://doi.org/10.3390/pr13041230
Chicago/Turabian StyleLuan, Zhixing, and Peng Wang. 2025. "Modeling the Temperature and Pressure Variations of Supercritical Carbon Dioxide in Coiled Tubing" Processes 13, no. 4: 1230. https://doi.org/10.3390/pr13041230
APA StyleLuan, Z., & Wang, P. (2025). Modeling the Temperature and Pressure Variations of Supercritical Carbon Dioxide in Coiled Tubing. Processes, 13(4), 1230. https://doi.org/10.3390/pr13041230





