Machine Learning and Industrial Data for Veneer Quality Optimization in Plywood Manufacturing
Abstract
:1. Introduction
1.1. Description of the Plywood Production Process
1.1.1. Maceration
1.1.2. Peeling
1.1.3. Drying
1.1.4. Bonding
1.1.5. Assembly, Pre-Pressing and Pressing
1.1.6. Quality in Veneer and Plywood
1.2. Machine Learning Approach
1.3. Least Absolute Shrinkage and Selection Operator (LASSO)
1.4. K-Nearest Neighbors (kNN)
1.5. Support Vector Machines (SVMs)
1.6. Random Forest
1.7. XGBoost
1.8. Logistic Regression
1.9. Machine Learning in Plywood Industry
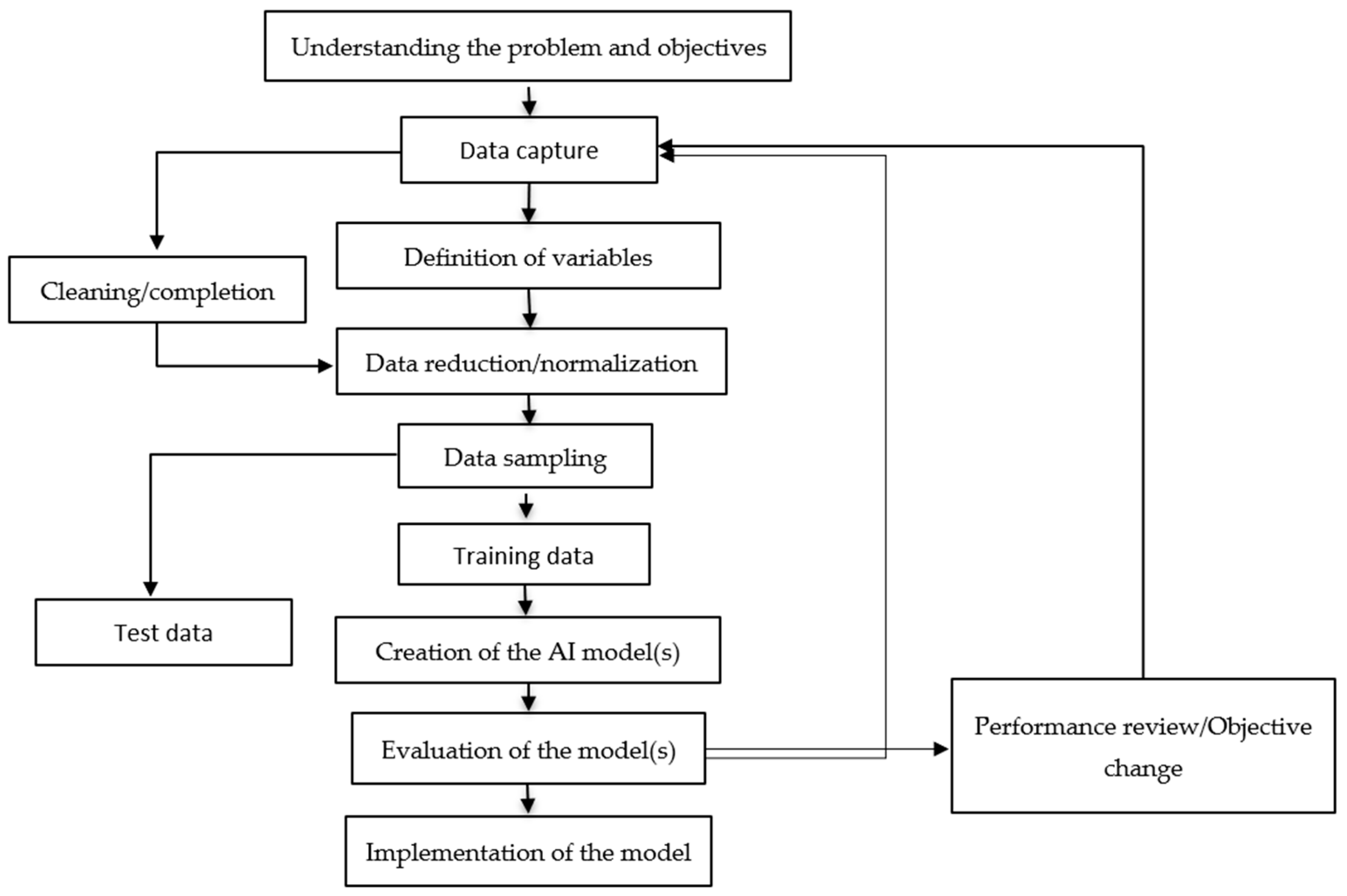
2. Resources and Data Processing
2.1. Computational and ML Resources
Data Model, Data Flow and Collection
2.2. Collected Variables
2.3. Data Preprocessing
2.4. Experimental Design
- Data Collection Interval: (1) every 5 min;
- Data Split: 70% training data, 30% test data;
- Algorithms Used: Random Forest, XGBoost, K-Nearest Neighbors (KNN), Support Vector Machine (SVM), Lasso, and Logistic Regression;
- KPI: Sheet Quality;
- Performance Metrics: Accuracy, Precision, Recall, F1-score.
3. Results and Discussion
3.1. Data Reduction
3.2. LASSO
| Algorithm 1. LASSO Regression |
| Input: - X: Feature matrix (n x p) where n is the number of samples and p is the number of features - y: Target variable (n x 1) - λ (lambda): Regularization parameter controlling sparsity - Max_iterations: Maximum number of optimization steps - Tolerance: Convergence threshold Output: - β: Estimated coefficient vector (p x 1) Steps: 1. Initialize β (coefficients) to zeros or small random values. 2. Standardize the feature matrix X (zero mean and unit variance for each feature). 3. Repeat until convergence or Max_iterations is reached: a. For each feature j in X: i. Compute the partial residual: r_j = y − (X * β) + (X_j * β_j) ii. Compute the ordinary least squares estimate: β_j = (1/n) * Σ (X_j * r_j) iii. Apply the soft-thresholding function: β_j = sign(β_j) * max(|β_j| − λ, 0) b. Check for convergence: - If the maximum absolute change in β between iterations is smaller than Tolerance, stop. 4. Return the final β values. End Algorithm |
3.3. Data Processing
3.4. Metrics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ramos-Maldonado, M.; Aguilera-Carrasco, C. Trends and Opportunities of Industry 4.0 in Wood Manufacturing Processes; Intechopen: London, UK, 2021. [Google Scholar] [CrossRef]
- Orejuela-Escobar, L.; Venegas-Vásconez, D.; Méndez, M.A. Opportunities of Artificial Intelligence in Valorisation of Biodiversity, Biomass and Bioresidues—Towards Advanced Bio-Economy, Circular Engineering, and Sustainability. Int. J. Sustain. Energy Environ. Res. 2024, 13, 105–113. [Google Scholar] [CrossRef]
- Lu, Z.; Lin, F.; Ying, H. Design of Decision Tree via Kernelized Hierarchical Clustering for Multiclass Support Vector Machines. Cybern. Syst. 2007, 38, 187–202. [Google Scholar] [CrossRef]
- Shalev-Shwartz, S.; Ben-David, S. Understanding Machine Learning: From Theory to Algorithms; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-05713-5. [Google Scholar]
- Frey, U.J.; Klein, M.; Deissenroth, M. Modelling Complex Investment Decisions in Germany for Renewables with Different Machine Learning Algorithms. Environ. Model. Softw. 2019, 118, 61–75. [Google Scholar] [CrossRef]
- Gradov, D.V.; Yusuf, Y.O.; Ohjainen, J.; Suuronen, J.; Eskola, R.; Roininen, L.; Koiranen, T. Modelling of a Continuous Veneer Drying Unit of Industrial Scale and Model-Based ANOVA of the Energy Efficiency. Energy 2022, 244, 122673. [Google Scholar] [CrossRef]
- Venegas-Vásconez, D.; Orejuela-Escobar, L.; Valarezo-Garcés, A.; Guerrero, V.H.; Tipanluisa-Sarchi, L.; Alejandro-Martín, S. Biomass Valorization through Catalytic Pyrolysis Using Metal-Impregnated Natural Zeolites: From Waste to Resources. Polymers 2024, 16, 1912. [Google Scholar] [CrossRef]
- Ramos Maldonado, M.; Duarte Sepúlveda, T.; Gatica Neira, F.; Venegas Vásconez, D. Machine Learning Para Predecir La Calidad Del Secado de Chapas En La Industria de Tableros Contrachapados de Pinus Radiata. Maderas Cienc. Tecnol. 2024, 26, 1–18. [Google Scholar] [CrossRef]
- Teihuel, J. Propuesta de Alternativas de Solución Para El Transporte de residuos de Madera Sólida En La Industria de Tableros. Bachelor’s Thesis, Universidad Austral de Chile, Los Rios Region, Chile, 2007. [Google Scholar]
- Moisan, R. Modelo de Determinación de Rendimiento Para El Proceso de Elaboración de Paneles En Planta Nueva Aldea. Bachelor’s Thesis, Universidad del Bío-Bío, Concepción City, Chile, 2007. [Google Scholar]
- Duarte, T. Uso de Técnicas de Machine Learning Para Predecir La Calidad de Tableros Contrachapados. Habilitación Profesional. Bachelor’s Thesis, Universidad del Bío-Bío, Concepción City, Chile, 2023. [Google Scholar]
- Navarrete, C. Evaluación de Método Predictivo Para Variables de Secado de Chapas En Planta de Paneles Arauco Nueva Aldea. Habilitación Profesional. Bachelor’s Thesis, Universidad del Bío-Bío, Concepción City, Chile, 2020. [Google Scholar]
- Kehr, R. Evaluación de Programas de Secado Continuo En Chapas de Pinus Radiata D. Don. Bachelor’s Thesis, Universidad Austral de Chile, Los Rios Region, Chile, 2007. [Google Scholar]
- Aydin, I. Effects of veneer drying at high temperature and chemical treatments on equilibrium moisture content of plywood. Maderas Cienc. Tecnol. 2014, 16, 445–452. [Google Scholar] [CrossRef]
- Demirkir, C.; Özsahin, Ş.; Aydin, I.; Colakoglu, G. Optimization of Some Panel Manufacturing Parameters for the Best Bonding Strength of Plywood. Int. J. Adhes. Adhes. 2013, 46, 14–20. [Google Scholar] [CrossRef]
- Lutz, J. Wood and Log Characteristics Affecting Veneer Production. In USDA Forest Service Research Paper; Forest Products Laboratory: Madison, WI, USA, 1971. [Google Scholar]
- Shi, S.; Walker, J. Wood-based composites: Plywood and veneer-based products. In Primary Wood Processing; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, S.; Li, X. Moisture Content Distribution and Its Effect on Veneer Properties. J. Wood Sci. 2017, 63, 49–55. [Google Scholar]
- Kollmann, F.F.P.; Côté, W.A. Solid Wood. In Principles of Wood Science and Technology; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Lai, W.; Zhao, H.; Zhang, Y. Influence of Wood Surface Characteristics on Plywood Quality. Wood Sci. Technol. 2019, 53, 47–64. [Google Scholar]
- Wu, S.J.; Gebraeel, N.; Lawley, M.A.; Yih, Y. A Neural Network Integrated Decision Support System for Condition-Based Optimal Predictive Maintenance Policy. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2007, 37, 226–236. [Google Scholar] [CrossRef]
- Minaei-Bidgoli, B.; Parvin, H.; Alinejad-Rokny, H.; Alizadeh, H.; Punch, W.F. Effects of Resampling Method and Adaptation on Clustering Ensemble Efficacy. Artif. Intell. Rev. 2014, 41, 27–48. [Google Scholar] [CrossRef]
- Parvin, H.; Alinejad-Rokny, H.; Minaei-Bidgoli, B.; Parvin, S. A New Classifier Ensemble Methodology Based on Subspace Learning. J. Exp. Theor. Artif. Intell. 2013, 25, 227–250. [Google Scholar] [CrossRef]
- Pillay, T.; Cawthra, H.C.; Lombard, A.T. Integration of Machine Learning Using Hydroacoustic Techniques and Sediment Sampling to Refine Substrate Description in the Western Cape, South Africa. Mar. Geol. 2021, 440, 106599. [Google Scholar] [CrossRef]
- Burghardt, E.; Sewell, D.; Cavanaugh, J. Agglomerative and Divisive Hierarchical Bayesian Clustering. Comput. Stat. Data Anal. 2022, 176, 107566. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-Level Classification of Skin Cancer with Deep Neural Networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Coleman, K.D.; Schmidt, K.; Smith, R.C. Frequentist and Bayesian Lasso Techniques for Parameter Selection in Nonlinearly Parameterized Models. IFAC-PapersOnLine 2016, 49, 416–421. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Lindström, E.; Höök, J. Unbiased Adaptive LASSO Parameter Estimation for Diffusion Processes; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 51, pp. 257–262. [Google Scholar]
- Zhang, Y.; Haghani, A. A Gradient Boosting Method to Improve Travel Time Prediction. Transp. Res. Part C Emerg. Technol. 2015, 58, 308–324. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Ali, A.; Hamraz, M.; Khan, D.; Debani, W.; Khan, Z. A Random Projection k Nearest Neighbours Ensemble for Classification via Extended Neighbourhood Rule. arXiv 2023, arXiv:2303.12210. [Google Scholar] [CrossRef]
- Jodas, D.S.; Passos, L.A.; Adeel, A.; Papa, J.P. PL-KNN: A parameterless nearest neighbors classifier. In Proceedings of the 2022 29th International Conference on Systems, Signals and Image Processing (IWSSIP), Sofia, Bulgaria, 1–3 June 2022. [Google Scholar] [CrossRef]
- Liu, Z.; Kou, J.; Yan, Z.; Wang, P.; Liu, C.; Sun, C.; Shao, A.; Klein, B. Enhancing XRF Sensor-Based Sorting of Porphyritic Copper Ore Using Particle Swarm Optimization-Support Vector Machine (PSO-SVM) Algorithm. Int. J. Min. Sci. Technol. 2024, 34, 545–556. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Mahesh, C.B.; Srikanth, B.; Nwa-David, C.; Obimba-Wogu, J.; Shakeri, J. Support Vector Machine (SVM) Prediction of Coefficients of Curvature and Uniformity of Hybrid Cement Modified Unsaturated Soil with NQF Inclusion. Clean Eng. Technol. 2021, 5, 100290. [Google Scholar] [CrossRef]
- Zheng, M.; Luo, X. Joint Estimation of State of Charge (SOC) and State of Health (SOH) for Lithium Ion Batteries Using Support Vector Machine (SVM), Convolutional Neural Network (CNN) and Long Sort Term Memory Network (LSTM) Models. Int. J. Electrochem. Sci. 2024, 19, 100747. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene Selection and Classification of Microarray Data Using Random Forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Wang, Q.; Zou, X.; Chen, Y.; Zhu, Z.; Yan, C.; Shan, P.; Wang, S.; Fu, Y. XGBoost Algorithm Assisted Multi-Component Quantitative Analysis with Raman Spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2024, 323, 124917. [Google Scholar] [CrossRef]
- Wang, Z.H.; Liu, Y.F.; Wang, T.; Wang, J.G.; Liu, Y.M.; Huang, Q.X. Intelligent Prediction Model of Mechanical Properties of Ultrathin Niobium Strips Based on XGBoost Ensemble Learning Algorithm. Comput Mater Sci 2024, 231, 112579. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John WiIley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Joanne Peng, C.-Y.; Lee, K.L.; Ingersoll, G. An Introduction to Logistic Regression Analysis and Reporting. J. Educ. Res. 2002, 96, 3–14. [Google Scholar] [CrossRef]
- Urra-González, C.; Ramos-Maldonado, M. A Machine Learning Approach for Plywood Quality Prediction. Maderas Cienc. Tecnol. 2023, 25, 36. [Google Scholar] [CrossRef]
- Demir, A. Determination of the Effect of Valonia Tannin When Used as a Filler on the Formaldehyde Emission and Adhesion Properties of Plywood with Artificial Neural Network Analysis. Int. J. Adhes. Adhes. 2023, 123, 103346. [Google Scholar] [CrossRef]
- Manrique Rojas, E. Machine Learning: Análisis de Lenguajes de Programación y Herramientas Para Desarrollo. Rev. Ibérica Sist. Tecnol. Informação 2019, 28, 586–599. [Google Scholar]
- Venegas-Vásconez, D.; Arteaga-Pérez, L.E.; Aguayo, M.G.; Romero-Carrillo, R.; Guerrero, V.H.; Tipanluisa-Sarchi, L.; Alejandro-Martín, S. Analytical Pyrolysis of Pinus Radiata and Eucalyptus Globulus: Effects of Microwave Pretreatment on Pyrolytic Vapours Composition. Polymers 2023, 15, 3790. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach, 4th ed.; Pearson Educational Inc.: London, UK, 2021; ISBN 9780134610993. [Google Scholar]
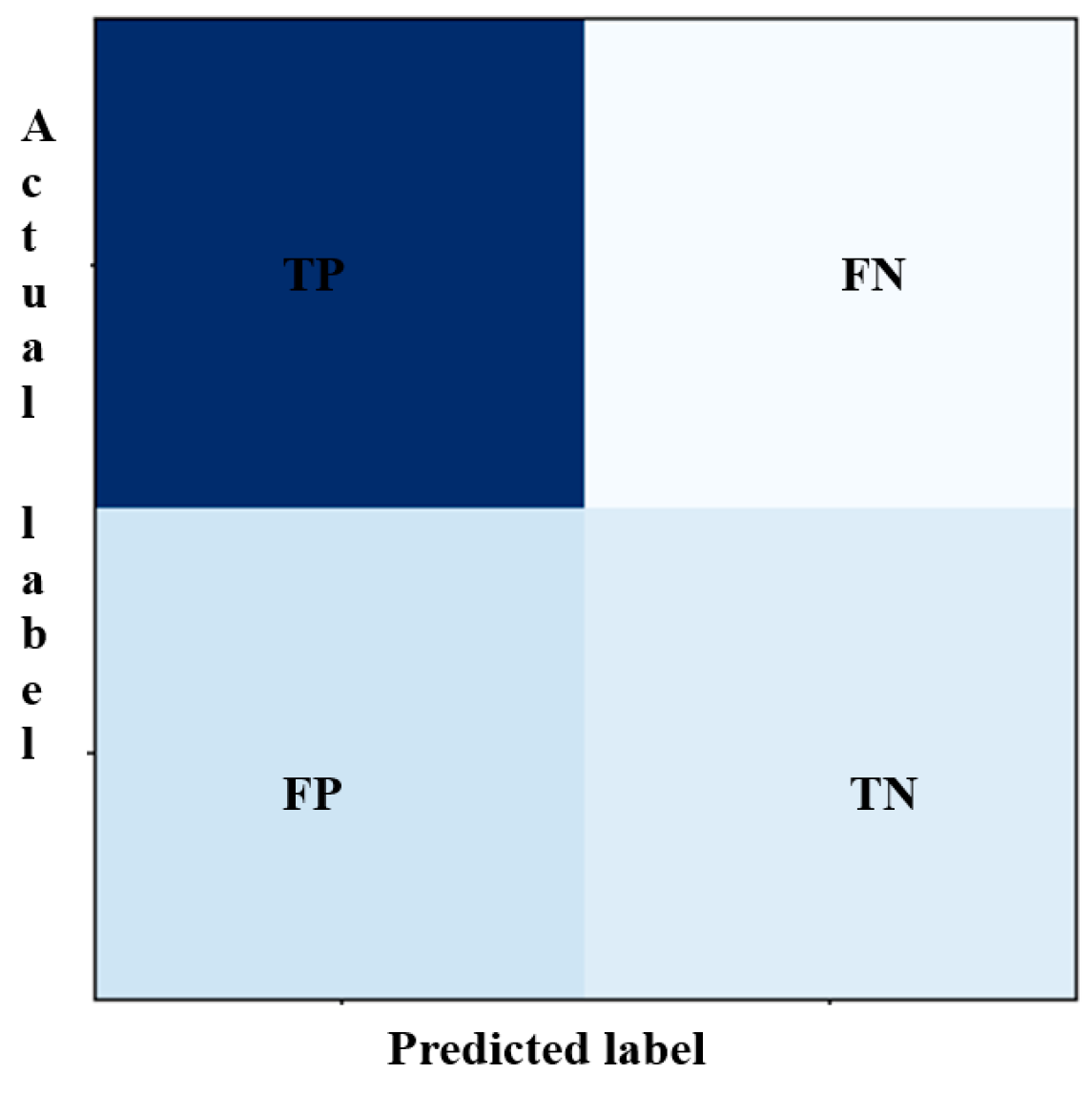
- Luque, A.; Carrasco, A.; Martín, A.; de las Heras, A. The Impact of Class Imbalance in Classification Performance Metrics Based on the Binary Confusion Matrix. Pattern Recognit. 2019, 91, 216–231. [Google Scholar] [CrossRef]
- Nakamura, K. A Practical Approach for Discriminating Tectonic Settings of Basaltic Rocks Using Machine Learning. Appl. Comput. Geosci. 2023, 19, 100132. [Google Scholar] [CrossRef]
- Düntsch, I.; Gediga, G. Confusion Matrices and Rough Set Data Analysis. J. Phys. Conf. Ser. 2019, 1229, 012055. [Google Scholar] [CrossRef]
- Lu, G.; Zeng, L.; Dong, S.; Huang, L.; Liu, G.; Ostadhassan, M.; He, W.; Du, X.; Bao, C. Lithology Identification Using Graph Neural Network in Continental Shale Oil Reservoirs: A Case Study in Mahu Sag, Junggar Basin, Western China. Mar. Pet. Geol. 2023, 150, 106168. [Google Scholar] [CrossRef]
- Bressan, T.S.; Kehl de Souza, M.; Pirelli, T.J.; Junior, F.C. Evaluation of Machine Learning Methods for Lithology Classification Using Geophysical Data. Comput. Geosci. 2020, 139, 104475. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Allen, P.G.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar] [CrossRef]




| Variable | Impact on Quality |
|---|---|
| Temperature | Elevated temperatures during the maceration improve wood fiber softening and adhesion, but excessive heat may degrade fibers, weakening structural integrity and visual quality. |
| Time | Longer maceration enhances fiber softening and adhesion, but excessive durations can lead to fiber breakdown, compromising structure and esthetics. |
| Intrinsic variable of wood | Uniform, defect-free wood improves maceration results, while defects like knots or cracks increase veneer flaws and reduce structural integrity. |
| Variable | Impact on Quality |
|---|---|
| Rotation speed | Ensures uniform cuts and minimizes defects. Excessive speeds cause tear-out; low speeds lead to poor peeling and adhesion. |
| Knife angle | Optimal angles create clean cuts and uniform thickness. Incorrect angles result in tearing and uneven surfaces. |
| Feed rate | Consistent feed rates prevent defects. High feed rates cause roughness; low rates lead to overheating and degradation. |
| Knife position | Proper positioning ensures uniform thickness. Too deep positioning damages fibers; too shallow causes poor peeling. |
| Density | High-density woods improve strength and cut quality, while low-density woods increase defects and reduce integrity. |
| Initial temperature | Preheating softens fibers for smoother cuts and better bonding. Low temperatures cause rigidity and defects. |
| Variable | Impact on Quality |
|---|---|
| Temperature | Optimal drying temperatures remove moisture effectively, preventing defects like warping and splitting. Excessive heat causes fiber degradation, while low temperatures may leave residual moisture. |
| Initial humidity | High moisture levels cause uneven drying, while low moisture content leads to rapid drying, damaging fibers and weakening adhesion. Optimal moisture content ensures uniform drying and reduces defects. |
| Vent layout | Proper veneer arrangement ensures uniform airflow and heat distribution, reducing defects. Improper layout causes uneven drying, leading to compromised structural integrity and visual quality. |
| Feed rate | An optimal feed rate ensures consistent airflow and temperature, preventing defects. Too high a rate leads to insufficient drying, while too slow a rate causes over-drying and fiber degradation. |
| Air speed | Proper air speed ensures efficient moisture removal and uniform drying, reducing defects. Excessive air speed causes fiber damage, while insufficient air speed leads to uneven drying and structural issues. |
| Variable | Impact on Quality |
|---|---|
| Adhesive flow | Ensures proper penetration into wood fibers, improving mechanical strength. Insufficient flow weakens bonds and risks delamination; excessive flow causes uneven glue distribution and reduced panel strength [9]. |
| Sheet metal temperature | Low temperatures hinder adhesive flow and penetration, weakening bonds. High temperatures cause premature curing, leading to uneven distribution and reduced adhesion strength [10]. |
| Assembly time | Short times prevent proper adhesive wetting, weakening bonds, while long times cause premature drying, reducing effectiveness. Optimal timing ensures strong bonds and structural integrity [9]. |
| Open timeout | Short open times limit adhesive spread, while long times cause premature drying, weakening bonds. Proper timing ensures effective adhesion [11]. |
| Relative humidity | High humidity weakens bonds and risks delamination, while low humidity causes rapid adhesive drying, reducing fiber penetration. Optimal control improves durability [10]. |
| Room temperature | Low temperatures hinder curing, weakening bonds, while high temperatures accelerate curing, reducing working time and causing uneven distribution. Optimal temperature ensures quality adhesion [11]. |
| Variable | Impact on Quality |
|---|---|
| Pre-pressing time | Adequate pre-pressing time ensures even adhesive distribution. Too little or too much time can weaken bonds [9]. |
| Open wait time | A short open wait time prevents tack development, while long wait causes premature drying, increasing delamination risk [10]. |
| Closed wait time | A short-closed wait time leads to uneven adhesive distribution; long wait causes premature setting, reducing effectiveness [9]. |
| Press cycle time | Insufficient press time can result in incomplete adhesive curing, leading to weak bonds. Excessive press time can cause over-compression, reducing panel thickness and affecting mechanical properties [11]. |
| Press cycle by pressure | Adequate pressure ensures proper adhesive flow and bonding between layers. Insufficient pressure may lead to weak adhesion, while excessive pressure can damage the veneers, compromising structural integrity [10]. |
| Dish position | Proper dish positioning ensures even pressure distribution across the assembly. Misalignment can lead to uneven pressure application, resulting in defects such as warping, delamination, or reduced structural integrity [10]. |
| Plate temperature | Optimal temperature activates adhesive. Low temperatures hinder viscosity; high temperatures degrade adhesive [11]. |
| Pressing pressure | Adequate pressure ensures uniform contact and optimal adhesive distribution; excessive pressure damages veneers [11]. |
| Actual thickness of board in press | Proper thickness ensures even pressure distribution for optimal adhesion. If the board is too thick, it may not receive enough pressure, causing weak bonding. If too thin, excessive pressure can damage veneers or result in uneven adhesive curing [10]. |
| Nominal thickness | Maintaining the specified nominal thickness ensures uniform pressure distribution during pressing, while variations can lead to weak joints and uneven adhesive curing, affecting visual quality [11]. |
| Post-pressing thickness | Post-pressing thickness must meet specified standards to ensure dimensional stability. Inadequate thickness can lead to warping or weak joints, compromising durability and bond strength [11]. |
| Variable | Abbreviation | Units | Subprocess |
|---|---|---|---|
| Maceration temperature | MT | °C | Maceration |
| Maceration time | Mt | h | Maceration |
| Rotation speed | Rs1 and Rs2 | rpm | Peeling |
| Knife angle | Ka1 and Ka2 | ° | Peeling |
| Feed rate | Fr1 and Fr2 | m/min | Peeling |
| Mantle temperature | MT1 and MT2 | °C | Peeling |
| Horizontal opening of the lathe | Ho1 and Ho2 | mm | Peeling |
| Linear meters veneer produced | Lm1 and Lm2 | m | Peeling |
| Log diameter | Lg1 and Lg2 | cm | Peeling |
| Nominal thickness of veneer | Nt1 and Nt2 | mm | Peeling |
| Drying temperature | DT151, DT152, DT153, DT181, DT182, DT183, DT241, DT242 and DT243 | °C | Drying |
| Moisture veneer | MV151, MV152, MV153, MV181, MV182, MV183, MV241, MV242 and MV243 | % | Drying |
| Vapor pressure | VP151, VP152, VP153, VP181, VP182, VP183, VP241, VP242 and VP243 | bar | Drying |
| Dryer speed | Ds24 | m/s | Drying |
| Steam inlet temperature | SiT24 | °C | Drying |
| Steam inlet pressure | Sip24 | °C | Drying |
| Vent opening | VO24 | % | Drying |
| TS | Maceration Time, h | Maceration Temperature °C | Rotation Speed Rs1, rpm | Knife Angle Ka1, ° | Feed Rate Fr1 | Mantle TemperatureMT1, °C | Horizontal Opening of the Lathe Ho1, mm | Log Diameter Lg1 cm | Nominal Thickness Nt1, mm |
|---|---|---|---|---|---|---|---|---|---|
| 2024-04-09 17:10:00 | 17.9 | 79.2 | 320 | 0.39 | 250 | 49 | −0.45 | 51.8 | 2.55 |
| 2024-04-09 17:15:00 | 17.9 | 78.9 | 320 | −0.5 | 250 | 49 | −0.45 | 51.8 | 2.55 |
| 2024-04-09 17:20:00 | 17.9 | 78.8 | 320 | −0.49 | 250 | 47 | −0.45 | 55.2 | 2.55 |
| Algorithm | Actual Label | Predicted Label | |
|---|---|---|---|
| 0 | 1 | ||
| kNN | 0 | 2493 | 362 |
| 1 | 647 | 605 | |
| SVM | 0 | 2791 | 64 |
| 1 | 993 | 259 | |
| RF | 0 | 2601 | 254 |
| 1 | 724 | 528 | |
| XGB | 0 | 2558 | 297 |
| 1 | 702 | 550 | |
| Logic | 0 | 2734 | 121 |
| 1 | 975 | 277 | |
| LASSO | 0 | 2757 | 98 |
| 1 | 1.009 | 243 | |
| Algorithm | Accuracy | Precision | Recall | F1-Score |
|---|---|---|---|---|
| KNN | 0.75 | 0.63 | 0.48 | 0.55 |
| SVM | 0.74 | 0.80 | 0.21 | 0.33 |
| RF | 0.76 | 0.68 | 0.42 | 0.52 |
| XGB | 0.76 | 0.65 | 0.44 | 0.52 |
| Logic | 0.73 | 0.22 | 0.34 | 0.34 |
| Lasso | 0.73 | 0.19 | 0.31 | 0.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Maldonado, M.; Gutiérrez, F.; Gallardo-Venegas, R.; Bustos-Avila, C.; Contreras, E.; Lagos, L. Machine Learning and Industrial Data for Veneer Quality Optimization in Plywood Manufacturing. Processes 2025, 13, 1229. https://doi.org/10.3390/pr13041229
Ramos-Maldonado M, Gutiérrez F, Gallardo-Venegas R, Bustos-Avila C, Contreras E, Lagos L. Machine Learning and Industrial Data for Veneer Quality Optimization in Plywood Manufacturing. Processes. 2025; 13(4):1229. https://doi.org/10.3390/pr13041229
Chicago/Turabian StyleRamos-Maldonado, Mario, Felipe Gutiérrez, Rodrigo Gallardo-Venegas, Cecilia Bustos-Avila, Eduardo Contreras, and Leandro Lagos. 2025. "Machine Learning and Industrial Data for Veneer Quality Optimization in Plywood Manufacturing" Processes 13, no. 4: 1229. https://doi.org/10.3390/pr13041229
APA StyleRamos-Maldonado, M., Gutiérrez, F., Gallardo-Venegas, R., Bustos-Avila, C., Contreras, E., & Lagos, L. (2025). Machine Learning and Industrial Data for Veneer Quality Optimization in Plywood Manufacturing. Processes, 13(4), 1229. https://doi.org/10.3390/pr13041229








