Closed-Loop Solar Tracking Control Strategy to Correct Drift in a CPV System Using Image Processing
Abstract
:1. Introduction
2. Methodology
2.1. Description of the Fresnel Tracking System
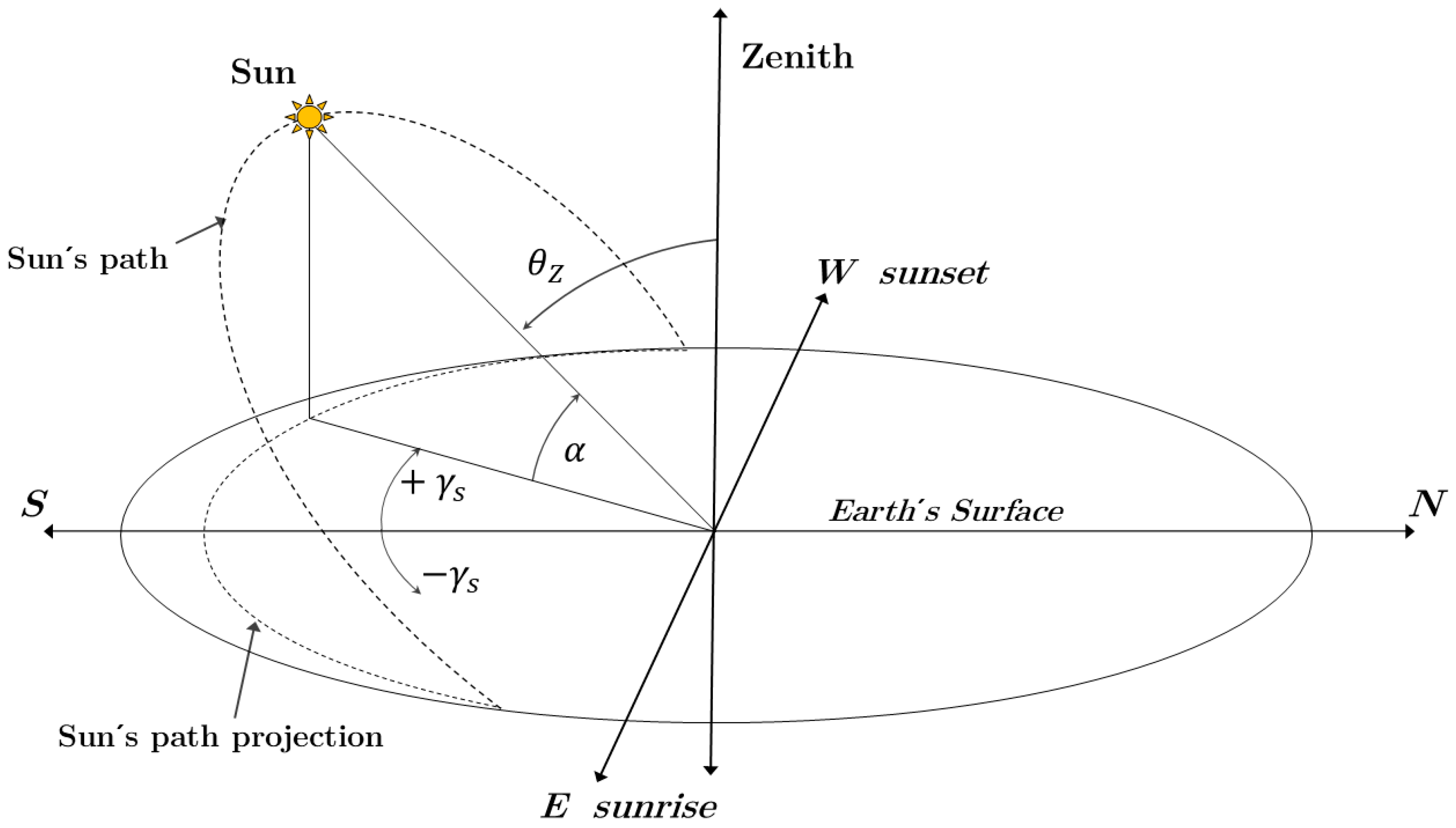
2.1.1. Solar Tracking Strategy
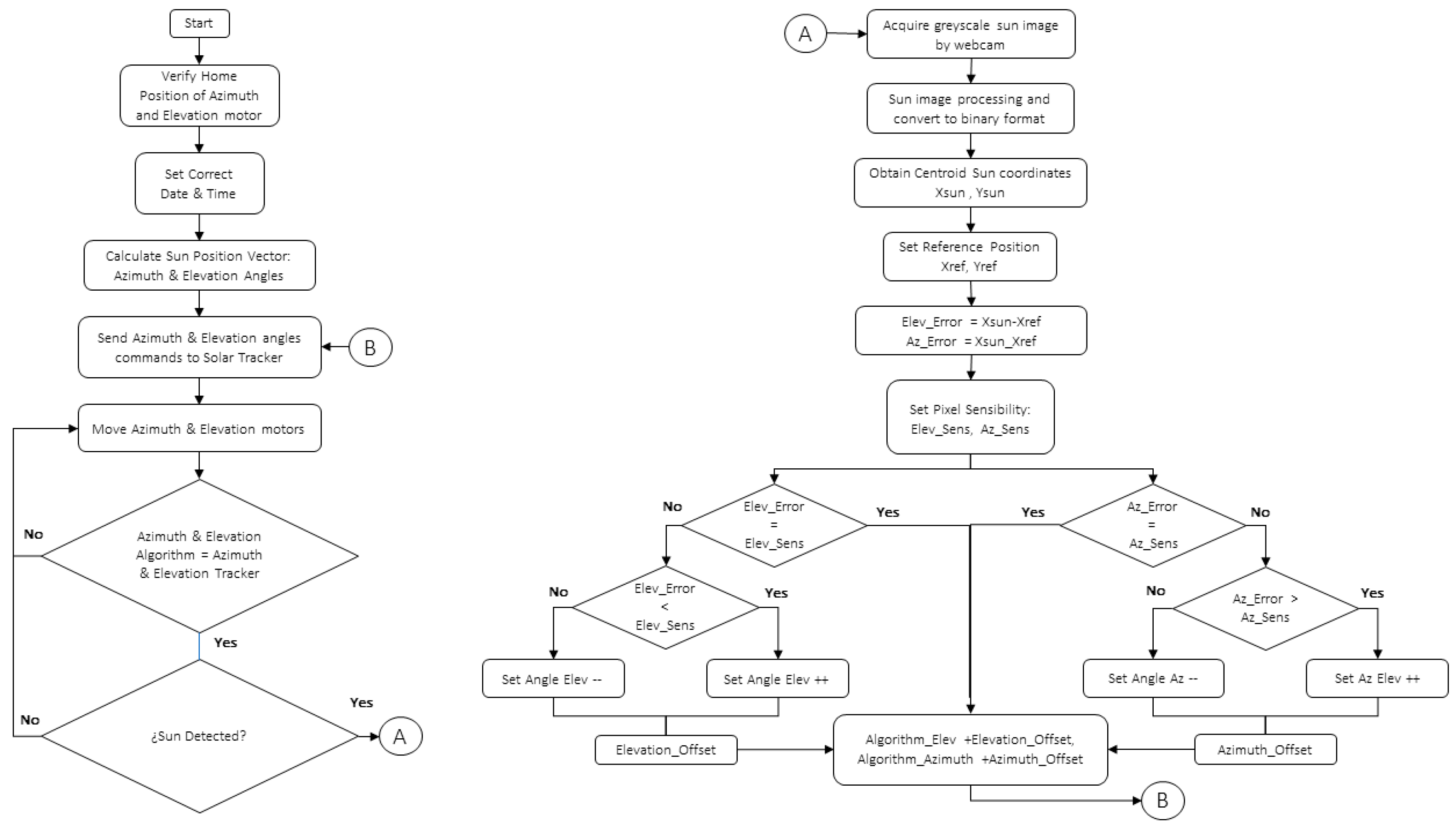
2.1.2. Solar Tracking Control System Configuration
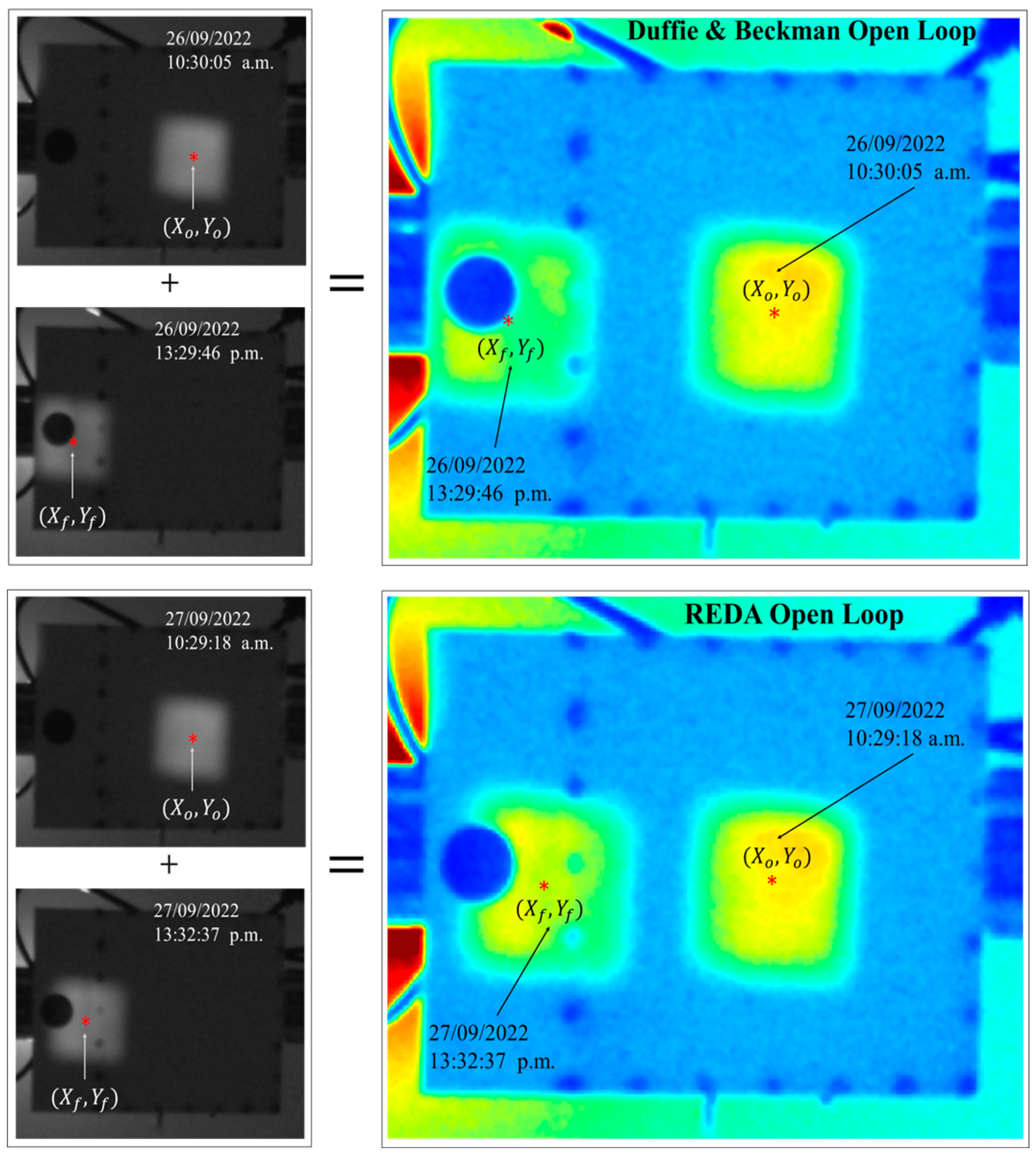
2.1.3. Experimental Design
2.1.4. Real-Time Digital Image Processing
Image Acquisition
Image Mask Function
Threshold Function
Centroid Function
Lookup Table Function
Shape Detection Function
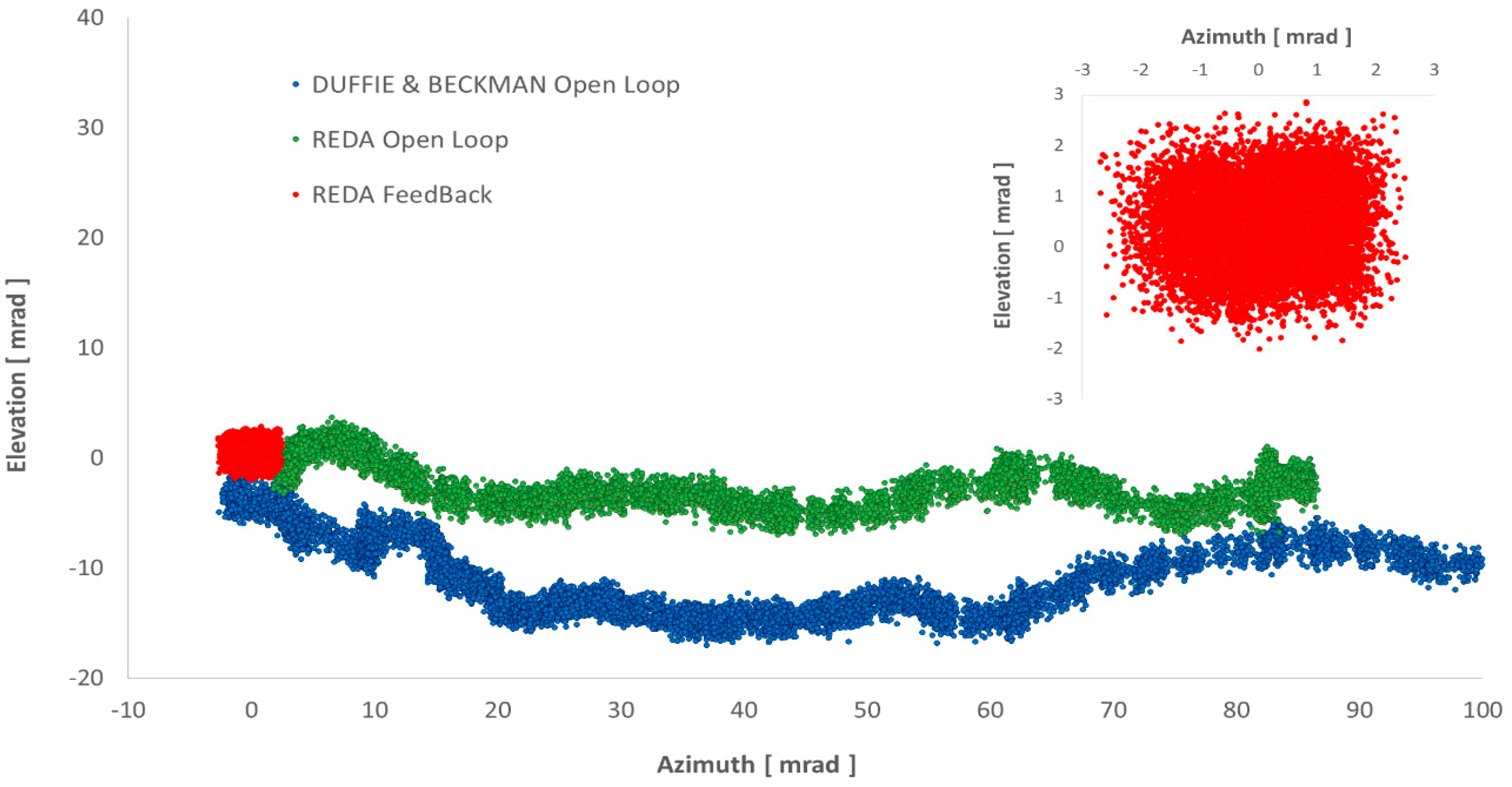
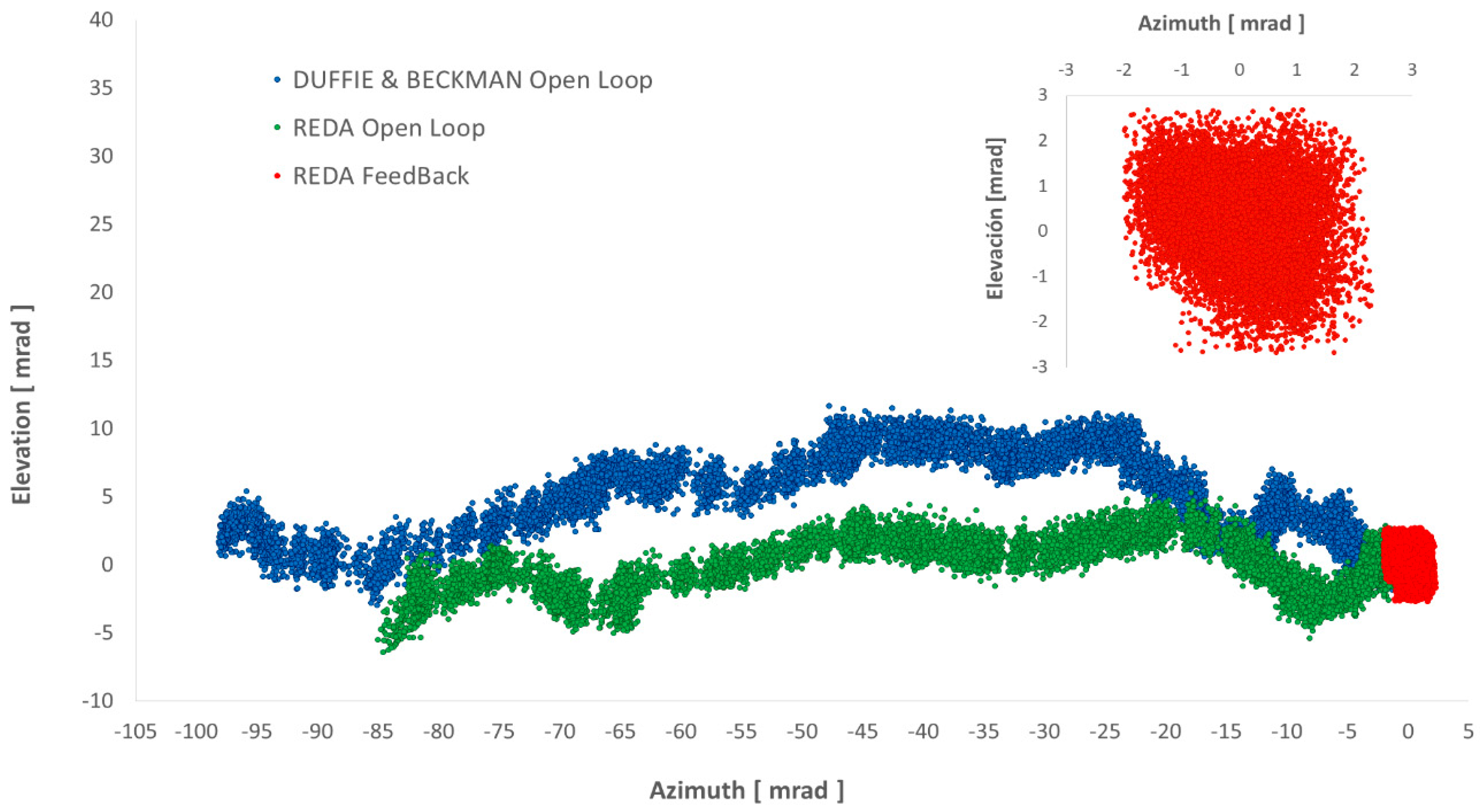
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| PV | Photovoltaic |
| CPV | Concentration photovoltaic |
| CNN | Convolutional Neural Networks |
| HCPV | High-concentration photovoltaic |
| FRESNEL | Focusing Retractile heliostat as Evaluator System for Non-imaging concentrated solar Electric generators |
| SAPOE | Semicircular arrays of the primary optical element |
| POE | Primary optical element |
| SEO | Second optical element |
| δ | Solar declination |
| w | Hour angle, ° |
| N | Julian day |
| Zenith angle, ° | |
| Azimuth angle, ° | |
| Elevation angle, ° | |
| Latitude | |
| Lloc | Local Longitude |
| Lstd | Standard Longitude |
| Pi constant | |
| NREL | National Renewable Energy Laboratory |
| SPA | Solar position algorithm |
| eSPA | Elevation angle SPA, ° |
| azSPA | Azimuth angle SPA, ° |
| Topocentric declination angle, ° | |
| Topocentric hour angle, ° | |
| Pixel element in matrix of an image | |
| Im | Bidirectional matrix of an image |
| Threshold value | |
| Pixel value of an image, 0-255 | |
| Binary image in threshold function | |
| Coordinate X of centroid image | |
| Coordinate Y of a centroid image | |
| D&B | Duffie & Beckman |
| Reference pixel in X | |
| Reference pixel in Y | |
| Final reference pixel in X | |
| Final reference pixel in Y |
References
- Carballo, J.A.; Bonilla, J.; Berenguel, M.; Fernández-Reche, J.; García, G. New approach for solar tracking systems based on computer vision, low cost hardware and deep learning. Renew. Energy 2019, 133, 1158–1166. [Google Scholar] [CrossRef]
- El Jaouhari, Z.; Zaz, Y.; Moughyt, S.; El Kadmiri, O.; El Kadmiri, Z. Dual-axis solar tracker design based on a digital hemispherical imager. J. Sol. Energy Eng. 2019, 141, 011001. [Google Scholar] [CrossRef]
- Nsengiyumva, W. Che International Renewable Energy Agency. Available online: https://www.irena.org/data (accessed on 27 February 2025).
- Cancro, C.; Palladino, V.; Borriello, A.; Romano, A.; Mongibello, L. Design of a novel hybrid concentrated photovoltaic-thermal system equipped with energy storage, optimized for use in residential contexts. Solar 2024, 4, 526–554. [Google Scholar] [CrossRef]
- Tilli, F. GSE/Giosuè Maugeri—RSE, National Survey Report of PV Power Applications in Italy. 2018. Available online: https://iea-pvps.org/wp-content/uploads/2020/01/NSR_Italy_2018.pdf (accessed on 27 February 2025).
- Nsengiyumva, W.; Chen, S.G.; Hu, L.; Chen, X. Recent advancements and challenges in Solar Tracking Systems (STS): A review. Renew. Sust. Energ. Rev. 2018, 81, 250–279. [Google Scholar] [CrossRef]
- Sidek, M.H.M.; Azis, N.; Hasan, W.Z.; Ab Kadir, M.Z.A.; Shafie, S.; Radzi, M.A.A. Automated positioning dual-axis solar tracking system with precision elevation and azimuth angle control. Energy 2017, 124, 160–170. [Google Scholar] [CrossRef]
- Foundation, C.; Lee, S.K.; Han, Y.H.; Lee, W.; Ryu, W. Foundation, Passive Solar Tracking System to Enhance Solar Cell Output. US20140238488A1 17 January 2017. [Google Scholar]
- Melo, A.G.; Filho, D.O.; De Oliveira Júnior, M.M.; Zolnier, S.; Ribeiro, A. Development of a closed and open loop solar tracker technology Acta Sci. Technol. 2017, 39, 177–183. [Google Scholar] [CrossRef]
- Chowdhury, M.E.H.; Khandakar, A.; Hossain, B.; Abouhasera, R. A low-cost closed-loop solar tracking system based on the sun position algorithm. J. Sens. 2019, 2019, 3681031. [Google Scholar] [CrossRef]
- González-Camarillo, H.; Calleja, R.; Pérez-Enciso, R.A.; Pérez-Rábago, C.; Estrada-Gasca, C.A. Corrección de la deriva en sistemas de seguimiento solar a través de control de lazo cerrado. In Proceedings of the XVII Congreso Ibérico y XIII Congreso Iberoamericano de Energía Solar, Online, 3–5 November 2020; pp. 601–609. [Google Scholar]
- Azizi, K.; Ghaffari, A. Design and manufacturing of a high-precision sun tracking system based on image processing. Int. J. Photoenergy 2013, 2013, 754549. [Google Scholar] [CrossRef]
- Pérez-Enciso, R.; Brito-Bazan, E.; Pérez-Rábago, C.A.; Arancibia-Bulnes, C.A.; Riveros-Rosas, D.; Estrada, C.A. Correction of the concentrated sunlight spot’s drift of the IER-UNAM’s solar furnace. Appl. Therm. Eng. 2015, 75, 1187–1191. [Google Scholar] [CrossRef]
- Rubio, F.R.; Ortega, M.G.; Gordillo, F.; López-Martínez, M. Application of new control strategy for sun tracking. Energ. Convers. Manag. 2007, 48, 2174–2184. [Google Scholar] [CrossRef]
- Oh, S.J.; Lee, Y.J.; Chen, J.K.; Kim, Y.M.; Lim, S.H.; Chun, W. Development of an embedded solar tracker for the enhancement of solar energy utilization. Int. J. Energy Res. 2012, 36, 249–258. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, Z.; Jin, P. Error analysis and auto correction of hybrid solar tracking system using photo sensors and orientation algorithm. Energy 2019, 182, 585–593. [Google Scholar] [CrossRef]
- Adrian, W.Y.W.; Durairajah, V.; Gobee, S. Autonomous dual axis solar tracking system using optical sensor and sun trajectory, in Lecture Notes in Electrical Engineering. In Proceedings of the 8th International Conference on Robotic, Vision, Signal Processing & Power Applications; Springer: Singapore, 2014; pp. 507–520. [Google Scholar] [CrossRef]
- Kumar, V.S.S. Automatic dual axis sun tracking system using LDR Sensor. Int. J. Curr. Eng. Technol. 2011, 4, 3214–3217. [Google Scholar] [CrossRef]
- Mishra, J.; Thakur, R.; Deep, A. Arduino based dual axis smart solar tracker. Int. J. Adv. Eng. Manag. Sci. 2017, 3, 532–535. [Google Scholar] [CrossRef]
- Gabe, I.J.; Bühler, A.; Chesini, D.; Frosi, F. Design and implementation of a low-cost dual-axes autonomous solar tracker. In Proceedings of the 8th International Symposium on Power Electronics for Distributed Generation System, Florianopolis, Brazil, 17–20 April 2017. [Google Scholar]
- Jamroen, C.; Komkum, P.; Kohsri, S.; Himananto, W.; Panupintu, S.; Unkat, S. A low-cost dual-axis solar tracking system based on digital logic design: Design and implementation. Sustain. Energy Technolo. Assess. 2020, 37, 1000618. [Google Scholar] [CrossRef]
- Ahmed, R.; Oh, S.J.; Mehmood, M.U.; Kim, Y.; Jeon, G.; Joo Han, H.; Hoon Lim, S. Computer vision and photosensor based hybrid control strategy for a two-axis solar tracker—Daylighting application. Sol. Energy 2021, 224, 175–183. [Google Scholar] [CrossRef]
- Garcia-Gil, G.; Ramirez, J.M. Fish-eye camera and image processing for commanding a solar tracker. Heliyon 2019, 5, e01398. [Google Scholar] [CrossRef]
- Abdollahpour, M.; Golzarian, M.R.; Rohani, A.; Abootorabi Zarchi, H. Development of a machine vision dual-axis solar tracking system. Sol. Energy 2018, 169, 136–143. [Google Scholar] [CrossRef]
- Fuentes-Morales, R.F.; Diaz-Ponce, A.; Peña-Cruz, M.I.; Rodrigo, P.M.; Valentín-Coronado, L.M.; Martell-Chavez, F.; Pineda-Arellano, C.A. Control algorithms applied to active solar tracking systems: A review. Sol. Energy 2020, 212, 203–219. [Google Scholar] [CrossRef]
- Garrido, R.; Díaz, A. Cascade closed-loop control of solar trackers applied to HCPV systems. Renew. Energy 2016, 97, 689–696. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; Wiley: Hoboken, NJ, USA, 1980; Available online: http://eu.wiley.com/WileyCDA/WileyTitle/productCd-0470873663.html (accessed on 5 January 2013).
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Posada-Gómez, R.; Sandoval-González, O.O.; Martínez Sibaja, A.; Portillo-Rodríguez, O.; Alor-Hernández, G. Digital Image Processing Using LabView; InTech: Vienna, Austria, 2011. [Google Scholar] [CrossRef]





| Array | Section (m) | No. of Mirrors | Array | Section (m) | of Mirrors |
|---|---|---|---|---|---|
| 0 | 0.55 | 40 | 8 | 1.07 | 116 |
| 1 | 0.60 | 64 | 9 | 1.14 | 124 |
| 2 | 0.66 | 72 | 10 | 1.21 | 132 |
| 3 | 0.72 | 80 | 11 | 1.29 | 140 |
| 4 | 0.79 | 84 | 12 | 1.37 | 148 |
| 5 | 0.86 | 92 | 13 | 1.45 | 156 |
| 6 | 0.93 | 100 | 14 | 1.53 | 164 |
| 7 | 1.00 | 108 | 15 | 1.61 | 168 |
| Solar Axis Tracker | Displacement [mrad] | Displacement [°] | Displacement [m] |
|---|---|---|---|
| (a) Duffie & Beckman algorithm in open-loop | |||
| Azimuth | 100 | 5.71 | 0.1003 |
| Elevation | 15 | 0.84 | 0.0147 |
| (b) SPA algorithm in open-loop | |||
| Azimuth | 87 | 5 | 0.0879 |
| Elevation | 13 | 0.72 | 0.0127 |
| (c) SPA algorithm in closed-loop | |||
| Azimuth | 4 | 0.25 | 0.0043 |
| Elevation | 5 | 0.31 | 0.0054 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Camarillo, H.; Pérez-Rábago, C.A.; Calleja-Valdez, R.; Pérez-Enciso, R.A.; García-Gutiérrez, R.; Estrada-Gasca, C.A.; Galindo-Luna, Y.R. Closed-Loop Solar Tracking Control Strategy to Correct Drift in a CPV System Using Image Processing. Processes 2025, 13, 944. https://doi.org/10.3390/pr13040944
González-Camarillo H, Pérez-Rábago CA, Calleja-Valdez R, Pérez-Enciso RA, García-Gutiérrez R, Estrada-Gasca CA, Galindo-Luna YR. Closed-Loop Solar Tracking Control Strategy to Correct Drift in a CPV System Using Image Processing. Processes. 2025; 13(4):944. https://doi.org/10.3390/pr13040944
Chicago/Turabian StyleGonzález-Camarillo, Héctor, Carlos A. Pérez-Rábago, Ramiro Calleja-Valdez, Ricardo Arturo Pérez-Enciso, Rafael García-Gutiérrez, Claudio A. Estrada-Gasca, and Yuridiana R. Galindo-Luna. 2025. "Closed-Loop Solar Tracking Control Strategy to Correct Drift in a CPV System Using Image Processing" Processes 13, no. 4: 944. https://doi.org/10.3390/pr13040944
APA StyleGonzález-Camarillo, H., Pérez-Rábago, C. A., Calleja-Valdez, R., Pérez-Enciso, R. A., García-Gutiérrez, R., Estrada-Gasca, C. A., & Galindo-Luna, Y. R. (2025). Closed-Loop Solar Tracking Control Strategy to Correct Drift in a CPV System Using Image Processing. Processes, 13(4), 944. https://doi.org/10.3390/pr13040944






