Determination and Analysis of Solubility of HC-290 (Propane) in [hmim][Tf2N]
Abstract
1. Introduction
2. Experimental Method
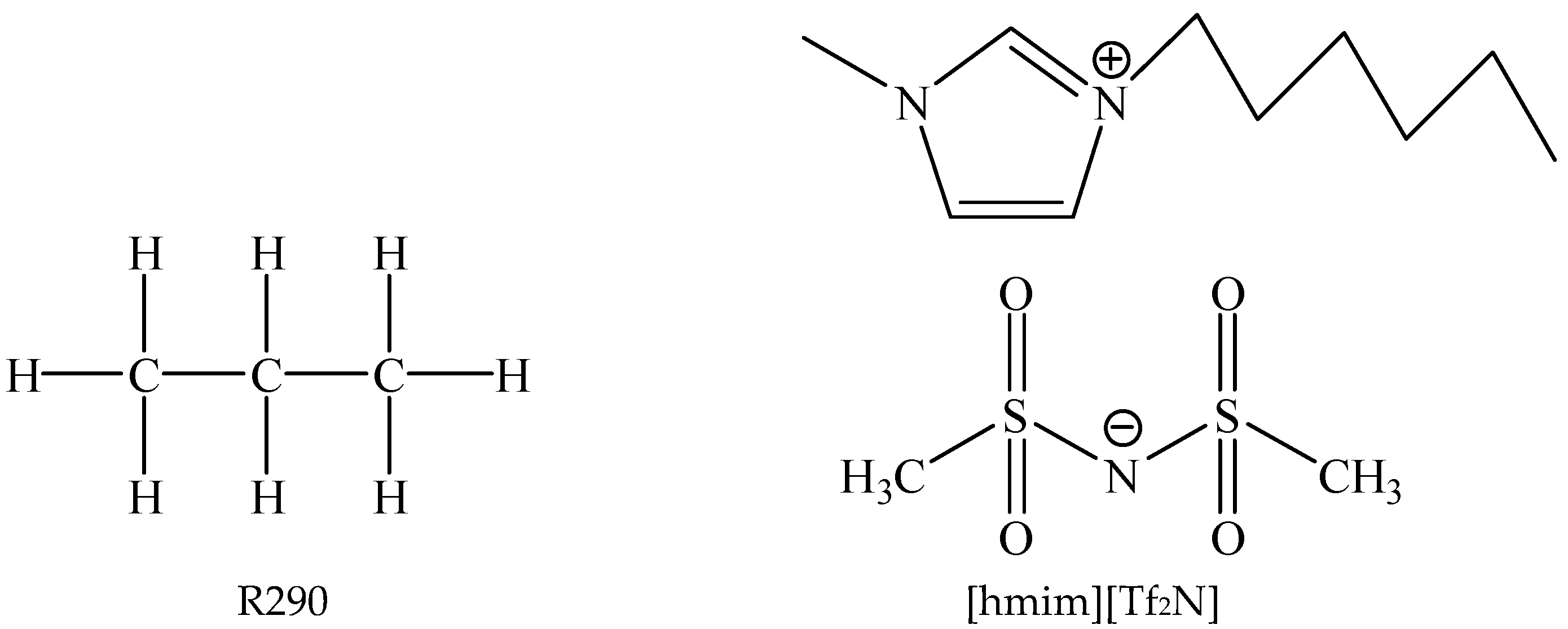
2.1. Experimental Samples
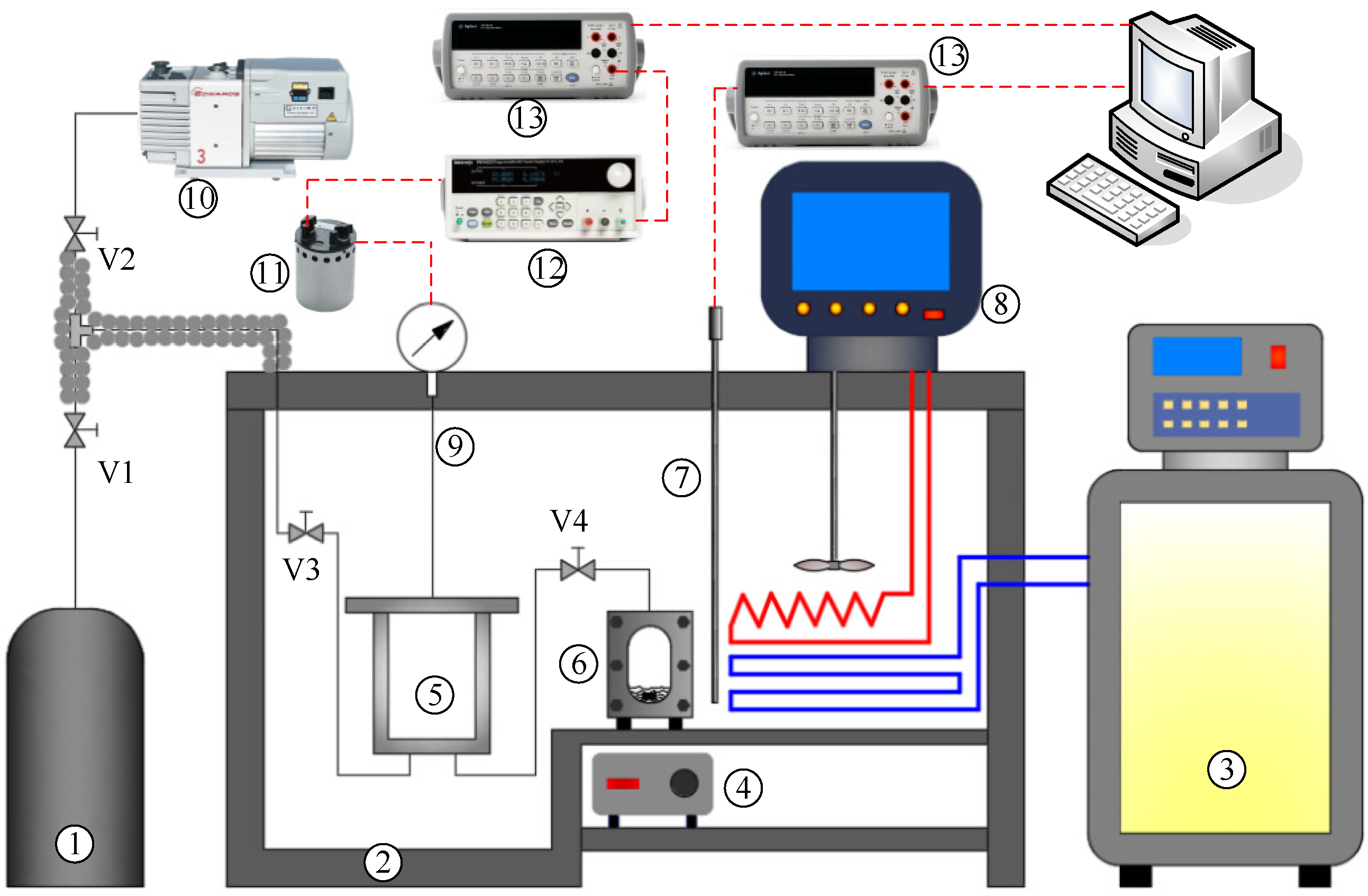
2.2. Experimental Setup
3. Experimental Results and Discussion
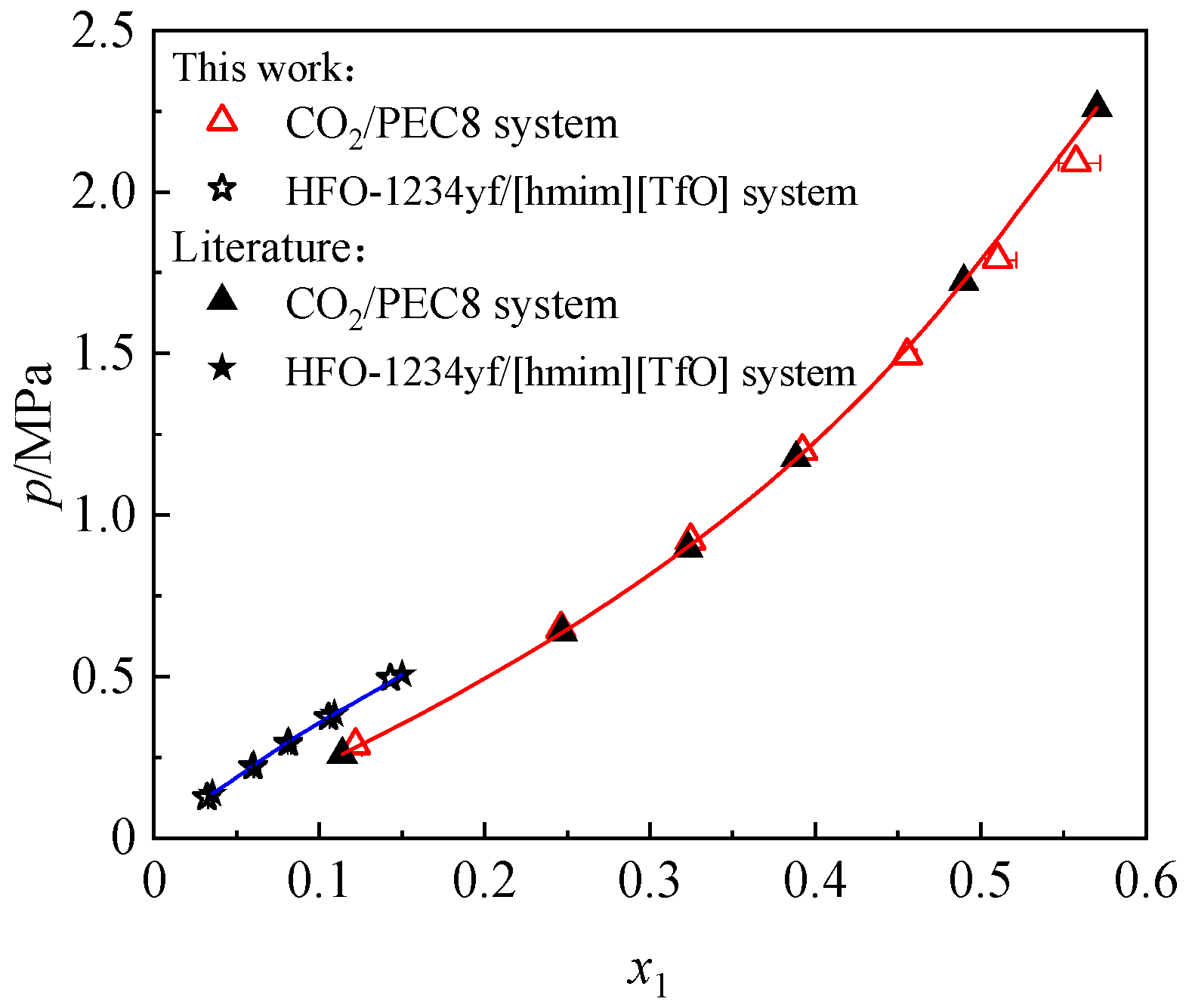
3.1. Experimental Data and Correlation
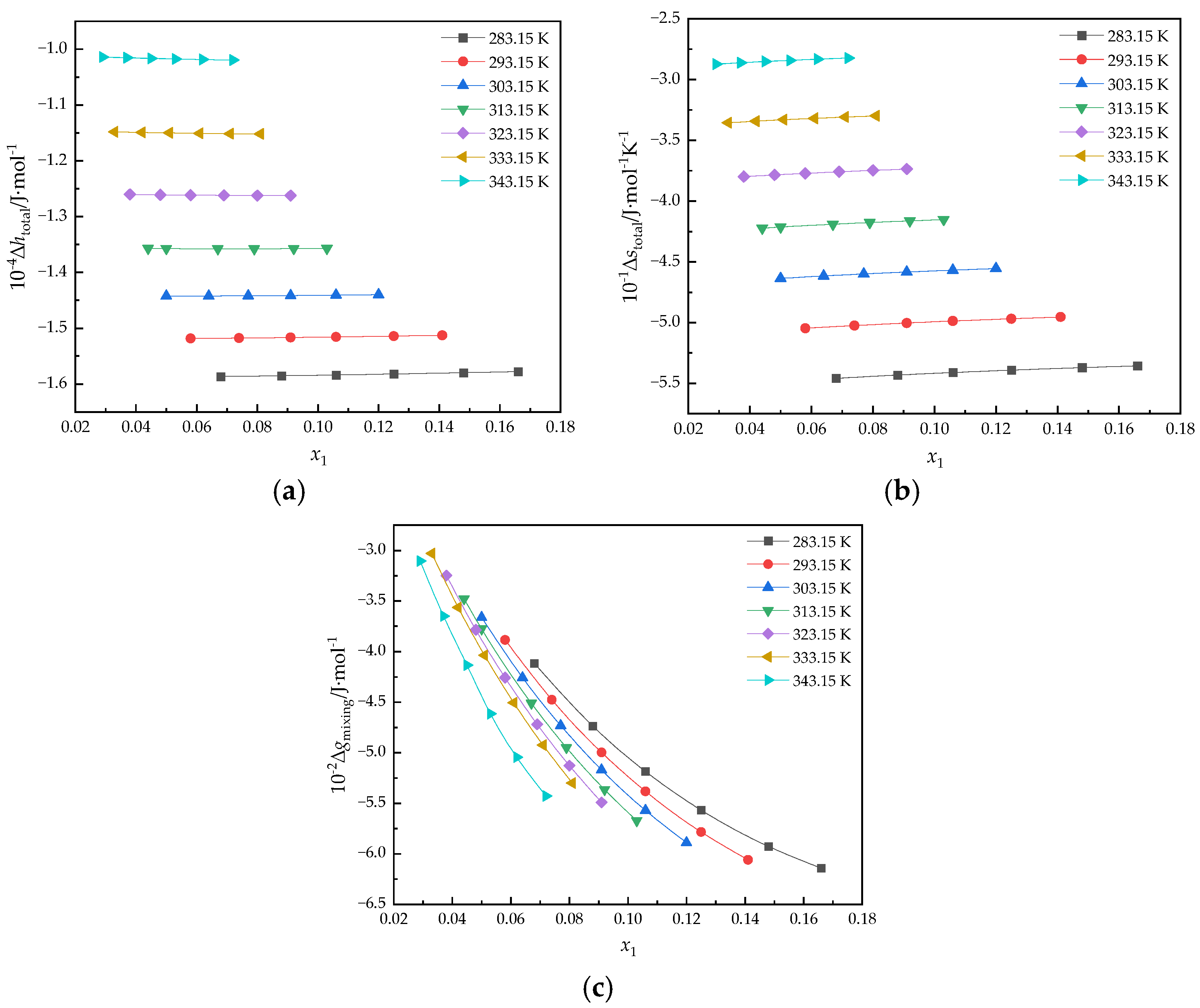
3.2. Derived Thermodynamic Properties of HC-290/[hmim][Tf2N]
3.3. Comparison of the Solubility of Different Refrigerants in [hmim][Tf2N]
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Srikhirin, P.; Aphornratana, S.; Chungpaibulpatana, S. A review of absorption refrigeration technologies. Renew. Sustain. Energy Rev. 2001, 5, 343–372. [Google Scholar]
- Wang, R.; Oliveira, R. Adsorption refrigeration—An efficient way to make good use of waste heat and solar energy. Prog. Energy Combust. Sci. 2006, 32, 424–458. [Google Scholar]
- Sun, J.; Fu, L.; Zhang, S. A review of working fluids of absorption cycles. Renew. Sustain. Energy Rev. 2012, 16, 1899–1906. [Google Scholar]
- Wang, K.; Abdelaziz, O.; Kisari, P.; Vineyard, E.A. State-of-the-art review on crystallization control technologies for water/LiBr absorption heat pumps. Int. J. Refrig. 2011, 34, 1325–1337. [Google Scholar]
- Earle, M.J.; Seddon, K.R. Ionic liquids. Green solvents for the future. Pure Appl. Chem. 2000, 72, 1391–1398. [Google Scholar]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H.; Watanabe, M.; Simon, P.; Angell, C.A. Energy applications of ionic liquids. Energy Env. Sci. 2014, 7, 232–250. [Google Scholar]
- Wu, W.; You, T.; Zhang, H.Y.; Li, X.T. Comparisons of different ionic liquids combined with trans-1,3,3,3-tetrafluoropropene (R1234ze(E)) as absorption working fluids. Int. J. Refrig. 2018, 88, 45–57. [Google Scholar]
- Park, S.; Choi, H.W.; Lee, J.W.; Cho, H.U.; Lee, N.S.; Kang, Y.T. Performance analysis of ionic liquids for simultaneous cooling and heating absorption system. Energy 2023, 271, 127005. [Google Scholar]
- Ren, W.; Scurto, A.M. Phase equilibria of imidazolium ionic liquids and the refrigerant gas, 1,1,1,2-tetrafluoroethane (R-134a). Fluid Phase Equilib. 2009, 286, 1–7. [Google Scholar]
- Liu, X.; He, M.; Lv, N.; Qi, X.; Su, C. Vapor−Liquid Equilibrium of Three Hydrofluorocarbons with [HMIM][Tf2N]. J. Chem. Eng. Data 2015, 60, 1354–1361. [Google Scholar]
- Liu, X.; Bai, L.; Liu, S.; He, M. Vapor–Liquid Equilibrium of R1234yf/[HMIM][Tf2N] and R1234ze(E)/[HMIM][Tf2N] Working Pairs for the Absorption Refrigeration Cycle. J. Chem. Eng. Data 2016, 61, 3952–3957. [Google Scholar] [CrossRef]
- He, M.; Pan, P.; Yang, F.; Wang, T.; Liu, X. Gaseous Absorption of trans-1-Chloro-3,3,3-trifluoropropene in Three Immidazolium-Based Ionic Liquids. J. Chem. Eng. Data 2018, 63, 1780–1788. [Google Scholar] [CrossRef]
- Liu, X.; Pan, P.; Yang, F.; He, M. Solubilities and diffusivities of R227ea, R236fa and R245fa in 1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide. J. Chem. Thermodyn. 2018, 123, 158–164. [Google Scholar] [CrossRef]
- Liu, X.; He, M.; Lv, N.; Qi, X.; Su, C. Solubilities of R-161 and R-143a in 1-Hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide. Fluid Phase Equilib. 2015, 388, 37–42. [Google Scholar] [CrossRef]
- Liu, X.; He, M.; Lv, N.; Qi, X.; Su, C. Solubilities of isobutane and cyclopropane in ionic liquids. J. Chem. Thermodyn. 2015, 88, 30–35. [Google Scholar] [CrossRef]
- Kumełan, J.; Pérez-Salado Kamps, Á.; Tuma, D.; Maurer, G. Solubility of the Single Gases Methane and Xenon in the Ionic Liquid [hmim][Tf2N]. Ind. Eng. Chem. Res. 2007, 46, 8236–8240. [Google Scholar] [CrossRef]
- Henni, N.; Henni, A.; Ibrahim, H. Selectivities of Carbon Dioxide over Ethane in Three Methylimidazolium-Based Ionic Liquids: Experimental Data and Modeling. Molecules 2024, 29, 4152. [Google Scholar] [CrossRef]
- Anderson, J.L.; Dixon, J.K.; Brennecke, J.F. Solubility of CO2, CH4, C2H6, C2H4, O2, and N2 in 1-Hexyl-3-methylpyridinium Bis(trifluoromethylsulfonyl)imide: Comparison to Other Ionic Liquids. Acc. Chem. Res. 2007, 40, 1208–1216. [Google Scholar] [CrossRef]
- Florusse, L.J.; Raeissi, S.; Peters, C.J. High-Pressure Phase Behavior of Ethane with 1-Hexyl-3-methylimidazolium Bis(trifluoromethylsulfonyl)imide. J. Chem. Eng. Data 2008, 53, 1283–1285. [Google Scholar] [CrossRef]
- Henni, N.; Henni, A.; Ibrahim, H. Solubility of carbon dioxide in promising methylimidazolium-based ionic liquids. Fluid Phase Equilib. 2023, 565, 113619. [Google Scholar] [CrossRef]
- Shokouhi, M.; Vahidi, M.; Neshati, K.; Zhalehrajabi, E. Diffusion Coefficient and Absorption of Carbonyl Sulfide in 1-Hexyl-3-methylimidazolium Bis (Trifluoromethyl) Sulfonylimide ([hmim][Tf2N]). J. Chem. Eng. Data 2023, 68, 586–600. [Google Scholar] [CrossRef]
- Yim, J.H.; Lim, J.S. CO2 solubility measurement in 1-hexyl-3-methylimidazolium ([HMIM]) cation based ionic liquids. Fluid Phase Equilib. 2013, 352, 67–74. [Google Scholar] [CrossRef]
- Kumełan, J.; Pérez-Salado Kamps, Á.; Tuma, D.; Maurer, G. Solubility of CO2 in the ionic liquid [hmim][Tf2N]. J. Chem. Thermodyn. 2006, 38, 1396–1401. [Google Scholar] [CrossRef]
- Aki, S.N.V.K.; Mellein, B.R.; Saurer, E.M.; Brennecke, J.F. High-Pressure Phase Behavior of Carbon Dioxide with Imidazolium-Based Ionic Liquids. J. Phys. Chem. B 2004, 108, 20355–20365. [Google Scholar] [CrossRef]
- Shiflett, M.B.; Yokozeki, A. Solubility of CO2 in Room Temperature Ionic Liquid [hmim][Tf2N]. J. Phys. Chem. B 2007, 111, 2070–2074. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Agrawal, A.; Saini, V.; Praveen Kumar, S.; Velkin, V.I.; Shcheklein, S.E. A domestic refrigerator’s potential of using hydrocarbon blends as refrigerants. J. Therm. Anal. Calorim. 2024, 149, 12803–12813. [Google Scholar] [CrossRef]
- Issa, A.B.; Liang, C.K.; Groll, E.A.; Ziviani, D. Residential heat pump and air conditioning systems with propane (R290) refrigerant: Technology review and future perspective. App. Therm. Eng. 2025, 266, 125560. [Google Scholar] [CrossRef]
- Al-Dadah, R.K.; Jackson, G.; Rezk, A. Solar powered vapor absorption system using propane and alkylated benzene AB300 oil. App. Therm. Eng. 2011, 31, 1936–1942. [Google Scholar] [CrossRef][Green Version]
- Liu, X.Y.; Lv, N.; Bai, L.H.; He, M.G. Solubilities of propane and cyclopropane in 1-hexyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate. Int. J. Refrig. 2016, 67, 69–76. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, J.; Wei, Q.M.; Wang, X.P. Solubility for propane and isobutane in [P66614]Cl from 278.15 to 348.15 K. J. Chem. Eng. Data 2021, 66, 1273–1279. [Google Scholar] [CrossRef]
- Safarov, J.; Kul, I.; Talibov, M.; Shahverdiyev, A.; Hassel, E. Vapor pressures and activity coefficients of methanol in binary mixtures with 1-hexyl-3-methylimidazolium bis(trifluoromethysulfony)imide. J. Chem. Eng. Data 2015, 60, 1648–1663. [Google Scholar]
- Wang, X.D.; Zhang, Y.H.; Zhi, H.Q.; Wang, X.P. Absorption separation of binary refrigerant blends using 1-butyl-3-methylimidazolium thiocyanate ionic liquid. J. Chem. Eng. Data 2025, 70, 398–407. [Google Scholar]
- Jia, X.C.; Du, Y.H.; Wang, X.P. Selective absorption of ionic liquids in separating R-1243zf or R-161 from refrigerant blends. J. Chem. Thermodyn. 2024, 196, 107307. [Google Scholar]
- Wang, X.P.; Jia, X.C.; Wang, D.B. Experimental investigation on the solubility of R290 in two mineral oils. Int. J. Refrig. 2021, 124, 13–19. [Google Scholar]
- Lemmon, E.W.; Bell, I.H.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP. Version 10.0; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019. [Google Scholar]
- Bich, W.; Cox, M.G.; Dybkaer, R.; Elster, C.; Estler, W.T.; Hibbert, B.; Imai, H.; Kool, W.; Michotte, C.; Nielsen, L.; et al. Revision of the ‘Guide to the Expression of Uncertainty in Measurement’. Metrologia 2012, 49, 702–705. [Google Scholar]
- Fedel, L.; Pernechele, F.; Bobbo, S.; Scattolini, M.; Stryjek, R. Solubility of carbon dioxide in pentaerythritol tetraoctanoate. Fluid Phase Equilib. 2009, 277, 55–60. [Google Scholar]
- Liu, X.Y.; Zheng, Y.; Bai, L.H.; He, M.G. Performance comparison of two absorption-compression hybrid refrigeration systems using R1234yf/ionic liquid as working pair. Energ. Convers. Manag. 2019, 181, 319–330. [Google Scholar]
- Vetere, A. The NRTL equation as a predictive tool for vapor–liquid equilibria. Fluid Phase Equilib. 2004, 218, 33–39. [Google Scholar]
- Pransnitz, J.M.; Lichtenthaler, R.N.; de Azevedo, E.G. Molecular Thermodynamics of Fluid Phase Equilibria, 3rd ed.; Prentice Hall PTR: Hoboken, NJ, USA, 1999. [Google Scholar]
- Krichevsky, I.R.; Kasarnovsky, J.S. Thermodynamical calculations of solubilities of nitrogen and hydrogen in water at high pressures. J. Am. Chem. Soc. 1935, 57, 2168–2171. [Google Scholar]
- Ji, X.; Adidharma, H. Thermodynamic modeling of CO2 solubility in ionic liquid with hetero segmented statistical associating fluid theory. Fluid Phase Equilib. 2010, 293, 141–150. [Google Scholar]



| Refrigerants | Authors | Years | T/K | p/MPa | Mole Fraction x1 |
|---|---|---|---|---|---|
| HFC-134a | Ren and Scurto [9] | 2009 | 298.15–343.15 | 0.042–1.878 | 0.0247–0.7642 |
| HFC-227ea | Liu et al. [13] | 2018 | 303.15–343.15 | 0.058–0.485 | 0.042–0.284 |
| HFC-236fa | Liu et al. [13] | 2018 | 303.15–343.15 | 0.030–0.315 | 0.046–0.279 |
| HFC-245fa | Liu et al. [13] | 2018 | 303.15–343.15 | 0.016–0.144 | 0.049–0.196 |
| HFC-143a | Liu et al. [14] | 2015 | 302.7–343.0 | 0.130–1.545 | 0.0434–0.3561 |
| HFC-125 | Liu et al. [10] | 2015 | 302.6–332.8 | 0.1091–0.9172 | 0.0576–0.3282 |
| HFC-152a | Liu et al. [10] | 2015 | 302.3–343.4 | 0.0376–0.3074 | 0.0573–0.2528 |
| HFC-161 | Liu et al. [14] | 2015 | 302.2–344.3 | 0.030–0.673 | 0.0305–0.3878 |
| HFC-32 | Liu et al. [10] | 2015 | 302.5–344.1 | 0.1144–1.2208 | 0.0923–0.4972 |
| HFO-1233zd(E) | He et al. [12] | 2018 | 303.12–343.17 | 0.009–0.130 | 0.010–0.113 |
| HFO-1234ze(E) | Liu et al. [11] | 2016 | 292.98–353.23 | 0.0497–0.6937 | 0.0228–0.3312 |
| HFO-1234yf | Liu et al. [11] | 2016 | 292.29–353.21 | 0.0993–0.9251 | 0.0376–0.3536 |
| HC-600a | Liu et al. [15] | 2015 | 303.2–343.5 | 0.0482–0.4524 | 0.014–0.103 |
| HC-50 | Kumelan et al. [16] | 2007 | 293.3–413.25 | 0.886–9.300 | 0.0632–0.5106 * |
| HC-170 | Henni et al. [17] | 2024 | 303.15–343.15 | 0.0199–1.3009 | 0.003–0.139 |
| HC-50 | Anderson et al. [18] | 2007 | 298.15–333.15 | 0.0202–0.988 | 0.00116–0.0246 |
| HC-170 | Florusse et al. [19] | 2008 | 293.19–368.40 | 0.388–13.070 | 0.0995–0.4016 |
| RC-270 | Liu et al. [15] | 2015 | 303.5–343.3 | 0.1473–1.1578 | 0.028–0.206 |
| CO2 | Henni et al. [20] | 2022 | 303.15–343.15 | 0.0195–1.4009 | 0.005–0.311 |
| CO2 | Shokouhi et al. [21] | 2023 | 313.15–353.15 | 0.265–0.843 | 0.053–0.155 |
| CO2 | Yim et al. [22] | 2013 | 303.15–373.15 | 0.42–45.28 | 0.165–0.824 |
| CO2 | Kumelan et al. [23] | 2006 | 293.15–413.2 | 0.601–9.911 | 0.2459–4.6574 * |
| CO2 | Aki et al. [24] | 2004 | 298.1–333.3 | 1.315–11.558 | 0.1993–0.7586 |
| CO2 | Shiflett et al. [25] | 2007 | 281.9–348.6 | 0.0089–1.9764 | 0.001–0.539 |
| Source of Uncertainty | Relative Value | Source of Uncertainty | Relative Value |
|---|---|---|---|
| u(ρ1) | 0.03% | u(m2) | 0.001% |
| u() | 0.01% | u(Vgc) | 0.1% |
| u(VIL) | 0.05% | u(Vec) | 0.1% |
| p/MPa | x1 | p/MPa | x1 | p/MPa | x1 | p/MPa | x1 |
|---|---|---|---|---|---|---|---|
| 283.15 K | 293.15 K | 303.15 K | 313.15 K | ||||
| 0.121 | 0.068 | 0.129 | 0.058 | 0.135 | 0.050 | 0.142 | 0.044 |
| 0.160 | 0.088 | 0.170 | 0.074 | 0.179 | 0.064 | 0.188 | 0.05 |
| 0.198 | 0.106 | 0.211 | 0.091 | 0.222 | 0.077 | 0.233 | 0.067 |
| 0.236 | 0.125 | 0.251 | 0.106 | 0.265 | 0.091 | 0.278 | 0.079 |
| 0.280 | 0.148 | 0.298 | 0.125 | 0.314 | 0.106 | 0.330 | 0.092 |
| 0.319 | 0.166 | 0.340 | 0.141 | 0.359 | 0.120 | 0.378 | 0.103 |
| 323.15 K | 333.15 K | 343.15 K | |||||
| 0.148 | 0.038 | 0.155 | 0.033 | 0.161 | 0.029 | ||
| 0.197 | 0.048 | 0.205 | 0.042 | 0.213 | 0.037 | ||
| 0.244 | 0.058 | 0.254 | 0.051 | 0.264 | 0.045 | ||
| 0.290 | 0.069 | 0.303 | 0.061 | 0.315 | 0.053 | ||
| 0.346 | 0.080 | 0.360 | 0.071 | 0.375 | 0.062 | ||
| 0.395 | 0.091 | 0.412 | 0.081 | 0.428 | 0.072 | ||
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| α | −0.0172 | A0 | 7.001 |
| τ12,0 | 17.726 | A1 | −1827 |
| τ12,1 | −0.0132 | B0 | −11,044 |
| τ12,2 | 1.0963 | B1 | 70.97 |
| τ21,0 | −23.0298 | B2 | −0.1087 |
| τ21,1 | 0.02296 | ||
| τ21,2 | −0.00000423 |
| T/K | x1 | ∆hcon | ∆scon | ∆hmixing | ∆gmixing | ∆smixing | ∆htotal | ∆stotal |
|---|---|---|---|---|---|---|---|---|
| /J∙mol−1 | /J∙mol−1∙K−1 | /J∙mol−1 | /J∙mol−1 | /J∙mol−1∙K−1 | /J∙mol−1 | /J∙mol−1∙K−1 | ||
| 283.15 | 0.068 | −15,887.91 | −56.11 | 21.37 | −411.64 | 1.53 | −15,866.54 | −54.58 |
| 283.15 | 0.088 | −15,887.91 | −56.11 | 35.15 | −473.60 | 1.80 | −15,852.75 | −54.32 |
| 283.15 | 0.106 | −15,887.91 | −56.11 | 49.75 | −518.50 | 2.01 | −15,838.15 | −54.11 |
| 283.15 | 0.125 | −15,887.91 | −56.11 | 67.07 | −556.78 | 2.20 | −15,820.84 | −53.91 |
| 283.15 | 0.148 | −15,887.91 | −56.11 | 90.17 | −592.70 | 2.41 | −15,797.73 | −53.70 |
| 283.15 | 0.166 | −15,887.91 | −56.11 | 109.56 | −614.12 | 2.56 | −15,778.35 | −53.56 |
| 293.15 | 0.058 | −15,184.07 | −51.80 | 1.62 | −388.41 | 1.33 | −15,182.45 | −50.46 |
| 293.15 | 0.074 | −15,184.07 | −51.80 | 8.16 | −447.58 | 1.55 | −15,175.91 | −50.24 |
| 293.15 | 0.091 | −15,184.07 | −51.80 | 17.43 | −499.74 | 1.76 | −15,166.64 | −50.03 |
| 293.15 | 0.106 | −15,184.07 | −51.80 | 27.38 | −538.19 | 1.93 | −15,156.69 | −49.87 |
| 293.15 | 0.125 | −15,184.07 | −51.80 | 42.05 | −578.38 | 2.12 | −15,142.02 | −49.68 |
| 293.15 | 0.141 | −15,184.07 | −51.80 | 55.95 | −605.91 | 2.26 | −15,128.12 | −49.54 |
| 303.15 | 0.05 | −14,407.91 | −47.52 | −14.70 | −366.20 | 1.16 | −14,422.61 | −46.36 |
| 303.15 | 0.064 | −14,407.91 | −47.52 | −13.39 | −425.78 | 1.36 | −14,421.31 | −46.16 |
| 303.15 | 0.077 | −14,407.91 | −47.52 | −10.38 | −473.13 | 1.53 | −14,418.29 | −46.00 |
| 303.15 | 0.091 | −14,407.91 | −47.52 | −5.37 | −517.00 | 1.69 | −14,413.28 | −45.83 |
| 303.15 | 0.106 | −14,407.91 | −47.52 | 1.84 | −557.06 | 1.84 | −14,406.07 | −45.68 |
| 303.15 | 0.12 | −14,407.91 | −47.52 | 10.12 | −588.88 | 1.98 | −14,397.79 | −45.55 |
| 313.15 | 0.044 | −13,541.35 | −43.24 | −28.54 | −347.83 | 1.02 | −13,569.89 | −42.22 |
| 313.15 | 0.05 | −13,541.35 | −43.24 | −30.32 | −377.55 | 1.11 | −13,571.66 | −42.13 |
| 313.15 | 0.067 | −13,541.35 | −43.24 | −32.93 | −451.02 | 1.34 | −13,574.27 | −41.90 |
| 313.15 | 0.079 | −13,541.35 | −43.24 | −32.76 | −494.96 | 1.48 | −13,574.11 | −41.76 |
| 313.15 | 0.092 | −13,541.35 | −43.24 | −30.87 | −536.45 | 1.61 | −13,572.22 | −41.63 |
| 313.15 | 0.103 | −13,541.35 | −43.24 | −27.98 | −567.26 | 1.72 | −13,569.33 | −41.52 |
| 323.15 | 0.038 | −12,562.33 | −38.87 | −39.87 | −324.78 | 0.88 | −12,602.20 | −37.99 |
| 323.15 | 0.048 | −12,562.33 | −38.87 | −46.53 | −378.42 | 1.03 | −12,608.86 | −37.85 |
| 323.15 | 0.058 | −12,562.33 | −38.87 | −51.76 | −425.83 | 1.16 | −12,614.09 | −37.72 |
| 323.15 | 0.069 | −12,562.33 | −38.87 | −55.94 | −471.99 | 1.29 | −12,618.27 | −37.59 |
| 323.15 | 0.08 | −12,562.33 | −38.87 | −58.59 | −512.83 | 1.41 | −12,620.91 | −37.47 |
| 323.15 | 0.091 | −12,562.33 | −38.87 | −59.79 | −549.06 | 1.51 | −12,622.12 | −37.36 |
| 333.15 | 0.033 | −11,431.60 | −34.31 | −49.13 | −302.99 | 0.76 | −11,480.74 | −33.55 |
| 333.15 | 0.042 | −11,431.60 | −34.31 | −59.12 | −356.24 | 0.89 | −11,490.73 | −33.42 |
| 333.15 | 0.051 | −11,431.60 | −34.31 | −67.78 | −403.63 | 1.01 | −11,499.38 | −33.31 |
| 333.15 | 0.061 | −11,431.60 | −34.31 | −75.90 | −450.60 | 1.12 | −11,507.50 | −33.19 |
| 333.15 | 0.071 | −11,431.60 | −34.31 | −82.52 | −492.50 | 1.23 | −11,514.13 | −33.08 |
| 333.15 | 0.081 | −11,431.60 | −34.31 | −87.74 | −530.03 | 1.33 | −11,519.34 | −32.99 |
| 343.15 | 0.029 | −10,082.14 | −29.38 | −57.03 | −310.39 | 0.66 | −10,139.17 | −28.72 |
| 343.15 | 0.037 | −10,082.14 | −29.38 | −69.77 | −364.90 | 0.77 | −10,151.91 | −28.61 |
| 343.15 | 0.045 | −10,082.14 | −29.38 | −81.31 | −413.40 | 0.88 | −10,163.46 | −28.51 |
| 343.15 | 0.053 | −10,082.14 | −29.38 | −91.70 | −461.48 | 0.97 | −10,173.85 | −28.42 |
| 343.15 | 0.062 | −10,082.14 | −29.38 | −102.07 | −504.39 | 1.06 | −10,184.21 | −28.32 |
| 343.15 | 0.072 | −10,082.14 | −29.38 | −112.02 | −542.84 | 1.16 | −10,194.16 | −28.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Shi, J.; Wang, X. Determination and Analysis of Solubility of HC-290 (Propane) in [hmim][Tf2N]. Processes 2025, 13, 945. https://doi.org/10.3390/pr13040945
Shi W, Shi J, Wang X. Determination and Analysis of Solubility of HC-290 (Propane) in [hmim][Tf2N]. Processes. 2025; 13(4):945. https://doi.org/10.3390/pr13040945
Chicago/Turabian StyleShi, Wei, Jianrong Shi, and Xiaopo Wang. 2025. "Determination and Analysis of Solubility of HC-290 (Propane) in [hmim][Tf2N]" Processes 13, no. 4: 945. https://doi.org/10.3390/pr13040945
APA StyleShi, W., Shi, J., & Wang, X. (2025). Determination and Analysis of Solubility of HC-290 (Propane) in [hmim][Tf2N]. Processes, 13(4), 945. https://doi.org/10.3390/pr13040945






