Terpene-Based Biofuel Additives (Citral, Limonene, and Linalool) with Chloroform: Experimental and Modeling Study of Volumetric and Transport Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Apparatus and Procedure
3. Results and Discussion
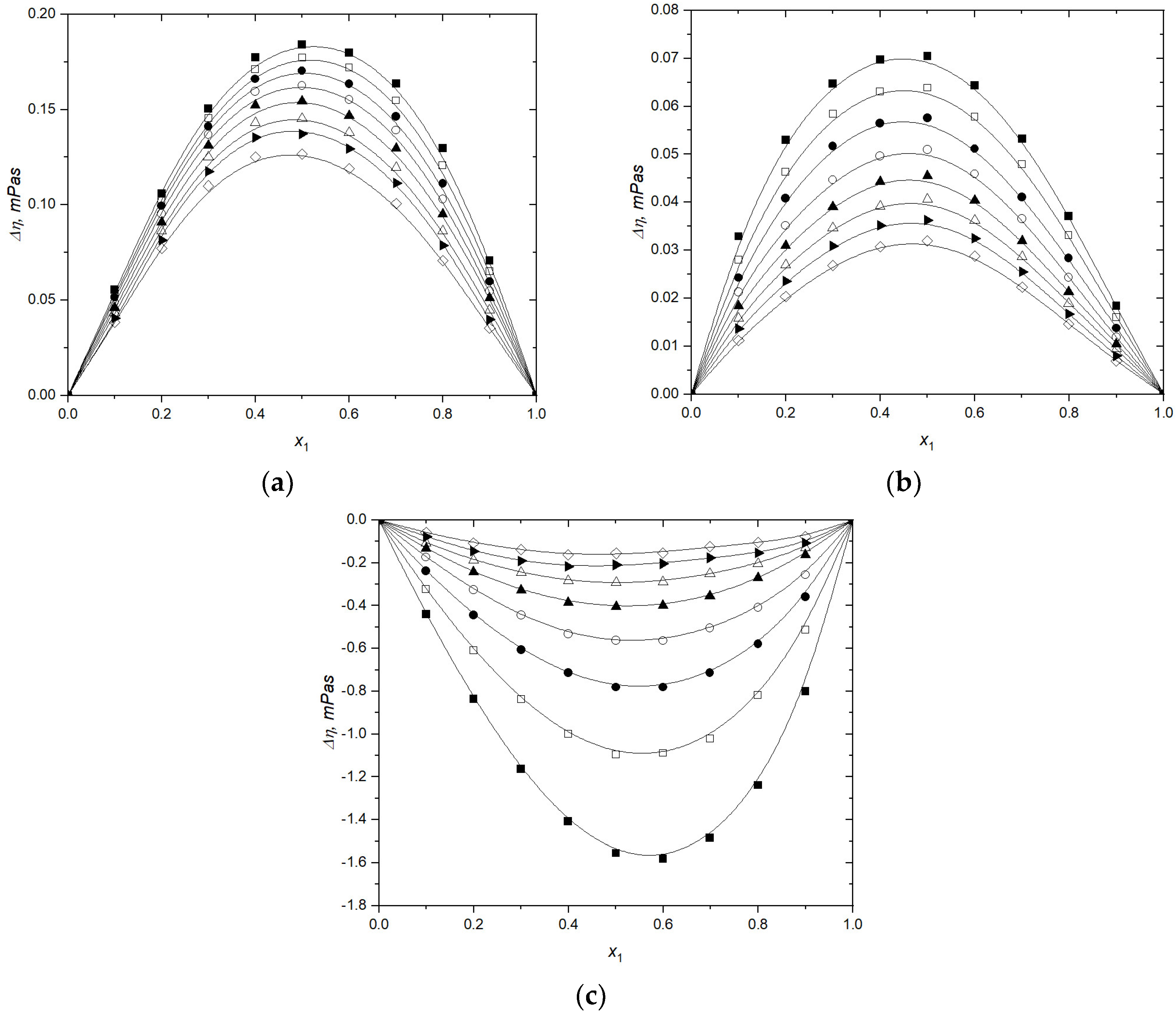
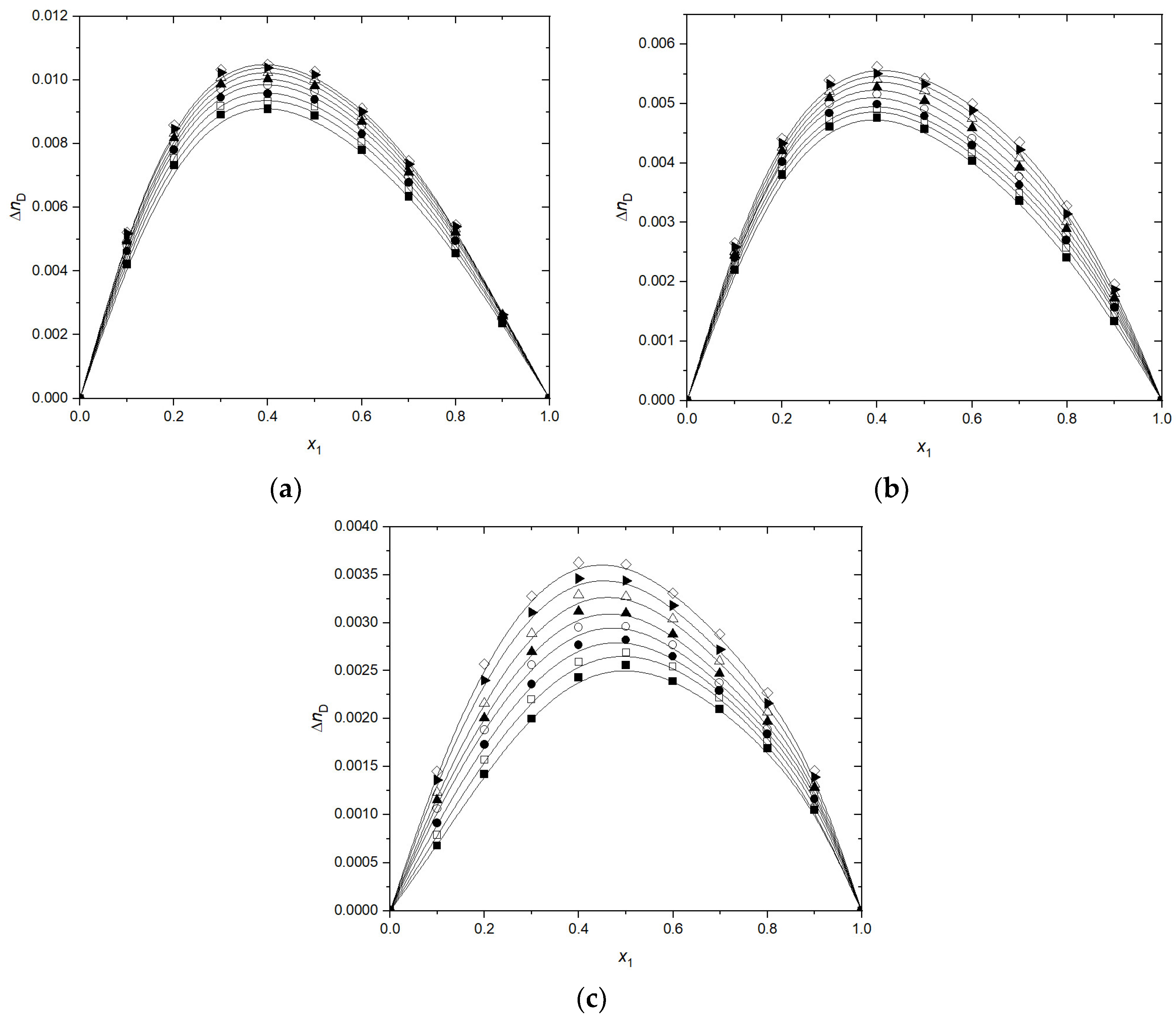
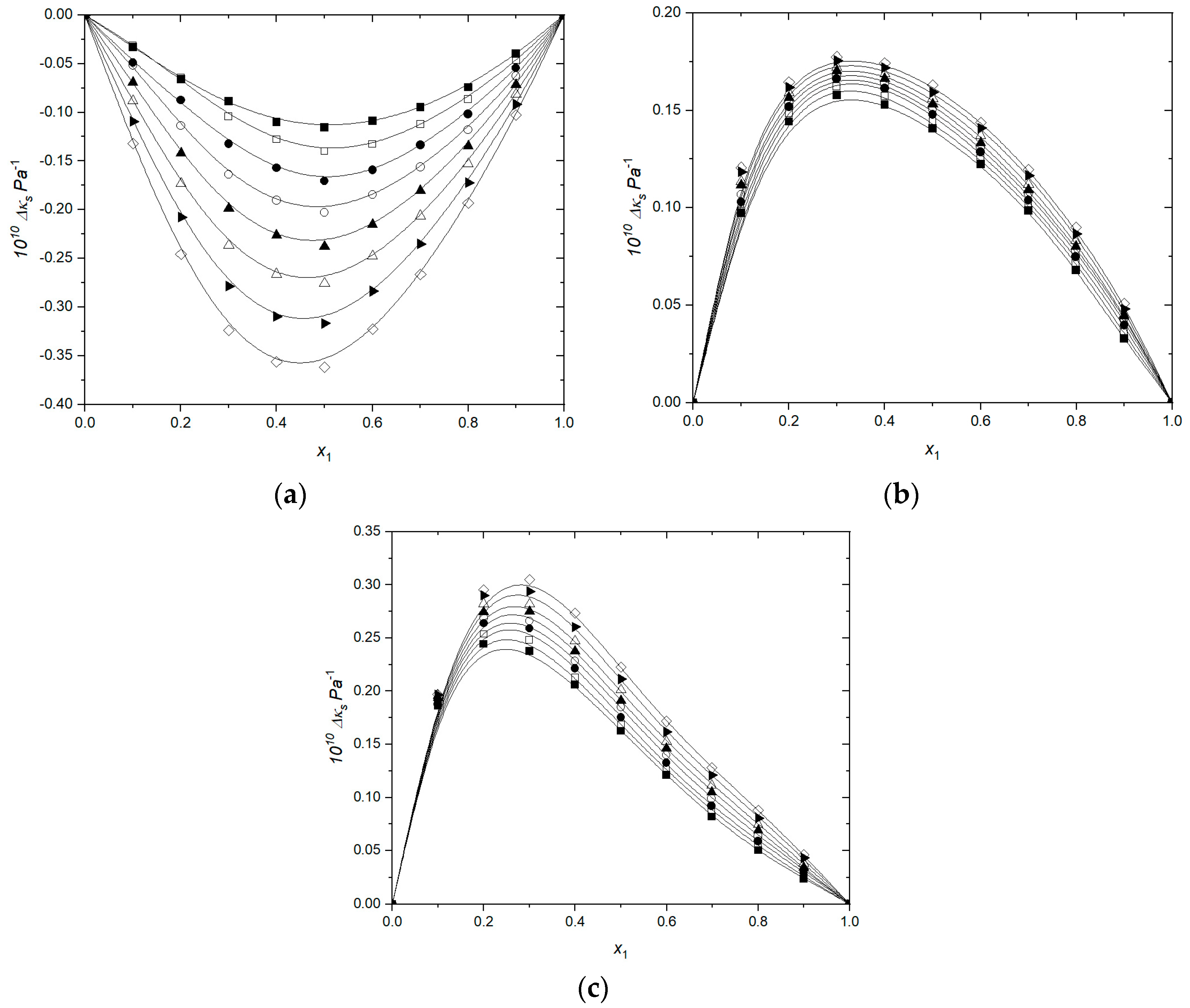
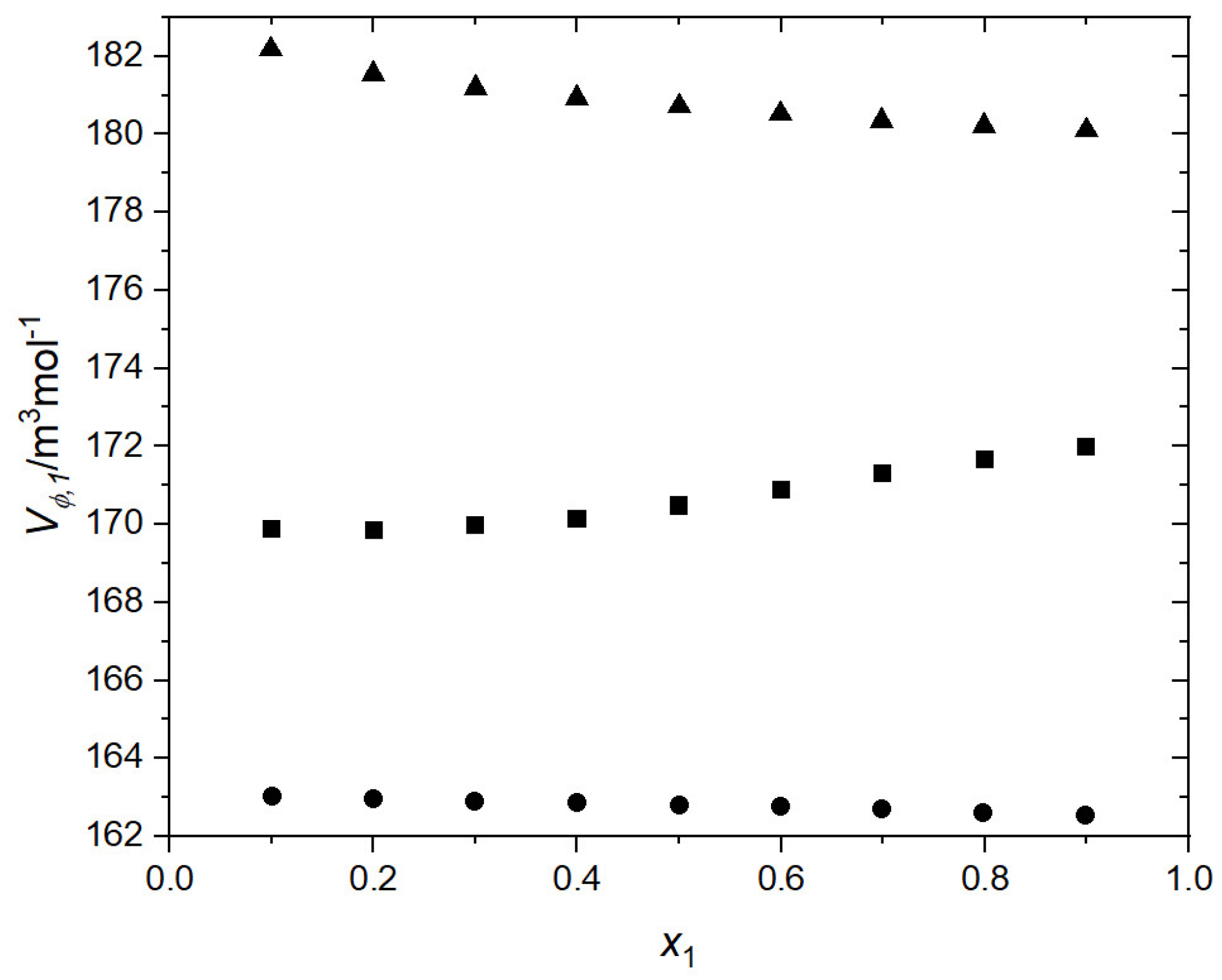
3.1. Volumetric and Transport Properties
3.2. Volumetric and Transport Properties Correlation by Heric–Brewer–Jouyban–Acree Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tracy, N.; Chen, D.; Crunkleton, D.; Price, G. Hydrogenated monoterpenes as diesel fuel additives. Fuel 2009, 88, 2238–2240. [Google Scholar] [CrossRef]
- Meyemans, H.; Baldwin, L.; Harvey, B. Low-Temperature Properties of Renewable High-Density Fuel Blends. Energy Fuels 2013, 27, 883–888. [Google Scholar] [CrossRef]
- Tisserand, R.; Young, R. Essential Oil Safety; Churchill Livingstone: London, UK, 2013. [Google Scholar]
- Ganjewala, D. Cymbopogon Essential oils: Compositions and bioactivities. Int. J. Essent. Oil Ther. 2009, 3, 56–65. [Google Scholar]
- Katsukawa, M.; Nakata, R.; Takizawa, Y.; Hori, K.; Takahashi, S.; Inoue, H. Citral, a component of lemongrass oil, activates PPAR α and γ suppresses COX-2 expression. Biochim. Biophys. Acta 2011, 1801, 1214–1220. [Google Scholar] [CrossRef] [PubMed]
- Saddiq, A.; Khayyat, S. Chemical and antimicrobial studies of monoterpene: Citral. Pestic. Biochem. Physiol. 2010, 98, 89–93. [Google Scholar] [CrossRef]
- Nazaroff, W.; Weschler, C. Cleaning products and air fresheners: Exposure to primary and secondary air pollutants. Atmos. Environ. 2004, 38, 2841–2865. [Google Scholar] [CrossRef]
- Filipsson, A.; Bard, J.; Karlsson, S. Limonene, 5th ed.; World Health Organization: Geneva, Switzerland, 1998; p. 32. [Google Scholar]
- Hirota, R.; Roger, N.; Nakamura, H.; Song, H.; Sawamura, M.; Suganuma, N. Anti-inflammatory effects of limonene from yuzu (Citrus junos Tanaka) essential oil on eosinophils. J. Food Sci. 2010, 75, H87–H92. [Google Scholar] [CrossRef]
- Roberto, D.; Micucci, P.; Sebastian, T.; Graciela, F.; Anesini, C. Antioxidant activity of limonene on normal murine lymphocytes: Relation to H2O2 modulation and cell proliferation. Basic Clin. Pharmacol. Toxicol. 2010, 106, 38–44. [Google Scholar] [CrossRef]
- Cheng, B.; Lin, C.; Yeh, T.; Cheng, S.; Chang, S. Potential source of S-(+) linalool from Cinnamomum osmophloeum ct. linalool leaf: Essential oil profile and enantiomeric purity. J. Agric. Food Chem. 2012, 60, 7623–7628. [Google Scholar] [CrossRef]
- Hussain, A.; Anwar, F.; Sherazi, S.; Przybylski, R. Chemical composition, antioxidant and antimicrobial activities of basil (Ocimum basilicum) essential oils depends on seasonal variations. Food Chem. 2008, 108, 986–995. [Google Scholar] [CrossRef]
- Bakkali, F.; Averbeck, S.; Averbeck, D.; Idaomar, M. Biological efects of essential oils—A review. Food Chem. Toxicol. 2008, 46, 446–475. [Google Scholar] [CrossRef] [PubMed]
- Silva, F.; Ferreira, S.; Duarte, A.; Mendonca, D.; Domingues, F. Antifungal activity of Coriandrum sativum essential oil, its mode of action against Candida species and potential synergism with amphotericin B. Phytomedicine 2011, 19, 42–47. [Google Scholar] [CrossRef]
- Guimarães, A.; Quintans, J.; Quintans-Júnior, L. Monoterpenes with analgesic activity—A systematic review. Phytother. Res. 2013, 27, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Yasar, A.; Ucuncu, O.; Gulec, C.; Inceer, H.; Ayaz, S.; Yayl, N. GC-MS Analysis of Chloroform Extracts in Flowers, Stems, and Roots of Tripleurospermum callosum. Pharm. Biol. 2005, 43, 108–112. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A. Algebraic representation of thermodynamic properties and the classification of solutions. Ind. Eng. Chem. 1948, 40, 345–348. [Google Scholar] [CrossRef]
- Grozdanic, N.; Radovic, I.; Knezevic-Stevanovic, A.; Kijevcanin, M. Volumetric properties of binary mixtures of tetrahydrofuran, dimethyl adipate, 1-butanol and 2-butanol from (288.15 to 323.15) K and modeling by Prigogine-Flory-Patterson (PFP) and Extended Real Association Solution (ERAS) models. J. Mol. Liq. 2021, 340, 117313. [Google Scholar] [CrossRef]
- Ilic-Pajic, J.; Radovic, I.; Grozdanic, N.; Stajic-Trosic, J.; Kijevcanin, M. Volumetric and thermodynamic properties of binary mixtures of p-cymene with α-pinene, limonene and citral at atmospheric pressure and temperatures up to 323.15 K. J. Mol. Liq. 2021, 344, 117486. [Google Scholar] [CrossRef]
- Clara, R.; Marigliano, A.G.; Solimo, H. Density, Viscosity, and Refractive Index in the Range (283.15 to 353.15) K and Vapor Pressure of r-Pinene, d-Limonene, (±)-Linalool, and Citral Over the Pressure Range 1.0 kPa Atmospheric Pressure. J. Chem. Eng. Data 2009, 54, 1087–1090. [Google Scholar] [CrossRef]
- Florido, P.M.; Andrade, I.M.G.; Capellini, M.C.; Carvalho, F.H.; Aracava, K.K.; Koshima, C.C.; Rodrigues, C.E.C.; Goncalves, C.B. Viscosities and densities of systems involved in the deterpenation of essential oils by liquid-liquid extraction: New UNIFAC-VISCO parameters. J. Chem. Thermodyn. 2014, 72, 152–160. [Google Scholar] [CrossRef]
- Sousa, A.T.; Nieto de Castro, C.A. Density of alpha-Pinene, beta-Pinene, Limonene, and Essence of Turpentine. Int. J. Thermophys. 1992, 13, 295–301. [Google Scholar] [CrossRef]
- Sevgili, L.; Sahin, S.; Kirbaslar, S.I. Liquid-Liquid Equilibria of (Limonene + Linalool + Ethylene Glycol or Diethylene Glycol or Triethylene Glycol or 1,2-Propylene Glycol) Ternary Systems. J. Chem. Eng. Data 2008, 53, 737–741. [Google Scholar] [CrossRef]
- Li, H.; Tamura, K. Ternary and Quaternary (Liquid + Liquid) Equilibria for (Water + Ethanol + α-Pinene, +β-Pinene, or +Limonene) and (Water + Ethanol + α-Pinene + Limonene) at the Temperature 298.15 K. J. Chem. Thermodyn. 2006, 38, 1036–1041. [Google Scholar] [CrossRef]
- Arce, A.; Marchiaro, A.; Soto, A. Liquid-Liquid Equilibria of Linalool+Ethanol+Water, Water+Ethanol+Limonene, and Limonene+Linalool+Water Systems. J. Solut. Chem. 2004, 33, 561–569. [Google Scholar] [CrossRef]
- Kodama, D.; Shinobu, Y.; Miyakoshi, Y.; Kato, M. Vapor-Liquid Equilibria for Ethanol + Limonene and 1-Propanol + Limonene. Netsu Bussei 2003, 17, 266–269. [Google Scholar] [CrossRef]
- Comelli, F.; Francesconi, R.; Castellari, C. Densities, Viscosities, and Excess Molar Enthalpies of Binary Mixtures Containing Essential Oils at (298.15 and 313.15) K. The (S)-(−)-Limonene + Cineole, (S)-(−)-Limonene + Linalool, and Cineole + Linalool Systems. J. Chem. Eng. Data 2001, 46, 868–872. [Google Scholar] [CrossRef]
- Comelli, F.; Ottani, S.; Francesconi, R.; Castellari, C. Densities, Viscosities, and Refractive Indices of Binary Mixtures Containing n-Hexane + Components of Pine Resins and Essential Oils at 298.15 K. J. Chem. Eng. Data 2002, 47, 93–97. [Google Scholar] [CrossRef]
- Garcia-Abarrio, S.M.; Viloria, L.; Haya, M.L.; Urieta, J.S.; Mainar, A.M. Thermophysical behavior of the mixture 3,7-dimethyl-1,6-octadien-3-ol with ethanol. Fluid Phase Equilibria 2011, 308, 78–89. [Google Scholar] [CrossRef]
- Smiljanic, J.; Kijevcanin, M.; Djordjevic, B.; Grozdanic, D.; Serbanovic, S. Densities and Excess Molar Volumes of the Ternary Mixture 2-Butanol +Chloroform + Benzene and Binary Mixtures 2-Butanol + Chloroform, or +Benzene over the Temperature Range (288.15 to 313.15) K. J. Chem. Eng. Data 2008, 53, 1965–1969. [Google Scholar] [CrossRef]
- Exarchos, N.; Tasioula-Margari, M.; Demetropoulos, I. Viscosities and Densities of Dilute Solutions of Glycerol Trioleate + Octane, + p-Xylene, + Toluene, and + Chloroform. J. Chem. Eng. Data 1995, 40, 567–571. [Google Scholar] [CrossRef]
- Clara, R.A.; Marigliano, A.C.G.; Solimo, H.N. Density, Viscosity, Vapor-liquid Equilibrium, Excess Molar Volume, Viscosity Deviation, and Their Correlations for the Chloroform+2-Butanone Binary System. J. Chem. Eng. Data 2006, 51, 1473–1478. [Google Scholar] [CrossRef]
- Clara, R.; Gomez-Marigliano, A.; Morales, D.; Solimo, H. Density, Viscosity, Vapor-Liquid Equilibrium, and Excess Molar Enthalpy of [Chloroform + Methyl tert-Butyl Ether]. J. Chem. Eng. Data 2010, 55, 5862–5867. [Google Scholar] [CrossRef]
- Dragoescu, D.; Gheorghe, D.; Bendova, M.; Wagner, Z. Speeds of sound, isentropic compressibilities and refractive indices for some binary mixtures of nitromethane with chloroalkane at temperatures from 298.15 to 318.15 K. Comparison with theories. Fluid Phase Equilibria 2015, 385, 105–119. [Google Scholar] [CrossRef]
- Mohammadi, D.; Hamzehloo, M. Densities, Viscosities, and Refractive Indices of Binary and Ternary Mixtures of Methanol, Acetone, and Chloroform at Temperatures from (298.15–318.15) K and Ambient Pressure. Fluid Phase Equilibria 2019, 483, 14–30. [Google Scholar] [CrossRef]
- Ma, D.; Zhu, C.; Fu, T.; Yuan, X.; Ma, Y. Volumetric and viscometric properties of binary and ternary mixtures of monoethanolamine, 2-(diethylamino) ethanol and water from (293.15 to 333.15) K. J. Chem. Thermodyn. 2019, 138, 350–365. [Google Scholar] [CrossRef]
- Poling, B.; Prausnitz, J.; O’Connell, J. The Property of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Grozdanić, N.; Simić, Z.; Kijevčanin, M.; Radović, I. High Pressure Densities and Derived Thermodynamic Properties of Pure (1R)-(+)-α-Pinene, (1S)-(−)-β-Pinene, and Linalool: Experiment and Modeling. J. Chem. Eng. Data 2024, 69, 854–863. [Google Scholar] [CrossRef]
- Pikkaralnen, L. Densities and Viscosities of Binary Mixtures of N,N-Dimethylacetamide with Aliphatic Alcohols. J. Chem. Eng. Data 1983, 28, 344–347. [Google Scholar] [CrossRef]
- Jouyban, A.; Khoubnasabjafari, M.; Vaez-Gharamaleki, Z.; Fekari, Z.; Acree, W.E., Jr. Calculation of the Viscosity of Binary Liquids at Various Temperatures Using Jouyban-Acree Model. Chem. Pharm. Bull. 2005, 53, 519–523. [Google Scholar] [CrossRef]
- Normazlan, W.W.; Sairi, N.; Alias, Y.; Udaiyappan, A.; Jouyban, A.; Khoubnasabjafari, M. Composition and Temperature Dependence of Density, Surface Tension, and Viscosity of EMIM DEP/MMIM DMP + Water + 1-Propanol/2-Propanol Ternary Mixtures and Their Mathematical Representation Using the Jouyban–Acree Model. J. Chem. Eng. Data 2014, 59, 2337–2348. [Google Scholar] [CrossRef]



| Chemical Name | Supplier | CAS Registry n0 | Molar Mass/g−1 | Initial Mass Fraction Purity |
|---|---|---|---|---|
| Citral (mixture of geranial and neral) | Acros Organics | 5392-40-5 | 152.24 | 0.95 |
| (+)-limonene | Acros Organics | 5989-27-5 | 136.24 | 0.96 |
| Linalool | Acros Organics | 78-70-6 | 154.25 | 0.97 |
| Chloroform | Fisher Scientific | 67-66-3 | 119.38 | 0.995 |
| Component | T b/K | 10−3 ρ c/kg·m−3 | η d/mPa·s | nD e | u f/m·s | ||||
|---|---|---|---|---|---|---|---|---|---|
| Exp. | Lit. | Exp. | Lit. | Exp. | Lit. | Exp. | Lit. | ||
| Citral | 293.15 | 0.88794 | 0.8884 [20] | 2.2809 | 2.225 [20] | 1.4879 | 1.48669 [20] | ||
| 298.15 | 0.88394 | 0.8847 [20] | 2.0282 | 2.111 [20] | 1.4854 | 1.48485 [20] | |||
| 303.15 | 0.87994 | 0.8804 [20] | 1.8328 | 1.807 [20] | 1.4829 | 1.48294 [20] | |||
| 313.15 | 0.87193 | 0.8723 [20] | 1.5285 | 1.502 [20] | 1.4781 | 1.47869 [20] | |||
| 323.15 | 0.86391 | 0.8643 [20] | 1.2955 | 1.274 [20] | 1.4732 | 1.47420 [20] | |||
| Limonene | 293.15 | 0.84255 | 0.8448 [20] 0.8402 [21] 0.8457 [22] | 1.4725 | 1.47274 [23] | ||||
| 298.15 | 0.83864 | 0.8410 [20] 0.8386 [21] 0.8422 [22] 0.8373 [24] 0.8372 [25] 0.8424 [26] | 0.8656 | 0.8599 [21] 0.8460 [27,28] | 1.4700 | 1.47027 [25] | |||
| 303.15 | 0.83472 | 0.8370 [20] 0.8377 [22] | |||||||
| 308.15 | 0.83079 | 0.8343 [22] | |||||||
| 313.15 | 0.82683 | 0.8290 [20] 0.8303 [22] | |||||||
| 323.15 | 0.81893 | 0.8211 [20] | |||||||
| Linalool | 293.15 | 0.86109 | 0.8618 [20] | 5.4116 | 5.53 [20] | 1.4615 | 1.46152 [20] 1.46272 [23] | ||
| 298.15 | 0.85687 | 0.8577 [20] 0.85809 [27] 0.85760 [28] | 4.3329 | 4.47 [20] 4.3493 [21] 4.4640 [27] 4.3810 [28] | 1.4590 | 1.45965 [20] 1.45970 [25] 1.4603 [27] 1.4605 [28] | 1314.3 | 1313.1 [29] | |
| 303.15 | 0.85263 | 0.8533 [20] | 3.5570 | 3.63 [20] | 1.4566 | 1.45665 [20] | |||
| 313.15 | 0.84412 | 0.8448 [20] 0.84543 [28] | 2.4966 | 2.541 [20] 2.552 [27] | 1.4516 | 1.45204 [20] 1.4535 [27] | 1259.8 | 1260.8 [29] | |
| 323.15 | 0.83548 | 0.8362 [20] | 1.8367 | 1.868 [20] | 1.4464 | 1.44738 [20] | |||
| Chloroform | 288.15 | 1.49787 | 1.49808 [30] | 0.6400 | 0.5962 [31] | ||||
| 293.15 | 1.48840 | 1.48864 [30] 1.4884 [32] | 0.6079 | 0.600 [33] | 1.4455 | 1.44589 [32] | |||
| 298.15 | 1.47889 | 1.47915 [30] | 0.5781 | 0.576 [33] | 983.0 | 984.42 [34] | |||
| 303.15 | 1.46933 | 1.46961 [30] 1.4694 [32] | 0.5520 | 0.552 [33] | 1.4392 | 1.43987 [32] | |||
| 308.15 | 1.45971 | 1.46003 [30] | 0.5268 | 0.533 [35] | 948.9 | 950.45 [34] | |||
| 313.15 | 1.45003 | 1.45041 [30] 1.4500 [32] | 0.5026 | 0.509 [33] | 1.4330 | 1.43386 [32] | |||
| 318.15 | 1.44028 | 0.4818 | 0.491 [33] | ||||||
| Function | T/K | A0 | A1 | A2 | σ | D/% |
|---|---|---|---|---|---|---|
| Citral (1) + chloroform (2) | ||||||
| 10−3 ρ/kg·m−3 | 288.15–323.15 | −67.0604 | 17.4571 | −8.4024 | 0.0006 | 0.0416 |
| η/mPa·s | 288.15–323.15 | 362.2231 | −162.6951 | 52.0481 | 0.0137 | 0.8713 |
| nD | 288.15–323.15 | 8.2593 | −3.4111 | 0.8729 | 0.0008 | 0.0409 |
| u/m·s−1 | 288.15–323.15 | 49.9569 | −7.6477 | −0.4393 | 4.4611 | 0.3033 |
| Limonene (1) + chloroform (2) | ||||||
| 10−3 ρ/kg·m−3 | 288.15–323.15 | −71.6699 | 17.1021 | −4.5862 | 0.0012 | 0.0926 |
| η/mPa·s | 288.15–323.15 | 105.6325 | −42.3770 | −1.1663 | 0.0062 | 0.6984 |
| nD | 288.15–323.15 | 4.3198 | −1.3223 | 0.9099 | 0.0005 | 0.0256 |
| u/m·s−1 | 288.15–323.15 | 23.3360 | −0.1104 | −5.0613 | 0.6580 | 0.0445 |
| Linalool (1) + chloroform (2) | ||||||
| 10−3 ρ/kg·m−3 | 288.15–323.15 | −88.2525 | 28.1124 | −9.7100 | 0.0017 | 0.1254 |
| η/mPa·s | 288.15–323.15 | 76.2210 | 15.4006 | −44.9597 | 0.0287 | 0.9696 |
| nD | 288.15–323.15 | 2.5822 | 0.0489 | 0.2538 | 0.0004 | 0.0240 |
| u/m·s−1 | 288.15–323.15 | 28.2242 | 7.4589 | −11.1498 | 0.4510 | 0.0319 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grozdanić, N.; Kijevčanin, M.; Radović, I. Terpene-Based Biofuel Additives (Citral, Limonene, and Linalool) with Chloroform: Experimental and Modeling Study of Volumetric and Transport Properties. Processes 2025, 13, 974. https://doi.org/10.3390/pr13040974
Grozdanić N, Kijevčanin M, Radović I. Terpene-Based Biofuel Additives (Citral, Limonene, and Linalool) with Chloroform: Experimental and Modeling Study of Volumetric and Transport Properties. Processes. 2025; 13(4):974. https://doi.org/10.3390/pr13040974
Chicago/Turabian StyleGrozdanić, Nikola, Mirjana Kijevčanin, and Ivona Radović. 2025. "Terpene-Based Biofuel Additives (Citral, Limonene, and Linalool) with Chloroform: Experimental and Modeling Study of Volumetric and Transport Properties" Processes 13, no. 4: 974. https://doi.org/10.3390/pr13040974
APA StyleGrozdanić, N., Kijevčanin, M., & Radović, I. (2025). Terpene-Based Biofuel Additives (Citral, Limonene, and Linalool) with Chloroform: Experimental and Modeling Study of Volumetric and Transport Properties. Processes, 13(4), 974. https://doi.org/10.3390/pr13040974







