Nonlinear Back-Calculation Anti-Windup Based on Operator Theory
Abstract
1. Introduction
- Nonlinear back-calculation anti-windup compensation based on operator theory is realized for nonlinear controllers.
- The proposed method is applied to ISMC, and its effectiveness is confirmed through simulations of tank system level control.
- The proposed method is applied to RCF, and its effectiveness is confirmed through simulations of tank system level control.
2. Preliminaries
2.1. Operator Definition
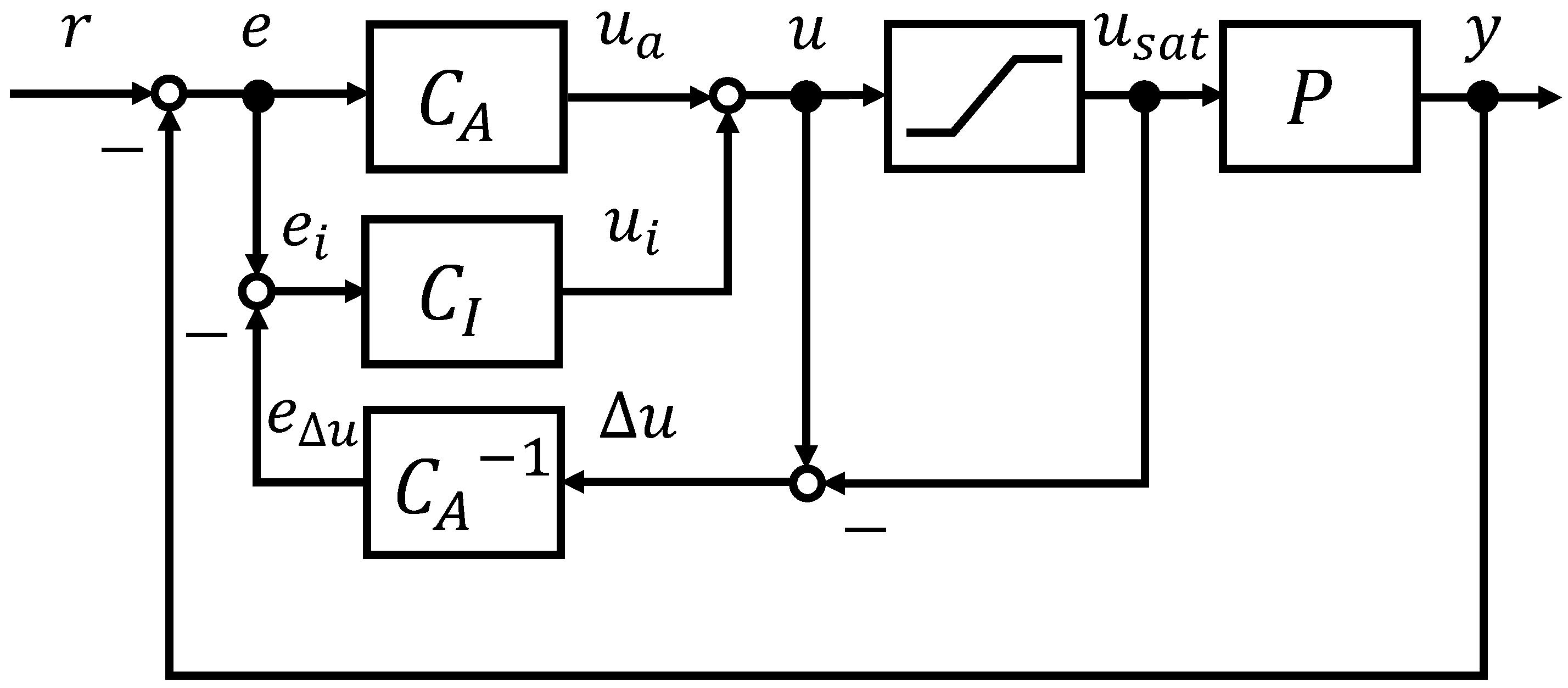
2.2. Back-Calculation Anti-Windup
3. Problem Statement
4. Main Results
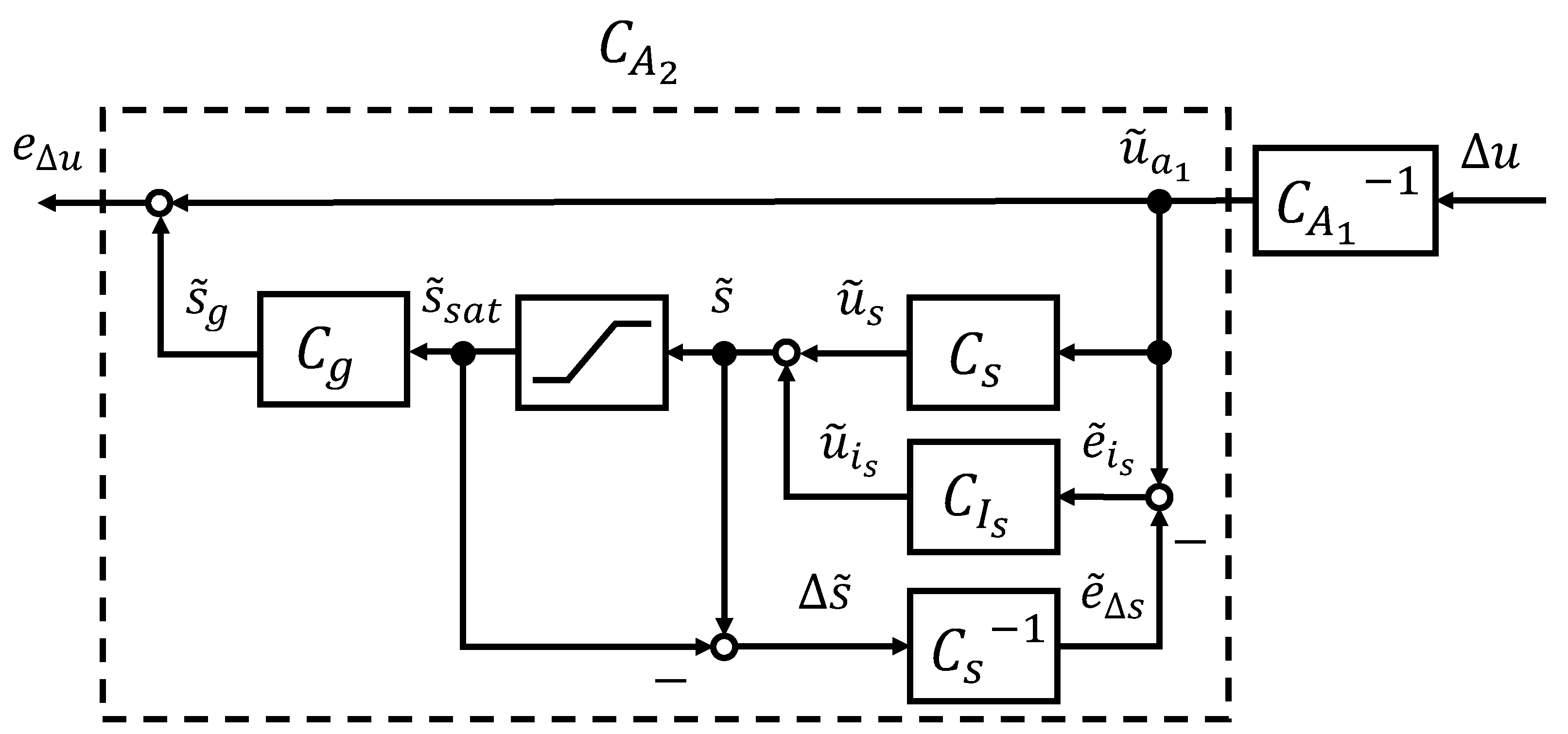
4.1. Nonlinear Back-Calculation Anti-Windup
4.2. Application to Integral Sliding Mode Control
4.3. Application to Right Coprime Factorization
5. Simulations
5.1. Simulations of Integral Sliding Mode Control
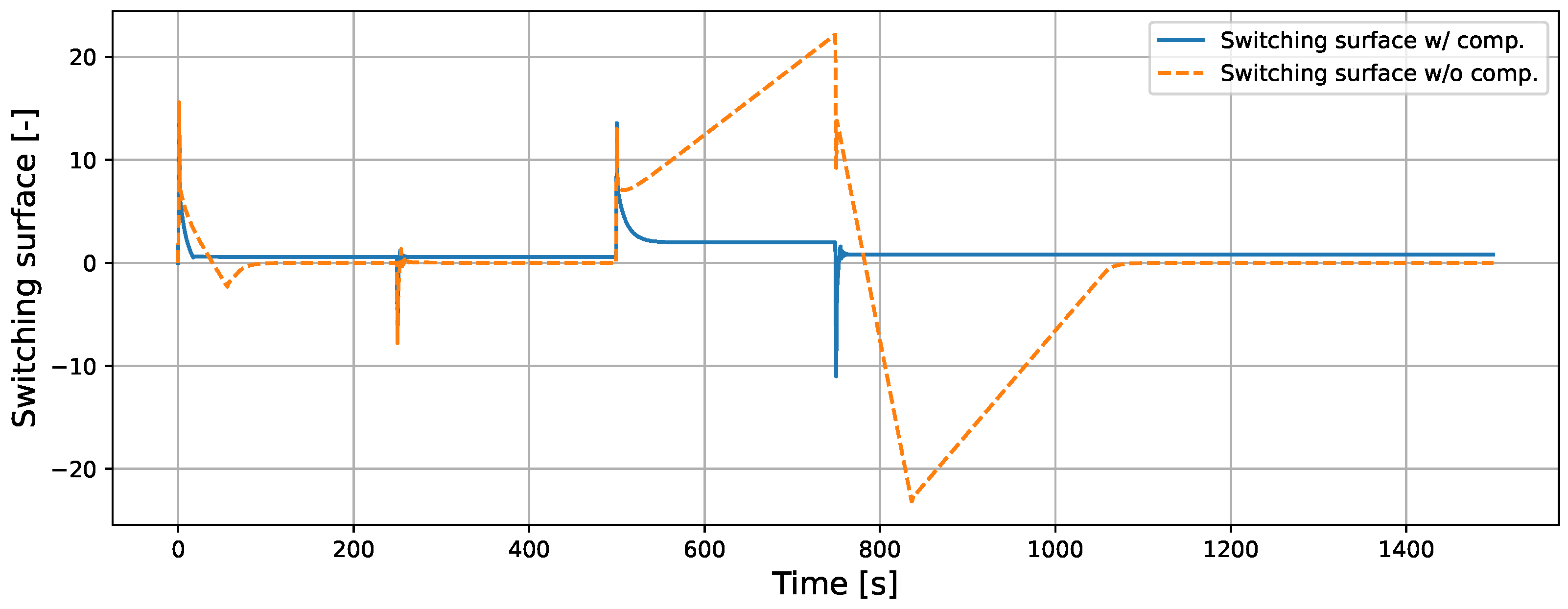
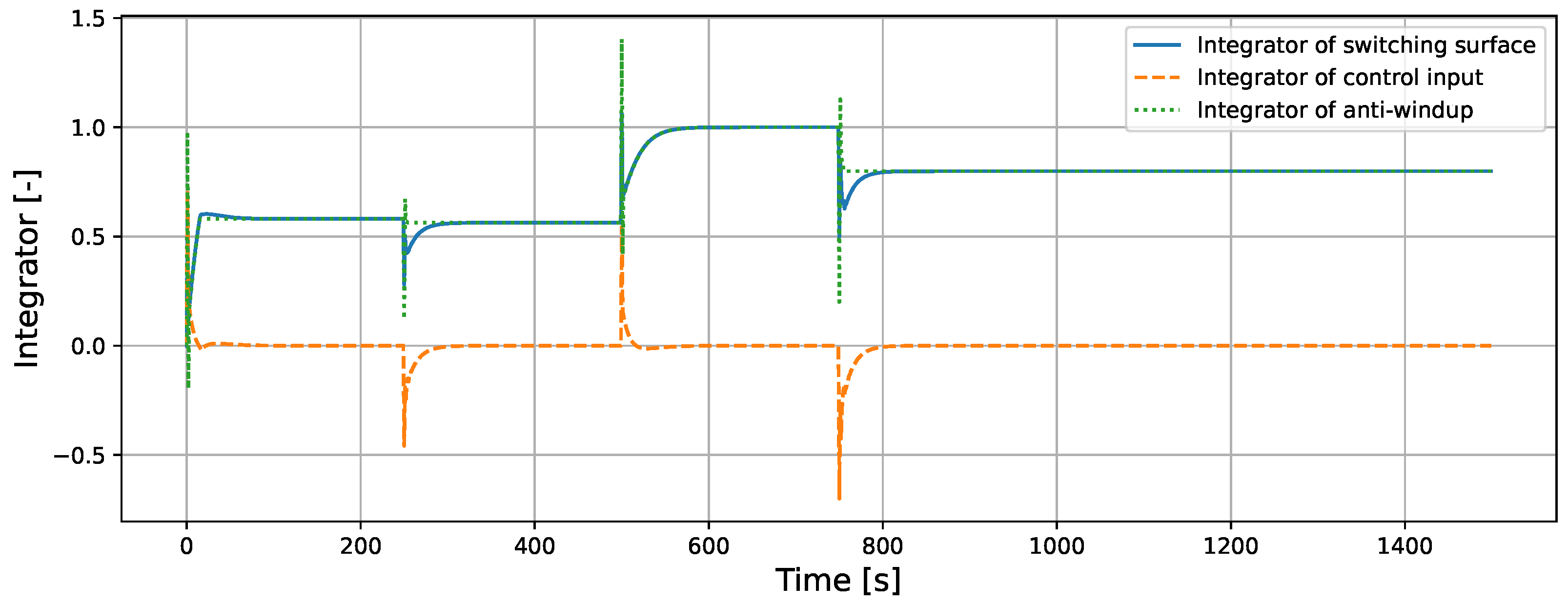
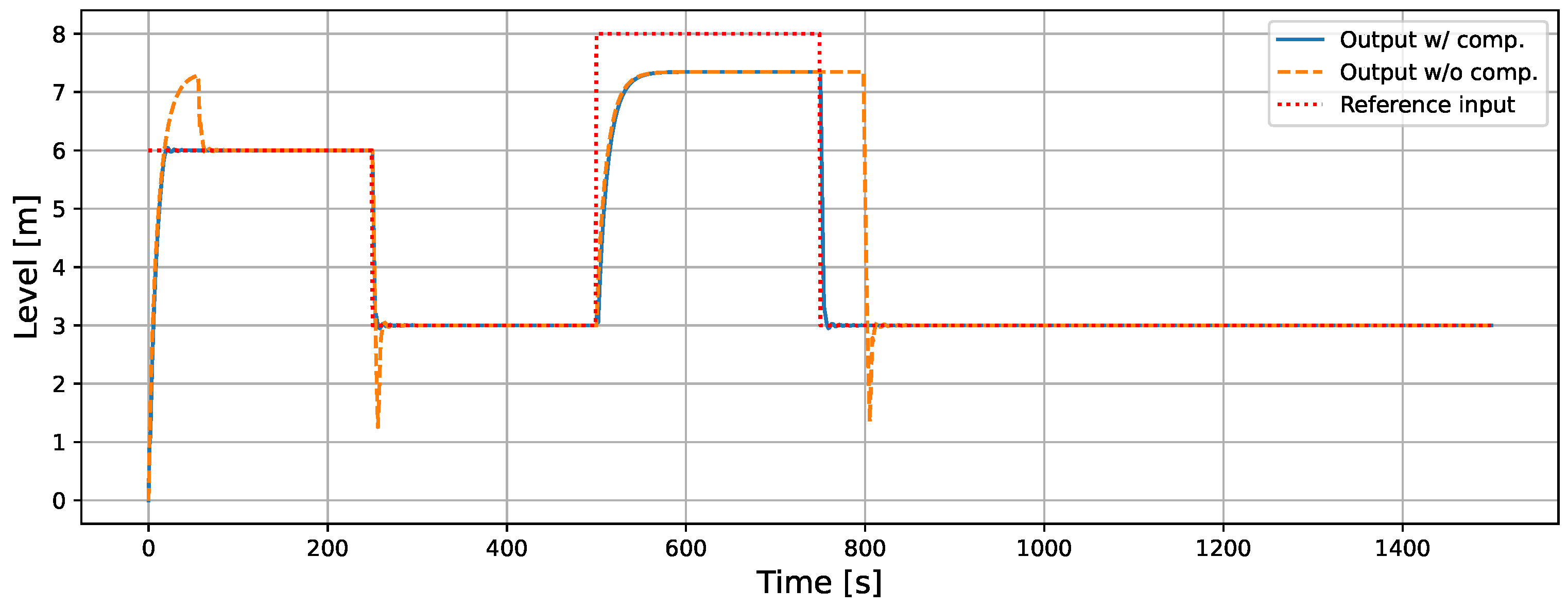
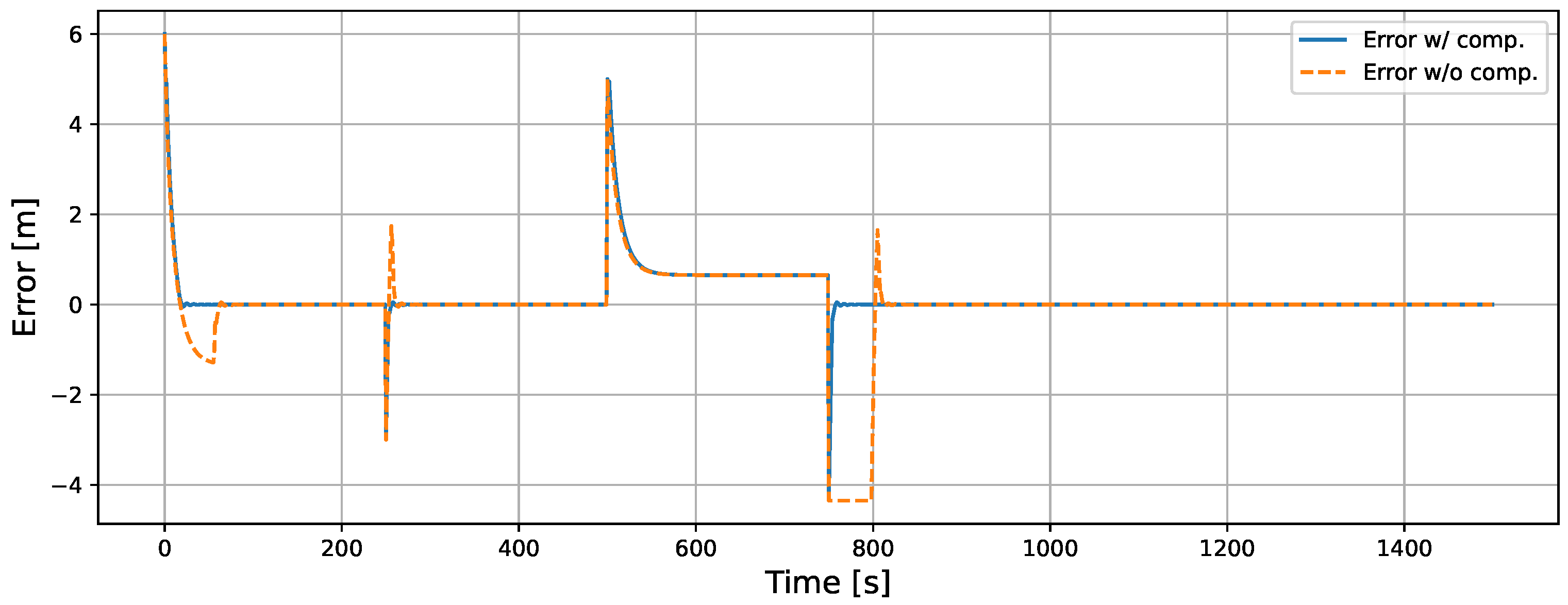
5.1.1. Comparison with and Without the Proposed Method in ISMC
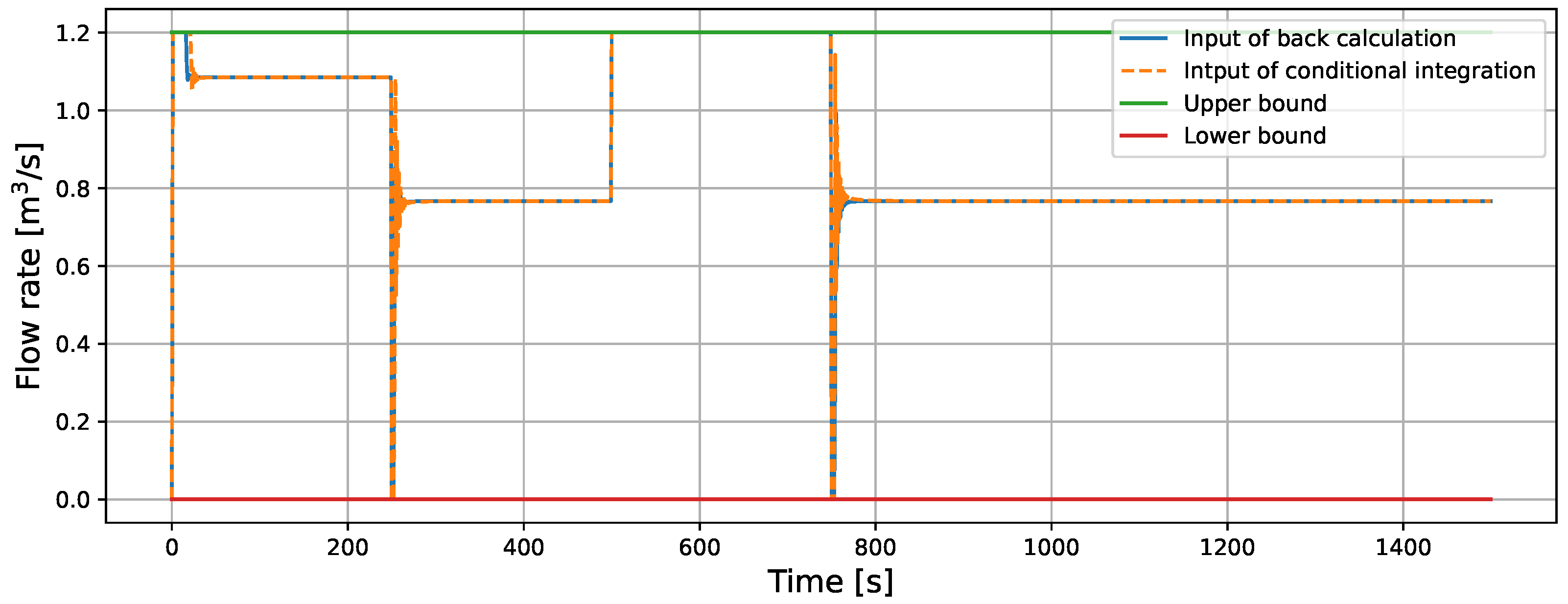
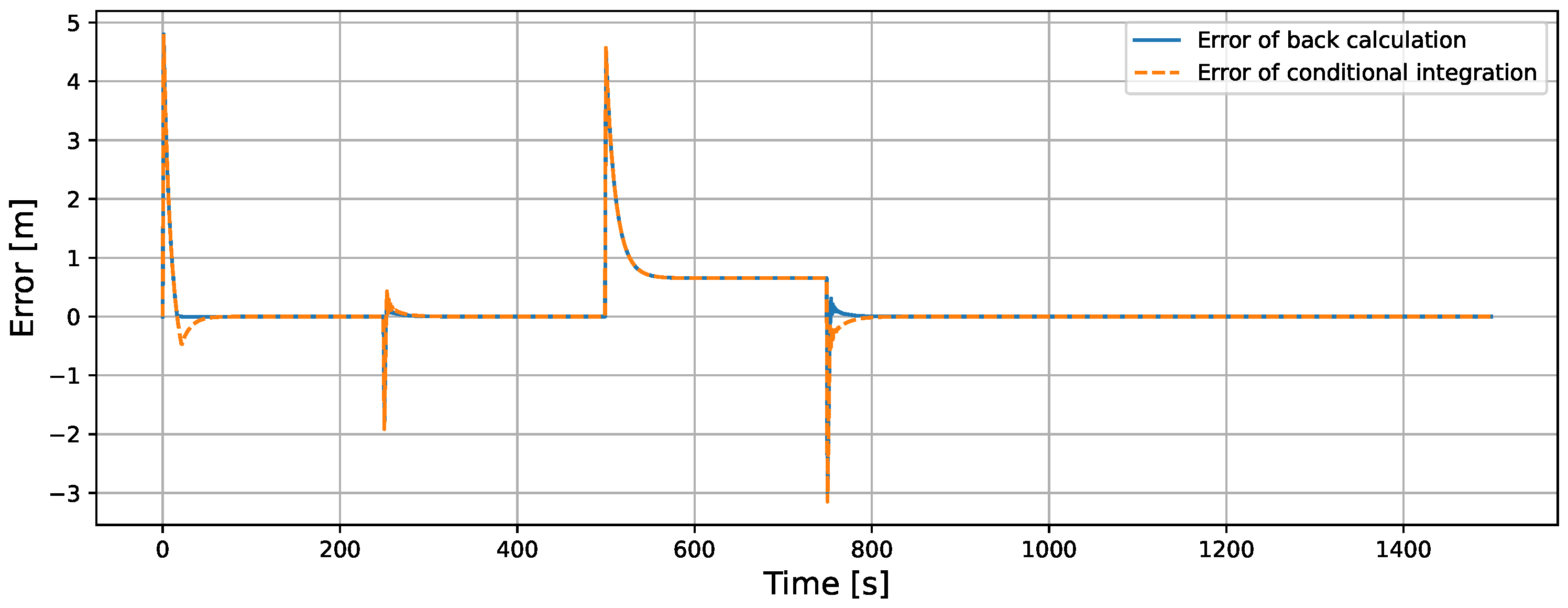
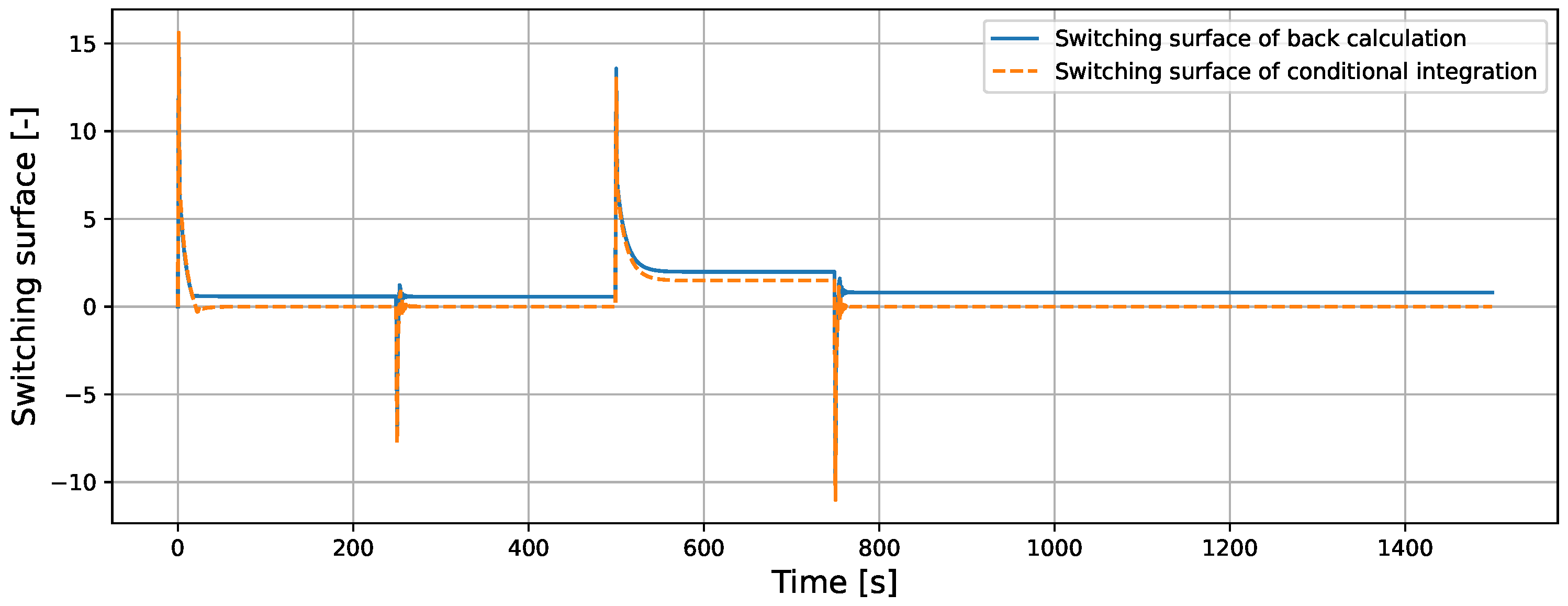
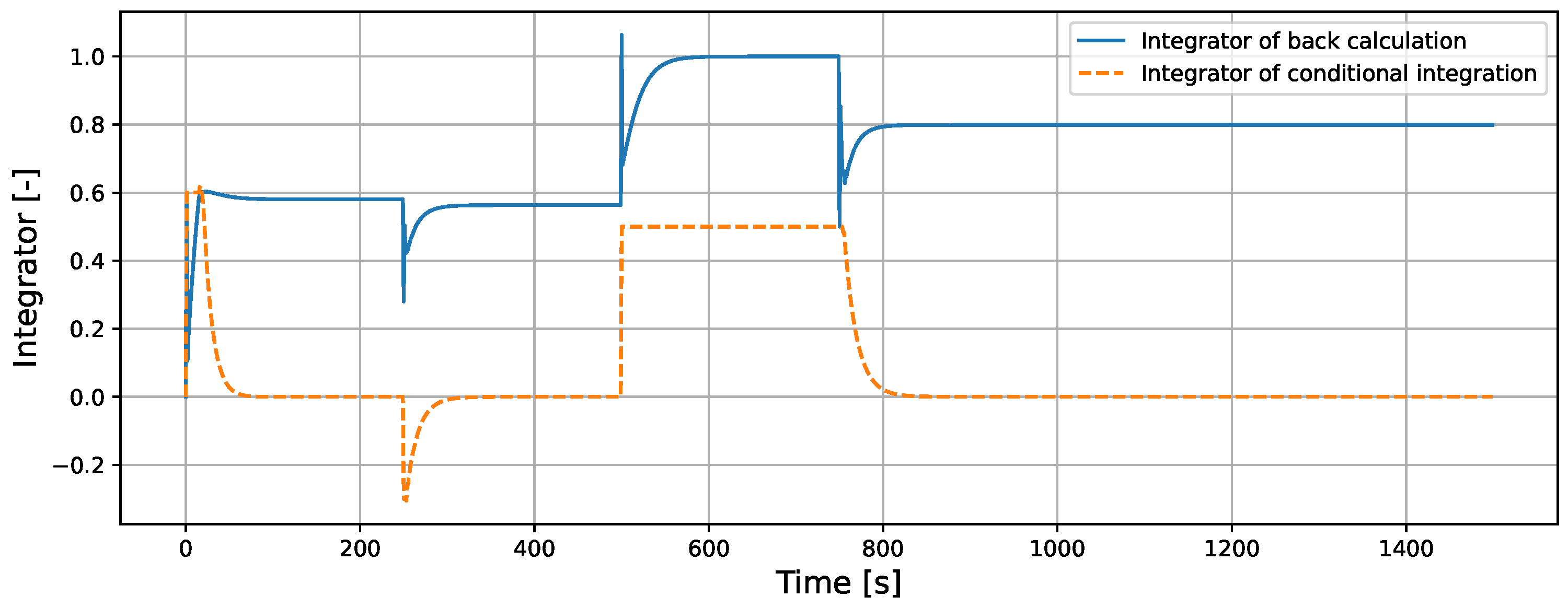
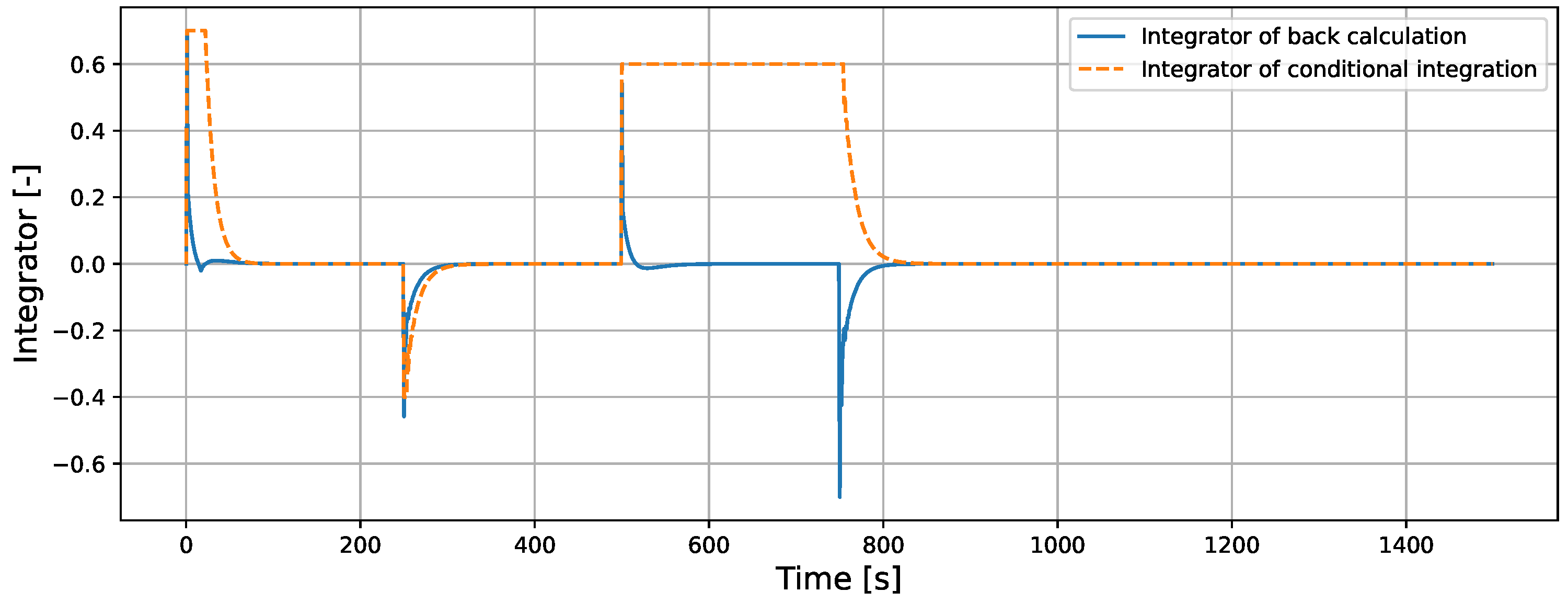
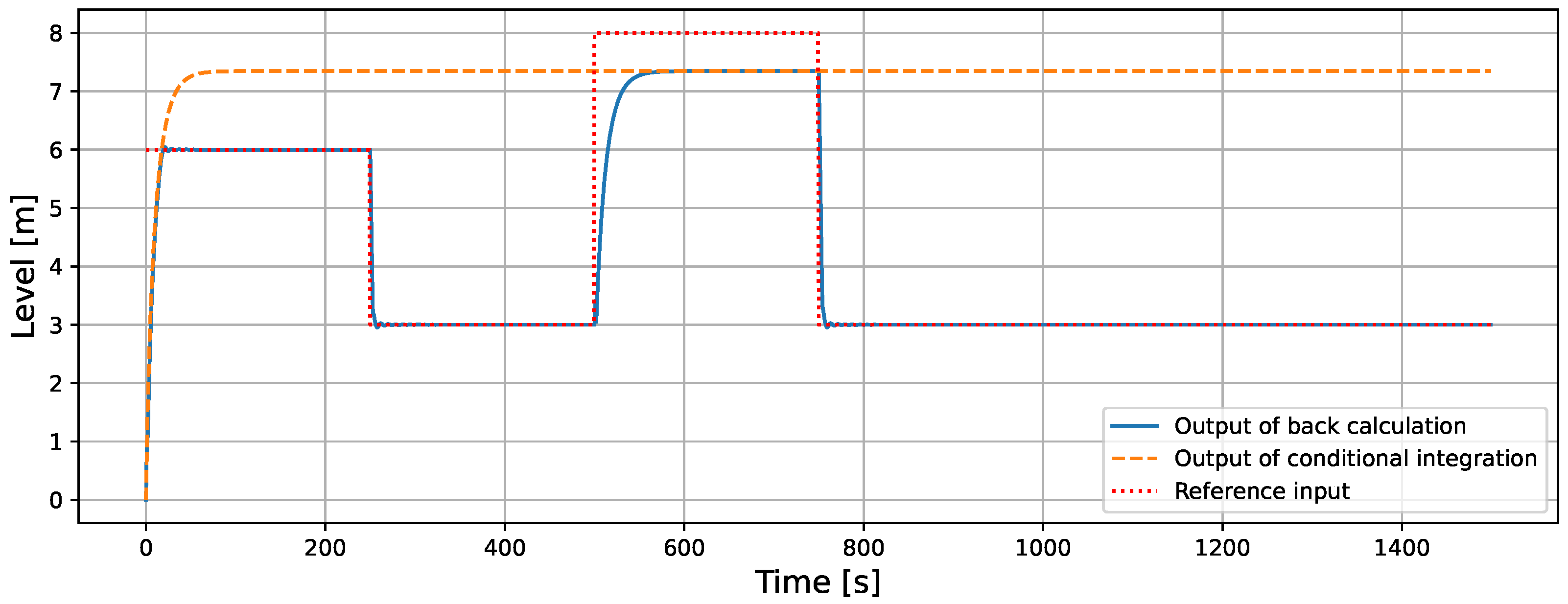
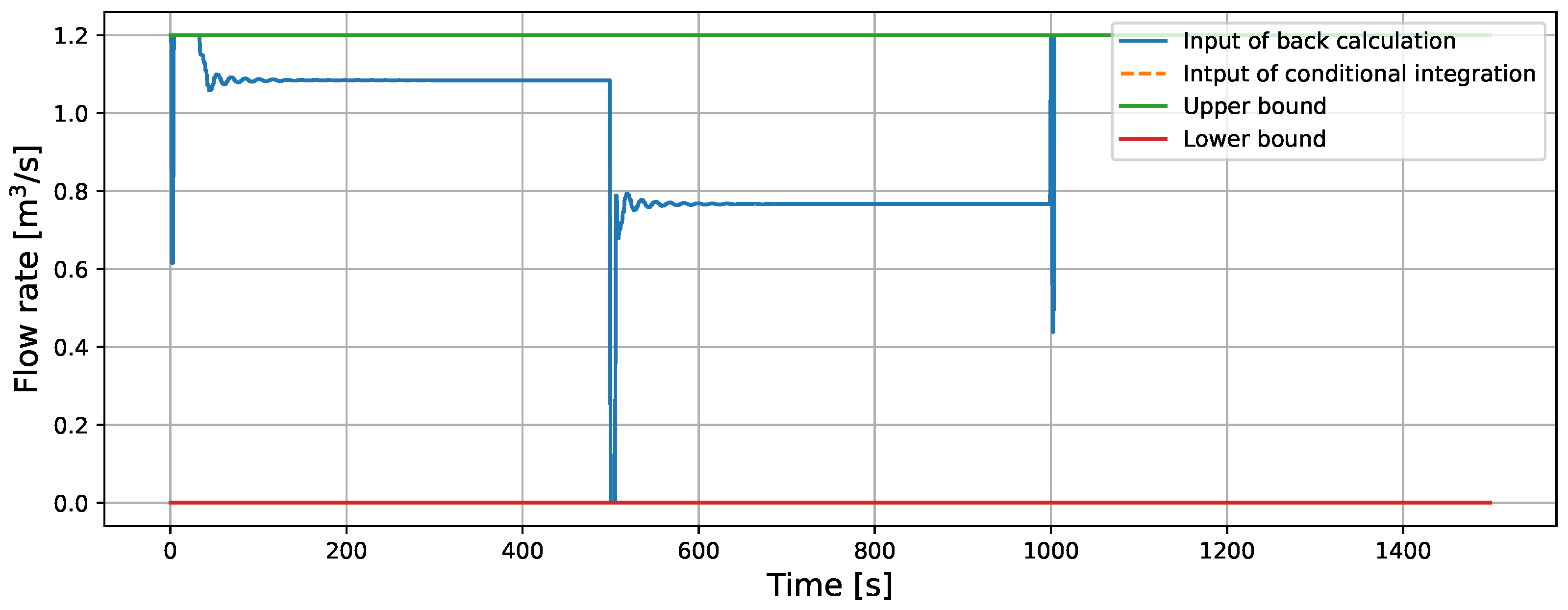
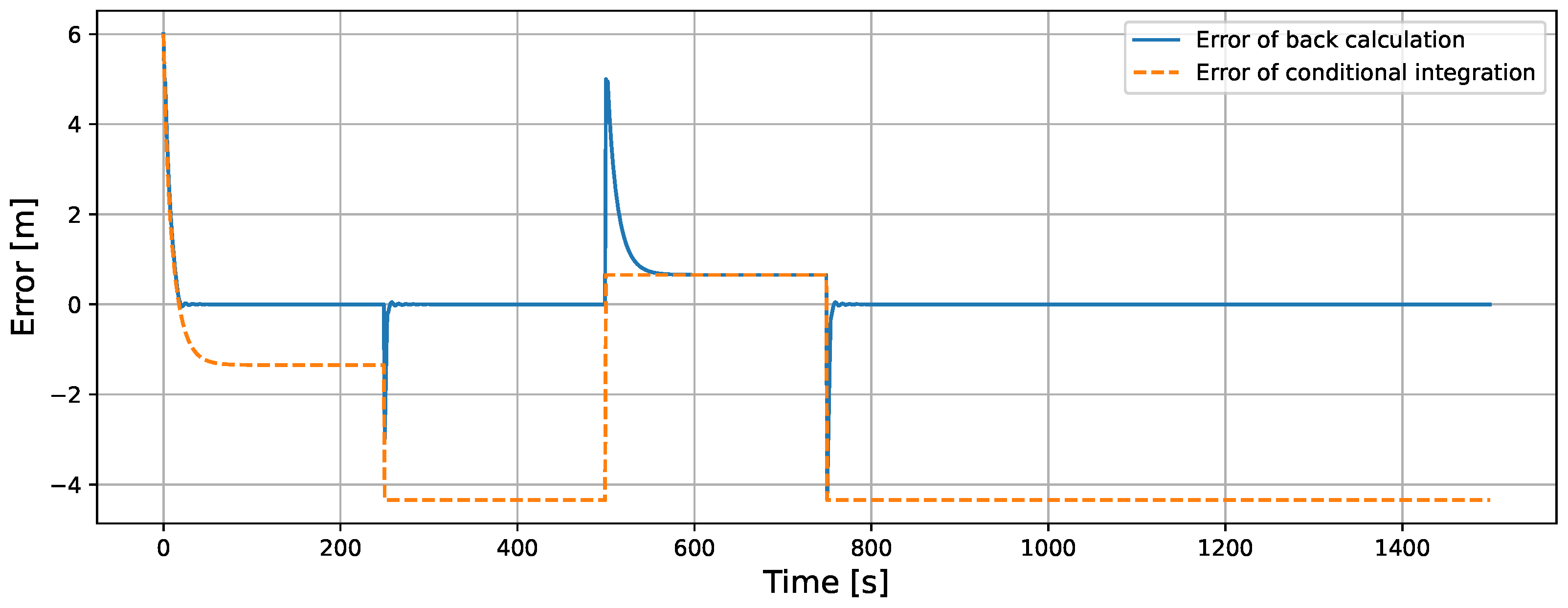
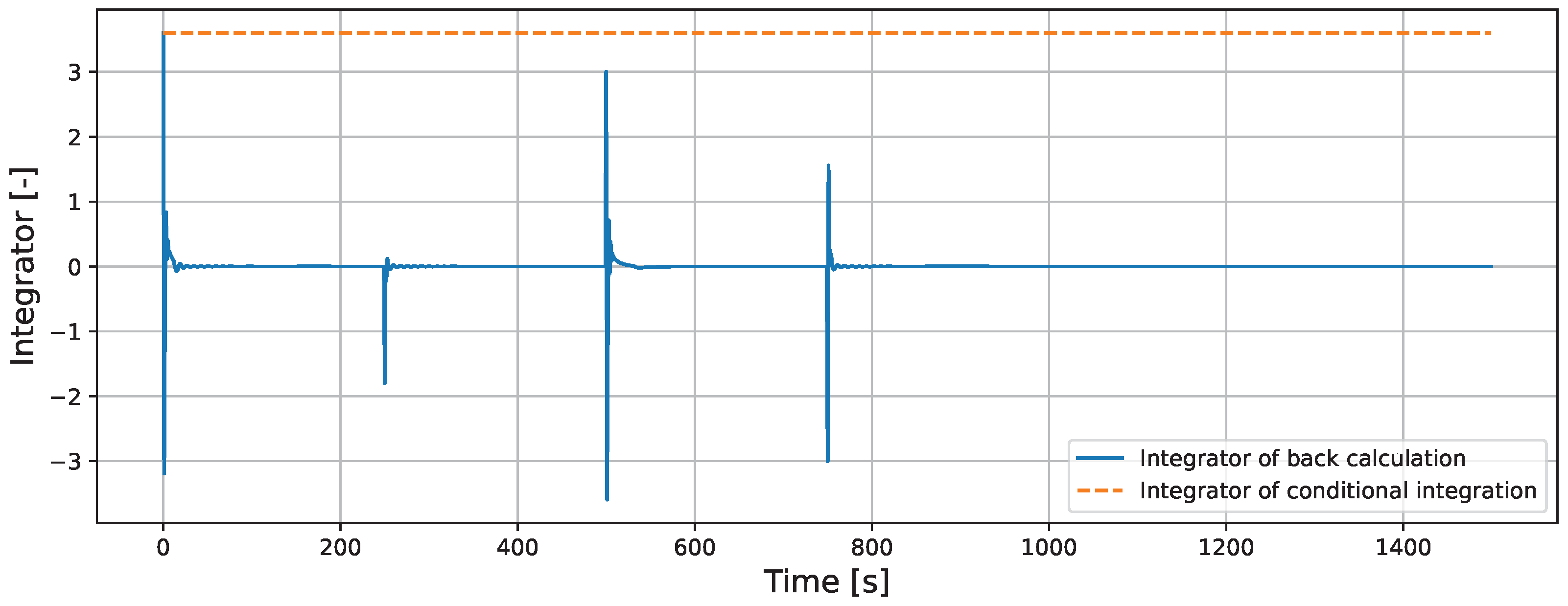
5.1.2. Comparison of Back-Calculation and Conditional Integration in ISMC
5.2. Simulations of Right Coprime Factorization
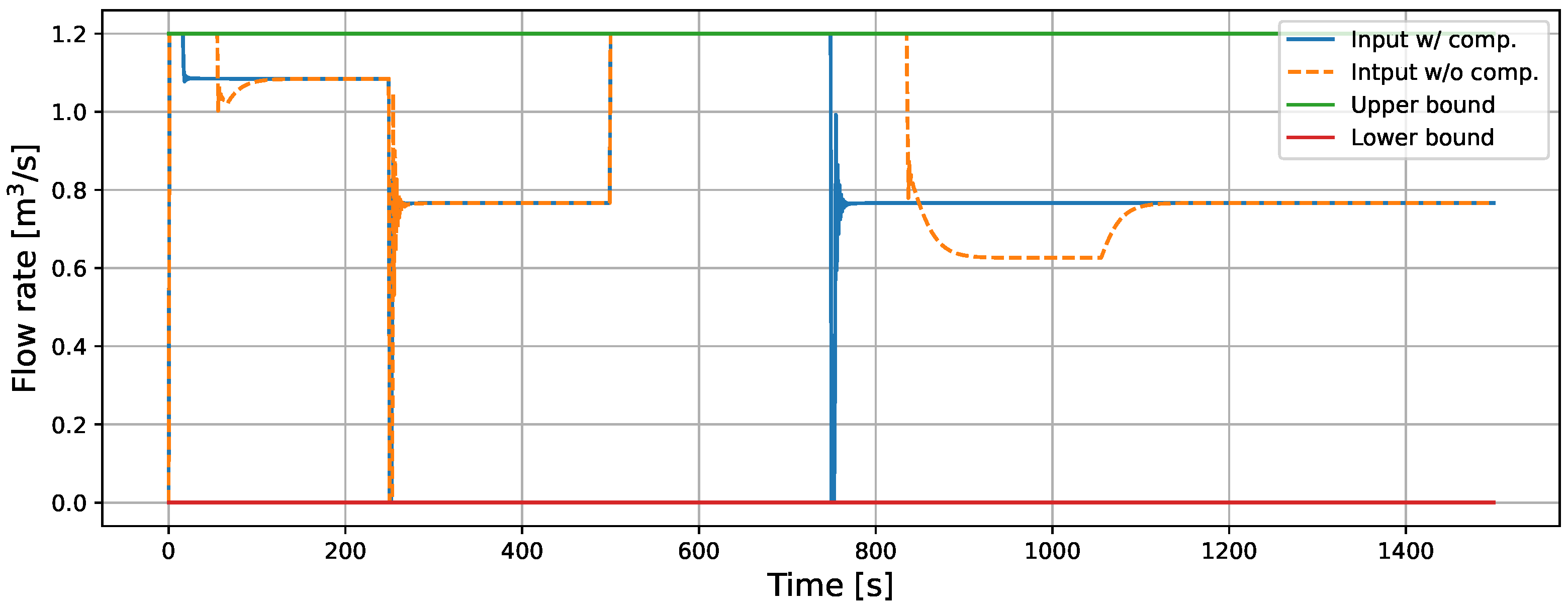
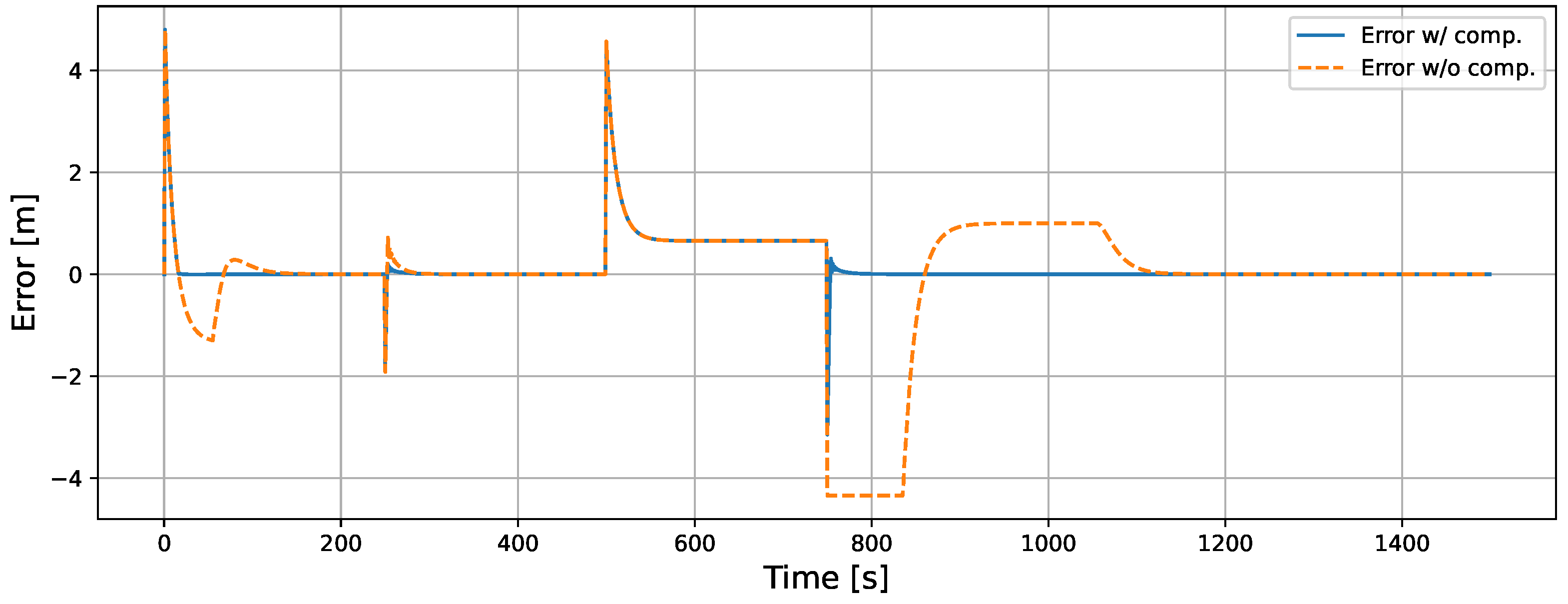
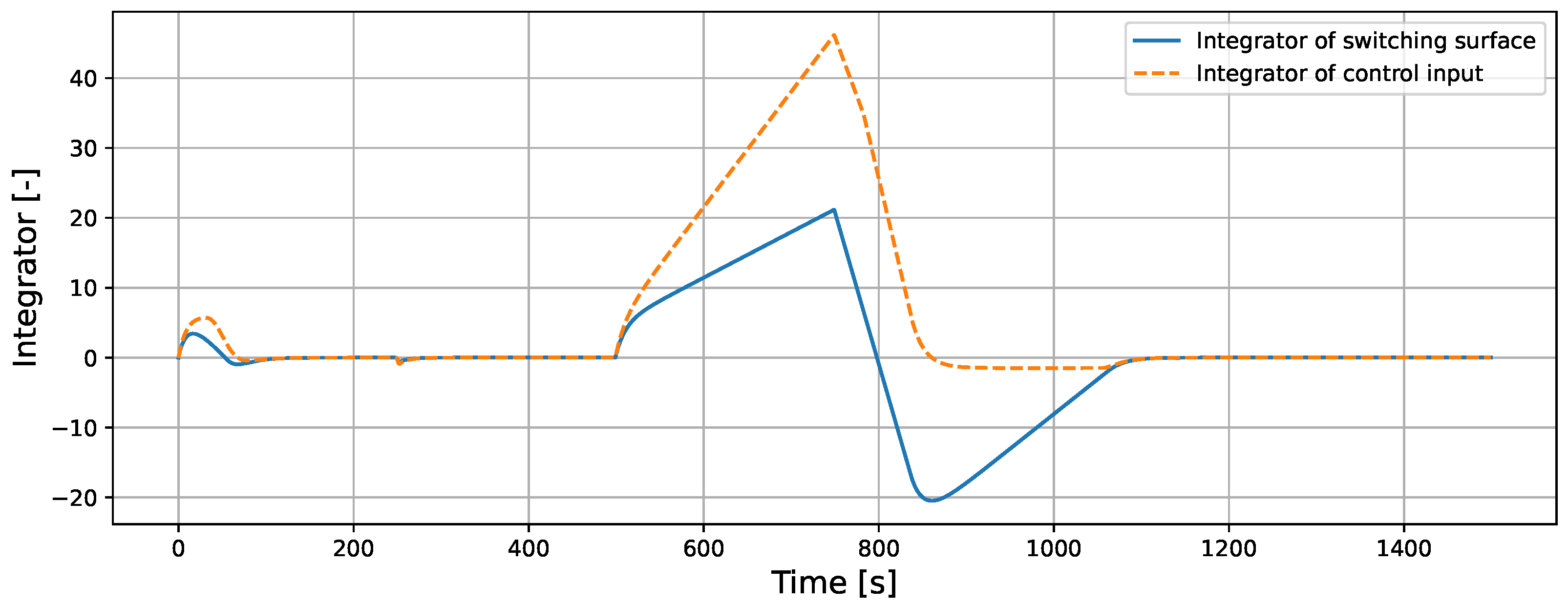
5.2.1. Comparison with and Without Anti-Windup Compensator in RCF
5.2.2. Comparison of Back-Calculation and Conditional Integration in RCF
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Markaroglu, H.; Guzelkaya, M.; Eksin, I.; Yesil, E. Tracking time adjustment in back calculation anti-windup scheme. In Proceedings of the 20th European Conference on Modelling and Simulation, Bonn, Germany, 28–31 May 2006. [Google Scholar]
- Åström, K.J.; Hägglund, T. The future of PID control. Control Eng. Pract. 2001, 9, 1163–1175. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar]
- Iqbal, J.; Ullah, M.; Khan, S.G.; Khelifa, B.; Ćuković, S. Nonlinear control systems-A brief overview of historical and recent advances. Nonlinear Eng. 2017, 6, 301–312. [Google Scholar] [CrossRef]
- Lin, Z.; Stoorvogel, A.A.; Saberi, A. Output regulation for linear systems subject to input saturation. Automatica 1996, 32, 29–47. [Google Scholar] [CrossRef]
- Hu, T.; Lin, Z. Control Systems with Actuator Saturation: Analysis and Design; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Tarbouriech, S.; Turner, M. Anti-windup design: An overview of some recent advances and open problems. IET Control Theory Appl. 2009, 3, 1–19. [Google Scholar] [CrossRef]
- García, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Fertik, H.A.; Ross, C.W. Direct digital control algorithm with anti-windup feature. ISA Trans. 1967, 6, 317–328. [Google Scholar]
- Rachev, E.; Petrov, V. Integral anti-windup correction in PI current controllers for electrical drives. In Proceedings of the 2020 12th Electrical Engineering Faculty Conference (BulEF), Varna, Bulgaria, 9–12 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Rundqwist, L. Anti-reset Windup for PID Controllers. IFAC Proc. Vol. 1990, 23, 453–458. [Google Scholar] [CrossRef]
- Gallun, S.E.; Matthews, C.W.; Senyard, C.P.; Slater, B. Windup protection and initialization for advanced digital control. Hydrocarb. Process. 1985, 67, 63–68. [Google Scholar]
- Phelan, R. Automatic Control Systems; Cornell Univ. Press: Ithaca, NY, USA, 1977. [Google Scholar]
- Deng, M.; Inoue, A.; Yanou, A.; Hirashima, Y. Continuous-time anti-windup generalized predictive control of non-minimum phase processes with input constraints. In Proceedings of the 42nd IEEE International Conference on Decision and Control (IEEE Cat. No.03CH37475), Maui, HI, USA, 9–12 December 2003; Volume 5, pp. 4457–4462. [Google Scholar]
- De Figueiredo, R.J.; Chen, G. Nonlinear Feedback Control Systems: An Operator Theory Approach; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Deng, M. Operator-Based Nonlinear Control Systems: Design and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Bu, N.; Zhang, Y.; Zhang, Y.; Morohoshi, Y.; Deng, M. Robust Control for Hysteretic Microhand Actuator Using Robust Right Coprime Factorization. IEEE Trans. Autom. Control 2024, 69, 3982–3988. [Google Scholar] [CrossRef]
- Jin, G.; Deng, M. Operator-based robust nonlinear free vibration control of a flexible plate with unknown input nonlinearity. IEEE/CAA J. Autom. Sin. 2020, 7, 442–450. [Google Scholar] [CrossRef]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; Man, Z. Terminal Sliding Mode Control – An Overview. IEEE Open J. Ind. Electron. Soc. 2021, 2, 36–52. [Google Scholar] [CrossRef]
- Niu, Y.; W C Ho, D.; Lam, J. Robust integral sliding mode control for uncertain stochastic systems with time-varying delay. Automatica 2005, 41, 873–880. [Google Scholar] [CrossRef]
- Baños, A. Stabilization of nonlinear systems based on a generalized Bezout identity. Automatica 1996, 32, 591–595. [Google Scholar] [CrossRef]







| Symbol | Quantity | Value |
|---|---|---|
| A | Cross-sectional area of the tank | 1 m2 |
| a | Cross-sectional area of the outlet | m2 |
| g | Acceleration due to gravity | m/s2 |
| Sampling period | 1 s | |
| Upper limit of the input | m3/s | |
| Lower limit of the input | 0 m3/s | |
| Design parameter of ISMC | 1.5 | |
| Design parameter of ISMC | ||
| Design parameter of ISMC |
| With Compensator | Without Compensator | |
|---|---|---|
| RMSE [m] | 0.49 | 1.23 |
| MAE [m] | 0.17 | 0.61 |
| Back-Calculation | Conditional Integration | |
|---|---|---|
| RMSE [m] | 0.486 | 0.488 |
| MAE [m] | 0.166 | 0.173 |
| With Compensator | Without Compensator | |
|---|---|---|
| RMSE [m] | 0.59 | 0.98 |
| MAE [m] | 0.19 | 0.35 |
| Back-Calculation | Conditional Integration | |
|---|---|---|
| RMSE [m] | 0.59 | 3.61 |
| MAE [m] | 0.19 | 3.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morohoshi, Y.; Deng, M. Nonlinear Back-Calculation Anti-Windup Based on Operator Theory. Processes 2025, 13, 1266. https://doi.org/10.3390/pr13051266
Morohoshi Y, Deng M. Nonlinear Back-Calculation Anti-Windup Based on Operator Theory. Processes. 2025; 13(5):1266. https://doi.org/10.3390/pr13051266
Chicago/Turabian StyleMorohoshi, Yuuki, and Mingcong Deng. 2025. "Nonlinear Back-Calculation Anti-Windup Based on Operator Theory" Processes 13, no. 5: 1266. https://doi.org/10.3390/pr13051266
APA StyleMorohoshi, Y., & Deng, M. (2025). Nonlinear Back-Calculation Anti-Windup Based on Operator Theory. Processes, 13(5), 1266. https://doi.org/10.3390/pr13051266







