Integrated Coordinated Control of Source–Grid–Load–Storage in Active Distribution Network with Electric Vehicle Integration
Abstract
1. Introduction
2. Related Works
2.1. Current Status of Renewable Energy Integration
2.2. Current Status of Electric Vehicle Integration
3. Electric Vehicle and Its Ordered and Disordered Optimization Models
3.1. Mathematical Model of Electric Vehicle
3.2. Disordered Charging Model of Electric Vehicle
- Set the travel day Td = 1 and determine the total number of vehicles N.
- Check if Td ≤ 7. If yes, set the vehicle counter n = 1 and proceed to step 3; otherwise, jump to step 10.
- For each vehicle (from 1 to N): Generate the first departure time t of the nth vehicle on the Td day according to the probability distribution. Determine the number of trips f of the vehicle on that day, and randomly set the initial battery state of charge SOC0. If n > N, jump to step 11.
- Set the starting point P as home. Initialize the trip counter i = 1 and set the initial driving distance S0 = 0.
- For each trip (from 1 to f): Determine the destination P of the ith trip according to the transition probability matrix. Generate the trip distance d, calculate the power consumption Pc and driving time dt. Calculate the arrival time t and check the battery state of charge SOC. If SOC does not meet the requirement that the next trip is lower than 0.3, charge at P. The charging time is determined by the stay time t, but not exceeding the time required to fully charge. Generate the charging load curve Li and update SOC.
- i = i + 1, return to step 5.
- For the current vehicle, integrate the charging load curves of all trips to generate the total charging curve for that day.
- n = n + 1, return to step 3.
- For the current travel day Td, integrate the charging curves of all vehicles.
- Td = Td + 1, return to step 2.
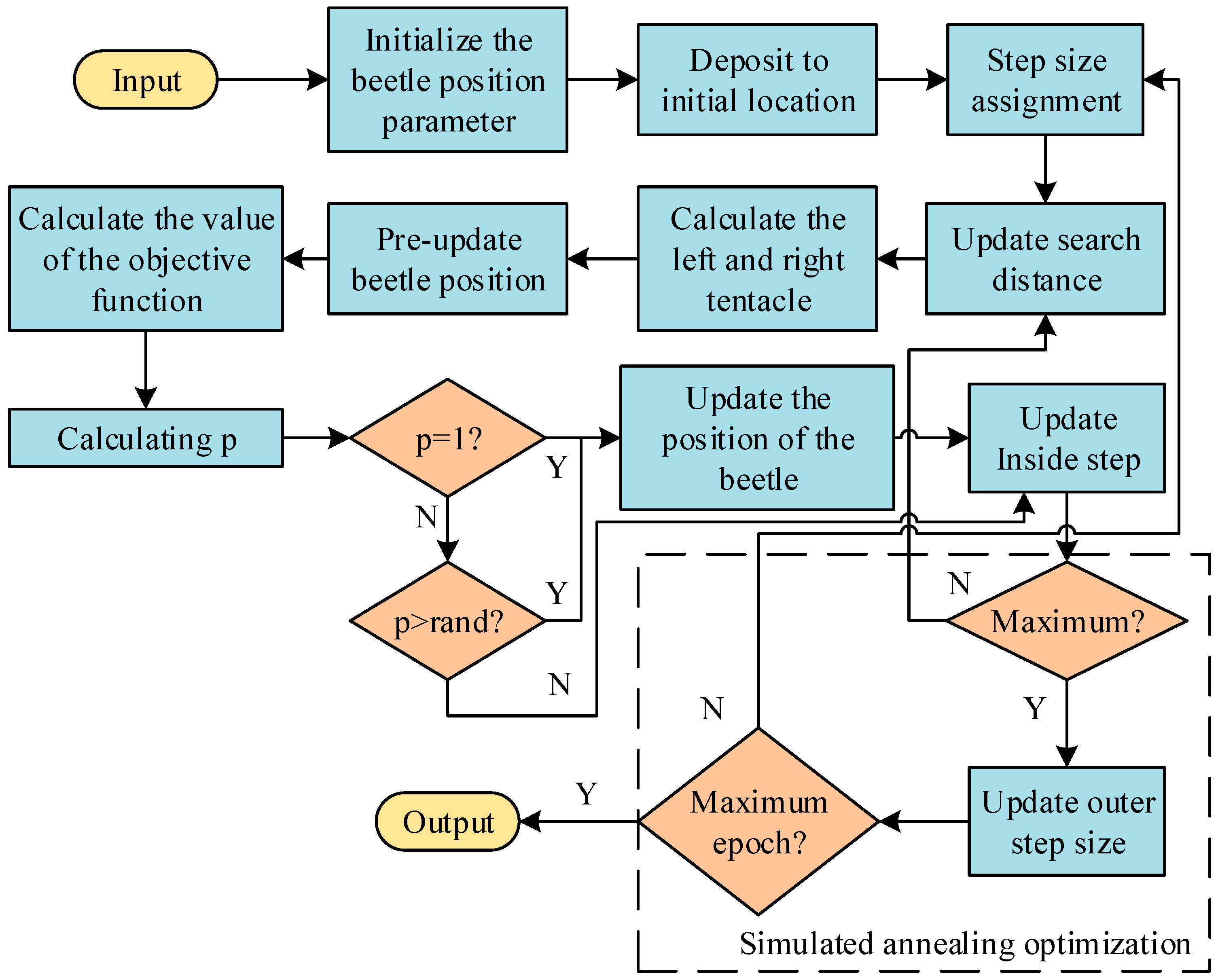
3.3. Ordered Charging and Discharging Model of Electric Vehicle
Objective Function and Constraints
- (1)
- Minimize the Peak-to-Valley Difference of the Load
- (2)
- Minimize the Standard Deviation of the Load Curve
- (3)
- Minimize the Charging Cost of Electric Vehicle Users
- a.
- EV State of Charge (SOC) Constraint
- b.
- EV Charging and Discharging State Constraint
3.4. Case Analysis
4. Research on the Coordinated Control of Source–Grid–Load–Storage in Active Distribution Network
4.1. Optimization Model of the Scheduling Layer in ADN
- (1)
- Mathematical Models of Various Devices in the Scheduling Layer
- a.
- EV Cluster
- b.
- Gas Turbine
- c.
- Flexible Load
- (2)
- Objective Function
4.2. Optimization Model of the Network Layer in ADN
- (1)
- Minimize the Coordinated Control Cost of ADN
- (2)
- Minimize the Cost of EV Cluster
- The power flow equation equality constraints are shown in Equations (19) and (20).
- (3)
- The node voltage constraint is shown in Equation (21).
- (4)
- The branch current constraint is shown in Equation (22).
- (5)
- The distributed generation power constraint is shown in Equation (23).
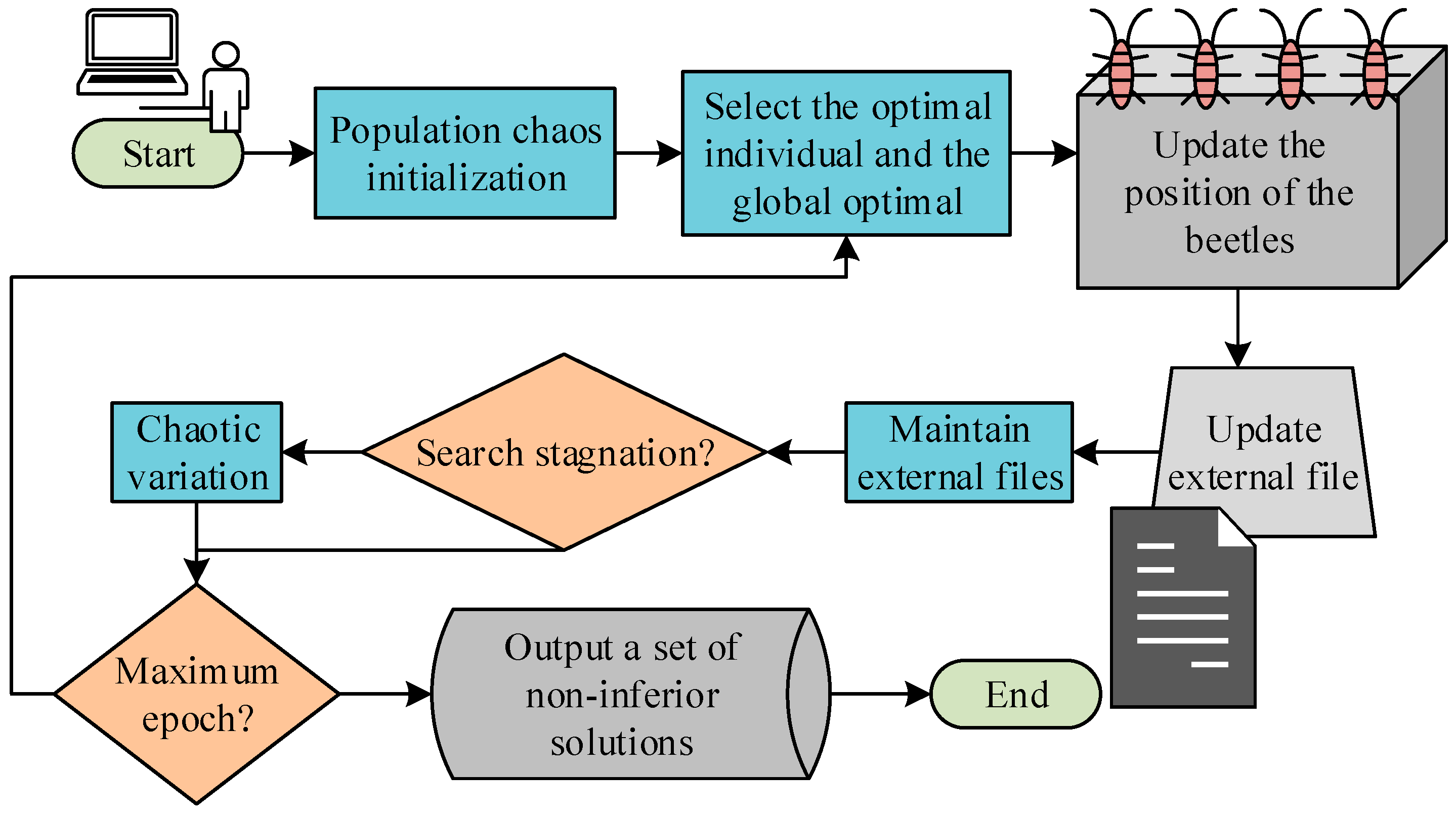
4.3. Calculation of the ADN Two-Layer Coordinated Control Model
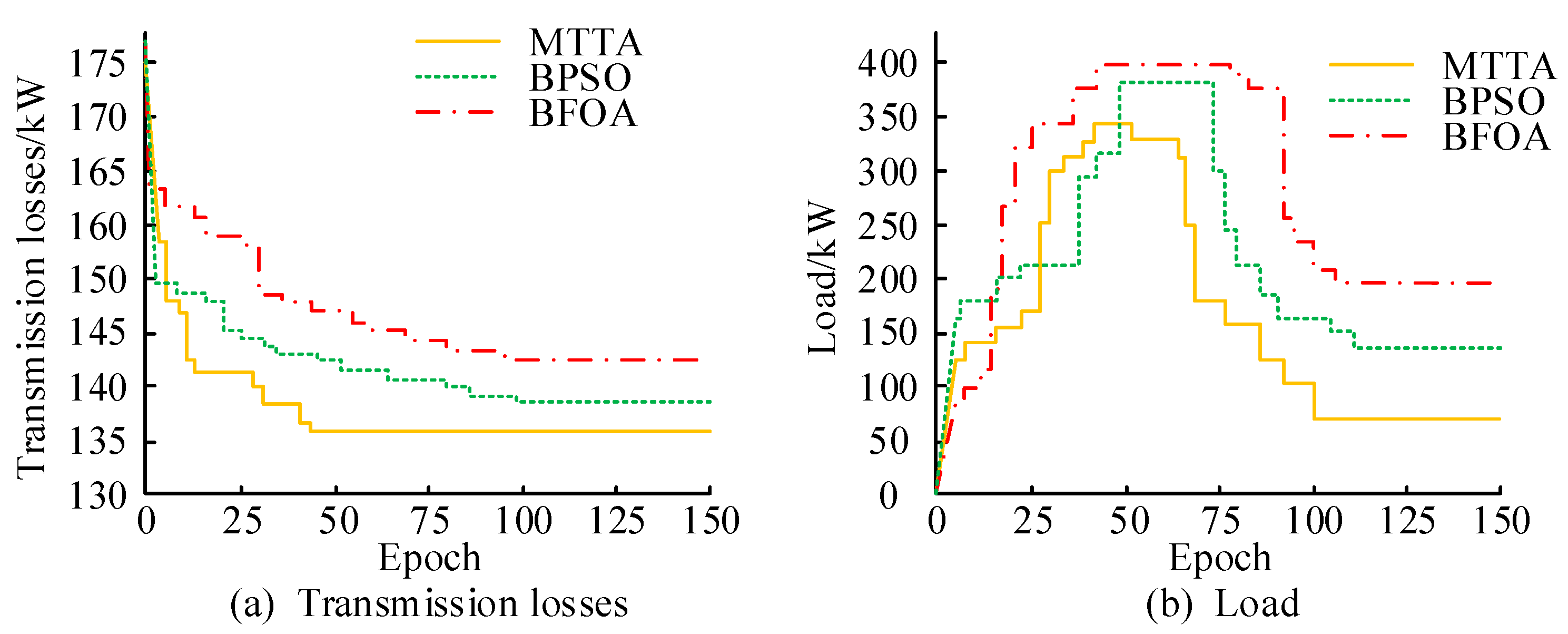
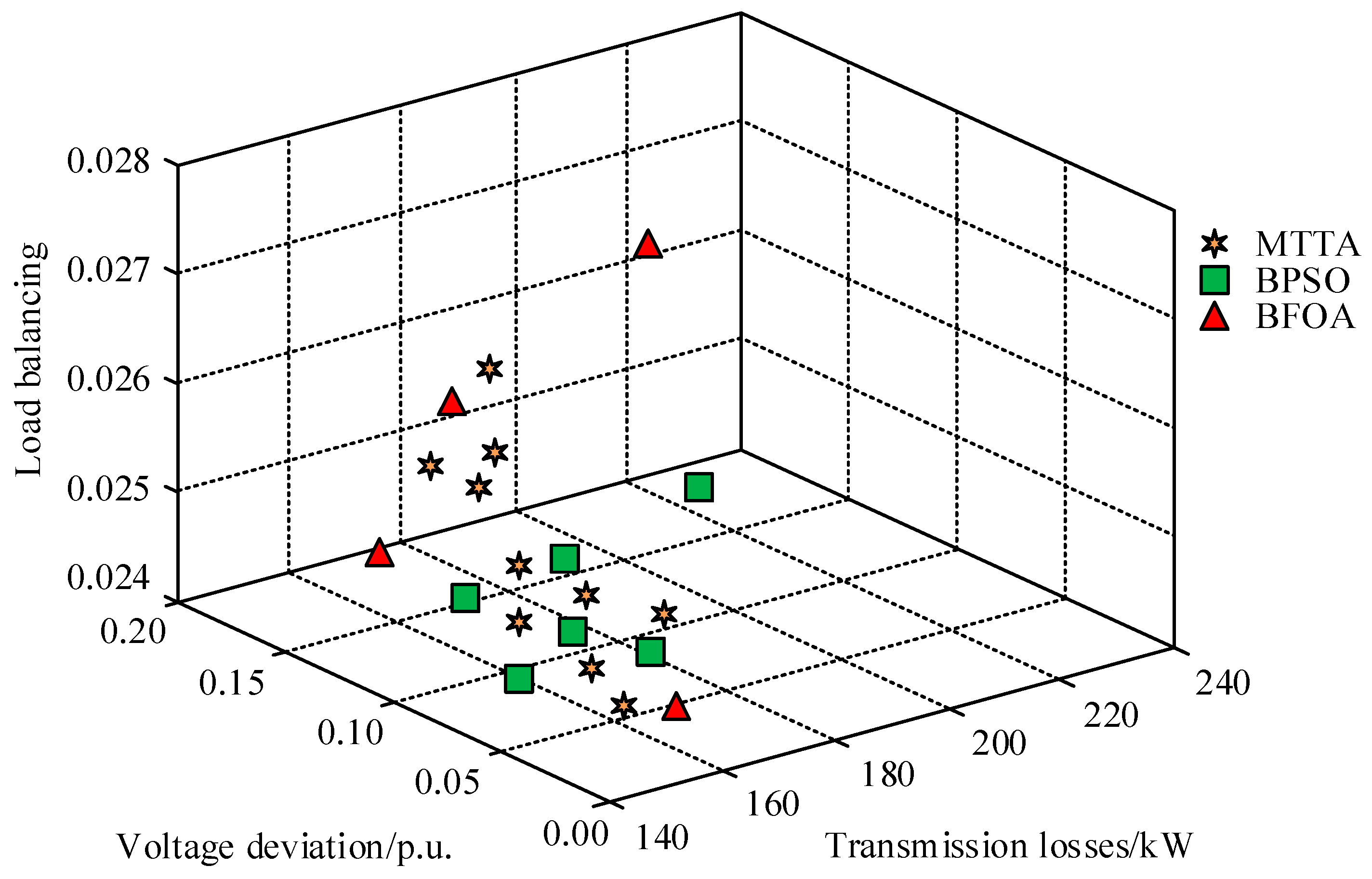
4.4. Case Analysis
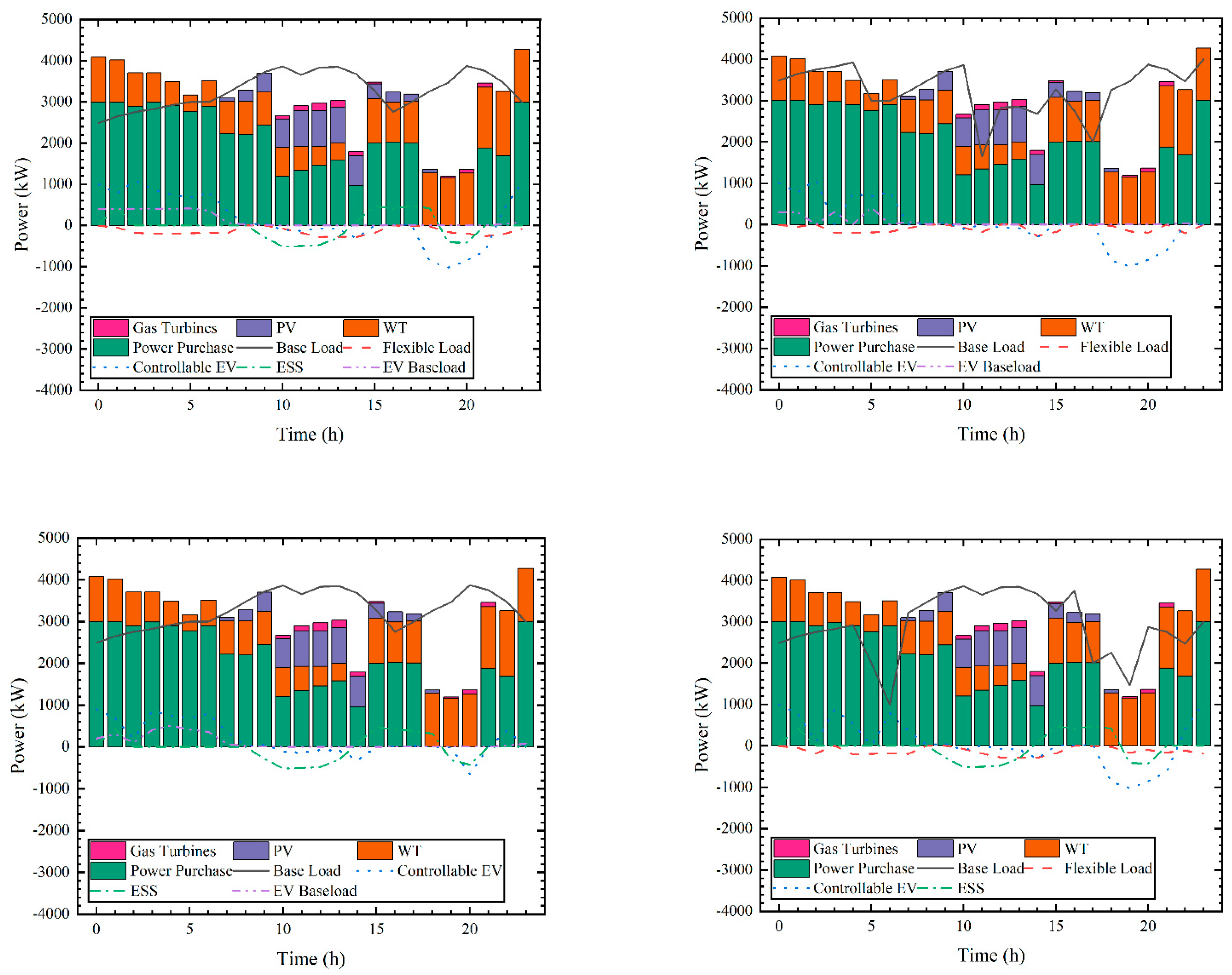
4.4.1. Scheduling Layer Result Analysis
- Scenario 1: Consider energy storage; optimize considering energy storage, flexible load, and EV cluster;
- Scenario 2: Do not consider energy storage;
- Scenario 3: Do not consider flexible load;
- Scenario 4: Do not consider EV cluster.
4.4.2. Network Layer Result Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xia, B.; Tang, Y.; Xiao, X.; Yang, C. Review of Optimal Scheduling Research on Smart Distribution Network with Electric Vehicles. Big Data Electr. Power 2019, 22, 87–92. [Google Scholar]
- Wang, Q.; Ma, S.; Liu, Q.; Fan, P.; Hui, Y. Research on Multi-objective Optimization of Active Distribution Network Based on Imperialist Competition Algorithm. Smart Power 2018, 46, 74–78. [Google Scholar]
- Lu, J.; Chu, W.; Yu, H.; Guo, J.; Ma, C. Multi-source Coordinated Optimal Scheduling of Active Distribution Network Based on Demand Side Response. Electr. Power Sci. Eng. 2018, 34, 30–37. [Google Scholar]
- Zhao, Q.; Wang, X.; Wang, X.; Lang, Y.; Jia, L. Optimal Scheduling of Microgrid with Different Clusters of Electric Vehicles. Renew. Energy Resour. 2019, 37, 379–385. [Google Scholar]
- Li, H.; She, C.; Zhang, T.; Luo, W. Research on Frequency Regulation Control Strategy of Electric Vehicles Participating in Power Grid Based on SOC. J. Chongqing Univ. 2018, 41, 66–72. [Google Scholar]
- Le Cam, A.; Southernwood, J.; Ring, D.; Clarke, D.; Creedon, R. Impact of Demand Response on Occupants’ Thermal Comfort in a Leisure Center. Energy Effic. 2021, 14, 91. [Google Scholar] [CrossRef]
- Zhong, Z.; Zhang, K.; Wu, Z.; Gan, G. Joint Optimal Scheduling Strategy of Wind—Thermal Power System Based on Improved LDW Particle Swarm Optimization Algorithm. Big Data Electr. Power 2017, 20, 50–55. [Google Scholar]
- Li, X.; Chen, M.; Cheng, S.; Chen, A. Optimal Scheduling Strategy of Microgrid with Electric Vehicles Based on Dual Incentive Cooperative Game. High Volt. Technol. 2020, 46, 10. [Google Scholar]
- Zhang, Q.; Xin, X.; Cheng, Z. Microgrid Reconfiguration Based on Depth-First Search and Grey Wolf Algorithm. J. Zhengzhou Univ. 2020, 41, 73–79. [Google Scholar]
- Kumar, M.; Kumar, A.; Sandhu, K.S. Impact of Distributed Generation on Nodal Prices in Hybrid Electricity Market. Mater. Today Proc. 2018, 5, 830–840. [Google Scholar] [CrossRef]
- Shen, H.; Yue, F.; Shi, L.; Liu, L.; Li, M.; Duan, Z.; Yuan, H. Comprehensive Optimal Planning of Multi-objective Distribution Network Reconfiguration and DG Regulation Considering Temporality of DG and Load. Mod. Electr. Power 2022, 39, 182–192. [Google Scholar]
- Rabiee, A.; Sadeghi, M.; Aghaei, J. Modified Imperialist Competitive Algorithm for Environmental Constrained Energy Management of Microgrids. J. Clean. Prod. 2018, 202, 27–292. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, X.; Han, X. Intelligent Charging Scheduling of Electric Vehicles for Distribution Network Loss Optimization. Guangdong Electr. Power 2016, 29, 94-97-103. [Google Scholar]
- Yu, X.; Yu, X.; Lu, Y.; Yen, G.G.; Cai, M. Differential Evolution Mutation Operators for Constrained Multi-objective Optimization. Appl. Soft Comput. 2018, 67, 452–466. [Google Scholar] [CrossRef]
- Yao, L.; Wang, X.; Ding, T.; Wang, Y.; Wu, X.; Liu, J. Stochastic Day—Ahead Scheduling of Integrated Energy Distribution Network with Identifying Redundant Gas Network Constraints. Smart Grid. IEEE Trans. 2019, 10, 4309–4322. [Google Scholar]
- Nguyen, C.L.; Lee, H.H.; Chun, T.W. Cost Optimized Battery Capacity and Short—Term Power Dispatch Control for Wind Farm. IEEE Trans. Ind. Appl. 2015, 51, 595–606. [Google Scholar] [CrossRef]
- Yang, X.; Ren, S.; Zhang, Y.; Zhao, B.; Huang, F.; Xie, L. Schedulable Capacity Model and Intra-day Priority Scheduling Strategy of Electric Vehicles. Autom. Electr. Power Syst. 2017, 41, 84–93. [Google Scholar]
- Yang, H.; Li, M.; Jiang, Z.; Zhang, P. Multi—Time Scale Optimal Scheduling of Regional Integrated Energy Systems Considering Integrated Demand Response. IEEE Access 2020, 8, 5080–5090. [Google Scholar] [CrossRef]
- Janfeshan, K.; Masoum, M. Hierarchical Supervisory Control System for PEVs Participating in Frequency Regulation of Smart Grids. IEEE Power Energy Technol. Syst. J. 2017, 4, 84–93. [Google Scholar] [CrossRef]
- Nisar, A.; Thomas, M.S. Comprehensive Control for Microgrid Autonomous Operation with Demand Response. IEEE Trans. Smart Grid 2017, 8, 2081–2089. [Google Scholar] [CrossRef]
- Wang, X.; Chen, N.; Li, Y.; Wang, C.; Wang, X. Multi—Source Optimal Scheduling Framework of Active Distribution Network Based on Situation Linkage. Power Syst. Technol. 2017, 41, 349–354. [Google Scholar]
- Li, C.; Chen, X.; Zhang, P.; Zhang, Q. Multi—Time Scale Optimal Scheduling of Demand Response Considering Wind Power Prediction Error. Power Syst. Technol. 2018, 42, 487–494. [Google Scholar]
- Dutta, A.; Debbarma, S. Frequency Regulation in Deregulated Market Using Vehicle to Grid Services in Residential Distribution Network. IEEE Syst. J. 2017, 12, 2812–2820. [Google Scholar] [CrossRef]
- Ko, H.; Pack, S.; Leung VC, M. Mobility—Aware Vehicle—To—Grid Control Algorithm in Microgrids. IEEE Trans. Intell. Transp. Syst. 2018, 19, 2165–2174. [Google Scholar] [CrossRef]
- Sun, B.; Dong, H.; Chen, G. Intra—Day Optimal Scheduling Model of Joint Operation of Electric Vehicle—Wind—Storage Hybrid System. Renew. Energy Resour. 2018, 36, 1033–1038. [Google Scholar]
- Wang, H.; Wang, S.; Pan, Z.; Wang, J. Optimal Scheduling Method for Improving the Flexibility of Distribution Network with High Penetration of Distributed Generation. Autom. Electr. Power Syst. 2018, 42, 86–93. [Google Scholar]
- Xu, X.; Song, Y.; Yao, L.; Suo, R.; Yan, Z. Source-Network-Load Coordination Method of Active Distribution Network Based on Multi—Layer Electricity Price Response Mechanism. Autom. Electr. Power Syst. 2018, 42, 9–17–24. [Google Scholar]
- Masrur, M.A.; Skowronska, A.G.; Hancock, J.; Kolhoff, S.W.; McGrew, D.Z.; Vandiver, J.C.; Gatherer, J. Military—Based Vehicle—To—Grid and Vehicle—To—Vehicle Microgrid-System Architecture and Implementation. IEEE Trans. Transp. Electrif. 2018, 4, 157–171. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, J.; Poor, H.V. Risk—Aware Day—Ahead Scheduling and Real—Time Dispatch for Electric Vehicle Charging. IEEE Trans. Smart Grid 2017, 5, 693–702. [Google Scholar] [CrossRef]
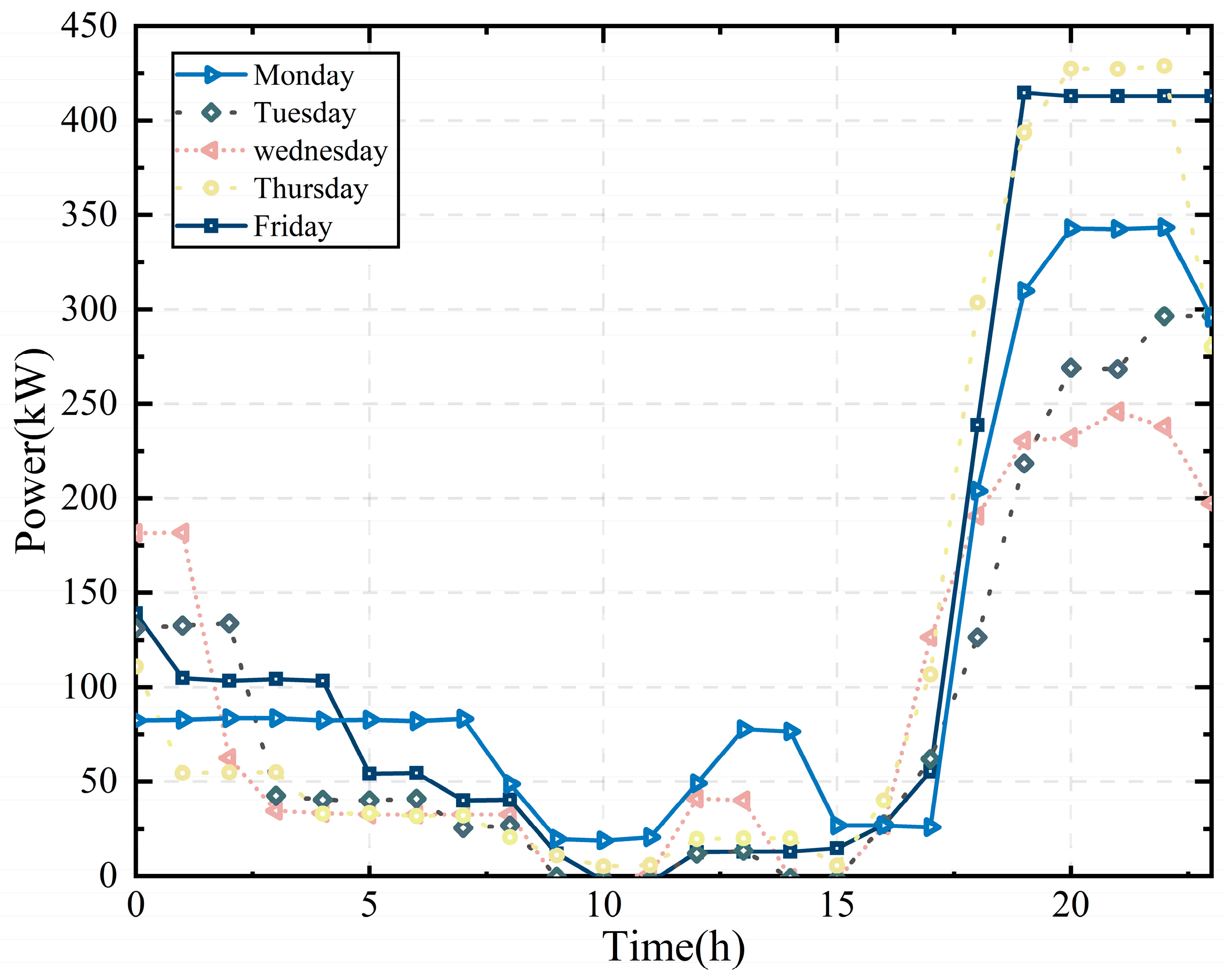
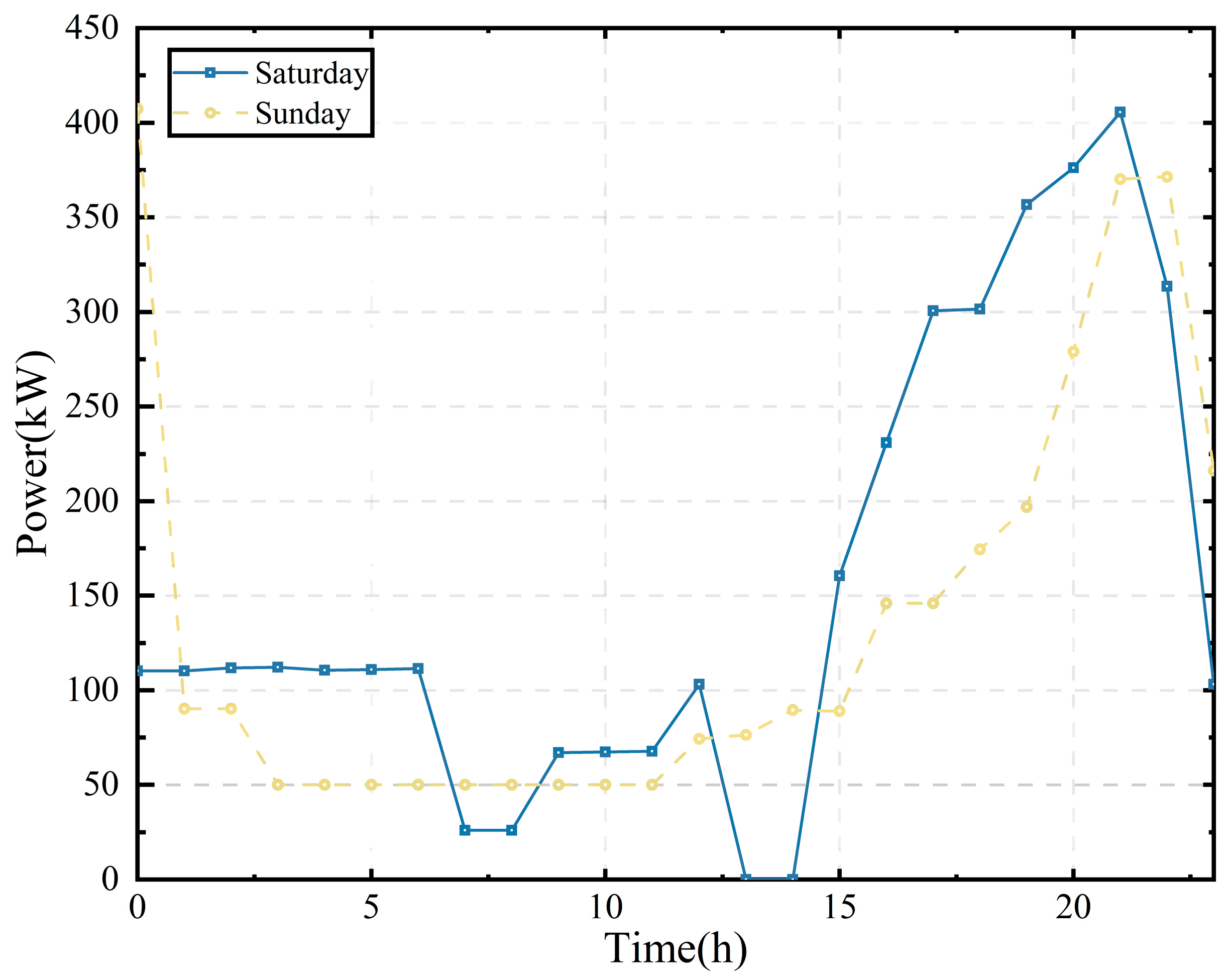


| Time | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
|---|---|---|---|---|---|---|---|
| Charging load | 2876 | 2196 | 3415 | 2757 | 2179 | 3864 | 3026 |
| Time | EV Load (kw.h) | Disorderly Charging | Orderly Charging | Discharge |
|---|---|---|---|---|
| Monday | 2876 | 45.23 | 35.78 | 30.37 |
| Tuesday | 2196 | 44.27 | 37.46 | 30.2 |
| Wednesday | 3415 | 46.08 | 36.42 | 32.15 |
| Thursday | 2757 | 45.87 | 37.94 | 28.76 |
| Friday | 2179 | 43.58 | 36.99 | 29.68 |
| Saturday | 3864 | 45.97 | 36.21 | 31.64 |
| Sunday | 3026 | 44.46 | 36.12 | 30.16 |
| Time | Disorderly Charging | Orderly Charging | Discharge |
|---|---|---|---|
| Monday | 555.84 | 366.84 | 272.50 |
| Tuesday | 542.44 | 393.32 | 269.07 |
| Wednesday | 594.34 | 421.39 | 284.78 |
| Thursday | 533.22 | 404.1 | 258.89 |
| Friday | 583.17 | 376.45 | 274.23 |
| Saturday | 570.47 | 379.43 | 279.87 |
| Sunday | 553.54 | 386 | 269.84 |
| Time | Disorderly Charging | Orderly Charging | Discharge |
|---|---|---|---|
| Monday | 3715.93 | 1040.54 | −458.75 |
| Tuesday | 2646.44 | 901.26 | −1053.82 |
| Wednesday | 4050.09 | 1402.8 | −112.28 |
| Thursday | 2633.89 | 901.81 | −1732.5 |
| Friday | 4013.12 | 1680.3 | −618.68 |
| Saturday | 4009.75 | 1478.86 | −616.16 |
| Sunday | 4719.75 | 1442 | −528.57 |
| Number of Experiments | MTTA | BPSO | BFOA | |||
|---|---|---|---|---|---|---|
| Mean | Standard | Mean | Standard | Mean | Standard | |
| 1 | 0.00000542 | 0.00000349 | 0.00006158 | 0.00001563 | 0.00061486 | 0.00012483 |
| 2 | 0.00000628 | 0.00000670 | 0.00005450 | 0.00009952 | 0.00091482 | 0.00001617 |
| 3 | 0.00000155 | 0.00000683 | 0.00000363 | 0.00002995 | 0.00003648 | 0.00051666 |
| 4 | 0.00000952 | 0.00000922 | 0.00009522 | 0.00006042 | 0.00031846 | 0.00064784 |
| 5 | 0.00000628 | 0.00000385 | 0.00003953 | 0.00006311 | 0.00016542 | 0.00016476 |
| Average | 0.00000582 | 0.00000603 | 0.00005088 | 0.00005371 | 0.00041523 | 0.00029405 |
| Scenario | ESS | Flexible Load | Electric Vehicle | Gas | Electricity Purchases | Total Cost |
|---|---|---|---|---|---|---|
| S1 | −602.368 | 1265.416 | 1201.2 | 2297.6 | 20,437.75 | 24,599.6 |
| S2 | 0 | 1480.92 | 2086.8 | 3040 | 21,250.63 | 27,858.35 |
| S3 | −506.579 | 0 | 1272.43 | 3472 | 22,302.63 | 26,540.48 |
| S4 | −602.368 | 1244.46 | 0 | 2480 | 22,906.35 | 26,028.45 |
| Scenario | Network Loss (kW-h) | EV User Costs (CNY) | System Control Costs (CNY) | Load Curve Standard Deviation | Total Voltage Deviation (%) |
|---|---|---|---|---|---|
| S1 | 1374.6 | −1142.8 | 25,083.945 | 612.3724 | 13.27 |
| S2 | 3441.3 | −1138.1 | 25,763.831 | 743.2586 | 25.85 |
| Scenario | ESS | Flexible Load | Electric Vehicle | Gas | Electricity Purchases | Total Cost |
|---|---|---|---|---|---|---|
| S1 | −602.368 | 1265.416 | 1201.2 | 2297.6 | 20,922.097 | 25,083.945 |
| S2 | −602.368 | 1265.416 | 1201.2 | 2297.6 | 21,601.983 | 25,763.831 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Luo, Y.; Yu, P.; Yu, R. Integrated Coordinated Control of Source–Grid–Load–Storage in Active Distribution Network with Electric Vehicle Integration. Processes 2025, 13, 1285. https://doi.org/10.3390/pr13051285
Wang S, Luo Y, Yu P, Yu R. Integrated Coordinated Control of Source–Grid–Load–Storage in Active Distribution Network with Electric Vehicle Integration. Processes. 2025; 13(5):1285. https://doi.org/10.3390/pr13051285
Chicago/Turabian StyleWang, Shunjiang, Yiming Luo, Peng Yu, and Ruijia Yu. 2025. "Integrated Coordinated Control of Source–Grid–Load–Storage in Active Distribution Network with Electric Vehicle Integration" Processes 13, no. 5: 1285. https://doi.org/10.3390/pr13051285
APA StyleWang, S., Luo, Y., Yu, P., & Yu, R. (2025). Integrated Coordinated Control of Source–Grid–Load–Storage in Active Distribution Network with Electric Vehicle Integration. Processes, 13(5), 1285. https://doi.org/10.3390/pr13051285








