Considering Active Support Capability and Intelligent Soft Open Point for Optimal Scheduling Strategies of Urban Microgrids
Abstract
:1. Introduction
- The active support capability evaluation and scheduling platform for urban microgrids is constructed. Through the operation condition monitoring module of the platform, the platform operator can obtain the real-time or historical operation data of distributed resources, providing data support for subsequent work.
- An evaluation model of the active support capability of urban microgrids is established. Some technical indicators are proposed for the active and reactive power support capabilities of urban microgrids to systematically evaluate the overall active support capability of urban microgrids, preparing the data basis and boundary conditions for the scheduling function.
- An active–reactive power coordinated optimization scheduling method for urban microgrids, considering the operating characteristics of distributed resources and incorporating an SOP, is proposed to obtain the optimal scheduling strategy. Based on the strategy, the operating costs of urban microgrids are reduced and the voltage deviation rate for urban microgrids is suppressed.
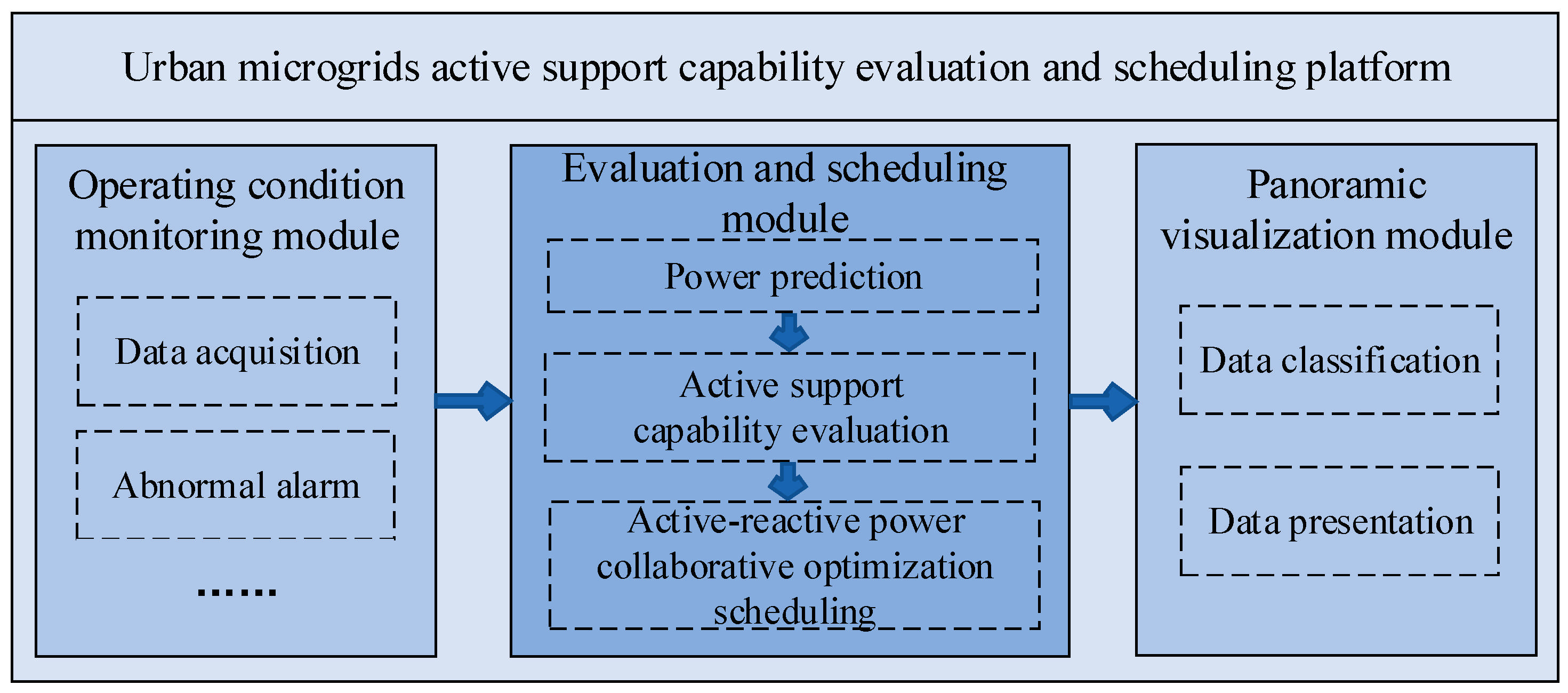
2. Evaluation and Control Platform for the Active Support Capability of Urban Microgrids
2.1. Operation Condition Monitoring Module
2.2. Evaluation and Scheduling Module
2.3. Panoramic Visualization Module
3. Active Support Capability Assessment
3.1. Active Power Support Capability Evaluation
3.1.1. BiLSTM Model
3.1.2. Active Power Support Capability Evaluation Model Based on BiLSTM Model
3.2. Reactive Power Support Capability Evaluation
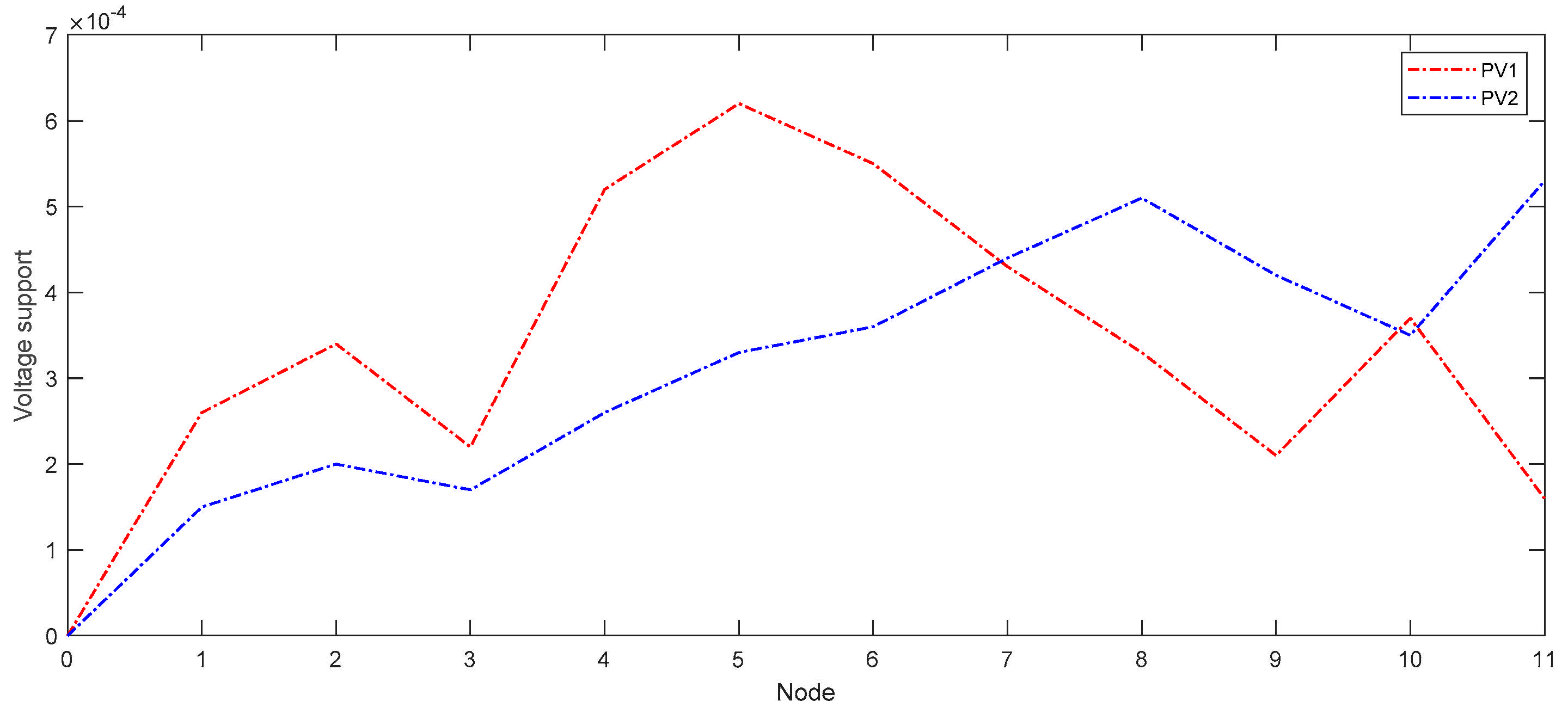
3.2.1. Voltage Support Degree
3.2.2. Reactive Power Regulation Ability
4. Active–Reactive Power Collaborative Optimization Scheduling
4.1. Objective Function
4.2. Constraint Condition
4.2.1. Power Flow Constraints
4.2.2. Photovoltaic Constraints
4.2.3. Energy Storage Constraints
4.2.4. Electric Vehicle Constraints
4.2.5. Temperature Control Load Constraint
4.2.6. SOP Constraints
4.3. Introduction of Stochasticity
5. Case Studies
5.1. Base Data
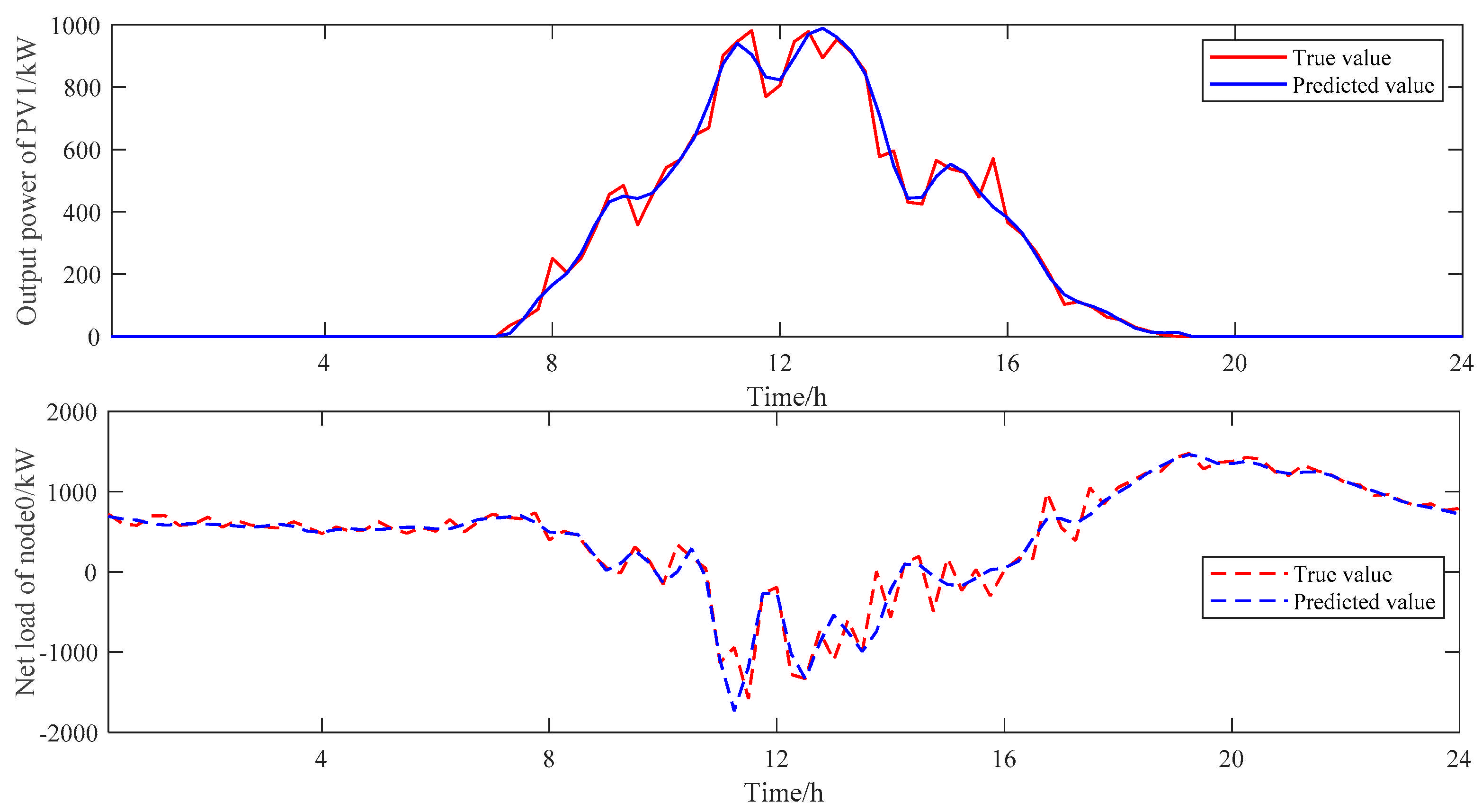
5.2. Active Support Capability Assessment Results
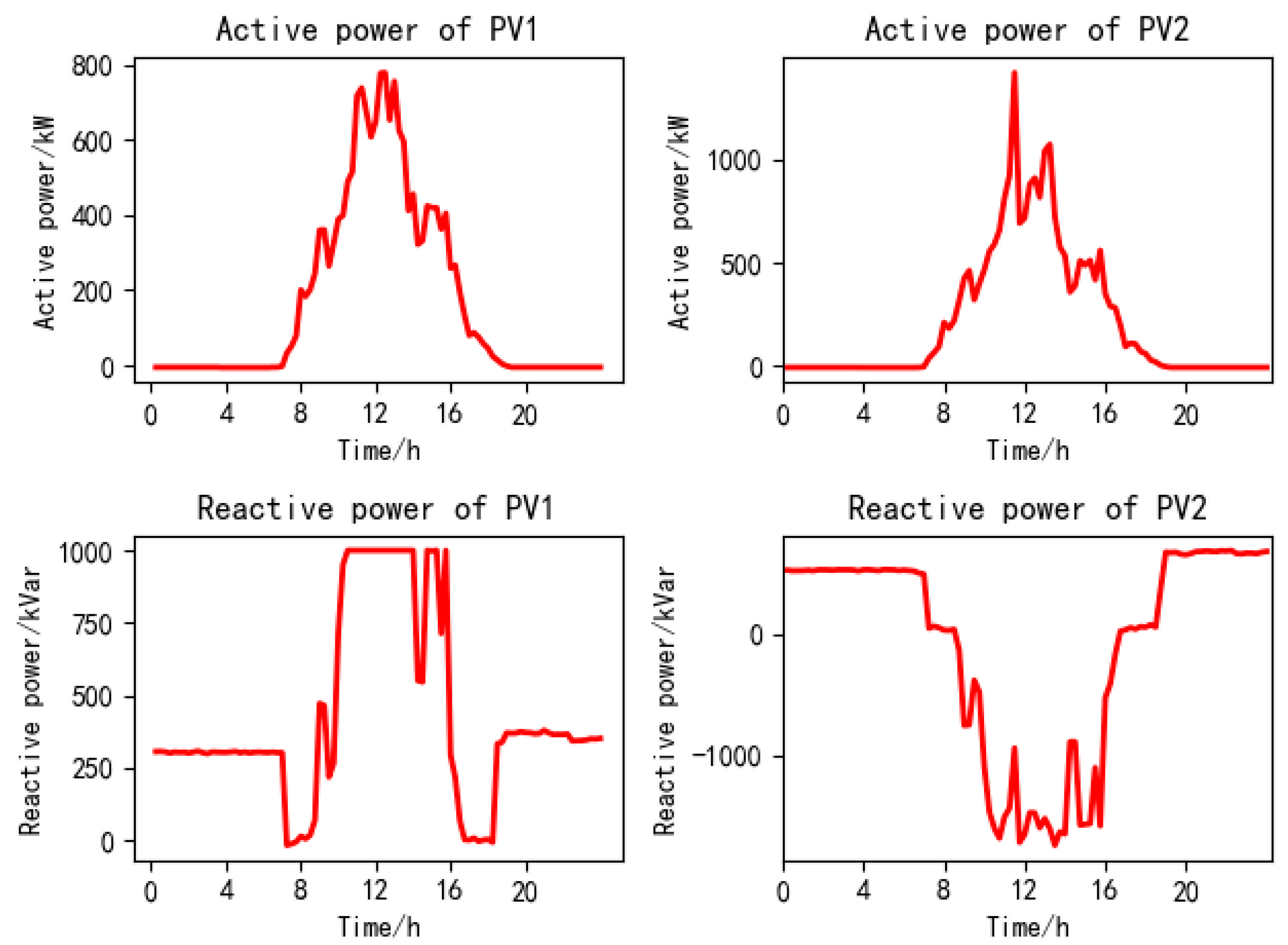
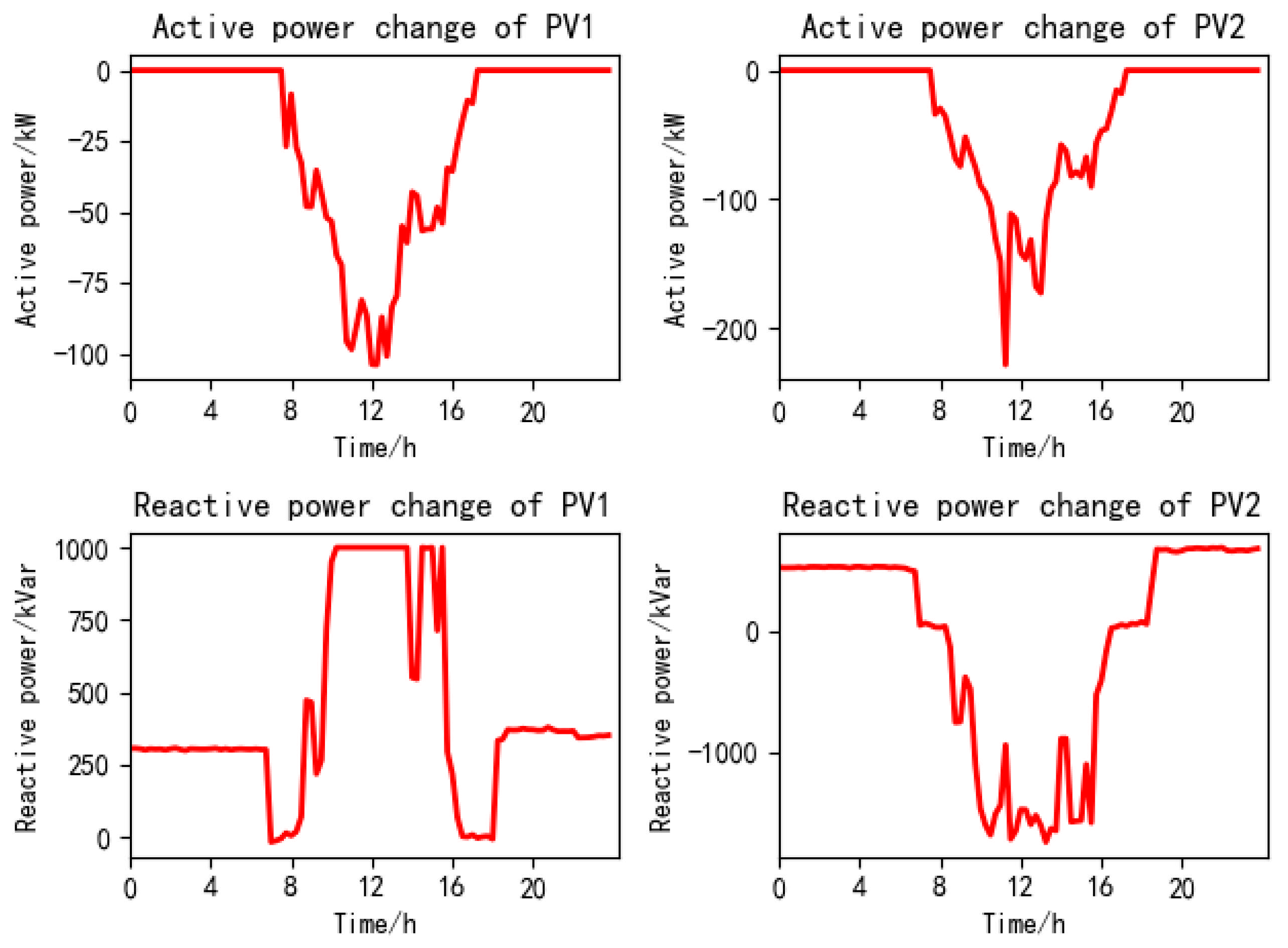
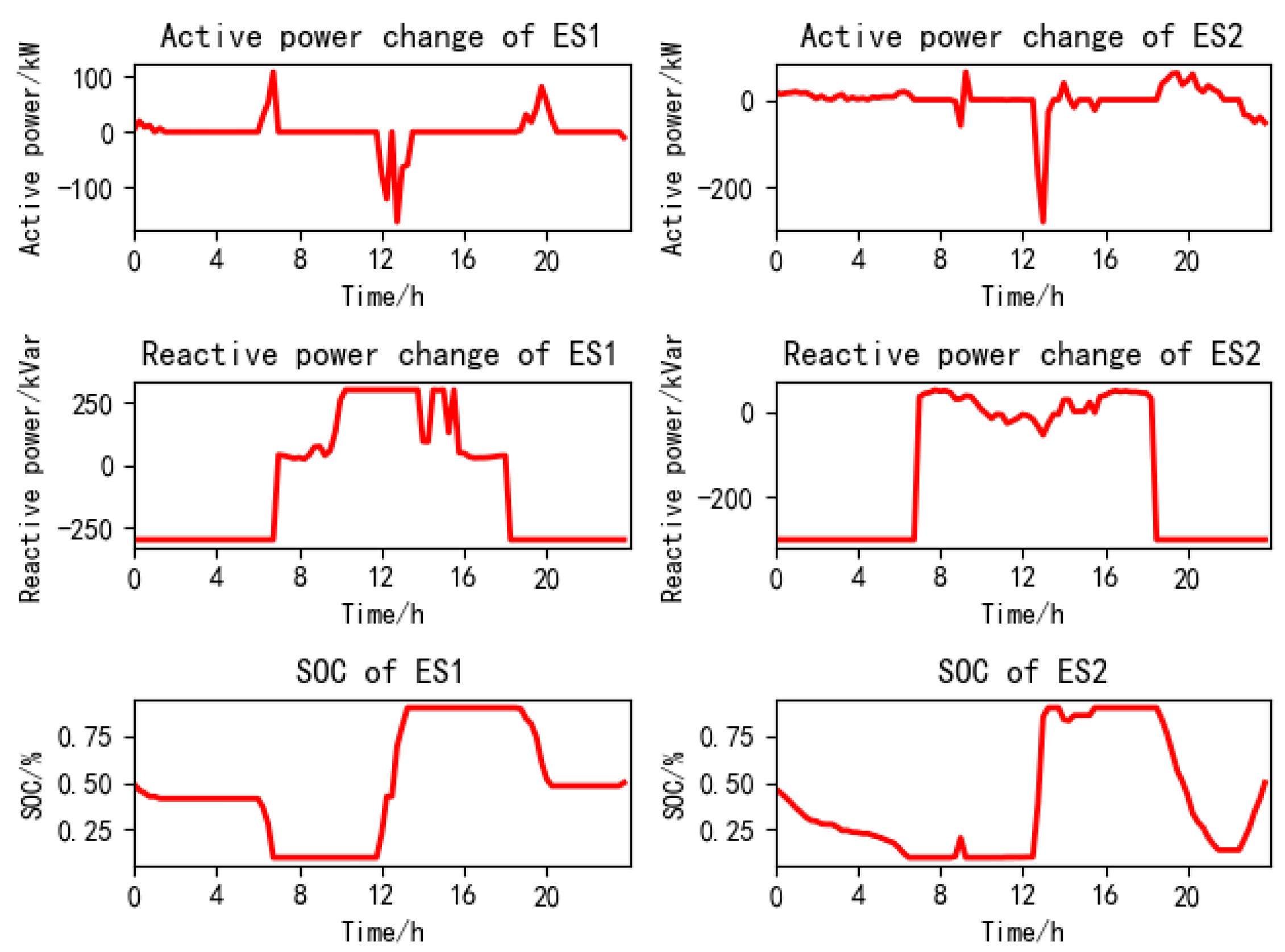
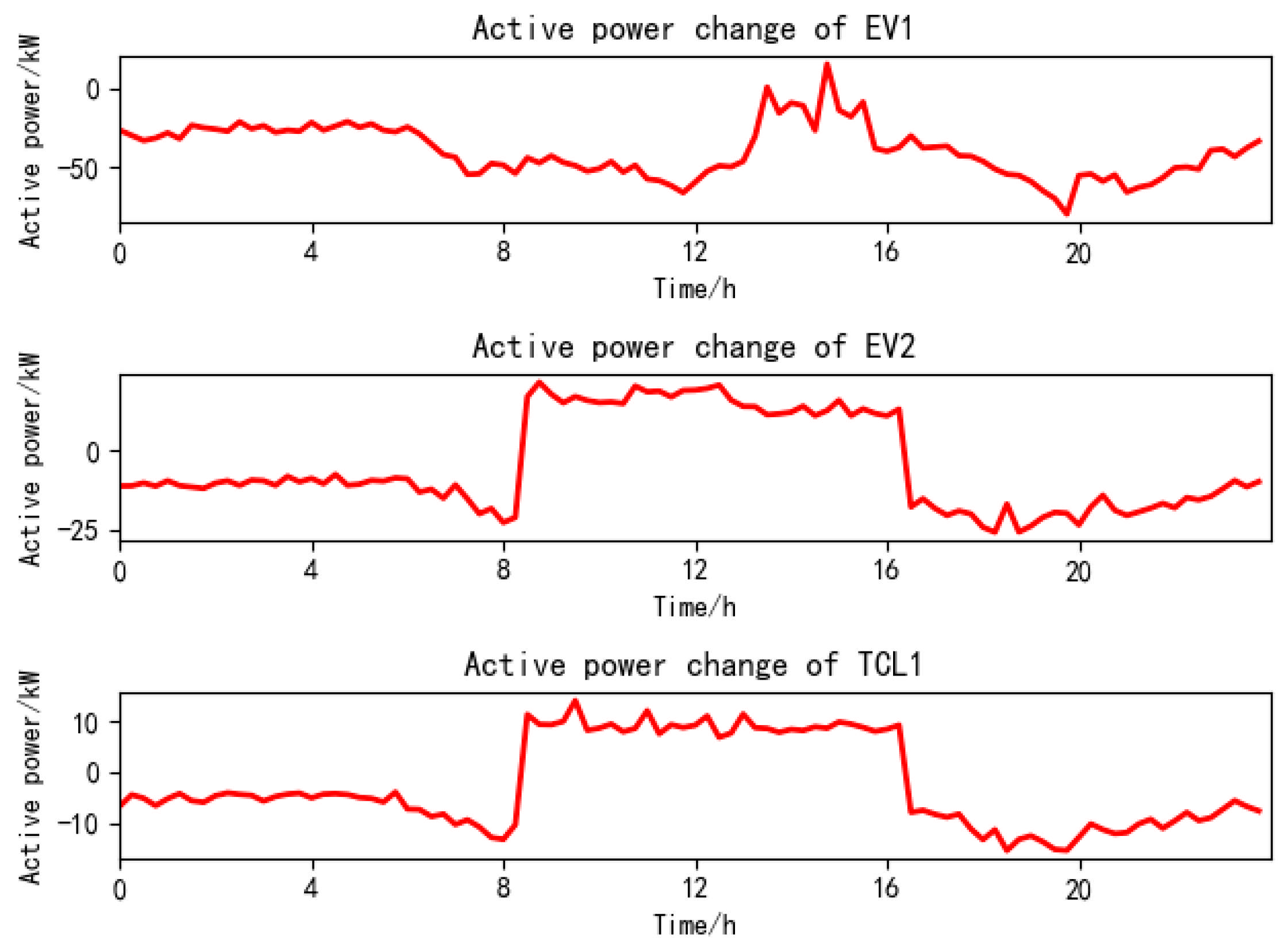
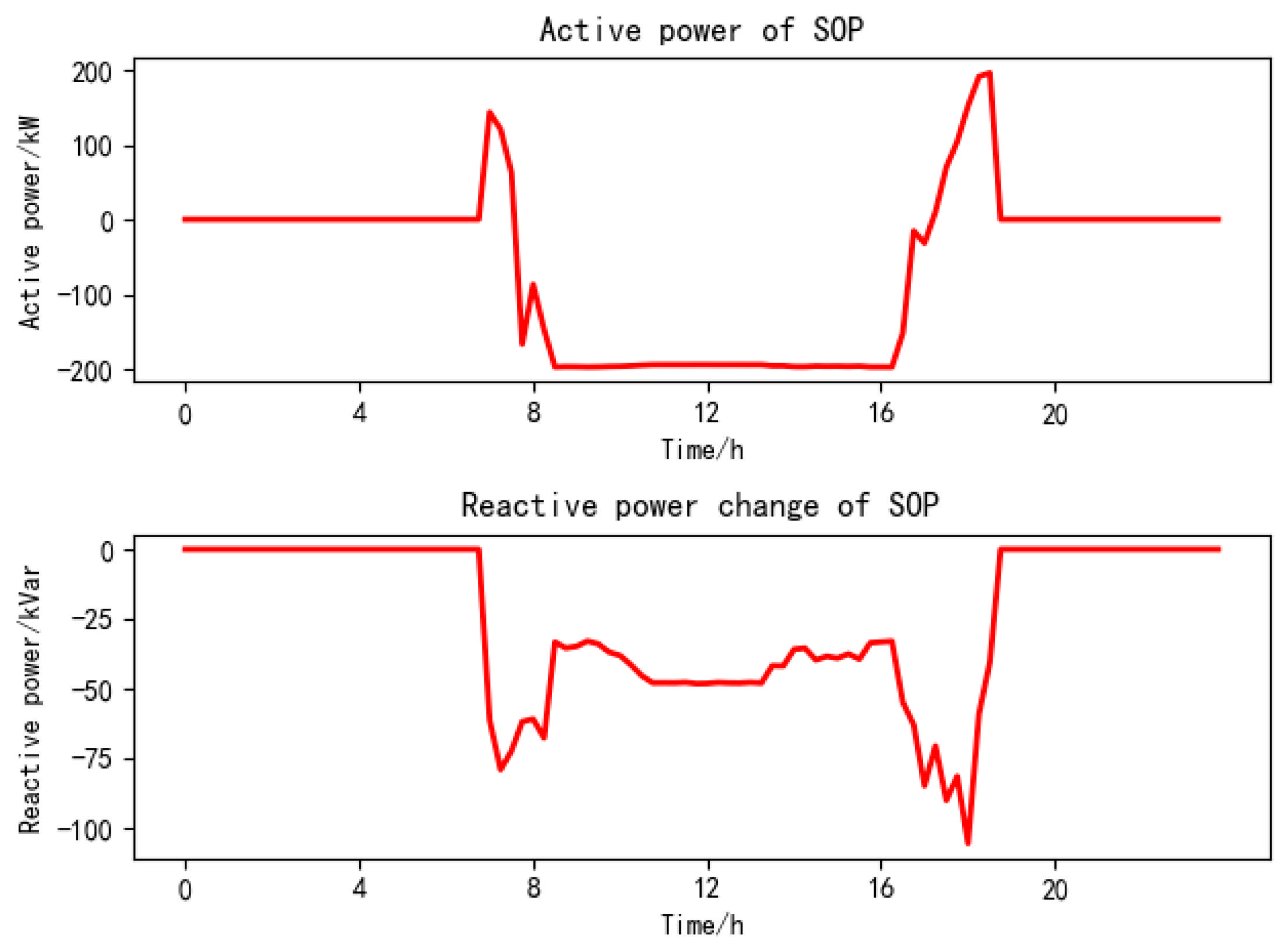
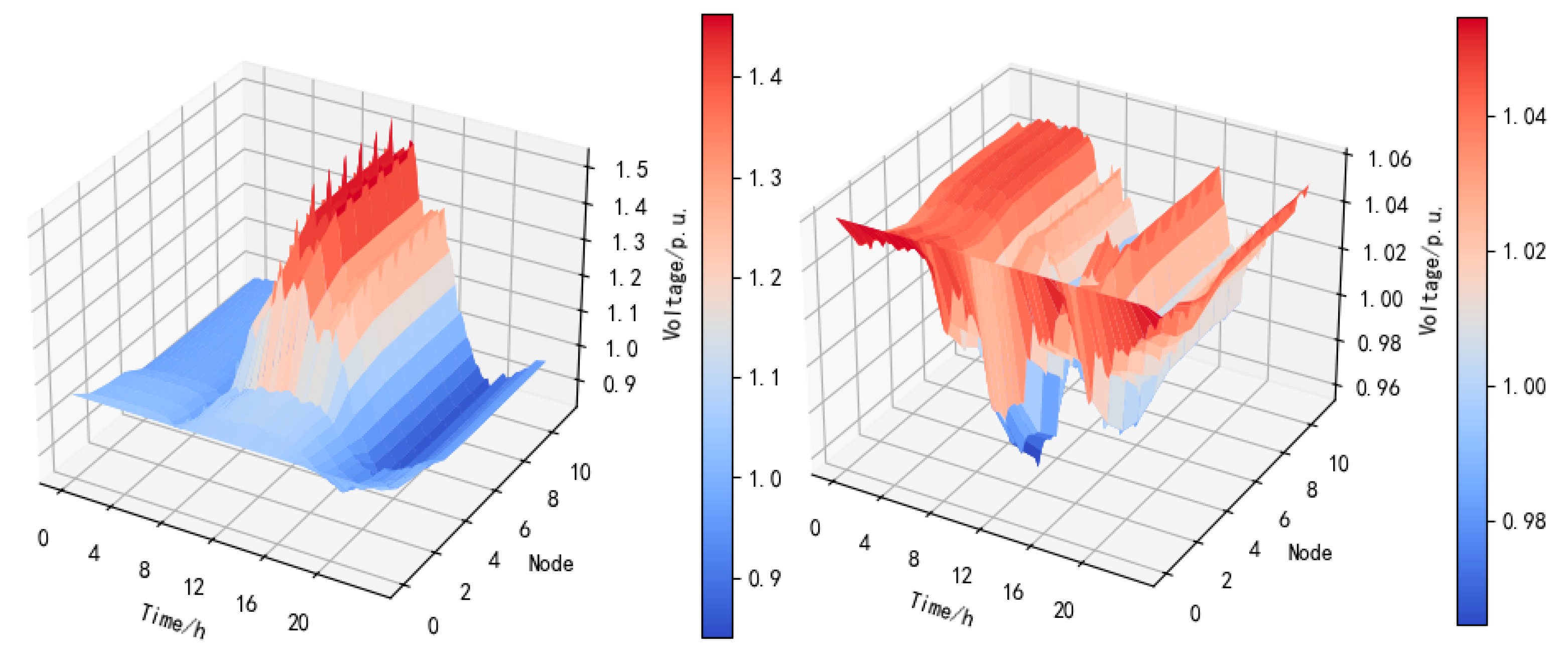
5.3. Collaborative Active–Reactive Power Optimization Scheduling Results
5.4. Comparative Results and Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameters | |
| Maximum/minimum adjustable reactive power of PV at time t of node i | |
| Active power output of PV at time t of node i | |
| Inverter capacity of PV/ES at node i | |
| Maximum/minimum adjustable reactive power of ES at time t of node i | |
| Conductance of line ij at time t | |
| // | Operating cost of PV/ES/SOP at time t of node i |
| // | Unit power cost of PV/ES/SOP |
| /// | Adjustment cost of PV/SOP/EV/TCL at time t |
| Rated voltage value of node i | |
| / | Upper limits of active/reactive power output of PV at time t of node i |
| Upper limit of PV active power reduction at time t of node i | |
| Upper/lower limits of charge power of ES at time t of node i | |
| Upper/lower limits of discharge power of ES at time t of node i | |
| / | Upper/lower limits of stored energy of ES at time t of node i |
| / | Charge/discharge efficiency of ES |
| Upper/lower limits of charging power of EV at time t of node i | |
| Charging efficiency of EV | |
| / | Upper/lower limits of operating power of TCL at time t of node i |
| Reference value of indoor temperature | |
| Dead zone value of indoor temperature | |
| / | Indoor/outdoor temperature |
| / | Equivalent thermal resistance/capacitance |
| Coefficient of performance of TCL | |
| Maximum/minimum reactive power allowed to be injected by node connected at ends of SOP | |
| Loss coefficient of SOP | |
| Capacity of SOP | |
| / | Predicted PV output |
| Variables | |
| Reactive power output of PV at time t of node i | |
| Active/reactive power of ES at time t of node i | |
| Voltage amplitude at time t of node i | |
| Phase angle of line ij at time t | |
| Active power regulation of SOP at time t of node i | |
| // | Active power adjustment of PV/EV/TC at time t of node i |
| / | Charge/discharge power of ES at time t of node i |
| Stored energy of ES at time t of node i | |
| Charging power of EV at time t of node i | |
| Storage energy of EV at time t of node i | |
| Operating power of TCL at time t of node i | |
| Active power injected by node i/j connected at both ends of SOP at time t | |
| / | Reactive power injected by node i/j connected at both ends of SOP at time t |
| / | Prediction errors of PV/load at time t of node i in scenario s |
| / | Actual PV output/load demand at time t of node i in scenario s |
| / | Binary parameters of interval l associated with each predicted PV output and load demand at time t of node i in scenario s |
| / | Probabilities of interval l associated with each predicted PV output and load demand at time t of node i in scenario s |
References
- Ru, N.; Zhang, Z.; Zhang, H. Carbon Emission Peak and Carbon Neutrality under the New Target and Vision. In Proceedings of the 2021 International Conference on Advanced Electrical Equipment and Reliable Operation (AEERO), Beijing, China, 15–17 October 2021; pp. 1–5. [Google Scholar]
- Jafari, M.R.; Parniani, M.; Ravanji, M.H. Decentralized Control of OLTC and PV Inverters for Voltage Regulation in Radial Distribution Networks with High PV Penetration. IEEE Trans. Power Deliv. 2022, 37, 4827–4837. [Google Scholar] [CrossRef]
- Bonthagorla, P.K.; Mikkili, S. Optimal PV Array Configuration for Extracting Maximum Power Under Partial Shading Conditions by Mitigating Mismatching Power Losses. CSEE J. Power Energy Syst. 2022, 8, 499–510. [Google Scholar]
- Fan, H.; Wu, H.; Li, S.; Han, S.; Ren, J.; Huang, S.; Zou, H. Optimal Scheduling Method of Combined Wind–Photovoltaic–Pumped Storage System Based on Improved Bat Algorithm. Processes 2025, 13, 101. [Google Scholar] [CrossRef]
- Aghamohamadi, M.; Mahmoudi, A.; Haque, M.H. Two-Stage Robust Sizing and Operation Co-Optimization for Residential PV–Battery Systems Considering the Uncertainty of PV Generation and Load. IEEE Trans. Industr. Inform. 2021, 17, 1005–1017. [Google Scholar] [CrossRef]
- Lee, J.-W.; Kim, M.-K. An Evolutionary Game Theory-Based Optimal Scheduling Strategy for Multiagent Distribution Network Operation Considering Voltage Management. IEEE Access 2022, 10, 50227–50241. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Yan, N.; Ma, R. Cooperative Dispatch of Distributed Energy Storage in Distribution Network With PV Generation Systems. IEEE Trans. Appl. Superconduct. 2021, 31, 1–4. [Google Scholar] [CrossRef]
- Linlin, Y.; Lihua, Z.; Gaojun, M.; Feng, Z.; Wanxun, L. Research on Multi-Objective Reactive Power Optimization of Power Grid With High Proportion of New Energy. IEEE Access 2022, 10, 116443–116452. [Google Scholar] [CrossRef]
- Sheng, H.; Wang, C.; Li, B.; Liang, J.; Yang, M.; Dong, Y. Multi-timescale Active Distribution Network Scheduling Considering Demand Response and User Comprehensive Satisfaction. IEEE Trans. Ind. Appl. 2021, 57, 1995–2005. [Google Scholar] [CrossRef]
- Jafarian, M.; Nouri, A.; Rigoni, V.; Keane, A. Real-Time Estimation of Support Provision Capability for Poor-Observable Distribution Networks. IEEE Trans. Power Syst. 2023, 38, 1806–1819. [Google Scholar] [CrossRef]
- Muzumdar, A.A.; Modi, C.N.; Vyjayanthi, C. Designing a Robust and Accurate Model for Consumer-Centric Short-Term Load Forecasting in Microgrid Environment. IEEE Syst. J. 2022, 16, 2448–2459. [Google Scholar] [CrossRef]
- Xia, M.; Shao, H.; Ma, X.; de Silva, C.W. A Stacked GRU-RNN-Based Approach for Predicting Renewable Energy and Electricity Load for Smart Grid Operation. IEEE Trans. Industr. Inform. 2021, 17, 7050–7059. [Google Scholar] [CrossRef]
- Rubasinghe, O.; Zhang, X.; Chau, T.K.; Chow, Y.H.; Fernando, T.; Iu, H.H.-C. A Novel Sequence to Sequence Data Modelling Based CNN-LSTM Algorithm for Three Years Ahead Monthly Peak Load Forecasting. IEEE Trans. Power Syst. 2024, 39, 1932–1947. [Google Scholar] [CrossRef]
- Petroșanu, D.-M.; Pîrjan, A. Electricity Consumption Forecasting Based on a Bidirectional Long-Short-Term Memory Artificial Neural Network. Sustainability 2021, 13, 104. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Guerrero, J.M. A Model Predictive Power Control Method for PV and Energy Storage Systems with Voltage Support Capability. IEEE Trans. Smart Grid 2020, 11, 1018–1029. [Google Scholar] [CrossRef]
- Dey, B.; Krishnamurthy, S.; Fose, N.; Ratshitanga, M.; Moodley, P. A Metaheuristic Approach to Analyze the Techno-Economical Impact of Energy Storage Systems on Grid-Connected Microgrid Systems Adapting Load-Shifting Policies. Processes 2025, 13, 65. [Google Scholar] [CrossRef]
- Ai, Y.; Du, M.; Pan, Z.; Li, G. The optimization of reactive power for distribution network with PV generation based on NSGA-III. CPSS TPEA 2021, 6, 193–200. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, Y.; Yi, Z.; Tu, Z.; Rong, S.; Zhao, G. Coordinated Operation Strategy of Energy Storages with Reactive Power Compensators in Joint Active and Reactive Power Market Environment. Processes 2025, 13, 16. [Google Scholar] [CrossRef]
- Martínez-Caballero, L.; Kot, R.; Milczarek, A.; Malinowski, M. Comparison of Energy Storage Management Techniques for a Grid-Connected PV- and Battery-Supplied Residential System. Electronics 2024, 13, 87. [Google Scholar] [CrossRef]
- Zhang, S.; Fang, Y.; Zhang, H.; Cheng, H.; Wang, X. Maximum Hosting Capacity of Photovoltaic Generation in SOP-Based Power Distribution Network Integrated With Electric Vehicles. IEEE Trans. Industr. Inform. 2022, 18, 8213–8224. [Google Scholar] [CrossRef]
- Meteorological Data. 2024. Available online: https://xihe-energy.com/ (accessed on 7 February 2025).
- Shi, H.; Xu, M.; Li, R. Deep Learning for Household Load Forecasting—A Novel Pooling Deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Hu, H.; Hu, Q.; Tan, G.; Zhang, Y.; Lin, Z. A Multi-Layer Model Based on Transformer and Deep Learning for Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2024, 25, 443–451. [Google Scholar] [CrossRef]
- Guo, J.; Han, M.; Zhan, G.; Liu, S. A Spatio-Temporal Deep Learning Network for the Short-Term Energy Consumption Prediction of Multiple Nodes in Manufacturing Systems. Processes 2022, 10, 476. [Google Scholar] [CrossRef]
- Dupačová, J.; Gröwe-Kuska, N.; Römisch, W. Scenario reduction in stochastic programming. Math. Program. 2003, 95, 493–511. [Google Scholar] [CrossRef]
- Ye, L.; Zhang, C.; Tang, Y.; Zhong, W.; Zhao, Y. Hierarchical Model Predictive Control Strategy Based on Dynamic Active Power Dispatch for Wind Power Cluster Integration. IEEE Trans. Power Syst. 2019, 34, 4617–4629. [Google Scholar] [CrossRef]
- Ding, T.; Liu, S.; Yuan, W.; Bie, Z.; Zeng, B. A Two-Stage Robust Reactive Power Optimization Considering Uncertain Wind Power Integration in Active Distribution Networks. IEEE Trans. Sustain. Energy 2016, 7, 301–311. [Google Scholar] [CrossRef]



| PV | Net Load | ||||
|---|---|---|---|---|---|
| Maximum Confidence Interval Range | Minimum Confidence Interval Range | Point Fluctuation Amplitude | Maximum Confidence Interval Range | Minimum Confidence Interval Range | Point Fluctuation Amplitude |
| 472.86 | 0.45 | 92.24 | 279.93 | 0.57 | 125.41 |
| Prediction Object | Evaluation Index | Prediction Method | |||||
|---|---|---|---|---|---|---|---|
| BiLSTM | LSTM | RNN | GRU | Transformer | GCN | ||
| PV | RMSE | 31.97 | 39.84 | 51.76 | 47.52 | 33.41 | 45.13 |
| MAE | 14.39 | 16.31 | 21.44 | 19.76 | 15.68 | 18.89 | |
| Net load | RMSE | 176.81 | 188.29 | 190.13 | 196.52 | 182.73 | 191.42 |
| MAE | 99.63 | 103.52 | 105.61 | 109.48 | 102.59 | 107.33 | |
| Scheme | Network Loss Cost ($) | Operating Cost of DERs ($) | Penalty Cost of Demand Response ($) | Total Cost ($) | Voltage Deviation Rate (%) |
|---|---|---|---|---|---|
| Scheme 1 | 1796.14 | 387.86 | 59.42 | 2243.42 | 3.26 |
| Scheme 2 | 2326.47 | 472.81 | 0 | 2799.28 | 11.85 |
| Scheme 3 | 1894.03 | 331.77 | 66.27 | 2292.07 | 3.43 |
| Scheme 4 | 1688.72 | 412.34 | 87.53 | 2188.59 | 6.89 |
| Scheme 5 | 2105.36 | 425.07 | 69.48 | 2599.91 | 3.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Si, T.; Qiu, Z.; Yu, L.; Zhou, Q.; Liu, X.; Zhang, K. Considering Active Support Capability and Intelligent Soft Open Point for Optimal Scheduling Strategies of Urban Microgrids. Processes 2025, 13, 1338. https://doi.org/10.3390/pr13051338
Zhu Z, Si T, Qiu Z, Yu L, Zhou Q, Liu X, Zhang K. Considering Active Support Capability and Intelligent Soft Open Point for Optimal Scheduling Strategies of Urban Microgrids. Processes. 2025; 13(5):1338. https://doi.org/10.3390/pr13051338
Chicago/Turabian StyleZhu, Zhuowen, Tuyou Si, Zejian Qiu, Lili Yu, Qian Zhou, Xiao Liu, and Kuan Zhang. 2025. "Considering Active Support Capability and Intelligent Soft Open Point for Optimal Scheduling Strategies of Urban Microgrids" Processes 13, no. 5: 1338. https://doi.org/10.3390/pr13051338
APA StyleZhu, Z., Si, T., Qiu, Z., Yu, L., Zhou, Q., Liu, X., & Zhang, K. (2025). Considering Active Support Capability and Intelligent Soft Open Point for Optimal Scheduling Strategies of Urban Microgrids. Processes, 13(5), 1338. https://doi.org/10.3390/pr13051338






