Numerical Simulation of a Wall-Flow Particulate Filter Made of Biomorphic Silicon Carbide Able to Fit Different Fuel/Biofuel Inputs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Description
2.2. Experimental Validation and Model Calibration for a bioSiC DPF
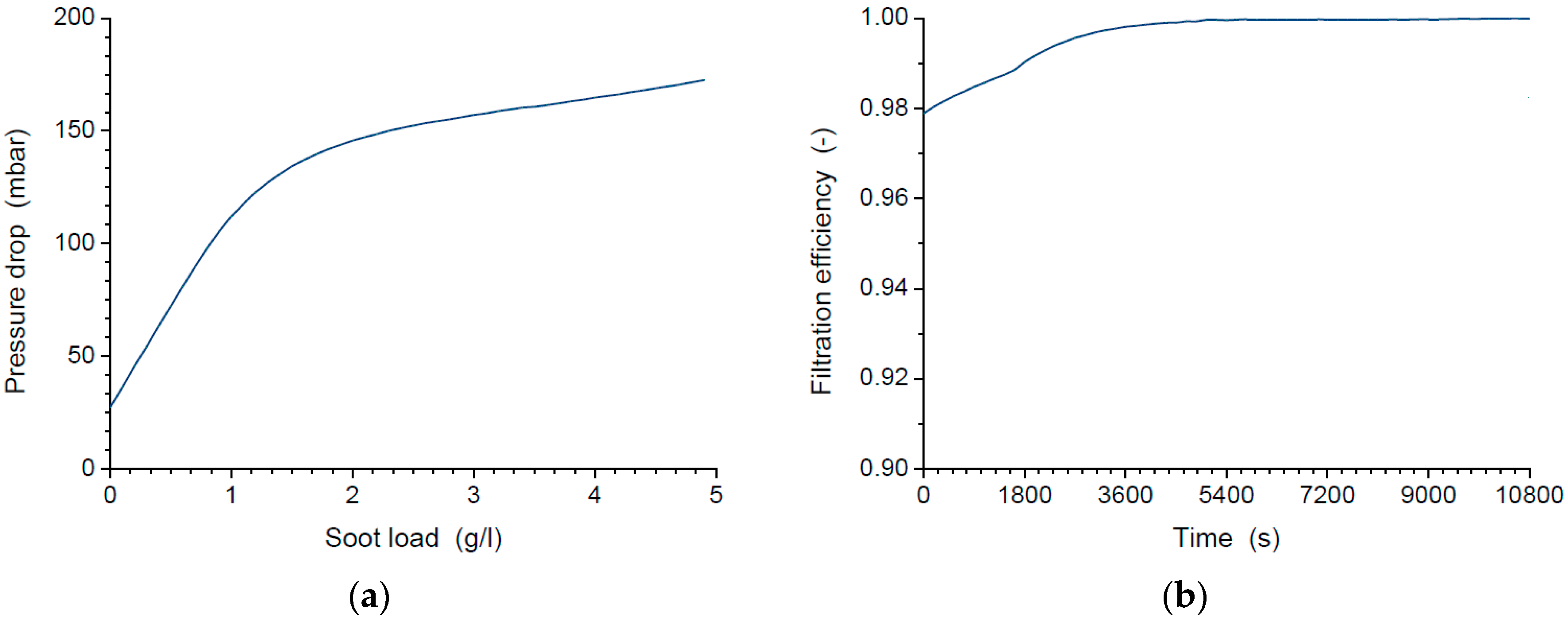
- The parameters related to the filtration efficiency are calibrated. The initial diffusion and interception collection efficiencies ( and ), as well as the diffusion mechanism exponent of the Peclet number (), are adjusted by matching up the initial filtration efficiency of the real filter, with the initial filtration efficiency of the modeled filter, for the different ranges of particle diameters. The filtration of small particles is mainly governed by the diffusion mechanism, while the filtration of larger particles is mainly governed by the interception mechanism. The exponent of the Peclet number affects the gradient of the efficiency curve on the right-hand side of the curve (from 10 to 100 nm). Then, the growth rate of the efficiency curve is adjusted by changing the gradient parameter in wall filtration efficiency (). Calibrating these parameters, the overlap between the theoretical evolution curve of the filtration efficiency and the real curve is achieved.
- The parameters related to the pressure drop are calibrated. If the permeability of the clean substrate is correct, the initial pressure drop resulting from the simulation should match with the real drop. From then on, there are two consecutive filtration stages. The first stage, the wall filtration stage, allows the calibration of the permeability of the loaded substrate (). Its value is adjusted by matching up the pressure drop of the real filter with the pressure drop of the modeled filter in the first growing part of the curves up to the transition phase. The second stage, the cake filtration stage, allows calibrating the soot permeability (). The soot permeability directly affects the gradient of the pressure drop during cake filtration, so the estimated value can be obtained by matching the experimental curve’s slope. Calibrating these parameters, the overlap between the theoretical evolution curve of the pressure drop and the experimental is achieved.
2.3. Extrapolation to a Real-Size Automotive DPF
- -
- A standard concentration of species (78% N2, 10% O2, 5% CO2, 6% H2O, 0.1% CO) was introduced
- -
- The volume flow rate was 175 m3 h−1 (0.035 kg s−1.) accordingly to the size of the new DPF. The estimation of the mass flow rate was derived from the engine map of a four-cylinder 1997 cc diesel engine (PSA DW10ATED) operating at 1800 rpm and 100 Nm [52].
- -
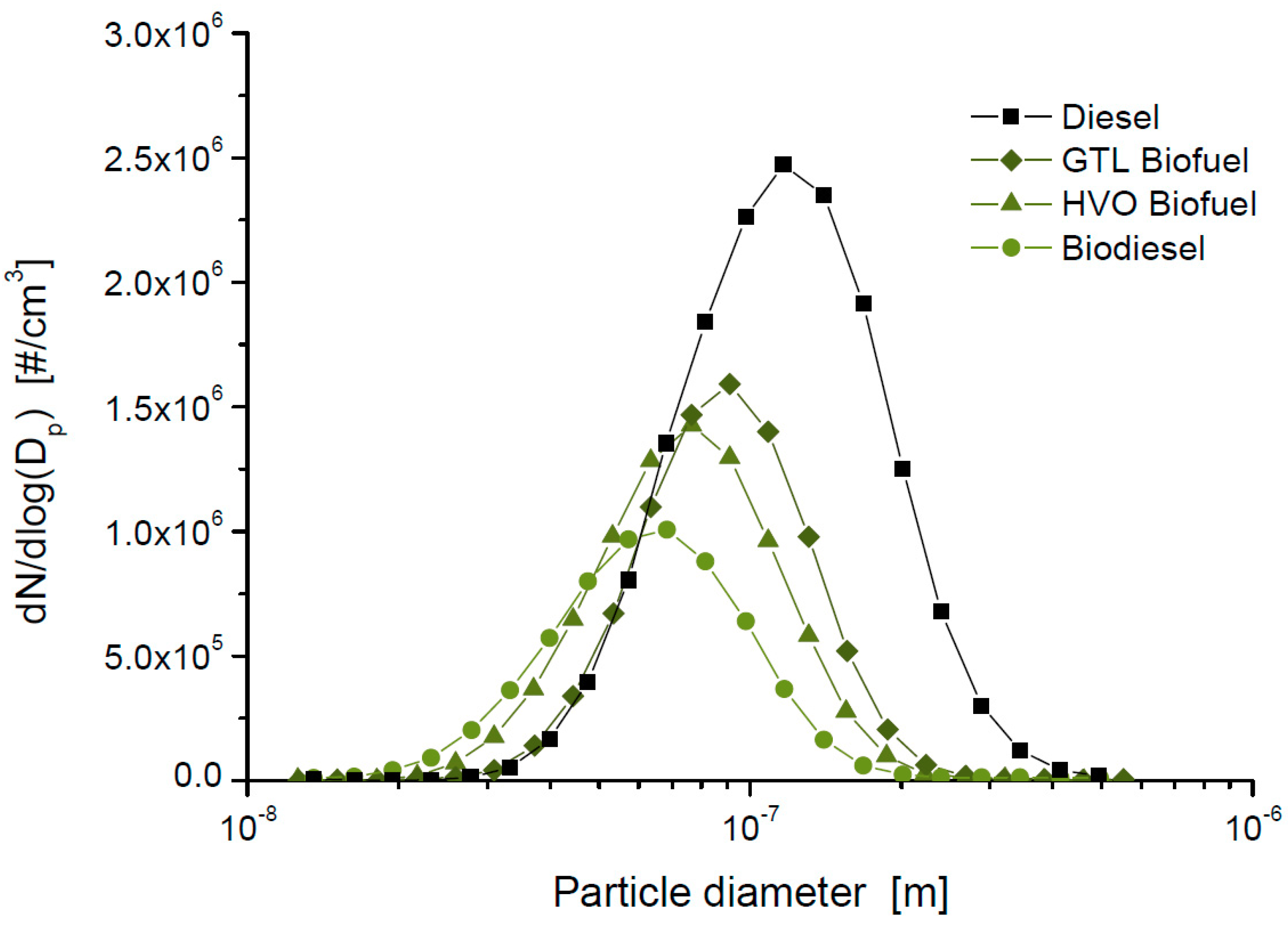
- The initial particle size distribution and concentration was set to the standard values of a commercial automotive, light-duty diesel engine. The parameters used to characterize the distribution curve were taken from a 90 CV four-cylinder 1248 cc diesel engine (General Motors Z13DTH), belonging to the Department of Applied Science and Technology (DISAT) of the Politecnico di Torino. Its particulate (PM) emissions were measured with a scanning mobility particle sizer (SMPS), showing a log-normal distribution with mean particle diameter equal to 80 nm and standard deviation equal to 1.41. From this distribution, multiplying by the effective density of the particles in each size range, a soot production of 4.15 g h−1 was calculated. The effective density was calculated with an empirical correlation [55]: .
- -
3. Results
Filtration Efficiency and Pressure Drop of a Full-Size bioSiC DPF
4. Discussion
4.1. Comparison with Commercial DPFs
4.2. Behavior under a New European Driving Cycle (NEDC)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameter for wall permeability correction (m kg−1) | |
| Parameter for wall permeability correction (m4 kg−2) | |
| Slip correction factor (m s (kg mole K)−0.5) | |
| Ergun coefficient (-) | |
| Parameter in the diffusional efficiency (-) | |
| Parameter in the direct interception efficiency (-) | |
| Channel width (m) | |
| Fiber diameter (m) | |
| Fractal dimension (-) | |
| Particle diffusion coefficient (m2 s−1) | |
| Permeability (m−2) | |
| Knudsen number (-) | |
| Kubawara hydrodynamic factor (-) | |
| Molecular weight (kg mole−1) | |
| Number of walls (-) | |
| Exponent of the Peclet number for the diffusion mechanism (-) | |
| Pressure (Pa) | |
| Peclet number (-) | |
| Soot primary particle radius (m) | |
| Interception parameter | |
| Gas constant (J mole−1 K−1) | |
| Maximum radius of aggregate cluster (m) | |
| Temperature (K) | |
| Velocity (m s−1) | |
| Thickness (m) | |
| Axial dimension | |
| Constant in the channel pressure drop correlation (-) | |
| Porosity (-) | |
| Dynamic viscosity (Pa s) | |
| Filtration efficiency (-) | |
| Density (kg m−3) | |
| Soot primary particle density (kg m−3) | |
| Subscripts | |
| Initial (clean) state | |
| Diffusion | |
| Identifier of the channel: 1 for inlet channels, and 2 for outlet channels | |
| Unit fiber | |
| Particles deposit | |
| Interception | |
| Soot layer | |
| Wall | |
References
- Barroso, J.M. Regulation No 459/2012. Off. J. Eur. Comm. 2012, 142, 16–24. [Google Scholar]
- United States: Cars and Light-Duty Trucks: Tier 3. Available online: www.dieselnet.com/standards/us/ld_t3 (accessed on 26 June 2019).
- Hooftman, N.; Messagie, M.; Van Mierlo, J.; Coosemans, T. A review of the European passenger car regulations—Real driving emissions vs local air quality. Renew. Sustain. Energy Rev. 2018, 86, 1–21. [Google Scholar] [CrossRef]
- European Automobile Manufacturers’ Association. WLTP Facts. Available online: http://wltpfacts.eu (accessed on September 15, 2019).
- Regulation (EU) 2016/1628 of the European Parliament and the council, of 14 September 2016. Off. J. Eur. Union 2016, 252, 53–117.
- Reşitoğlu, İ.A.; Altinişik, K.; Keskin, A. The pollutant emissions from diesel-engine vehicles and exhaust aftertreatment systems. Clean Technol. Environ. Policy 2015, 17, 15–27. [Google Scholar] [CrossRef] [Green Version]
- The European Parliament and the Council Directive 2003/30/EC of the European Parliament and of the Council of 8 May 2003 on the promotion of the use of biofuels or other renewable fuels for transport. Off. J. Eur. Union 2003, L 123, 42–46.
- Wu, F.; Wang, J.; Chen, W.; Shuai, S. A study on emission performance of a diesel engine fueled with five typical methyl ester biodiesels. Atmos. Environ. 2009, 43, 1481–1485. [Google Scholar] [CrossRef]
- Tayari, S.; Abedi, R.; Rahi, A. Comparative assessment of engine performance and emissions fueled with three different biodiesel generations. Renew. Energy 2020, 147, 1058–1069. [Google Scholar] [CrossRef]
- Verma, P.; Stevanovic, S.; Zare, A.; Dwivedi, G.; Van, T.C.; Davidson, M.; Rainey, T.; Brown, R.J.; Ristovski, Z.D. An overview of the influence of biodiesel, alcohols, and various oxygenated additives on the particulate matter emissions from diesel engines. Energies 2019, 12, 1987. [Google Scholar] [CrossRef] [Green Version]
- Ogunkunle, O.; Ahmed, N.A. A review of global current scenario of biodiesel adoption and combustion in vehicular diesel engines. Energy Rep. 2019, 5, 1560–1580. [Google Scholar] [CrossRef]
- Mofijur, M.; Rasul, M.G.; Hyde, J.; Azad, A.K.; Mamat, R.; Bhuiya, M.M.K. Role of biofuel and their binary (diesel-biodiesel) and ternary (ethanol-biodiesel-diesel) blends on internal combustion engines emission reduction. Renew. Sustain. Energy Rev. 2016, 53, 265–278. [Google Scholar] [CrossRef] [Green Version]
- E, J.; Pham, M.; Zhao, D.; Deng, Y.; Le, D.H.; Zuo, W.; Zhu, H.; Liu, T.; Peng, Q.; Zhang, Z. Effect of different technologies on combustion and emissions of the diesel engine fueled with biodiesel: A review. Renew. Sustain. Energy Rev. 2017, 80, 620–647. [Google Scholar] [CrossRef]
- Karavalakis, G.; Bakeas, E.; Fontaras, G.; Stournas, S. Effect of biodiesel origin on regulated and particle-bound PAH (polycyclic aromatic hydrocarbon) emissions from a Euro 4 passenger car. Energy 2011, 36, 5328–5337. [Google Scholar] [CrossRef]
- Durbin, T.D.; Collins, J.R.; Norbeck, J.M.; Smith, M.R. Effects of Biodiesel, Biodiesel Blends, and a Synthetic Diesel on Emissions from Light Heavy-Duty Diesel Vehicles. Environ. Sci. Technol. 2000, 34, 349–355. [Google Scholar] [CrossRef]
- Kontses, A.; Dimaratos, A.; Keramidas, C.; Williams, R.; Hamje, H.; Ntziachristos, L.; Samaras, Z. Effects of fuel properties on particulate emissions of diesel cars equipped with diesel particulate filters. Fuel 2019, 255, 115879. [Google Scholar] [CrossRef]
- Fontaras, G.; Karavalakis, G.; Kousoulidou, M.; Tzamkiozis, T.; Ntziachristos, L.; Bakeas, E.; Stournas, S.; Samaras, Z. Effects of biodiesel on passenger car fuel consumption, regulated and non-regulated pollutant emissions over legislated and real-world driving cycles. Fuel 2009, 88, 1608–1617. [Google Scholar] [CrossRef]
- Szabados, G.; Bereczky, Á.; Ajtai, T.; Bozóki, Z. Evaluation analysis of particulate relevant emission of a diesel engine running on fossil diesel and different biofuels. Energy 2018, 161, 1139–1153. [Google Scholar] [CrossRef]
- Buono, D.; Senatore, A.; Prati, M.V. Particulate filter behaviour of a Diesel engine fueled with biodiesel. Appl. Therm. Eng. 2012, 49, 147–153. [Google Scholar] [CrossRef]
- Guan, B.; Zhan, R.; Lin, H.; Huang, Z. Review of the state-of-the-art of exhaust particulate filter technology in internal combustion engines. J. Environ. Manag. 2015, 154, 225–258. [Google Scholar] [CrossRef]
- Lupše, J.; Campolo, M.; Soldati, A. Modelling soot deposition and monolith regeneration for optimal design of automotive DPFs. Chem. Eng. Sci. 2016, 151, 36–50. [Google Scholar] [CrossRef]
- Martirosyan, K.S.; Chen, K.; Luss, D. Behavior features of soot combustion in diesel particulate filter. Chem. Eng. Sci. 2010, 65, 42–46. [Google Scholar] [CrossRef]
- Guo, Y.; Stevanovic, S.; Verma, P.; Jafari, M.; Jabbour, N.; Brown, R.; Cravigan, L.; Alroe, J.; Godday, C.; Brown, R.; et al. An experimental study of the role of biodiesel on the performance of diesel particulate filters. Fuel 2019, 247, 67–76. [Google Scholar] [CrossRef]
- Ajtai, T.; Pintér, M.; Utry, N.; Kiss-Albert, G.; Gulyás, G.; Pusztai, P.; Puskás, R.; Bereczky, A.; Szabados, G.; Szabó, G.; et al. Characterisation of diesel particulate emission from engines using commercial diesel and biofuels. Atmos. Environ. 2016, 134, 109–120. [Google Scholar] [CrossRef]
- Bermúdez, V.; Serrano, J.R.; Piqueras, P.; Sanchis, E.J. On the impact of particulate matter distribution on pressure drop of wall-flow particulate filters. Appl. Sci. 2017, 7, 234. [Google Scholar] [CrossRef] [Green Version]
- Savic, N.; Rahman, M.M.; Miljevic, B.; Saathoff, H.; Naumann, K.H.; Leisner, T.; Riches, J.; Gupta, B.; Motta, N.; Ristovski, Z.D. Influence of biodiesel fuel composition on the morphology and microstructure of particles emitted from diesel engines. Carbon 2016, 104, 179–189. [Google Scholar] [CrossRef] [Green Version]
- Nyström, R.; Sadiktsis, I.; Ahmed, T.M.; Westerholm, R.; Koegler, J.H.; Blomberg, A.; Sandström, T.; Boman, C. Physical and chemical properties of RME biodiesel exhaust particles without engine modifications. Fuel 2016, 186, 261–269. [Google Scholar] [CrossRef]
- Deng, Y.; Zheng, W.; Jiaqiang, E.; Zhang, B.; Zhao, X.; Zuo, Q. Influence of geometric characteristics of a diesel particulate filter on its behavior in equilibrium state. Appl. Therm. Eng. 2017, 123, 61–73. [Google Scholar] [CrossRef]
- Tandon, P.; Heibel, A.; Whitmore, J.; Kekre, N.; Chithapragada, K. Measurement and prediction of filtration efficiency evolution of soot loaded diesel particulate filters. Chem. Eng. Sci. 2010, 65, 4751–4760. [Google Scholar] [CrossRef]
- Chiavola, O.; Chiatti, G.; Sirhan, N. Impact of Particulate Size During Deep Loading on DPF Management. Appl. Sci. 2019, 9, 3075. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Martín, A.; Orihuela, M.P.; Becerra-Villanueva, J.A.; Martínez-Fernández, J.; Ramírez-Rico, J. Permeability and mechanical integrity of porous biomorphic SiC ceramics for application as hot-gas filters. Mater. Des. 2016, 107, 450–460. [Google Scholar] [CrossRef]
- Orihuela, M.P.; Gómez-Martín, A.; Becerra-Villanueva, J.A.; Chacartegui, R.; Ramírez-Rico, J. Performance of biomorphic silicon carbide as particulate filter in diesel boilers. J. Environ. Manag. 2017, 203, 907–919. [Google Scholar] [CrossRef]
- Orihuela, M.P.; Gómez-Martín, A.; Miceli, P.; Becerra-Villanueva, J.A.; Chacartegui, R.; Fino, D.; Becerra, J.A.; Chacartegui, R.; Fino, D. Experimental measurement of the filtration efficiency and pressure drop of wall-flow Diesel Particulate Filters (DPF) made of biomorphic Silicon Carbide using laboratory generated particles. Appl. Therm. Eng. 2018, 131, 41–53. [Google Scholar] [CrossRef]
- Singh, M.; Martínez-Fernández, J.; Ramírez de Arellano-López, A. Environmentally conscious ceramics (ecoceramics) from natural wood precursors. Curr. Opin. Solid State Mater. Sci. 2003, 7, 247–254. [Google Scholar] [CrossRef]
- Ramírez de Arellano-López, A.; Martínez-Fernández, J.; González, P.; Domínguez, C.; Fernández-Quero, V.; Singh, M. Biomorphic SiC: A New Engineering Ceramic Material. Int. J. Appl. Ceram. Technol. 2005, 1, 56–67. [Google Scholar] [CrossRef]
- Bissett, E.J. Mathematical model of the thermal regeneration of a wall-flow monolith diesel particulate filter. Chem. Eng. Sci. 1984, 39, 1233–1244. [Google Scholar] [CrossRef]
- Bisset, E.J.; Shadman, F. Thermal regeneration of diesel-particulate monolithic filters. AIChE J. 1985, 31, 753–758. [Google Scholar] [CrossRef]
- Konstandopoulos, A.G.; Johnson, J.H. Wall-flow diesel particulate filters—Their pressure drop and collection efficiency. SAE Trans. 1989, 98, 625–647. [Google Scholar]
- Bollerhoff, T.; Markomanolakis, I.; Koltsakis, G. Filtration and regeneration modeling for particulate filters with inhomogeneous wall structure. Catal. Today 2012, 188, 24–31. [Google Scholar] [CrossRef]
- Exothermia SA. Available online: www.exothermia.com (accessed on 1 January 2017).
- Konstandopoulos, A.G.; Kostoglou, M.; Kladopoulou, E.; Vlachos, N. Advances in the science and technology of diesel particulate filter simulation. Adv. Chem. Eng. 2007, 33, 213–294. [Google Scholar]
- Koltsakis, G.; Haralampous, O.; Depcik, C.; Ragone, J.C. Catalyzed diesel particulate filter modeling. Rev. Chem. Eng. 2013, 29, 1–61. [Google Scholar] [CrossRef] [Green Version]
- Axisuite® Axitrap: Catalyzed Diesel Particulate Filter Simulation; Exothermia SA; 4.02.4.; Exothermia SA: Thessaloniki, Greece, 2015.
- Pulkrabek, W.W.; Ibele, W.E. The effect of temperature on the permeability a porous material. Int. J. Heat Mass Transf. 1987, 30, 1103–1109. [Google Scholar] [CrossRef]
- Steffens, J.; Coury, J.R. Collection efficiency of fiber filters operating on the removal of nano-sized aerosol particles: I—Homogeneous fibers. Sep. Purif. Technol. 2007, 58, 99–105. [Google Scholar] [CrossRef]
- Lee, K.W.; Liu, B.Y.H. Theoretical Study of Aerosol Filtration by Fibrous Filters. Aerosol Sci. Technol. 1982, 1, 147–161. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Rubow, K.L. Efficiency, pressure drop and figure of merit of high efficiency fibrous and membrane filter media. In Proceedings of the Fifth World Filtration Congress, Nice, France, 5–8 June 1990. [Google Scholar]
- Rodríguez-Fernández, J.; Lapuerta, M.; Sánchez-Valdepeñas, J. Regeneration of diesel particulate filters: Effect of renewable fuels. Renew. Energy 2017, 104, 30–39. [Google Scholar] [CrossRef]
- Schneider, J.; Weimer, S.; Drewnick, F.; Borrmann, S.; Helas, G.; Gwaze, P.; Schmid, O.; Andreae, M.O.; Kirchner, U. Mass spectrometric analysis and aerodynamic properties of various types of combustion-related aerosol particles. Int. J. Mass Spectrom. 2006, 258, 37–49. [Google Scholar] [CrossRef]
- Wentzel, M.; Gorzawski, H.; Naumann, K.H.; Saathoff, H.; Weinbruch, S. Transmission electron microscopical and aerosol dynamical characterization of soot aerosols. J. Aerosol Sci. 2003, 34, 1347–1370. [Google Scholar] [CrossRef]
- Gysel, M.; Laborde, M.; Mensah, A.A.; Corbin, J.C.; Keller, A.; Kim, J.; Petzold, A.; Sierau, B.; Sierau, B. Technical note: The single particle soot photometer fails to reliably detect PALAS soot nanoparticles. Atmos. Meas. Tech. 2012, 5, 3099–3107. [Google Scholar] [CrossRef] [Green Version]
- Stratakis, G.A.; Psarianos, D.L.; Stamatelos, A.M. Experimental investigation of the pressure drop in porous ceramic diesel particulate filters. Proc. Inst. Mech. Eng. D J. Automob. Eng. 2002, 216, 773–784. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, M.; Zhang, D. Effect of a homogeneous combustion catalyst on the characteristics of diesel soot emitted from a compression ignition engine. Appl. Energy 2014, 113, 751–757. [Google Scholar] [CrossRef]
- Lapuerta, M.; Martos, F.J.; Herreros, J.M. Effect of engine operating conditions on the size of primary particles composing diesel soot agglomerates. Aerosol Sci. 2007, 38, 455–466. [Google Scholar] [CrossRef]
- Haralampous, O.; Payne, S. Experimental testing and mathematical modelling of diesel particle collection in flow-through monoliths. Int. J. Engine Res. 2016, 17, 1045–1061. [Google Scholar] [CrossRef]
- Yang, J.; Stewart, M.; Maupin, G.; Herling, D.; Zelenyuk, A. Single wall diesel particulate filter (DPF) filtration efficiency studies using laboratory generated particles. Chem. Eng. Sci. 2009, 64, 1625–1634. [Google Scholar] [CrossRef]
- Mizutani, T.; Kaneda, A.; Ichikawa, S.; Miyairi, Y.; Ohara, E.; Takahashi, A.; Yuuki, K.; Matsuda, H.; Kurachi, H.; Toyoshima, T.; et al. Filtration Behavior of Diesel Particulate Filters (2). SAE Tech. Pap. 2007. [Google Scholar] [CrossRef]
- Dabhoiwala, R.H.; Johnson, J.H.; Naber, J.D.; Bagley, S.T. A Methodology to Estimate the Mass of Particulate Matter Retained in a Catalyzed Particulate Filter as Applied to Active Regeneration and On-Board Diagnostics to Detect Filter Failures. SAE Tech. Pap. Ser. 2008, 2008-01–0764, 1–23. [Google Scholar]
- Dabhoiwala, R.H.; Johnson, J.H.; Naber, J.D. Experimental Study Comparing Particle Size and Mass Concentration Data for a Cracked and Un-Cracked Diesel Particulate Filter. SAE Tech. Pap. Ser. 2009, 2009-01–0629, 1–12. [Google Scholar]
- Tsuneyoshi, K.; Takagi, O.; Yamamoto, K. Effects of Washcoat on Initial PM Filtration Efficiency and Pressure Drop in SiC DPF. SAE Tech. Pap. Ser. 2011, 2011-01–08, 1–10. [Google Scholar]
- www.testo.com Soot generator testo REXS–Reproducible EXhaust Simulator-Data sheet 1–2. Available online: https://static-int.testo.com/media/4d/22/d72019911546/testo-REXS-Datasheet-1981-9514.pdf (accessed on 10 December 2019).
- Haralampous, O.A.; Kandylas, I.; Koltsakis, G.C.; Samaras, Z. Diesel particulate filter pressure drop Part 1: Modelling and experimental validation. Int. J. Engine Res. 2004, 5, 149–162. [Google Scholar] [CrossRef]
- Wolff, T.; Friedrich, H.; Johannesen, L.; Hajizera, S. A New Approach to Design High Porosity Silicon Carbide Substrates; SAE Tech. Pap. 2010-01–0539; SAE International: Warrendale, PA, USA, 2010; pp. 1–11. [Google Scholar]
- Gil-Robles, J.M. Directive 98/69/EC. Off. J. Eur. Comm. 1998, 350, 1–56. [Google Scholar]
- Tucki, K.; Mruk, R.; Orynycz, O.; Wasiak, A.; Botwińska, K.; Gola, A. Simulation of the operation of a spark ignition engine fueled with various biofuels and its contribution to technology management. Sustainability 2019, 11, 2799. [Google Scholar] [CrossRef] [Green Version]
- Williams, R.; Hamje, H.; Zemroch, P.J.; Clark, R.; Samaras, Z.; Dimaratos, A.; Jansen, L.; Fittavolini, C. Effect of fuel properties on emissions from Euro 4 and Euro 5 diesel passenger cars. Transp. Res. Procedia 2016, 14, 3149–3158. [Google Scholar] [CrossRef] [Green Version]
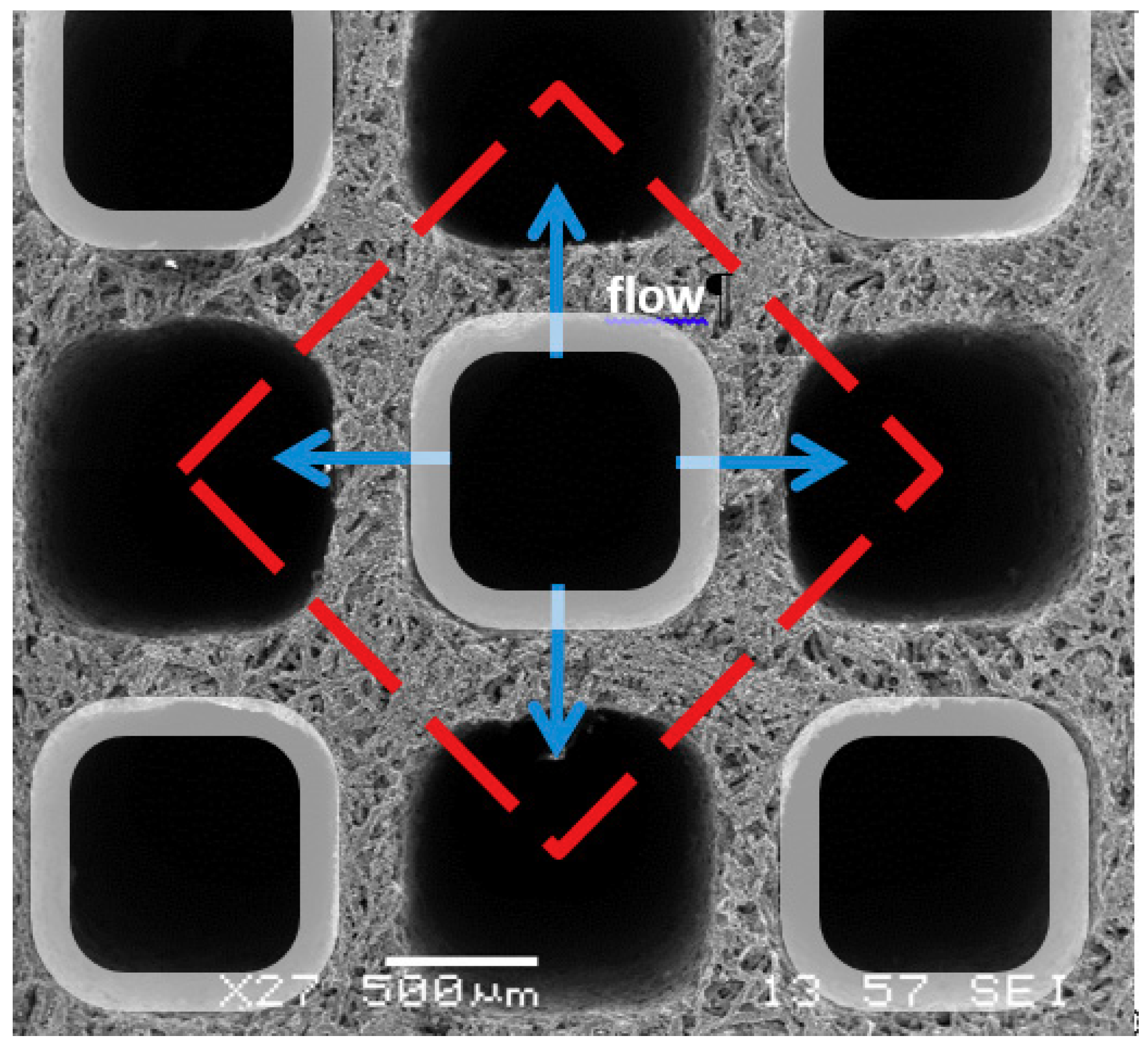

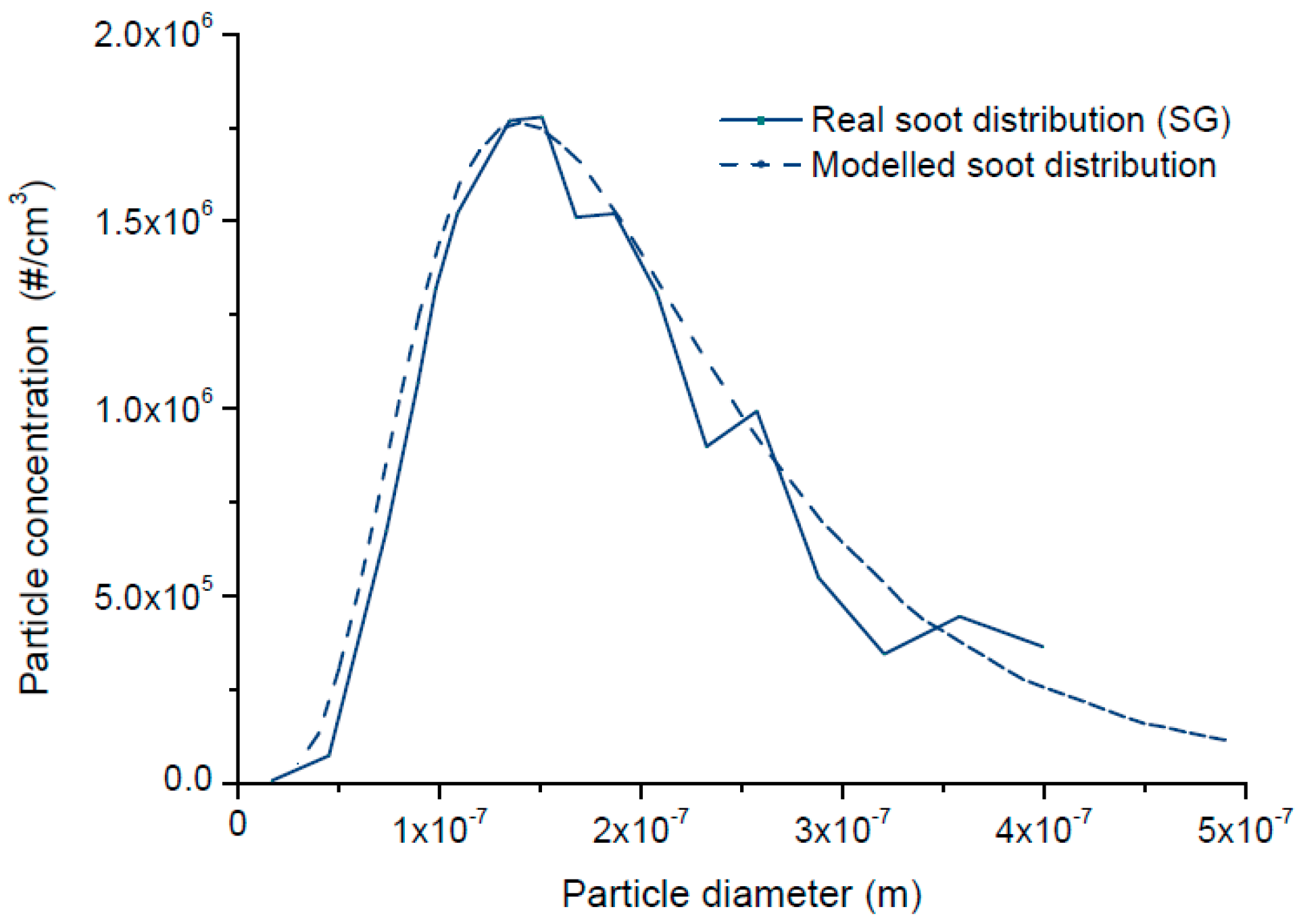


| Control Volume | Equation |
|---|---|
| Along the free path of the channels | Continuity equation: |
| Momentum conservation equation: | |
| Through porous media | Across the soot layer: |
| Across the substrate walls: | |
| Total pressure drop between the inlet and the outlet channel: |
| Filtration Mechanism | Equation |
|---|---|
| Diffusion | Diffusional efficiency [46]: |
| Peclet number: | |
| Parameter in the diffusional efficiency [47]: | |
| Direct interception | Direct interception efficiency [46]: |
| Interception parameter: | |
| Parameter in the direct interception efficiency [47]: |
| Properties and Composition | Diesel | HVO Biofuel | GTL Biofuel | Biodiesel |
|---|---|---|---|---|
| Standard | UNE EN 590 | UNE EN 15940 | UNE EN 15940 | UNE EN 14214 |
| Lower heating value (MJ/kg) | 43.04 | 43.96 | 44.03 | 37.26 |
| Sulfur (mg/kg) | <10 | <10 | <10 | <10 |
| Water (mg/kg) | 60 | 19.2 | 20 | 102 |
| C (% w/w) | 85.74 | 84.68 | 84.82 | 76.45 |
| H (% w/w) | 14.26 | 14.53 | 15.18 | 12.36 |
| O (% w/w) | 0 | 0 | 0 | 11.19 |
| Density at 15 °C (kg/m3) | 811 | 779.6 | 774 | 874.3 |
| Viscosity at 40 °C (mm2/s) | 2.02 | 2.99 | 2.34 | 4.5 |
| Inlet Settings | Value |
| Composition of the gas stream | Pure Argon |
| Volume flow rate | 5 L min−1 (0.1365 × 10−3 kg s−1) |
| Temperature | Room temperature: ~30 °C |
| Pressure | - |
| Soot mass flow | 0.004 g h−1 |
| Soot particle size distribution | Log-Normal (µ = 140 × 10−9 m; σ = 1.7) |
| Soot aggregate structure | Fractal dimension: 2.1 [49] Soot primary particle radius: 6.6 × 10−9 m Soot primary particle density: 1700 kg m−3 |
| DPF Settings | Value |
| Substrate length | 0.032 m |
| Plug length | 0.001 m |
| Substrate equivalent diameter | 0.00997 m |
| Cell density | 370 cpsi |
| Wall thickness | 0.00038 m (14.96 mil) |
| Substrate Properties Specific for bioSiC | Value |
| Initial permeability (clean) | 4 × 10−14 m2 |
| Substrate pore diameter | 15.7 × 10−6 m |
| Pore volume fraction | 0.49 |
| Inlet Settings—Simulating the Exhaust of a Real Engine (Light Duty) Fueled with Either Diesel or Biodiesel | |
| Composition of the gas stream | 78% N2, 10% O2, 5% CO2, 6% H2O, 0.1% CO |
| Volume flow rate | 175 m3h−1 (0.035 kg s−1) [52] |
| Temperature | 473 K (200 °C) |
| Pressure | - |
| Soot mass flow | 4.15 g h−1 |
| Soot particle size distribution | Log-Normal (µ = 80 × 10−9 m; σ = 1.41) |
| Soot aggregate structure | Fractal dimension: 2.07 [53] Soot primary particle radius: 12 × 10−9 m [54] Soot primary particle density: 2000 kg m−3 |
| DPF Settings | Value |
| Substrate length | 0.152 m (6″) |
| Plug length | 0.005 m |
| Substrate equivalent diameter | 0.144 m (5.66″) |
| Cell density | 370 cpsi |
| Wall thickness | 0.00038 m (14.96 mil) |
| Substrate Properties Specific for bioSiC | Value |
| Initial permeability (clean) | 4 × 10−14 m2 |
| Substrate pore diameter | 15.7 × 10−6 m |
| Pore volume fraction | 0.49 |
| Filtration Efficiency-Based Parameters | Pressure Drop-Based Parameters |
|---|---|
| Reference | Mizutani, 2007 [57] | Dabhoiwala, 2008/09 [58,59] | Tandon, 2010 [29] | Tsuneyoshi, 2011 [60] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Case Identification | Stationary engine test | Initial ΔP test | Soot load ΔP test | Heavy Duty, 20% load | Heavy Duty, 60% load | 275 cpsi ε = 51% d50 ~21.8 μm | 200 cpsi ε = 49% d50 ~13.4 μm | 300 cpsi ε = 51% d50 ~14 μm | Engine test | ΔP test | |
| Inlet settings | |||||||||||
| Composition of the gas stream | Exhaust gas | Air | Exhaust gas | Exhaust gas | Exhaust gas | Exhaust gas | Air | ||||
| Volume/mass flow rate (m3/h–kg/s) | 2000 rpm 50 Nm | 540–0.174 | 85.8–0.028 | 1469–0.245 | 2455–0.327 | 26.49–0.012 | 1400 rpm 190 Nm | 240–0.077 | |||
| Temperature (K–°C) | 298–25 | 473–200 | 563–290 | 707–434 | 298–25 | 623–350 | 298–25 | ||||
| Soot mass flow (g/h) | 0.6 | 15.46 | 18.25 | 1.5 [61] | |||||||
| Soot part size distribution | Log-Normal Mean (µ) (m) Std. deviation (σ) (-) | 70 - | - | Gas burner Soot gen. | 144 1.82 | Gas burner 80 1.8 | 80 - | - | |||
| Soot aggregate structure | Fractal dimension Primary part radius (m) Primary part density (kg/m3) | 20/35 | |||||||||
| DPF settings | |||||||||||
| Substrate material | SiC | Cordierite | SiC | ||||||||
| Substrate length (m–inch) | 0.152–6 | 0.3048–12 | 0.152–6 | 0.153–6 | |||||||
| Plug length (m) | |||||||||||
| Substrate diameter (m–inch) | 0.144–5.66 | 0.2667–10.5 | 0.144–5.66 | 0.144–5.66 | |||||||
| Cell density (cpsi–cpsc) | 300–46.5 | 200–31 | 275–42.6 | 200–31 | 300–46.5 | 300–46.5 | |||||
| Wall thickness (mm–mil) | 0.3048–12 | 0.3048–12 | 0.3048–12 | 0.3048–12 | 0.33–13 | 0.25–10 | |||||
| Reference | Haralampous, 2004 [62] | Wolff, 2010 [63] | Bollerhoff, 2012 [39] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case Identification | Transient ΔP (200 °C) | Transient ΔP (400 °C) | Lab test | Engine test XP-SiC | Engine test SiC | Initial ΔP test XP-SiC | Initial ΔP test SiC | |||
| Inlet settings | ||||||||||
| Composition of the gas stream | Exhaust gases | Exhaust gas | Exhaust gas | Exhaust gas | Air | Air | Exhaust gas | |||
| Volume/mass flow rate (m3/h–kg/s) | 245–0.05 approx. | 393–0.08 approx. | 362–0.0694 | 205–0.0417 | 205–0.0417 | 600–0.268 | 600–0.268 | 200–0.037 | ||
| Temperature (K–°C) | 473–200 | 673–400 | 513–240 | 473–200 | 473–200 | 298–25 | 298–25 | 523–250 | ||
| Soot mass flow (g/h) | 0 (filtered gases) | 9 | 2.4 | |||||||
| Soot part size distribution | Log-Normal Mean (µ) (m) Std. deviation (σ) (-) | - | Soot gen | 60 1.78 | ||||||
| Soot aggregate structure | Fractal dimension Primary part radius (m) Primary part density (kg/m3) | - | ||||||||
| DPF settings | ||||||||||
| Substrate material | SiC | XP-SiC | XP-SiC | SiC | XP-SiC | SiC | Cordierite | Improved SiC | ||
| Substrate length (m–inch) | 0.152–6 | 0.177–7 | 0.152–6 | |||||||
| Plug length (m) | 0.005 | |||||||||
| Substrate diameter (m–inch) | 0.144–5.66 | 0.144–5.66 | 0.144–5.66 | |||||||
| Cell density (cpsi–cpsc) | 200–31 | 300–46.5 | 200–31 | |||||||
| Wall thickness (mm–mil) | 0.38–15 | 0.33–13 | 0.33–13 | 0.3048–12 | 0.33–13 | 0.3048–12 | 0.3048–12 | 0.3556–14 | ||
| Bibliographic Source | Case from Table 7 | ΔP of the Reference DPF (kPa) | ΔP of a Similar bioSiC DPF (kPa) | Deviation |
|---|---|---|---|---|
| Mizutani, 2007 [57] | Soot load ΔP test | 1.5 | 1.5 | 0% |
| Mizutani, 2007 [57] | Initial ΔP test | 5.3 | 5.8 | +9.4% |
| Dabhoiwala, 2008 [58] | Heavy Duty, 20% load | 4.3 | 3.4 | −20.9% |
| Dabhoiwala, 2008 [58] | Heavy Duty, 60% load | 8.0 | 6.0 | −25.0% |
| Tsuneyoshi, 2011 [60] | ΔP test | 1.9 | 2.0 | +5.3% |
| Wolff, 2010 [63] | Lab test | 2.5 | 4.2 | +68.0% |
| Wolff, 2010 [63] | Initial ΔP test SiC | 4.9 | 9.0 | +83.7% |
| Wolff, 2010 [63] | Initial ΔP test XP-SiC | 4.5 | 9.2 | +104.4% |
| Bibliographic Source | Case from Table 7 | Initial Efficiency of the Reference DPF (%) | Initial Efficiency of a Similar bioSiC DPF (%) | Deviation |
|---|---|---|---|---|
| Tandon, 2010 [29] | 275 cpsi | 38 | 98.5 | +159% |
| Tandon, 2010 [29] | 200 cpsi | 50 | 98.2 | +96% |
| Tandon, 2010 [29] | 300 cpsi | 77 | 98.9 | +28% |
| Mizutani, 2007 [57] | Stationary engine test | 86 | 96.8 | +13% |
| Wolff, 2010 [63] | Engine test SiC | 53 | 95.8 | +81% |
| Wolff, 2010 [63] | Engine test XP-SiC | 60 | 96.5 | +61% |
| Wolff, 2010 [63] | Lab test | 90 | 94.0 | +4% |
| Bollerhoff, 2012 [39] | Cordierite | 60 | 96.6 | +61% |
| Bollerhoff, 2012 [39] | Improved SiC | 45 | 97.8 | +117% |
| Tsuneyoshi, 2011 [60] | Engine test | 55 | 94.7 | +72% |
| Dabhoiwala, 2009 [59] | Heavy Duty, 20% load | 52 | 94.6 | +82% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orihuela, M.P.; Haralampous, O.; Chacartegui, R.; Torres García, M.; Martínez-Fernández, J. Numerical Simulation of a Wall-Flow Particulate Filter Made of Biomorphic Silicon Carbide Able to Fit Different Fuel/Biofuel Inputs. Processes 2019, 7, 945. https://doi.org/10.3390/pr7120945
Orihuela MP, Haralampous O, Chacartegui R, Torres García M, Martínez-Fernández J. Numerical Simulation of a Wall-Flow Particulate Filter Made of Biomorphic Silicon Carbide Able to Fit Different Fuel/Biofuel Inputs. Processes. 2019; 7(12):945. https://doi.org/10.3390/pr7120945
Chicago/Turabian StyleOrihuela, M. Pilar, Onoufrios Haralampous, Ricardo Chacartegui, Miguel Torres García, and Julián Martínez-Fernández. 2019. "Numerical Simulation of a Wall-Flow Particulate Filter Made of Biomorphic Silicon Carbide Able to Fit Different Fuel/Biofuel Inputs" Processes 7, no. 12: 945. https://doi.org/10.3390/pr7120945
APA StyleOrihuela, M. P., Haralampous, O., Chacartegui, R., Torres García, M., & Martínez-Fernández, J. (2019). Numerical Simulation of a Wall-Flow Particulate Filter Made of Biomorphic Silicon Carbide Able to Fit Different Fuel/Biofuel Inputs. Processes, 7(12), 945. https://doi.org/10.3390/pr7120945







