The Influence and Optimization of Geometrical Parameters on Coast-Down Characteristics of Nuclear Reactor Coolant Pumps
Abstract
:1. Introduction
2. Research Method
2.1. Data Normalization
2.2. Path Analysis
3. Results
3.1. The Direct Impact Analysis of the Main Geometric Parameters of Nuclear Reactor Coolant Pump on Its Performance
3.2. Indirect Effect Analysis of the Geometric Parameters of the Nuclear Reactor Coolant Pump on Its Performance
3.3. Analysis of Residual Path Coefficient
3.4. Optimal Parameter Selection
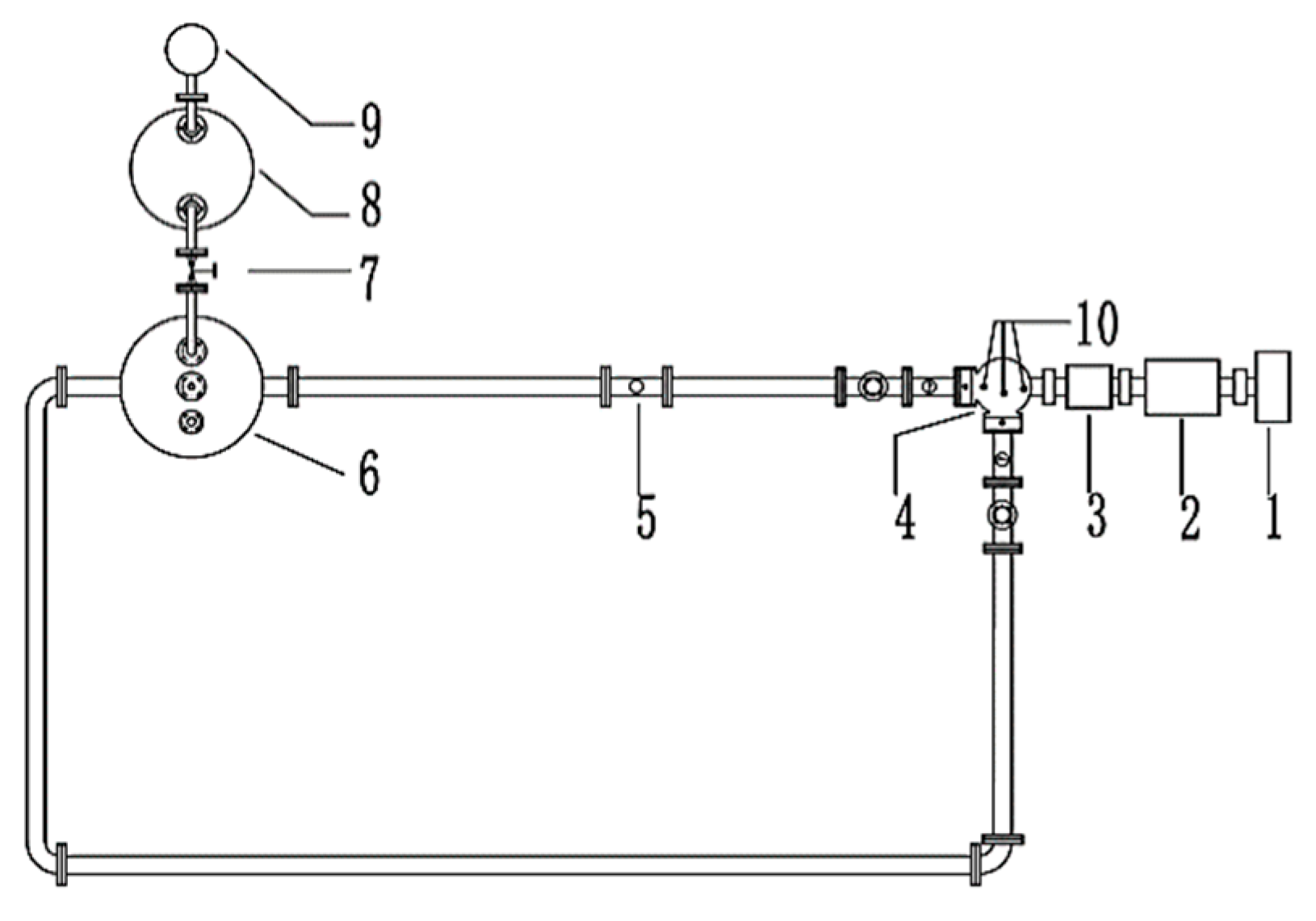
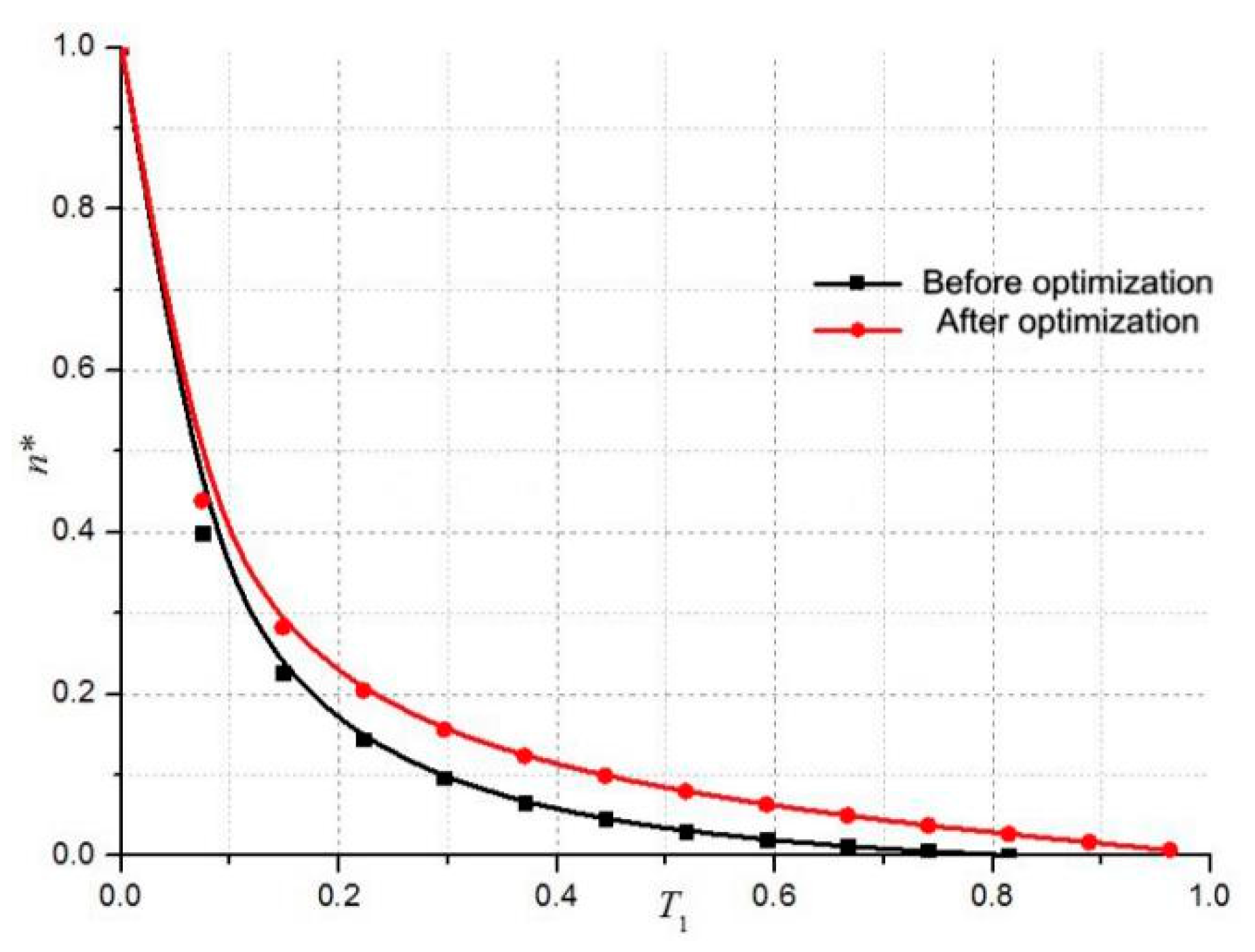
4. Experiment Verification
5. Conclusions
- (1)
- According to the energy conservation law, the calculation equation of coast-down time and the energy utilization of the inertia moment storage were listed, and the basis of coast-down optimization was given based on the reducing energy loss in the coast-down transition. Hydraulic optimization design of the reactor coolant pump impeller was carried out by combining orthogonal optimization test and CFD simulation software, while the hydraulic characteristics of the calculation model were also completed.
- (2)
- The correlation between the impeller geometric parameters and efficiency, head, and different geometric parameters was computed, and the main parameters affecting efficiency and the pressure head were determined. By the path analysis on the results of hydraulic characteristics, the direct influence of geometric parameters on efficiency and head and the indirect influence of the geometric parameters on other parameters that changed the efficiency and head were ascertained.
- (3)
- The efficiency of the pump was the target, the head was the constraint condition, and, combined with the calculation results of the partial correlation analysis and path analysis, the optimal parameters were selected as γ = 23º, β2 = 30º, φ = 115º, Z = 5, b2 = 200 mm, D2 = 770 mm, D0 = 555 mm, and Y = 1.002, respectively.
Author Contributions
Funding
Conflicts of Interest
References
- Gao, H.; Gao, F.; Zhao, X.; Chen, J.; Gao, X. Analysis of reactor coolant pump transient performance in primary coolant system during start-up period. Ann. Nucl. Energy 2013, 54, 202–208. [Google Scholar] [CrossRef]
- Tsukamoto, H.; Matsunaga, S.; Yoneda, H.; Hata, S. Transient characteristics of a centrifugal pump during starting/stopping periods: Analysis based on rotating circular cascade model and criterion for quasi-steady change. Trans. Jpn. Soc. Mech. Eng. B 1986, 52, 1291–1299. [Google Scholar] [CrossRef]
- Wu, D.; Wang, L.; Hao, Z.; Li, Z.; Bao, Z. Experimental study on hydrodynamic performance of a cavitating centrifugal pump during transient operation. J. Mech. Sci. Technol. 2010, 24, 575–582. [Google Scholar] [CrossRef]
- Li, Z.; Wu, D.; Wang, L.; Huang, B. Numerical simulation of the transient flow in a centrifugal pump during starting period. J. Fluids Eng. 2010, 132, 081102. [Google Scholar] [CrossRef]
- Chalghoum, I.; Elaoud, S.; Akrout, M.; Taieb, E.H. Transient behavior of a centrifugal pump during starting period. Appl. Acoust. 2016, 109, 82–89. [Google Scholar] [CrossRef]
- Elaoud, S.; Hadj-Taïeb, E. Influence of pump starting times on transient flows in pipes. Nucl. Eng. Des. 2011, 241, 3624–3631. [Google Scholar] [CrossRef]
- Farhadi, K.; Bousbia-Salah, A.; D’Auria, F. A model for the analysis of pump start-up transients in Tehran Research Reactor. Prog. Nucl. Energy 2007, 49, 499–510. [Google Scholar] [CrossRef]
- Farhadi, K. Transient behaviour of a parallel pump in nuclear research reactors. Prog. Nucl. Energy 2011, 53, 195–199. [Google Scholar] [CrossRef]
- Farhadi, K. The effect of retarding torque during a flow transient for Tehran research reactor. Ann. Nucl. Energy 2011, 38, 175–184. [Google Scholar] [CrossRef]
- Alatrash, Y.; Kang, H.O.; Yoon, H.G.; Seo, K.; Chi, D.Y.; Yoon, J. Experimental and analytical investigations of primary coolant pump coastdown phenomena for the Jordan research and training reactor. Nucl. Eng. Des. 2015, 286, 60–66. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, R.; Fu, Q.; Wang, X.; An, C.; Chen, J. Research on the structure design of the LBE reactor coolant pump in the lead base heap. Nucl. Eng. Technol. 2018, 51, 546–555. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, R.; Wang, X.; Fu, Q.; Li, M.; Si, X. Study on gas-liquid two-phase all-characteristics of CAP1400 nuclear main pump. Nucl. Eng. Des. 2017, 319, 140–148. [Google Scholar] [CrossRef]
- Lu, Y.; Zhu, R.; Wang, X.; Fu, Q.; Ye, D. Study on the complete rotational characteristic of coolant pump in the gas-liquid two-phase operating condition. Ann. Nucl. Energy 2019, 123, 180–189. [Google Scholar]
- Kim, J.H.; Ahn, H.J.; Kim, K.Y. High-efficiency design of a mixed-flow pump. Sci. China Technol. Sci. 2010, 53, 24–27. [Google Scholar] [CrossRef]
- Varchola, M.; Hlbocan, P. Geometry design of a mixed flow pump using experimental results of on internal impeller flow. Procedia Eng. 2012, 39, 168–174. [Google Scholar] [CrossRef]
- Long, Y.; Yin, J.L.; Wang, D.Z.; Li, T.B. Study on the effect of the impeller and diffuser blade number on reactor coolant pump performances. In Proceedings of the 7th International Conference on Pumps and Fans (ICPF 2015), Hangzhou, China, 18–21 October 2015. [Google Scholar]
- Zhou, F.M.; Wang, X.F. The effects of blade stacking lean angle to 1400 MW canned nuclear coolant pump hydraulic performance. Nucl. Eng. Des. 2017, 325, 232–244. [Google Scholar] [CrossRef]
- Zhu, R.S.; Xing, S.B.; Fu, Q.; Li, T.B.; Wang, X.L. Study on transient flow characteristics of AP1000 nuclear reactor coolant pump under exhaust transit condition. At. Energy Sci. Technol. 2016, 50, 1040–1046. [Google Scholar]
- Gao, H.; Gao, F.; Zhao, X.; Chen, J.; Cao, X. Transient flow analysis in reactor coolant pump systems during flow coastdown period. Nucl. Eng. Des. 2011, 241, 509–514. [Google Scholar] [CrossRef]
- Long, Y.; Zhu, R.; Wang, D.; Yin, J.; Li, T. Numerical and experimental investigation on the diffuser optimization of a reactor coolant pump with orthogonal test approach. J. Mech. Sci. Technol. 2016, 30, 4941–4948. [Google Scholar]
- Kang, C.; Mao, N.; Zhang, W.; Gu, Y. The influence of blade configuration on cavitation performance of a condensate pump. Ann. Nucl. Energy 2017, 110, 789–797. [Google Scholar] [CrossRef]
- Zhang, K.; Yuan, J.; Sun, W.; Si, Q. Internal flow characteristics of residual heat removal pump during different starting periods. J. Drain. Irrig. Mach. Eng. 2017, 35, 192–199. [Google Scholar]
- Fu, Q.; Zhang, B.; Zhu, R.; Cao, L. Effect of rotating speed on cavitation performance of nuclear reactor coolant pump. J. Drain. Irrig. Mach. Eng. 2016, 34, 651–656. [Google Scholar]

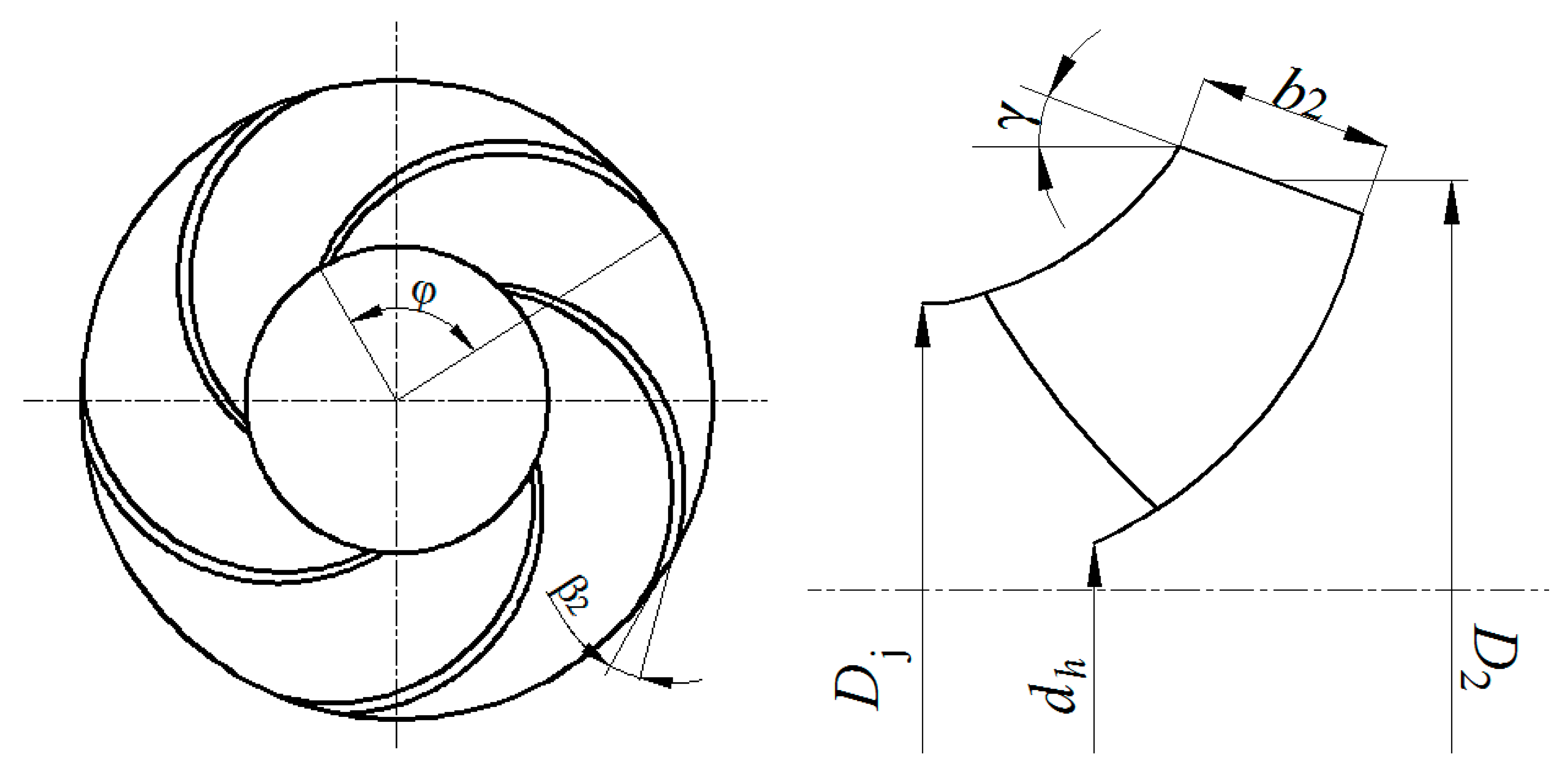
| γ/° | β2/° | φ/° | Z | D2/mm | b2/mm | Dj/mm | Area Ratio Y | Index | ||
|---|---|---|---|---|---|---|---|---|---|---|
| η1 | H | |||||||||
| 1 | 20 | 20 | 115 | 4 | 760 | 190 | 555 | 0.927 | 79.45 | 94.89 |
| 2 | 20 | 25 | 120 | 5 | 765 | 190 | 560 | 0.916 | 81.09 | 109.48 |
| 3 | 20 | 30 | 125 | 6 | 770 | 195 | 550 | 0.916 | 82.76 | 134.33 |
| 4 | 23 | 30 | 125 | 5 | 765 | 195 | 550 | 0.932 | 84.38 | 111.69 |
| 5 | 23 | 25 | 120 | 6 | 760 | 200 | 560 | 1.002 | 84.70 | 138.02 |
| 6 | 23 | 20 | 115 | 4 | 760 | 200 | 555 | 0.952 | 84.04 | 100.39 |
| 7 | 26 | 20 | 115 | 4 | 770 | 190 | 555 | 0.914 | 82.24 | 101.80 |
| 8 | 26 | 25 | 120 | 5 | 765 | 190 | 560 | 0.925 | 82.16 | 112.89 |
| 9 | 26 | 30 | 120 | 6 | 765 | 195 | 550 | 0.935 | 82.32 | 136.20 |
| 10 | 20 | 20 | 125 | 6 | 770 | 195 | 550 | 0.916 | 80.67 | 101.59 |
| 11 | 23 | 30 | 125 | 4 | 770 | 200 | 560 | 0.931 | 83.10 | 95.47 |
| 12 | 26 | 25 | 115 | 5 | 760 | 200 | 555 | 0.956 | 82.90 | 119.49 |
| 13 | 20 | 30 | 115 | 6 | 770 | 190 | 555 | 0.905 | 84.22 | 137.83 |
| 14 | 23 | 30 | 120 | 5 | 765 | 190 | 560 | 0.921 | 83.69 | 124.90 |
| 15 | 26 | 25 | 120 | 6 | 760 | 195 | 550 | 0.946 | 82.27 | 120.81 |
| 16 | 20 | 20 | 115 | 4 | 770 | 195 | 550 | 0.916 | 83.98 | 101.89 |
| 17 | 23 | 20 | 125 | 5 | 765 | 200 | 560 | 0.941 | 83.11 | 100.60 |
| 18 | 26 | 25 | 125 | 4 | 760 | 200 | 555 | 0.956 | 81.31 | 103.49 |
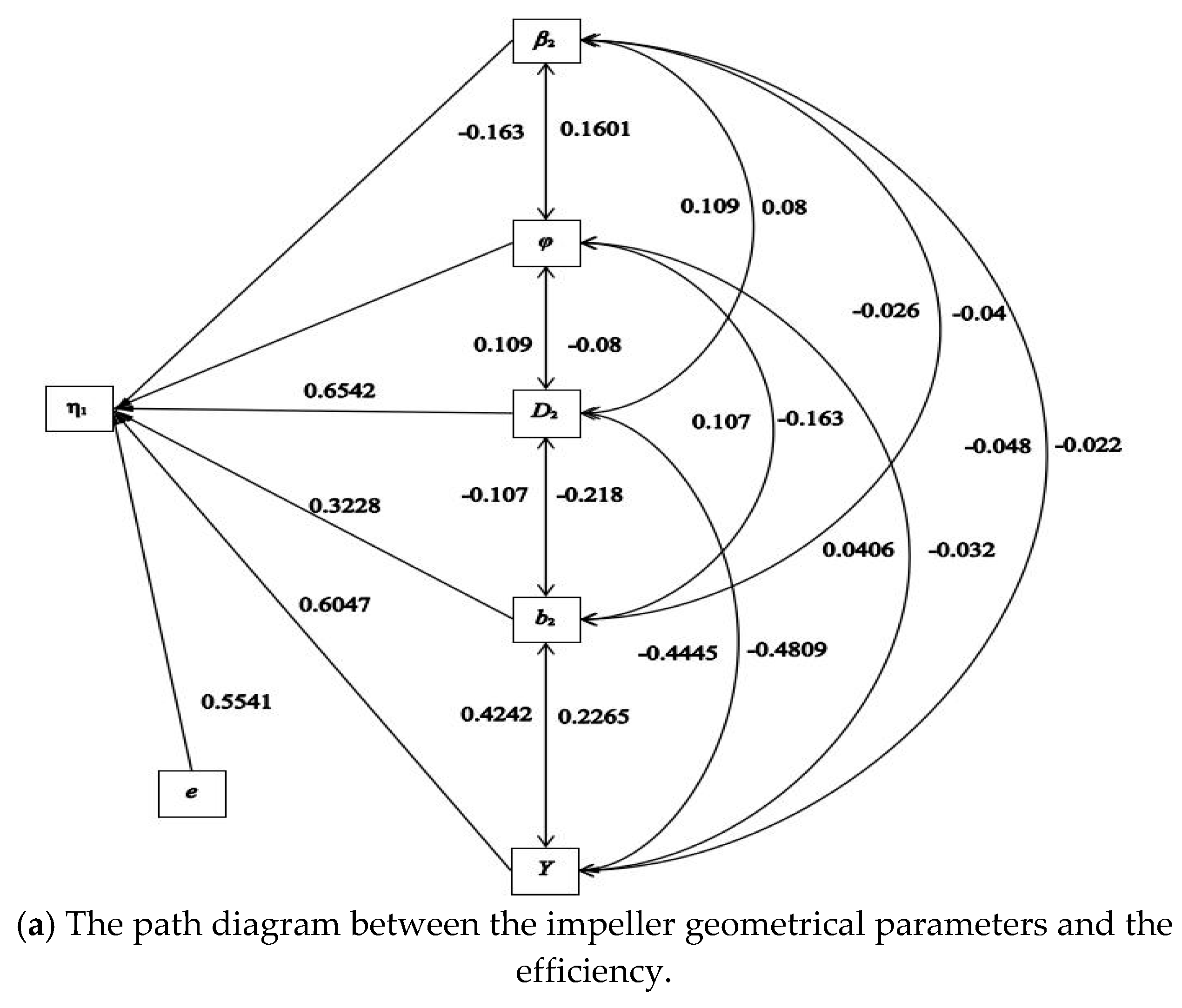
| Factor | Direct Effect | Indirect Effect | |||||||
| γ → H | β2→H | φ → H | Z → H | D2→H | b2→H | D0→H | Y → H | ||
| γ | 0.0076 | 0.0424 | 0.0000 | −0.0502 | −0.0748 | −0.0365 | −0.0031 | 0.1825 | |
| β2 | 0.5091 | 0.0006 | −0.1244 | 0.2510 | 0.0299 | 0.0122 | 0.0000 | −0.0349 | |
| φ | −0.3731 | 0.0000 | 0.1697 | 0.1506 | 0.0299 | −0.0487 | 0.0000 | 0.0295 | |
| Z | 0.6025 | −0.0006 | 0.2121 | −0.1041 | 0.015 | 0.0122 | 0.0092 | 0.0322 | |
| D2 | 0.1795 | −0.0032 | 0.0849 | −0.0622 | 0.0502 | 0.0487 | 0.0061 | −0.3235 | |
| b2 | −0.1461 | 0.0019 | −0.0424 | −0.1244 | −0.0502 | −0.0598 | 0.0000 | 0.3087 | |
| D0 | −0.0368 | 0.0006 | 0.0000 | 0.0000 | −0.1506 | −0.0299 | 0.0000 | 0.1007 | |
| Y | 0.4401 | 0.0032 | −0.0404 | −0.0250 | 0.0441 | −0.1320 | −0.1025 | −0.0084 | |
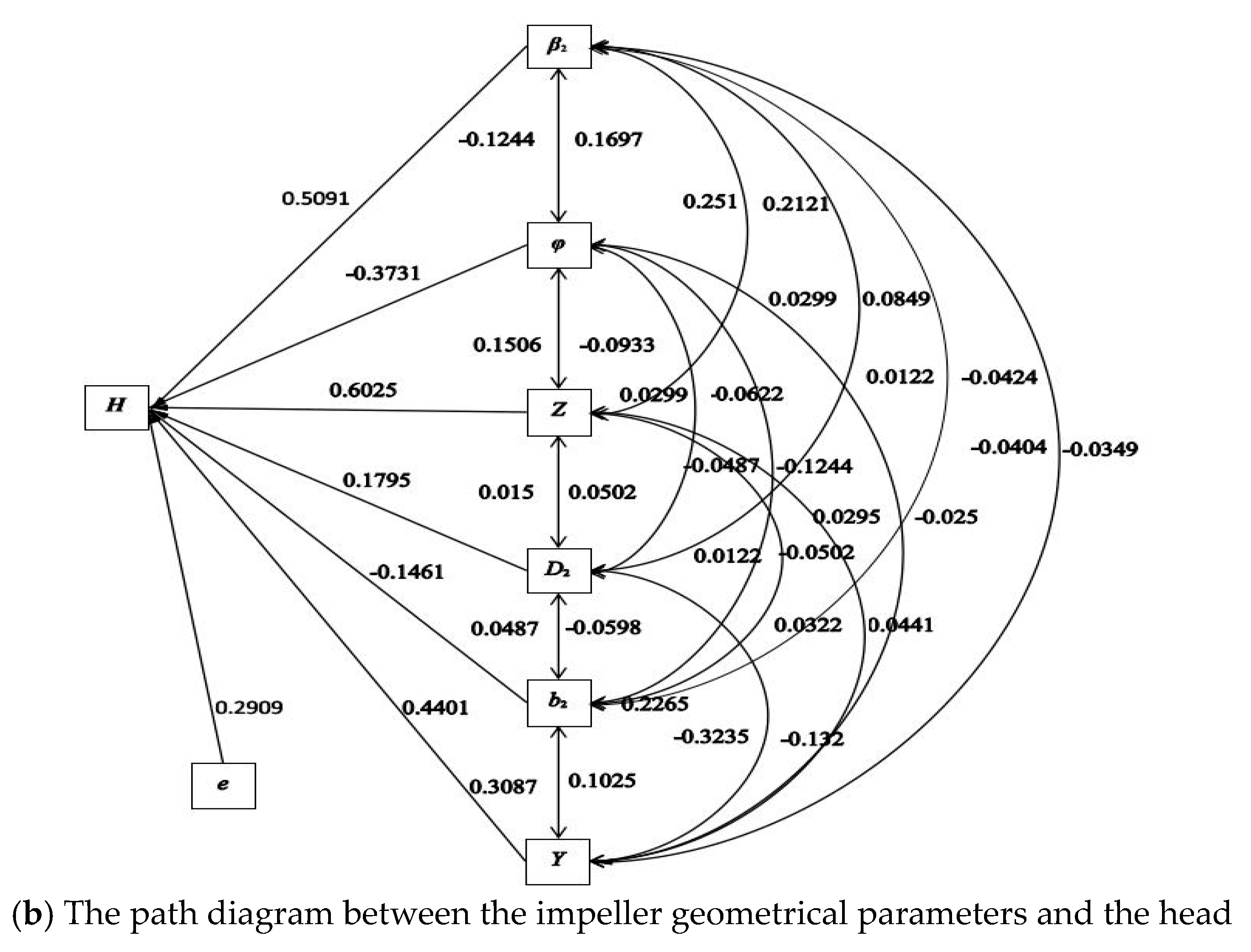
| Factor | Direct Effect | Indirect Effect | |||||||
| γ → η1 | β2→ η1 | φ → η1 | Z → η1 | D2→ η1 | b2→ η1 | D0→ η1 | Y → η1 | ||
| γ | −0.0528 | 0.0400 | 0.0000 | 0.0001 | −0.2726 | 0.1070 | 0.0040 | 0.2509 | |
| β2 | 0.4803 | −0.0044 | −0.1636 | −0.0005 | 0.1090 | −0.0269 | 0.0000 | −0.048 | |
| φ | −0.4908 | 0.0000 | 0.1601 | −0.0003 | 0.1090 | 0.1076 | 0.0000 | 0.0406 | |
| Z | −0.0011 | 0.0044 | 0.2001 | −0.1227 | 0.0545 | −0.0269 | −0.0120 | 0.0443 | |
| D2 | 0.6542 | 0.022 | 0.0800 | −0.0818 | −0.0001 | −0.1076 | −0.0080 | −0.4445 | |
| b2 | 0.3228 | −0.0132 | −0.0400 | −0.1636 | 0.0001 | −0.2181 | 0.0000 | 0.4242 | |
| D0 | 0.0480 | −0.0044 | 0.000 | 0.0000 | 0.0003 | −0.1090 | 0.0000 | 0.1383 | |
| Y | 0.6047 | −0.0219 | −0.0381 | −0.0329 | −0.0001 | −0.4809 | 0.2265 | 0.0110 | |
| Performance | Determine Path Coefficient | Residual Path Coefficient |
|---|---|---|
| H | 0.8421 | 0.2909 |
| η1 | 0.6678 | 0.5541 |
| Factor | γ | β2 | φ | Z | D2 | b2 | D0 | Y |
|---|---|---|---|---|---|---|---|---|
| Optimal results | 23° | 30° | 115° | 5 | 770 mm | 200 mm | 555 mm | 1.002 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Si, X.; Wang, X.; Zhu, R.; Fu, Q.; Zhong, H. The Influence and Optimization of Geometrical Parameters on Coast-Down Characteristics of Nuclear Reactor Coolant Pumps. Processes 2019, 7, 327. https://doi.org/10.3390/pr7060327
Zhao Y, Si X, Wang X, Zhu R, Fu Q, Zhong H. The Influence and Optimization of Geometrical Parameters on Coast-Down Characteristics of Nuclear Reactor Coolant Pumps. Processes. 2019; 7(6):327. https://doi.org/10.3390/pr7060327
Chicago/Turabian StyleZhao, Yuanyuan, Xiangyu Si, Xiuli Wang, Rongsheng Zhu, Qiang Fu, and Huazhou Zhong. 2019. "The Influence and Optimization of Geometrical Parameters on Coast-Down Characteristics of Nuclear Reactor Coolant Pumps" Processes 7, no. 6: 327. https://doi.org/10.3390/pr7060327
APA StyleZhao, Y., Si, X., Wang, X., Zhu, R., Fu, Q., & Zhong, H. (2019). The Influence and Optimization of Geometrical Parameters on Coast-Down Characteristics of Nuclear Reactor Coolant Pumps. Processes, 7(6), 327. https://doi.org/10.3390/pr7060327





