Study on Wear Properties of the Flow Parts in a Centrifugal Pump Based on EDEM–Fluent Coupling
Abstract
:1. Introduction
2. Models and Methods
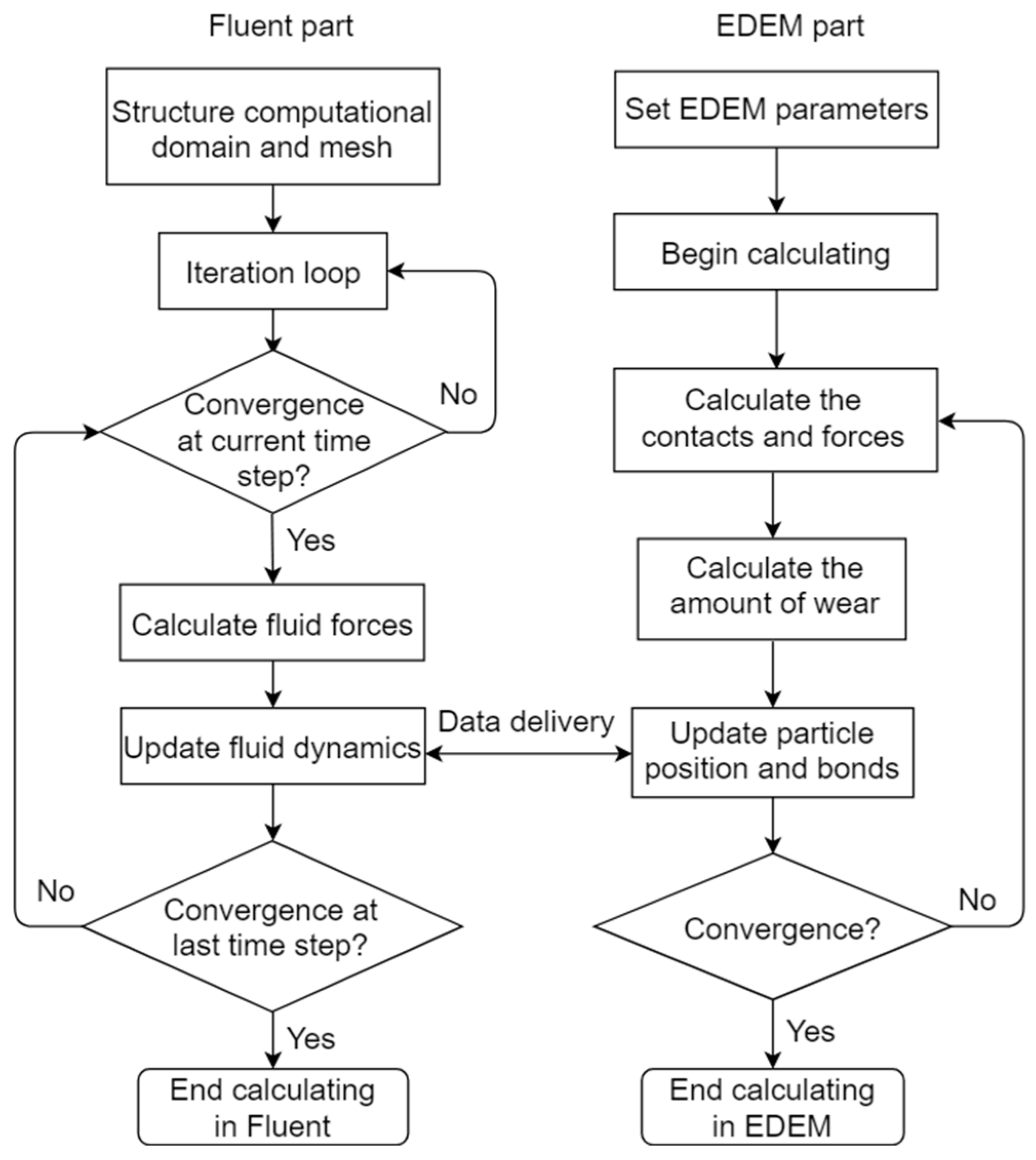
2.1. EDEM–Fluent Coupling Method
2.2. Wear Model
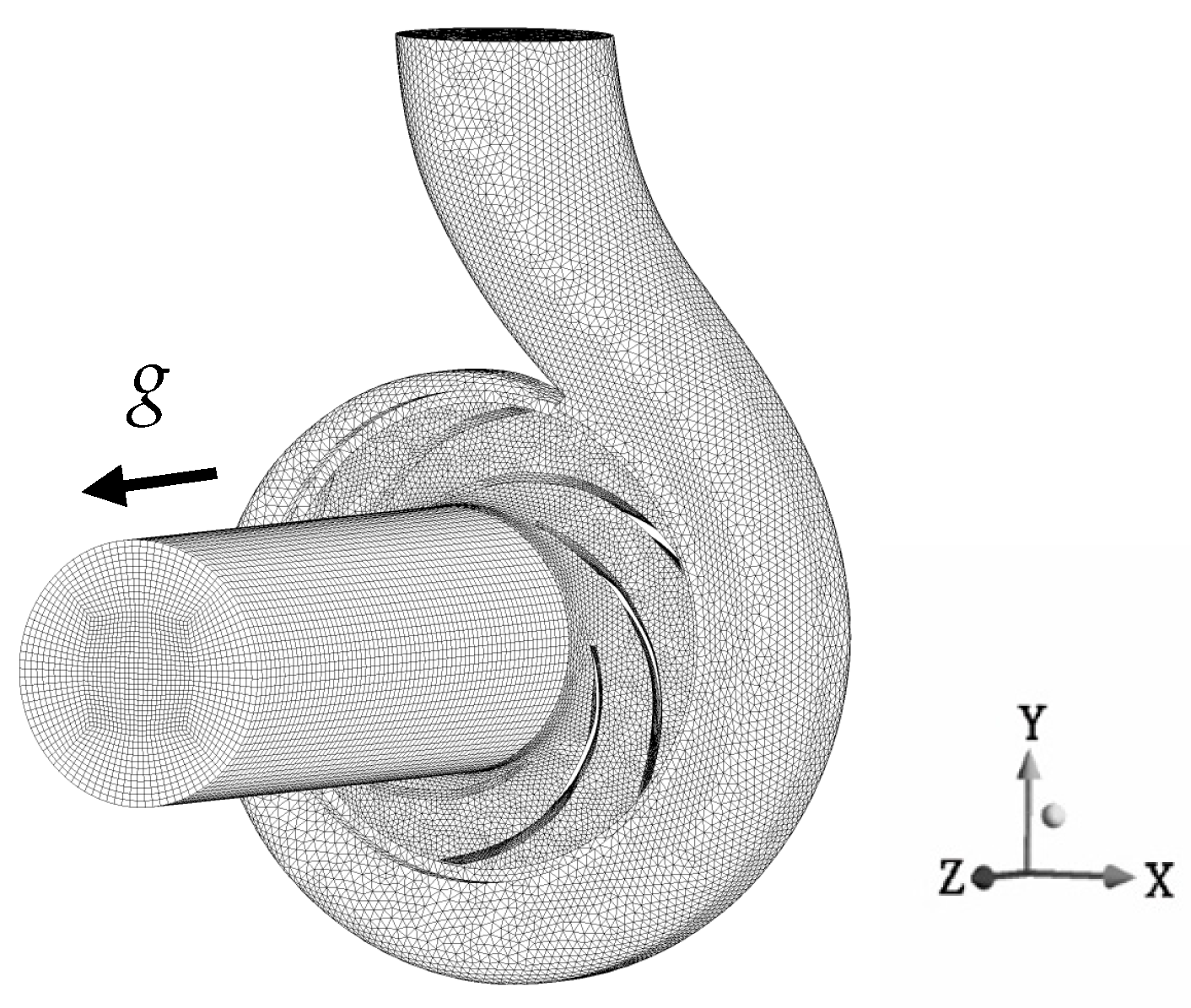
2.3. Computational Model and Meshing
2.4. Material Properties and Interactions
3. Results and Analyses
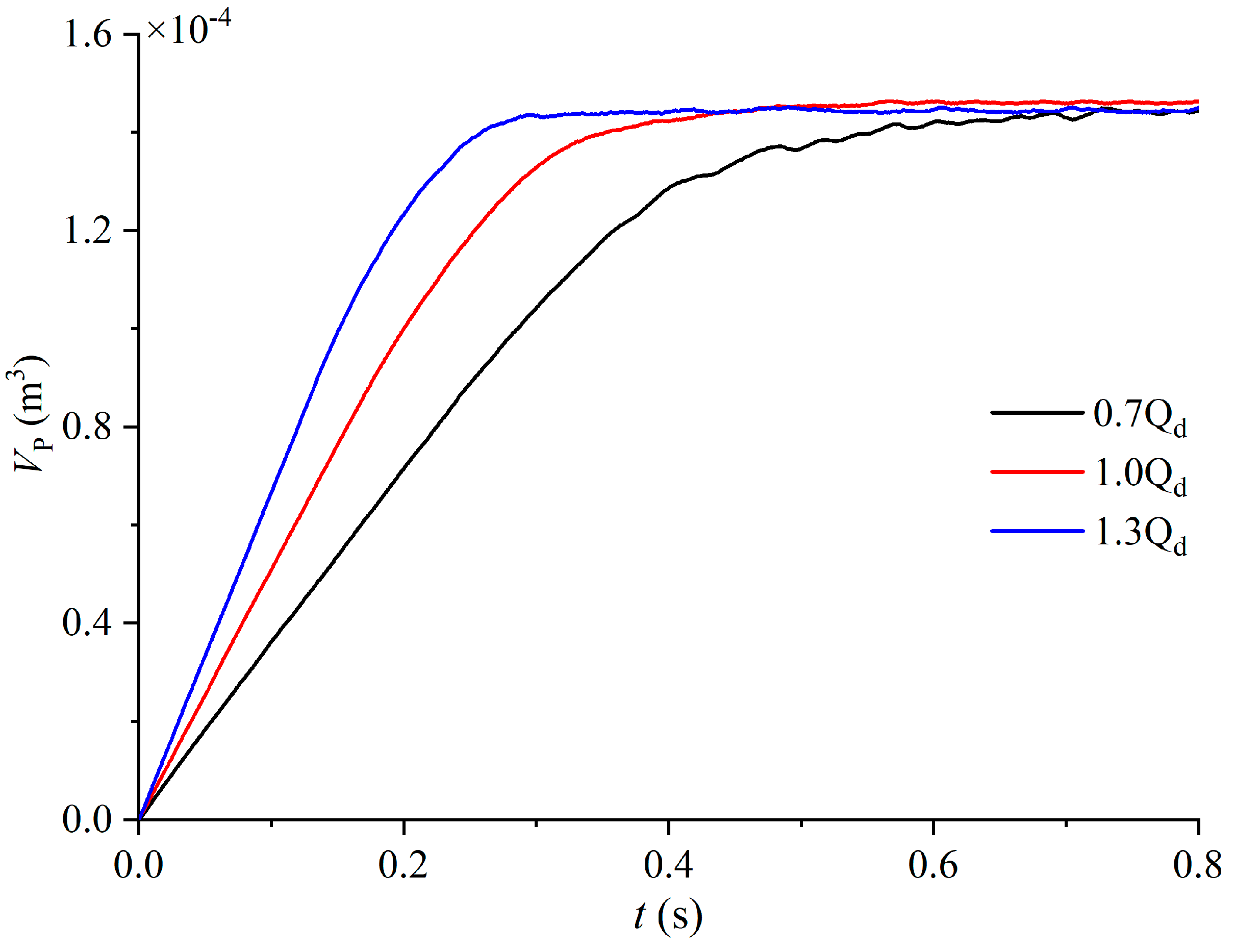
3.1. Particle Distribution
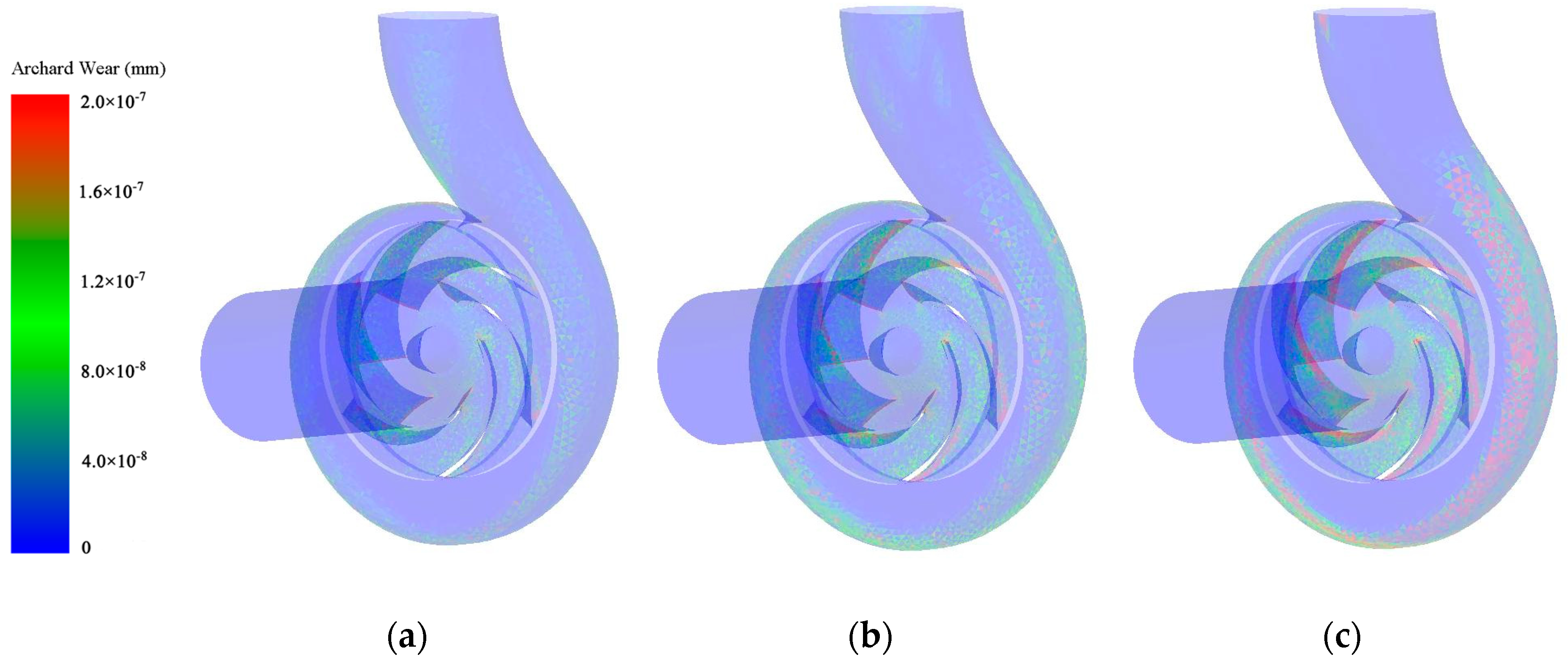
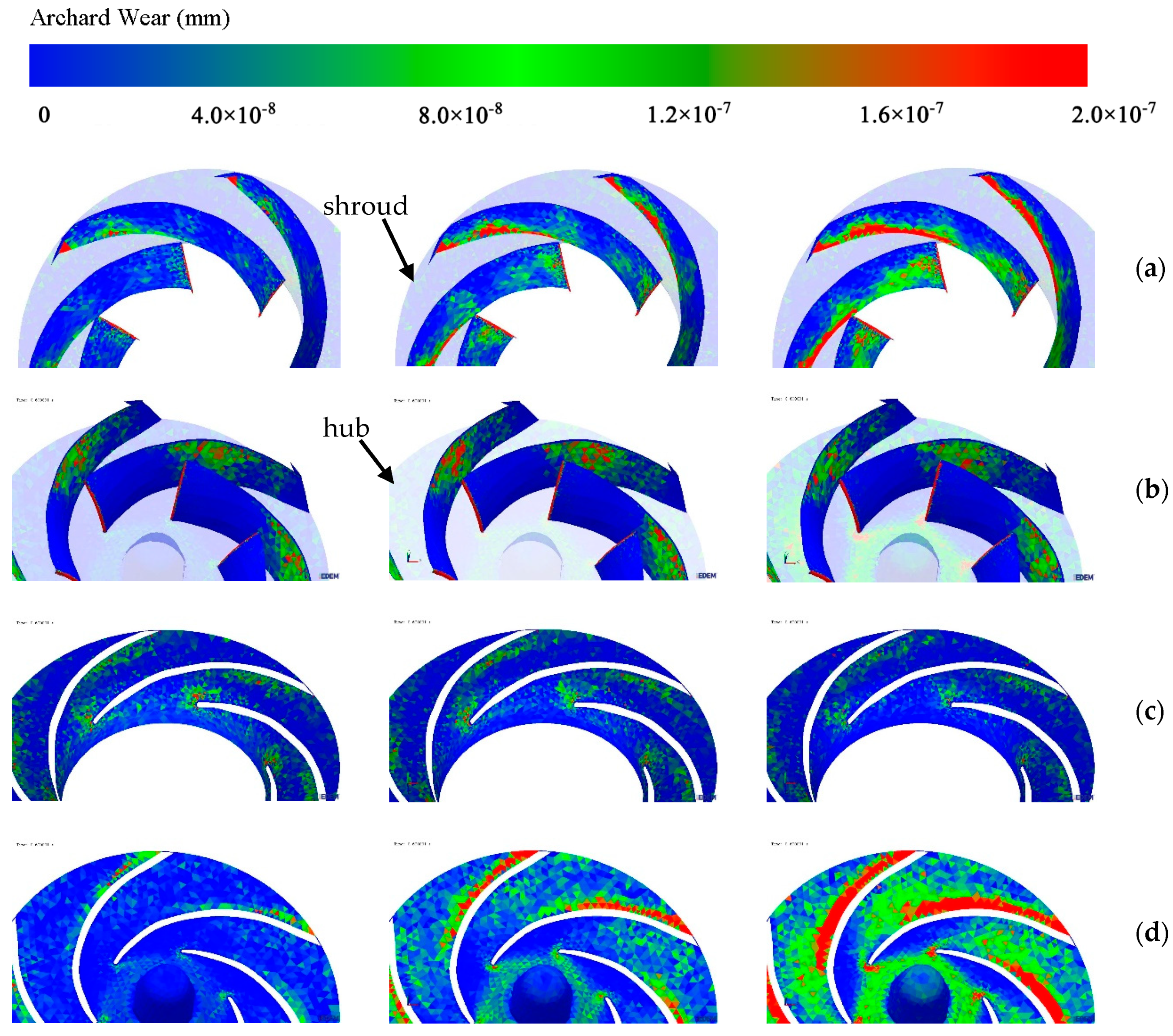
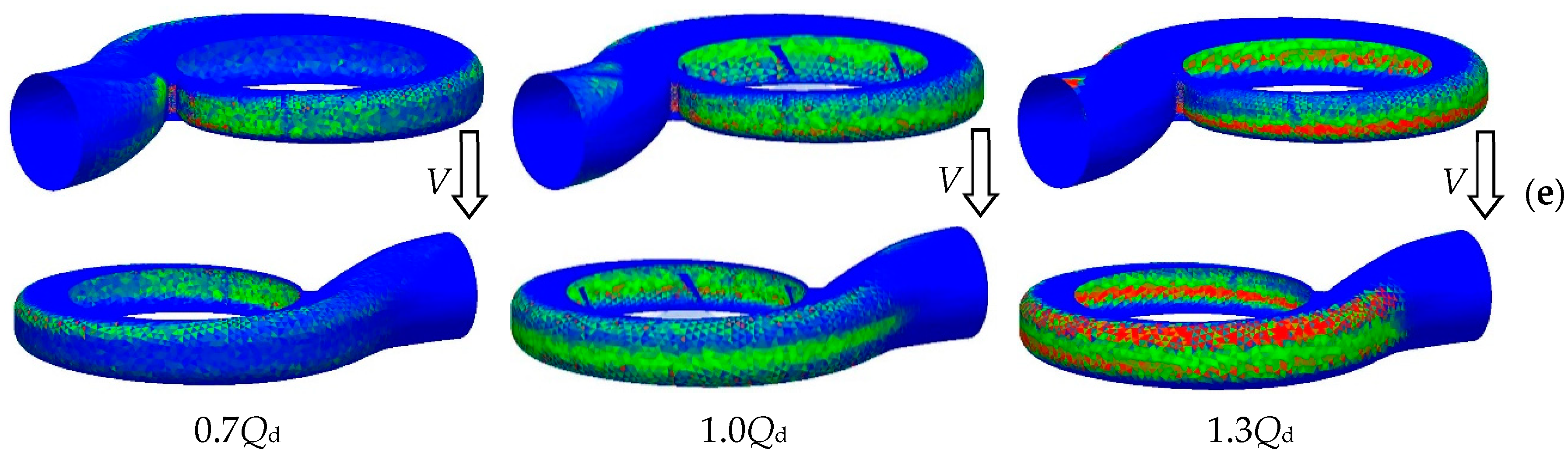
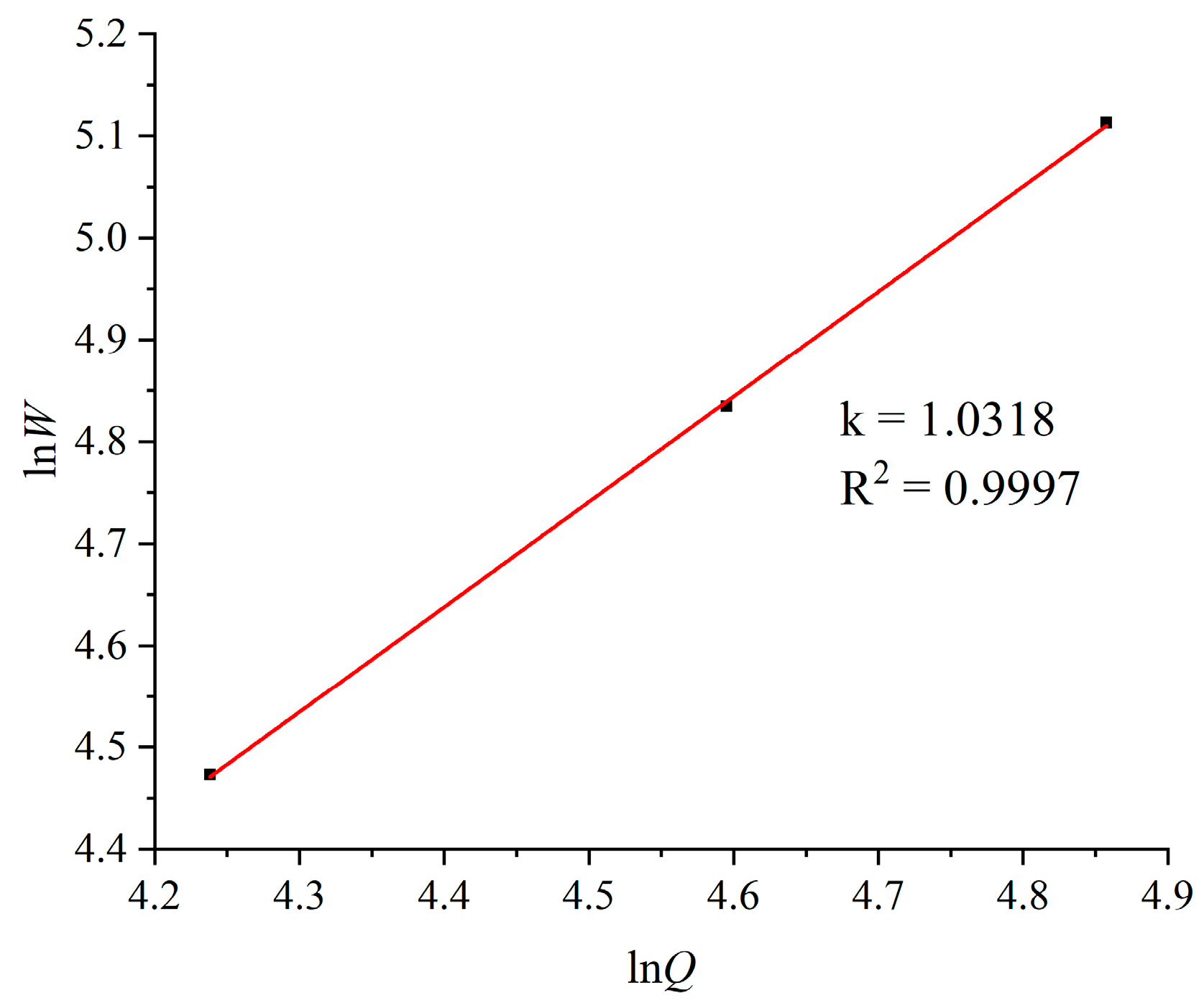
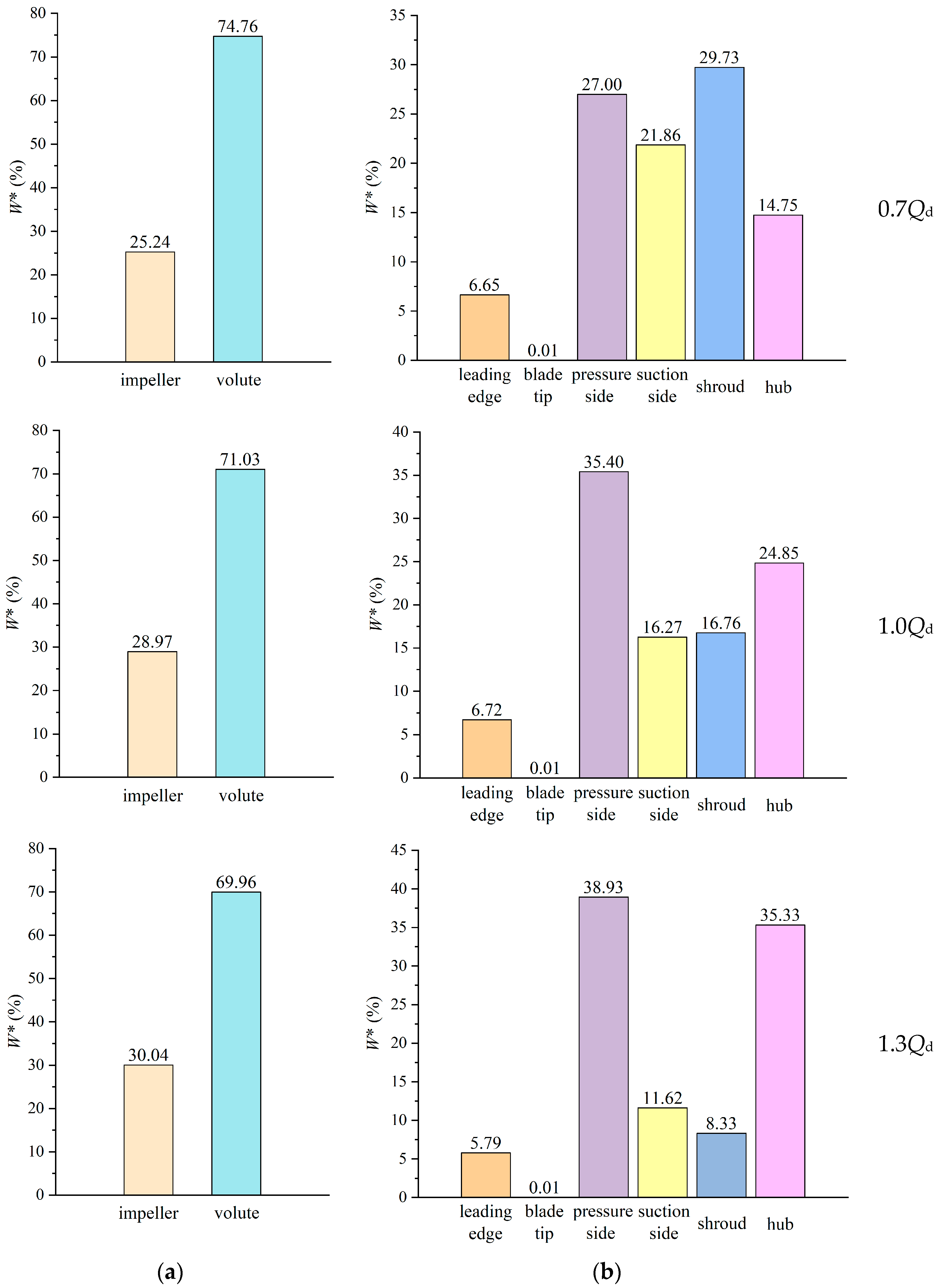
3.2. Wear Analysis of Flow Parts
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, S.; Su, X.H.; Qiu, G.Q. Transient numerical simulation for solid-liquid flow in a centrifugal pump by DEM-CFD coupling. Eng. Appl. Comput. Fluid Mech. 2015, 9, 411–418. [Google Scholar] [CrossRef] [Green Version]
- Ning, C.; Wang, Y. Performance analysis on solid-liquid mixed flow in a centrifugal pump. Iop Conf. Ser. Mater. Sci. Eng. 2016, 129, 012062. [Google Scholar] [CrossRef] [Green Version]
- Cheah, K.W.; Lee, T.S.; Winoto, S.H. Numerical study of inlet and impeller flow structures in centrifugal pump at design and off-design points. Int. J. Fluid Mach. Syst. 2011, 4, 25–32. [Google Scholar] [CrossRef]
- Huang, S.J.; Shao, C.L. Solid-liquid two-phase flow characteristics in centrifugal pump with multi-component medium. Trans. Chin. Soc. Agric. Eng. 2016, 32, 77–84. [Google Scholar]
- Torabi, R.; Nourbakhsh, S.A. The effect of viscosity on performance of a low specific speed centrifugal pump. Int. J. Rotating Mach. 2016. [Google Scholar] [CrossRef]
- Noon, A.A.; Kim, M.H. Erosion wear on centrifugal pump casing due to slurry flow. Wear 2016, 364, 103–111. [Google Scholar] [CrossRef]
- Shen, Z.J.; Chu, W.L. Effect of particle parameters on erosion wear and performance of screw centrifugal pump. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018; AMER SOC Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar]
- Peng, G.J.; Luo, Y.Y.; Wang, Z.W. Research on wear properties of centrifugal dredge pump based on liquid-solid two-phase fluid simulations. Iop Conf. Ser. Mater. Sci. Eng. 2015, 72. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, S.; Mohapatra, S.K. Study on role of particle shape in erosion wear of austenitic steel using image processing analysis technique. Proc. Inst. Mech. Eng. Part. J. J. Eng. Tribol. 2019, 233, 712–725. [Google Scholar] [CrossRef]
- Lei, H.M.; Xiao, Y.X.; Chen, F.N.; Ahn, S.H.; Wang, Z.W.; Gui, Z.H.; Luo, Y.Y.; Zhao, X.R. Numerical simulation of solid-liquid two-phase flow in a centrifugal pump with different wear blades degree. Iop Conf. Ser. Earth Environ. Sci. 2018, 163. [Google Scholar] [CrossRef]
- Pagalthivarthi, K.V.; Gupta, P.K.; Tyagi, V.; Navi, M.R. CFD prediction of erosion wear in centrifugal slurry pumps for dilute slurry flows. J. Comput. Multiph. Flows. 2011, 3, 225–245. [Google Scholar] [CrossRef]
- Lai, F.; Zhu, X.Y.; Xu, X.; Li, G.J. Erosion wear and performance simulation of centrifugal pump for solid-liquid flow. In Proceedings of the ASME Power Conference, Lake Buena Vista, FL, USA, 24–28 June 2018; AMER SOC Mechanical Engineers: New York, NY, USA, 2018. [Google Scholar]
- Luo, X.W.; Xu, H.Y.; Yan, Z.M.; Li, S.S. Analysis on the Wear Characteristic of ADI Blade for Slurry Pump. J. Hydroelectr. Eng. 2001, 1, 79–85. [Google Scholar]
- Roco, M.C.; Addie, G.; Dennis, J.; Nair, P.; Bhra, F.; Snamprogetti, I. Modeling erosion wear in centrifugal slurry pumps. Hydrotransport 1984, 9, 291–316. [Google Scholar]
- Ahmad, K.; Baker, R.C.; Goulas, A. Computation and experimental results of wear in a slurry pump impeller. Proc. Inst. Mech. Eng. Part. C: J. Mech. Eng. Sci. 1986, 200, 439–445. [Google Scholar] [CrossRef]
- Azimian, M.; Bart, H.J. Erosion investigations by means of a centrifugal accelerator erosion tester. Wear 2015, 328, 249–256. [Google Scholar] [CrossRef]
- Tao, Y.; Yuan, S.; Zhang, J.F.; Zhang, F.; Tao, J.P. Numerical simulation and test on impeller wear of slurry pump. Trans. Chin. Soc. Agric. Eng. 2014, 30, 63–69. [Google Scholar]
- Zhu, Z.C.; Cui, B.; Li, Y. Experimental study on hydraulic performance and wear of double-channel pump delivering solid-liquid media. J. Mech. Eng. 2009, 45, 65–69. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Kafui, K.D.; Thornton, C.; Adams, M.J. Discrete particle-continuum fluid modelling of gas–solid fluidised beds. Chem. Eng. Sci. 2002, 57, 2395–2410. [Google Scholar] [CrossRef]
- Finnie, I. Some observations on the erosion of ductile metals. Wear 1972, 19, 81–90. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. Erosion prediction in turbomachinery resulting from environmental solid particles. J. Aircr. 1975, 12, 471–478. [Google Scholar] [CrossRef]
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Chen, G.; Schott, D.L.; Lodewijks, G. Sensitivity analysis of DEM prediction for sliding wear by single iron ore particle. Eng. Comput. 2017, 34, 2031–2053. [Google Scholar] [CrossRef] [Green Version]




| Material | Poisson’s Ratio | Shear Modulus (mpa) | Density (kg/m3) | Diameter (mm) | Volume Fraction At Pump Inlet (%) |
|---|---|---|---|---|---|
| pump | 0.30 | 70.0 × 103 | 7800 | ||
| particle | 0.40 | 21.3 | 1500 | 1.0–3.0 | 2 |
| Interaction | Coefficient of Restitution | Coefficient of Static Friction | Coefficient of Rolling Friction |
|---|---|---|---|
| particle–particle | 0.44 | 0.27 | 0.01 |
| particle–pump | 0.50 | 0.15 | 0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.; Huang, J.; Guo, J.; Mo, Y. Study on Wear Properties of the Flow Parts in a Centrifugal Pump Based on EDEM–Fluent Coupling. Processes 2019, 7, 431. https://doi.org/10.3390/pr7070431
Huang S, Huang J, Guo J, Mo Y. Study on Wear Properties of the Flow Parts in a Centrifugal Pump Based on EDEM–Fluent Coupling. Processes. 2019; 7(7):431. https://doi.org/10.3390/pr7070431
Chicago/Turabian StyleHuang, Si, Jiaxing Huang, Jiawei Guo, and Yushi Mo. 2019. "Study on Wear Properties of the Flow Parts in a Centrifugal Pump Based on EDEM–Fluent Coupling" Processes 7, no. 7: 431. https://doi.org/10.3390/pr7070431
APA StyleHuang, S., Huang, J., Guo, J., & Mo, Y. (2019). Study on Wear Properties of the Flow Parts in a Centrifugal Pump Based on EDEM–Fluent Coupling. Processes, 7(7), 431. https://doi.org/10.3390/pr7070431





