Review and Modeling of Crystal Growth of Atropisomers from Solutions
Abstract
1. Introduction
2. Literature
- They usually require the knowledge of crystal structure data, which is usually not available for substances in early stage of development.
- They are often valid under idealized conditions, often neglecting the effect of crystallization media and mixing (BFDH and AE theories) or assuming low supersaturation (models based on BCF theory).
- They often assume a size-independent growth rate (MPB models, RGEC).
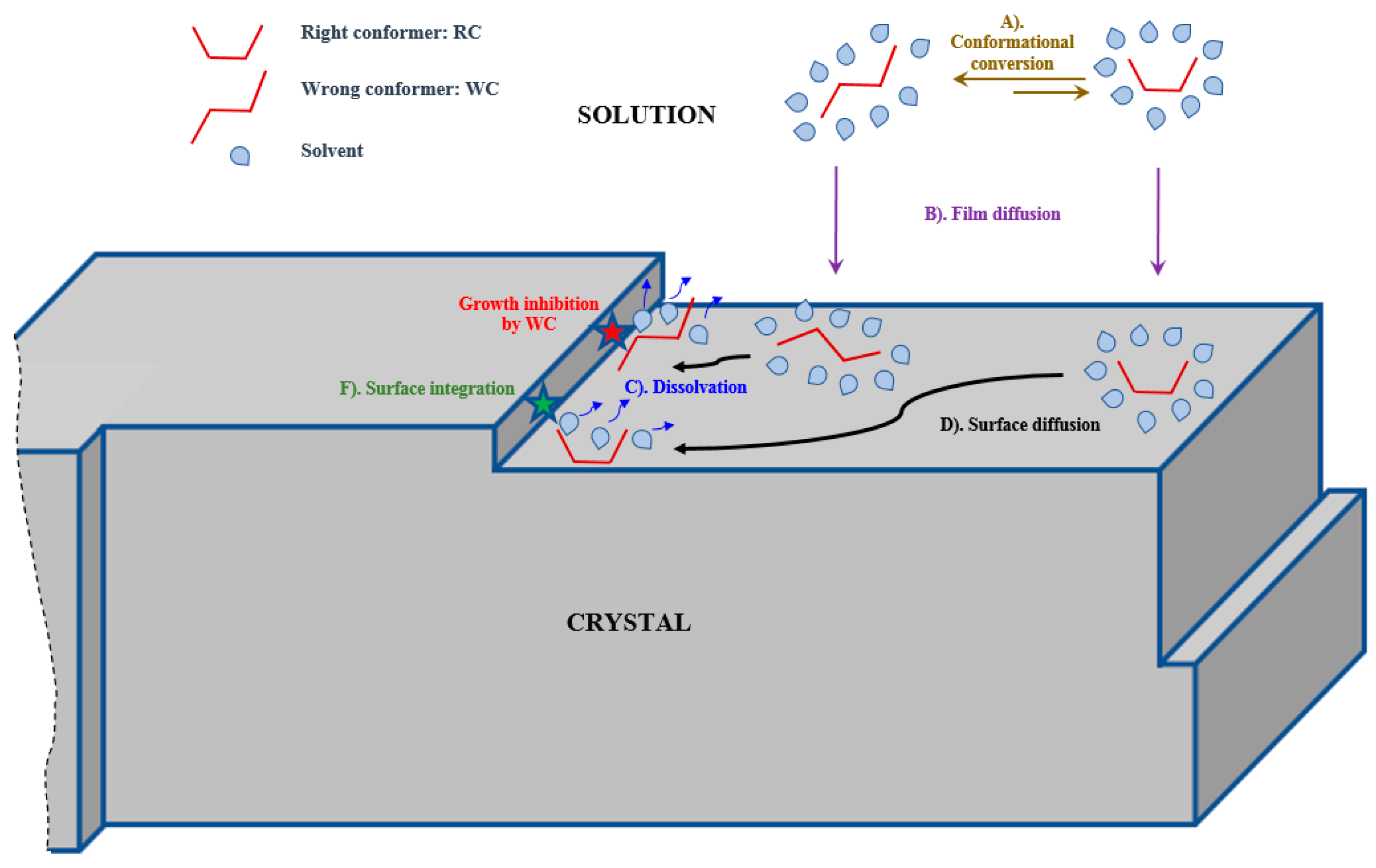
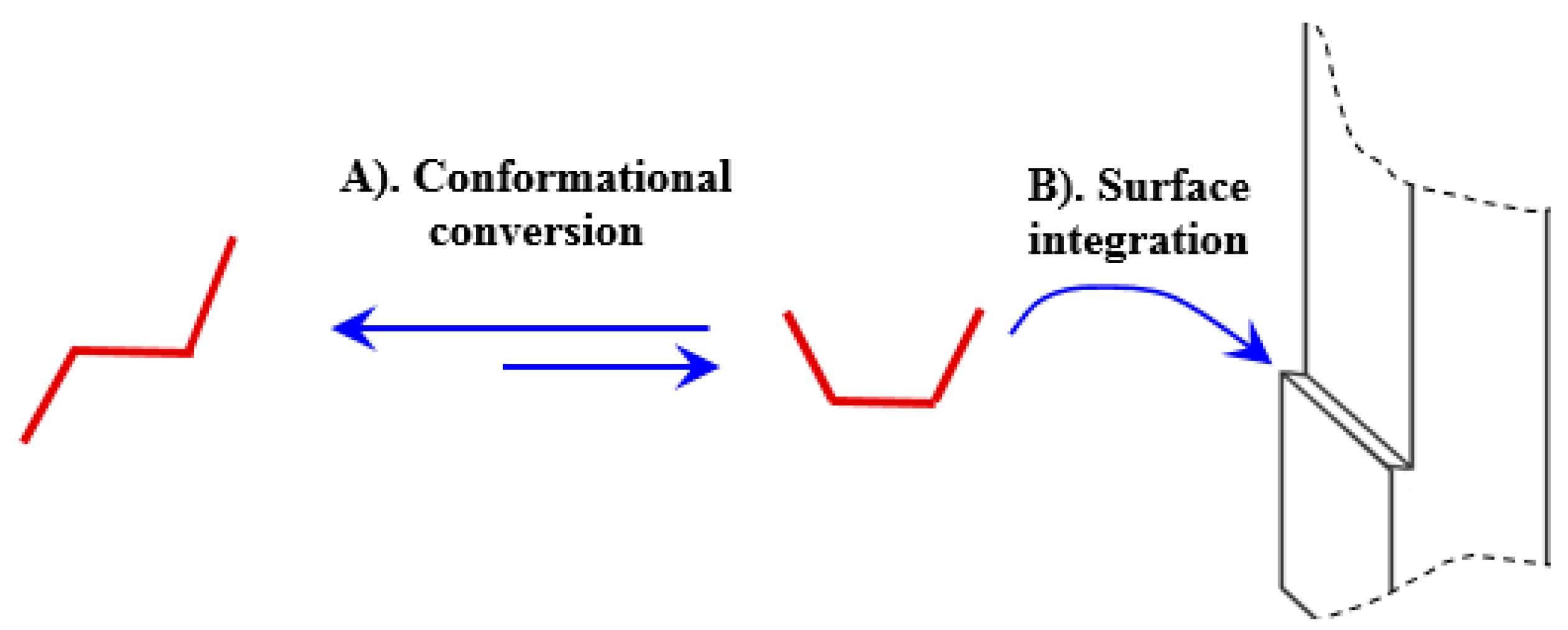
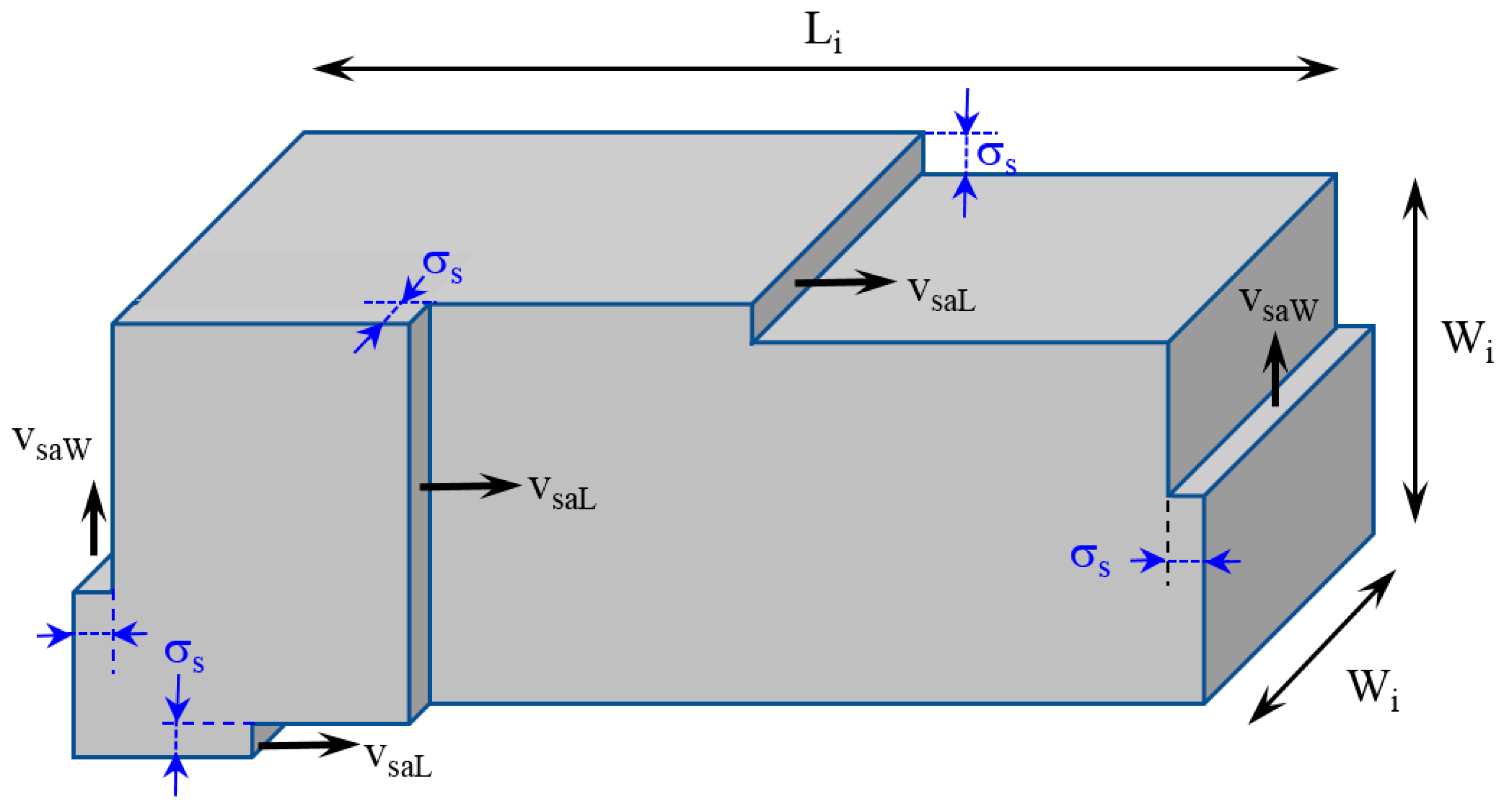
3. Mathematical Modeling
- Low supersaturation is maintained during crystallization.
- Crystal growth is the main phenomenon occurring (nucleation, agglomeration and breakage can be neglected).
- Concentration is uniform in the crystallizer.
- -
- is the concentration at the interface film/surface;
- -
- Vm is the solute molecular volume;
- -
- Lm is the molecular length;
- -
- is the activation energy for solute integration on face F;
- -
- is the distance between kinks on face F;
- -
- is the molecular vibration frequency.
- -
- Ψ is the WC growth inhibition term (-);
- -
- is the is a parameter dependent on the equilibrium between conformers (-);
- -
- is a parameter dependent on the solute.
- -
- F is an index referring to the face F (L or W);
- -
- is the ratio of solute integration coefficients of face F between temperatures and ;
- -
- is the ratio related to constant of equilibrium K between temperatures and .
Parameter Estimation
- Limit the scanning of kL to lower in the range of kW/3 to kW since kL must be lower than kW and computation results that returned unrealistically high aspect ratios for ratios kW/kL > 3.
- Utilize a two-tier estimation algorithm with a 1st low-resolution estimation to narrow the location of the global minima followed by a high-resolution scan to identify the minima of the objective function.
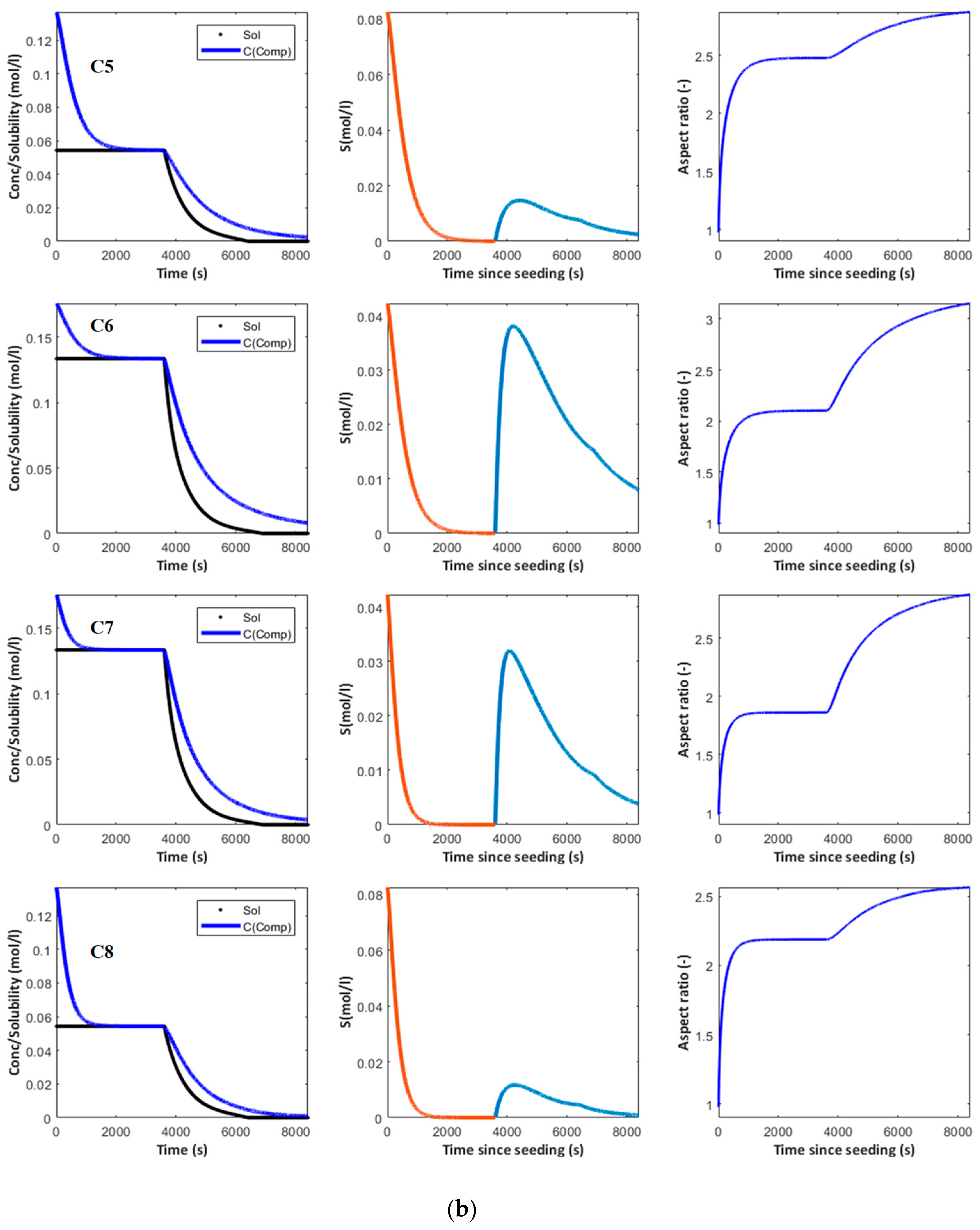
4. Simulation
4.1. Supersaturation, Crystal Size and Aspect Ratio
- Dissolution of the solute in an appropriate solvent.
- Addition of a given amount of anti-solvent to generate supersaturation.
- Addition of seeds.
- Aging of the seeds to consume supersaturation and increase the seed surface available for growth.
- Addition of anti-solvent at given rate to drive crystallization to completion.
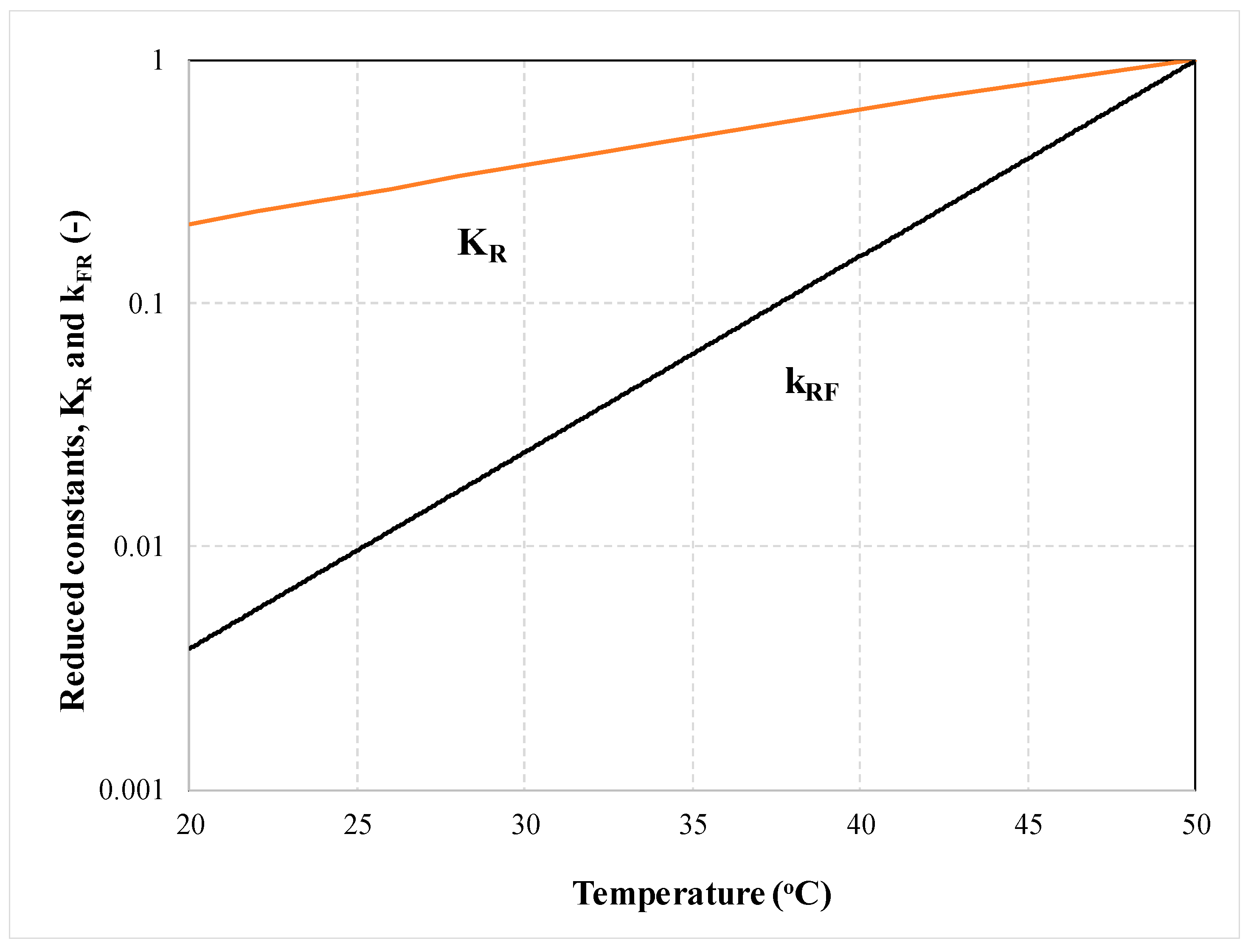
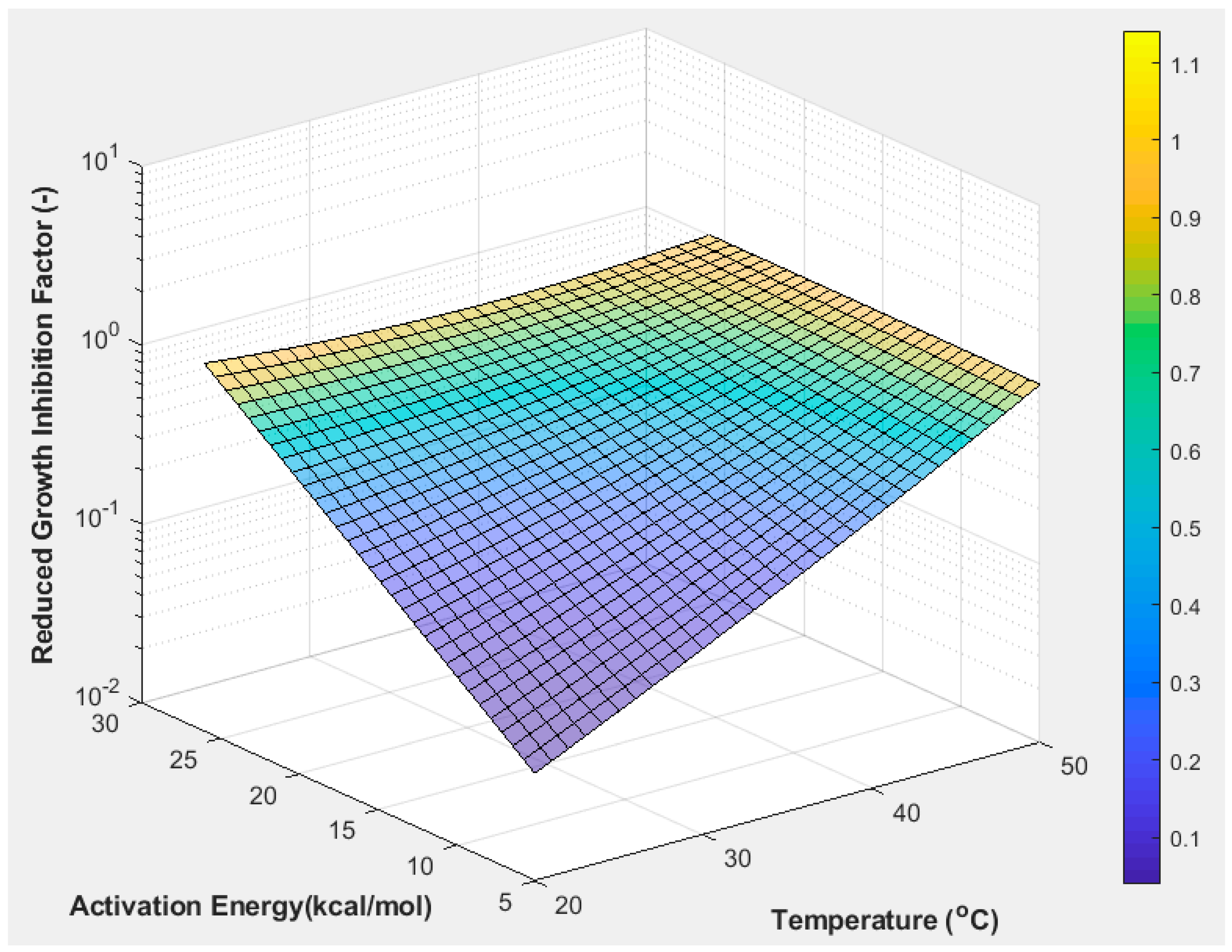
4.2. Crystal Growth Inhibition by the Wrong Conformer
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Ar | Aspect ratio | (-) |
| AR | Anti-solvent addition rate | (m3/(s kg)) |
| C | Concentration | (mol/L) |
| Cint | Concentration at the interface film/surface | (mol/L) |
| C* | Solubility | (mol/m3) |
| Cm | Constant related to the solute | (m5s−1) |
| E | Objective function: Sum of error between experimental and computed data | (mol/L) |
| Ea | Activation energy for solute integration | (kcal/mol) |
| Eb | Energy barrier to conformational change | (kcal/mol) |
| hfinal | Total number of experimental acquisition of concentration | (-) |
| keq | Constant of equilibrium between conformers | (-) |
| K | Constant related to constant of equilibrium | (-) |
| k | Solute integration coefficient | (mol/m3/((mol/L) s)) |
| ke | Ratio of solute integration coefficients | (-) |
| KR | Reduced constant of equilibrium | |
| kR | Reduced solute integration coefficient | (-) |
| Lm | Molecular length | (m) |
| L | Length | (m) |
| mcr | Mass of crystals | (kg) |
| Nc | Number of classes of particles | (-) |
| R | Universal gas constant | (kcal/(mol K)) |
| RSS | Relative supersaturation | (%) |
| S | Absolute supersaturation | (mol/L) |
| SL | Seed loading | (%) |
| sfinal | Total number of experimental acquisition of aspect ratio | (-) |
| T | Temperature | (K, °C) |
| t | time | (s) |
| TRC | Temperature of rotamers’ coalescence | (K, °C) |
| V | Volume | (m3) |
| Vm | Solute molecular volume | (m3/mol) |
| vsa | Step advance velocity | (m/s) |
| W | Width | (m) |
| x | Mass fraction | (-) |
| Greek letters | ||
| ρcr | Density of crystals | (kg/m3) |
| Ψ | WC-induced growth inhibition coefficient | (-) |
| ΘR | Reduced WC-induced growth inhibition coefficient | (-) |
| λo | Distance between kinks on face F | (m) |
| υm | Molecular vibration frequency | (s−1) |
| σs | Thickness of step | (m) |
| Subscripts | ||
| AS | Related to anti-solvent | |
| exp | Related to experimental value | |
| comp | Related to computed value | |
| F | Related to face F (L or W) | |
| h | Related to increment of experimental measurement of concentration | |
| i | Index for class of particles | |
| o | Related to initial state | |
| L | Refers to faces L | |
| s | Related to increment of experimental measurement of aspect ratio | |
| Slt | Related to solute | |
| Solu | Related to solution | |
| Solv | Related to solvent | |
| W | Refers to faces W | |
References
- Häuy, A. Essai d’une Théorie sur la Structure des Cristaux Appliquée à Plusieurs Genres de Substances Cristallisées; Chez Gogné: Paris, France, 1783. [Google Scholar]
- Wulff, G.Z. Zur Frage der Geschwindigkeit des Wachstums und der Auflösung der Kristallflächen. Krist. Min. 1901, 34, 499–530. [Google Scholar]
- Gibbs, J.W. Collected Works; Longmans Green: New York, NY, USA, 1906. [Google Scholar]
- Donnay, J.D.H.; Harker, D. A new law of crystal morphology, extending the law of Bravais. Am. Min. 1937, 22, 151–155. [Google Scholar]
- Bravais, A. Etudes Cristallographiques; Gauthier-Villar: Paris, France, 1866. [Google Scholar]
- Friedel, M.G. Etudes sur les lois de Bravais. Bull. Soc. Fr. Miner. 1907, 30, 326–455. [Google Scholar]
- Hartman, P.; Perdok, W.G. On the relations between structure and morphology of crystals. I. Acta Crystallogr. 1955, 8, 49–52. [Google Scholar] [CrossRef]
- Hartman, P.; Perdok, W.G. On the relations between structure and morphology of crystals. II. Acta Crystallogr. 1955, 8, 521–524. [Google Scholar] [CrossRef]
- Hartman, P.; Perdok, W.G. On the relations between structure and morphology of crystals. III. Acta Crystallogr. 1955, 8, 525–529. [Google Scholar] [CrossRef]
- Clydesdale, G.; Roberts, K.J.; Docherty, R. HABIT95—A program for predicting the morphology of molecular crystals as a function of the growth environment. J. Cryst. Growth 1996, 166, 78–83. [Google Scholar] [CrossRef]
- Clydesdale, G.; Roberts, K.J.; Docherty, R. HABIT95, Quantum Chemistry Program Exchange. Program No. 670; QC Plumbing & Electrical: Bloomington, IN, USA, 1996. [Google Scholar]
- Clydesdale, G.; Roberts, K.J.; Docherty, R. HABIT—A program for predicting the morphology of molecular crystals. Comput. Phys. Commun. 1991, 64, 311–328. [Google Scholar] [CrossRef]
- SHAPE for Windows 7.1. 2006. Available online: www.shapesoftware.com (accessed on 25 April 2019).
- Accelrys. Available online: http://www.accelrys.com/cerius2/ (accessed on 25 April 2019).
- Docherty, R.; Roberts, K.J.; Dowty, E. Morang—A computer-program designed to aid in the determinations of crystal morphology. Comput. Phys. Commun. 1988, 51, 423–430. [Google Scholar] [CrossRef]
- Hammond, R.B.; Pencheva, K.; Roberts, K.J. A structural-kinetic approach to model face-specific solution/crystal surface energy associated with the crystallization of acetyl salicylic acid from supersaturated aqueous/ethanol solution. Cryst. Growth Des. 2006, 6, 1324–1334. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applications—Overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Meenan, P.A.; Anderson, S.R.; Klug, D.L. The influence of impurities and solvents on crystallization. In Handbook of Industrial Crystallization; Myerson, A.S., Ed.; Butterworth-Heinemann: Boston, MA, USA, 2001. [Google Scholar]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The growth of crystals and the equilibrium structure of their surfaces. Philos. Trans. 1951, 243, 299–358. [Google Scholar] [CrossRef]
- Kuvadia, Z.B.; Doherty, M.F. Spiral growth model for faceted crystals of non-centrosymmetric organic molecules grown from solution. Cryst. Growth Des. 2011, 11, 2780–2802. [Google Scholar] [CrossRef]
- Kuvadia, Z.B.; Doherty, M.F. Reformulating multidimensional population balances for predicting crystal size and shape. AIChE J. 2013, 59, 3468–3474. [Google Scholar] [CrossRef]
- Sizemore, J.P.; Doherty, M.F. An engineering model for predicting the shape of solution-grown organic crystals in the presence of an additive. VDI Berichte 2005, 1901I, 477–480. [Google Scholar]
- Sizemore, J.P.; Doherty, M.F. A new model for the effect of molecular imposters on the shape of faceted molecular crystals. Cryst. Growth Des. 2009, 9, 2637–2645. [Google Scholar] [CrossRef]
- Winn, D.; Doherty, M.F. A new technique for predicting the shape of solution-grown organic crystals. AIChE J. 1998, 44, 2501–2514. [Google Scholar] [CrossRef]
- Winn, D.; Doherty, M.F. Modeling of crystal shape of organic materials grown from solution. AIChE J. 2000, 46, 1348–1367. [Google Scholar] [CrossRef]
- Winn, D.; Doherty, M.F. Predicting the shape of organic crystals grown from polar solvents. Chem. Eng. Sci. 2002, 57, 1805–1813. [Google Scholar] [CrossRef]
- Snyder, R.C.; Doherty, M.F. Predicting crystal growth by spiral motion. Proc. R. Soc. A Math. Phys. Eng. Sci. 2009, 465, 1145–1171. [Google Scholar] [CrossRef]
- Lovette, M.A.; Doherty, M.F. Predictive modeling of supersaturation-dependent crystal shapes. Cryst. Growth Des. 2012, 12, 656–669. [Google Scholar] [CrossRef]
- Ma, C.Y.; Wang, X.Z.; Roberts, K.J. Multi-dimensional population balance modeling of the growth of rod-like L-glutamic acid crystals using growth rates estimated from in-process imaging. Adv. Powder Technol. 2007, 18, 707–723. [Google Scholar] [CrossRef]
- Ma, C.Y.; Wang, X.Z. Crystal Growth Rate Dispersion Modeling Using Morphological Population Balance. AIChE J. 2008, 54, 2321–2334. [Google Scholar] [CrossRef]
- Ma, C.Y.; Wang, X.Z.; Roberts, K.J. Morphological Population Balance for Modeling Crystal Growth in Face Directions. AIChE J. 2008, 54, 209–222. [Google Scholar] [CrossRef]
- Wang, X.Z.; Ma, C.Y. Morphological Population Balance Model in Principal Component Space. AIChE J. 2009, 54, 2321–2334. [Google Scholar] [CrossRef]
- Ma, C.Y.; Roberts, K.J. Combining Morphological Population Balances with Face-Specific Growth Kinetics Data to Model and Predict the Crystallization Processes for Ibuprofen. Ind. Eng. Chem. Res. 2018, 57, 16379–16394. [Google Scholar] [CrossRef]
- Ma, C.Y.; Roberts, K.J. Morphological population balance modelling of the effect of crystallisation environment on the evolution of crystal size and shape of para-aminobenzoic acid. Comput. Chem. Eng. 2019, 126, 356–370. [Google Scholar] [CrossRef]
- Chan, E.J.; Tejwani, R.; Derdour, L. Use of Molecular Simulation in Calculating a Characteristic Relative Growth Effect Curvature to Correlate Factors Influencing Crystalline Growth and Other Properties. Cryst. Growth Des. 2015, 15, 5754–5766. [Google Scholar] [CrossRef]
- Szilágyi, B.; Nagy, Z.K. Aspect Ratio Distribution and Chord Length Distribution Driven Modeling of Crystallization of Two-Dimensional Crystals for Real-Time Model-Based Applications. Cryst. Growth Des. 2018, 18, 5311–5321. [Google Scholar]
- Szilágyi, B.; Agachi, P.S.; Lakatos, B.G. Numerical analysis of crystallization of high aspect ratio crystals with breakage. Powder Technol. 2015, 283, 152–162. [Google Scholar] [CrossRef]
- Borsos, A.; Lakatos, B.G. Investigation and simulation of crystallization of high aspect ratio crystals with fragmentation. Chem. Eng. Sci. 2014, 92, 1133–1141. [Google Scholar] [CrossRef]
- Sato, K.; Nagai, H.; Hasegawa, K.; Tomori, K.; Kramer, H.J.M.; Jansen, J.P. Two-dimensional population balance model with breakage of high aspect ratio crystals for batch crystallization. Chem. Eng. Sci. 2008, 63, 3271–3278. [Google Scholar] [CrossRef]
- Briesens, H. Simulation of crystal size and shape by means of a reduced two-dimensional population balance model. Chem. Eng. Sci. 2006, 61, 104–112. [Google Scholar] [CrossRef]
- Gunawan, R.; Fusman, I.; Braatz, R.D. High Resolution Algorithms for Multidimensional Population Balance Equations. AIChE J. 2004, 50, 2738–2749. [Google Scholar] [CrossRef]
- Szilágyi, B.; Lakatos, B.G. Batch cooling crystallization of plate-like crystals: A simulation study. Period. Polytech. Chem. Eng. 2015, 59, 151–158. [Google Scholar] [CrossRef]
- Oullion, M.; Puel, F.; Févotte, G.; Righini, S.; Carvin, P. Industrial batch crystallization of a plate-like organic product. In situ monitoring and 2D-CSD modeling. Part 2: Kinetic modeling and identification. Chem. Eng. Sci. 2007, 62, 833–845. [Google Scholar] [CrossRef]
- Patience, D.B.; Rawlings, J.B. Particle shape monitoring and control in crystallization processes. AIChE J. 2001, 47, 2125–2130. [Google Scholar] [CrossRef]
- Puel, F.; Marchal, P.; Klein, J.P. Habit transient analysis in industrial crystallization using two dimensional crystal size technique. Trans. Icheme 1997, 75, 193–205. [Google Scholar] [CrossRef]
- Puel, F.; Févotte, G.; Klein, J.P. Simulation and analysis of industrial crystallization processes though multidimensional population equations. Part 1: A resolution algorithm based on the method of classes. Chem. Eng. Sci. 2003, 58, 3715–3727. [Google Scholar] [CrossRef]
- Mattews, H.B.; Rawlings, J.B. Batch crystallization of a photochemical: Modeling, control, and filtration. AIChE J. 1998, 44, 1119–1127. [Google Scholar] [CrossRef]
- Shoji, M.; Takiyama, H. The Application of Two-Dimensional Population Balance Model to Study the Effect of temperature Profile on the Crystal Size Distribution and Aspect Ratio. Cryst. Growth Des. 2012, 12, 5241–5246. [Google Scholar] [CrossRef]
- Kean, E.S.; Fisher, K.; West, R. Molecular conformation and electronic structure. The solid state spectrum of a planar anil. J. Am. Chem. Soc. 1972, 94, 3247–3249. [Google Scholar]
- Derdour, L.; Skliar, D. A review of the effect of multiple conformers on crystallization from solution and strategies for crystallizing slow inter-converting conformers. Chem. Eng. Sci. 2014, 106, 275–292. [Google Scholar] [CrossRef]
- Fukuyama, Y.; Asakawa, Y. Novel neurotrophic isocuparane-type sesquiterpene dimers, mastigophorenes A, B, c and D, Isolated from the Liverwort Mastigophora didados. J. Chem. Soc. Perkin Trans. 1991, 11, 2737–2741. [Google Scholar] [CrossRef]
- Albert, J.S.; Ohnmacht, C.; Bernstein, P.R.; Rumsey, W.L.; Aharony, D.; Alelyunas, Y.; Russell, D.J.; Potts, W.; Sherwood, S.A.; Shen, L.; et al. Structural analysis and optimization of NK1 receptor antagonists through modulation of atropisomer interconversion properties. J. Med. Chem. 2004, 47, 519–529. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.S.; Tay, L.D.; Hughes, D.; Donahue, S. Simulaiton of the impact of atropisomer interconversion of plasma exposure of atropisomers of an endothelin receptor antagonist. J. Clin. Pharm. 2004, 44, 680–688. [Google Scholar] [CrossRef] [PubMed]
- Bringmann, G.; Price-Mortimer, A.J.; Keller, P.A.; Gresser, M.J.; Garner, J.; Breuning, M. Atroposelective synthesis of axially chiral biaryl compounds. Angew. Chem. Int. Ed. 2005, 44, 5384–5427. [Google Scholar] [CrossRef] [PubMed]
- Vrudhula, V.M.; Dasgupta, B.; Qian-Cutrone, J.; Kozlowski, E.S.; Boissard, C.G.; Dworetzky, S.I.; Wu, D.; Gao, Q.; Kimura, R.; Gribkoff, V.K.; et al. Atropisomeric 3-(β-hydroxyethyl)-4-arylquinolin-2-ones as Maxi-K Potassium Channel Openers. J. Med. Chem. 2007, 50, 1050–1057. [Google Scholar] [CrossRef]
- Xing, L.; Shieh, H.S.; Selness, S.R.; Devraj, R.V.; Walker, J.K.; Devada, B.; Hope, H.R.; Compton, R.P.; Schinlder, J.F.; Hirsch, J.L.; et al. Structural bioinformatics-based prediction of exceptional selectivity of p38 MAP kinase inhibitor PH-797804. Biochemistry 2009, 48, 6402–6411. [Google Scholar] [CrossRef]
- Clayden, J.; Moran, W.J.; Edwards, P.J.; LaPlante, S.R. The challenge of atropisomerism in drug discovery. Angew. Chem. Int. Ed. 2009, 48, 6398–6401. [Google Scholar] [CrossRef]
- Laplante, S.R.; Fader, L.D.; Fandrick, K.R.; Fandrick, D.R.; Hucke, O.; Kemper, R.; Miller, S.P.F.; Edwards, P.J.J. Assessing atropisomer axial chirality in drug discovery and development. Med. Chem. 2011, 54, 7005–7022. [Google Scholar] [CrossRef] [PubMed]
- Laplante, S.E.; Edwards, P.J.; Fader, L.D.; Jakalian, A.; Hucke, O. Revealing atropisomer axial chirality in drug discovery. Chem. Med. Dev. 2011, 6, 505–513. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Itoyama, R.; Yamahira, M.; Tanaka, J.; Loaëc, N.; Lozach, O.; Durieu, E.; Fukuda, T.; Ishibashi, F. Synthesis, resolution, and biological evaluation of atropisomeric (a R)-and (aS)-16-methyllamellarins n: Unique effects of the axial chirality on the selectivity of protein kinases inhibition. J. Med. Chem. 2013, 56, 7289–7301. [Google Scholar] [CrossRef] [PubMed]
- Zask, A.; Murphy, J.; Ellestad, G.A. Biological stereoselectivity of atropisomeric natural products and drugs. Chirality 2013, 25, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.E.; Marquez, I.; Lokensgard, M.E.; Rheingold, A.L.; Hecht, D.A.; Gustafson, J.L. Exploiting atropisomerism to increase the target selectivity of kinase inhibitors. Angew. Chem. Int. Ed. 2015, 54, 11754–11759. [Google Scholar] [CrossRef] [PubMed]
- LaPlante, S.R.; Forgione, P.; Boucher, C.; Coulombe, R.; James Gillard, J.; Hucke, O.; Jakalian, A.; Joly, M.A.; Kukolj, G.; Lemke, C.; et al. Enantiomeric atropisomers inhibit HCV polymerase and/or HIV matrix: Characterizing hindered bond rotations and target selectivity. J. Med. Chem. 2014, 57, 1944–1951. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zeng, W.; Li, S.; Shen, L.; Gu, Z.; Zhang, Y.; Li, J.; Chen, S.; Jia, X. Discovery and assessment of atropisomers of (±)-lesinurad. ACS Med. Chem. Lett. 2017, 8, 299–303. [Google Scholar] [CrossRef]
- Glunz, P.E. Recent encounters with atropisomerism in drug discovery. Bioorg. Med. Chem. Lett. 2018, 8, 53–60. [Google Scholar] [CrossRef]
- Wisniewski, S.R.; Carrasquillo-Flores, R.; Gonzalez, F.L.; Ramirez, A.; Casey, M.; Soumeillant, M.; Razler, T.M.; Mack, B. Adventures in Atropisomerism: Development of a Robust, Diastereoselective, Lithium-Catalyzed Atropisomer-Forming Active Pharmaceutical Ingredient Step. Org. Process Res. Dev. 2018, 22, 1426–1431. [Google Scholar] [CrossRef]
- Chandrasekhar, J.; Dick, R.; Van Veldhuizen, J.; Koditek, D.; Lepist, E.I.; McGrath, M.E.; Patel, L.; Phillips, G.; Sedillo, K.; Somoza, J.R.; et al. Atropisomerism by Design: Discovery of a Selective and Stable Phosphoinositide 3-Kinase (PI3K) β Inhibitor. J. Med. Chem. 2018, 61, 6858–6868. [Google Scholar] [CrossRef]
- Toenjes, S.T.; Gustafson, J.L. Atropisomerism in medicinal chemistry: Challenges and opportunities. Future Med. Chem. 2018, 10, 409–422. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Reutzel-Edens, S.M.; Mitchell, C.A. Crystallization and polymorphism of conformationally flexible molecules: Problems, patterns and strategies. Org. Proc. Res. Dev. 2000, 4, 396–402. [Google Scholar] [CrossRef]
- Nangia, A. Conformational polymorphism in organic molecules. Acc. Chem. Res. 2007, 41, 595–604. [Google Scholar] [CrossRef] [PubMed]
- Derdour, L.; Pack, S.K.; Skliar, D.; Lai, C.J.; Kiang, S. Crystallization from solutions containing multiple conformers: A new modeling approach for solubility and supersaturation. Chem. Eng. Sci. 2011, 66, 88–102. [Google Scholar] [CrossRef]
- Derdour, L.; Skliar, D. Crystallization from solutions containing multiple conformers. Part I. Modeling of crystal growth and supersaturation. Cryst. Growth Des. 2012, 12, 5180–5187. [Google Scholar] [CrossRef]
- Derdour, L.; Sivakumar, C.; Skliar, D.; Pack, S.K.; Lai, C.J.; Vernille, J.P.; Kiang, S. Crystallization from solutions containing multiple conformers. Part II. Experimental study and model validation. Cryst. Growth Des. 2012, 12, 5188–5196. [Google Scholar] [CrossRef]
- Back, K.; Davey, R.J.; Grecu, T.; Hunter, C.A.; Taylor, L.S. Molecular Conformation and Crystallization: The Case of Ethenzamide. Cryst. Growth Des. 2012, 12, 6110–6117. [Google Scholar] [CrossRef]
- Li, P.; Hwang, J.; Maier, J.M.; Zhao, C.; Kaborda, D.V.; Smith, M.D.; Pellechia, P.J.; Shimizu, K.D. Correlation between Solid-State and Solution Conformational Ratios in a Series of N-(o-Tolyl) Succinimide Molecular Rotors. Cryst. Growth Des. 2015, 15, 3561–3564. [Google Scholar] [CrossRef]
- Cesàro, A.; Bellich, B.; Giannini, G.; Maiocchi, A. Conformational Disorder and Atropisomerism in Pharmaceutical Compounds. In Disordered Pharmaceutical Materials; Descamps, M., Ed.; Wiley-VCH: Weinheim, Germany, 2015; pp. 161–181. [Google Scholar]
- Wicker, J.G.P.; Cooper, R.I. Beyond Rotatable Bond Counts: Capturing 3D Conformational Flexibility in a Single Descriptor. J. Chem. Inf. Model. 2016, 56, 2347–2352. [Google Scholar] [CrossRef]
- Zimmer, G.C.; Pagliari, A.B.; Bender, C.R.; Salbego, P.R.S.; Orlando, T.; Hörner, M.; Zanatta, N.; Bonacorso, H.G.; Martins, M.A.P. Insights on conformation in the solid state: A case study—s-cis and/or s-trans crystallization of 5(3)-aryl-(5)-carboxyethyl-1-tert-butylpyrazoles. Cryst. Eng. Commun. 2018, 20, 5154–5168. [Google Scholar] [CrossRef]
- Thompson, H.P.G.; Day, G.M. Which conformations make stable crystal structures? Mapping crystalline molecular geometries to the conformational energy landscape. Chem. Sci. 2014, 5, 3173–3182. [Google Scholar] [CrossRef]
- Rosbottom, I.; Toroz, D.; Hammond, R.B.; Roberts, K.J. Conformational and structural stability of the single molecule and hydrogen bonded clusters of para aminobenzoic acid in the gas and solution phases. CrystEngComm 2018, 20, 7543–7555. [Google Scholar] [CrossRef]
- Martins, M.A.P.; Pagliari, A.B.; Belladona, A.L.; Tier, A.Z.; Meyer, A.R.; Rodrigues, L.V.; Horner, M.; Frizzo, C.P.; Bonacorso, H.G.; Zanatta, N. Supramolecular self-assembly and thermodynamic properties of 5-aryl-1-(1,1-dimethylethyl)-1H-pyrazoles in the crystalline state. J. Mol. Struct. 2019, 1195, 570–581. [Google Scholar] [CrossRef]
- Du, W.; Cruz-Cabeza, A.J.; Woutersen, S.; Davey, R.J.; Yin, Q. Can the study of self-assembly in solution lead to a good model for the nucleation pathway? The case of tolfenamic acid. Chem. Sci. 2015, 6, 3515–3524. [Google Scholar] [CrossRef] [PubMed]
- Kessler, H. Detection of hindered rotation and inversion by NMR spectroscopy. Angew. Chem. Int. Ed. 1970, 9, 219–235. [Google Scholar] [CrossRef]
- Oki, M. Recent advances in atropisomerism. In Topics in Stereochemistry; Eliel, E.L., Allinger, N.L., Wilen, S.H., Eds.; Wiley Interscience: New York, NY, USA, 1983; pp. 1–81. [Google Scholar]
- Binsch, G. Band-shape analysis. In Dynamic Nuclear Magnetic Resonance Spectroscopy; Jackman, L.M., Cotton, F.A., Eds.; Academic Press: New York, NY, USA, 1975; pp. 45–81. [Google Scholar]
- Kuhn, R. Molekulare assymmetrie. In Stereochemie; Freudenber, H., Ed.; Franz Deuticke: Leipzig, Germany; Wien, Austria, 1933; pp. 803–824. [Google Scholar]
- Bernstein, J.; Hagler, A.T. Conformational polymorphism. The influence of crystal structure on molecular conformation. J. Am. Chem. Soc. 1978, 100, 673–681. [Google Scholar] [CrossRef]
- Bernstein, J.; Anderson, R.E.; Eckhardt, C.J. Confomational influences on electronic spectra and structure. Polymorphs of N-(p-Chlorobenzylidene)-p-chloroaniline. J. Am. Chem. Soc. 1978, 101, 551–554. [Google Scholar]
- Desiraju, G.R. Supramolecular Synthons in Crystal Engineering-A New Organic Synthesis. Angew. Chem. Int. Ed. 1995, 34, 2311–2327. [Google Scholar] [CrossRef]
- Buttar, D.; Charlton, M.H.; Docherty, R.; Starbuck, J.J. Theoretical investigations of conformational aspects of polymorphism. Part 1: O-acetamidobenzamide. Chem. Soc. Perkin Trans. 2 1988, 763–772. [Google Scholar] [CrossRef]
- Holman, K.T.; Pivovar, A.M.; Michael, M.D. Engineering crystal symmetry and polar order in molecular host frameworks. Science 2001, 294, 1907–1911. [Google Scholar] [CrossRef]
- Steiner. T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- Long, S.; Li, T. Controlled Formation of the Acid-Pyridine Heterosynthon over the Acid-Acid Homosynthon in 2-Anilinonicotinic Acids. Cryst. Growth Des. 2009, 9, 4993–4997. [Google Scholar] [CrossRef]
- Bar, I.; Bernstein, J. Conformational polymorphism. 5. Crystal energetics of an isomorphic system including disorder. J. Phys. Chem. 1984, 88, 243–248. [Google Scholar] [CrossRef]
- Bar, I.; Bernstein, J. Conformational polymorphism VI: The crystal and molecular structures of Form II, Form 111, and Form V of 4-Amino-N-2-pyridinylbenzenesulfonamide (Sulfapyridine). J. Pharm. Sci. 1985, 74, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, J.; Davey, R.J.; Henck, J.O. Concomitant polymorphs. Angew. Chem. Int. Ed. 1999, 38, 3440–3461. [Google Scholar] [CrossRef]
- Bernstein, J.; Davey, R.J.; Henck, J.O. Gleichzeitig auftretende polymorphe modifikationen. Angew. Chem. 1999, 111, 3646–3669. [Google Scholar] [CrossRef]
- Starbuck, J.; Docherty, R.; Charlton, M.H.; Buttar, D. Theoretical investigation of conformational aspects of polymorphism. Part 2. Diarylamines. J. Chem. Soc. Perkin Trans. 2 1999, 677–691. [Google Scholar] [CrossRef]
- Lewis, T.C.; Derek, A.T.; Price, S.L. An experimental and theoretical search for polymorphs of barbituric acid: The challences of even limited conformational flexibility. Cryst. Growth Des. 2004, 4, 979–987. [Google Scholar] [CrossRef]
- Roy, S.; Banerjee, R.; Nangia, A.; Kruger, G.J. Conformational, Concomitant Polymorphs of 4,4-Diphenyl-2,5-cyclohexadienone: Conformation and Lattice Energy Compensation in the Kinetic and Thermodynamic Forms. Chem. Eur. J. 2006, 12, 3777–3788. [Google Scholar] [CrossRef]
- Roberts, K.J.; Docherty, R.; Bennema, P.; Jetten, L.A.M. The importance of considering growth-induced conformational change in predicting the morphology of benzophenone. J. Phys. D Appl. Phys. 1993, 26, B7–B21. [Google Scholar] [CrossRef]
- Mc Pherson, A. Crystallization of Biological Macromolecules; CSHL Press: New York, NY, USA, 1999. [Google Scholar]
- Allen, T. Particle Size Measurement, 4th ed.; Chapman & Hall: New York, NY, USA, 1990. [Google Scholar]
- Concistré, M.; De Lorenzo, L.; De Luca, G.; Longeri, M.; Pileio, G.; Raos, G. Conformational analysis of 2,2’-Bithiophene: A 1H liquid crystal NMR study using the 13C satellite spectra. J. Phys. Chem. A 2005, 109, 9953–9963. [Google Scholar] [CrossRef] [PubMed]
- Brás, E.M.; Henriques, M.S.C.; Paixão, J.A.; Fausto, R. High Z′ Crystal Structure of a New Polymorph of a Thioimidazole Disulfide: Importance of Conformational Flexibility. Cryst. Growth Des. 2018, 18, 4167–4173. [Google Scholar] [CrossRef]
- Bazargani, M.F.; Talavat, L.; Naderi, S.; Khavasi, H.R. 2-[(1H-Imidazol-2-yl)disulfanyl]-1H-2-[(1H-Imidazol-2-yl)disulfanyl]-1H-imidazole. Acta Cryst. 2011, E67, o2585. [Google Scholar]
- Kitamura, M.; Furukawa, H.; Asaeda, M. Solvent effect of ethanol on crystallization and growth process of L-histidine polymorphs. J. Cryst. Growth 1994, 141, 193–199. [Google Scholar] [CrossRef]
- Kishikawa, K.; Yoshizaki, K.; Kohmoto, S.; Yamamoto, M.; Yamaguchi, K.; Yamada, K. Control of the rotational barrier and spatial disposition of the N-(2’-methylphenyl) group in succinimides by substituent and solvent effects. J. Chem. Soc. Perkin Trans. 1997, 1, 1233–1239. [Google Scholar] [CrossRef]
- Hunter, C.A.; McCabe, J.F.; Spitaleri, A. Solvent effects of the structures of pre-nucleation aggregates of carbamazepine. CrystEngComm 2012, 14, 7115–7117. [Google Scholar] [CrossRef]
- Spitaleri, A.; Hunter, C.A.; McCabe, J.F.; Packer, M.J.; Cockroft, S.L. A 1H NMR study of crystal nucleation in solution. CrystEngComm 2004, 6, 489–493. [Google Scholar] [CrossRef]
- Zeglinski, J.; Kuhs, M.; Khamar, D.; Hegarty, A.C.; Devi, R.K.; Rasmuson, A.C. Crystal nucleation of tolbutamide in solution: Relationship to solvent, solute conformation, and solution structure. Chem. Eur. J. 2018, 24, 4916–4926. [Google Scholar] [CrossRef] [PubMed]
- Mattei, M.; Li, T. Polymorph Formation and Nucleation Mechanism of Tolfenamic Acid in Solution: An Investigation of Pre-nucleation Solute Association. Pharm. Res. 2012, 29, 460–470. [Google Scholar] [CrossRef]
- Zeglinski, J.; Kuhs, M.; Devi, K.R.; Khamar, D.; Hegarty, A.C.; Thompson, D.; Rasmuson, A.C. Probing Crystal Nucleation of Fenoxycarb from Solution through the Effect of Solvent. Cryst. Growth Des. 2019, 19, 2037–2049. [Google Scholar] [CrossRef]
- Petit, S.; Coquerel, G.; Harman, P. Nucleation and crystal growth of molecular solvates with several conformations both in solution and in solid state: Application to some hydrated coper (II) sulfoxinates. J. Cryst. Growth 1994, 137, 585–594. [Google Scholar] [CrossRef]
- Hurshouse, M.B.; Huth, L.S.; Threlfall, T.L. Why do organic compounds crystallise well or badly or ever so slowly? Why is crystallisation nevertheless such a good purification technique? Org. Proc. Res. Dev. 2009, 13, 1231–1240. [Google Scholar] [CrossRef]
- Walter, W.; Gerhard Maerten, G. Thioformylierung von Aminen und Untersuchungen über die cis-trans-Isomerie an der Thioamidgruppe. Liebigs Ann. Chem. 1963, 669, 66–75. [Google Scholar] [CrossRef]
- Walter, W.; Gerhard Maerten, G.; Rose, H. NMR-spektroskopische Untersuchungen an cis- und trans-N-Methyl-N-benzyl-thioformamid. Zuordnung der Konfigurationen und Kinetik der Umwandlung. Liebigs Ann. Chem. 1966, 691, 25–32. [Google Scholar] [CrossRef]
- Walter, W.; Becker, R.F. Über die struktur der thioamide und ihrer derivate. XX. Untersuchungen zur behinderten rotation bei ortho-substituierten n-alkyl-thioformaniliden. Tetrahedron 1972, 28, 1705–1720. [Google Scholar] [CrossRef]
- Mannschreck, A. Separation of rotational isomers of amides, thioamides, and nitrosamines. Angew. Chem. Int. Ed. 1965, 4, 985. [Google Scholar]
- Mannschreck, A. Protonenresonanz-Untersuchungen zur innerbn rotation II. 1. Zur trennung rotationsisomerer amide der mesitylencabonsäure. Tetrahedron Lett. 1965, 19, 1341–1347. [Google Scholar] [CrossRef]
- Jaeschke, A.; Muensch, H.; Schmid, H.G.; Friebolin, H.; Mannschreck, A. The conformers of a nitrosamine and a carboxamide: Comparison of NMR line shape and equilibration methods. J. Mol. Spectrosc. 1969, 31, 14–31. [Google Scholar] [CrossRef]
- Staab, H.A.; Lauer, D. Stabile rotationisomere von carbonsaureamiden. Tetrahedron Lett. 1966, 38, 4593–4598. [Google Scholar] [CrossRef]
- Bungard, C.J.; Morris, J.C. Total synthesis of the 7,3’-linked naphthylisoquinoline alkaloid ancistrocladidine. J. Org. Chem. 2006, 71, 7354–7363. [Google Scholar] [CrossRef]
- Mannschreck, A.; Münsch, H.; Mattheus, A. Trennung der konformationsisomeren eines Nitrosamins. Angew. Chem. 1966, 78, 751. [Google Scholar] [CrossRef]
- Parker, J.S.; Smith, N.A.; Welham, M.J.; Moss, W.O. A new approach to the rapid parallel development of four neurokinin antagonists. Part 5. preparation of ZM374979 cyanoacid and selective crystallisation of ZM374979 atropisomers. Org. Proc. Res. Dev. 2004, 8, 45–50. [Google Scholar] [CrossRef]
- Ischenko, V.; Englert, U.; Jansen, M. Conformational dimorphism of 1,1,3,3,5,5-Hexachloro-1,3,5-trigermacyclohexane: Solvent-induced crystallization of a metastable polymorph containing boat-shaped molecules. Chem. Eur. J. 2005, 11, 1375–1383. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Galera, A.J.; Gomez-Rodríguez, J.M. Surface Diffusion of Simple Organic Molecules on Graphene on Pt(111). J. Phys. Chem. C 2011, 115, 23036–23042. [Google Scholar] [CrossRef]
- Derdour, L.; Buono, F. An investigation of the applicability of microcalorimetry for the measurement of supersaturation of during batch crystallization from solution. Cryst. Growth Des. 2012, 12, 1899–1912. [Google Scholar] [CrossRef]
- Garside, J.; Mersmann, A.; Nyvlt, J. Measurement of Crystal Growth and Nucleation Rates, 2nd ed.; IChemE: Rugby, UK, 2002. [Google Scholar]
- Davey, R.J.; Garside, J. From Molecules to Crystallisers—An Introduction to Crystallisation; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Kossel, W. Zur Energetik von oberflächenvorgängen. Ann. Phys. 1934, 21, 457–480. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Butterworth Heinemann: Oxford, UK, 2001. [Google Scholar]
- Bennema, P.; Gilmer, G.H. Kinetics of crystal growth. In Crystal Growth, an Introduction; Harman, P., Ed.; North-Holland: Amsterdam, The Netherlands, 1973. [Google Scholar]




| Authors | Eb (kcal/mol) | Purity of Atropisomer in Crystal | Proportion of Crystal Atropisomer in Solution |
|---|---|---|---|
| Walter and maerten [116] | NR | Pure | NR |
| Walter et al. [117] | 25.16 | Pure | 50% |
| Walter and Becker [118] | 22.31 | Pure | 50% |
| Mannschreck [119,120] | 22.9 at 38.5 | Pure | 64% in CCl4 at 38.2 °C |
| Jaeschke et al. [121] | 23.4–22.8 | Pure | 41% at 50 °C in |
| 1-Chloronaphthalen/Benzotricholide (1:1) | |||
| Staab and Lauer [122] | 32 at 120 °C | Pure * | 66% in THF at RT |
| Mannschreck [119,120] | 26.8–27.3 | Pure | 68% at 50 °C in CDCl3 |
| Xing et al. [56] | >25 | Pure | 50% |
| Bungard and Morris [123] | NR | Pure | 50% |
| Mannschreck [119,120] | NR | 94% | 81% at 36 °C in CCl4 |
| Mannschreck et al. [124] | 22.3–23.2 | 94% | NR |
| 23.9–24.2 | Pure * | 62.5% in CCl4 at 36.5 °C | |
| Parker et al. [125] | NR | 89% | NR |
| NR | 97% | 40% at 60 °C | |
| Ischenko et al. [126] | 11 (Chair major) | Pure | 50% |
| Jaeschke et al. [121] | 22 | Pure | 57.1% at 50 °C in Hexachlorobutadiene |
| Derdour and Skliar [50] | NMR: 16.8 ab initio: 22.4 | Pure | 15.6% |
| Li et al. [75] | 20–21 [108] | Pure | Dominant (14 rotors) Mixture (16 rotors) |
| Zimmer et al. [78] | 5.51 | Pure | 100% |
| Conditions # | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
| SL (% input) | 1 | 1 | 2 | 2 | 1 | 1 | 2 | 2 |
| AR (mL/(mn) | 1 | 1 | 1 | 1 | 3 | 3 | 3 | 3 |
| RSSo (%) | 151.9 | 31.7 | 31.7 | 151.9 | 151.9 | 31.7 | 31.7 | 151.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derdour, L.; Chan, E.J.; Skliar, D. Review and Modeling of Crystal Growth of Atropisomers from Solutions. Processes 2019, 7, 611. https://doi.org/10.3390/pr7090611
Derdour L, Chan EJ, Skliar D. Review and Modeling of Crystal Growth of Atropisomers from Solutions. Processes. 2019; 7(9):611. https://doi.org/10.3390/pr7090611
Chicago/Turabian StyleDerdour, Lotfi, Eric J. Chan, and Dimitri Skliar. 2019. "Review and Modeling of Crystal Growth of Atropisomers from Solutions" Processes 7, no. 9: 611. https://doi.org/10.3390/pr7090611
APA StyleDerdour, L., Chan, E. J., & Skliar, D. (2019). Review and Modeling of Crystal Growth of Atropisomers from Solutions. Processes, 7(9), 611. https://doi.org/10.3390/pr7090611




