Handling Constraints and Raw Material Variability in Rotomolding through Data-Driven Model Predictive Control
Abstract
1. Introduction
2. Preliminaries
2.1. Rotational Molding
2.1.1. Surface Void Analysis
2.1.2. Ultrasonic Spectroscopy
2.1.3. Impact Test
2.1.4. Rheology
2.2. Subspace Identification Approach for Batch Processes
2.3. Model Identification
3. Model Predictive Control Design for Rotational Molding Process
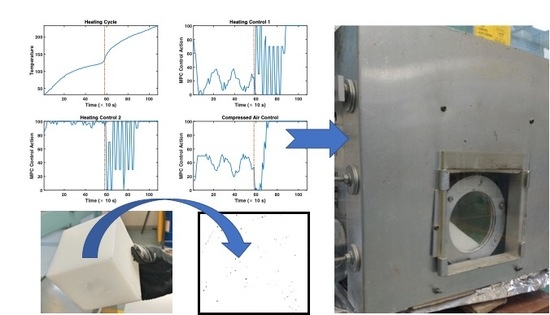
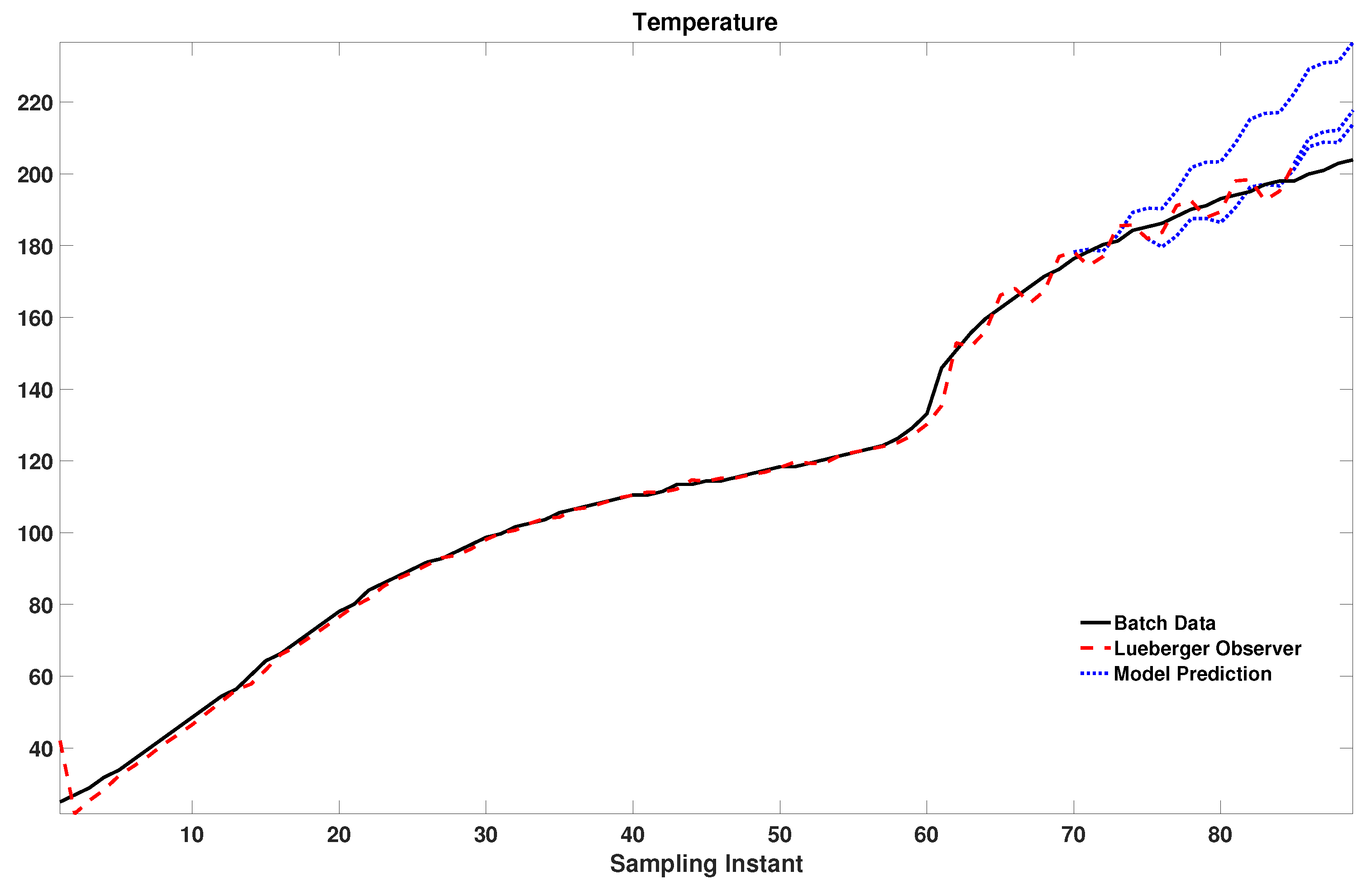
4. Closed-Loop Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gomes, F.P.; Garg, A.; Mhaskar, P.; Thompson, M.R. Quality Monitoring of Rotational Molded Parts Using a Nondestructive Technique. In Proceedings of the ANTEC 2018, Orlando, FL, USA, 7–10 May 2018; Society of Plastics Engineers: Brookfield, CT, USA, 2018. ISBN 123-0-1234567-8-9. [Google Scholar]
- Garg, A.; Gomes, F.P.; Mhaskar, P.; Thompson, M.R. Model predictive control of uni-axial rotational molding process. Comput. Chem. Eng. 2019, 121, 306–316. [Google Scholar] [CrossRef]
- Bonvin, D. Optimal operation of batch reactors—A personal view. J. Process Control 1998, 8, 355–368. [Google Scholar] [CrossRef]
- Aumi, S.; Mhaskar, P. Integrating Data-Based Modeling and Nonlinear Control Tools For Batch Process Control. AIChE J. 2012, 58, 2105–2119. [Google Scholar] [CrossRef]
- Aumi, S.; Corbett, B.; Mhaskar, P.; Clarke-Pringle, T. Data-based modeling and control of Nylon-6, 6 batch polymerization. IEEE Trans. Control Syst. Technol. 2013, 21, 94–106. [Google Scholar] [CrossRef]
- Abu-Al-Nadi, D.I.; Abu-Fara, D.I.; Rawabdeh, I.; Crawford, R.J. Control of rotational molding using adaptive fuzzy systems. Adv. Polym. Technol. 2005, 24, 266–277. [Google Scholar] [CrossRef]
- Flores-Cerrillo, J.; MacGregor, J.F. Control of particle size distributions in emulsion semibatch polymerization using mid-course correction policies. Ind. Eng. Chem. Res. 2002, 41, 1805–1814. [Google Scholar] [CrossRef]
- Flores-Cerrillo, J.; MacGregor, J.F. Latent variable MPC for trajectory tracking in batch processes. J. Process Control 2005, 15, 651–663. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User; Pearson Education: London, UK, 1998. [Google Scholar]
- Kadali, R.; Huang, B.; Rossiter, A. A data driven subspace approach to predictive controller design. Control Eng. Pract. 2003, 11, 261–278. [Google Scholar] [CrossRef]
- Pour, N.D.; Huang, B.; Shah, S.L. Subspace Approach to Identification of Step-Response Model from Closed-Loop Data. Ind. Eng. Chem. Res. 2010, 49, 8558–8567. [Google Scholar] [CrossRef]
- Corbett, B.; Mhaskar, P. Subspace identification for data-driven modeling and quality control of batch processes. AIChE J. 2016, 62, 1581–1601. [Google Scholar] [CrossRef]
- Garg, A.; Corbett, B.; Mhaskar, P.; Hu, G.; Flores-Cerrillo, J. Subspace-based model identification of a hydrogen plant startup dynamics. Comput. Chem. Eng. 2017, 106, 183–190. [Google Scholar] [CrossRef]
- Garg, A.; Mhaskar, P. Subspace Identification-Based Modeling and Control of Batch Particulate Processes. Ind. Eng. Chem. Res. 2017, 56, 7491–7502. [Google Scholar] [CrossRef]
- Garg, A.; Mhaskar, P. Utilizing big data for batch process modeling and control. Comput. Chem. Eng. 2018, 119, 228–236. [Google Scholar] [CrossRef]
- Gomes, F.P.; West, W.T.; Thompson, M.R. Effects of annealing and swelling to initial plastic deformation of polyethylene probed by nonlinear ultrasonic guided waves. Polymer 2017, 131, 160–168. [Google Scholar] [CrossRef]
- Tangirala, A.K. Principles of System Identification: Theory and Practice; Taylor & Francis: Abingdon, UK, 2014. [Google Scholar]
- Qin, S.J. An overview of subspace identification. Comput. Chem. Eng. 2006, 30, 1502–1513. [Google Scholar] [CrossRef]
- Raghavan, H.; Tangirala, A.K.; Bhushan Gopaluni, R.; Shah, S.L. Identification of chemical processes with irregular output sampling. Control Eng. Pract. 2006, 14, 467–480. [Google Scholar] [CrossRef]
- Larimore, W. Canonical variate analysis in identification, filtering, and adaptive control. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; Volume 2, pp. 596–604. [Google Scholar] [CrossRef]
- Overschee, P.V.; Moor, B.D. Two subspace algorithms for the identification of combined deterministic-stochastic systems. In Proceedings of the 31st IEEE Conference on Decision and Control, Tucson, AZ, USA, 16–18 December 1992; Volume 311, pp. 75–93. [Google Scholar] [CrossRef]
- Verhagen, M.; Dewilde, P. Subspace model identification Part 1. The output-error state-space model identification class of algorithms. Int. J. Control 1992, 56, 1187–1210. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. A unifying theorem for three subspace system identification algorithms. Automatica 1995, 31, 1853–1864. [Google Scholar] [CrossRef]
- Wang, J.; Qin, S.J. A new subspace identification approach based on principal component analysis. J. Process Control 2002, 12, 841–855. [Google Scholar] [CrossRef]
- Qin, S.J.; Lin, W.; Ljung, L. A novel subspace identification approach with enforced causal models. Automatica 2005, 41, 2043–2053. [Google Scholar] [CrossRef]
- Moonen, M.; De Moor, B.; Vandenberghe, L.; Vandewalle, J. On- And Off-Line Identification Of Linear State Space Models. Int. J. Control 1989, 49, 219–232. [Google Scholar] [CrossRef]
- Mhaskar, P.; Garg, A.; Corbett, B. Modeling and Control of Batch Processes; Advances in Industrial Control; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Kheradmandi, M.; Mhaskar, P. Adaptive Model Predictive Batch Process Monitoring and Control. Ind. Eng. Chem. Res. 2018, 57, 14628–14636. [Google Scholar] [CrossRef]
- Gomes, F.P.; Garg, A.; Mhaskar, P.; Thompson, M.R. Data-Driven Advances in Manufacturing for Batch Polymer Processing Using Multivariate Nondestructive Monitoring. Ind. Eng. Chem. Res. 2019. [Google Scholar] [CrossRef]




| Batches | ||||
|---|---|---|---|---|
| Batch 1 | 3596 | |||
| Batch 2 | 4260 | |||
| Batch 3 | 4276 | |||
| Batch 4 | 4230 | |||
| Batch 5 | 4441 | |||
| Batch 6 | 4377 | |||
| Batch 7 | 4387 |
| Batches | ||||
|---|---|---|---|---|
| Actual | 4681 | |||
| Predicted () | 4740 | |||
| Predicted () | 4296 | |||
| Predicted () | 4292 |
| Batches | ||||
|---|---|---|---|---|
| MPC Batch 1 | 4681 | |||
| MPC Batch 2 | 7730 | |||
| MPC Batch 3 | 4722 | |||
| MPC Batch 4 | 4726 | |||
| MPC Batch 5 | 5262 |
| Batches | Blending % | |||
|---|---|---|---|---|
| MPC Batch 1 | 2 | |||
| MPC Batch 2 | 2 | |||
| MPC Batch 3 | 4 | |||
| MPC Batch 4 | 4 | |||
| MPC Batch 5 | 6 | |||
| MPC Batch 6 | 6 | |||
| MPC Batch 7 | 8 | |||
| MPC Batch 8 | 8 | |||
| MPC Batch 9 | 10 | |||
| MPC Batch 10 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garg, A.; Abdulhussain, H.A.; Mhaskar, P.; Thompson, M.R. Handling Constraints and Raw Material Variability in Rotomolding through Data-Driven Model Predictive Control. Processes 2019, 7, 610. https://doi.org/10.3390/pr7090610
Garg A, Abdulhussain HA, Mhaskar P, Thompson MR. Handling Constraints and Raw Material Variability in Rotomolding through Data-Driven Model Predictive Control. Processes. 2019; 7(9):610. https://doi.org/10.3390/pr7090610
Chicago/Turabian StyleGarg, Abhinav, Hassan A. Abdulhussain, Prashant Mhaskar, and Michael R. Thompson. 2019. "Handling Constraints and Raw Material Variability in Rotomolding through Data-Driven Model Predictive Control" Processes 7, no. 9: 610. https://doi.org/10.3390/pr7090610
APA StyleGarg, A., Abdulhussain, H. A., Mhaskar, P., & Thompson, M. R. (2019). Handling Constraints and Raw Material Variability in Rotomolding through Data-Driven Model Predictive Control. Processes, 7(9), 610. https://doi.org/10.3390/pr7090610