Modeling and Economic Optimization of the Membrane Module for Ultrafiltration of Protein Solution Using a Genetic Algorithm
Abstract
:1. Introduction
2. Process Configuration and Model Calculation
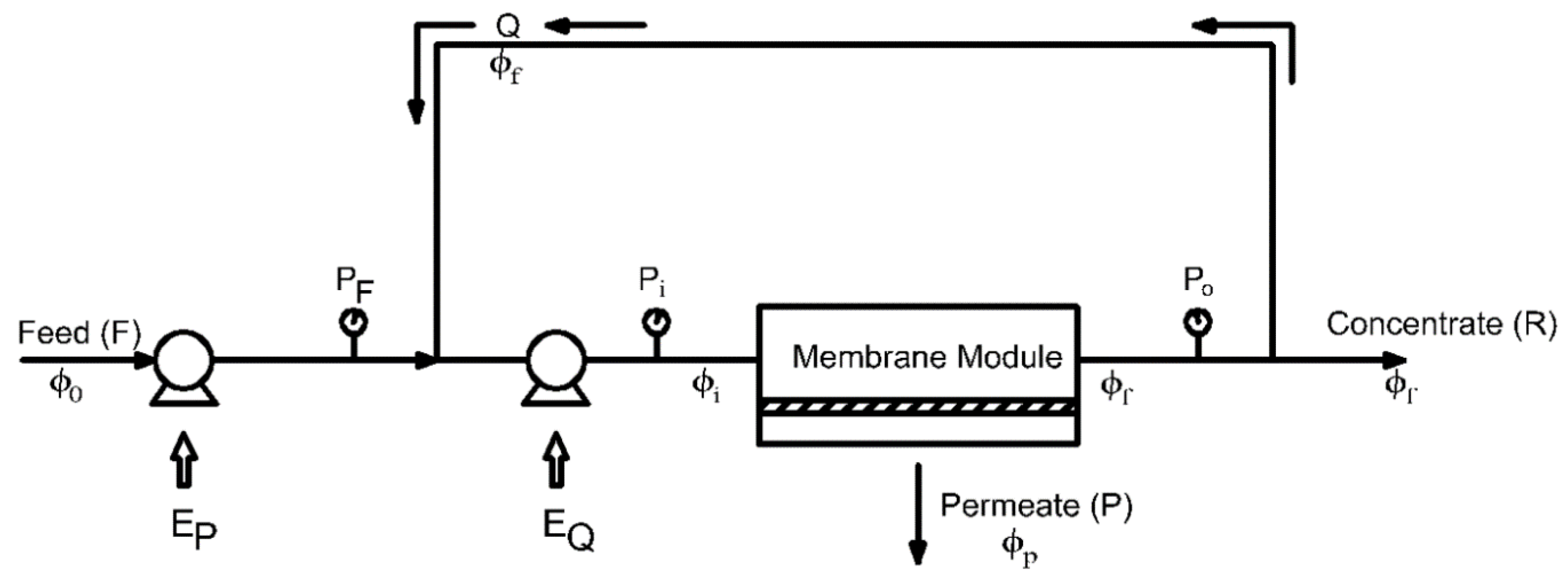
2.1. Membrane Plant Configuration
2.2. Modeling of Membrane Modules
- EP, EQ are the power supplied by the feed pump and recirculation pump, respectively
- PF, Pi, Po are the pressure at the outlet of the feed pump, at the inlet and outlet of the membrane module, respectively
- ΔPdrop is the pressure drop in the membrane module
2.3. Cost Estimation
2.3.1. Operating Cost
2.3.2. Capital Cost
Pump Capital Cost
- I: a cost index ratio for updating the cost to the recent year
- f1: an adjust factor for pump construction material
- f2: an adjust factor for suction pressure range
- L: a factor used to incorporate labor costs
- Q: flow capacity of the pump [m3/h]
- P: pressure outlet of the pump [kPa]
Capital Cost of Other Equipment
- Pipes and valves
- Instruments and controls
- Tanks and frames
- Miscellaneous
Annual Capital Cost
3. Formulizations of the Problem
3.1. Fix Parameters and Design Variables
3.2. Objective Function
3.3. Constraints
3.4. Optimization by Genetic Algorithm
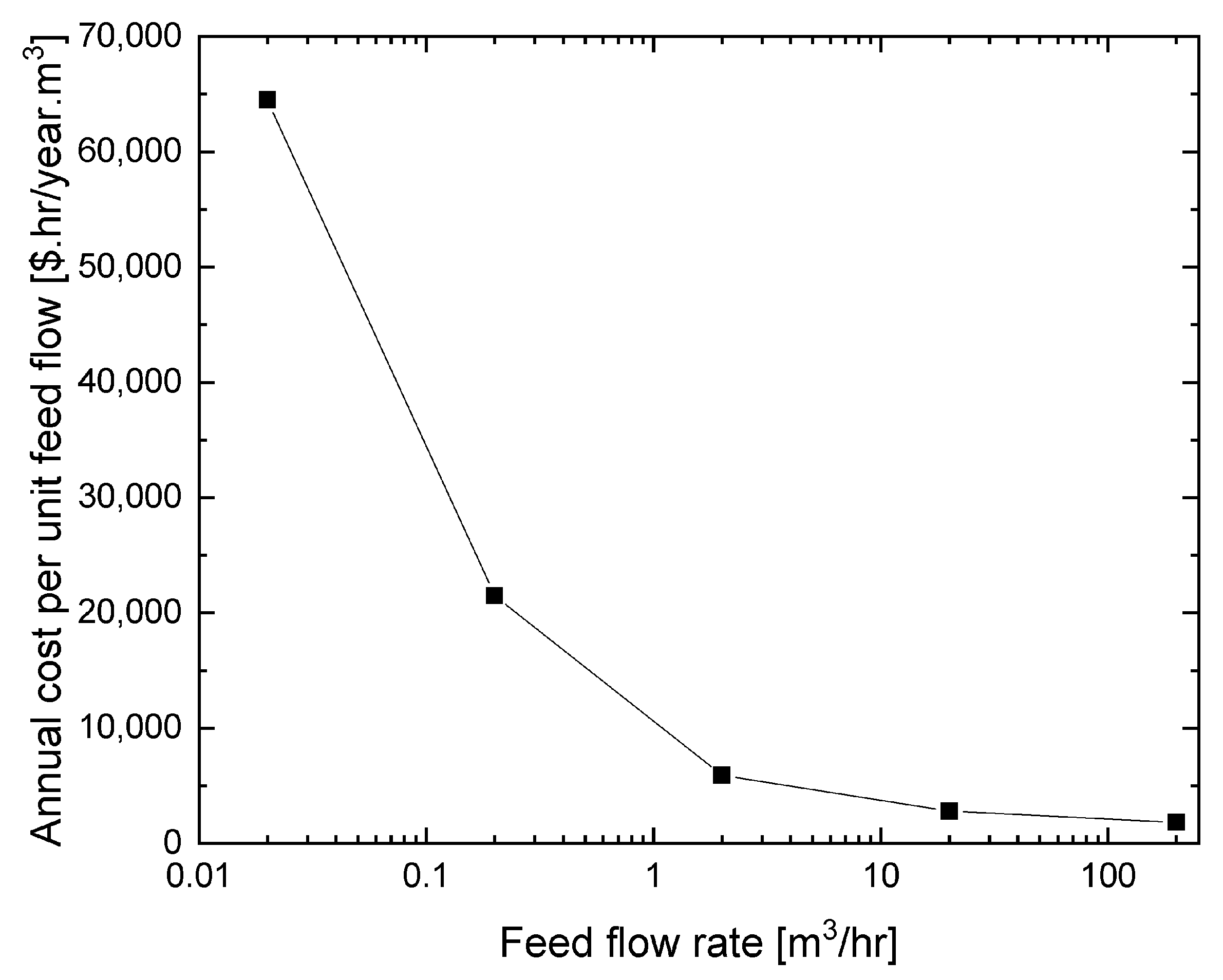
4. Results and Discussion
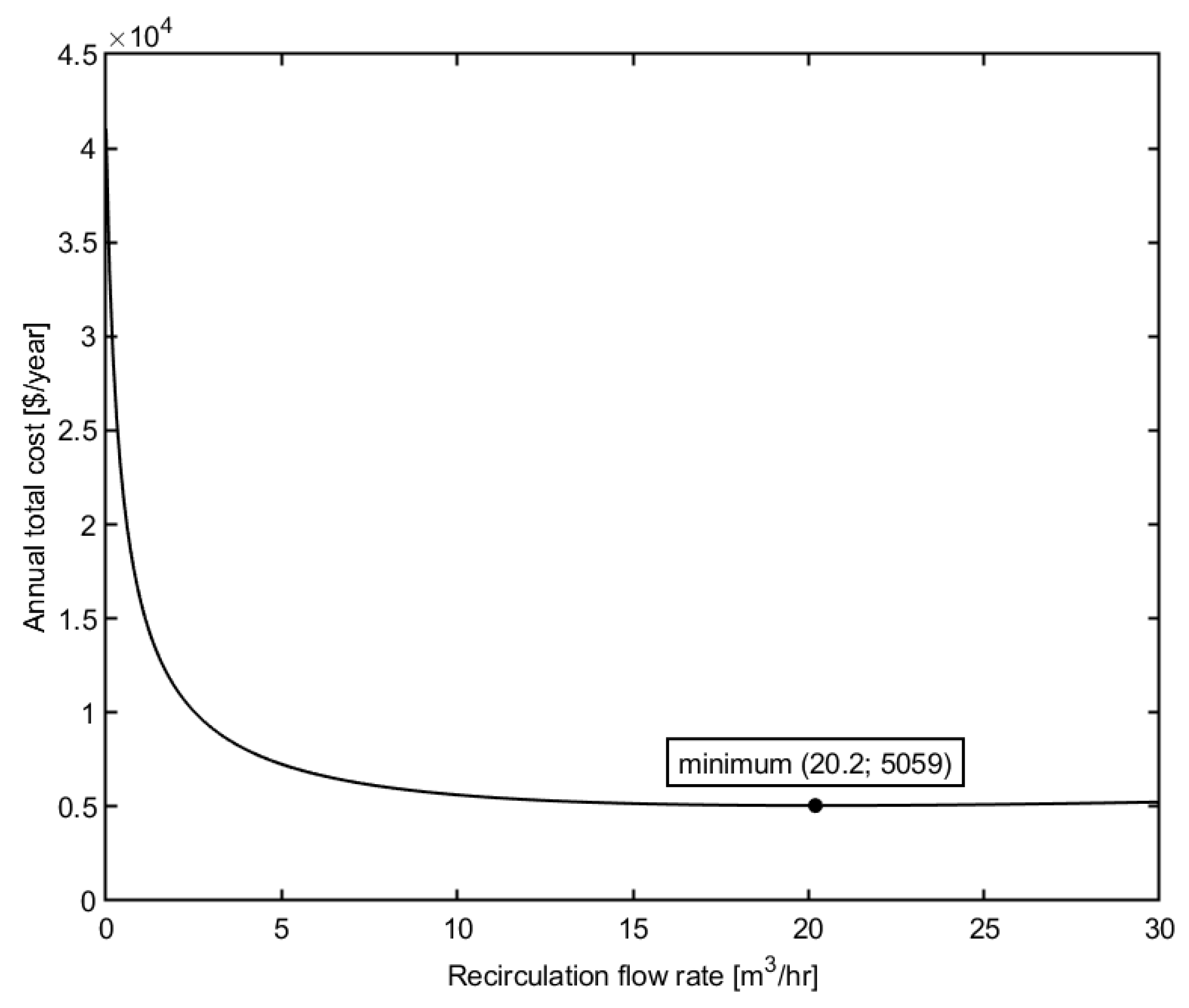
4.1. Effect of Recirculation Flow Rate on the Total Cost
4.2. Effect of Module Inlet Pressure Operation
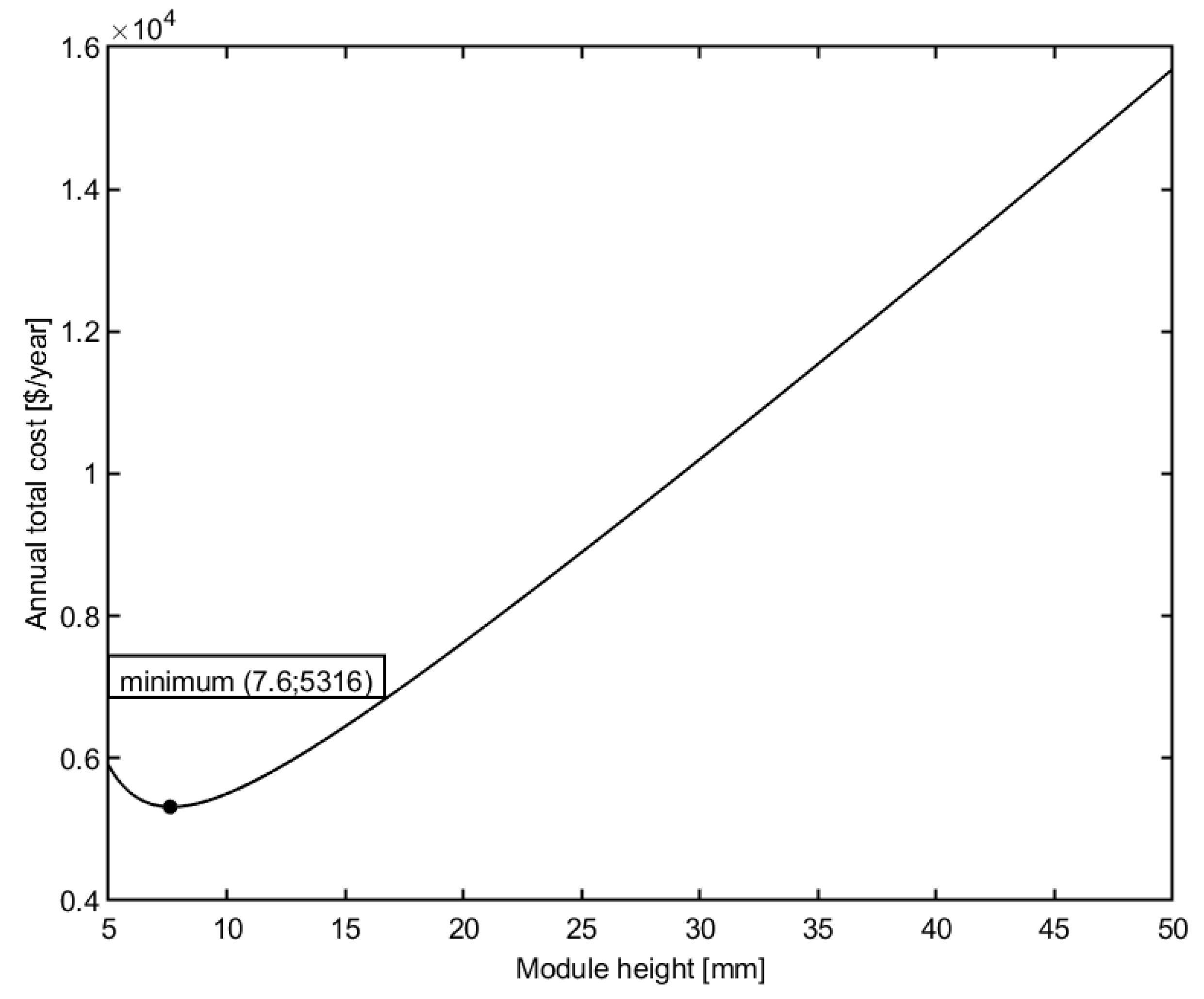
4.3. Effect of Module Height
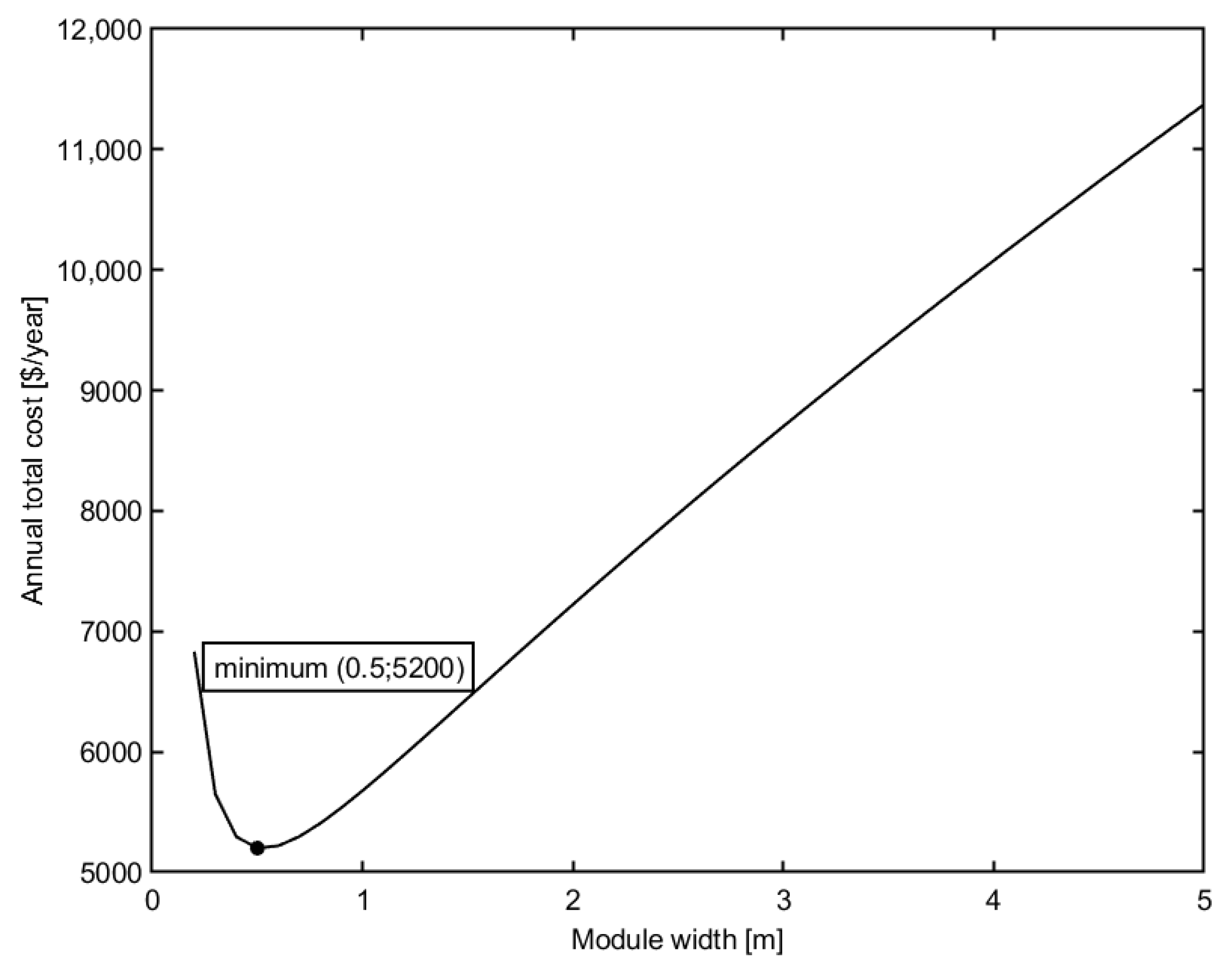
4.4. Effect of Module Width
4.5. Optimum Design
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mores, P.L.; Arias, A.M.; Scenna, N.J.; Caballero, J.A.; Mussati, S.F.; Mussati, M.C. Membrane-Based Processes: Optimization of Hydrogen Separation by Minimization of Power, Membrane Area, and Cost. Processes 2018, 6, 221. [Google Scholar] [CrossRef] [Green Version]
- Ramírez-Santos, Á.A.; Bozorg, M.; Addis, B.; Piccialli, V.; Castel, C.; Favre, E. Optimization of multistage membrane gas separation processes. Example of application to CO2 capture from blast furnace gas. J. Membr. Sci. 2018, 566, 346–366. [Google Scholar] [CrossRef]
- Ohs, B.; Lohaus, J.; Wessling, M. Optimization of membrane based nitrogen removal from natural gas. J. Membr. Sci. 2016, 498, 291–301. [Google Scholar] [CrossRef]
- Wiley, D.E.; Fell, C.J.D.; Fane, A.G. Optimisation of membrane module design for brackish water desalination. Desalination 1985, 52, 249–265. [Google Scholar] [CrossRef]
- Nguyen, T.-A.; Yoshikawa, S.; Karasu, K.; Ookawara, S. A simple combination model for filtrate flux in cross-flow ultrafiltration of protein suspension. J. Membr. Sci. 2012, 403–404, 84–93. [Google Scholar] [CrossRef]
- Nguyen, T.-A.; Yoshikawa, S.; Ookawara, S. Steady State Permeate Flux Estimation in Cross-Flow Ultrafiltration of Protein Solution. Sep. Sci. Technol. 2014, 49, 1469–1478. [Google Scholar] [CrossRef]
- Sethi, S.; Wiesner, M.R. Performance and Cost Modeling of Ultrafiltration. J. Environ. Eng. 1995, 121, 874–883. [Google Scholar] [CrossRef]
- Zeman, L.J.; Zydney, A.L. Microfiltration and Ultrafiltration: Principles and Applications; Taylor & Francis: New York, NY, USA, 1996. [Google Scholar]
- Cheryan, M. Ultrafiltration and Microfiltration Handbook; Taylor & Francis: New York, NY, USA, 1998. [Google Scholar]
- Nguyen, T.-A.; Yoshikawa, S.; Ookawara, S. Effect of operating conditions in membrane module performance. Asean Eng. J. Part B 2015, 4, 4–13. [Google Scholar]
- Sumathi, S.; Hamsapriya, T.; Surekha, P. Evolutionary Intelligence: An Introduction to Theory and Applications with Matlab; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Apostol, T.M. Mathematical Analysis; Addison-Wesley: Boston, MA, USA, 1974. [Google Scholar]
- Karasu, K. A study on permeation phenomena in cross-flow ultrafiltration producing a compressible cake layer. Ph.D. Thesis, Tokyo Institute of Technology, Tokyo, Japan, 2010. [Google Scholar]
- Porter, M.C. Concentration Polarization with Membrane Ultrafiltration. Prod. R&D 1972, 11, 234–248. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics; McGraw Hill: New York, NY, USA, 2011. [Google Scholar]
- Pritchard, P.J. Fox and McDonald’s Introduction to Fluid Mechanics, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Buzzi-Ferraris, G.; Manenti, F. Differential and Differential-Algebraic Systems for the Chemical Engineer: Solving Numerical Problems; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- U.S. Energy Information Administration. Average Price of Electricity to Ultimate Customers: Total by End-Use Sector. In Electric Power Monthly; Table 5.6.A.; U.S. Department of Energy: Washington, DC, USA, 2019. [Google Scholar]
- Park, C.S. Fundamentals of Engineering Economics: International Edition; Pearson Education Limited: London, UK, 2013. [Google Scholar]
- Guthrie, K.M. Process Plant Estimating, Evaluation, and Control; Craftsman Book Company of America: Carlsbad, CA, USA, 1974. [Google Scholar]
- Perry, R.H.; Chilton, C.H.; Perry, J.H. Chemical Engineers’ Handbook, 5th ed.; McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2007. [Google Scholar]
- Holland, F.A.; Wilkinson, J.K. Process Economics. In Perry’s Chemical Engineers’ Handbook, 7th ed.; Perry, R.H., Green, D.W., Eds.; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Mir, L.; Michaels, S.L.; Goel, V.; Kaiser, R. Crossflow Microfiltration: Applications, Design, and Cost. In Membrane Handbook; Ho, W.S.W., Sirkar, K.K., Eds.; Springer: Boston, MA, USA, 1992; pp. 571–594. [Google Scholar]
- Sethi, S. Transient Permeate Flux Analysis, Cost Estimation, and Design Optimization in Crossflow Membrane Filtration. Ph.D. Thesis, Rice University, Houston, TX, USA, 1997. [Google Scholar]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]

| Notation | Name and Units |
|---|---|
| F | Feed flow rate (m3/h) |
| R | Retentate (concentrate) flow rate (m3/h) |
| Q | Recirculation flow rate (m3/h) |
| P | Permeation flow rate (m3/h) |
| PF | Pressure at outlet of feed pump (kPa) |
| Pi | Pressure at the inlet of membrane module (kPa) |
| Po | Pressure at the inlet of membrane module (kPa) |
| EP | Energy supplied by feed pump (kW) |
| EQ | Energy supplied by recirculation pump (kW) |
| ϕ0 | initial concentration of protein solution (m3/m3) |
| ϕi | inlet concentration of protein solution (m3/m3) |
| ϕf | final concentration of protein solution (m3/m3) |
| ϕP | protein concentration of permeate flux (m3/m3) |
| Parameters | Value |
|---|---|
| Feed flow rate (m3/h) | 0.02–200 |
| Inlet pressure (kPa) | 200–1000 |
| Recirculation flow rate (m3/h) | 0–50 |
| Initial solid fraction (m3/m3) | 0.1 |
| Final solid fraction (m3/m3) | 0.4 |
| Plant design year (year) | 20 |
| Interest rate (%) | 8 |
| Energy price ($/kWh) | 0.08 |
| Efficiency of pumps (%) | 70 |
| Operating temperature (°C) | 25 |
| Module height (mm) | 0–100 |
| Module width (m) | 0–30 |
| Feed [m3/h] | ϕ0 [-] | ϕf [-] | Pressure [kPa] | Recirculation [m3/h] | Width [m] | Height [mm] | Total Cost [$/yr] |
|---|---|---|---|---|---|---|---|
| 0.02 | 0.1 | 0.4 | 523 | 2.8 | 0.1 | 5.0 | 1.29 × 103 |
| 0.2 | 0.1 | 0.4 | 1000 | 4.9 | 0.1 | 8.9 | 4.30 × 103 |
| 2 | 0.1 | 0.4 | 1000 | 0.2 | 0.1 | 6.9 | 1.18 × 104 |
| 20 | 0.1 | 0.4 | 987 | 0.2 | 1.3 | 5.0 | 5.60 × 104 |
| 200 | 0.1 | 0.4 | 1000 | 0.8 | 11.1 | 5.0 | 3.65 × 105 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, T.-A.; Yoshikawa, S. Modeling and Economic Optimization of the Membrane Module for Ultrafiltration of Protein Solution Using a Genetic Algorithm. Processes 2020, 8, 4. https://doi.org/10.3390/pr8010004
Nguyen T-A, Yoshikawa S. Modeling and Economic Optimization of the Membrane Module for Ultrafiltration of Protein Solution Using a Genetic Algorithm. Processes. 2020; 8(1):4. https://doi.org/10.3390/pr8010004
Chicago/Turabian StyleNguyen, Tuan-Anh, and Shiro Yoshikawa. 2020. "Modeling and Economic Optimization of the Membrane Module for Ultrafiltration of Protein Solution Using a Genetic Algorithm" Processes 8, no. 1: 4. https://doi.org/10.3390/pr8010004
APA StyleNguyen, T.-A., & Yoshikawa, S. (2020). Modeling and Economic Optimization of the Membrane Module for Ultrafiltration of Protein Solution Using a Genetic Algorithm. Processes, 8(1), 4. https://doi.org/10.3390/pr8010004





