Non-Intrusive Monitoring Algorithm for Resident Loads with Similar Electrical Characteristic
Abstract
:1. Introduction
2. Fundamental of NILM
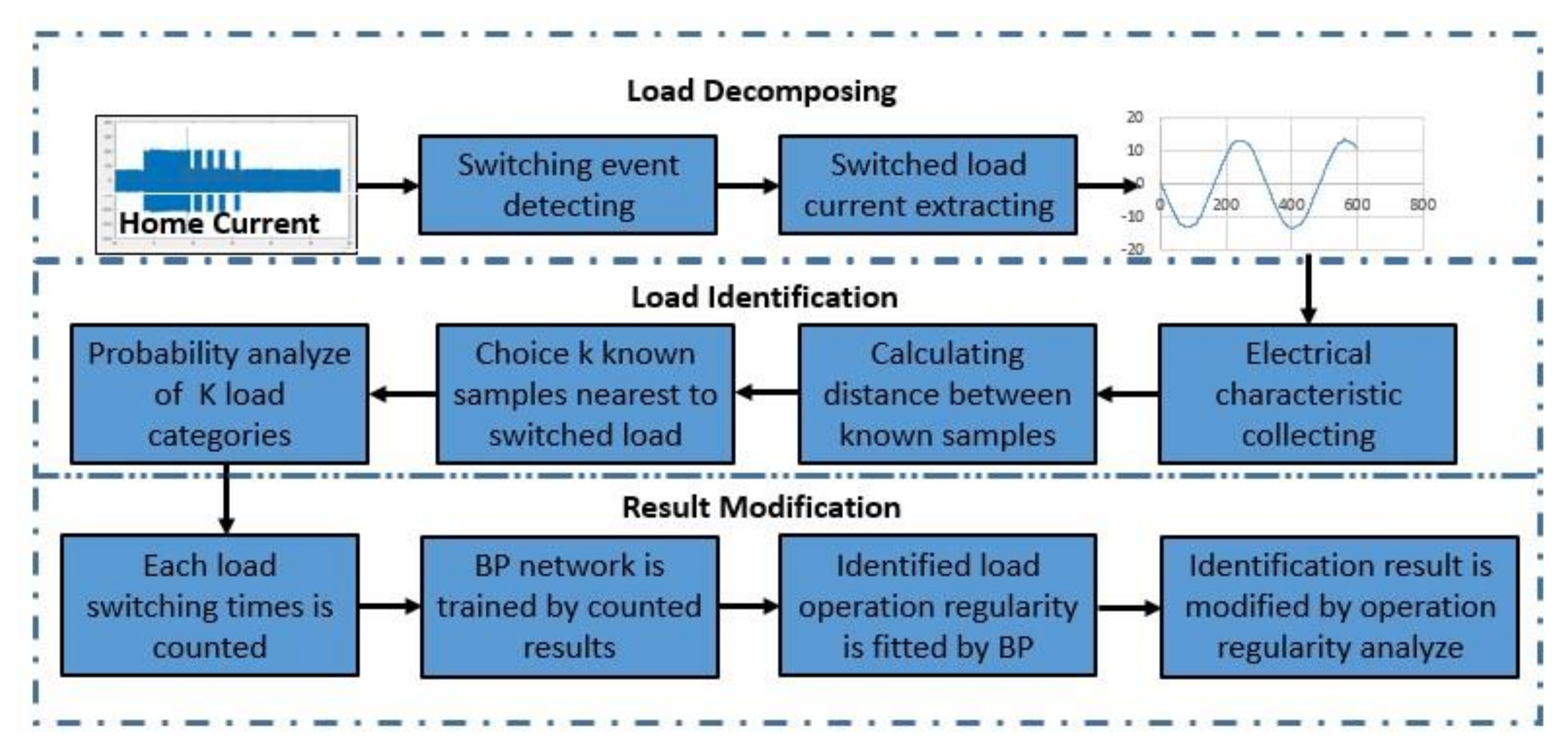
3. Similar Load Characteristics Identification Method Based on Load Switching Probability Distribution Curve
3.1. Switching Event Detecting and Combined Signal Decomposition
3.2. Load Identification Using KNN Algorithm
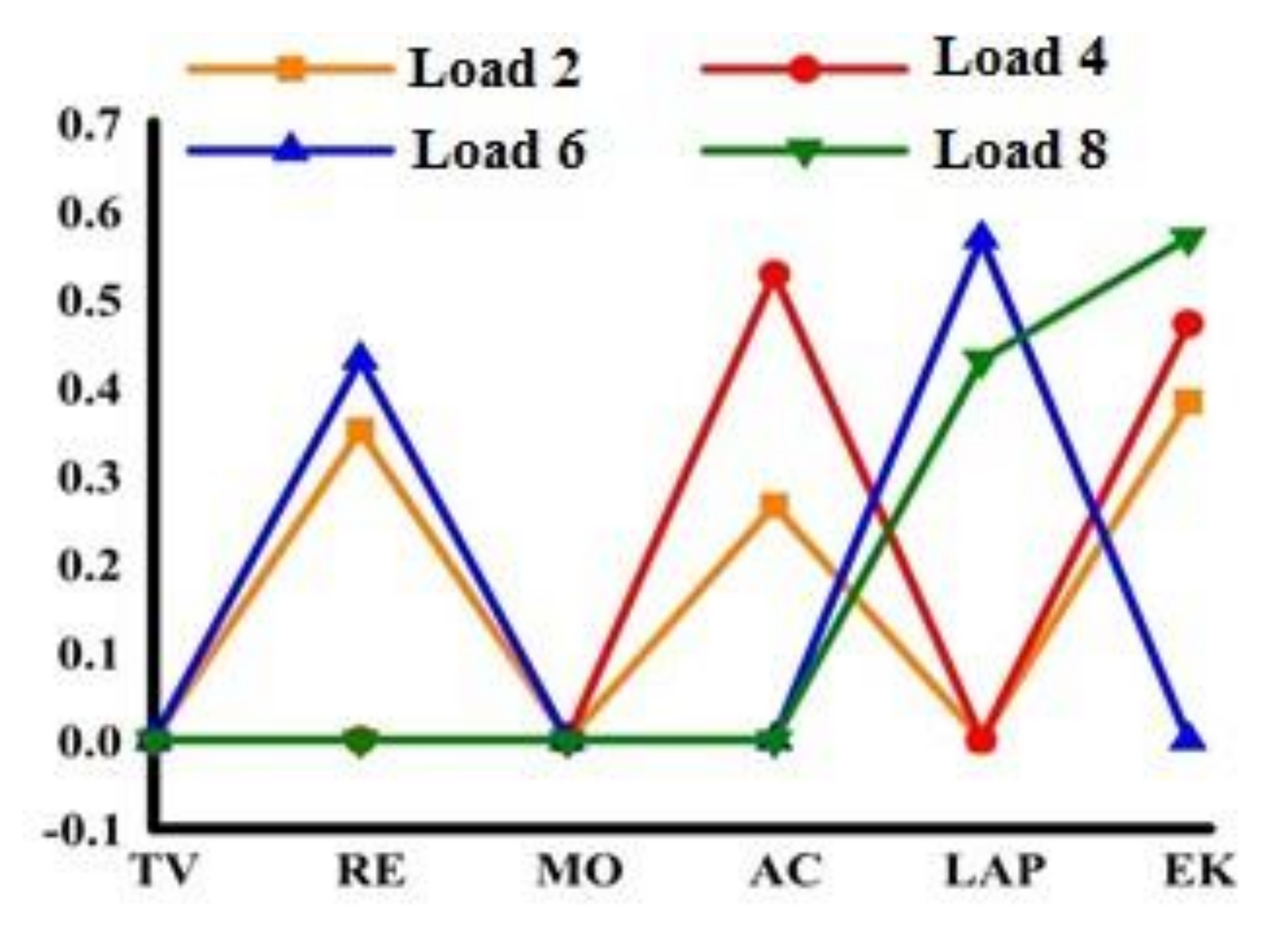
3.3. Load Identification Based on Electrical Properties and Switching Probabilities
4. Experiment and Analysis
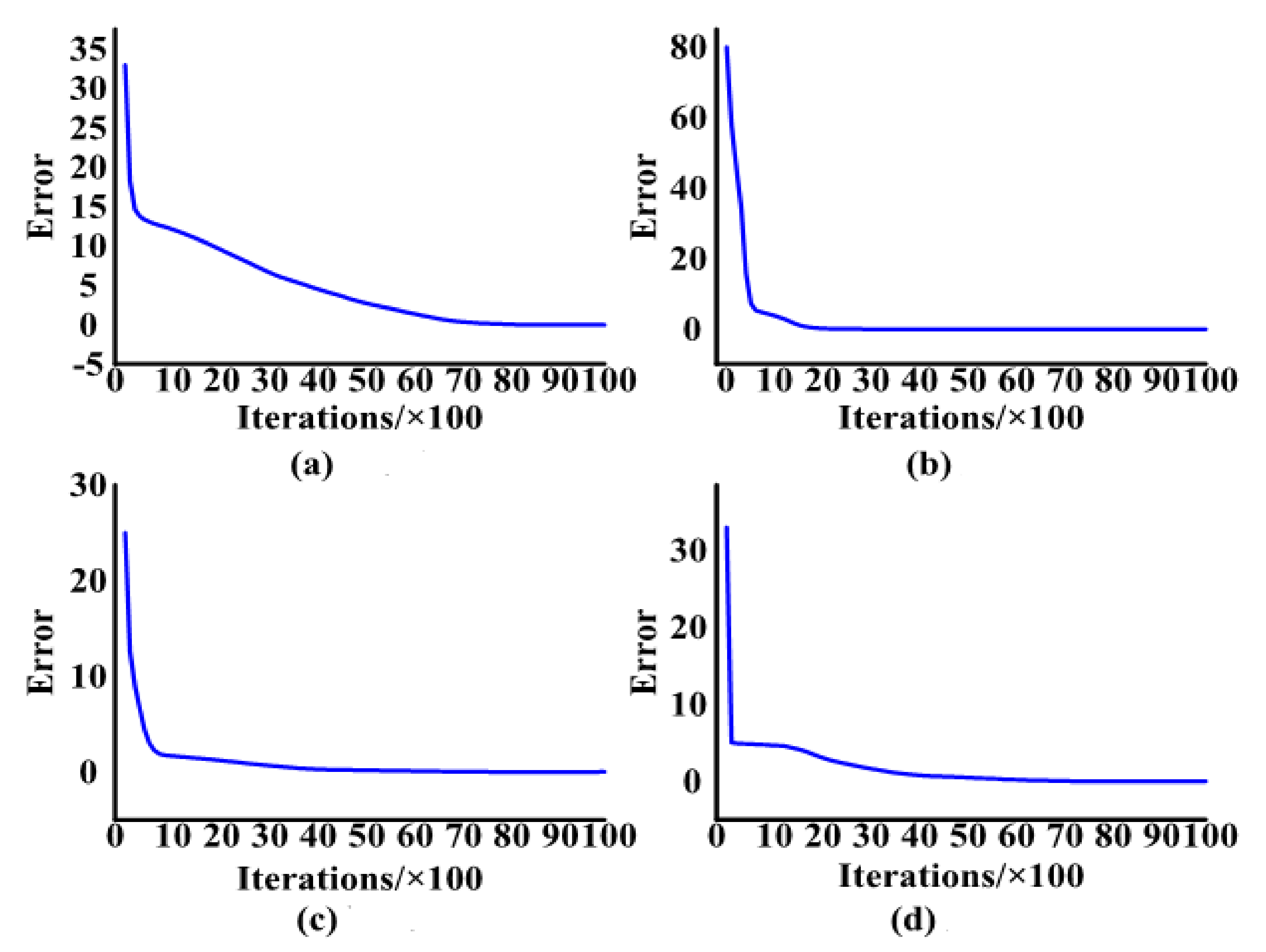
4.1. Verification of Signal Decomposition Effect
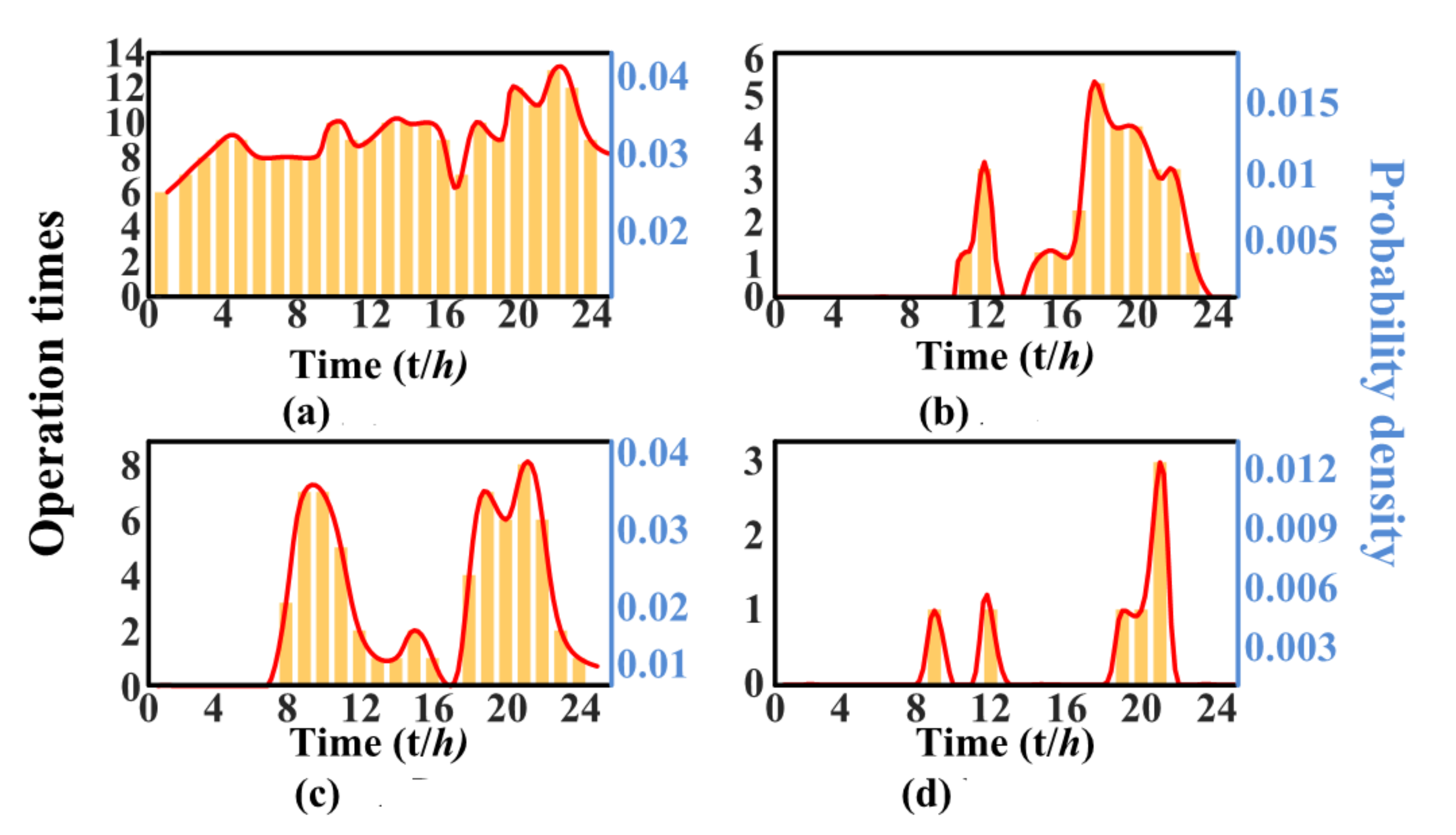
4.2. Verification of Initial Load Identification
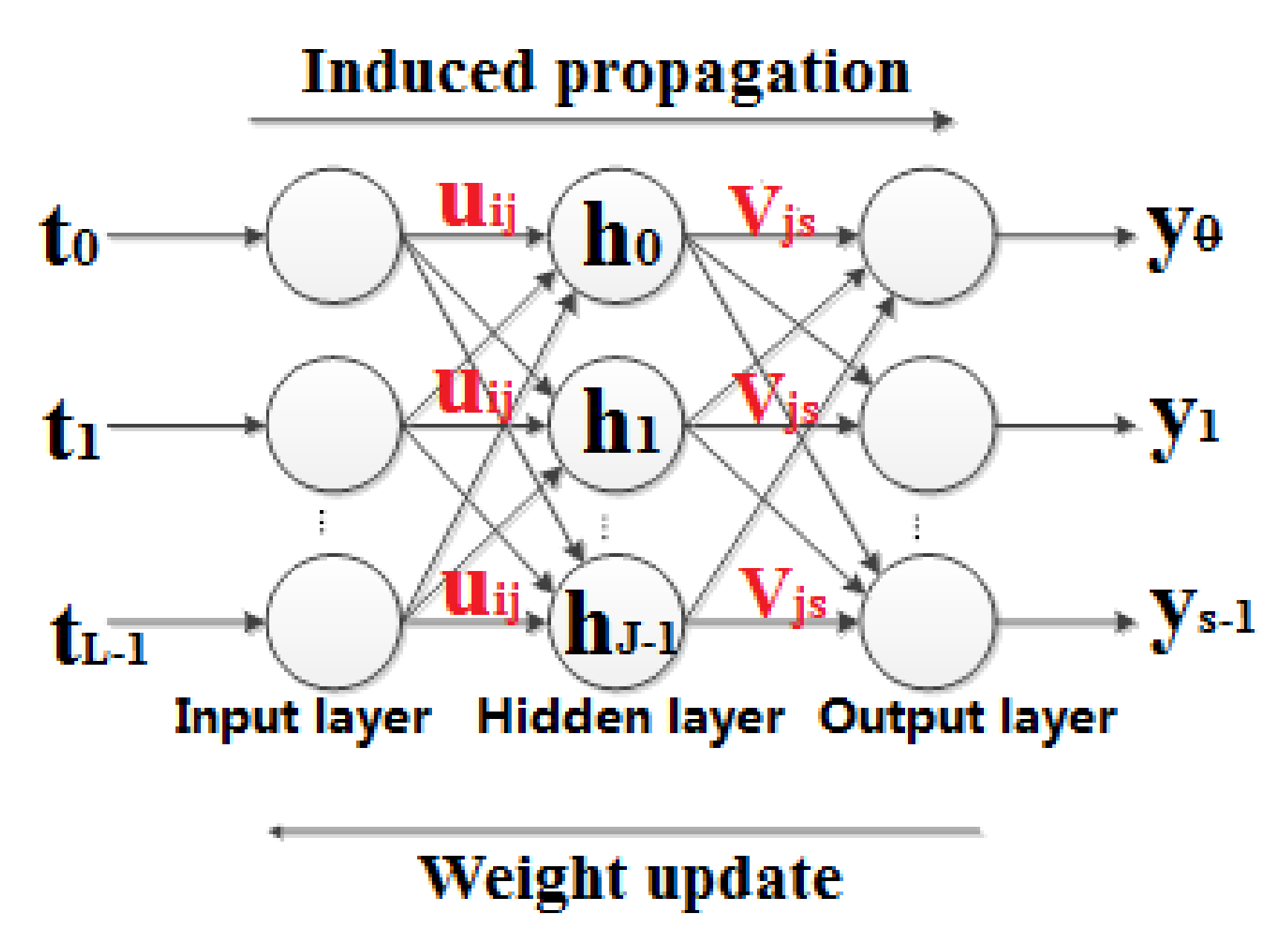
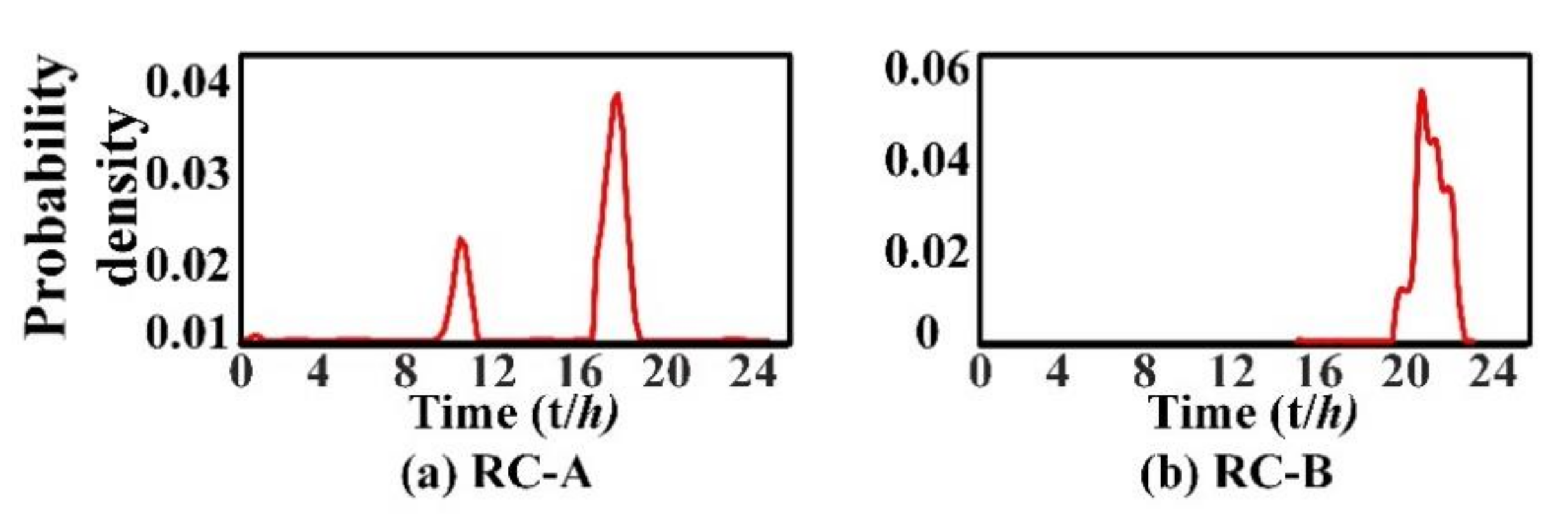
4.3. Verification of Modification Method
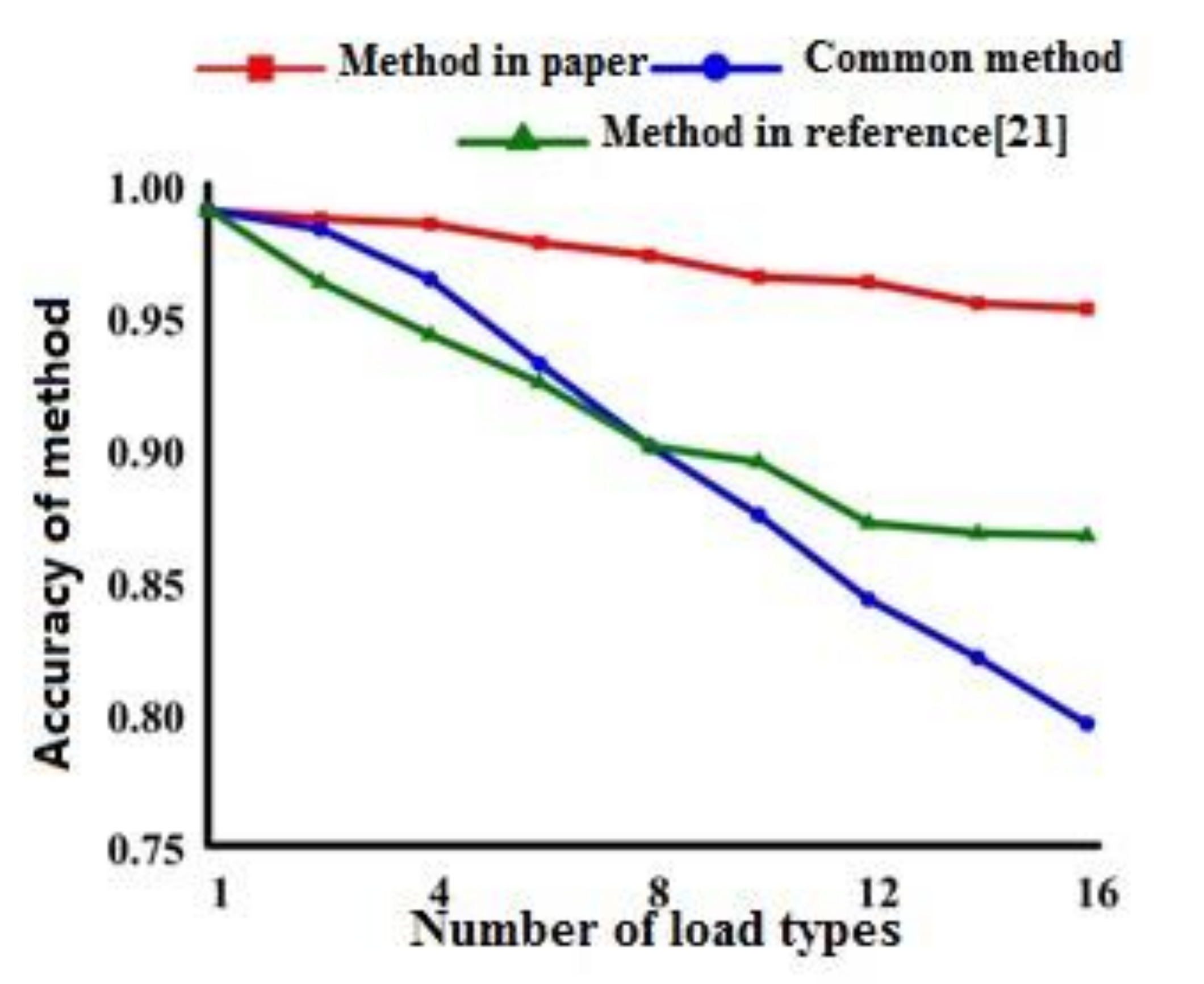
4.4. Comparison with Existing Algorithms
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zeng, M.; Shi, L.; He, Y. Status, challenges and countermeasures of demand-side management development in China. Renew. Sustain. Energy Rev. 2015, 47, 284–294. [Google Scholar]
- Wu, C.; Zhang, H.; Hou, Y.; Cao, L.; Liu, F. Analysis of Binjin UHVDC restart failure and relevant suggestions on secure and stable operation of power grid. Energy Procedia 2018, 145, 452–457. [Google Scholar]
- Hart, G. Nonintrusive appliance load monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar]
- Hong, Y.; Chou, J.J. Nonintrusive energy monitoring for microgrids using hybrid self-organizing feature-mapping networks. Energies 2012, 5, 2578–2593. [Google Scholar]
- Figueiredo, M.; De Almeida, A.; Ribeiro, B. Home electrical signal disaggregation for non-intrusive load monitoring (NILM) systems. Neurocomput 2012, 96, 66–73. [Google Scholar]
- Jian, L.; Ng, S.; Kendall, G.; Cheng, J. Load Signature Study-Part I: Basic Concept, Structure, and Methodology. IEEE Trans. Power Deliv. 2010, 25, 551–560. [Google Scholar]
- Semwal, S.; Singh, M.; Prasad, R.S. Group control and identification of residential appliances using a nonintrusive method. Turk. J. Electr. Eng. Comput. Sci. 2015, 23, 1805–1816. [Google Scholar]
- Chang, H.; Chen, K.; Tsai, Y.; Lee, W. A new measurement method for power signatures of nonintrusive demand monitoring and load identification. IEEE Trans. Ind. Appl. 2012, 48, 764–771. [Google Scholar]
- Chang, H.; Yang, H. Applying a non-intrusive energy-management system to economic dispatch for a cogeneration system and power utility. Appl. Energy 2009, 86, 2335–2343. [Google Scholar]
- Chang, H. Genetic algorithms and non-intrusive energy management system based economic dispatch for cogeneration units. Energy 2011, 36, 181–190. [Google Scholar]
- Srinivasan, D.; Ng, W.S.; Liew, A.C. Neural-network-based signature recognition for harmonic source identification. IEEE Trans. Power Deliv. 2006, 21, 398–405. [Google Scholar]
- Ruzzelli, A.G.; Nicolas, C.; Schoofs, A.; O’Hare, G.M.P. Real-time recognition and profiling of appliances through a single electricity sensor. In Proceedings of the 7th Annual IEEE Communications Society Conference on Sensor: Mesh and Ad Hoc Communications and Networks (SECON), Boston, MA, USA, 21–25 June 2010; pp. 1–9. [Google Scholar]
- Gabaldo’n, A.; Molina, R.; Mari’n-Parra, A.; Valero-Verdu’, S.; A’lvarez, C. Residential end-uses disaggregation and demand response evaluation using integral transforms. J. Mod. Power Syst. Clean Energy 2017, 5, 91–104. [Google Scholar]
- Hassan, T.; Javed, F.; Arshad, N. An empirical investigation of V-I trajectory based load signatures for non-intrusive load monitoring. IEEE Trans. Smart Grid 2013, 5, 870–878. [Google Scholar]
- He, D.; Du, L.; Yang, Y.; Harley, R.; Habetler, T. Front-end electronic circuit topology analysis for model-driven classification and monitoring of appliance loads in smart buildings. IEEE Trans. Smart Grid 2012, 4, 2286–2293. [Google Scholar]
- Rahimpour, A.; Qi, H.; Fugate, D.; Kuruganti, T. Non-intrusive energy disaggregation using non-negative matrix factorization with sum-to-k constraint. IEEE Trans. Power Syst. 2017, 32, 4430–4441. [Google Scholar]
- Wu, X.; Jiao, D.; Liang, K.; Han, X. A fast online load identification algorithm based on V-I characteristics of high-frequency data under user operational constraints. Energy 2019, 188, 116012. [Google Scholar]
- Wen, X.; Lu, G.; Liu, J.; Yan, P. Graph modeling of singular values for early fault detection and diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2020, 145, 106956. [Google Scholar]
- Yu, F.; Xu, X. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar]
- Peng, Y.; Hao, Z.; Yun, X. Lock-Free Parallelization for Variance-Reduced Stochastic Gradient Descent on Streaming Data. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 2220–2231. [Google Scholar]
- Ahmadi, H.; Marti, J.R. Load Decomposition at Smart Meters Level Using Eigenloads Approach. IEEE Trans. Power Syst. 2015, 30, 3425–3436. [Google Scholar]


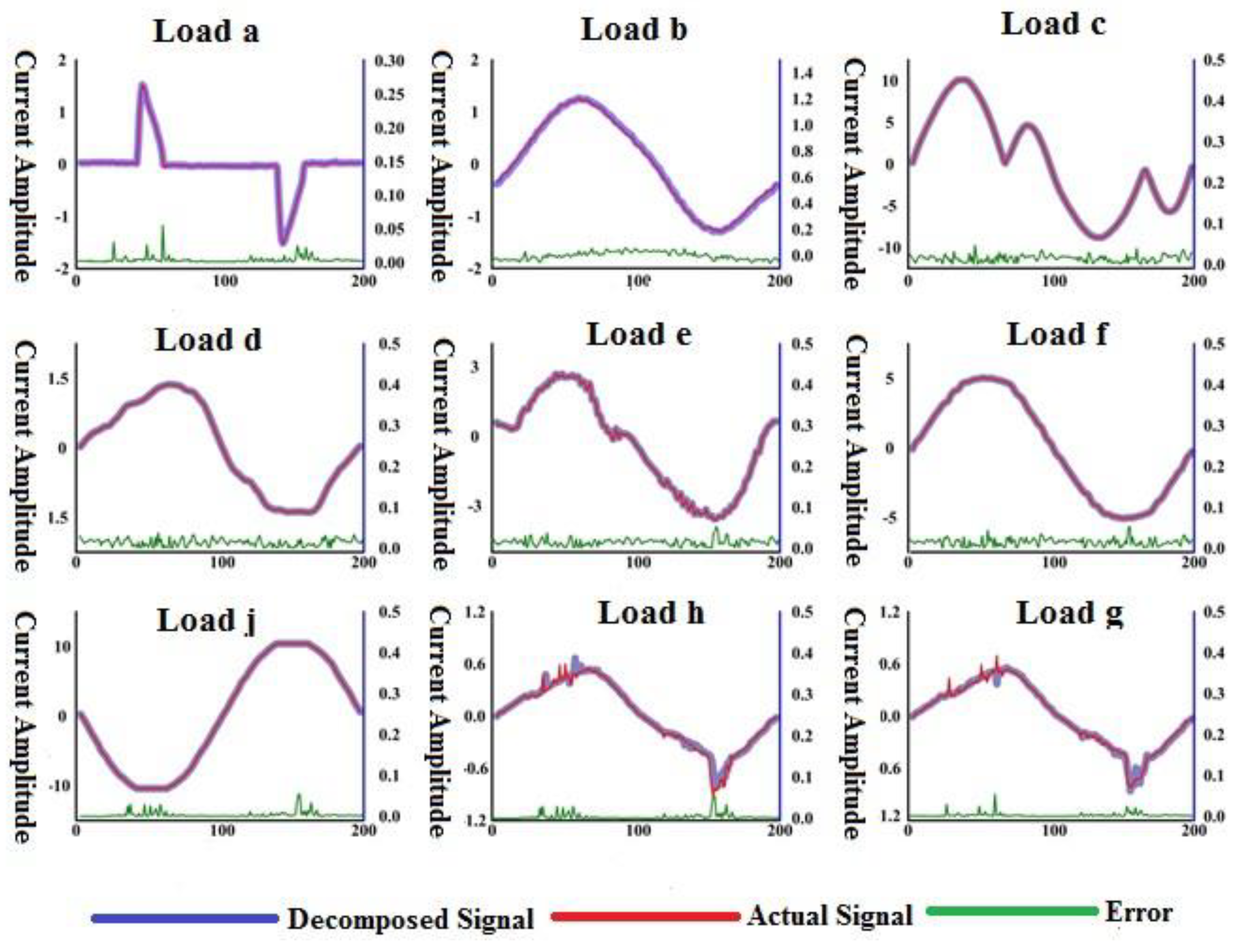
| Decomposed Current | R | RMSE |
|---|---|---|
| No. 1 | 0.941 | 0.389 |
| No. 2 | 0.903 | 0.521 |
| No. 3 | 0.994 | 0.029 |
| No. 4 | 0.982 | 0.076 |
| No. 5 | 0.975 | 0.113 |
| No. 6 | 0.936 | 0.452 |
| No. 7 | 0.927 | 0.417 |
| No. 8 | 0.918 | 0.458 |
| No. 9 | 0.953 | 0.289 |
| Decomposed Current | R | RMSE |
|---|---|---|
| No. 1 | 0.997 | 0.0032 |
| No. 2 | 0.963 | 0.0127 |
| No. 3 | 0.994 | 0.0092 |
| No. 4 | 0.992 | 0.0077 |
| No. 5 | 0.965 | 0. 0182 |
| No. 6 | 0.986 | 0.0176 |
| No. 7 | 0.997 | 0.0098 |
| Home Appliance | 1st Harmonic | 2nd Harmonic | 3rd Harmonic | 4th Harmonic |
|---|---|---|---|---|
| TV | 0.345 | 0.009 | 0.310 | 0.008 |
| RE | 1.205 | 0.033 | 0.079 | 0.007 |
| MO | 7.620 | 0.682 | 2.943 | 0.103 |
| AC | 4.477 | 0.691 | 0.334 | 0.187 |
| LAP | 2.769 | 0.172 | 0.432 | 0.272 |
| EK | 5.146 | 0.005 | 0.089 | 0.001 |
| TV | RE | MO | AC | LAP | EK | |
|---|---|---|---|---|---|---|
| Decomposed current 1 | 0.131/0.078 | 0 | 0 | 0 | 0 | 0 |
| Decomposed current 2 | 0 | 0.118/0.109 | 0 | 0.156/0.156 | 0 | 0.108/0.095 |
| Decomposed current 3 | 0 | 0 | 0.103/0.086 | 0 | 0 | 0 |
| Decomposed current 4 | 0 | 0 | 0 | 0.108/0.079 | 0 | 0.132/0.122 |
| Decomposed current 5 | 0 | 0.143/0.112 | 0 | 0.118/0.074 | 0 | 0 |
| Decomposed current 6 | 0 | 0.133/0.133 | 0 | 0 | 0.101/0.089 | 0 |
| Decomposed current 7 | 0 | 0.132/0.132 | 0 | 0 | 0.117/0.086 | 0 |
| Decomposed current 8 | 0 | 0 | 0 | 0 | 0.148/0.148 | 0.112/0.101 |
| Decomposed current 9 | 0 | 0 | 0 | 0 | 0.140/0.1140 | 0.108/0.086 |
| TV | RE | MO | AC | LAP | RC | STE | |
|---|---|---|---|---|---|---|---|
| Decomposed current 1 | 0 | 0.681 | 0 | 0.319 | 0 | 0 | 0 |
| Decomposed current 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| Decomposed current 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Decomposed current 4 | 0 | 0.221 | 0 | 0.779 | 0 | 0 | 0 |
| Decomposed current 5 | 0 | 0.125 | 0 | 0 | 0.875 | 0 | 0 |
| Decomposed current 6 | 0 | 0 | 0 | 0.112 | 0 | 0.453 | 0.435 |
| Decomposed current 7 | 0 | 0 | 0 | 0.075 | 0 | 0.505 | 0.420 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Nhl | 2 | Initial learning rate | 0.0001 |
| Nneu1 | 32 | Epochs | 10,000 |
| Nneu2 | 64 | Dropout Rate | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Lo, K.L. Non-Intrusive Monitoring Algorithm for Resident Loads with Similar Electrical Characteristic. Processes 2020, 8, 1385. https://doi.org/10.3390/pr8111385
Wu S, Lo KL. Non-Intrusive Monitoring Algorithm for Resident Loads with Similar Electrical Characteristic. Processes. 2020; 8(11):1385. https://doi.org/10.3390/pr8111385
Chicago/Turabian StyleWu, Sheng, and Kwok L. Lo. 2020. "Non-Intrusive Monitoring Algorithm for Resident Loads with Similar Electrical Characteristic" Processes 8, no. 11: 1385. https://doi.org/10.3390/pr8111385
APA StyleWu, S., & Lo, K. L. (2020). Non-Intrusive Monitoring Algorithm for Resident Loads with Similar Electrical Characteristic. Processes, 8(11), 1385. https://doi.org/10.3390/pr8111385




