A Charge-Based Mechanistic Study into the Effects of Process Parameters on Fiber Accumulating Geometry for a Melt Electrohydrodynamic Process
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Preparation
2.2. Melt Electrohydrodynamic System Configuration
2.3. Imaging and Data Measurement
3. Results
3.1. Effect of Deposition Time and Collector Temperature on Bulk Geometry of the Fiber Deposit
3.2. Effect of Voltage on Bulk Geometry of Fiber Deposit
3.3. Observation of Jet States and Its Dependence on Collector Temperature
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Robinson, T.M.; Hutmacher, D.W.; Dalton, P.D. The Next Frontier in Melt Electrospinning: Taming the Jet. Adv. Funct. Mater. 2019, 29, 1904664. [Google Scholar] [CrossRef] [Green Version]
- Alexander, F.A., Jr.; Johnson, L.; Williams, K.; Packer, K. A Parameter Study for 3D-Printing Organized Nanofibrous Collagen Scaffolds Using Direct-Write Electrospinning. Materials 2019, 12, 4131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piyasin, P.; Yensano, R.; Pinitsoontorn, S. Size-Controllable Melt-Electrospun Polycaprolactone (PCL) Fibers with a Sodium Chloride Additive. Polymers 2019, 11, 1768. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ibrahim, Y.S.; Hussein, E.A.; Zagho, M.M.; Abdo, G.G.; Elzatahry, A.A. Melt Electrospinning Designs for Nanofiber Fabrication for Different Applications. Int. J. Mol. Sci. 2019, 20, 2455. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jun, I.; Han, H.; Edwards, J.R.; Jeon, H. Electrospun Fibrous Scaffolds for Tissue Engineering: Viewpoints on Architecture and Fabrication. Int. J. Mol. Sci. 2018, 19, 745. [Google Scholar] [CrossRef] [Green Version]
- Mao, M.; He, J.; Li, X.; Zhang, B.; Lei, Q.; Liu, Y.; Li, D. The emerging frontiers and applications of high-resolution 3D printing. Micromachines 2017, 8, 113. [Google Scholar] [CrossRef]
- Brown, T.D.; Edin, F.; Detta, N.; Skelton, A.D.; Hutmacher, D.W.; Dalton, P.D. Melt electrospinning of poly(ε-caprolactone) scaffolds: Phenomenological observations associated with collection and direct writing. Mater. Sci. Eng. C 2015, 45, 698–708. [Google Scholar] [CrossRef]
- Jin, Y.; Gao, Q.; Xie, C.; Li, G.; Du, J.; Fu, J. Fabrication of heterogeneous scaffolds using melt electrospinning writing: Design and optimization. Mater. Des. 2020, 185, 108274. [Google Scholar] [CrossRef]
- Tourlomousis, F.; Jia, C.; Karydis, T.; Mershin, A.; Wang, H.; Kalyon, D.M.; Chang, R.C. Machine learning metrology of cell confinement in melt electrowritten three-dimensional biomaterial substrates. Microsyst. Nanoeng. 2019, 5, 15. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; De Botelho, A.; Braga, F.; Van Blitterswijk, C.; Mota, C.; Wieringa, P.A.; Moroni, L. Direct Writing Electrospinning of Scaffolds with Multidimensional Fiber Architecture for Hierarchical Tissue Engineering. ACS Appl. Mater. Interfaces 2017, 9, 38187–38200. [Google Scholar] [CrossRef]
- Rogalski, J.J. PA6 Nanofibre Production: A Comparison between Rotary Jet Spinning and Electrospinning. Fibers 2018, 6, 37. [Google Scholar] [CrossRef] [Green Version]
- Muerza-Cascante, M.L.; Haylock, D.; Hutmacher, D.W.; Dalton, P.D. Melt Electrospinning and Its Technologization in Tissue Engineering. Tissue Eng. Part B Rev. 2015, 21, 187–202. [Google Scholar] [CrossRef] [PubMed]
- Paşcu, E.I.; Cahill, P.A.; Stokes, J.; McGuinness, G.B. Towards functional 3D-stacked electrospun composite scaffolds of PHBV, silk fibroin and nanohydroxyapatite: Mechanical properties and surface osteogenic differentiation. J. Biomater. Appl. 2016, 30, 1334–1339. [Google Scholar] [CrossRef] [PubMed]
- Gwiazda, M.; Kumar, S.; Świeszkowski, W.; Ivanovski, S.; Vaquette, C. The effect of melt electrospun writing fiber orientation onto cellular organization and mechanical properties for application in Anterior Cruciate Ligament tissue engineering. J. Mech. Behav. Biomed. Mater. 2020, 104. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, Z.; Wan, Y.; Zhang, Y.; Wang, Z.; Klausen, L.H.; Huang, P.; Dong, M.; Han, X.; Cui, B.; et al. A hierarchically ordered compacted coil scaffold for tissue regeneration. NPG Asia Mater. 2020, 12, 4–13. [Google Scholar] [CrossRef]
- Zaiss, S.; Brown, T.D.; Reichert, J.C.; Berner, A. Poly(ε-caprolactone) scaffolds fabricated by melt electrospinning for bone tissue engineering. Materials 2016, 9, 232. [Google Scholar] [CrossRef] [Green Version]
- Afghah, F.; Dikyol, C.; Altunbek, M.; Koc, B. Biomimicry in Bio-Manufacturing: Developments in Melt Electrospinning Writing Technology Towards Hybrid Biomanufacturing. Appl. Sci. 2019, 9, 3540. [Google Scholar] [CrossRef] [Green Version]
- Applications, B.; Partheniadis, I.; Nikolakakis, I.; Laidmäe, I. A Mini-Review: Needleless Electrospinning of Nanofibers for Pharmaceutical and Biomedical Applications. Processes 2020, 8, 673. [Google Scholar] [CrossRef]
- Wunner, F.M.; Wille, M.; Noonan, T.G.; Bas, O.; Dalton, P.D.; De-juan-pardo, E.M.; Hutmacher, D.W. Melt Electrospinning Writing of Highly Ordered Large Volume Scaffold Architectures. Adv. Mater. 2018, 30, 1706570. [Google Scholar] [CrossRef]
- Ding, H.; Cao, K.; Zhang, F.; Boettcher, W.; Chang, R.C. A Fundamental Study of Charge Effects on Melt Electrowritten Polymer Fibers. Mater. Des. 2019, 178, 107857. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Kim, J.H. Identification of sagging in melt-electrospinning of microfiber scaffold. Mater. Sci. Eng. C 2019, 103, 109785. [Google Scholar] [CrossRef] [PubMed]
- Collins, G.; Federici, J.; Imura, Y.; Catalani, L.H. Charge generation, charge transport, and residual charge in the electrospinning of polymers: A review of issues and complications. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
- Lubasova, D.; Netravali, A.N. A Novel Method for Electrospinning Nanofibrous 3-D Structures. Fibers 2020, 8, 27. [Google Scholar] [CrossRef]
- Li, X.; Zheng, Y.; Mu, X.; Xin, B.; Lin, L. Investigation into Jet Motion and Fiber Properties Induced by Electric Fields in Melt Electrospinning. Ind. Eng. Chem. Res. 2020, 59, 2163–2170. [Google Scholar] [CrossRef]
- Hochleitner, G.; Youssef, A.; Hrynevich, A.; Haigh, J.N.; Jungst, T.; Groll, J.; Dalton, P.D. Fibre pulsing during melt electrospinning writing. BioNanoMaterials 2016, 17, 159–171. [Google Scholar] [CrossRef]
- Tourlomousis, F.; Ding, H.; Kalyon, D.M.; Chang, R.C. Melt Electrospinning Writing Process Guided by a “Printability Number”. J. Manuf. Sci. Eng. 2017, 139, 081004. [Google Scholar] [CrossRef] [Green Version]
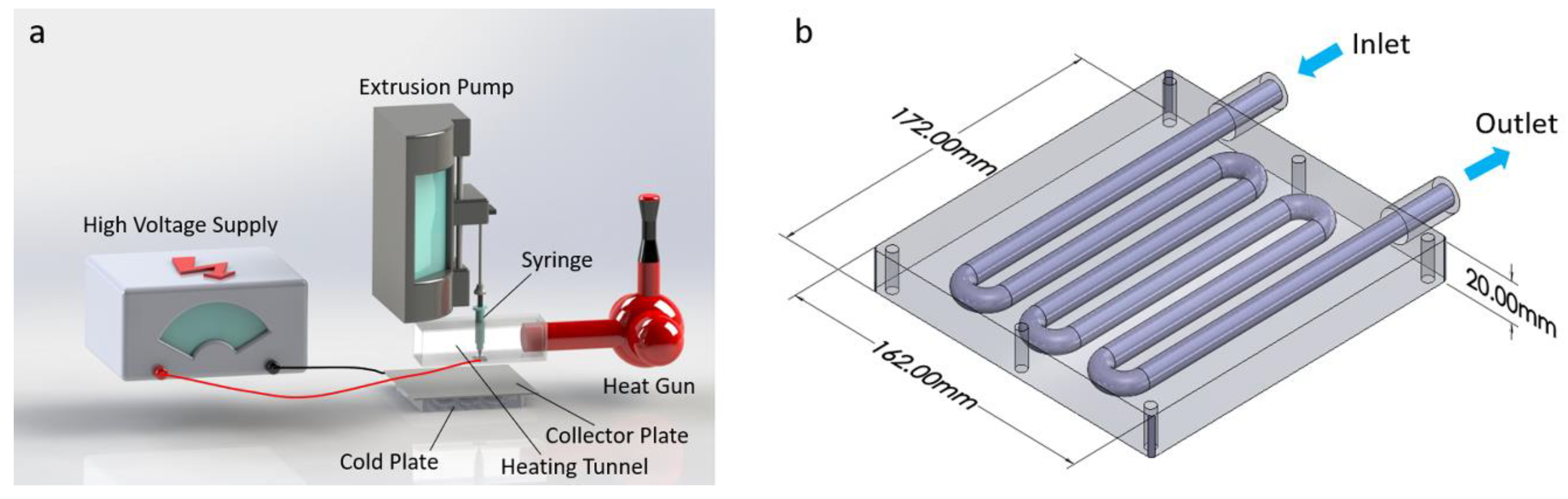




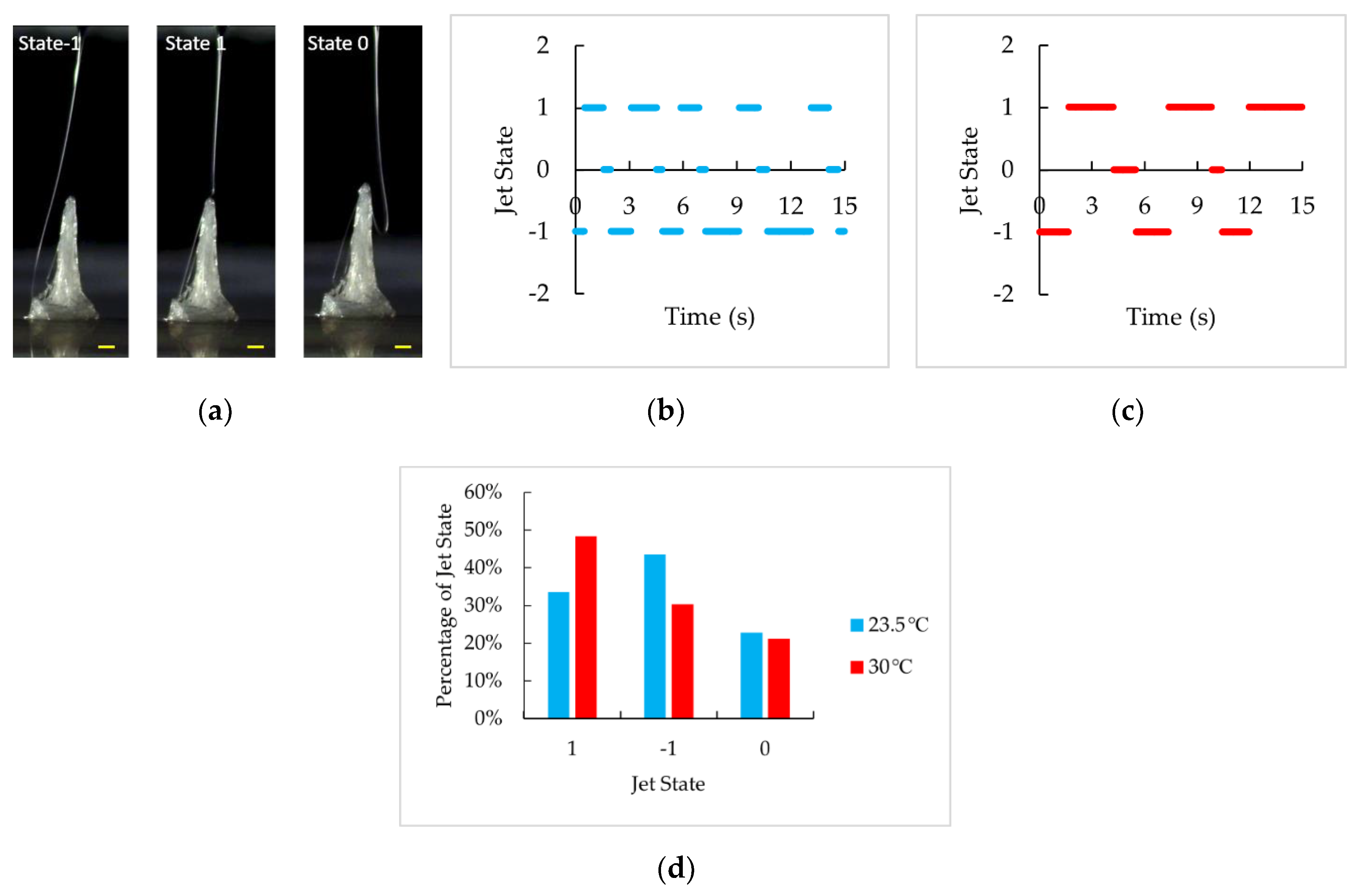


| Parameters | Values |
|---|---|
| Polymer temperature (Tp) | 94.7 ± 1 °C (measured) |
| Applied Voltage (V) | 12 kV, unless otherwise stated |
| Volumetric flow rate (Qv) | 25 µL/h |
| Tip-to-collector distance (Dtc) | 20 mm |
| Inter-fiber distance (Sf) | 60–500 µm |
| Set temperature (Ts) | 160 °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, K.; Zhang, F.; Chang, R.C. A Charge-Based Mechanistic Study into the Effects of Process Parameters on Fiber Accumulating Geometry for a Melt Electrohydrodynamic Process. Processes 2020, 8, 1440. https://doi.org/10.3390/pr8111440
Cao K, Zhang F, Chang RC. A Charge-Based Mechanistic Study into the Effects of Process Parameters on Fiber Accumulating Geometry for a Melt Electrohydrodynamic Process. Processes. 2020; 8(11):1440. https://doi.org/10.3390/pr8111440
Chicago/Turabian StyleCao, Kai, Fucheng Zhang, and Robert C. Chang. 2020. "A Charge-Based Mechanistic Study into the Effects of Process Parameters on Fiber Accumulating Geometry for a Melt Electrohydrodynamic Process" Processes 8, no. 11: 1440. https://doi.org/10.3390/pr8111440
APA StyleCao, K., Zhang, F., & Chang, R. C. (2020). A Charge-Based Mechanistic Study into the Effects of Process Parameters on Fiber Accumulating Geometry for a Melt Electrohydrodynamic Process. Processes, 8(11), 1440. https://doi.org/10.3390/pr8111440




