Analysis of Flow and Wear Characteristics of Solid–Liquid Two-Phase Flow in Rotating Flow Channel
Abstract
:1. Introduction
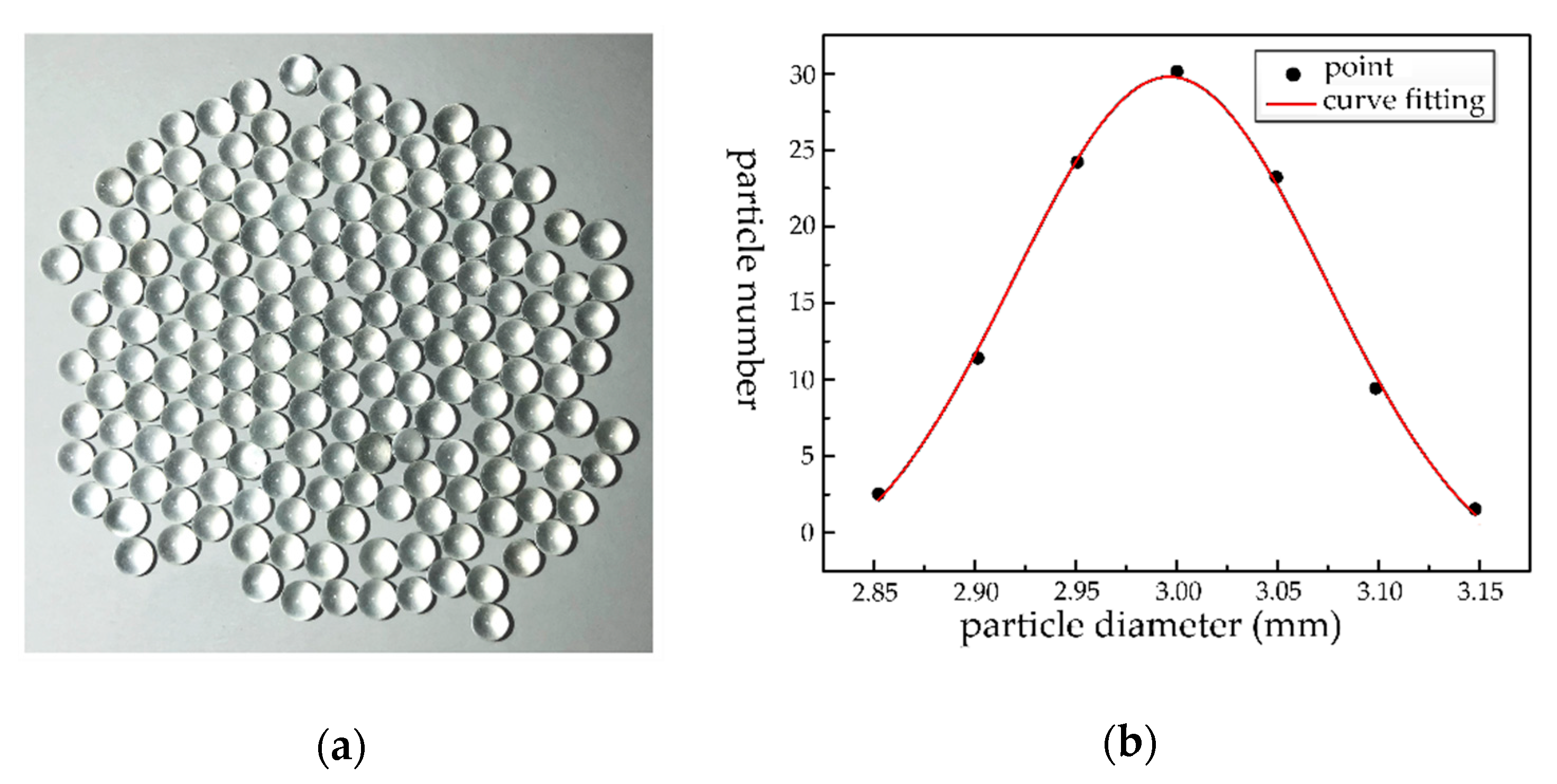
2. Experimental Methods
3. Model Design and Numerical Method
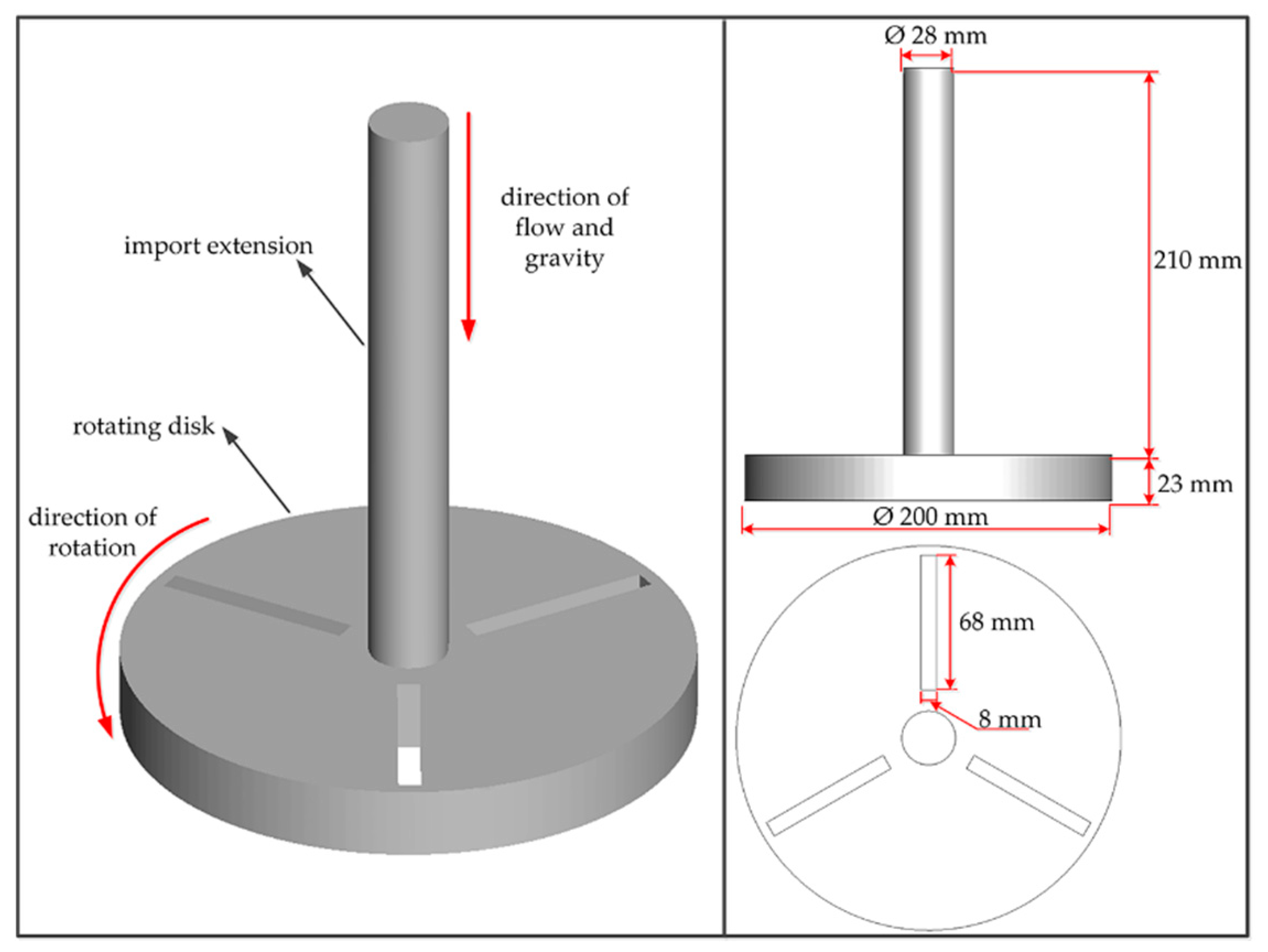
3.1. Computational Domain Model
3.2. Numerical Methods
3.2.1. Mathematical Formulation
3.2.2. Simulation Parameters
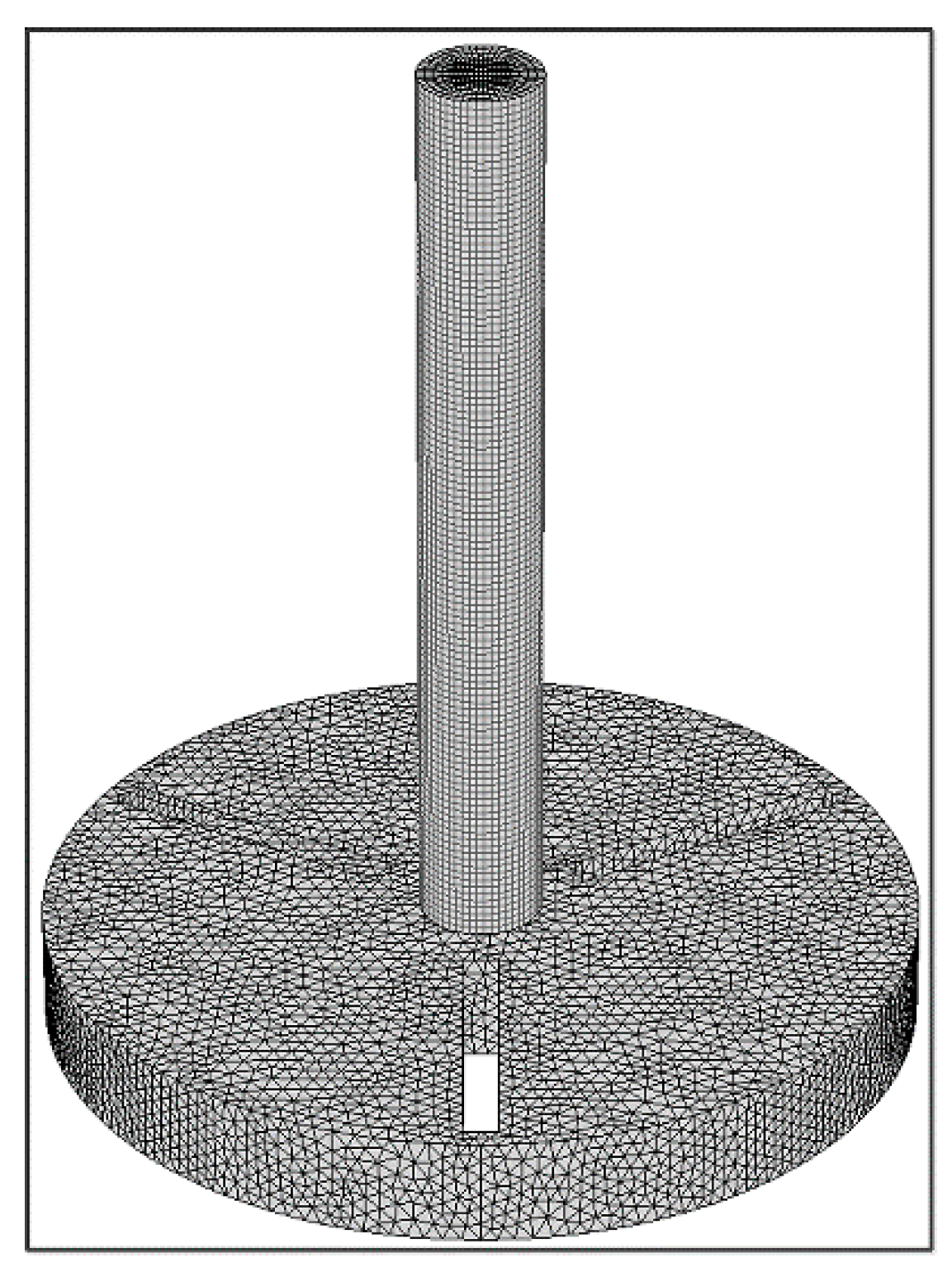
3.3. Mesh Generation
3.4. Calculation Method Verification
4. Results and Analysis
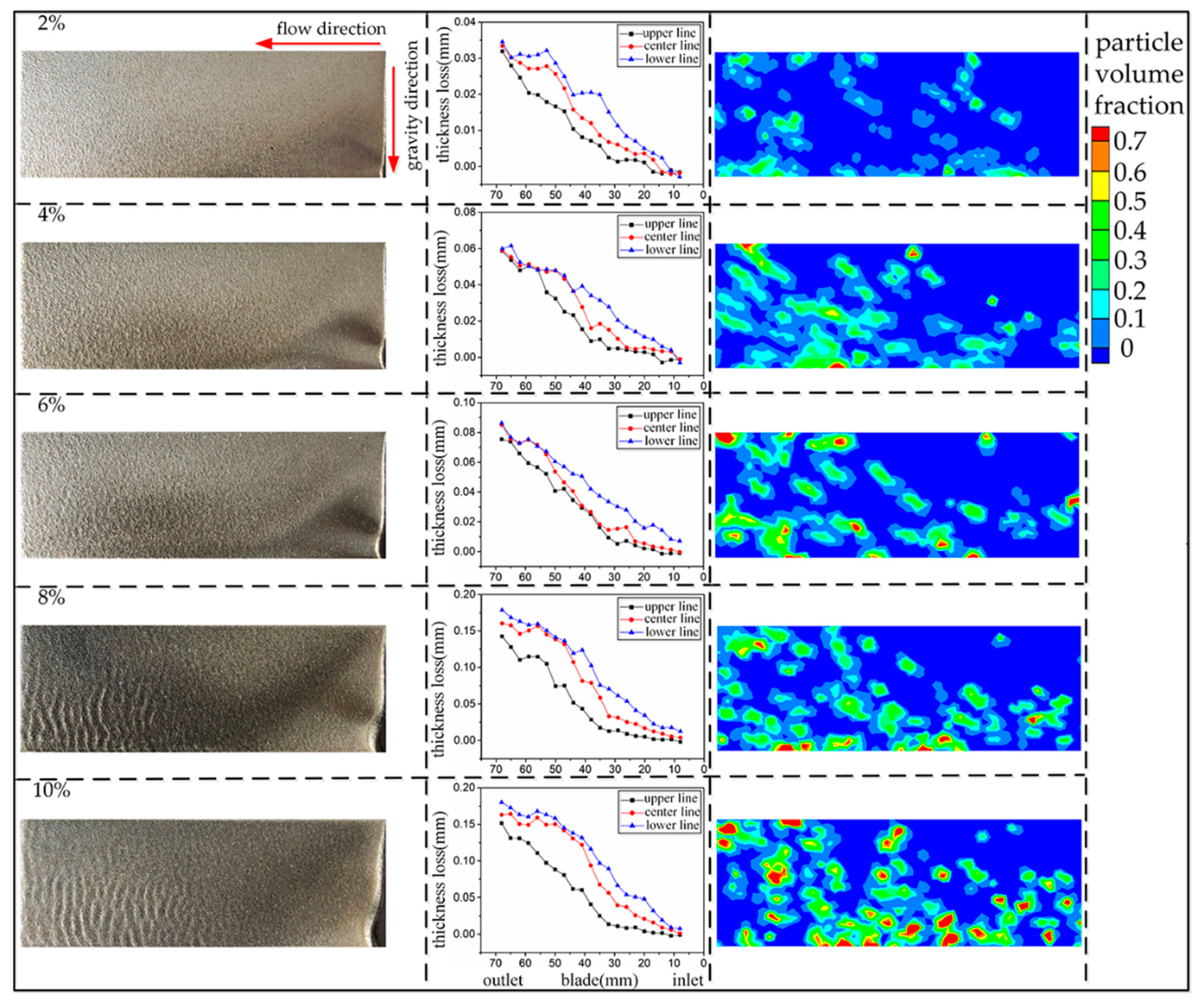
4.1. Effect of Rotation Speed on Particle Distribution and Volume Concentration
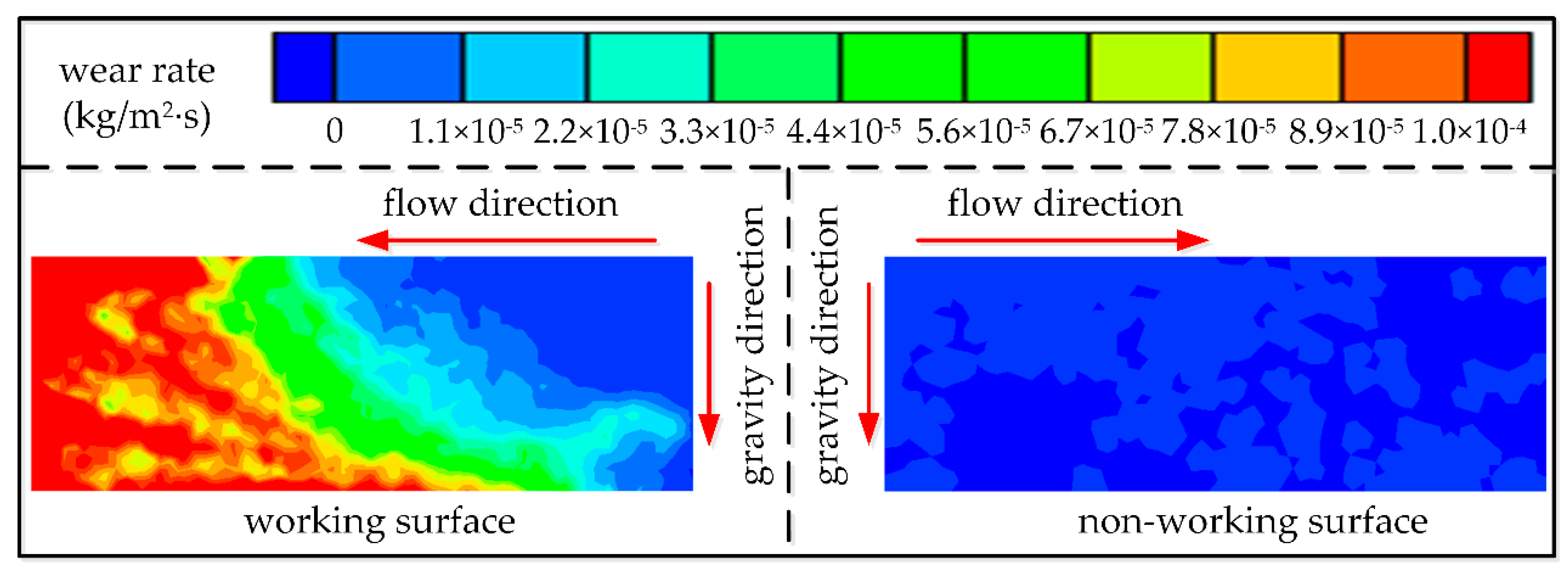
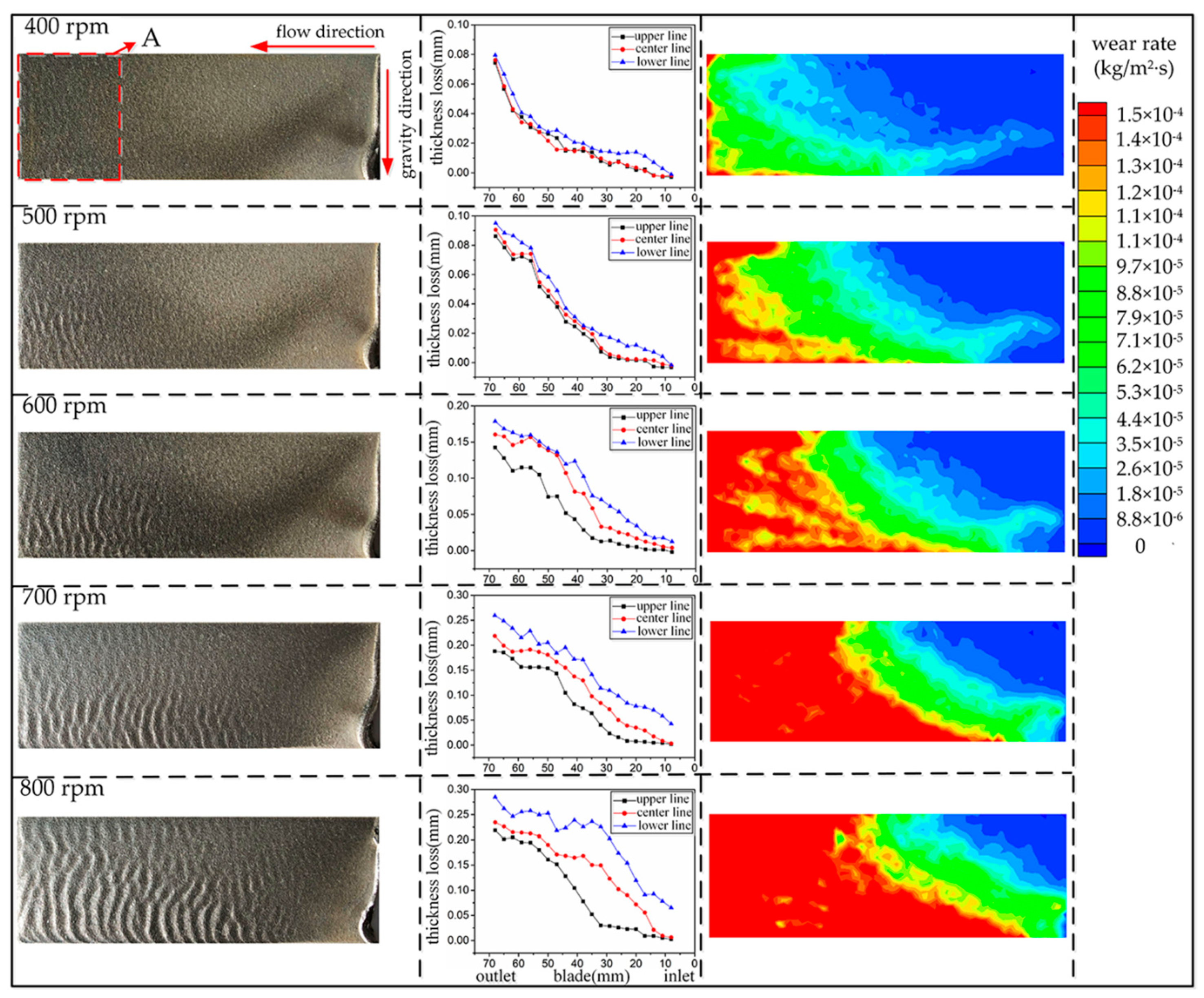
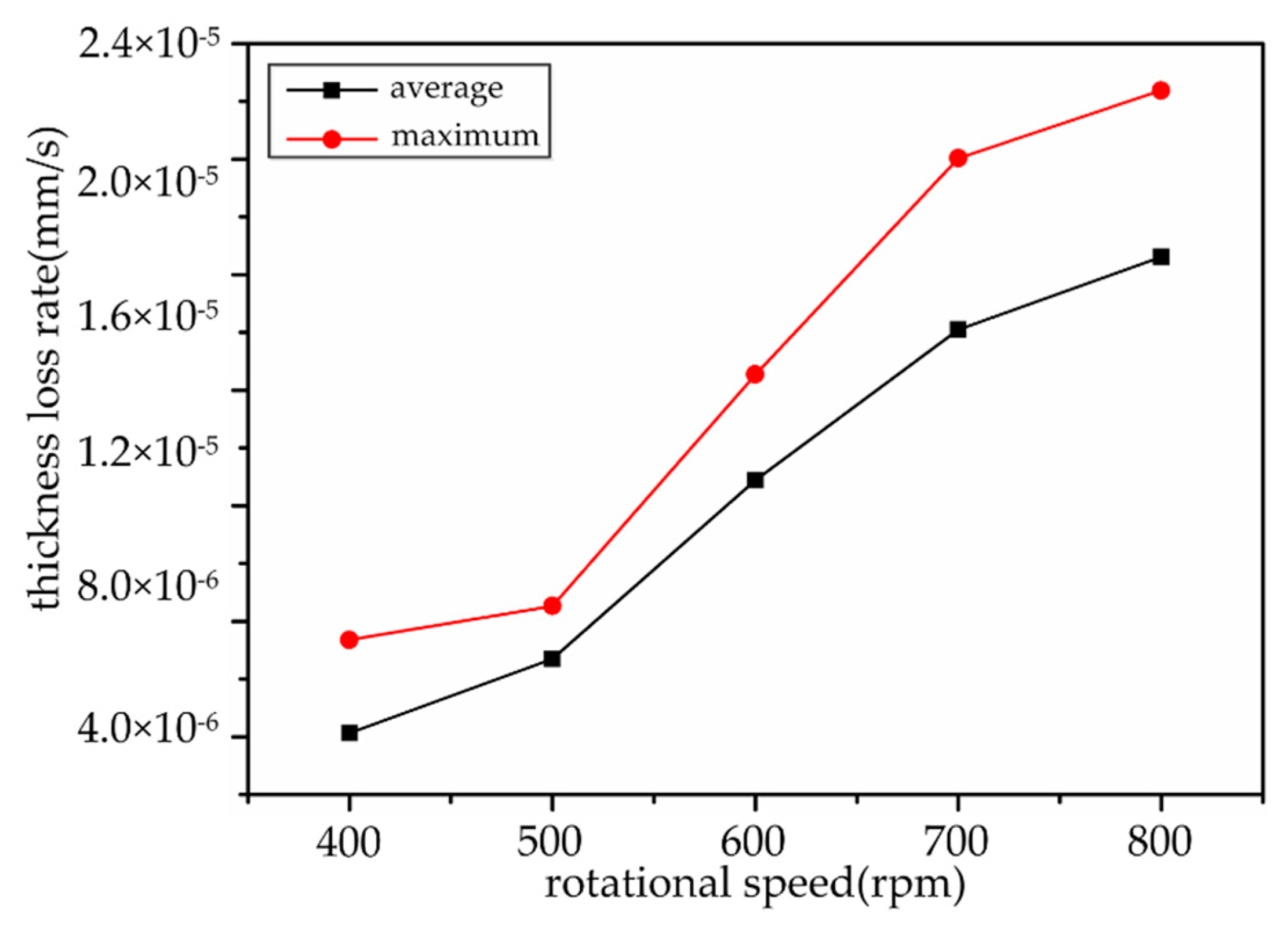
4.2. Effect of Rotation Speed on Blade Wear
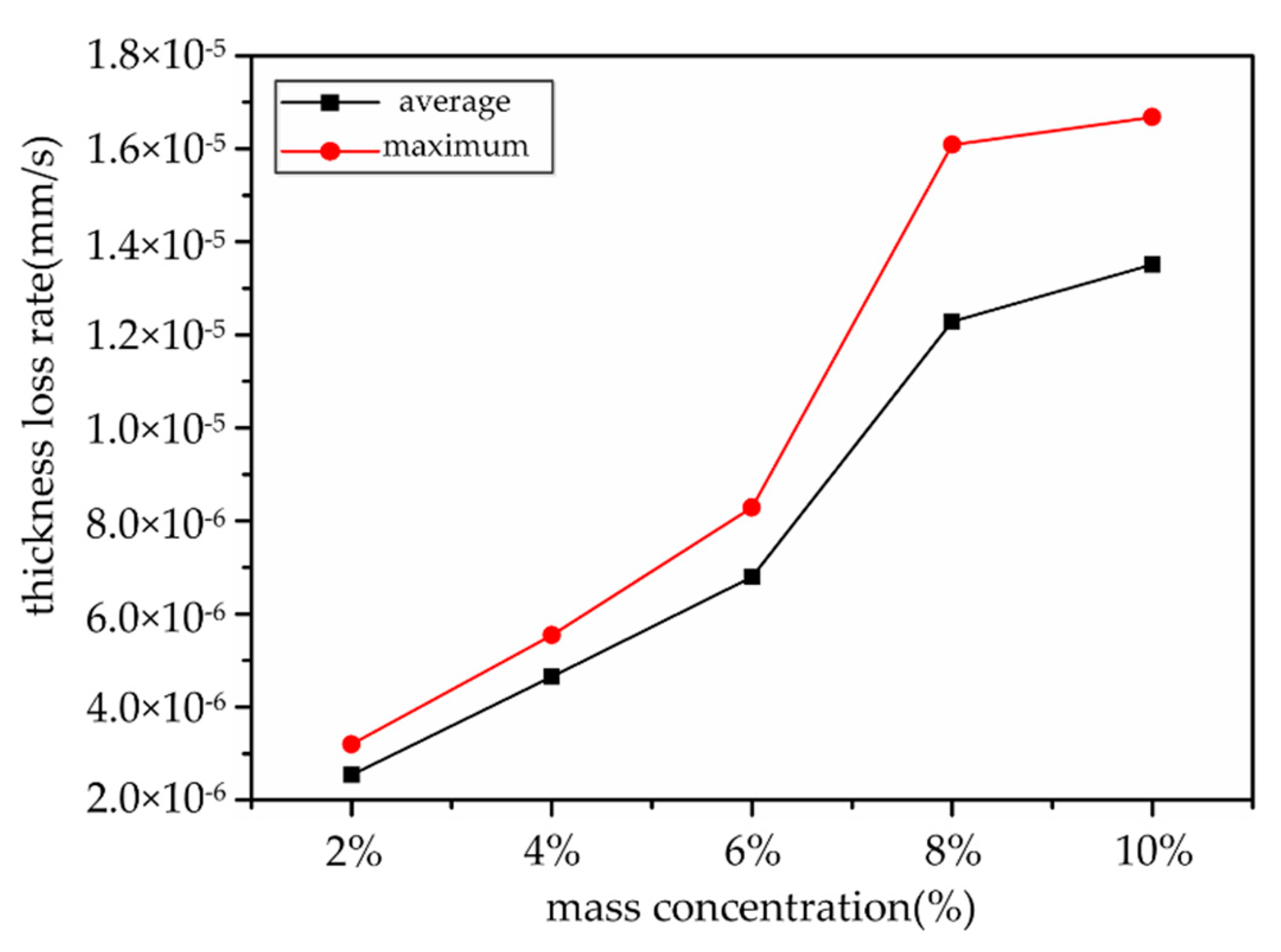
4.3. Effect of Particle Concentration on Blade Wear
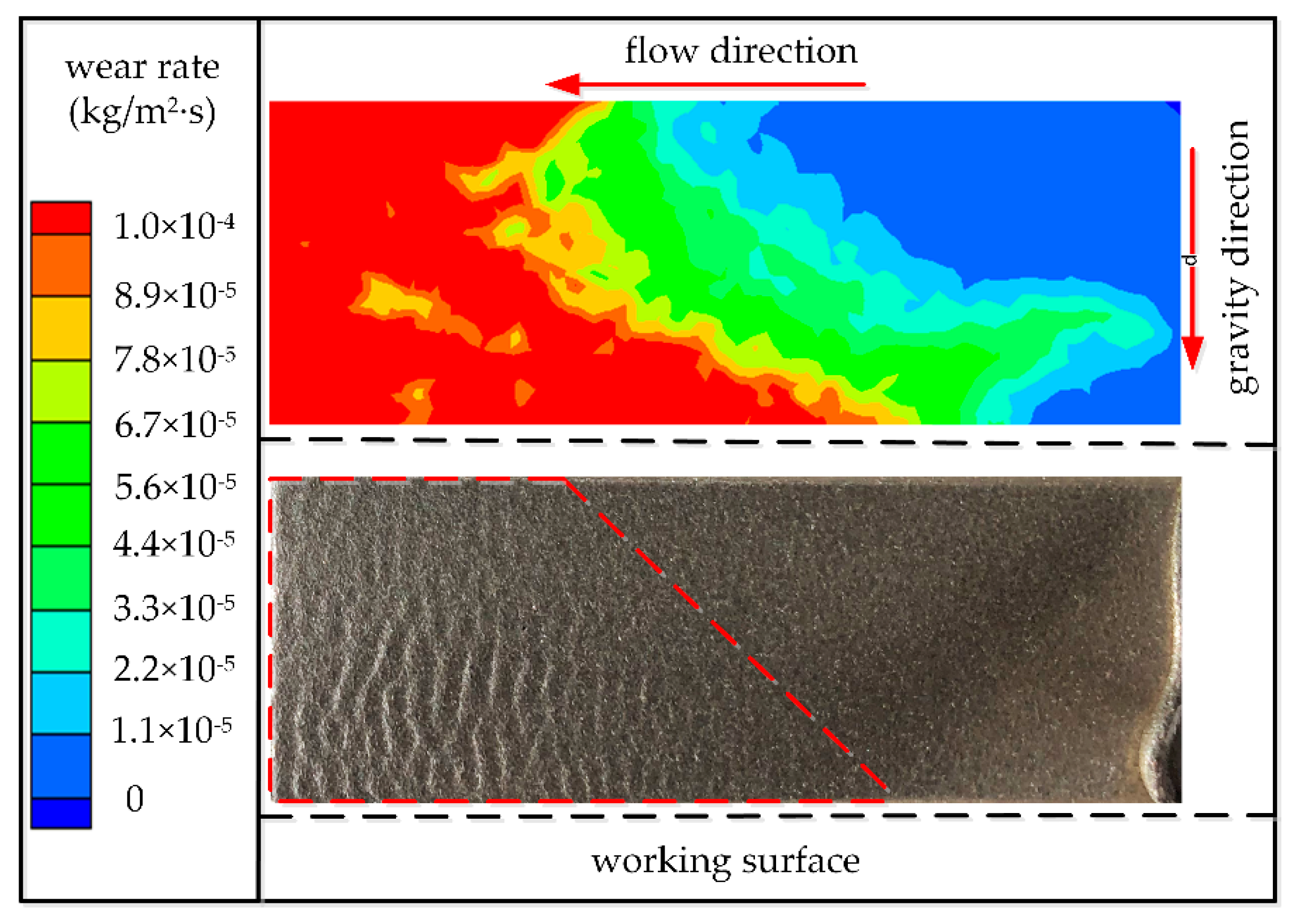
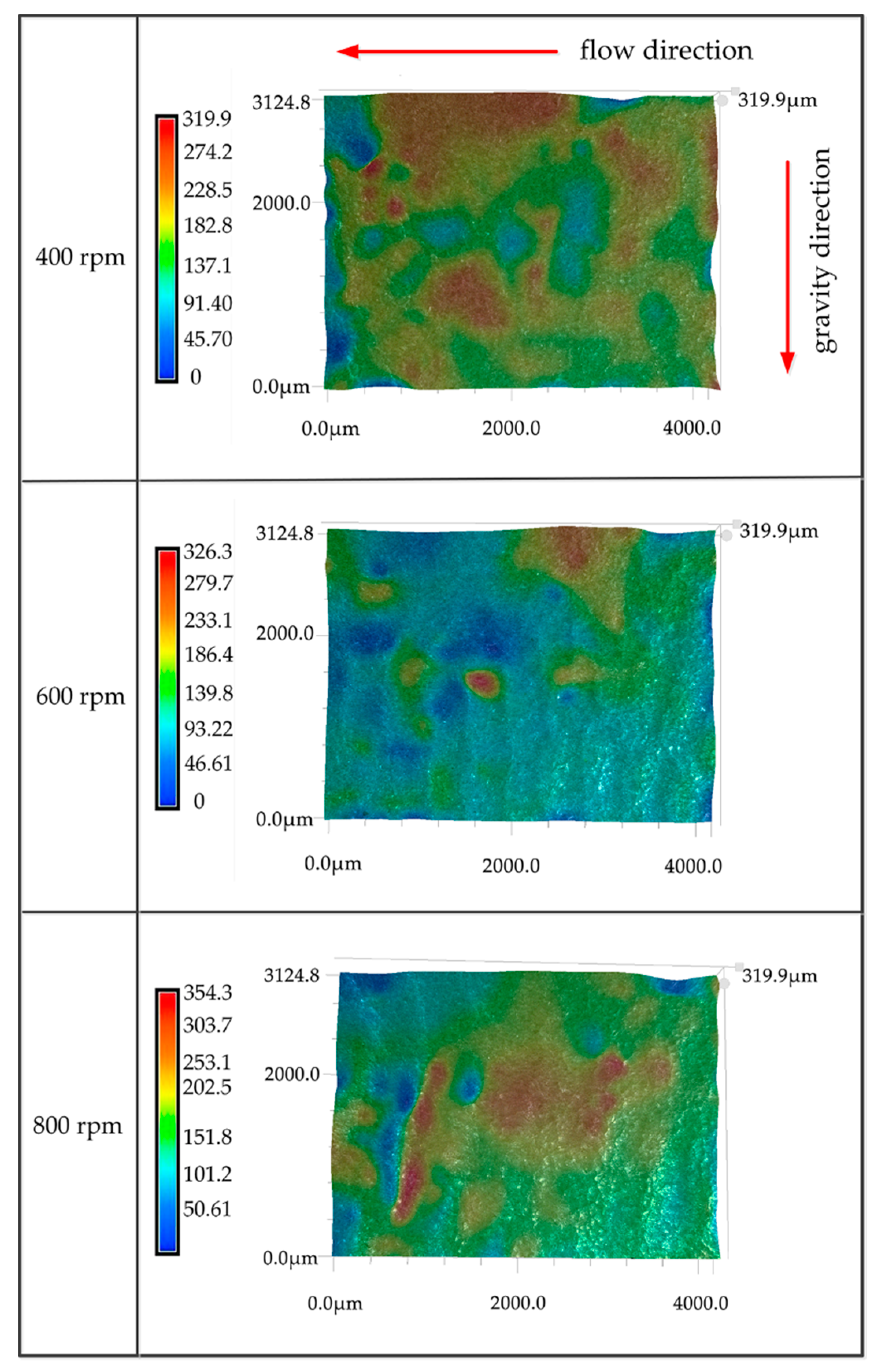
4.4. Analysis of Different Micro-Topographies of Wear Surface Caused by Different Rotation Speeds
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tarodiya, R.; Gandhi, B.K. Hydraulic performance and erosive wear of centrifugal slurry pumps—A review. Powder Technol. 2017, 305, 27–38. [Google Scholar] [CrossRef]
- Tarodiya, R.; Gandhi, B.K. Experimental investigation of centrifugal slurry pump casing wear handling solid-liquid mixtures. Wear 2019, 434, 202972. [Google Scholar] [CrossRef]
- Xiao, Y.; Guo, B.; Ahn, S.-H.; Luo, Y.; Wang, Z.; Shi, G.; Li, Y. Slurry Flow and Erosion Prediction in a Centrifugal Pump after Long-Term Operation. Energies 2019, 12. [Google Scholar] [CrossRef] [Green Version]
- Khalid, Y.A.; Sapuan, S.M. Wear analysis of centrifugal slurry pump impellers. Ind. Lubr. Tribol. 2007, 59, 18–28. [Google Scholar] [CrossRef]
- Xing, D.; Hai-lu, Z.; Xin-yong, W. Finite element analysis of wear for centrifugal slurry pump. Procedia Earth Planet. Sci. 2009, 1, 1532–1538. [Google Scholar] [CrossRef] [Green Version]
- Tressia, G.; Penagos, J.J.; Sinatora, A. Effect of abrasive particle size on slurry abrasion resistance of austenitic and martensitic steels. Wear 2017, 376–377, 63–69. [Google Scholar] [CrossRef]
- Chandel, S.; Singh, S.N.; Seshadri, V. Experimental Study of Erosion Wear in a Centrifugal Slurry Pump Using Coriolis Wear Test Rig. Part. Sci. Technol. 2012, 30, 179–195. [Google Scholar] [CrossRef]
- Tian, H.H.; Addie, G.R.; Barsh, E.P. A new impact erosion testing setup through Coriolis approach. Wear 2007, 263, 289–294. [Google Scholar] [CrossRef]
- Azimian, M.; Bart, H.-J. Erosion investigations by means of a centrifugal accelerator erosion tester. Wear 2015, 328, 249–256. [Google Scholar] [CrossRef]
- Serrano, R.O.; Santos, L.P.; de Faria Viana, F.M.; Pinto, M.A.; Martinez, C.B. Case study: Effects of sediment concentration on the wear of fluvial water pump impellers on Brazil’s Acre River. Wear 2018, 408, 131–137. [Google Scholar] [CrossRef]
- Deng, T.; Bingley, M.S.; Bradley, M.S.A. Influence of particle dynamics on erosion test conditions within the centrifugal accelerator type erosion tester. Wear 2001, 249, 1059–1069. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; He, Z.; He, W. Abrasion characteristic analyses of solid-liquid two-phase centrifugal pump. J. Therm. Sci. 2011, 20, 283–287. [Google Scholar] [CrossRef]
- Guangjie, P.; Zhengwei, W.; Yexiang, X.; Yongyao, L. Abrasion predictions for Francis turbines based on liquid–solid two-phase fluid simulations. Eng. Fail. Anal. 2013, 33, 327–335. [Google Scholar] [CrossRef]
- Cai, X.; Zhou, S.P.; Li, S. Study on the influence of back blade shape on the wear characteristics of centrifugal slurry pump. IOP Conf. Ser. Mater. Sci. Eng. 2016, 129. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.H.; Zhu, M.Y. Numeration Simulation of Solid-Liquid Two-Phase Flow in Centrifugal Sewerage Pump. Appl. Mech. Mater. 2010, 44, 345–348. [Google Scholar] [CrossRef]
- Zhao, B.J.; Huang, Z.F.; Chen, H.L.; Hou, D.H. Numerical investigation of solid-liquid two phase flow in a non-clogging centrifugal pump at off-design conditions. IOP Conf. 2012, 15, 062020. [Google Scholar] [CrossRef]
- Pagalthivarthi, K.V.; Gupta, P.K.; Tyagi, V.; Ravi, M.R. CFD prediction of erosion wear in centrifugal slurry pumps for dilute slurry flows. J. Comput. Multiph. Flows 2011, 3, 225–246. [Google Scholar] [CrossRef] [Green Version]
- Ahlert, K.R. Effects of Particle Impingement Angle and Surface Wetting on Solid Particle Erosion of AISI 1018 Steel; The University of Tulsa: Tulsa, OK, USA, 1994. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Zhu, X.; Li, Y. Analysis of Flow and Wear Characteristics of Solid–Liquid Two-Phase Flow in Rotating Flow Channel. Processes 2020, 8, 1512. https://doi.org/10.3390/pr8111512
Wang P, Zhu X, Li Y. Analysis of Flow and Wear Characteristics of Solid–Liquid Two-Phase Flow in Rotating Flow Channel. Processes. 2020; 8(11):1512. https://doi.org/10.3390/pr8111512
Chicago/Turabian StyleWang, Peng, Xinyu Zhu, and Yi Li. 2020. "Analysis of Flow and Wear Characteristics of Solid–Liquid Two-Phase Flow in Rotating Flow Channel" Processes 8, no. 11: 1512. https://doi.org/10.3390/pr8111512
APA StyleWang, P., Zhu, X., & Li, Y. (2020). Analysis of Flow and Wear Characteristics of Solid–Liquid Two-Phase Flow in Rotating Flow Channel. Processes, 8(11), 1512. https://doi.org/10.3390/pr8111512




