The Impact of Local Hydrodynamics on High-Rate Activated Sludge Flocculation in Laboratory and Full-Scale Reactors
Abstract
:1. Introduction
2. Materials and Methods
2.1. High Rate Activated Sludge System under Study
2.2. Dispersed Suspended Solids Test
2.3. Jar Tests
2.4. Particle Size Distribution
2.5. Computational Fluid Dynamics Modeling
2.5.1. Steady State Model Development
2.5.2. CFD Model of the Jar Test
2.5.3. CFD Model of the Full Scale Mixers
3. Results and Discussion
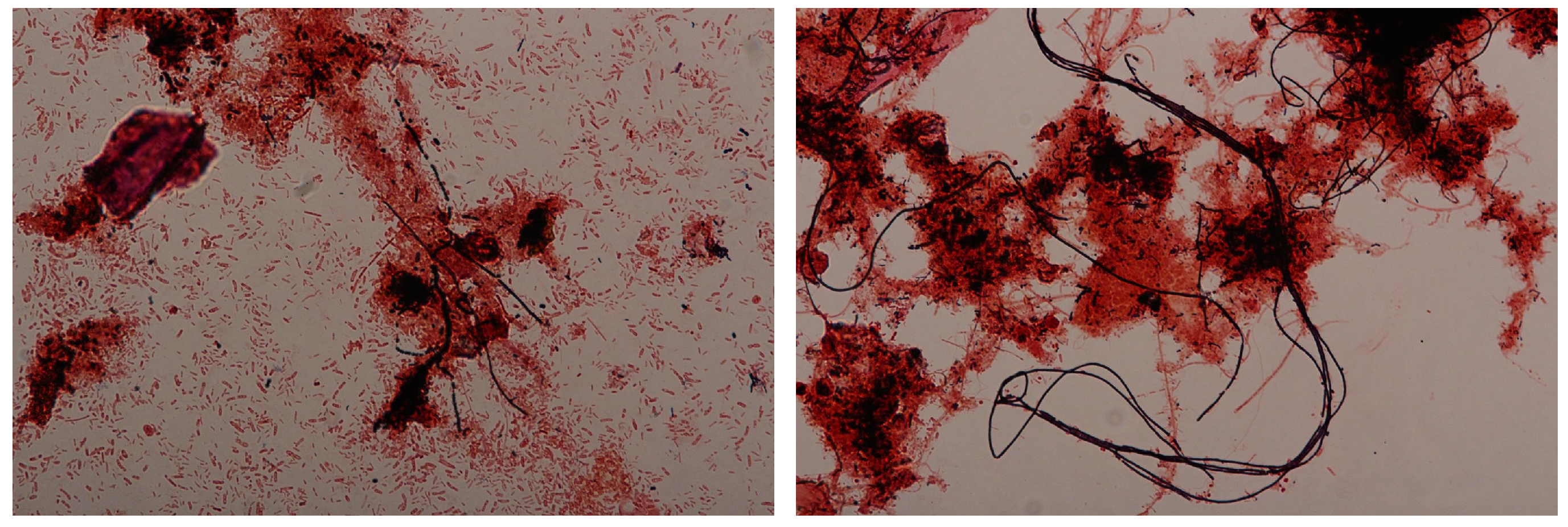
3.1. Flocculation State of High Rate vs. Conventional Activated Sludge
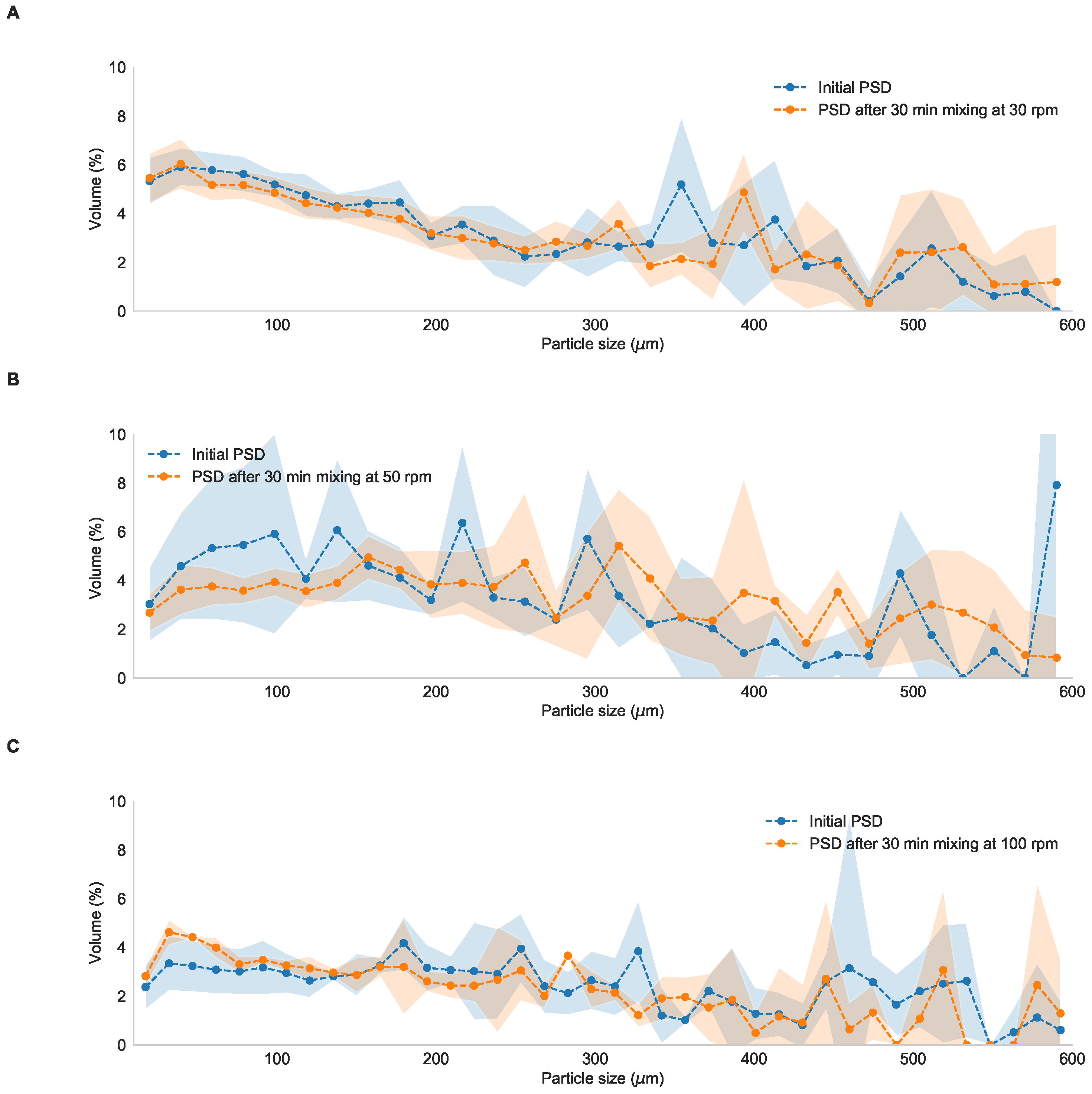
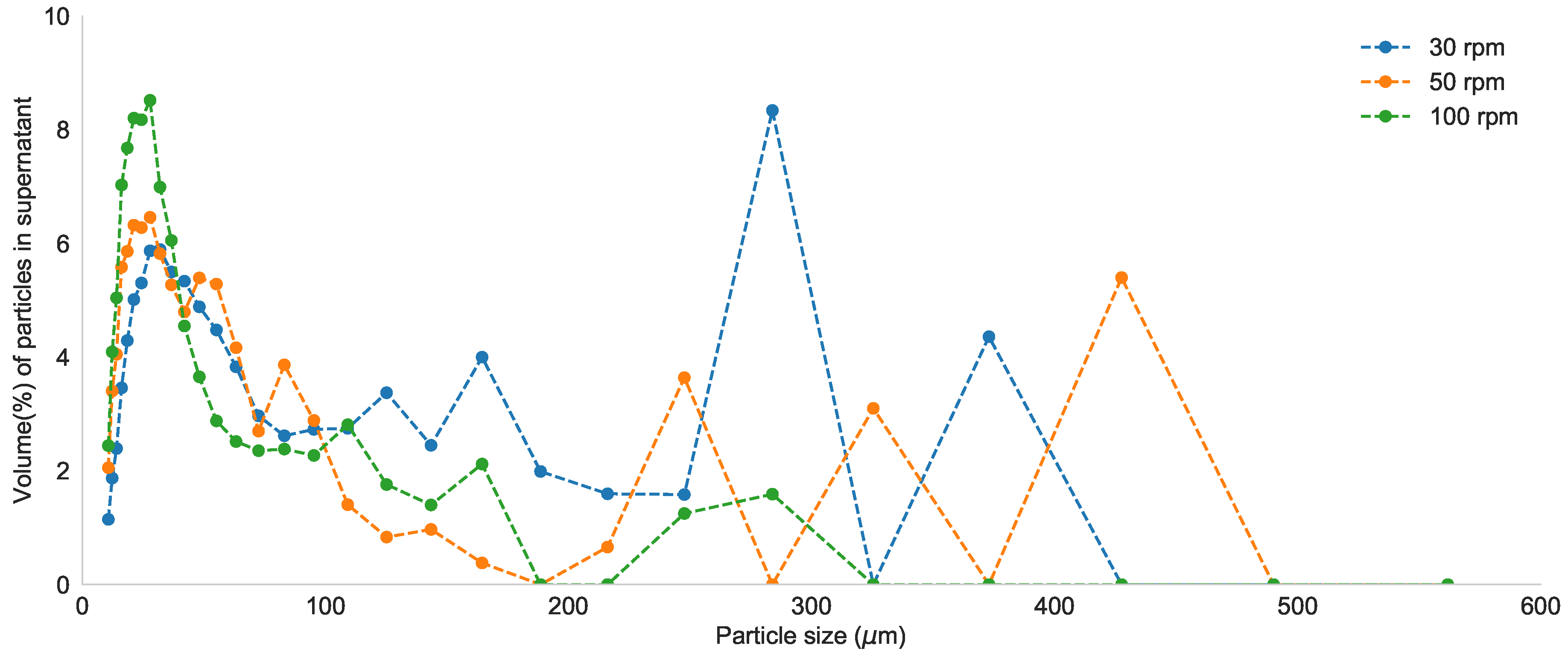
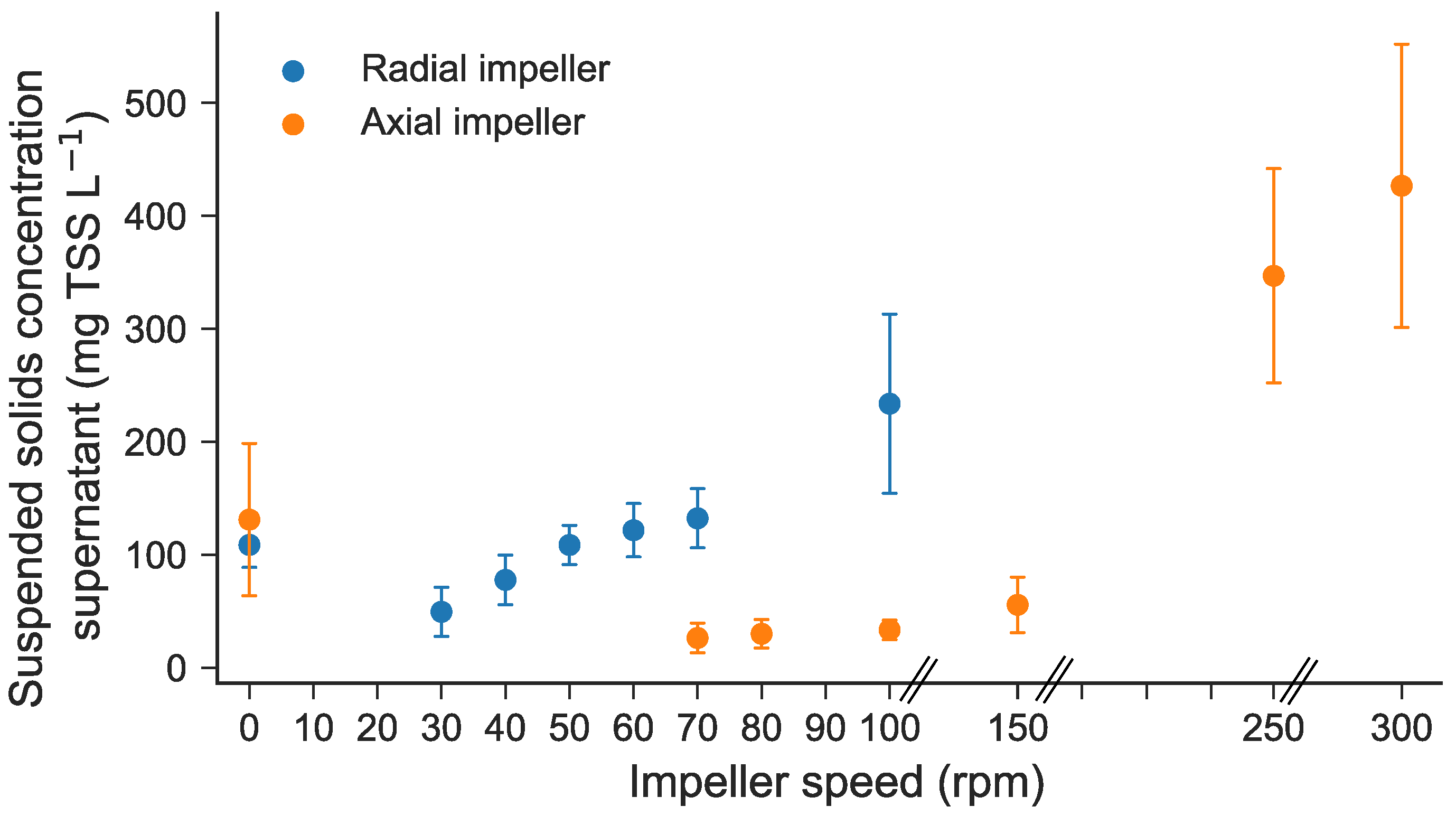
3.2. Impact of Mixing on the Flocculation State
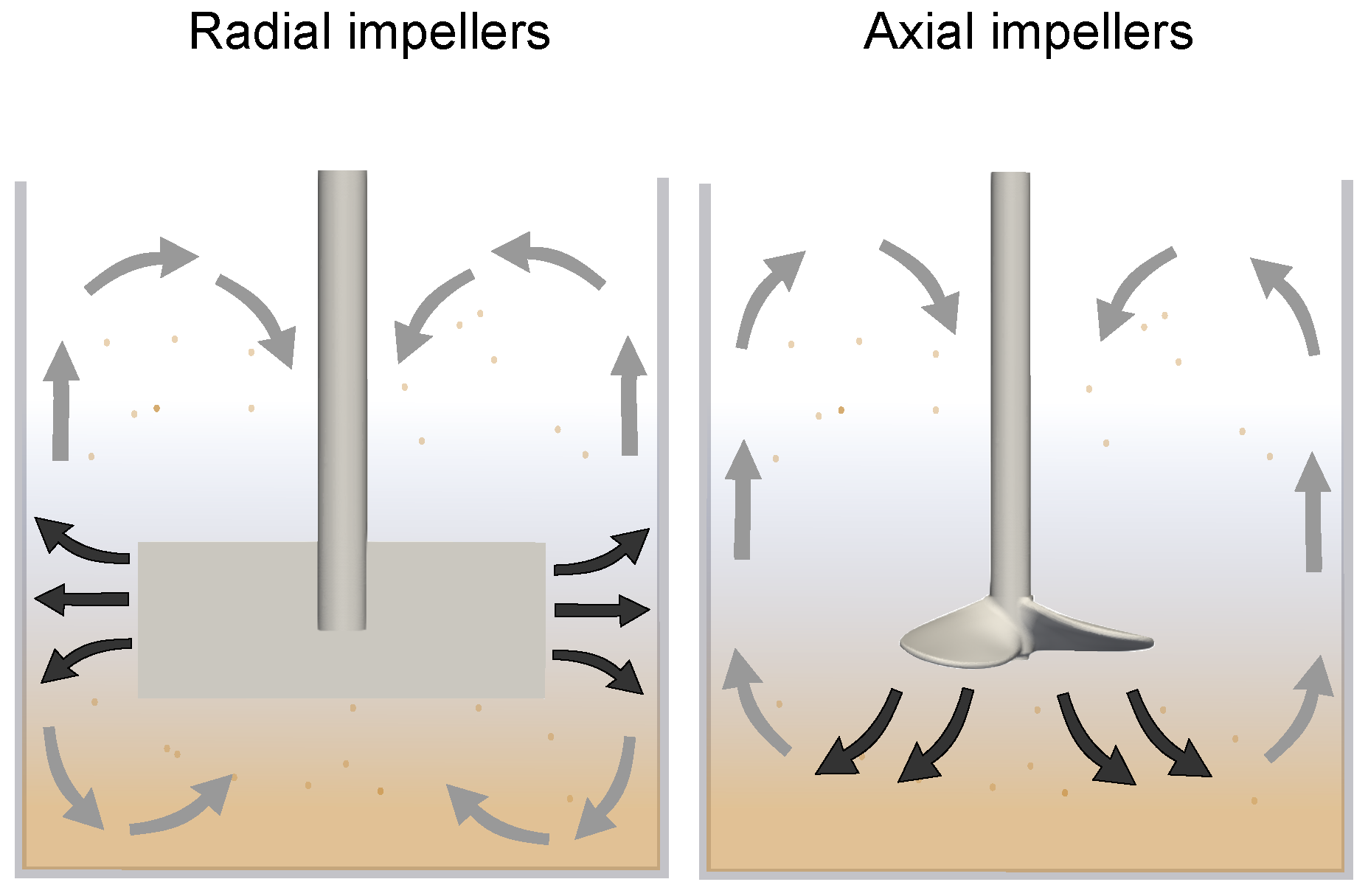
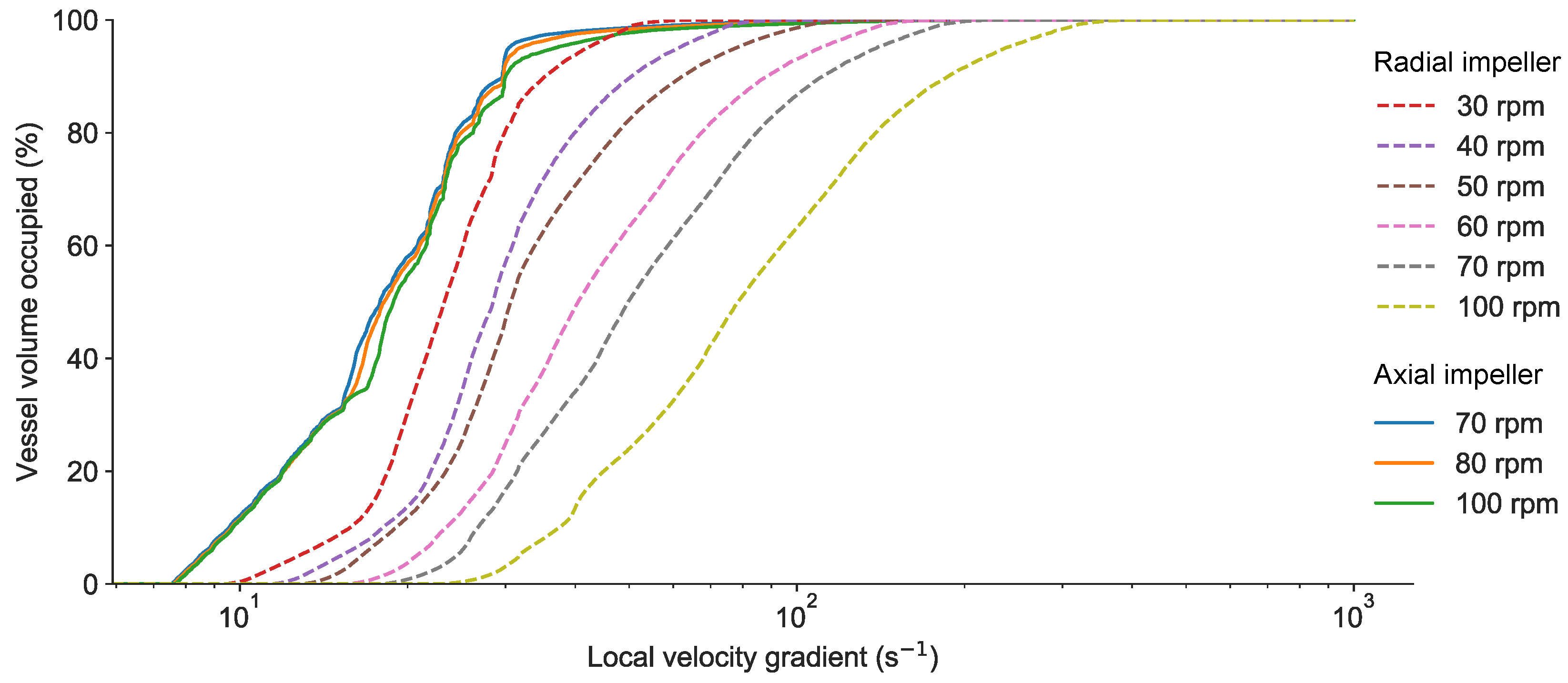
3.3. Impact of Local Velocity Gradients
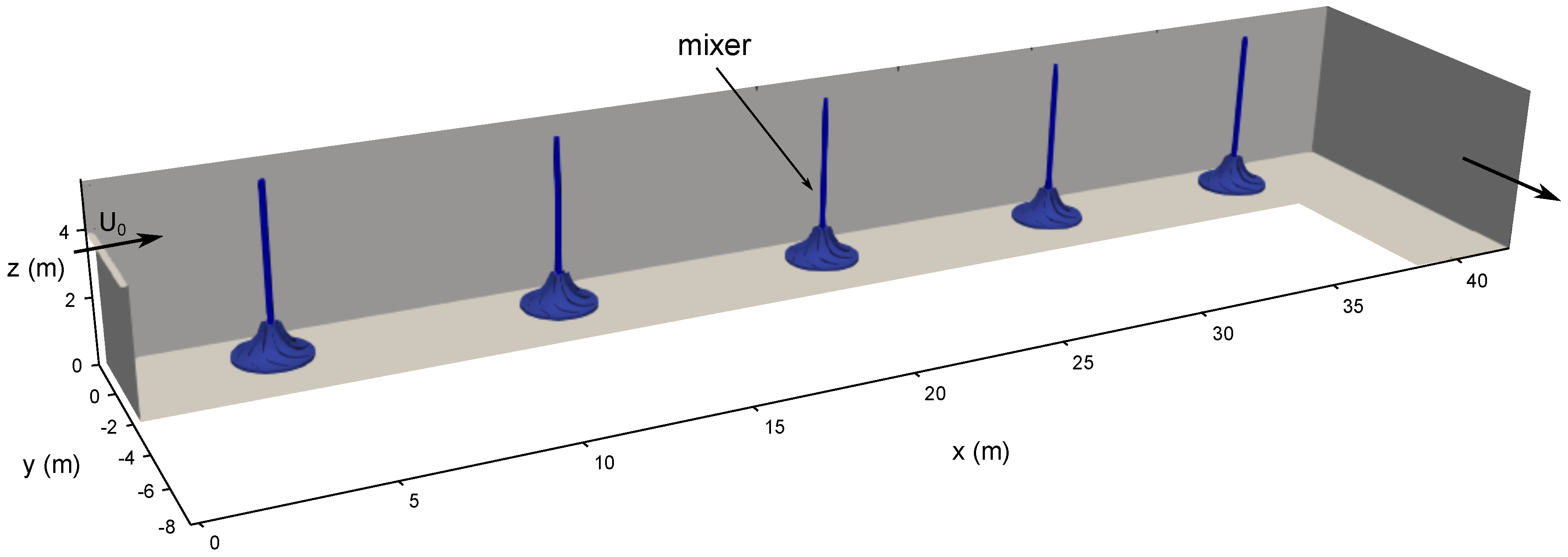
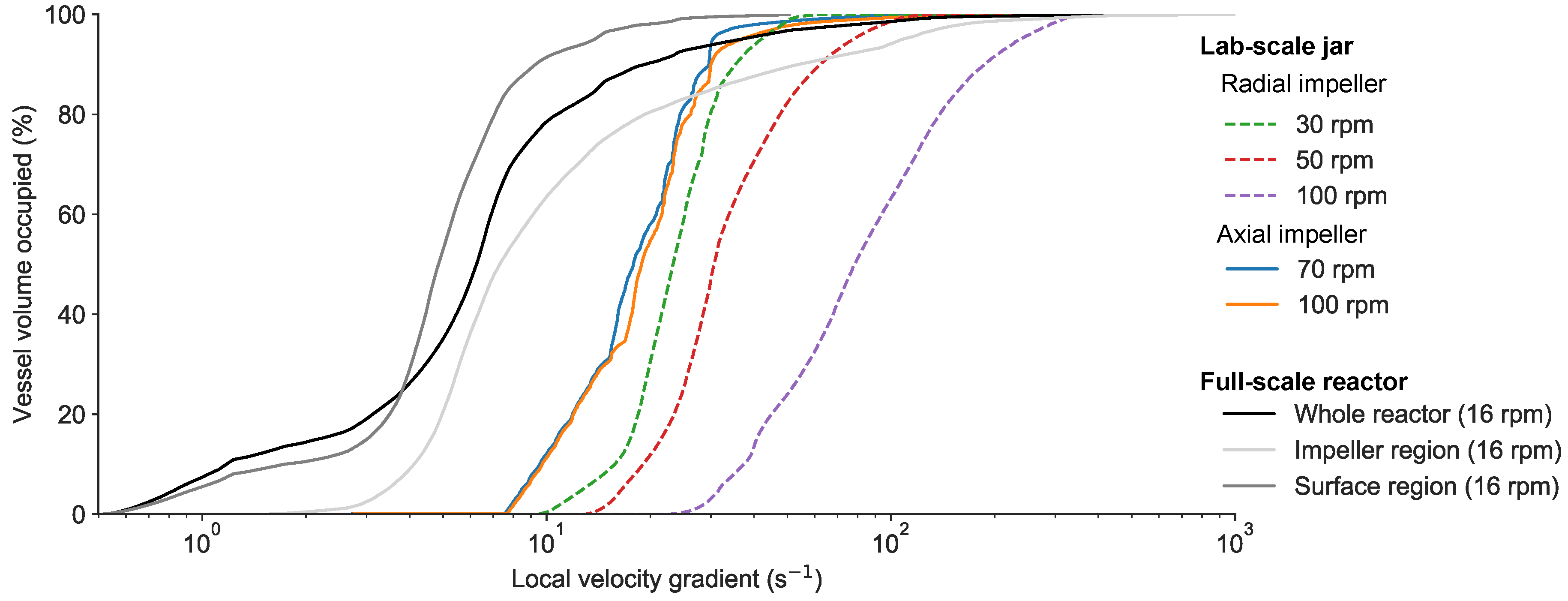
3.4. Comparison to a Full Scale Reactor
3.5. Consequences for Flocculation Modeling
4. Conclusions
- The distribution of the velocity gradients within a jar test highly impacted the flocculation state of the sludge (and thus, the equilibrium between floc aggregation and breakage rates).
- The axial impeller appeared to be more appropriate for HRAS flocculation over a range of impeller speeds as it produced a more homogeneous distribution of local velocity gradients compared to the radial impeller.
- CFD is an excellent tool to acquire information on the distribution of local velocity gradients, which is necessary to describe the floc formation process of HRAS sludge accurately, including aggregation and breakage rates.
- Standard methods for flocculation jar tests should be updated with detailed information on the jar test configuration and appropriate recommendations for impeller type and velocity. A model based strategy can be used to link the information gained on lab scale to full scale systems.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Spicer, P.T.; Pratsinis, S.E. Shear-induced flocculation: The evolution of floc structure and the shape of the size distribution at steady state. Water Res. 1996, 1354, 1049–1056. [Google Scholar] [CrossRef]
- Thomas, D.N.; Judd, S.J.; Fawcett, N. Flocculation modeling: A review. Water Res. 1999, 33, 1579–1592. [Google Scholar] [CrossRef]
- Spicer, P.; Keller, W.; Pratsinis, S. The Effect of Impeller Type on Floc Size and Structure during Shear-Induced Flocculation. J. Colloid Interface Sci. 1996, 184, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Wahlberg, E.J.; Merrill, D.T.; Parker, D. Troubleshooting activated sludge secondary clarifier performance using simple diagnostic tests. In Proceedings of the 68th Annual WEF Conference and Exposition, Miami Beach, FL, USA, 21–25 October 1995; pp. 435–444. [Google Scholar]
- Moruzzi, R.B.; de Oliveira, A.L.; da Conceição, F.T.; Gregory, J.; Campos, L.C. Fractal dimension of large aggregates under different flocculation conditions. Sci. Total Environ. 2017, 609, 807–814. [Google Scholar] [CrossRef] [Green Version]
- Parker, D.; Butler, R.; Finger, R.; Fisher, R. Design and operations experience with flocculator-clarifiers in large plants. Water Sci. Technol. 1995, 33, 163–170. [Google Scholar] [CrossRef]
- Das, D.; Keinath, T.; Parker, D.; Wahlberg, E. Floc breakup in activated sludge plants. Water Environ. Res. 1993, 65, 138–145. [Google Scholar] [CrossRef]
- Khiewwijit, R.; Temmink, H.; Rijnaarts, H.; Keesman, K.J. Energy and nutrient recovery for municipal wastewater treatment: How to design a feasible plant layout? Environ. Model. Softw. 2015, 68, 156–165. [Google Scholar] [CrossRef]
- Böhnke, B. Das Adsorptions-Belebungsverfahrene. Korresp. Abwasser 1977, 24, 33–42. [Google Scholar]
- Jimenez, J.; Miller, M.; Bott, C.; Murthy, S.; De Clippeleir, H.; Wett, B. High-rate activated sludge system for carbon management-Evaluation of crucial process mechanisms and design parameters. Water Res. 2015, 87, 476–482. [Google Scholar] [CrossRef]
- Meerburg, F.; Van Winckel, T.; Vercamer, J.; Nopens, I.; Vlaeminck, S. Toward energy-neutral wastewater treatment: A high rate contact stabilization process to maximally recover sewage organics. Bioresour. Technol. 2015, 179, 373–381. [Google Scholar] [CrossRef]
- Liao, B.Q.; Droppo, I.G.; Leppard, G.G.; Liss, S.N. Effect of solids retention time on structure and characteristics of sludge flocs in sequencing batch reactors. Water Res. 2006, 40, 2583–2591. [Google Scholar] [CrossRef] [PubMed]
- Meerburg, F.; Vlaeminck, S.; Roume, H.; Seuntjens, D.; Pieper, D.H.; Jauregui, R.; Vilchez-Vargas, R.; Boon, N. High-rate activated sludge communities have a distinctly different structure compared to low-rate sludge communities, and are less sensitive towards environmental and operational variables. Water Res. 2016, 100, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Mancell-egala, W.; Su, C.; Takacs, I.; Novak, J.; Kinnear, D.; Murthy, S.; De Clippeleir, H. Settling regimen transitions quantify solid separation limitations through correlation with floc size and shape. Water Res. 2017, 109, 54–68. [Google Scholar] [CrossRef]
- Agrawal, S.; Seuntjens, D.; De Cocker, P.; Lackner, S.; Vlaeminck, S.E. Success of mainstream partial nitritation/anammox demands integration of engineering, microbiome and modeling insights. Curr. Opin. Biotechnol. 2018, 50, 214–221. [Google Scholar] [CrossRef]
- Van Winckel, T.; Liu, X.; Vlaeminck, S.; Takács, I.; Al-Omari, A.; Sturm, B.; Kjellerup, B.; Murthy, S.; De Clippeleir, H. Overcoming floc formation limitations in high rate activated sludge systems. Chemosphere 2019, 215, 342–352. [Google Scholar] [CrossRef] [PubMed]
- Sancho, I.; Lopez-Palau, S.; Arespacochaga, N.; Cortina, J.L. New concepts on carbon redirection in wastewater treatment plants: A review. Sci Total Environ. 2019, 647, 1373–1384. [Google Scholar] [CrossRef] [PubMed]
- Camp, T.; Stein, P. Velocity gradients and internal work in fluid motion. J. Boston Soc. Civ. Eng. 1943, 30, 219–237. [Google Scholar]
- Bouyer, D.; Liné, A.; Do-Quang, Z. Experimental analysis of floc size distribution under different hydrodynamics in a mixing tank. AIChE J. 2004, 50, 2064–2081. [Google Scholar] [CrossRef]
- Coufort, C.; Bouyer, D.; Liné, A. Flocculation related to local hydrodynamics in a Taylor-Couette reactor and in a jar. Chem. Eng. Sci. 2005, 60, 2179–2192. [Google Scholar] [CrossRef]
- Bridgeman, J.; Jefferson, B.; Parsons, S. The development and application of CFD models for water treatment flocculators. Adv. Eng. Softw. 2010, 41, 99–109. [Google Scholar] [CrossRef]
- He, C.; Wood, J.; Marsalek, J.; Rochfort, Q. Using CFD Modeling to Improve the Inlet Hydraulics and Performance of a Storm-Water Clarifier. J. Environ. Eng. 2008, 134, 722–730. [Google Scholar] [CrossRef]
- Joshi, J.B.; Nere, N.K.; Rane, C.V.; Murthy, B.N.; Mathpati, C.S.; Patwardhan, A.W.; Ranade, V.V. CFD simulation of stirred tanks: Comparison of turbulence models (Part II: Axial flow impellers, multiple impellers and multiphase dispersions). Can. J. Chem. Eng. 2011, 89, 754–816. [Google Scholar] [CrossRef]
- Joshi, J.B.; Nere, N.K.; Rane, C.V.; Murthy, B.N.; Mathpati, C.S.; Patwardhan, A.W.; Ranade, V.V. CFD simulation of stirred tanks: Comparison of turbulence models. Part I: Radial flow impellers. Can. J. Chem. Eng. 2011, 89, 23–82. [Google Scholar] [CrossRef]
- Ducoste, J.J.; Clark, M.M.; Weetman, R.J. Turbulence in Flocculators: Effects of Tank Size and Impeller Type. AIChE J. 1997, 43, 328–338. [Google Scholar] [CrossRef]
- Coufort, C.; Dumas, C.; Bouyer, D.; Liné, A. Analysis of floc size distributions in a mixing tank. Chem. Eng. Process. Process Intensif. 2008, 47, 287–294. [Google Scholar] [CrossRef]
- Kilander, J.; Blomström, S.; Rasmuson, A. Scale-up behavior in stirred square flocculation tanks. Chem. Eng. Sci. 2007, 62, 1606–1618. [Google Scholar] [CrossRef]
- Bridgeman, J.; Jefferson, B.; Parsons, S. Assessing floc strength using CFD to improve organics removal. Chem. Eng. Res. Des. 2008, 86, 941–950. [Google Scholar] [CrossRef]
- Marshall, E.; Bakker, A. Computational Fluid Mixing. In Handbook of Industrial Mixing: Science and Practice; Paul, E.L., Atiemo-obeng, V.A., Kresta, S.M., Eds.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2004; pp. 257–343. [Google Scholar] [CrossRef]
- Oyegbile, B.; Ay, P.; Narra, S. Flocculation kinetics and hydrodynamic interactions in natural and engineered flow systems: A review. Environ. Eng. Res. 2016, 21, 1–14. [Google Scholar] [CrossRef] [Green Version]
- De Graaff, M.S.; van den Brand, T.P.; Roest, K.; Zandvoort, M.H.; Duin, O.; van Loosdrecht, M.C. Full-Scale Highly-Loaded Wastewater Treatment Processes (A-Stage) to Increase Energy Production from Wastewater: Performance and Design Guidelines. Environ. Eng. Sci. 2016, 33, 571–577. [Google Scholar] [CrossRef]
- Seuntjens, D.; Bundervoet, B.L.; Mollen, H.; De Mulder, C.; Wypkema, E.; Verliefde, A.; Nopens, I.; Colsen, J.G.; Vlaeminck, S.E. Energy efficient treatment of A-stage effluent: Pilot scale experiences with shortcut nitrogen removal. Water Sci. Technol. 2016, 73, 2150–2158. [Google Scholar] [CrossRef]
- Parker, D.; Kaufman, W.; Jenkins, D. Characteristics of Biological Flocs in Turbulent Regime; Technical Report; University of California: Berkeley, CA, USA, 1970. [Google Scholar]
- APHA. Standard Methods for the Examination of Water and Wastewater, 22nd ed.; American Public Health Association: Washington, DC, USA; American Water Works Association: Washington, DC, USA; Water Environment Federation: Washington, DC, USA, 2012; p. 1496. [Google Scholar]
- Torfs, E.; Nopens, I.; Winkler, M.K.; Vanrolleghem, P.A.; Balemans, S.; Smets, I.Y. Settling tests. In Experimental Methods in Wastewater Treatment; van Loosdrecht, M., Nielsen, P., Lopez-Vazquez, C.M., Brdjanovic, D., Eds.; IWA Publishing: London, UK, 2016; pp. 235–262. [Google Scholar]
- Deglon, D.A.; Meyer, C.J. CFD modeling of stirred tanks: Numerical considerations. Min. Eng. 2006, 19, 1059–1068. [Google Scholar] [CrossRef]
- Aubin, J.; Fletcher, D.F.; Xuereb, C. Modeling turbulent flow in stirred tanks with CFD: The influence of the modeling approach, turbulence model and numerical scheme. Exp. Therm. Fluid Sci. 2004, 28, 431–445. [Google Scholar] [CrossRef] [Green Version]
- Bridgeman, J.; Jefferson, B.; Parsons, S.A. Computational Fluid Dynamics modeling of flocculation in water treatment: A review. Eng. Appl. Comput. Fluid Mech. 2009, 3, 220–241. [Google Scholar]
- Alleyne, A.A.; Xanthos, S.; Ramalingam, K.; Temel, K.; Li, H.; Tang, H.S. Numerical investigation on flow generated by invent mixer in full scale wastewater stirred tank. Eng. Appl. Comput. Fluid Mech. 2014, 8, 503–517. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Xue, L.; Gorczyca, B.; Nan, J.; Shi, Z. Comparative analysis on flocculation performance in unbaffled square stirred tanks with different height-to-width ratios: Experimental and CFD investigations. Chem. Eng. Res. Des. 2018, 132, 518–535. [Google Scholar] [CrossRef]
- He, W.; Xue, L.; Gorczyca, B.; Nan, J.; Shi, Z. Experimental and CFD studies of floc growth dependence on baffle width in square stirred-tank reactors for flocculation. Sep. Purif. Technol. 2018, 190, 228–242. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Limited: Essex, UK, 2007; p. 520. [Google Scholar]
- Greenshields, C.J. The OpenFOAM Foundation User Guide 7.0; The OpenFOAM Foundation Ltd.: London, UK, 10 July 2019. [Google Scholar]
- Cagnetta, C.; Saerens, B.; Meerburg, F.A.; Decru, S.O.; Broeders, E.; Menkveld, W.; Vandekerckhove, T.G.; De Vrieze, J.; Vlaeminck, S.E.; Verliefde, A.R.; et al. High-rate activated sludge systems combined with dissolved air flotation enable effective organics removal and recovery. Bioresour. Technol. 2019, 291. [Google Scholar] [CrossRef]
- Faust, L.; Temmink, H.; Zwijnenburg, A.; Kemperman, A.J.B.; Rijnaarts, H.H.M. High loaded MBRs for organic matter recovery fromsewage: Effect of solids retention time on bioflocculation and on the role of extracellular polymers. Water Res. 2014, 56, 258–266. [Google Scholar] [CrossRef]
- Mikkelsen, L.H. The shear sensitivity of activated sludge: Relations to filterability, rheology and surface chemistry. J. Colloid Interface Sci. 2001, 182, 1–14. [Google Scholar]
- Nopens, I.; Biggs, C.; De Clercq, B.; Govoreanu, R.G.; Wilén, B.; Lant, P.; Vanrolleghem, P. Modelling the activated sludge flocculation process combining laser diffraction particle sizing and population balance modeling (PBM). Water Sci. Technol. 2002, 45, 41–49. [Google Scholar] [CrossRef]
- Li, D.H.; Ganczarczyk, J.J. Size distribution of activated sludge flocs. Res. J. Water Pollut. Control Fed. 1991, 63, 806–814. [Google Scholar]
- Marchisio, D.L.; Vigil, R.D.; Fox, R.O. Quadrature method of moments for aggregation-breakage processes. J. Colloid Interface Sci. 2003, 258, 322–334. [Google Scholar] [CrossRef]
- Lee, B.J.; Toorman, E.; Molz, F.J.; Wang, J. A two-class population balance equation yielding bimodal flocculation of marine or estuarine sediments. Water Res. 2011, 45, 2131–2145. [Google Scholar] [CrossRef] [PubMed]
- Ramalingam, K.; Xanthos, S.; Gong, M.; Fillos, J.; Beckmann, K.; Deur, A.; McCorquodale, J.A. Critical modeling parameters identified for 3D CFD modeling of rectangular final settling tanks for New York City wastewater treatment plants. Water Sci. Technol. 2012, 65, 1087–1094. [Google Scholar] [CrossRef] [PubMed]
- Castellano, S.; Sheibat-Othman, N.; Marchisio, D.; Buffo, A.; Charton, S. Description of droplet coalescence and breakup in emulsions through a homogeneous population balance model. Chem. Eng. J. 2018, 354, 1197–1207. [Google Scholar] [CrossRef]
- Rehman, U. Next Generation Bioreactor Models for Wastewater Treatment Systems by Means of Detailed Combined Modelling of Mixing and Biokinetics. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2016. [Google Scholar]



| Radial Impeller | Axial Impeller | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| N (rpm) | 30 | 40 | 50 | 60 | 70 | 100 | 70 | 80 | 100 |
| G () | 23 | 28 | 30 | 40 | 50 | 78 | 17 | 18 | 19 |
| G () | 69 | 105 | 148 | 200 | 257 | 465 | 180 | 254 | 421 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balemans, S.; Vlaeminck, S.E.; Torfs, E.; Hartog, L.; Zaharova, L.; Rehman, U.; Nopens, I. The Impact of Local Hydrodynamics on High-Rate Activated Sludge Flocculation in Laboratory and Full-Scale Reactors. Processes 2020, 8, 131. https://doi.org/10.3390/pr8020131
Balemans S, Vlaeminck SE, Torfs E, Hartog L, Zaharova L, Rehman U, Nopens I. The Impact of Local Hydrodynamics on High-Rate Activated Sludge Flocculation in Laboratory and Full-Scale Reactors. Processes. 2020; 8(2):131. https://doi.org/10.3390/pr8020131
Chicago/Turabian StyleBalemans, Sophie, Siegfried E. Vlaeminck, Elena Torfs, Leonie Hartog, Laura Zaharova, Usman Rehman, and Ingmar Nopens. 2020. "The Impact of Local Hydrodynamics on High-Rate Activated Sludge Flocculation in Laboratory and Full-Scale Reactors" Processes 8, no. 2: 131. https://doi.org/10.3390/pr8020131
APA StyleBalemans, S., Vlaeminck, S. E., Torfs, E., Hartog, L., Zaharova, L., Rehman, U., & Nopens, I. (2020). The Impact of Local Hydrodynamics on High-Rate Activated Sludge Flocculation in Laboratory and Full-Scale Reactors. Processes, 8(2), 131. https://doi.org/10.3390/pr8020131







