Methodologies for the Design of Solar Receiver/Reactors for Thermochemical Hydrogen Production
Abstract
:1. Introduction
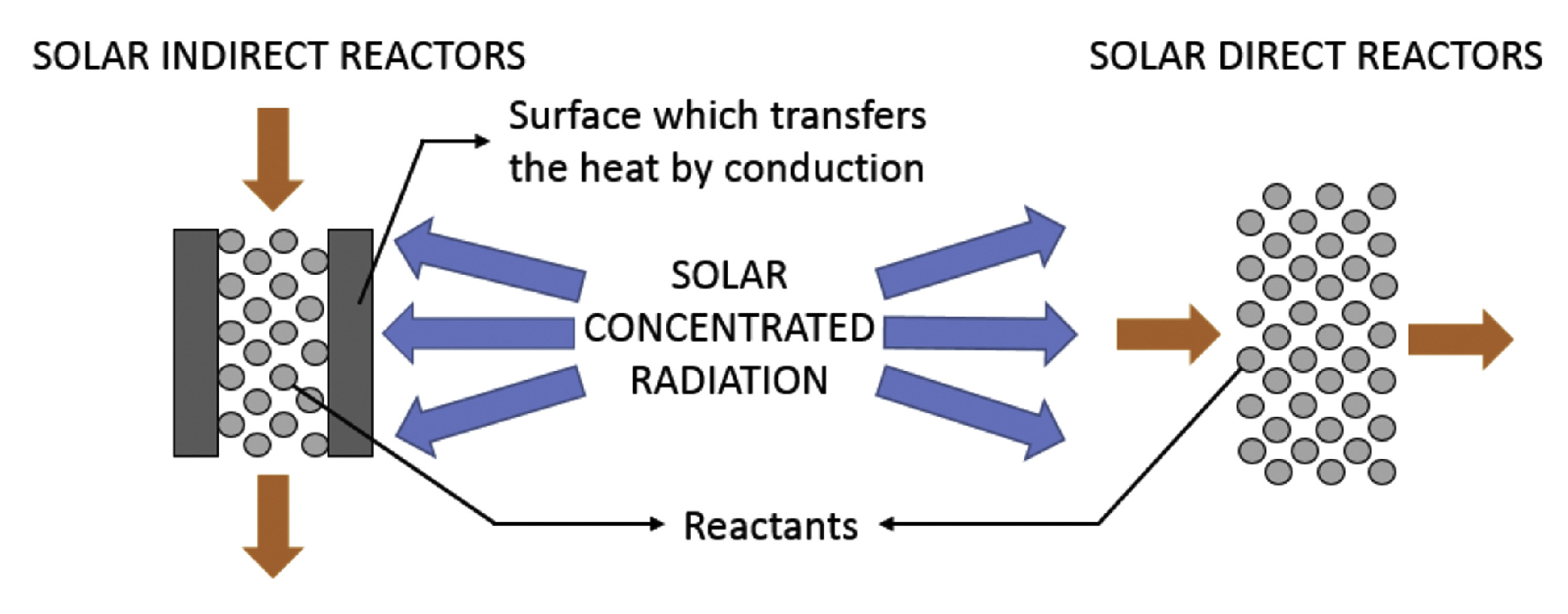
2. Generalities of Solar Receiver/Reactors
- Capacity to reach the required reaction temperatures
- Material resistance
- The possibility of scaling up
- Low energy losses, mainly achieved by reducing re-radiation
- Low cost
3. Overview of Proposed Reactor Configurations for Thermochemical Hydrogen Production
3.1. Reactor/Receivers for Solar Gasification
3.2. Reactor/Receivers for Solar Reforming
3.3. Reactors/Receivers for Solar Cracking
3.4. Reactor/Receivers for Direct Solar Thermolysis
- Quenching of product followed by low-temperature separation
- (a)
- Quenching by auxiliary jets
- (b)
- Injection of hot product gas into water
- (c)
- Reaction near an immersed target and cooling of the gas by the surrounding body of water
- (d)
- Dissociation of a jet of steam at low temperature on a hot target and cooling of the product gas coming in contact with the jet
- High-temperature separation
- (a)
- Separation of H2 using a microporous membrane
- (b)
- Separation of O2 using an electrodiffusion membrane
- (c)
- Separation of H2 using a non-porous metallic membrane
- (d)
- Separation by creation of a high-speed jet
- (e)
- Separation by centrifugation
3.5. Reactor/Receivers for Water-Splitting Redox Cycles
- two-step WSTCs, in which two reactions, one endothermic and the other exothermic, are required to achieve the production of H2 and O2. These processes have the advantage of producing hydrogen and oxygen in two distinct steps, thereby avoiding the requirement of a high temperature gas separation. They may be further divided into redox cycles and hybrid Westinghouse cycles.
- -
- Redox cycles that make use of metal oxides are currently the most widely studied two-step WSTCs. In this case, the first reaction is the endothermic step of the process and consists of the reduction of the oxide, with consequent release of O2. This reaction is also known as the activation step. The second reaction is the exothermic step, during which the reduced oxide is newly oxidized, forming H2 and regenerating the original oxide. Materials that have been considered for application in the thermochemical production of hydrogen include Fe [63,64,65,66,67,68,69], Ce [70,71,72,73], Zn [74,75,76,77,78,79,80,81,82,83,84,85,86], Ti [87], Mn [65,68,88], Co [68], and Sn [83,84,89,90] oxides, as well as ferrites [91,92,93]. These cycles generally operate between the lower temperature of the oxidation step and the higher temperature of the reduction step. More recently, the isothermal splitting of water has been proposed to avoid the irreversible heat and time losses related to the cyclic rotation between the low and high temperatures of the two-step cycles. The process is made possible by (partial) pressure swings between the reduction and oxidation processes. This concept is at the basis of the mixed sodium manganese ferrite cycle, first proposed by Tamaura and co-workers [94] and extensively studied by Varsano and co-workers [95,96,97]. Analyses of water splitting cycles based on gas composition pressure swings have been presented in [98,99,100], and thorough discussions of such cycles isothermally were reported in [101,102].
- -
- The first hybrid Westinghouse cycle to have been proposed was the sulfur cycle, in which sulfurous acid and water react electrolytically, producing hydrogen and sulfuric acid. The latter is vaporized to produce steam and sulfur trioxide, which is then reduced at higher temperatures into sulfur dioxide and oxygen. The final mixture is separated, and sulfur dioxide is recycled to the electrolyzer [103].
- Multi-step WSTCs consist of more than two reaction step. Their drawbacks are mainly related to the potentially lower efficiency of the process, but lower operating temperatures may be achieved compared to those usually required by two-step processes. In addition to the older three-step sulfur-iodine cycle [104], Mn-oxide based three-step cycles have been more recently proposed [62,105,106]. The use of nanoparticles was also found to have a beneficial effect on lowering the maximum temperature of the cycle [107].
4. Generalities on Solar Receiver/Reactor Modeling
- Heating of the reactive material
- To describe the heating received by the reactive material, it is necessary to study the irradiation distribution. As described in detail by Lanchi et al. [110], the absorbed radiation is a purely optical quantity. It is generally evaluated through a Monte Carlo ray-tracing technique. Its distribution depends on the geometric characteristics of the concentrating facility and of the receiver, as well as the characteristics of the absorber material (absorbance and reflectivity). These, in turn, depend not only on the nature of the material itself, but also on its state of oxidation and potential deposition of particles. For indirectly heated reactors, heat conduction from the irradiated surface to the reactive material must also be described. For directly radiated reactors, the effect of possible fouling of the cavity window should be accounted for.
- Heat losses to the environment through convection
- Naturally, some heat losses take place toward the environment, which is at a lower temperature level compared to the receiver surface. Heat losses through the outer walls of receivers are generally neglected as these are insulated. On the other hand, particularly in the case of indirectly irradiated cavities, the inner wall is exposed to still air, and heat loss through natural convection must be accounted for.
- Heat losses to the environment through thermal re-radiation
- The receiver emits radiation towards the environment. The heat loss due to thermal re-emission may be evaluated as [110]:where f is a factor quantifying the fraction of radiation that is emitted from the cavity toward the environment, is the Boltzmann constant, is the wall emissivity, is the wall temperature, and is the sky effective radiative temperature and is approximately equal to the ambient temperature.
- Fluidodynamics
- As mentioned above, the type of reaction and the operating conditions determine whether solar receivers/reactors should be designed as fixed bed reactors, fluidized bed reactors, or particle reactors. Depending on the chosen configuration, the flow conditions may have a significant effect on the overall behavior of the system.
- Reaction rate
- The rate of reaction is often studied separately, and the rate expression developed is employed in the model of the solar receiver/reactor.
5. Selected Examples
- Select a general configuration
- Identify the criterion based on which the “optimal” reactor characteristics can be defined
- Develop a model to describe the behavior of the reactor
- Analyze the results of the models and the effect of changes in the geometry
- Select the “optimal” configuration
- Maximize energy conversion efficiency
- Minimize losses associated with process irreversibilities, i.e., exergy analysis
- Minimize thermo-mechanical stress
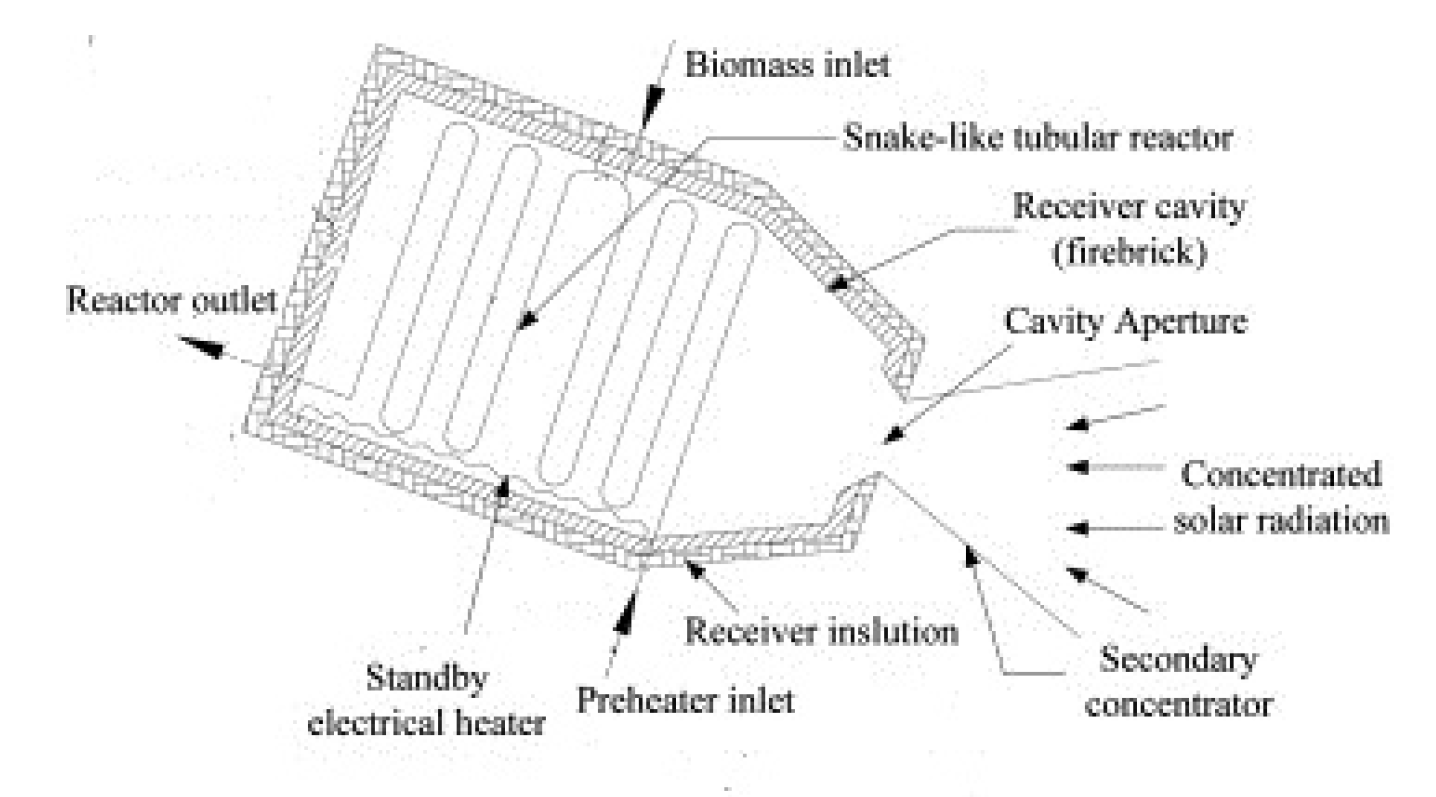
5.1. Tubular Reactor/Receiver for Steam Reforming [114]
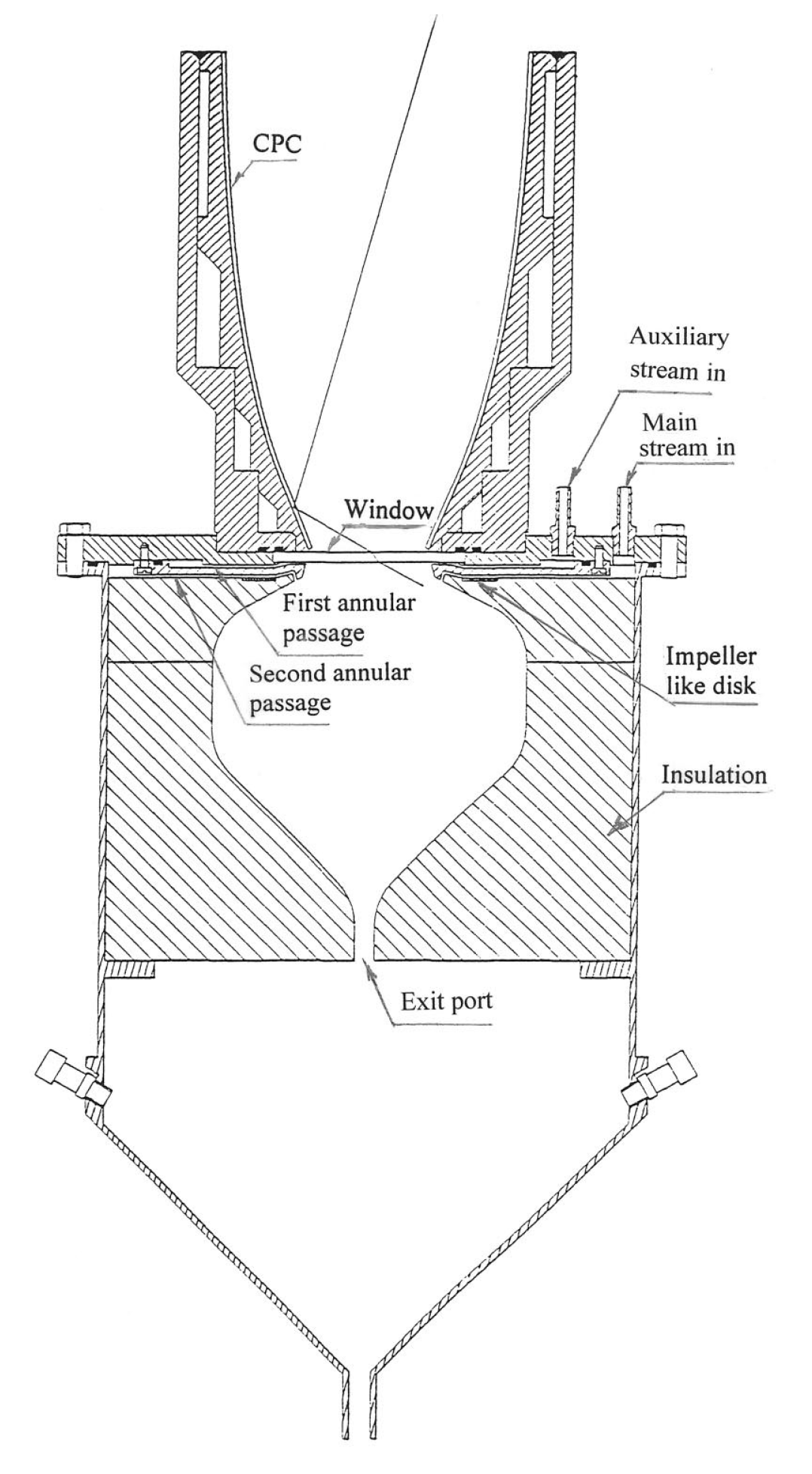
5.2. Directly Heated Receiver/Reactor for Thermochemical Water-Splitting [4]
- is the intercepted power on the absorber surface, defined as the ratio between the power absorbed and the power entering the secondary concentrator.
- is the dimensionless surface area of the absorber normalized with respect to the inlet aperture area of the secondary concentrator. This parameter is important because the absorber surface area is proportional to the reactive area. A higher value of is therefore equivalent to a higher amount of reactive material.
- The subscript 60 refers to the fact that for the irradiation to be useful for the reaction, it cannot exceed a maximum value, , to avoid overheating and consequent damage of the reactive material, and it cannot decrease below a minimum value, to avoid an excessive drop in reaction rate. For this reason, the radiative flux was considered to be useful if included between and 60% of
5.3. Receiver/Reactor for the Gasification of Solid Particles [116]
- particle size
- feeding rate
- input power
- geometry of the cavity’s longitudinal section (radius and length) at constant reactor volume
- Extent of feed conversion,
- Solar-to-chemical energy conversion efficiency (Equation (1))
- upgrade factor, defined as the ratio between the calorific content of the gaseous products and that of the solid feed:
5.4. Indirectly Heated Receiver/Reactor for an Isothermal Redox Cycle [119]
- With regards to the material morphology, porous particles were chosen over solid particles, a porous ceria monolith, and a reticulate porous ceramic (RPC), due to the good combination of large surface area per unit of mass, favorable for the reaction kinetics, rapid heat transfer, and low pressure drops.
- Specific gas flow rates and duration of each cycle step were selected to maximize CO production on the basis of results obtained on 1 g of porous ceria particles tested in an infrared imaging furnace. The validity of scaling these results to a larger reactor was confirmed in previous works by some of the same authors [120,121].
- Based on the optimization described in the previous step, the mass of porous ceria particles required for the 3 kW prototype was established.
- The length-to-radius ratio of the cavity was selected to be equal to two, to obtain an apparent absorptivity close to unity.
- The diameter of the cavity aperture was selected to accommodate a solar power input of 3 kW at an average flux of 3 MW/m2.
- Tube radii were selected from standard tube sizes based on considerations relative to the ease of operation, but also from an estimation of the mechanical stresses.
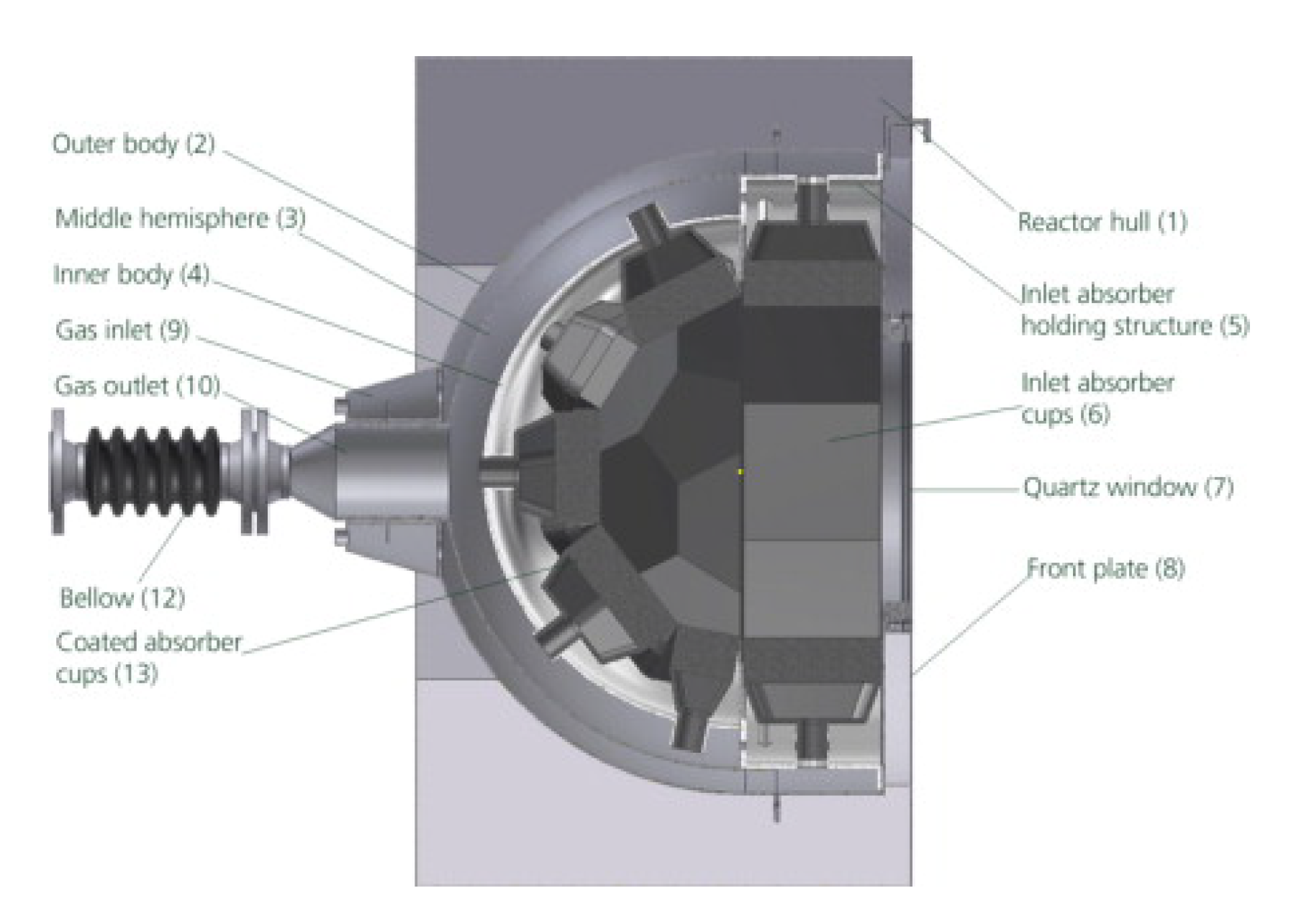
5.5. Directly Heated Particle Receiver/Reactor [122]
6. Conclusions
- Energy conversion efficiency
- Energy losses associated with process irreversibilities
- Thermo-mechanical stress
- Reactant conversion
- Temperature uniformity within the reactor
- Ratio between the calorific content of the products and the reactants
- Receiver shape and dimensions
- Mode of reactant feed
- Particle morphology in the case of solid reactants
Funding
Conflicts of Interest
References
- Steinfeld, A. Solar thermochemical production of hydrogen-a review. Sol. Energy 2005, 78, 603–615. [Google Scholar] [CrossRef]
- Villafan Vidales, H.I.; Arancibia Bulnes, C.A.; Riveros Rosas, D.; Romero Paredes, H.; Estrada, C.A. An overview of the solar thermochemical processes for hydrogen and syngas production: Reactors, and facilities. Renew. Sustain. Energy Rev. 2017, 75, 894–908. [Google Scholar] [CrossRef]
- Romero, M.; Steinfeld, A. Concentrating solar thermal power and thermochemical fuels. Energy Environ. Sci. 2012, 5, 9234–9245. [Google Scholar] [CrossRef]
- Houaijia, A.; Sattler, C.; Roeb, M.; Lange, M.; Breuer, S.; Säck, J.P. Analysis and improvement of a high-efficiency solar cavity reactor design for a two-step thermochemical cycle for solar hydrogen production from water. Sol. Energy 2013, 97, 26–38. [Google Scholar] [CrossRef]
- Kodama, T.; Bellan, S.; Gokon, N.; Cho, H.S. Particle reactors for solar thermochemical processes. Sol. Energy 2017, 156, 113–132. [Google Scholar] [CrossRef]
- Tapia, E.; Iranzo, A.; Pino, F.J.; Rosa, F.; Salva, J.A. Methodology for thermal design of solar tubular reactors using CFD technique. Int. J. Hydrog. Energy 2016, 41, 19525–19538. [Google Scholar] [CrossRef]
- Giaconia, A.; Monteleone, G.; Morico, B.; Salladini, A.; Shabtai, K.; Sheintuch, M.; Boettge, D.; Adler, J.; Palma, V.; Voutetakis, S.; et al. Multi-fuelled solar steam reforming for pure hydrogen production using solar salts as heat transfer fluid. Energy Procedia 2015, 69, 1750–1758. [Google Scholar] [CrossRef]
- Said, S.A.; Simakov, D.S.; Waseeuddin, M.; Roman-Leshkov, Y. Solar molten salt heated membrane reformer for natural gas upgrading and hydrogen generation: A CFD model. Sol. Energy 2016, 124, 163–176. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. Modelling and optimization of hydrogen yield in membrane steam reforming reactors. Can. J. Chem. Eng. 2017, 95, 1676–1682. [Google Scholar] [CrossRef]
- Murmura, M.A.; Cerbelli, S.; Annesini, M.C. Designing the optimal geometry of a membrane reactor for hydrogen production from a pre-reformed gas mixture based on the extent of the reaction boundary layer. Chem. Eng. Process.-Process Intensif. 2017, 120, 148–160. [Google Scholar] [CrossRef]
- Aiman, W.R.; Thorsness, C.B.; Gregg, D.W. Solar coal gasification: Plant design and economics. AIChE J. 1981, 77, 36–46. [Google Scholar]
- Beattie, W.H.; Berjoan, R.; Coutures, J.P. High-temperature solar pyrolysis of coal. Sol. Energy 1983, 31, 137–143. [Google Scholar] [CrossRef]
- Gregg, D.W.; Taylor, R.W.; Campbell, J.H.; Taylor, J.R.; Cotton, A. Solar gasification of coal, activated carbon, coke and coal and biomass mixtures. Sol. Energy 1980, 25, 353–364. [Google Scholar] [CrossRef]
- Murray, J.P.; Fletcher, E.A. Reaction of steam with cellulose in a fluidized bed using concentrated sunlight. Energy 1994, 19, 1083–1098. [Google Scholar] [CrossRef]
- Kodama, T.; Aoki, A.; Shimizu, T.; Kitayama, Y.; Komarneni, S. Efficient thermochemical cycle for CO2 gasification of coal using a redox system of reactive iron-based oxide. Energy Fuels 1998, 12, 775–781. [Google Scholar] [CrossRef]
- Matsunami, J.; Yoshida, S.; Oku, Y.; Yokota, O.; Tamaura, Y.; Kitamura, M. Coal gasification by CO2 gas bubbling in molten salt for solar/fossil energy hybridization. Sol. Energy 2000, 68, 257–261. [Google Scholar] [CrossRef]
- Kodama, T.; Funatoh, A.; Shimizu, K.; Kitayama, Y. Kinetics of metal oxide-catalyzed CO2 gasification of coal in a fluidized-bed reactor for solar thermochemical process. Energy Fuels 2001, 15, 1200–1206. [Google Scholar] [CrossRef]
- Piatkowski, N.; Wieckert, C.; Steinfeld, A. Experimental investigation of a packed-bed solar reactor for the steam-gasification of carbonaceous feedstocks. Fuel Process. Technol. 2009, 90, 360–366. [Google Scholar] [CrossRef]
- Epstein, M.; Spiewak, I.; Funken, K.; Ortner, J. Review of the technology for solar gasification of carbonaceous materials. In Proceedings of the Solar Engineering Conference, San Francisco, CA, USA, 27–30 March 1994; pp. 79–91. [Google Scholar]
- Gordillo, E.D.; Belghit, A. A bubbling fluidized bed solar reactor model of biomass char high temperature steam-only gasification. Fuel Process. Technol. 2011, 92, 314–321. [Google Scholar] [CrossRef]
- Gokon, N.; Izawa, T.; Abe, T.; Kodama, T. Steam gasification of coal cokes in an internally circulating fluidized bed of thermal storage material for solar thermochemical processes. Int. J. Hydrog. Energy 2014, 39, 11082–11093. [Google Scholar] [CrossRef]
- Kodama, T.; Enomoto, S.I.; Hatamachi, T.; Gokon, N. Application of an internally circulating fluidized bed for windowed solar chemical reactor with direct irradiation of reacting particles. J. Sol. Energy Eng. 2008, 130, 014504. [Google Scholar] [CrossRef]
- Chen, J.; Lu, Y.; Guo, L.; Zhang, X.; Xiao, P. Hydrogen production by biomass gasification in supercritical water using concentrated solar energy: System development and proof of concept. Int. J. Hydrog. Energy 2010, 35, 7134–7141. [Google Scholar] [CrossRef]
- Melchior, T.; Perkins, C.; Lichty, P.; Weimer, A.W.; Steinfeld, A. Solar-driven biochar gasification in a particle-flow reactor. Chem. Eng. Process. Process Intensif. 2009, 48, 1279–1287. [Google Scholar] [CrossRef]
- Melchior, T.; Perkins, C.; Weimer, A.W.; Steinfeld, A. A cavity-receiver containing a tubular absorber for high-temperature thermochemical processing using concentrated solar energy. Int. J. Therm. Sci. 2008, 47, 1496–1503. [Google Scholar] [CrossRef]
- Simakov, D.S.A.; Wright, M.M.; Ahmed, S.; Mokheimer, E.M.A.; Román-Leshkov, Y. Solar thermal catalytic reforming of natural gas: A review on chemistry, catalysis and system design. Catal. Sci. Technol. 2015, 5, 1991–2016. [Google Scholar] [CrossRef]
- Agrafiotis, C.; von Storch, H.; Roeb, M.; Sattler, C. Solar thermal reforming of methane feedstocks for hydrogen and syngas production: A review. Renew. Sustain. Energy Rev. 2014, 29, 656–682. [Google Scholar] [CrossRef]
- Al-Ali, K.; Kodama, S.; Kaneko, H.; Sekiguchi, H.; Tamaura, Y.; Chiesa, M. Solar upgrade of methane using dry reforming in direct contact bubble reactor-receiver. In Proceedings of the SolarPACES, Marrakech, Morocco, 11–14 September 2012. [Google Scholar]
- Kodama, T.; Koyanagi, T.; Shimizu, T.; Kityama, Y. CO2 reforming of methane in a molten carbonate salt bath for use in solar thermochemical process. Energy Fuels 2001, 15, 60–65. [Google Scholar] [CrossRef]
- Karni, J.; Kribus, A.; Dorono, P.; Rubin, R.; Titerman, A.; Sagie, D. The DIAPR: A high-pressure, high-temperature solar receiver. J. Sol. Energy Eng. 1997, 119, 74–78. [Google Scholar] [CrossRef]
- Karni, J.; Kribus, A.; Rubin, R.; Dorno, P. The “Porcupine”: A novel high-flux absorber for volumetric solar receivers. J. Sol. Energy Eng. 1998, 120, 85–95. [Google Scholar] [CrossRef] [Green Version]
- Berman, A.; Karn, R.K.; Epstein, M. A new catalyst system for high-tempertuare solar reforming of methane. Energy Fuels 2006, 20, 455–462. [Google Scholar] [CrossRef]
- Abanades, G.; Flamant, G. Hydrogen production from solar thermal dissociation of methane in a high-temperature fluid-wall chemical reactor. Chem. Eng. Process. Process Intensif. 2008, 47, 490–498. [Google Scholar] [CrossRef]
- Hirsch, D.; Steinfeld, A. Solar-hydrogen production by thermal decomposition of natural gas using a vortex-flow reaction. Int. J. Hydrog. Energy 2004, 29, 47–55. [Google Scholar] [CrossRef]
- Dahl, J.K.; Buechler, K.J.; Weimer, A.W.; Lewandowski, A.; Bingham, C. Solar thermal dissociation of methane in a fluid-wall aerosol flow reactor. Int. J. Hydrog. Energy 2004, 29, 725–736. [Google Scholar] [CrossRef]
- Maag, G.; Znganeh, G.; Steinfeld, A. Solar thermal cracking of methane in a particle-flow reactor for the co-production of hydrogen and carbon. Int. J. Hydrog. Energy 2009, 34, 7676–7685. [Google Scholar] [CrossRef]
- Rodat, S.; Abanades, S.; Flamant, G. Experimental evaluation of indirect heating tubular reactors for solar methane pyrolysis. Int. J. Chem. React. Eng. 2010, 8. [Google Scholar] [CrossRef]
- Rodat, S.; Abanades, S.; Flamant, G. Co-production of hydrogen and carbon black from solar thermal methane splitting in a tubular reactor prototype. Sol. Energy 2011, 85, 645–652. [Google Scholar] [CrossRef]
- Rodat, S.; Abanades, S.; Coulie, J.; Flamant, G. Kinetic modelling of methane decomposition in a tubular solar reactor. Chem. Eng. J. 2009, 146, 120–127. [Google Scholar] [CrossRef]
- Yeheskel, J.; Epstein, M. Thermolysis of methane in a solar reactor for mass-production of hydrogen and carbon nano-materials. Carbon 2011, 49, 4695–4703. [Google Scholar] [CrossRef]
- Costandy, J.; El Ghazal, N.; Mohamed, M.T.; Menon, A.; Shilapuram, V.; Ozalp, N. Effect of reactor geometry on the temperature distribution of hydrogen producing solar reactors. Int. J. Hydrog. Energy 2012, 37, 16581–16590. [Google Scholar] [CrossRef]
- Valdés-Parada, F.J.; Romero-Paredes, H.; Espinosa-Paredes, G. Numerical simulation of a tubular solar reactor for methane cracking. Int. J. Hydrog. Energy 2011, 36, 3354–3363. [Google Scholar] [CrossRef]
- Olsvik, O.; Rokstad, O.A.; Holmen, A. Pyrolysis of methane in a presence of hydrogen. Chem. Eng. Technol. 1995, 18, 349–358. [Google Scholar] [CrossRef]
- Holmen, A.; Olsvik, O.; Rostad, O.A. Pyrolysis of natural gas: Chemistry and process concepts. Fuel Process. Technol. 1995, 42, 249–267. [Google Scholar] [CrossRef]
- Bertocchi, R. Carbon particles cloud generation for a solar particle receiver. J. Sol. Energy Eng. 2002, 124, 230–236. [Google Scholar] [CrossRef]
- Bertocchi, R.; Karni, J.; Kribur, A. Experimental evaluation of a non-isothermal high temperature solar particle receiver. Energy 2004, 29, 687–700. [Google Scholar] [CrossRef]
- Fletcher, E.A.; Moen, R.L. Hydrogen and oxygen from water. Science 1977, 197, 1050–1056. [Google Scholar] [CrossRef] [PubMed]
- Ihara, S. On the study of hydrogen production from water using solar thermal energy. Int. J. Hydrog. Energy 1980, 5, 527–534. [Google Scholar] [CrossRef]
- Jellinek, H.H.G.; Kachi, H. The catalytic thermal decomposition of water and the production of hydrogen. Int. J. Hydrog. Energy 1984, 9, 667–688. [Google Scholar] [CrossRef]
- Lede, J.; Lapicque, F.; Villermaux, J. Production of hydrogen by direct thermal decomposition of water. Int. J. Hydrog. Energy 1983, 8, 675–679. [Google Scholar] [CrossRef]
- Kogan, A. Direct solar thermal splitting of water and on-site separation of the products–II experimental feasibility study. Int. J. Hydrog. Energy 1998, 23, 89–98. [Google Scholar] [CrossRef]
- Lede, J.; Villermaux, J.; Quazene, R.; Hossain, M.A.; Ouahes, R. Production of hydrogen by simple impingement of a turbulent jet of steam upon a high temperature zirconia surface. Int. J. Hydrog. Energy 1987, 12, 3–11. [Google Scholar] [CrossRef]
- Ohya, H.; Yatabe, M.; Aihara, M.; Negishi, Y.; Takeuchi, T. Feasibility of hydrogen production above 2500 K by direct thermal decomposition reaction in membrane reactor using solar energy. Int. J. Hydrog. Energy 2002, 27, 369–376. [Google Scholar] [CrossRef]
- Fan, J.; Ohya, H.; Suga, T.; Ohashi, H.; Yamashita, K.; Tsuchiya, S.; Aihara, M.; Takeuchi, T.; Negishi, Y. High flux zirconia composite membrane for hydrogen separation at elevated temperature. J. Membr. Sci. 2000, 170, 113–125. [Google Scholar] [CrossRef]
- Warner, J.W.; Berry, R.S. Hydrogen separation and the direct high-temperature splitting of water. Int. J. Hydrog. Energy 1986, 11, 91–100. [Google Scholar] [CrossRef]
- Diver, R.B.; Pederson, S.; Kappauf, T.; Fletcher, E.A. Hydrogen and oxygen from water-IV, quenching the effluent from a solar furnace. Energy 1983, 8, 947–955. [Google Scholar] [CrossRef]
- Baykara, S.Z.; Bilgen, E. An overall assessment of hydrogen production by solar water thermolysis. Int. J. Hydrog. Energy 1984, 14, 881–891. [Google Scholar] [CrossRef]
- David, R.; Houzelot, J.L.; Villermaux, J. A novel and simple jet-stirred reactor for homogeneous and heterogeneous reactions with short residence times. Chem. Eng. Sci. 1979, 34, 867–876. [Google Scholar] [CrossRef]
- Kogan, A.; Spiegler, E.; Wolfshtein, M. Direct solar thermal splitting of water and on-site separation of the products. III. Improvement of reactor efficiency by steam entrainment. Int. J. Hydrog. Energy 2000, 25, 739–745. [Google Scholar] [CrossRef]
- Baykara, S.Z. Experimental solar water thermolysis. Int. J. Hydrog. Energy 2004, 29, 1459–1469. [Google Scholar] [CrossRef]
- Bilgen, E.; Ducarroir, M.; Foex, M.; Sibieude, F.; Trombe, F. Use of solar energy for direct and two-step water decomposition cycles. Int. J. Hydrog. Energy 1977, 2, 251–257. [Google Scholar] [CrossRef]
- Olmos, F.; Hennessy, B.P.; Manousiouthakis, I.V.; Somiari, I.; Manousiouthakis, V.I. Thermodynamic feasibility of a water-splitting thermochemical cycle based on sodium carbonate decomposition. Int. J. Hydrog. Energy 2019, 44, 4041–4061. [Google Scholar] [CrossRef]
- Nakamura, T. Hydrogen production from water utilizing solar heat at high temperatures. Sol. Energy 1977, 19, 467–475. [Google Scholar] [CrossRef]
- Steinfeld, A.; Sanders, S.; Palumbo, R. Design aspects of solar thermochemcial engineering - A case study: two-step water-splitting cycle using the Fe3O4/FeO redox system. Sol. Energy 1999, 65, 43–53. [Google Scholar] [CrossRef]
- Sibieude, F.; Ducarroir, M.; Tofighi, A.; Ambriz, J. High-temperature experiments witha solar furnace: Decomposition of Fe3O4, Mn3O4, CdO. Int. J. Hydrog. Energy 1982, 7, 79–88. [Google Scholar] [CrossRef]
- Abandades, S.; Villafan-Vidales, I. CO2 valorisation based on Fe3O4/FeO thermochemical redox reactions using concentrated solar energy. Int. J. Energy Resour. 2013, 37, 598–608. [Google Scholar] [CrossRef]
- Charvin, P.; Abanades, S.; Florent, L.; Flamant, G. Analysis of a solar chemical processes for hydrogen production from water splitting thermochemical cycles. Energy Convers. Manag. 2008, 49, 1547–1556. [Google Scholar] [CrossRef]
- Charvan, P.; Abanades, S.; Lemort, F.; Flamant, G. Hydrogen production by three-step solar thermochemical cycles using hydroxides and metal oxide system. Energy Fuels 2007, 21, 2919–2928. [Google Scholar] [CrossRef]
- Charvin, P.; Abanades, S.; Flamant, G.; Lemort, F. Two-step water splitting thermochemical cycle based on iron oxide redox pair for solar hydrogen production. Energy 2007, 32, 1124–1133. [Google Scholar] [CrossRef]
- Abanades, S.; Flamant, G. Thermochemical hydrogen production from a two-step solar-driven water-splitting cycle based on cerium oxides. Sol. Energy 2006, 80, 1611–1623. [Google Scholar] [CrossRef]
- Kaneko, H.; Miura, T.; Fuse, A.; Ishihara, H.; Taku, S.; Fukuzumi, H. Rotary-type solar reactor for solar hydrogen production with two-step water splitting process. Energy Fuels 2007, 2007, 2287–2293. [Google Scholar] [CrossRef]
- Furler, P.; Scheffe, J.; Gorbar, M.; Moes, L.; Vogt, U.; Steinfeld, A. Solar thermochemical CO2 splitting utilizing a reticulated porous ceria redox system. Energy Fuels 2012, 26, 7051–7059. [Google Scholar] [CrossRef]
- Furler, P.; Scheffe, J.; Steinfeld, A. Syngas production by simultaneous splitting of H2O and CO2 via ceria redox reactions in a high-temperature solar reactor. Energy Environ. Sci. 2012, 5, 6098–6103. [Google Scholar] [CrossRef]
- Steinfeld, A. Solar hydrogen production via a two-step water-splitting thermochemical cycle based on Zn/ZnO redox reactions. Int. J. Hydrog. Energy 2002, 27, 611–619. [Google Scholar] [CrossRef]
- Perkins, C.; Weimer, A. Likely near-term solar-thermal water splitting technologies. Int. J. Hydrog. Energy 2004, 29, 1587–1599. [Google Scholar] [CrossRef]
- Weidenkaff, A.; Steinfeld, A.; Wokaun, A.; Eichler, B.; Reller, A. The direct solar thermal dissociation of ZnO: Condensation and crystallization of Zn in the presence of oxygen. Sol. Energy 1999, 65, 59–69. [Google Scholar] [CrossRef]
- Palumbo, R.; Lede, J.; Boutin, O.; Elorza-Ricart, E.; Steinfeld, A.; Möller, S.; Weidenkaff, A.; Fletcher, E.A.; Bielicki, J. The production of Zn form ZnO in a single step high temperature solar decomposition process. Chem. Eng. Sci. 1998, 53, 2503–2518. [Google Scholar] [CrossRef]
- Lede, J.; Boutin, O.; Elorza-Ricart, E.; Ferrer, M. Solar thermal splitting of zinc oxide: A review of some of the rate controlling factors. J. Sol. Energy Eng. 2001, 123, 91–97. [Google Scholar] [CrossRef]
- Moller, S.; Palumbo, R. The development of a solar chemical reactor for the direct thermal dissociation of zinc oxide. J. Sol. Energy Eng. 2001, 123, 83–90. [Google Scholar] [CrossRef]
- Müller, R.; Haeberling, P.; Palumbo, R.D. Further advances toward the development of a direct heating solar thermal chemical reactor for the thermal dissociation of ZnO(s). Sol. Energy 2006, 80, 500–511. [Google Scholar] [CrossRef]
- Koepf, E.; Advani, S.G.; Steinfeld, A.; Prasad, A.K. A novel beam-down, gravity feed, solar thermochemical receiver/reactor for direct solid particle decomposition: Design, modeling and experimentation. Int. J. Hydrog. Energy 2012, 37, 16871–16887. [Google Scholar] [CrossRef]
- Loutzenhiser, P.G.; Gálvez, M.E.; Hishier, I.; Graf, A.; Steinfeld, A. CO2 splitting in an aerosol flow reactor via two-step Zn/ZnO solar thermochemical cycle. Chem. Eng. Sci. 2010, 65, 1855–1864. [Google Scholar] [CrossRef]
- Abanades, S.; Chambon, M. CO2 dissociation and upgrading from two-step solar thermochemical processes based on ZnO/Zn and SnO2/SnO redox pairs. Energy Fuels 2010, 24, 6667–6674. [Google Scholar] [CrossRef]
- Chambon, M.; Abanades, S.; Flamant, G. Thermal dissociation of compressed ZnO and SnO2 powders in a moving-front solar thermochemical reactor. Environ. Energy Eng. 2011, 57, 2264–2273. [Google Scholar] [CrossRef]
- Perkins, C.; Lichty, P.R.; Weimer, A.W. Thermal ZnO dissociation in a rapid aerosol reactor as a part of a solar hydrogen production. Int. J. Hydrog. Energy 2008, 33, 499–510. [Google Scholar] [CrossRef]
- Chambon, M.; Abanades, S.; Flamant, G. Design of a lab-scale rotary cavity-type solar reactor for continuous thermal dissociation of volatile oxides under reduced pressure. J. Sol. Energy Eng. 2010, 132, 021006. [Google Scholar] [CrossRef]
- Palumbo, R.; Rouanet, A.; Pichelin, G. The solar thermal decomposition of TiO2 above 2200 K and its use in the production of Zn from ZnO. Energy Int. J. 1995, 20, 857–868. [Google Scholar] [CrossRef]
- Alonso, E.; Hutter, C.; Romero, M.; Steinfeld, A.; Gonzalez-Aguilar, J. Kinetics of Mn2O3-Mn3O4 redox reactions performed under concentrated thermal radiative flux. Energy Fuels 2013, 27, 4884–4890. [Google Scholar] [CrossRef]
- Charvin, P.; Abanades, S.; Lemont, F.; Flamant, G. Experimental study of SnO2/SnO/Sn thermochemical systems for solar production of hydrogen. AIChE J. 2008, 54, 2759–2767. [Google Scholar] [CrossRef]
- Abanades, S. CO2 and H2O reduction by solar thermochemical looping using SnO2/SnO redox reactions: Thermogravimetric analysis. Int. J. Hydrog. Energy 2012, 37, 8223–8231. [Google Scholar] [CrossRef]
- Kaneko, H.; Yokoyama, T.; Fuse, A.; Ishihar, H.; Hasegawa, N.; Tamaura, Y. Synthesis of new ferrite, Al-Cu ferrite, and its oxygen deficiency for solar H2 generation from H2O. Int. J. Hydrog. Energy 2006, 31, 2256–2265. [Google Scholar] [CrossRef]
- Kodama, T.; Kondoh, Y.; Yamamoto, R.; Andou, H.; Satou, N. Thermochemical hydrogen production by a redox system of ZrO2-supported Co(II)-ferrite. Sol. Energy 2005, 78, 623–631. [Google Scholar] [CrossRef]
- Alvani, A.; Enna, G.; La Barbera, A.; Marongiu, G.; Padella, F.; Varsano, F. Synthesis and characterization of nanocrystalline MnFe2O4: Advances in thermochemical water splitting. Int. J. Hydrog. Energy 2005, 30, 1407–1411. [Google Scholar] [CrossRef]
- Tamaura, Y.; Ueda, Y.; Matsunami, J.; Hasegawa, N.; Nezuka, M.; Sano, T.; Tsuji, M. Solar hydrogen production by using ferrites. Sol. Energy 1999, 65, 55–57. [Google Scholar] [CrossRef]
- Varsano, F.; Padella, F.; Alvani, C.; Bellusci, M.; La Barbera, A. Chemical aspects of the water-splitting thermochemical cycle based on sodium manganese ferrite. Int. J. Hydrog. Energy 2012, 37, 11595–11601. [Google Scholar] [CrossRef]
- Varsano, F.; Murmura, M.A.; Brunetti, B.; Padella, F.; La Barbera, A.; Alvani, C.; Annesini, M.C. Hydrogen production by water splitting on manganese ferrite-sodium carbonate mixture: Feasibility tests in a packed bed solar reactor-receiver. Int. J. Hydrog. Energy 2014, 39, 20920–20929. [Google Scholar] [CrossRef]
- Murmura, M.A.; Varsano, F.; Padella, F.; La Barbera, A.; Alvani, C.; Annesini, M.C. Hydrogen production by the sodium manganese ferrite thermochemical cycle-experimental rate and modeling. Ind. Eng. Chem. Res. 2014, 53, 10310–10317. [Google Scholar] [CrossRef]
- Hoskins, A.L.; Millican, S.L.; Czernik, C.E.; Alshankiti, I.; Netter, J.C.; Wendelin, T.J.; Musgrave, C.B.; Weimer, A.W. Continuous on-sun solar thermochemical hydrogen production via an isothermal redox cycle. Appl. Energy 2019, 249, 368–376. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Dey, S. Solar thermochemical splitting of water to generate hydrogen. Proc. Natl. Acad. Sci. USA 2017, 114, 13385–13393. [Google Scholar] [CrossRef] [Green Version]
- Roeb, M.; Sattler, C. Isothermal water splitting. Science 2013, 341, 470–471. [Google Scholar] [CrossRef]
- Muhich, C.L.; Evanko, B.W.; Weston, K.C.; Lichty, P.; Liang, X.; Martinek, J.; Musgrave, C.B.; Weimer, A.W. Efficient generation of H2 by splitting water with and isothermal redox cycle. Science 2013, 341, 540–542. [Google Scholar] [CrossRef]
- Alshankiti, I.; Ehrhart, B.D.; Weimer, A.W. Isothermal redox for H2O and CO2 splitting - a review and perpective. Sol. Energy 2017, 156, 21–29. [Google Scholar] [CrossRef]
- Brecher, L.E.; Spewock, S.; Warde, C.J. The Westinghouse sulfur cycle for the thermochemical decomposition of water. Int. J. Hydrog. Energy 1977, 2, 7–15. [Google Scholar] [CrossRef]
- Huang, C.; Raissi, A.T. Analysis of sulfur-iodine thermochemical cycle for solar hydrogen production. Part I:decomposition of sulfuric acis. Sol. Energy 2005, 78, 632–646. [Google Scholar] [CrossRef]
- Xu, B.; Bhawe, Y.; Davis, M.E. Spinel metal oxide-alkali carbonate-based, low-temperature thermochemical cycles for water splitting and CO2 reduction. Chem. Mater. 2013, 25, 1564–1571. [Google Scholar] [CrossRef] [Green Version]
- Kreider, P.B.; Funke, H.H.; Cuche, K.; Schmidt, M.; Steinfeld, A.; Weimer, A.W. Manganese oxide based thermochemical hydrogen production cycle. Int. J. Hydrog. Energy 2011, 36, 7028–7037. [Google Scholar] [CrossRef]
- Dey, S.; Rajesh, S.; Rao, C.N.R. Significant reduction in the operating temperature of the Mn(II)/Mn(III) oxide-based thermochemical water splitting cycle brought about by the use of nanoparticles. J. Mater. Chem. A 2016, 4, 16830–16833. [Google Scholar] [CrossRef]
- Muhich, C.L.; Ehrhart, B.D.; Alshankiti, I.; Ward, B.J.; Musgrave, C.B.; Weimer, A.W. A review and perspective of efficient hydrogen generation via solar thermal water splitting. WIREs Energy Environ. 2016, 5, 261–287. [Google Scholar] [CrossRef]
- Agrafiotis, C.; Roeb, M.; Konstandopoulos, A.G.; Nalbandian, L.; Zaspalis, V.T.; Sattler, C.; Stobbe, P.; Steeled, A.M. Solar water splitting for hydrogen production with monolithic reactors. Sol. Energy 2005, 79, 409–421. [Google Scholar] [CrossRef]
- Lanchi, M.; Varsano, F.; Brunetti, B.; Murmura, M.A.; Annesini, M.C.; Turchetti, L.; Grena, R. Thermal characterization of a cavity receiver for hydrogen production by thermochemical cycles operating at moderate temperatures. Sol. Energy 2013, 92, 256–268. [Google Scholar] [CrossRef]
- Martinek, J.; Viger, R.; Weimer, A.W. Transient simulation of a tubular packed bed solar receiver for hydrogen generation via metal oxide thermochemical cycles. Sol. Energy 2014, 105, 613–631. [Google Scholar] [CrossRef]
- Lichty, P.; Perkins, C.; Woodruff, B.; Bingham, C.; Weimer, A. Rapid high temperature solar thermal biomass gasification in a prototype cavity reactor. J. Sol. Energy Eng. 2010, 132, 011012. [Google Scholar] [CrossRef]
- Martinek, J.; Weimer, A.W. Design considerations for a multiple tube solar reactor. Sol. Energy 2013, 90, 68–83. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Sun, J.; Lei, J.; Ju, Y.; Jin, H. A new solar receiver/reactor structure for hydrogen production. Energy Convers. Manag. 2017, 133, 118–126. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Y.; Lei, J.; Jin, H. Numerical investigation of the thermophysical characteristics of the mid-and-low temperature solar receiver/reactor for hydrogen production. Int. J. Heat Mass Transf. 2016, 97, 379–390. [Google Scholar] [CrossRef]
- Z’Graggen, A.; Steinfeld, A. Hydrogen production by steam-gasification of carbonaceous materials using concentrated solar energy–V. Reactor modeling, optimization, and scale-up. Int. J. Hydrog. Energy 2008, 33, 5484–5492. [Google Scholar] [CrossRef]
- Z’Graggen, A.; Haueter, P.; Trommer, D.; Romero, M.; De Jesus, J.C.; Steinfeld, A. Hydrogen production by steam-gasification of petroleum coke using concentrated solar powe – II Reactor design, testing, and modeling. Int. J. Hydrog. Energy 2006, 31, 797–811. [Google Scholar] [CrossRef]
- Z’Graggen, A.; Haueter, P.; Maag, G.; Vidal, A.; Romero, M.; Steinfeld, A. Hydrogen production by steam-gasification of petroleum coke using concentrated solar power–III. Reactor experimentation with slurry feeding. Int. J. Hydrog. Energy 2007, 32, 992–996. [Google Scholar] [CrossRef]
- Bader, R.; Bala Chandran, R.; Venstrom, L.J.; Sedler, S.J.; Krenzke, P.T.; De Smith, R.M.; Banerjee, A.; Chase, T.R.; Davidson, J.H.; Lipiński, W. Design of a solar reactor to split CO2 via isothermal redox cycling of Ceria. J. Sol. Energy Eng. 2015, 137, 031007. [Google Scholar] [CrossRef]
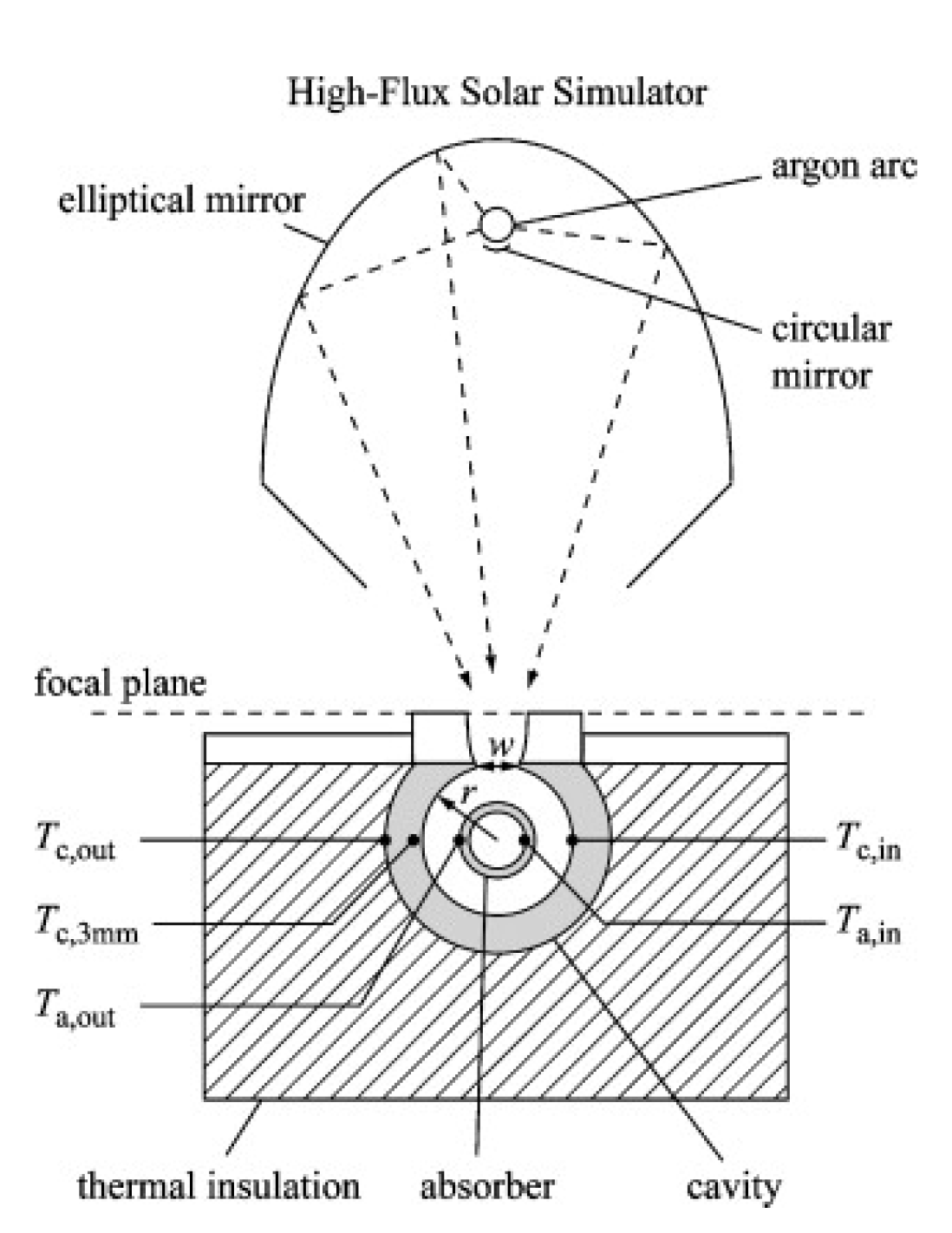
- Krueger, K.R.; Davidson, J.H.; Lipinski, W. Design of a new 45 kWe high-flux solar simulator for high-temperature solar thermal and thermochemical research. J. Sol. Energy Eng. 2011, 133, 011013. [Google Scholar] [CrossRef] [Green Version]
- Krueger, K.R.; Lipinski, W.; Davidson, J.H. Operational performance of the University of Minnesota 45 kWe high-flux solar simulator. J. Sol. Energy Eng. 2013, 135, 044501. [Google Scholar] [CrossRef]
- Kogan, A.; Kogan, M. The tornado flow configuration – an effective methof for screening of a solar reactor window. J. Sol. Energy Eng. 2002, 124, 206–214. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murmura, M.A.; Annesini, M.C. Methodologies for the Design of Solar Receiver/Reactors for Thermochemical Hydrogen Production. Processes 2020, 8, 308. https://doi.org/10.3390/pr8030308
Murmura MA, Annesini MC. Methodologies for the Design of Solar Receiver/Reactors for Thermochemical Hydrogen Production. Processes. 2020; 8(3):308. https://doi.org/10.3390/pr8030308
Chicago/Turabian StyleMurmura, M.A., and M.C. Annesini. 2020. "Methodologies for the Design of Solar Receiver/Reactors for Thermochemical Hydrogen Production" Processes 8, no. 3: 308. https://doi.org/10.3390/pr8030308
APA StyleMurmura, M. A., & Annesini, M. C. (2020). Methodologies for the Design of Solar Receiver/Reactors for Thermochemical Hydrogen Production. Processes, 8(3), 308. https://doi.org/10.3390/pr8030308





