Integrating Support Vector Regression with Genetic Algorithm for Hydrate Formation Condition Prediction
Abstract
:1. Introduction
2. Theoretical Basis
- (1)
- Random chromosome coding of individuals in the initial population using the binary principle to form a genotype string that mimics the chromosome of a biological gene, which is an individual in the biological population.
- (2)
- On the basis of step 1), the N initial genotype character strings are randomly generated to form an initial population containing N individuals.
- (3)
- The fitness function is defined, and the superiority and inferiority of the individuals in the population are evaluated (i.e., the solution of optimised parameters) by calculating the fitness values of the individuals.
- (4)
- Individuals are selected with a certain probability based on the fitness value. a smaller fitness value corresponds to a higher probability of being selected for the next-generation population.
- (5)
- On the basis of step (4), the individuals of the population are optimised through crossover and mutation with a certain probability to obtain individuals with better adaptability.
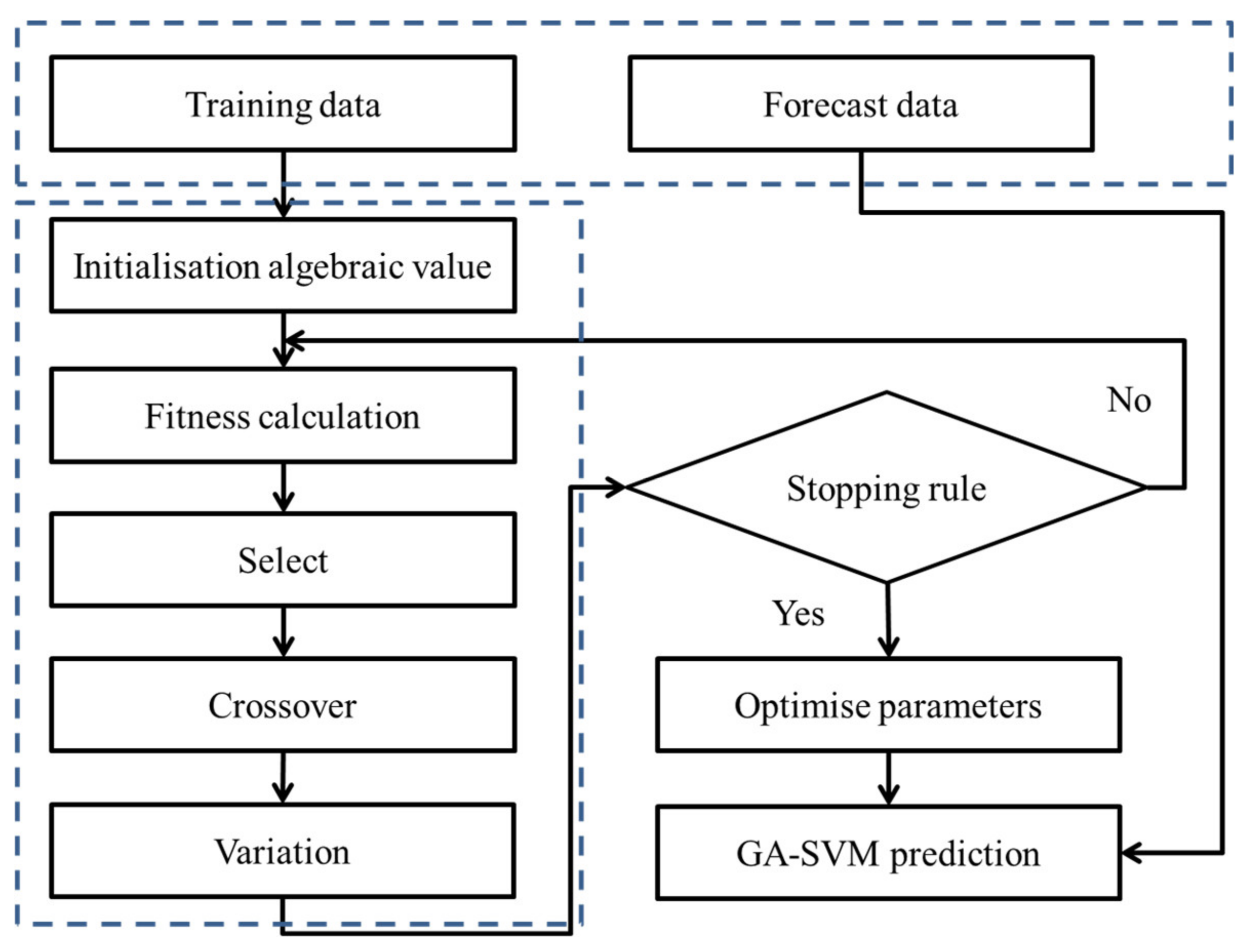
3. Model Building
3.1. Dataset and Variable Selection
3.2. Model Parameter Optimisation
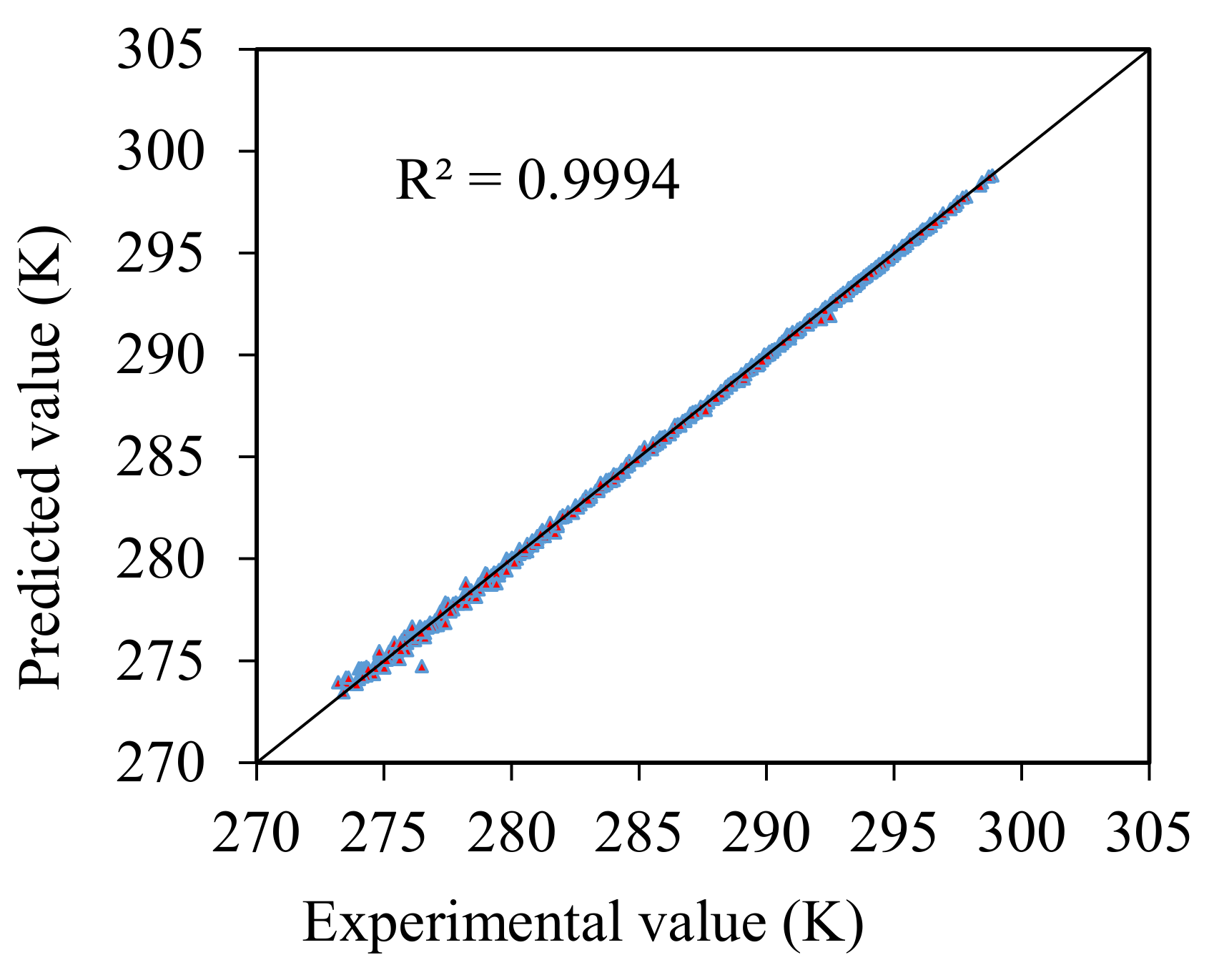
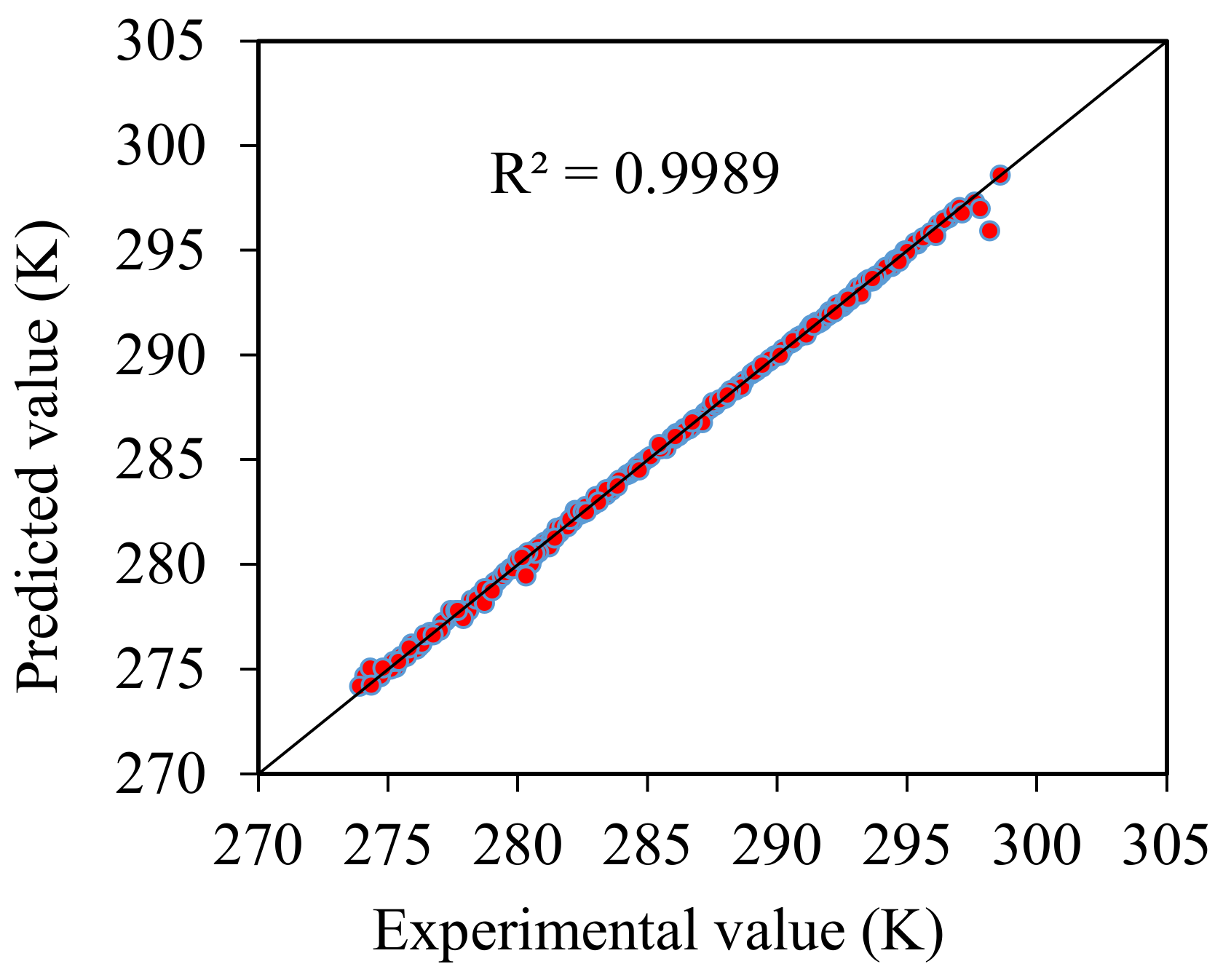
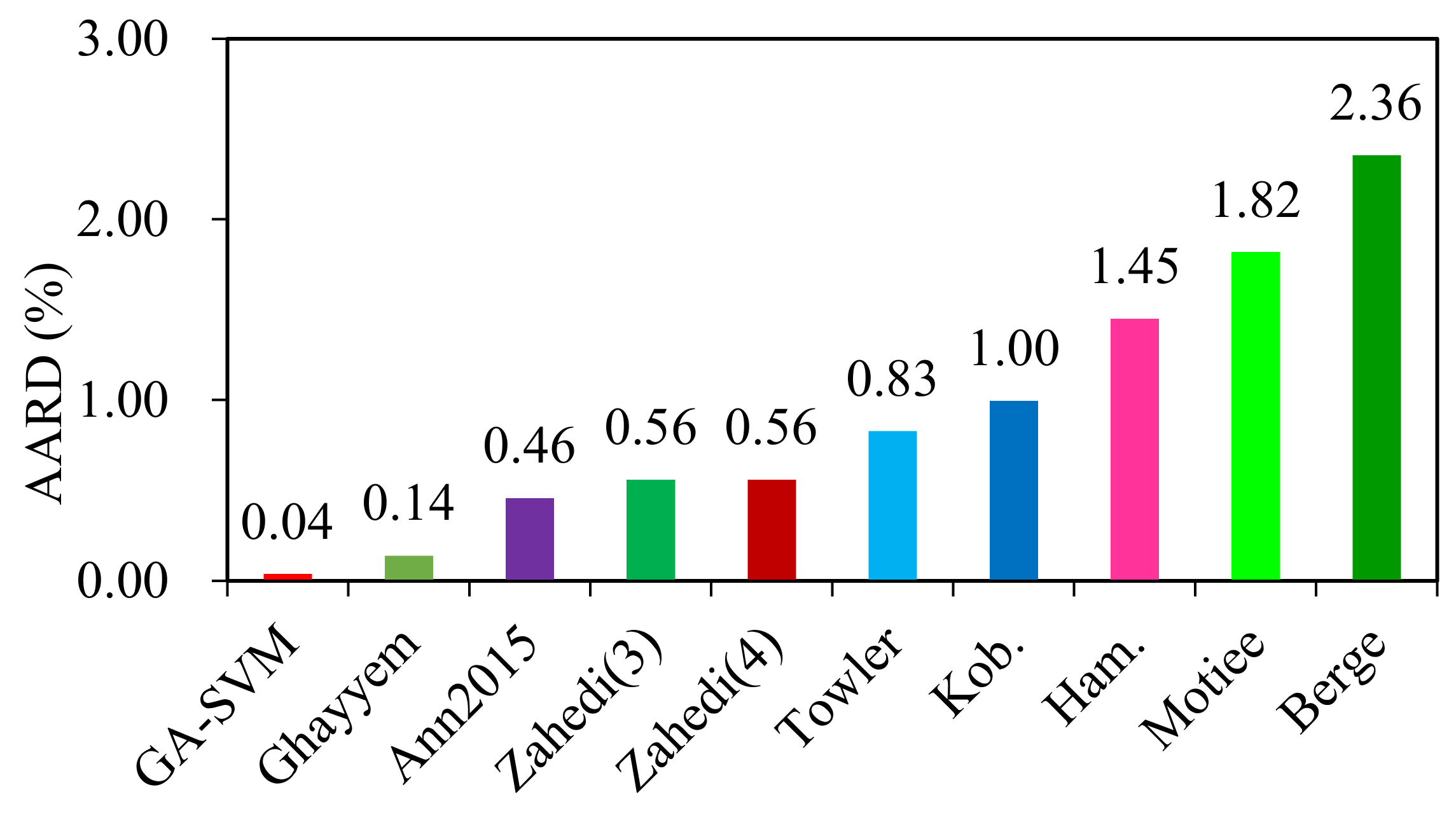
4. Analysis of Results
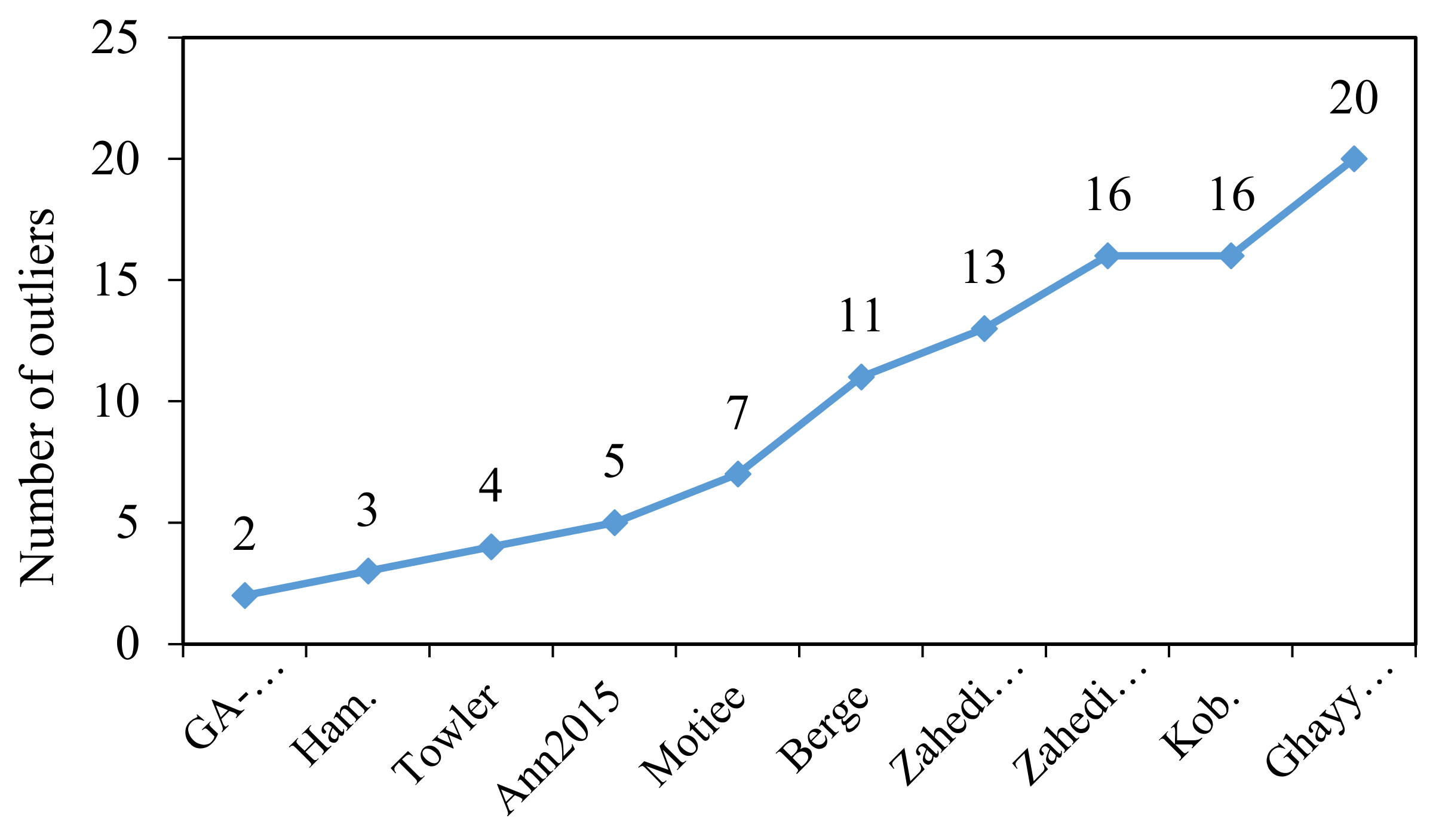
5. Outlier Detection
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Naeiji, P.; Varaminian, F. Experimental study and kinetics modeling of gas hydrate formation of methane-ethane mixture. J. Non-Equilib. Thermodyn. 2013, 38, 273–286. [Google Scholar]
- Kar, S.; Kakati, H.; Mandal, A.; Laik, S. Experimental and modeling study of kinetics for methane hydrate formation in a crude oil-in-water emulsion. Pet. Sci. 2016, 13, 489–495. [Google Scholar]
- Wu, W.; Guan, J.; Liang, D. The experimental research for structure H hydrate formation. J. Eng. Thermophys. 2018, 44–48. [Google Scholar]
- Mottahedin, M.; Varaminian, F.; Mafakheri, K. Modeling of methane and ethane hydrate formation kinetics based on non-equilibrium thermodynamics. J. Non-Equilib. Thermodyn. 2011, 36, 3–22. [Google Scholar]
- Obanijesu, E.O.; Gubner, R.; Barifcani, A.; Pareek, V.; Tade, M.O. The influence of corrosion inhibitors on hydrate formation temperature along the subsea natural gas pipelines. J. Pet. Sci. Eng. 2014, 120, 239–252. [Google Scholar]
- Ma, S.; Huang, J.; Zhang, F. Prediction and prevention of hydrate forming in deep water gas well test. J. Xi’an Shiyou Univ. 2017, 6, 93–98. [Google Scholar]
- Ghavipour, M.; Ghavipour, M.; Chitsazan, M.; Najibi, S.H.; Ghidary, S.S. Experimental study of natural gas hydrates and a novel use of neural network to predict hydrate formation conditions. Chem. Eng. Res. Des. 2013, 91, 264–273. [Google Scholar]
- Rashid, S.; Fayazi, A.; Harimi, B.; Hamidpour, E.; Younesi, S. Evolving a robust approach for accurate prediction of methane hydrate formation temperature in the presence of salt inhibitor. J. Nat. Gas Sci. Eng. 2014, 18, 194–204. [Google Scholar]
- Gai, S. Study on the Formation Mechanism and Forecast of Gas Hydrate in Gas Well Borehole in the Sulige Gasfield. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2008. [Google Scholar]
- Bahadori, A.; Vuthaluru, H.B. A novel correlation for estimation of hydrate forming condition of natural gases. J. Nat. Gas Chem. 2009, 18, 453–457. [Google Scholar]
- Ghayyem, M.; Izadmehr, M.; Tavakoli, R. Developing a simple and ac-curate correlation for initial estimation of hydrate formation tempera-ture of sweet natural gases using an eclectic approach. J. Nat. Gas Sci. Eng. 2014, 21, 184–192. [Google Scholar]
- Amin, J.S.; Nejad, S.K.B.; Veiskarami, M.; Bahadori, A. Prediction of hydrate formation temperature based on an improved empirical correlation by imperialist competitive algorithm. Pet. Sci. Technol. 2016, 34, 162–169. [Google Scholar]
- Guo, P.; Ran, W.; Liu, H. Research advance of the prediction of nature gas hydrate formation condition. Sci. Technol. Eng. 2018, 18, 138–144. [Google Scholar]
- Yu, X.; Zhao, J.; Guo, J. Comparison of prediction models for gas hydrate formation conditions. Oil Gas Storage Transport. 2002, 20–24. [Google Scholar]
- Pi, Y.; Liao, K.; Sun, O. Prediction model for natural gas hydrate formation conditions and applicability evaluation. Nat. Gas Oil 2012, 30, 16–18. [Google Scholar]
- Klauda, J.B.; Sandler, S.I. A Fugacity Model for Gas Hydrate Phase Equilibria. Ind. Eng. Chem. Res. 2000, 39, 3377–3386. [Google Scholar]
- Mekala, P.; Sangwai, J.S. Prediction of phase equilibrium of clathrate hydrates of multicomponent natural gases containing CO2 and H2S. J. Petroleum Sci. Eng. 2014, 116, 81–89. [Google Scholar]
- Gao, L.; Zhang, Y.; Zheng, Y. Study on the forecasting model and control of hydrate in gas pipelines. Contemp. Chem. Ind. 2018, 47, 360–364. [Google Scholar]
- Bian, X.; Han, B.; Du, Z. Prediction of hydrate formation condition of sour natural gases by using support vector machine (SVM). China Sci. 2016, 11, 1017–1020. [Google Scholar]
- Mesbah, M.; Soroush, E.; Rezakazemi, M. Development of a least squares support vector machine model for prediction of natural gas hydrate formation temperature. Chin. J. Chem. Eng. 2017, 25, 1238–1248. [Google Scholar]
- Akbari, M.; Saedodin, S.; Panjehpour, A.; Hassani, M.; Afrand, M.; Torkamany, M.J. Numerical simulation and designing artificial neural network for estimating melt pool geometry and temperature distribution in laser welding of Ti6Al4V alloy. Opt. Int. J. Light Electron Opt. 2016, 127, 11161–11172. [Google Scholar]
- Zahedi, G.; Karami, Z.; Yaghoobi, H. Prediction of hydrate formation temperature by both statistical models and artificial neural network approaches. Energy Convers. Manag. 2009, 50, 2052–2059. [Google Scholar]
- ZareNezhad, B.; Aminian, A. Accurate prediction of sour gas hydrate equilibrium dissociation conditions by using an adaptive neuro fuzzy inference system. Energy Convers. Manag. 2012, 57, 143–147. [Google Scholar]
- Bian, X.Q.; Han, B.; Du, Z.M.; Jaubert, J.N.; Li, M.J. Integrating support vector regression with genetic algorithm for CO2-oil minimum miscibility pressure (MMP) in pure and impure CO2 streams. Fuel 2016, 182, 550–557. [Google Scholar]
- Boyle, B.H. Support Vector Machines: Data Analysis, Machine Learning, and Applications; Nova Science Publishers: Freiburg, Germany, 2011. [Google Scholar]
- Han, B. Theoretical Model of Saturaetd Water Content in High Temperature and Pressure Sour Natural Gas. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2017. [Google Scholar]
- Burges, C.J.C. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar]
- Darrell, W. A Genetic Algorithm Tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar]
- Chen, K.Y. Forecasting systems reliability based on support vector regression with genetic algorithms. Reliab. Eng. Syst. Saf. 2007, 92, 423–432. [Google Scholar]
- Eslamimanesh, A.; Gharagheizi, F.; Mohammadi, A.H.; Richon, D. A statistical method for evaluation of the experimental phase equilibrium data of simple clathrate hydrates. Chem. Eng. Sci. 2012, 80, 402–408. [Google Scholar]
- Sun, C.Y.; Chen, G.J.; Lin, W.; Guo, T.M. Hydrate formation conditions of sour natural gases. J. Chem. Eng. Data 2003, 48, 600–602. [Google Scholar]
- Sorousha, E.; Mesbahb, M.; Shokrollahib, A.; Rozync, J.; Leed, M.; Kashiwaoe, T.; Bahadoric, A. Evolving a robust modeling tool for prediction of natural gas hydrate formation conditions. Unconv. Oil Gas Resour. 2015, 12, 45–55. [Google Scholar]
- Towler, B.F.; Mokhatab, S. Quickly estimate hydrate formation conditions in natural gases. Hydrocarb. Process. 2005, 84, 61–62. [Google Scholar]
- Kobayashi, R.; Song, K.Y.; Sloan, E.D. Phase behavior of water/hydrocarbon systems. Pet. Eng. Handb. 1987, 25, 12–14. [Google Scholar]
- Hammerschmidt, E.G. Formation of gas hydrates in natural gas transmission lines. J. Ind. Eng. Chem. 1934, 26, 851–855. [Google Scholar]
- Motiee, M. Estimate possibility of hydrates. Hydrocarb. Process 1991, 70, 98–99. [Google Scholar]
- Berge, B.K. Hydrate Prediction on a Microcomputer; SPE-15306-MS; Society of Petroleum Engineers: Denver, CO, USA, 1986; pp. 213–224. [Google Scholar]
- Robinson, D.B.; Hutton, J.B. Hydrate formation in systems containing methane, hydrogen sulphide and carbon dioxide. J. Can. Pet. Technol. 1967, 6, 6–9. [Google Scholar]

| Variable | Relative Molecular Weight of Gas Sample (g/mol) | Pressure (KPa) | Temperature (K) |
|---|---|---|---|
| Range | 15.64–28.97 | 367.65–33,948.90 | 273.20–298.84 |
| Parameter Type | Optimise Parameters | Parameter Value (Range) |
|---|---|---|
| Variable value | Input data form | [−1,1] |
| genetic algorithm (GA) parameters | Evolutionary algebra | 200 |
| Population size | 20 | |
| Selection probability | 0.9 | |
| Cross probability | 0.7 | |
| Mutation probability | 0.035 | |
| support vector machine (SVM) parameters | Best C | 854.8931 |
| Best ε | 0.003592 | |
| Best γ | 9.1190 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Zhu, S.; Li, C.; Han, B. Integrating Support Vector Regression with Genetic Algorithm for Hydrate Formation Condition Prediction. Processes 2020, 8, 519. https://doi.org/10.3390/pr8050519
Cao J, Zhu S, Li C, Han B. Integrating Support Vector Regression with Genetic Algorithm for Hydrate Formation Condition Prediction. Processes. 2020; 8(5):519. https://doi.org/10.3390/pr8050519
Chicago/Turabian StyleCao, Jie, Shijie Zhu, Chao Li, and Bing Han. 2020. "Integrating Support Vector Regression with Genetic Algorithm for Hydrate Formation Condition Prediction" Processes 8, no. 5: 519. https://doi.org/10.3390/pr8050519
APA StyleCao, J., Zhu, S., Li, C., & Han, B. (2020). Integrating Support Vector Regression with Genetic Algorithm for Hydrate Formation Condition Prediction. Processes, 8(5), 519. https://doi.org/10.3390/pr8050519





