Extensional Magnetorheology as a Tool for Optimizing the Formulation of Ferrofluids in Oil-Spill Clean-Up Processes
Abstract
1. Introduction
2. Materials and Methods
2.1. Fluids
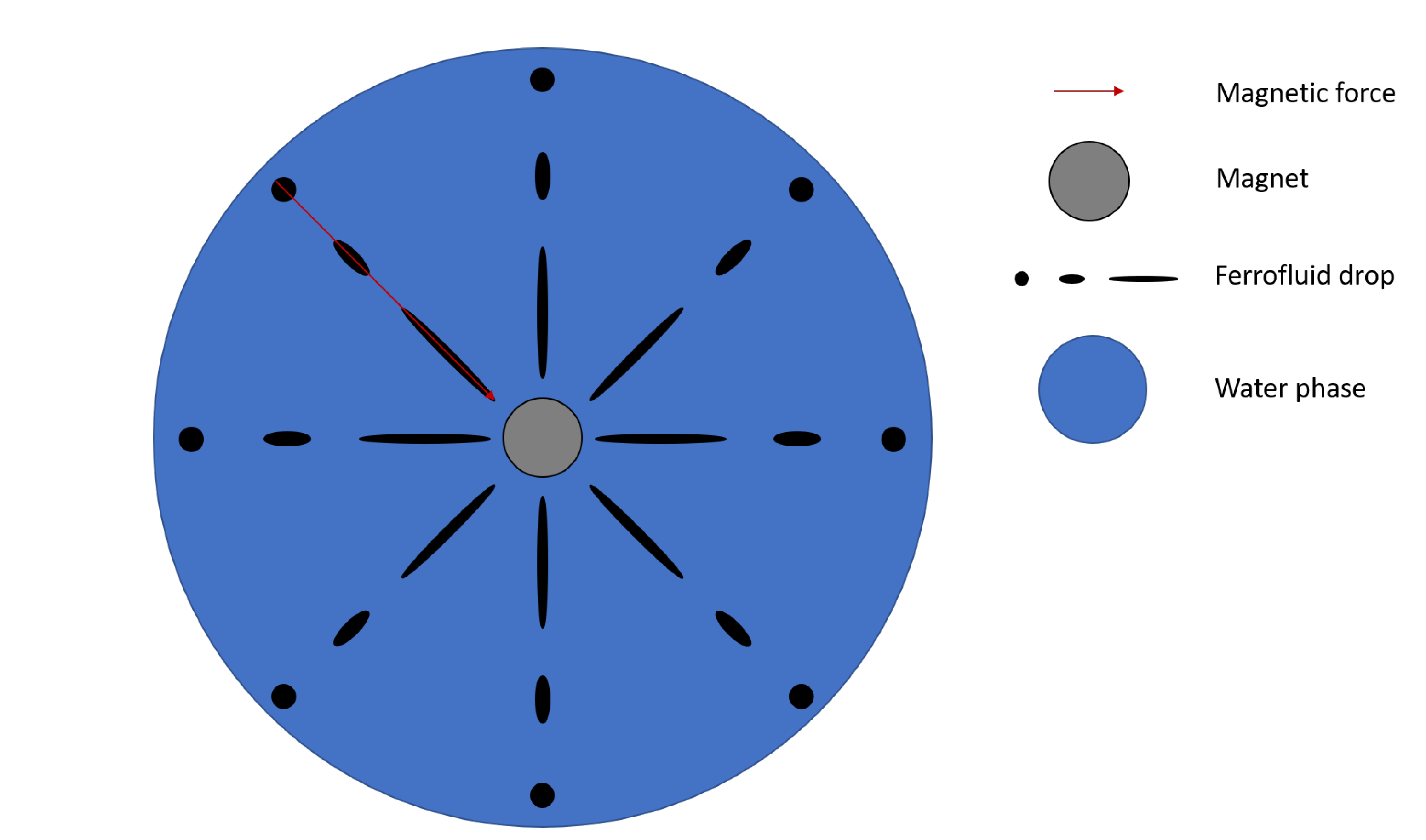
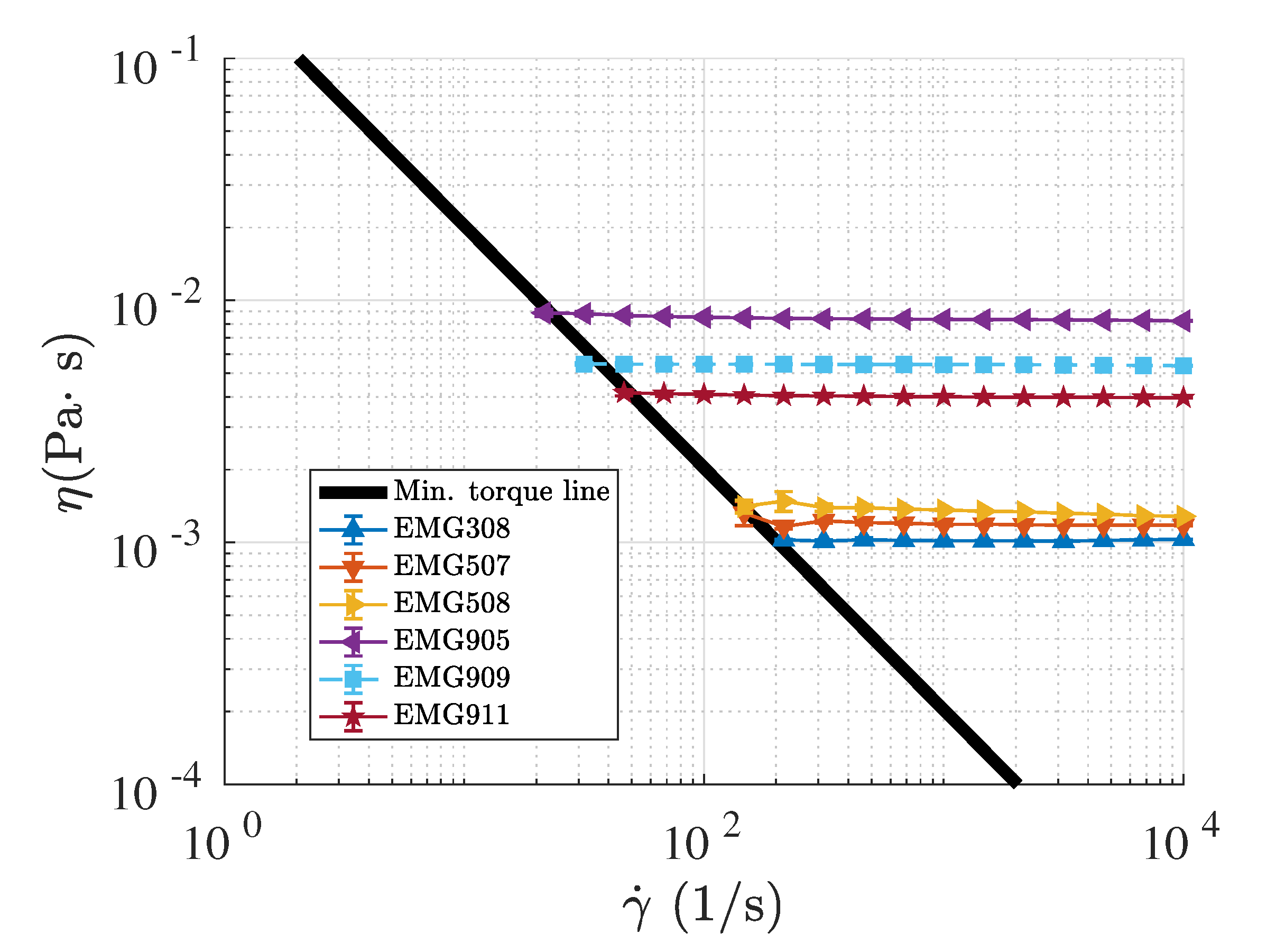
2.2. Capillary Breakup Extensional Magneto-Rheometry
Slow Retraction Method (SRM)
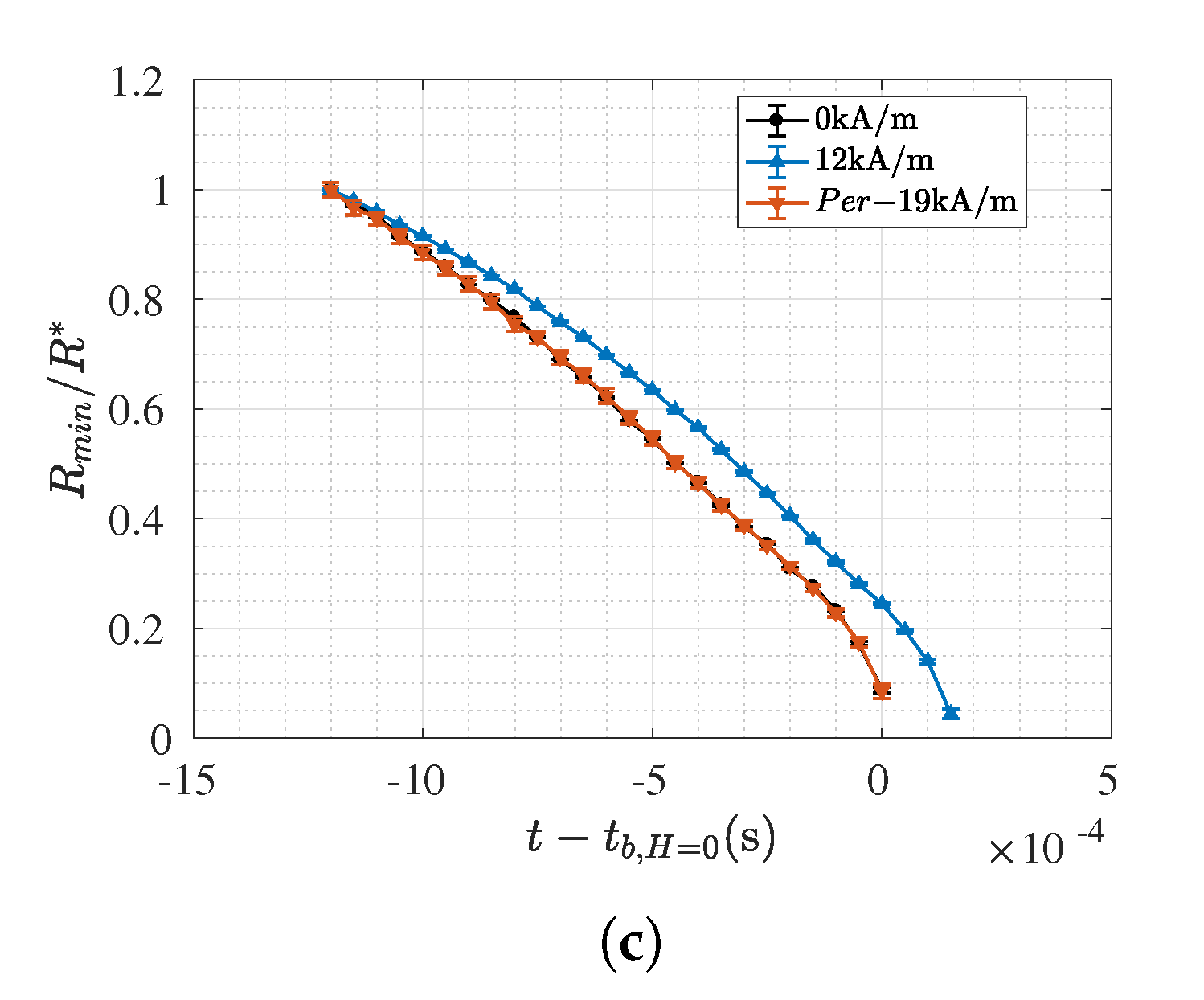
3. Results and Discusion
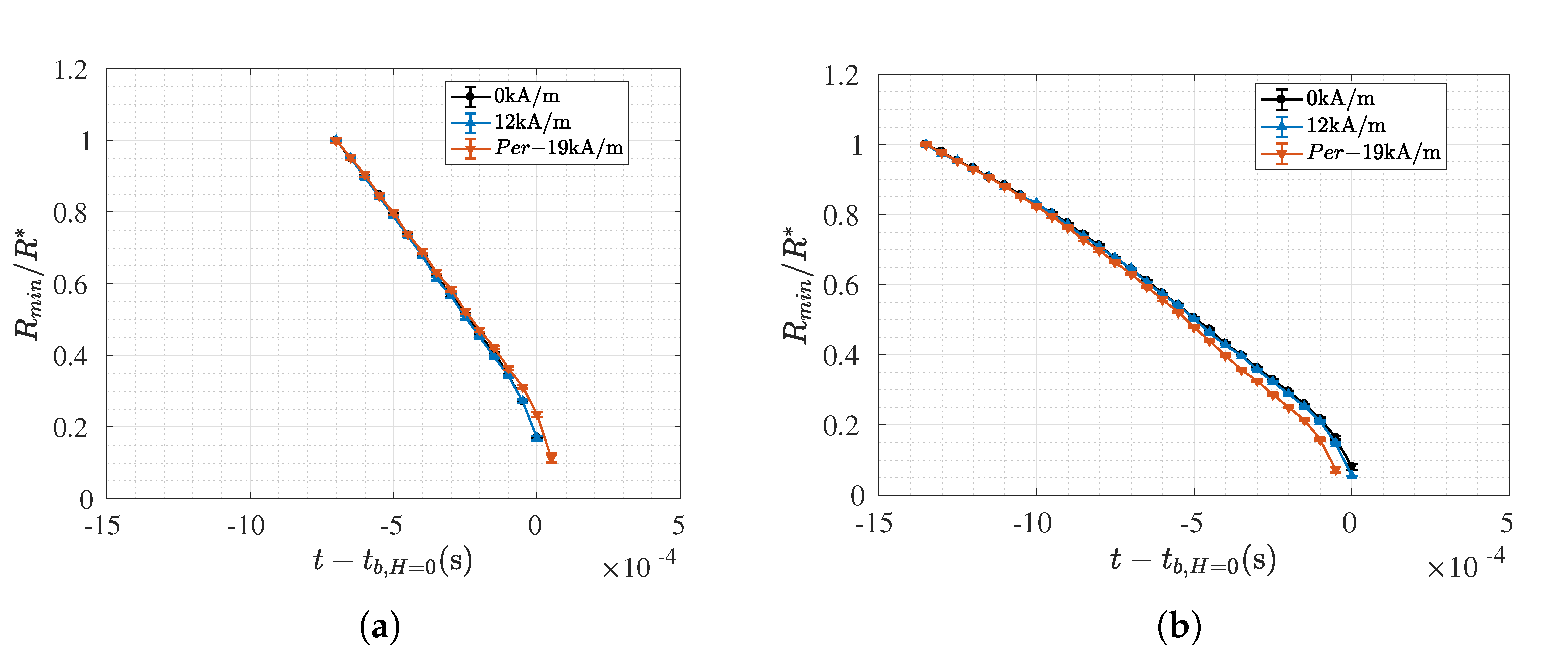
3.1. Oil Based Samples
3.2. Water Based Samples
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CaBER | Capillary Breakup Extensional Rheometer |
| ExMRFx | Extensional Magneto-Rheological Fixture |
| FFs | Ferrofluids |
| SRM | Slow Retraction Method |
| MVE | Magnetoviscous effect |
| eMVE | extensional Magnetoviscous effect |
References
- Konishi, M.; Kishimoto, M.; Tamesui, N.; Omasa, T.; Shioya, S.; Ohtake, H. The separation of oil from an oil–water–bacteria mixture using a hydrophobic tubular membrane. Biochem. Eng. J. 2005, 24, 49–54. [Google Scholar] [CrossRef]
- Carrier, G.; Fendell, F.; Mitchell, J. In Situ burning via towed boom of oil spilled at sea. Combust. Flame 1992, 90, 295–306. [Google Scholar] [CrossRef]
- Araruna, J.; Portes, V.; Soares, A.; Silva, M.; Sthel, M.; Schramm, D.; Tibana, S.; Vargas, H. Oil spills debris clean up by thermal desorption. J. Hazard. Mater. 2004, 110, 161–171. [Google Scholar] [CrossRef] [PubMed]
- Darmanin, T.; Nicolas, M.; Guittard, F. Electrodeposited polymer films with both superhydrophobicity and superoleophilicity. Phys. Chem. Chem. Phys. 2008, 10, 4322–4326. [Google Scholar] [CrossRef]
- Teas, C.; Kalligeros, S.; Zanikos, F.; Stournas, S.; Lois, E.; Anastopoulos, G. Investigation of the effectiveness of absorbent materials in oil spills clean up. Desalination 2001, 140, 259–264. [Google Scholar] [CrossRef]
- Zahn, M.; Alan Hatton, T.; Shahriar Rhointon, K. Magnetic collid petroleum oil Spill clean-up of ocean surface, depth, and shore regions. Patent WO 2012/115814 A1, 14 February 2012. [Google Scholar]
- Papell, S.S. Low viscosity magnetic fluid obtained by the colloidal suspension of magnetic particles. U.S. Patent 3,215,572, 2 November 1965. [Google Scholar]
- Charles, S.W. The Preparation of Magnetic Fluids. In Ferrofluids: Magnetically Controllable Fluids and Their Applications; Odenbach, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 3–18. [Google Scholar] [CrossRef]
- Taylor, R.; Coulombe, S.; Otanicar, T.; Phelan, P.; Gunawan, A.; Lv, W.; Rosengarten, G.; Prasher, R.; Tyagi, H. Small particles, big impacts: A review of the diverse applications of nanofluids. J. Appl. Phys. 2013, 113, 011301. [Google Scholar] [CrossRef]
- Voit, W.; Kim, D.K.; Zapka, W.; Muhammed, M.; Rao, K.V. Magnetic behavior of coated superparamagnetic iron oxide nanoparticles in ferrofluids. MRS Proc. 2001, 676, Y7.8. [Google Scholar] [CrossRef]
- Shahrivar, K.; Morillas, J.R.; Luengo, Y.; Gavilan, H.; Morales, P.; Bierwisch, C.; de Vicente, J. Rheological behavior of magnetic colloids in the borderline between ferrofluids and magnetorheological fluids. J. Rheol. 2019, 63, 547–558. [Google Scholar] [CrossRef]
- Behrens, S.; Bönnemann, H.; Matoussevitch, N.; Modrow, H.; Kempter, V.; Riehemann, W.; Wiedenmann, A.; Odenbach, S.; Will, S.; Eberbeck, D.; et al. Colloidal Magnetic Fluids: Basics, Development and Application of Ferrofluids; Springer: Berlin/Heidelberg, Germany, 2009; p. 430. [Google Scholar] [CrossRef]
- Iglesias, G.; López-López, M.; Delgado, A.; Durán, J. Description and performance of a fully automatic device for the study of the sedimentation of magnetic suspensions. Rev. Sci. Instruments 2011, 82. [Google Scholar] [CrossRef]
- López-López, M.T.; Gómez-Ramírez, A.; Rodríguez-Arco, L.; Durán, J.D.G.; Iskakova, L.; Zubarev, A. Colloids on the Frontier of Ferrofluids. Rheological Properties. Langmuir 2012, 28, 6232–6245. [Google Scholar] [CrossRef]
- Nogueras-Lara, F.; Rodríguez-Arco, L.; López-López, M.T. Dynamics of magnetic assembly of binary colloidal structures. EPL 2015, 111, 37002. [Google Scholar] [CrossRef]
- Mohammadfam, Y.; Heris, S.Z.; Khazini, L. Experimental Investigation of Fe3O4/hydraulic oil magnetic nanofluids rheological properties and performance in the presence of magnetic field. Tribol. Int. 2020, 142, 105995. [Google Scholar] [CrossRef]
- Hong, R.; Ren, Z.; Han, Y.; Li, H.; Zheng, Y.; Ding, J. Rheological properties of water-based Fe3O4 ferrofluids. Chem. Eng. Sci. 2007, 62, 5912–5924. [Google Scholar] [CrossRef]
- Susan-Resiga, D.; Vékás, L. Ferrofluid based composite fluids: Magnetorheological properties correlated by Mason and Casson numbers. J. Rheol. 2017, 61, 401–408. [Google Scholar] [CrossRef]
- Zhenkun, l.; Yao, J.; Li, D. Research on the Rheological Properties of a Perfluoropolyether Based Ferrofluid. J. Magn. Magn. Mater. 2016, 424. [Google Scholar] [CrossRef]
- Zhenkun, l.; Li, D.; Cui, H.; Zhang, Y.; Wang, H. Influence of the Carrier Fluid Viscosity on the Rotational and Oscillatory Rheological Properties of Ferrofluids. J. Nanosci. Nanotechnol. 2019, 19, 5572–5581. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J.; Segovia-Gutiérrez, J.P.; Pinho, F.T.; Alves, M.A.; de Vicente, J. Extensional rheometry of magnetic dispersions. J. Rheol. 2015, 59, 193–209. [Google Scholar] [CrossRef]
- Sadek, S.H.; Najafabadi, H.H.; Galindo-Rosales, F.J. Capillary breakup extensional magnetorheometry. J. Rheol. 2020, 64, 55–65. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J.; Moldenaers, P.; Vermant, J. Assessment of the dispersion quality in polymer nanocomposites. Macromol. Eng. 2011, 296, 331–340. [Google Scholar] [CrossRef]
- McKinley, G.H.; Tripathi, A. How to Extract the Newtonian Viscosity from Capillary Breakup Measurements In a Filament Rheometer. J. Rheol. 2000, 44, 653–671. [Google Scholar] [CrossRef]
- McKinley, G.H. Visco-Elasto-Capillary Thinning and Break-Up of Complex Fluids; Rheology Reviews; The British Society of Rheology: Aberystwyth, UK, 2005. [Google Scholar]
- Rodd, L.; Scott, T.; Cooper-White, J.; McKinley, G.H. Capillary break-up rheometry of low-viscosity elastic fluids. Appl. Rheol. 2005, 15, 17–27. [Google Scholar] [CrossRef]
- Campo-Deaño, L.; Clasen, C. The slow retraction method (SRM) for the determination of ultra-short relaxation times in capillary breakup extensional rheometry experiments. J. Non-NEwtonian Fluid Mech. 2010, 165, 1688–1699. [Google Scholar] [CrossRef]
- Li, Y.; Sprittles, J.E. Capillary breakup of a liquid bridge: Identifying regimes and transitions. J. Fluid Mech. 2016, 797, 29–59. [Google Scholar] [CrossRef]
- McKinley, G. Free surface flows of complex fluids. Rheol. Bull. 2005, 74, 6–10. [Google Scholar]
- Ilg, P.; Odenbach, S. Ferrofluid Structure and Rheology. In Colloidal Magnetic Fluids: Basics, Development and Application of Ferrofluids; Odenbach, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–77. [Google Scholar] [CrossRef]
- Odenbach, S.; Thurm, S. Magnetoviscous Effects in Ferrofluids. In Ferrofluids: Magnetically Controllable Fluids and Their Applications; Odenbach, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 185–201. [Google Scholar] [CrossRef]
- Santiago-Quinones, D.; Raj, K.; Rinaldi, C. A comparison of the magnetorheology of two ferrofluids with different magnetic field-dependent chaining behavior. Rheol. Acta 2013, 52. [Google Scholar] [CrossRef]
- Anna, S.; McKinley, G. Elasto-capillary thinning and breakup of model elastic liquids. J. Rheol. 2001, 45, 115. [Google Scholar] [CrossRef]


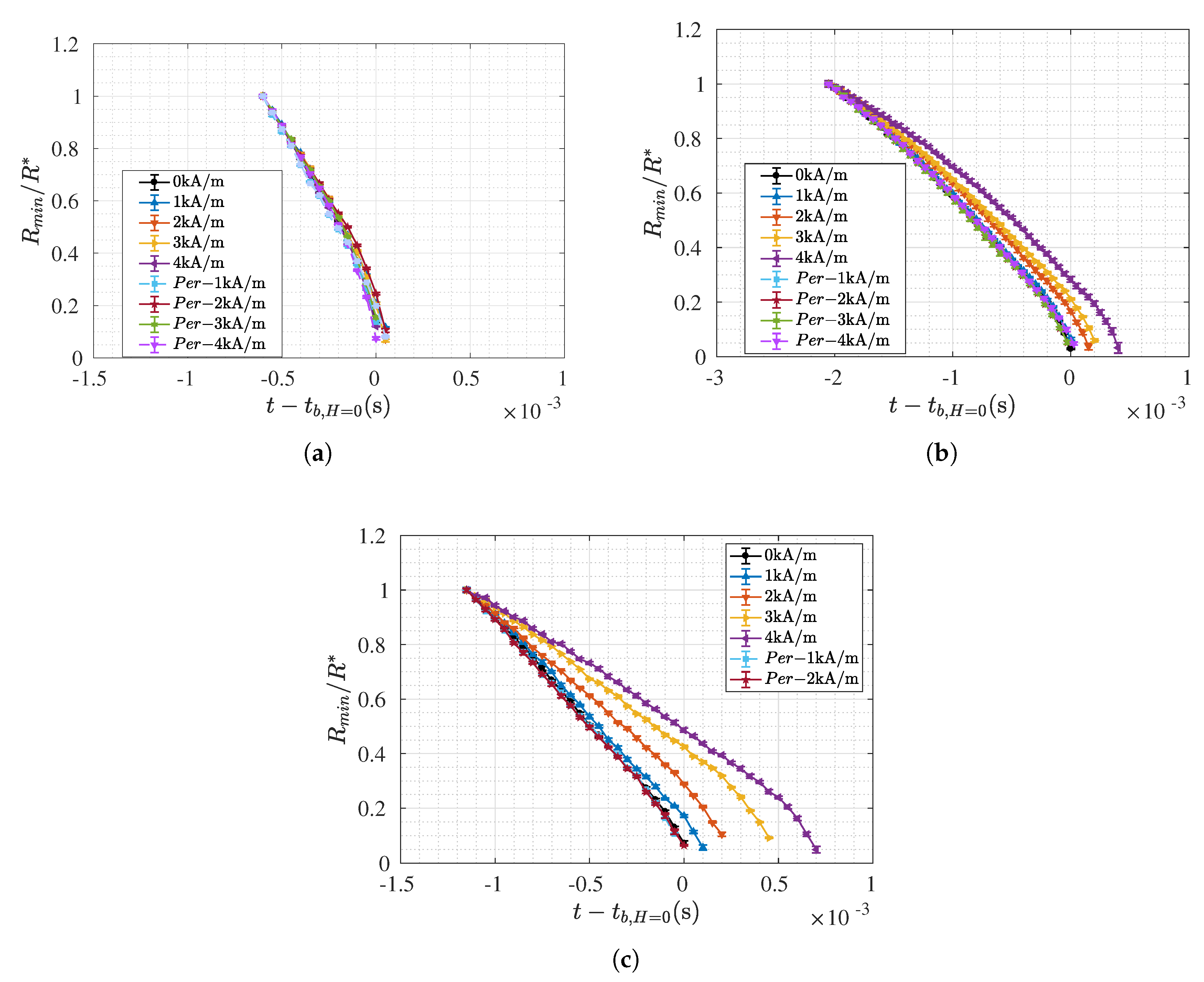

| EMG-905 | EMG-909 | EMG-911 | EMG-308 | EMG-507 | EMG-508 | |
|---|---|---|---|---|---|---|
| (kg/m) at 25 C | 1200 | 1020 | 890 | 1060 | 1120 | 1070 |
| (mPas) at 22 C | 9.81 ± 0.07 | 5.90 ± 0.02 | 4.04 ± 0.04 | 1.02 ± 0.01 | 1.20 ± 0.01 | 1.35 ± 0.02 |
| (mN/m) | 22.76 | 23.66 | 23.75 | 58.64 | 58.66 | 50.48 |
| a (nm) | ∼10 | ∼10 | ∼10 | ∼10 | ∼10 | ∼10 |
| (mT) | 44 | 22 | 11 | 6.6 | 11 | 6.6 |
| 3.52 | 1.38 | 0.50 | 0.50 | 1.63 | 0.88 | |
| (% vol) | 7.8 | 3.9 | 2 | 1.2 | 2 | 1.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Ortiz, J.H.; Galindo-Rosales, F.J. Extensional Magnetorheology as a Tool for Optimizing the Formulation of Ferrofluids in Oil-Spill Clean-Up Processes. Processes 2020, 8, 597. https://doi.org/10.3390/pr8050597
García-Ortiz JH, Galindo-Rosales FJ. Extensional Magnetorheology as a Tool for Optimizing the Formulation of Ferrofluids in Oil-Spill Clean-Up Processes. Processes. 2020; 8(5):597. https://doi.org/10.3390/pr8050597
Chicago/Turabian StyleGarcía-Ortiz, José Hermenegildo, and Francisco José Galindo-Rosales. 2020. "Extensional Magnetorheology as a Tool for Optimizing the Formulation of Ferrofluids in Oil-Spill Clean-Up Processes" Processes 8, no. 5: 597. https://doi.org/10.3390/pr8050597
APA StyleGarcía-Ortiz, J. H., & Galindo-Rosales, F. J. (2020). Extensional Magnetorheology as a Tool for Optimizing the Formulation of Ferrofluids in Oil-Spill Clean-Up Processes. Processes, 8(5), 597. https://doi.org/10.3390/pr8050597






