Correlations for Total Entropy Generation and Bejan Number for Free Convective Heat Transfer of an Eco-Friendly Nanofluid in a Rectangular Enclosure under Uniform Magnetic Field

Abstract

In this paper, focusing on the study of entropy generation (EGN), the convection flow of an eco-friendly nanofluid (N-F) in a rectangular enclosure is studied numerically. The nanoparticles (N-Ps) used are silver N-P, which are obtained in an eco-friendly manner from natural materials. By suspending these N-Ps in an equal mixture of water and ethylene glycol (E-G), the N-F has been prepared. There are two constant-temperature triangular obstacles with height w and base H that are placed on the hot wall. There is a magnetic field (M-F) in the x-direction. To simulate the N-F flow, eco-friendly N-P relations are used, and the equations are solved using the volume control method and the SIMPLE algorithm. The variables include Rayleigh number (Ra), Hartmann number (Ha), H, W, and the volume fraction of silver N-Ps. The effect of these parameters is evaluated on the EGN and Bejan number (Be). Finally, a correlation is expressed for the EGN for a range of variables. The most important results of this paper demonstrate that the addition of silver eco-friendly N-Ps intensifies the EGN so that the addition of 3% of N-Ps enhances the EGN by 3.8%. An increment in the obstacle length reduces the Be barrier while increasing the Ha, which enhances the Be when the convection is strong. Increasing the height of the obstacle intensifies entropy generation.

1. Introduction

In recent years, researchers have paid more attention to nanotechnology. Nanotechnology has applications in many industries, including medicine, aerospace, military, construction, food, heat transfer, renewable energy, etc. [1,2,3,4,5]. One of the applications of nanoparticles (N-Ps) in manufacturing is the preparation of nanofluids (N-Fs). N-Fs are widely used in heat transfer industries [6,7,8,9,10]. One of the important applications of nanofluids is their use in closed enclosures, which are used to enhance the improvement of thermal and refrigeration equipment [11,12,13,14,15]. Ghasemi and Aminossadati [16] investigated the effect of N-Fs in a square enclosure. They changed the percentage of N-Ps in the base fluid and found that a higher volume percentage leads to more heat transfer in the enclosure. Additionally, a rise in the Rayleigh number (Ra) leads to an increase in the vortices’ velocity, suggesting an increase in heat transfer. Among the various N-Ps, some researchers have used eco-friendly N-Ps in their research. These N-Ps are made from natural materials and are environmentally friendly. Various materials have been utilized as N-Ps in investigations in the realm of N-Fs. Silver N-Ps have been increasingly popular in recent years because of their unique characteristics and many uses, which include medical equipment, heating systems, and apparel. The reduction of silver ions in solution or at high temperatures in gaseous settings is the general approach for producing silver N-Ps [17]. However, some researchers have proposed a new method for preparing these N-Ps from tea leaves. Mashayekhi et al. [18] studied the effect of using eco-friendly N-F on heat transfer rate. Their results demonstrated that using this N-F instead of base fluid enhances the rate of heat transfer. In another study, Essa et al. [19] assessed the effect of using eco-friendly coffee-based colloid on solar steel was studied. They mentioned the advantages of using this N-F as organic and the low cost of preparation. In another study, Kosinska et al. [20] investigated the effect of using coffee colloids eco-friendly N-Fs in a direct solar absorption collector. They used this N-F to reduce preparation costs and preserve the environment along with the desirable properties of this N-F. Other researchers have also used gold eco-friendly N-Ps in their studies [21]. The magnetic field (M-F) can apply a force to different materials called the Lorentz force. This force is very important in N-F flows, especially in the natural flow, and can fundamentally change the flow. One of the fascinating issues for researchers is the use of M-F in enclosures to investigate its influence and Hartmann number (Ha) changes on the natural flow field [22,23,24,25]. The influence of the M-F on various enclosure geometries was investigated by several researchers [26,27,28]. The impact of Ra and Ha on heat transfer rate, flow field, and temperature in an enclosure was investigated by Ghasemi and Aminossadati [29]. They found that an enhancement in the Ha weakens the flow field and also reduces the Nusselt number (Nu). The use of N-Fs can also enhance the Nu.

The increasing need for energy on the one hand, and the increment in environmental pollution on the other hand, have prompted researchers to improve the efficiency of various devices as much as possible [30,31,32,33,34]. One of the solutions to enhance the efficiency is the evaluation of entropy generation (EGN) and the rate of irreversibility created in these devices. The researchers determined EGN in heat transfer devices to estimate their efficiency [35,36,37,38]. The study of EGN in enclosures has also been one of the interesting topics for researchers in recent years [39,40,41,42,43]. Aghakhani et al. [44] evaluated the EGN of a N-F in a closed enclosure under a M-F. Their findings indicated that increasing the enclosure’s convection intensity increases the rate of EGN and heat transmission at the same time. Additionally, an increase in Ra lowers the quantity of Bejan number (Be).

The use of N-Ps in different industries has been growing in recent years, and also, the researches have been increased in the field of different N-Ps [45]. One of the problems with using N-Ps is their environmental concerns. One of the best ways to prevent environmental damage by using industrial N-Ps is to use N-Ps synthesized from natural materials. One of these N-Ps is silver N-Ps that can be produced using an industrial method from tea leaves. Due to this issue, it was decided to use an eco-friendly N-F in this study, which contains silver N-Ps obtained from natural materials dispersed in a mixture of water and ethylene glycol (E-G). In addition, considering the need to enhance the use of various devices in this article, the focus is on EGN. Therefore, in this paper, the impact of the natural flow of an eco-friendly N-F in an enclosure with two triangular blades is evaluated on EGN. The effect of the M-F on N-F flow is examined. Finally, by changing the Ra and Ha as well as the dimensions of the triangular blades, the EGN and the Be are investigated, and a correlation for EGN is provided. In summary, the use of eco-friendly N-Fs in the mentioned geometry is considered as the novelty of the present work.

2. Problem Description

The two-dimensional enclosure consists of a rectangular enclosure, with dimensions as shown in Figure 1. The enclosure has two walls of high temperature and low temperature and two insulated walls. Two triangular blades are mounted on the bottom wall. The distance between the sides of the blades is equal. The enclosure is saturated with eco-friendly silver N-Ps dispersed in 50:50 water and E-G. It is noteworthy that the N-Ps used are eco-friendly and synthesized from the environment. The enclosure is under a M-F in the direction as shown in Figure 1.

2.1. Governing Equations and Boundary Condition

The non-dimensional equations for the N-F flow, including the continuity, the momentum, and the energy equations, for steady laminar flow and incompressible Newtonian N-F, are as follows. Additionally, the effects of viscosity loss, radiative heat transfer, and volumetric forces except the gravitational force are neglected [40]:

$$U_X+V_Y=0,$$

(1)

$$U{U}_X+V{U}_Y=-{\mathrm{P}}_X+\frac{{\mathsf{\mu }}_{\mathrm{nf}}}{{\mathsf{\rho }}_{\mathrm{nf}}{\mathsf{\alpha }}_{\mathrm{f}}}\left({\mathrm{U}}_{XX}+{\mathrm{U}}_{YY}\right),$$

(2)

$$U{V}_X+V{V}_Y=-{\mathrm{P}}_Y+\frac{{\mathsf{\mu }}_{\mathrm{nf}}}{{\mathsf{\rho }}_{\mathrm{nf}}{\mathsf{\alpha }}_{\mathrm{f}}}\left({\mathrm{V}}_{XX}+{\mathrm{V}}_{YY}\right)+\frac{{\mathsf{\beta }}_{\mathrm{nf}}}{{\mathsf{\beta }}_{\mathrm{f}}}RaPr\theta +\frac{{\mathsf{\rho }}_{\mathrm{f}}}{{\mathsf{\rho }}_{\mathrm{nf}}}\frac{{\mathsf{\sigma }}_{\mathrm{nf}}}{{\mathsf{\sigma }}_{\mathrm{f}}}Pr{\mathrm{Ha}}^{2}V,$$

(3)

$${\mathrm{U}\mathsf{\theta }}_X+{\mathrm{V}\mathsf{\theta }}_X=\frac{{\mathsf{\alpha }}_{\mathrm{nf}}}{{\mathsf{\alpha }}_{\mathrm{f}}}\left({\mathsf{\theta }}_{XX}+{\mathsf{\theta }}_{YY}\right),$$

(4)

where X and Y indices mean the first derivation with respect to these parameters and XX and YY indices represent the second derivation with respect to these parameters. Equations (2) and (3) are momentum equations in the x- and y-directions. In the momentum equation in the Y-direction, there is a buoyancy term due to the gravitational force. There is also a magnetic field force in this equation. Equation (5) is used to non-dimensionalize the equations. Additionally, in Equation (6), the definitions of the Prandtl, Ra, Ha, and EGN parameters are presented.

$$\mathrm{X}=\frac{\mathrm{x}}{l}, \mathrm{Y}=\frac{\mathrm{y}}{l}, \mathrm{U}=\frac{\mathrm{u}l}{{\mathsf{\alpha }}_{\mathrm{f}}}, \mathrm{V}=\frac{\mathrm{v}l}{{\mathsf{\alpha }}_{\mathrm{f}}}, \mathrm{P}=\frac{p{l}^2}{{\mathsf{\rho }}_{\mathrm{nf}}{\mathsf{\alpha }}_{\mathrm{f}}^2}, \mathsf{\theta }=\frac{\mathrm{T}-{\mathrm{T}}_{\mathrm{c}}}{{\mathrm{T}}_{\mathrm{h}}-{\mathrm{T}}_{\mathrm{c}}},$$

(5)

$$Pr=\frac{{\vartheta }_f}{{\alpha }_f}, Ra=\frac{g{\beta }_f{l}^3({\mathrm{T}}_{\mathrm{h}}-{\mathrm{T}}_{\mathrm{c})}Pr}{{\vartheta }_f{}^2}, H{a}^2=\frac{{\sigma }_f{B}_0{}^2{l}^2}{{\mu }_f}, \Lambda =\frac{{\mathsf{\mu }}_{nf}{T}_0}{{\mathrm{k}}_f}{\left(\frac{{\mathsf{\alpha }}_{\mathrm{f}}}{L\left(T_h-T_C\right)}\right)}^2.$$

(6)

To solve the governing equations, boundary conditions must be used. Figure 2 shows the non-dimensionalized boundary conditions.

The amount of EGN in the general case is defined as follows. The total EGN includes three types of EGN: thermal EGN, EGN due to fluid friction, and EGN due to M-F.

$$S_g=\frac{{\mathrm{k}}_{nf}}{{\mathrm{k}}_f}\left({\left(\frac{\partial \mathsf{\theta }}{\partial \mathrm{X}}\right)}^2+{\left(\frac{\partial \mathsf{\theta }}{\partial \mathrm{Y}}\right)}^2\right)+\Lambda \left\{2\left[{\left(\frac{\partial U}{\partial \mathrm{X}}\right)}^2+{\left(\frac{\partial \mathrm{V}}{\partial \mathrm{Y}}\right)}^2\right]+{\left(\frac{\partial \mathrm{U}}{\partial \mathrm{Y}}+\frac{\partial \mathrm{V}}{\partial \mathrm{X}}\right)}^2\right\}+\Lambda \frac{{\sigma }_{nf}}{{\sigma }_f}\frac{{\mu }_f}{{\mu }_{nf}}H{a}^2{V}^2.$$

(7)

The above equation consists of three terms. Temperature changes cause thermal EGN. Velocity changes cause frictional ENG, and velocity changes for different magnetic fields cause magnetic field ENG. The EGN in the enclosure is expressed using the equation below.

$$\mathrm{S}\_\mathrm{T}={{\displaystyle \iint }}_0^1{S}_{g}dXdY.$$

(8)

The Be is defined as follows:

$$B{e}_a=\frac{S_{gen,Thermal}}{S_g},$$

(9)

$$Be={{\displaystyle \iint }}_0^{l}Be dXdY.$$

(10)

2.2. N-F Properties Equations

Eco-friendly silver N-Ps are used to make silver N-Fs in a 50% volume aqueous solution E-G. These N-Ps are obtained from tea leaves in different stages. The following are the relationships that can be used for this N-F [46,47,48]:

$${\sigma }_{nf}=\left(1-\mathsf{\phi }\right){\mathsf{\sigma }}_{\mathrm{f}}+{\mathsf{\phi }\mathsf{\sigma }}_p,$$

(11)

$${\mathsf{\rho }}_{\mathrm{nf}}=\left(1-\mathsf{\phi }\right){\mathsf{\rho }}_{\mathrm{f}}+{\mathsf{\phi }\mathsf{\rho }}_p,$$

(12)

$${(\mathsf{\rho }\mathsf{\beta })}_{\mathrm{nf}}=\left(1-\mathsf{\phi }\right){(\mathsf{\rho }\mathsf{\beta })}_{\mathrm{f}}+\mathsf{\phi }{(\mathsf{\rho }\mathsf{\beta })}_p,$$

(13)

$${\left({\mathsf{\rho }\mathrm{c}}_{\mathrm{p}}\right)}_{\mathrm{nf}}=\left(1-\mathsf{\phi }\right){\left({\mathsf{\rho }\mathrm{c}}_{\mathrm{p}}\right)}_{\mathrm{f}}+\mathsf{\phi }{\left({\mathsf{\rho }\mathrm{c}}_{\mathrm{p}}\right)}_p,$$

(14)

$${\mathsf{\alpha }}_{\mathrm{nf}}=\frac{{\mathrm{k}}_{\mathrm{nf}}}{{\left({\mathsf{\rho }\mathrm{c}}_{\mathrm{p}}\right)}_{\mathrm{nf}}},$$

(15)

$$\frac{{\mu }_{nf}}{{\mu }_f}=1-2.5\mathsf{\phi },$$

(16)

$$\frac{k_{nf}}{k_f}=0.981+0.00114\times T+30.661\times \mathsf{\phi }.$$

(17)

Correlations related to the thermal conductivity of N-F can be used for the ones with volume fractions up to 1%.

Table 1. Thermophysical properties of water/E–G and Ag [18,47,49,50,51,52,53].

	${\mathit{c}}_{\mathit{p} }\left(J/kg·K\right)$	$\mathit{k} \left(W/m\mathit{·}K\right)$	$\mathsf{\rho } \left(kg/m^3\right)$	$\mathsf{\mu } \left(kg/m\mathit{·}s\right)$	$\mathit{\sigma }{\left(\mathsf{\Omega }·m\right)}^{-1}$	9
E-G	2430.8	0.2532	1088	0.0141	9.2 × 10−5	-
Water	4179	0.613	997.1	0.001	0.05	-
Ag	235	429	10,500	-	1.6 × 10−4	40

lists the thermophysical characteristics of E-G and silver N-Ps.

2.3. Numerical Procedure

To solve dimensionless equations, the equations are first algebraized using the volume control method. Then, a home code is written in FORTRAN software to solve dimensionless equations using the SIMPLE algorithm with the help of boundary conditions. In this software, a structured mesh is generated. The convergence criterion to solve all equations, including continuity, momentum, and energy equations, is 10⁻⁸. Grid study and validation are performed, and the results are presented in the Appendix A.

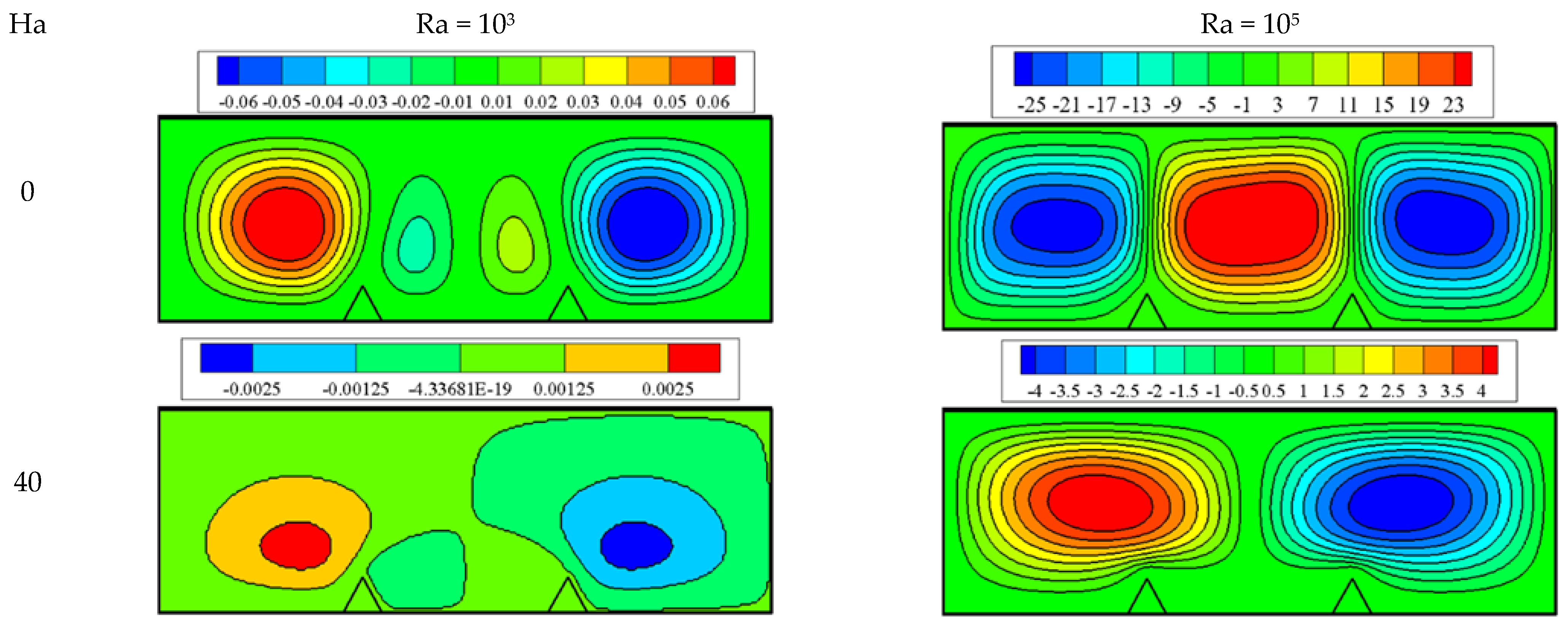
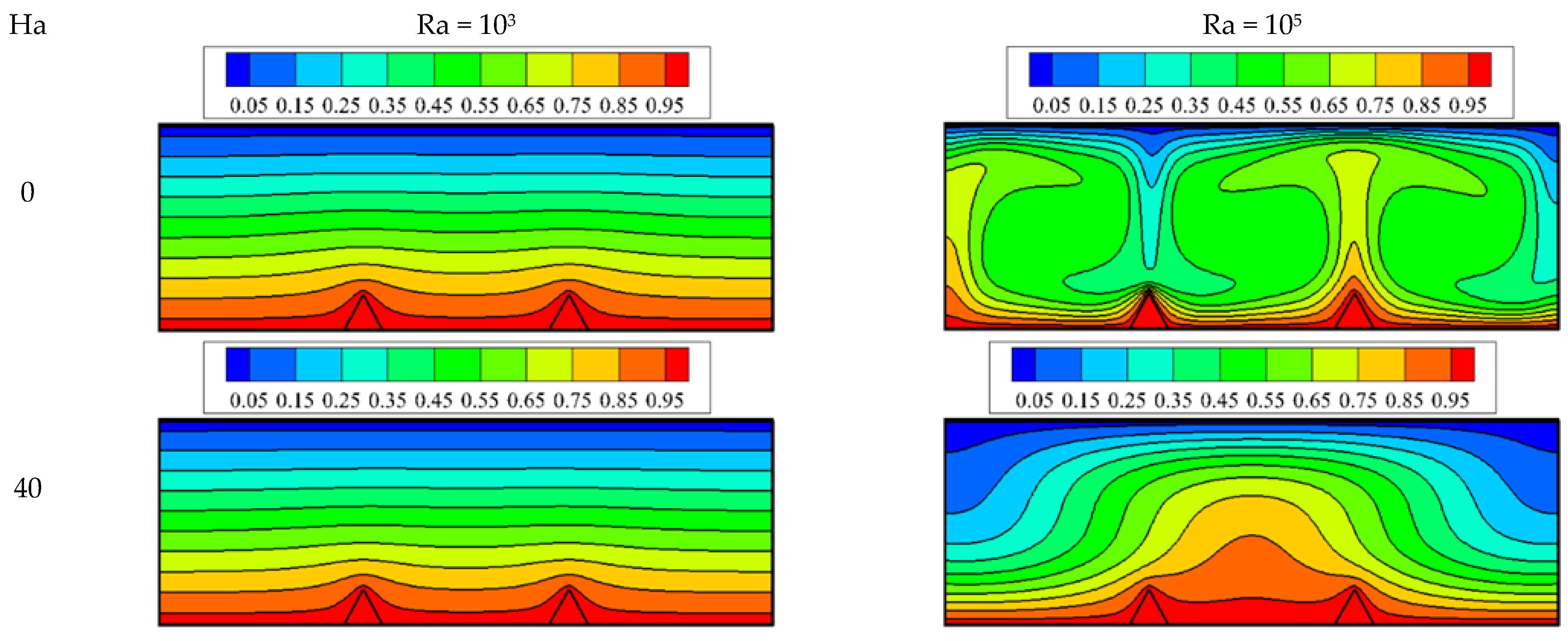
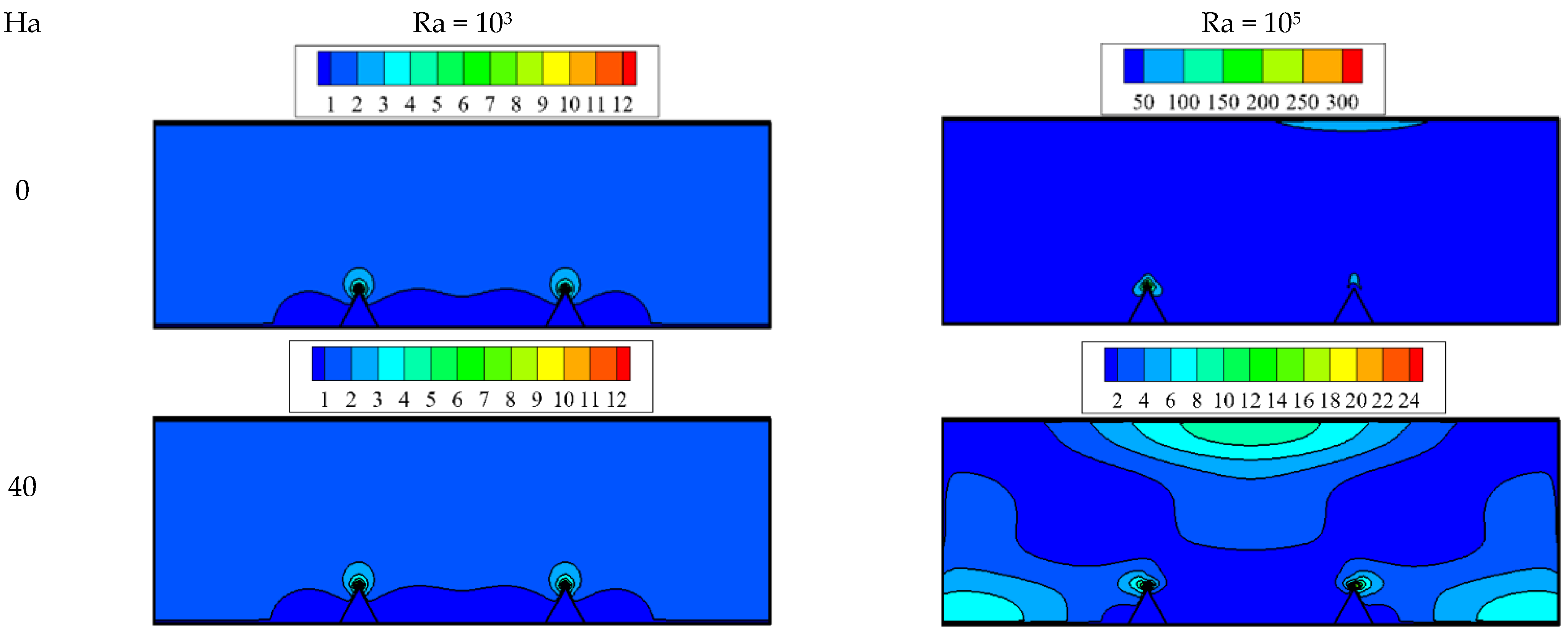
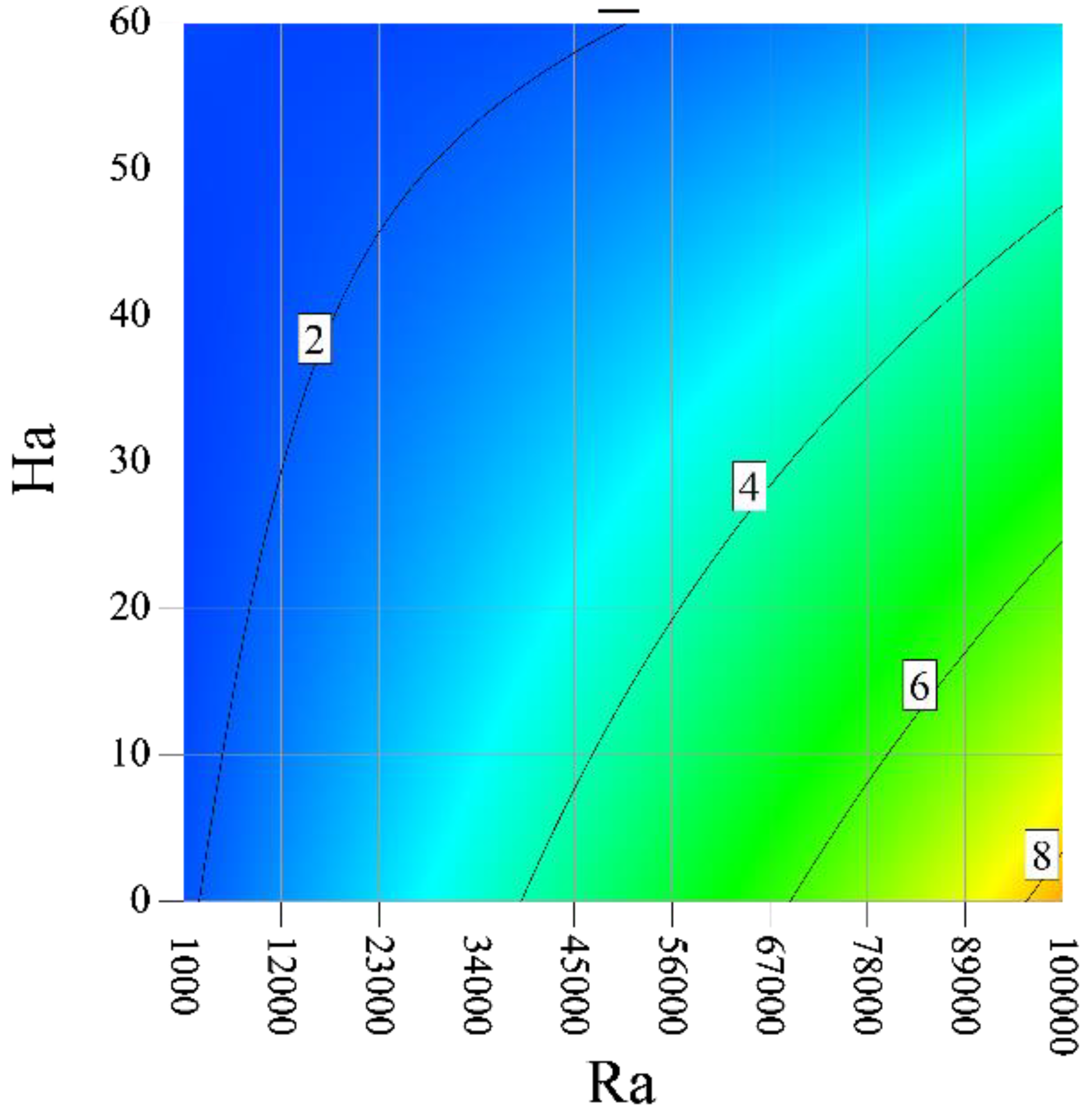
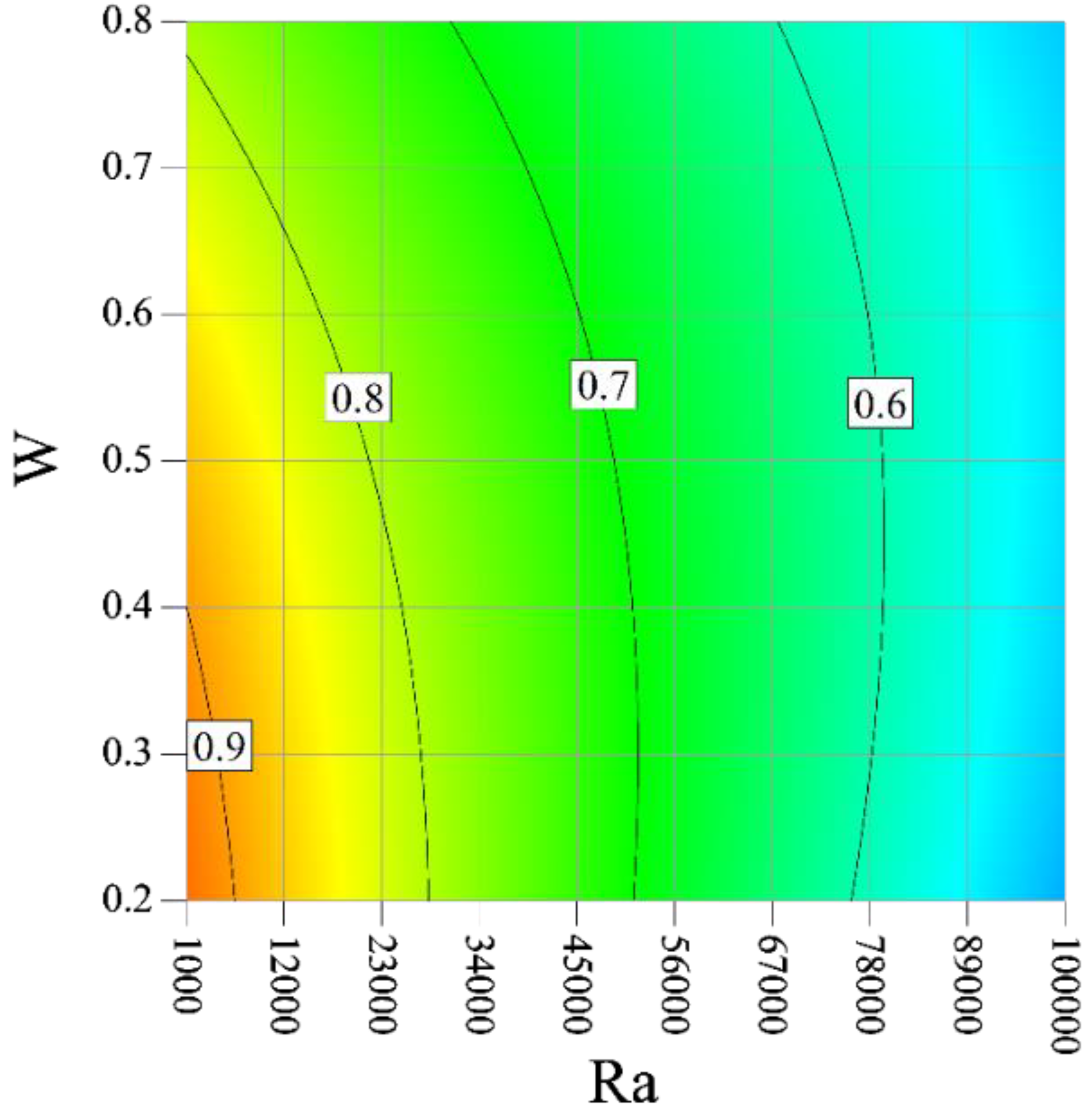
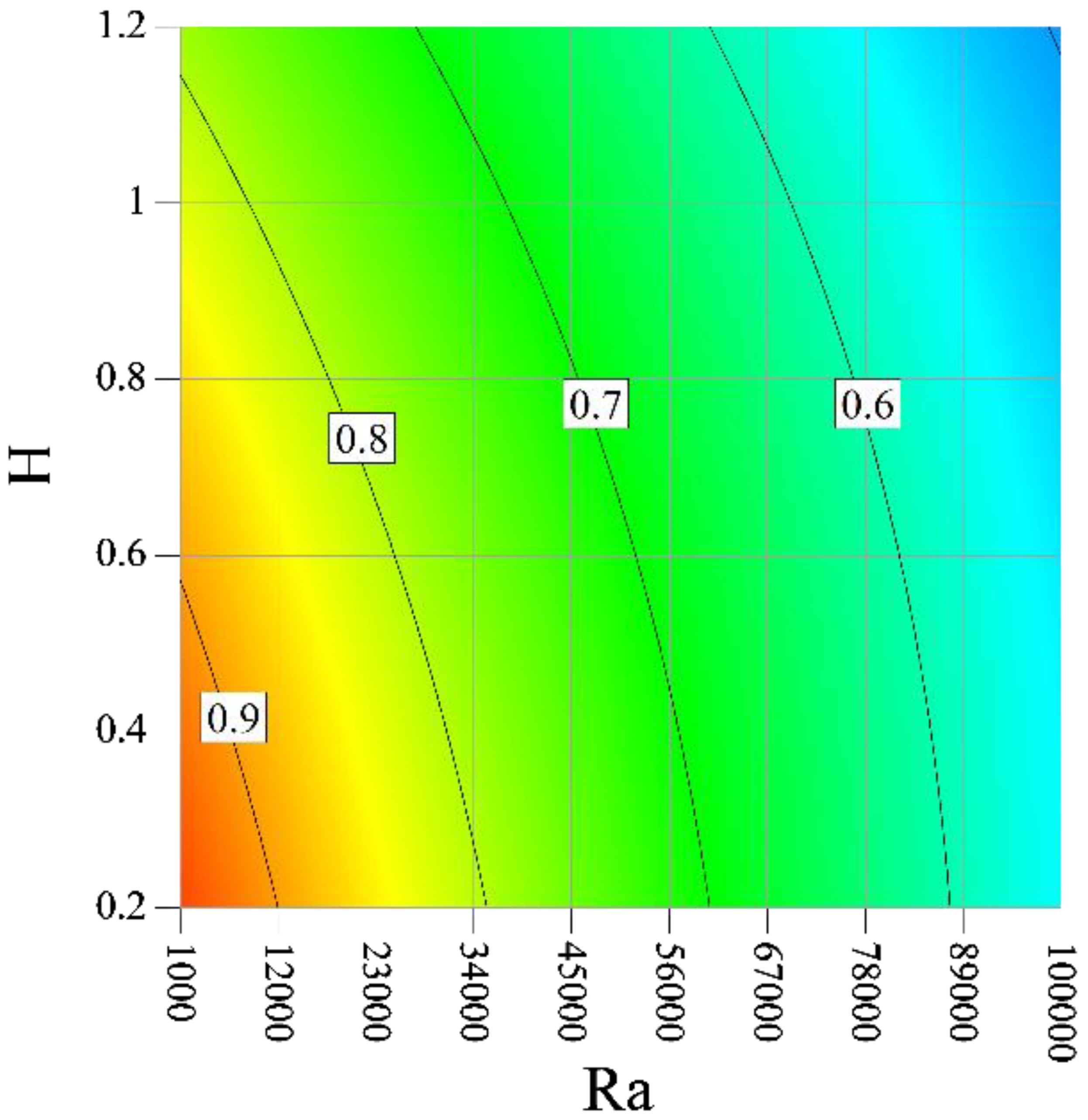
3. Results and Discussion

Figure 3 demonstrates the effect of Ra and Ha on the velocity field for H = W = 0.2. It can be seen that an enhancement in the Ha has a strong effect on the contours and reduces the amount of velocity. An increment in the Ra enhances the velocity. Changing the number of vortices from two to four vortices is another effect of changing Ra and Ha on the velocity field.

Figure 4 reveals the effect of Ra and Ha on the temperature field for H = W = 0.2 and a volume fraction of 0.3%. In the case of low Ra, the isotherms do not change with the Ha and remain as parallel lines. However, for Ra = 10⁵, the variations of the Ha affect the isotherms and change their shape. The changes of the Ra also affect the temperature contours, changing it from parallel lines to overlapping ones.

Figure 5 shows the effect of Ra and Ha on the EGN for H = W = 0.2 and a volume fraction of 0.3%. At low Ra. The variations of the Ha do not affect the place of EGN and the values of EN. However, at Ra = 10⁵, the Ha affects the place of EGN and the values of EN. High EGN occurs at the blade tip in all figures. Numerical values for Ra = 10⁵ and the absence of the M-F are much larger than the other cases.

Figure 6 demonstrates the EGN for different Ra and Ha when W = 0.5, H = 0.7, and the volume fraction is 0.3%. An enhancement in the Ra due to an increase in the velocity and an increment in the sudden changes in the temperature enhances the EGN. However, an increase in the Ha reduces the EGN due to the reduction in the velocity. Obviously, at Ra = 10⁵, where the velocity is higher, and the increase in Ha has a greater effect on the deceleration, the decrease in the EGN is lower. Thus, the maximum EGN corresponds to Ra = 10⁵ in the absence of the M-F.

Figure 7 shows the EGN for different Ra and various blade heights when Ha = 30, H = 0.7, and volume fraction is 0.3%. The trend of EGN changes with the Ra is an increasing trend. The EGN is enhanced with the height, which has less of an effect on EGN than the Ra. The enlargement of the blade causes sudden changes in temperature as well as velocity, producing irreversibility and an increase in EGN.

Figure 8 shows the EGN for different Ra and various blade lengths when Ha = 30, W = 0.5, and the volume fraction is 0.3%. The increasing trend of EGN with the Ra is observed. The change in blade length, however, has different effects on EGN at different Ra. At low Ra, an increase in the blade length first increases and then decreases EGN. While, at Ra greater than 45,000, the increase in blade length prevents a constant enhancing trend in EN. At Ra = 10⁵, the EGN is enhanced with the blade length.

Figure 9 shows the entropy for different Ha and various blade heights when Ra = 10⁵, H = 0.7, and volume fraction is 0.3%. As the Ha is enhanced, the amount of EGN is reduced. In addition, for all Ha and various strengths of the M-F, an increase in the blade height enhances the amount of EGN. The amount of EGN changes with the blade height has a constant trend for all Ha. The lowest EGN occurs at Ha = 60 and W = 0.2.

Figure 10 shows the EGN for different Ha and various blade lengths when Ra = 10⁵, W = 0.7, and the volume fraction is 0.3%. As the Ha is enhanced, the amount of EGN is reduced. An increase in the blade length reduces the EGN for lower Ha and weaker M-Fs. But, at high Ha and strong M-Fs, the enhancement of the blade length increases the EGN initially and then decreases. The highest EGN corresponds to Ha = 0 and the blade length of 0.2.

Figure 11 shows the EGN for different blade heights and lengths when Ra = 10⁵, Ha = 30, and the volume fraction is 0.3%. The variations of EGN with the blade height have an increasing trend so that for all blade lengths, increasing its height enhances the amount of EGN. An increment in the length of the blade initially enhances the EGN slightly and then reduces the EGN so that the EGN prevents the increasing trend to W = 0.4, and then the trend is reversed. The minimum EGN occurs at W = 1.2 and H = 0.2, while the maximum one occurs at W = 0.4 and H = 0.8.

Figure 12 illustrates the Be for different Ra and Ha when W = 0.5 and H = 0.7, and the volume fraction is 0.3%. The Be has a constant decreasing trend with the Ra, while the Be is reduced and is enhanced with the Ha. This trend is more visible at low Ra. At high Ra, an increasing trend takes place for the Be. The minimum value of the Be occurs at Ra = 10⁵ while its maximum occurs at Ra = 10³ and Ha = 60.

Figure 13 demonstrates the Be for different Ra and various blade heights when H = 0.7 and Ha = 30, and the volume fraction is 0.3%. It can be seen that the variation of the Be is under a decreasing trend with the Ra, but changing the blade height has a different effect on the Be, so that for high and low Ra, changing the blade height has a different impact on the Be. For high Ra, an enhancement in the blade height first intensifies the Be and then reduces it, while at low Ra, an increment in the blade height reduces the Be.

Figure 14 reveals the EGN for different Ra and various blade heights when H = 0.7 and Ha = 30, and volume fraction is 0.3%. The variations of the Be with the blade length have a constant decreasing trend so that an increase in the blade length reduces the amount of Be for all Ra. The declining trend of the Be is maintained with the Ra for various blade lengths.

Table 2. The EGN for different volume percentages of silver eco-friendly N-Ps at Ra = 105, Ha = 0, and W = H = 0.2.

$\mathit{\phi }$	S_T	$\frac{S\_T_{\mathit{\phi }}-S\_T_{\mathit{\phi }=0}}{S\_T_{\mathit{\phi }=0}}$
0	8.02	0
0.1	8.02	1.7
0.2	8.02	2.8
0.3	8.02	3.8
0.4	8.02	4.4
0.5	8.02	6.2

presents the EGN for different volume percentages of silver eco-friendly N-Ps at Ra = 10⁵, Ha = 0, and W = H = 0.2. It is observed that an increment in the amount of silver eco-friendly N-Ps in the fluid enhances the amount of EGN. Improving the heat transfer by adding silver N-Ps causes the temperature changes in the enclosure to intensify, and as a result, the amount of EGN, especially thermal EGN, is enhanced. For instance, the addition of 0.5% silver N-Ps to a mixture of water and E-G results in an enhancement in the EGN by 6.2% compared to the base fluid.

Equation (16) is a correlation to express the total EGN in terms of the Ra, the Ha, and the blade length and height.

$$\begin{array}{l}{\mathrm{S}}_{\mathrm{T}}=0.847+5.76\times {10}^{-5}Ra-0.01Ha+0.197W+0.67H-8.83\times {10}^{-7}\times Ra\times \\ Ha-3.66\times {10}^{-6}\times Ra\times W-1.05\times {10}^{-5}\times Ra\times H-6.45\times {10}^{-3}\times W\times Ha+.\\ 0.013\times H\times Ha-0.15\times W\times H+1.62\times {10}^{-10}\times R{a}^2+1.48\times {10}^{-4}\times H{a}^2+\\ 0.98\times W^2-0.54\times H^2\end{array}$$

(18)

It is noteworthy that an increment in ENG in different heat exchangers is undesirable. Enhancing ENG in the enclosure results in an enhancement of irreversibility. Increasing ENG ultimately leads to an intensification of energy loss. Thus, it is attempted to reduce the ENG in different devices so that the irreversibility is reduced, and the efficiency of the devices is enhanced. Using the above relation, it can be found how many variable parameters can have the minimum ENG in the enclosure.

4. Conclusions

In this paper, the EGN in a rectangular enclosure saturated with an eco-friendly N-F containing silver N-Ps dispersed in an equal mixture of water and E-G was evaluated. The triangular blades were installed on the bottom of the enclosure when a M-F was applied in the x-direction. By changing the percentage of silver N-Ps, blade dimensions, as well as Ra and Ha, the EGN and the Be were calculated, and the following results were obtained.

• The addition of silver eco-friendly N-Ps to a mixture of water and E-G enhances the amount of EGN, so that adding 0.3% of N-F enhances the amount of EGN by 3.8%;
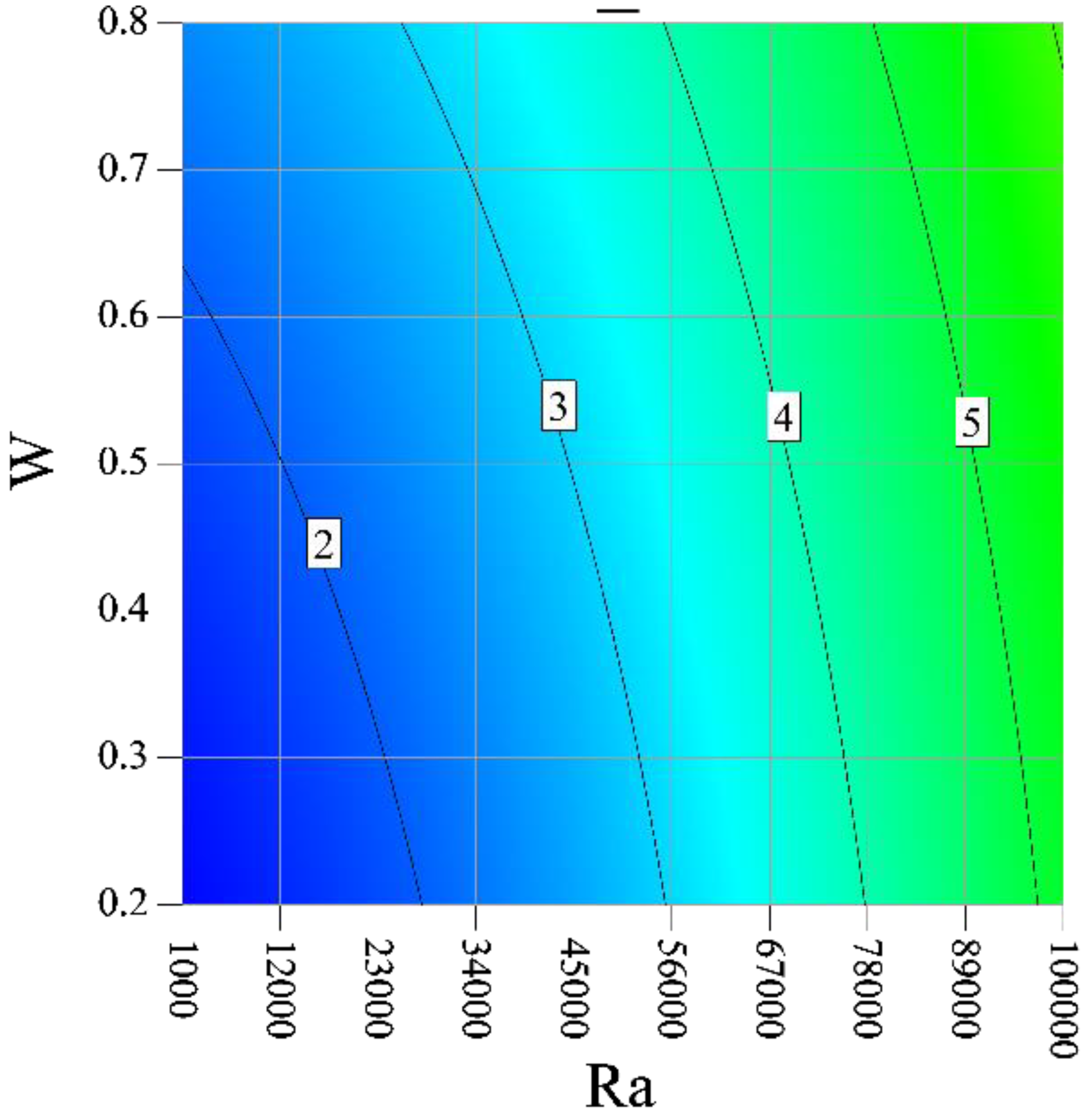
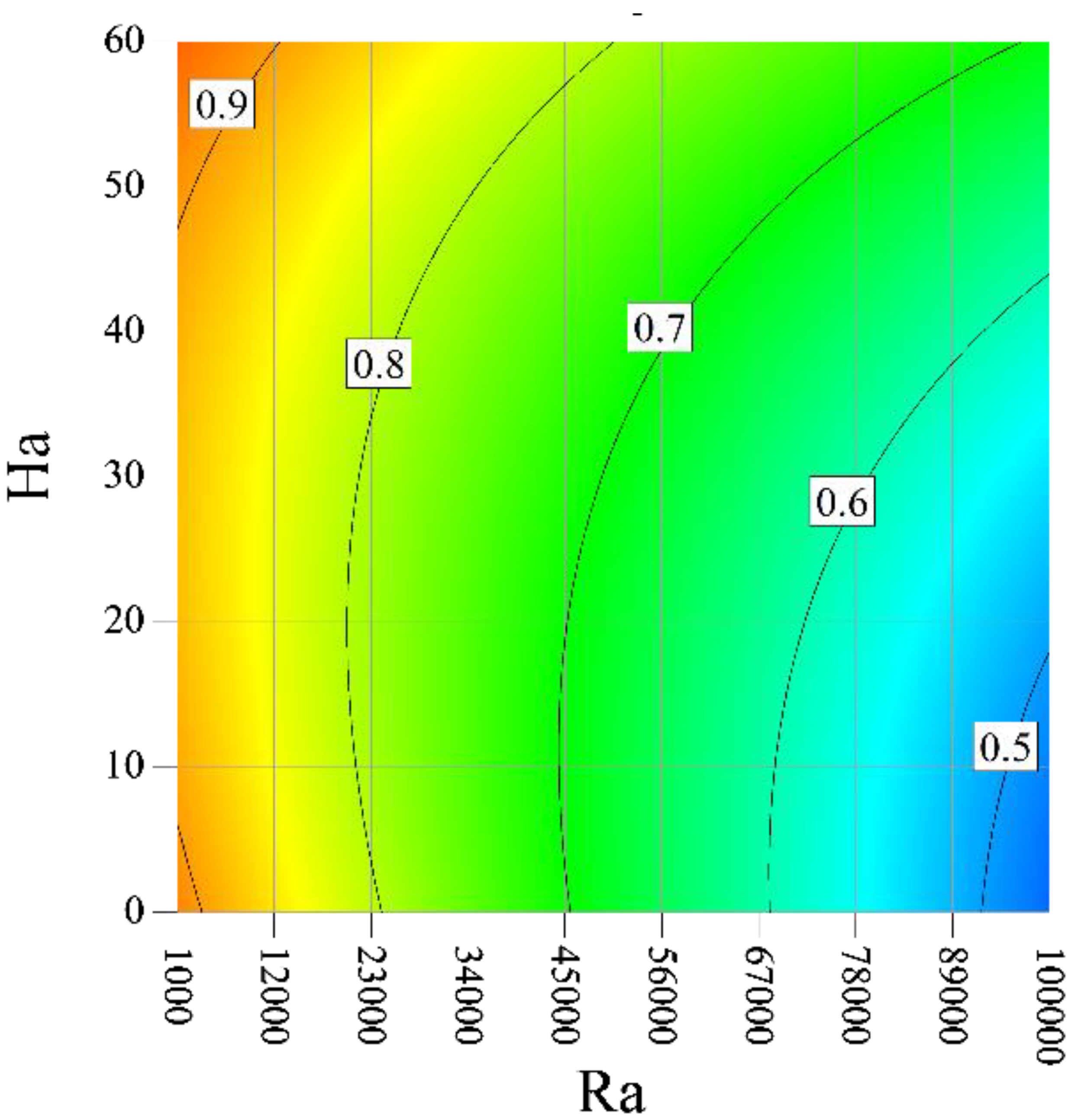
• An increment in the Ra enhances ENG and reduces the Be. The ENG has a decreasing trend with the Ha;
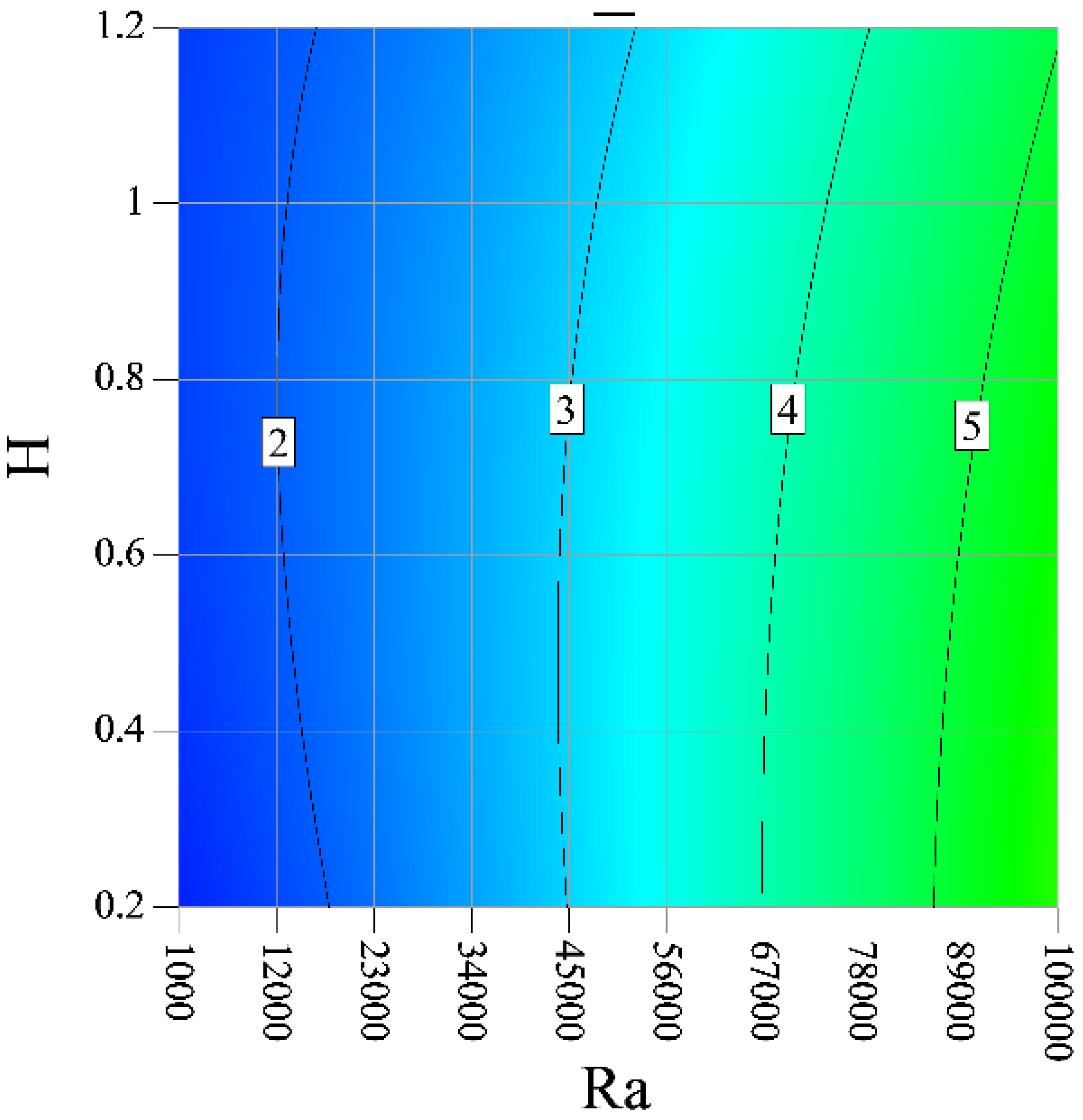
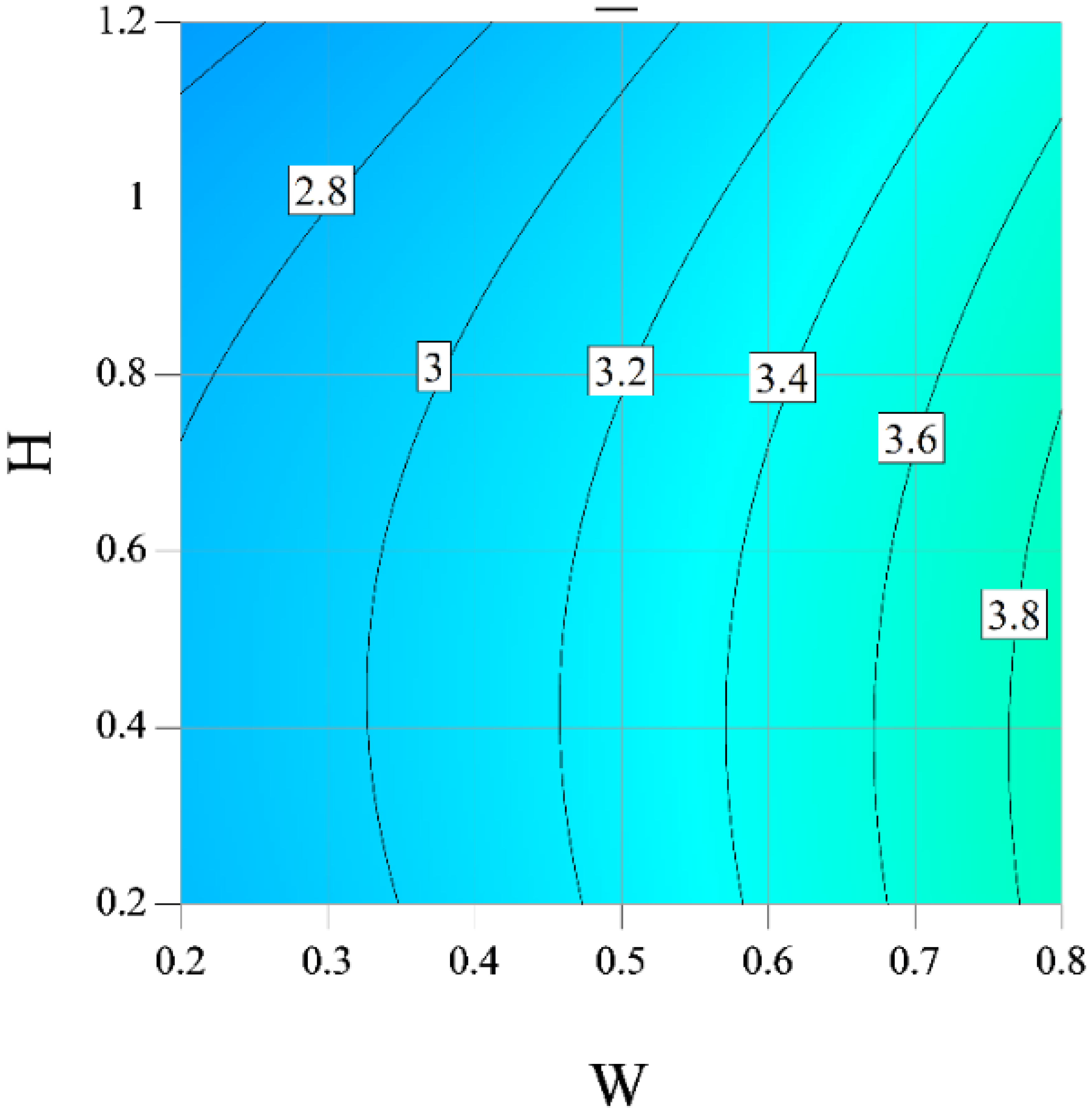
• An enhancement in the blade height causes the amount of EGN to enhance. An increment in the blade height results in a reduction in the Be at the low Ra, but the Be is first enhanced and reduced at high Ra;
• The increase of Ha at high Ra leads to an increase in the Be, but at low Ras, the Be first has a decreasing trend and then an increasing trend;
• Enhancing the fin length in strong convections decreases the ENG. An increment in the fin length results in a reduction in the Be.