Optimal Scheduling of the Peirce-Smith Converter in the Copper Smelting Process

Abstract

Copper losses during the Peirce-Smith converter (PSC) operation is of great concern in the copper smelting process. Two primary objectives of the PSC are to produce blister copper with a shorter batch time and to keep the copper losses at a minimum level. Due to the nature of the process, those two objectives are contradictory to each other. Moreover, actions inside the PSC are subject to several operational constraints that make it difficult to develop a scheduling framework for its optimal operation. In this work, a basic but efficient linear multi-period scheduling framework for the PSC is presented that finds the optimal timings of the PSC operations to keep the copper losses and the batch time at a minimum level. An industrial case study is used to illustrate the effectiveness of the proposed framework. This novel solution can be implemented in other smelting processes and used for the design of an inter-PSC scheduling framework.

1. Introduction

The copper industry is one of the backbones of the European processing industry, representing more than 12% of the worldwide production of refined copper [1]. This industry can utilize both high and low quality concentrates for its operation. At present, the global trend is that the high quality deposits of the copper will soon be depleted and the utilization of low quality concentrates will become a common practice [2,3]. At present, more than 60% of the concentrates come from low-grade deposits that have a high fraction of impurities (e.g., arsenic and bismuth) [4,5]. This utilization of low quality concentrates leads to higher operational costs in terms of copper losses, which remain a part of the slag as waste.

In the copper industry, the smelting process is used to extract copper from both high and low quality concentrates. Copper smelting operators that have access to high quality concentrates have a cost advantage since the lost copper possesses no significant value to the process operator; therefore, no extra technological investment is needed for its recovery. However, with the prospect of high quality deposits running out, this advantage can only be described as short-term. In fact, smelting operators have long-term advantages and turn a profit by utilizing low quality concentrates. This low quality concentrate utilization increases the relative importance of the copper losses and sets a need for minimizing the copper losses.

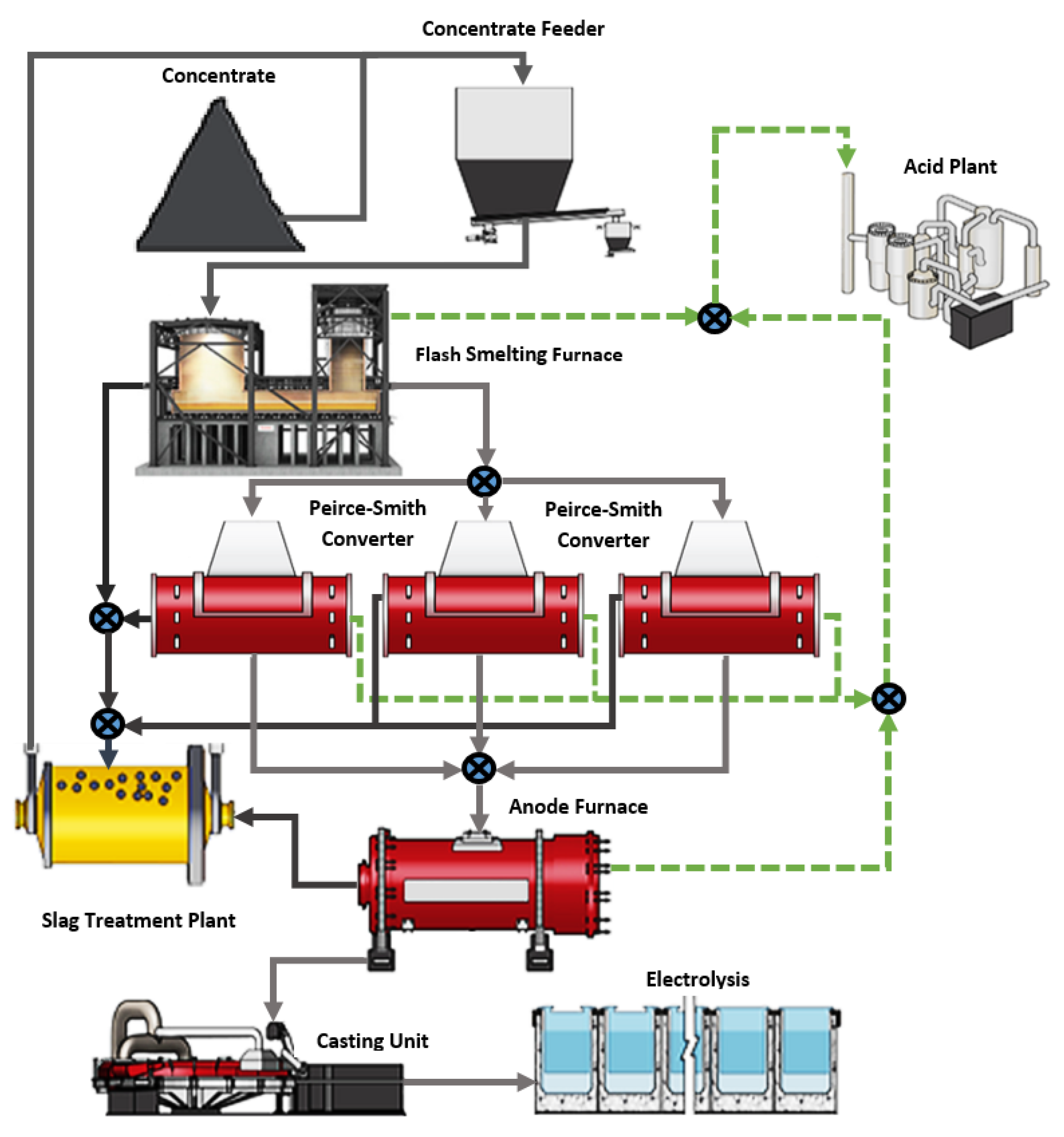
The copper smelting process is a large-scale complex industrial process that typically consists of a flash smelting furnace (FSF), Peirce-Smith converter (PSC), anode furnace, casting unit, electrolysis, slag treatment, and an acid plant, as shown in Figure 1. In this process, a major challenge is the scheduling of the PSC. Parallel functioning of the PSC units, high gas emissions, and the amount of copper that is lost during the PSC operation are some of the factors that contribute to this challenge [6,7,8]. Among those factors, copper losses affect its commercial viability and it is heavily dependent on the scheduling of its intra-operations.

In PSC, copper losses depend on numerous factors, such as the ratio of iron to silica in the slag, the operating temperature, the limitation of the mechanical structure, and other physical–chemical factors [10,11,12]. Furthermore, the amount of copper that is lost to the PSC slag is much higher than the amount of copper that is lost in other smelting units. For example, these losses are about 4–8 % in the PSC, while these same losses can vary from 1 to 2% in other units [7,8]. Copper losses that exceed 2–3% strongly affect the economics of the process [13]. Hence, neglecting the slag as waste is not an attractive solution since the slag contains a considerable amount of dissolved copper [7]. One way to recover the dissolved copper from the slag is to use a slag treatment unit. However, the slag treatment unit demands sufficient processing time, fundamental modifications, and capital investment for its effective operation [14,15].

Copper losses in the smelting process can be reduced either by improving the chemical nature of the process or by using innovative scheduling techniques. Davenport et al. [7] proposed chemical based strategies. These include minimizing slag generation, minimizing copper entrainment in the slag, and pyrometallurgical slag reduction. These strategies depend on the chemical nature of the process, and sometimes they cannot be adopted because of limitations in the quality of the concentrate, quality requirements, and other operational constraints. Lennartsson et al. [16] presented an interesting model for the PSC, which is based on thermodynamics. In this model formulation, PSC is divided into various operating zones and the content of various elements present in the matte is calculated. The results are then compared with the industrial data. Another thermodynamic based model for the PSC is presented by the Tan [17]. This model predicts the behavior of slag and matte in the PSC, their amount and composition, PSC temperature, and slag blow endpoint detection. The model is validated by industrial data and some industrial applications have also been presented.

In the literature, multiple solutions for the scheduling of the PSC can be found. Harjunkoski et al. [18] presented a continuous-time inter-PSC scheduling scheme for the copper production process with the objective of maximizing the production in the process. The problem was presented as a mixed-integer linear programming (MILP), which only captures the essential aspects of the process and optimizes the overall production processing time. Suominen et al. [19] presented an inter-PSC scheduling approach for the copper smelting process that optimizes the process time and the deviation from the target copper matte grade. That approach uses a continuous-time formulation, and the scheduling problem is formulated as a mixed-integer non-linear programming (MINLP). Navarra [20] introduced another MINLP formulation for the scheduling of the PSC that maximizes the production, while respecting the chemical, volumetric, and other operational constraints. All of the above studies ignore minimization of the copper losses; therefore, the effectiveness of these solutions is limited in many real copper smelter applications.

Motivated by the copper loss minimization in the slag, one technique to address this problem is to use practical scheduling techniques. In this study, a novel multi-period scheduling framework has been developed for the PSC using the discrete-time formulation (see, e.g., [21]). The proposed framework is developed using MILP techniques that keep the copper losses at minimum level by finding the optimal timings of the process operations.

The remainder of the paper is organized as follows: Section 2 briefly describes a general description of the PSC. The problem formulation is presented in Section 3. The mathematical formulation of the problem is discussed in Section 4, which is followed by describing a case study in which the framework is tested, and the simulation results are discussed. Section 5 presents the concluding remarks and provides an outlook for the future work.

2. Peirce-Smith Converter

A process diagram of the PSC is shown in Figure 2. The PSC involves a sequence of actions and phases, which are executed in a sequential order, and it always operates in batches. This unit is in service in more than 70% of copper smelters [22]. The purpose of the PSC is to oxidize part of the iron, sulfur, and other undesirable elements present in the matte to form slag, gases, and heat. Additional materials that are added to the PSC are silica, air, and industrial oxygen. Silica is added to accelerate metal oxide dissolution in the slag, which provides easy material discharge during the PSC operation and adequate matte/slag separation [23]. Industrial oxygen and air are used to control the PSC temperature for the purpose of keeping the matte and slag in the molten state. During the operation, the oxygen blast reacts with the iron and sulfur to produce a metal oxide that leaves the PSC in the form of slag (dissolved FeO and CuO) and off-gas (SO₂), which is used by the acid plant for the manufacture of sulfuric acid.

The process of converting FSF matte into blister copper is completed in two stages, called slag-making and copper-making. During the slag-making stage—iron and part of sulfur is oxidized first to produce slag in repetitive slag blow operations, while the sulfur is oxidized in a single long copper blow operation during the copper-making stage. The slag is removed periodically during the slag skimming operation. After the final slag skimming operation, the residual material is often referred to as white metal (high content of Cu₂S). Thereafter, the copper-making stage begins. During this stage, the chemical nature of the reaction remains the same where the remaining amount of the sulfur is oxidized by passing the white metal through the oxygen blast until the maximum threshold level of sulfur in the white metal is achieved. This final product is often referred to as blister copper (≈99%).

Temperature is one of the important parameters that has a direct influence on the PSC performance. During the slag-making stage, the temperature rises because of the iron and sulfur oxidation [24]. Increase in the PSC temperature results in high copper losses. On the other hand, decreasing the temperature leads to state change of the slag from molten to solid. Details about the temperature constraints and its effects can be found in the literature [7,20].

The slag-making stage is often split into three slag blows: the first, second, and third slag blow. To keep the temperature within the operational limits, the process operator defines the upper limit for the first two slag blows. Such action allows the process operator to maintain the PSC temperature within its operational limits. During the third slag blow, the temperature is kept in a feasible range by selecting an appropriate oxygen enrichment, while coolants (e.g., scrap with a high matte grade or slag from the anode furnace produced during the previous batch) are added during the copper blow to prevent excess of temperature. At the end of the copper-making stage, the PSC is emptied, and it is ready to produce the next batch of the blister copper.

Copper Losses

In the PSC, a decrease in the iron (Fe) content in the matte increases the copper (Cu) losses in the slag in a non-linear fashion [17]. The rate of those copper losses are smaller during the first slag blow than in the second slag blow, which in turn is smaller than in the third slag blow, as shown in Figure 3. The objective of the slag blows is to oxidize unwanted elements from the matte as quickly as possible. Due to the fact that PSC batches with shorter batch times are preferred, a general PSC operation will favor a longer duration of the first and second slag blows. However, such actions would result in too small iron content in the matte during the slag blows, which will lead to higher copper losses in the slag.

3. Problem Formulation

In this section, we define the problem statement and mathematical formulation of the scheduling problem.

Problem Statement

In this study, we consider a generic PSC installed in a copper smelting process. Although the real process is more complex in nature than the process framework considered in this work, it still reflects the main aspects of the real PSC operation.

Given: a PSC that follows a predefined sequence of actions that are carried out in a sequential order to produce a single batch of blister copper. During the PSC operation, it receives matte as a raw material from the FSF.

Determine: production schedule for a single batch of blister copper that delivers a product with a pre-defined quality and respects the process operational constraints.

Objective: in PSC, shortening the batch time magnifies the copper losses in a non-linear fashion. Hence, the objective is to minimize the copper losses and shorten the batch times simultaneously.

Note that in this formulation, the required product quality can be attained by oxidizing the mandatory amount of iron and sulfur from the matte, whereas the batch period can be optimized by avoiding unnecessary idle times.

Limitations: this framework assumes that the FSF operates at full capacity and it continuously produces matte with a perfectly known matte grade. This matte grade can change during its operation. There is always initial inventory available in FSF; thus, PSC operation can begin without any delay. Consequently, FSF internal process dynamics has no effect on PSC operation. In this work, it is assumed that the constant oxygen supply is available when required; hence, the rate of oxidation of elements in the PSC remain constant. During the slag skimming stage, all of the produced slag are removed from the PSC and moved to the slag treatment plant without any delay. The slag treatment plant, slag container, and SO₂ capturing unit have unlimited capacity; therefore, they are not considered in the present framework. The slag type does not change during the PSC operation.

Temperature raises inside the PSC during its operation, as discussed in Section 2. In this framework, it is assumed that the temperature is kept in a feasible range by pre-selecting an appropriate constant oxygen enrichment during the slag blow stages; therefore, temperature is not a decision variable in this framework. Moreover, by defining suitable maximum values for the first and second slag blow; the temperature reaching to its maximum threshold is avoided. It is also assumed that, in the copper-making stage, coolants are added when needed to keep the temperature in a feasible range. During each slag blow, a minimum amount of slag is produced. This is achieved by setting a minimum duration constraint for all of the slag blows.

4. Mathematical Formulation

In the literature, most of the scheduling problems with similar objectives are formulated using the big-M type of constraints. Such formulations are subject to weak linear relaxations and poor computational performances [25]. To maintain the model complexity at a low level, another way to formulate similar problems is to use a combination of two binary variables for scheduling every single process operation.

The main characteristics of this framework are:

• The processing times of PSC operations are deterministic, and vary depending upon the type of operation.
• The process schedule follows a pre-defined recipe that is already defined by the process operator.
• The schedule contains indefinite idle times if any operation from the pre-defined recipe is not performed in the prescribed way.

Here, PSC operations refer to the pre-defined tasks that must be carried out in a specific order to produce a single batch of the blister copper. The sets, variables, and parameters that are used in this framework are describe next.

Sets:

$z_i$ = operation in the PSC $\left\{z_i\mid z_i\in operation\forall operation\in \{loadin{g}_i,slagblo{w}_i,slagski{m}_i,copperblow\}and\left\{i\mid i\in {\mathbb{Z}}^{+},{\mathbb{Z}}^{+}=\{1,2,3,...,I\}\right\}\right\}$

t = discrete time $\left\{t\mid t\in {\mathbb{Z}}^{+},{\mathbb{Z}}^{+}=\{1,2,3,...,T\}\right\}$

j = set of equations for copper ratio scheme $\left\{j\mid j\in {\mathbb{Z}}^{+},{\mathbb{Z}}^{+}=\{1,2,3,...,J\}\right\}$

Variables:

$$b_{z_i}^t=\left\{\begin{array}{c}1ifoperation{z}_{i}isprocessedattimet\hfill \\ 0otherwise\hfill \end{array}\right.$$

$$s_{z_i}^t=\left\{\begin{array}{c}1if{b}_{z_i}^{t}isprocessedattimet\forall t=\{t,t+1,t+2,....,T\}\hfill \\ 0\forall t=\{1,2,3,...,t-1\}\hfill \end{array}\right.$$

$$idl{e}^t=\left\{\begin{array}{c}1if{b}_{z_i}^{t}isprocessedattimet\hfill \\ 0otherwise\hfill \end{array}\right.$$

$Mas{s}_m^t$ = accumulated mass of PSC matte at time t

$Mas{s}_{ele}^t$ = content of element $ele$ (iron, sulfur) in PSC matte at time t

$Mas{s}_{cu}^t$ = accumulated mass of copper losses in slag at time t

$A_j^t$ = copper loss trajectory

$C{u}_{ratio}^t$ = possible trade-off point

Parameters:

$r_{z_i}$ = rate of copper losses during operation $z_i$

$r_{ele}$ = rate of element $ele$ flow from matte to slag

$n_{z_i}$ = number that represents position of operation $z_i$$\left\{n_{z_i}\mid n_{z_i}\in {\mathbb{Z}}^{+},{\mathbb{Z}}^{+}=\{1,2,3,...,N\}\right\}$

$ma{x}_{z_i}$ = maximum processing time of operation $z_i$

$mi{n}_{z_i}$ = minimum processing time of operation $z_i$

$fi{x}_{z_i}$ = fixed processing time of operation $z_i$

$c_{z_i}$ = amount of matte transferred from FSF to PSC during operation $z_i$

$mg$ = matte grade

$a,b,B,C$ = positive real number $\left\{(a,b,B,C)\mid (a,b,B,C)\in {\mathbb{R}}^{+},{\mathbb{R}}^{+}=\{0.5,1,2,...,R^{+}\}\right\}$

In this formulation, there are three fundamental types of constraints: precedence sequence, material balance, and copper ratio scheme. The formulation of those constraints are discussed next.

4.1. Precedence Sequence

In this scheduling problem, only one operation $z_i$ can be processed at a given time t as shown in Equation (1). Every operation $z_i$ is processed for a duration as shown in Equations (2) and (3). If the process duration is not fixed, the framework estimates the optimal value.

$$\sum _{\begin{array}{c}{z}_i\in \\ operation\end{array}}{b}_{z_i}^t\le 1$$

(1)

$$\sum _{t=1}^t{b}_{z_i}^t=fi{x}_{z_i}\forall z_i\in loadin{g}_i,slagski{m}_i$$

(2)

$$mi{n}_{z_i}\le \sum _{t=1}^t{b}_{z_i}^t\le ma{x}_{z_i}\forall z_i\in slagblo{w}_i$$

(3)

For the precedence sequence of each PSC operations $z_i$, this framework uses a combination of two sets of binary variables. One set of binary variables, as represented by $b_{z_i}^t$, corresponds to the occurrence of operation $z_i$ at time t. The other set of binary variables $s_{z_i}^t$, which are also called start-up variables, are used to ensure that the PSC operations are processed in the order as presented by the process operator. Whenever the variable $b_{z_i}^t$ value is set to one at time t, the associated variable $s_{z_i}^t$ is also set to one at the same time that remains active until the final batch time as shown in Equation (4). A graphical illustration of the precedence sequence is provided in Figure 4. After the completion of operation $z_i$, the next operation can be scheduled as per constraint given in (5). In this expression, the summation of variables $s_{z_i}^t$ ensures that all of the preceding operations $b_{z_i}^t$ are scheduled prior to time $t\{1,2,...,t-1,t\}$.

$$s_{z_i}^t=s_{z_i}^{t-1}+b_{z_i}^t$$

(4)

$$\sum _{\begin{array}{c}{z}_i\in \\ operation\end{array}}\sum _{t=1}^t{s}_{z_i}^t\ge n_{z_i}\ast b_{z_i+1}^t$$

(5)

4.2. Material Balances

Material balances can be divided in three type of constraints as shown in Equations (6)–(8). All of them calculate the amount of material from the beginning of the batch until time $t\{1,2,...,t\}$. When the PSC batch begins, the previous quantity represents the corresponding initial inventory value. Equation (6) retains the matte quantity in the PSC. During the operation, a known amount of material $c_{z_i}$ is transferred from the FSF to the PSC. The input matte is composed of numerous unwanted elements and their content in matte depends on the matte grade $mg$. For example, the matte having 60% matte grade contains 15% iron and 25% sulfur [17]. The content of those unwanted elements in the PSC (e.g., $Mas{s}_{Fe}^t$, $Mas{s}_S^t$) is estimated by Equation (7). Equation (8) represents the accumulated mass of the copper lost to the slag. Here, the copper is lost at a rate $r_{z_i}$.

$$\begin{array}{cc}\hfill Mas{s}_m^t& =Mas{s}_m^{t-1}+\sum _{\begin{array}{c}{z}_i^{\prime }\in \\ operation\end{array}}\sum _{t=1}^t{c}_{z_i^{\prime }}\ast b_{z_i^{\prime }}^t-\sum _{\begin{array}{c}{z}_i\in \\ operation\end{array}}\sum _{t=1}^t(r_{z_i}+r_{ele})\ast b_{z_i}^t\hfill \\ \hfill & \forall z_i^{\prime }\in loadin{g}_i,z_i\notin loadin{g}_i\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill Mas{s}_{elm}^t& =Mas{s}_{elm}^{t-1}+\sum _{\begin{array}{c}{z}_i^{\prime }\in \\ operation\end{array}}\sum _{t=1}^t(a\ast mg+b)\ast b_{z_i^{\prime }}^t-\sum _{\begin{array}{c}{z}_i\in \\ operation\end{array}}\sum _{t=1}^t(r_{z_i}+r_{ele})\ast b_{z_i}^t\hfill \\ \hfill & \forall z_i^{\prime }\in loadin{g}_i,z_i\notin loadin{g}_i\hfill \end{array}$$

(7)

$$\begin{array}{c}\hfill Mas{s}_{cu}^t=Mas{s}_{cu}^{t-1}+\sum _{\begin{array}{c}{z}_i\in \\ operation\end{array}}\sum _{t=1}^t{r}_{z_i}\ast b_{z_i}^t\forall z_i\in slagblo{w}_i\end{array}$$

(8)

4.3. Copper Ratio Scheme

During the slag-making stage, iron is oxidized from the matte and added to the slag. This flow of iron decreases the iron content in matte and, thus, increases the matte grade. This increase in the matte grade increases the copper losses in the slag [13]. As the iron content in the matte begins approaching the near zero-level value, the matte grade starts reaching to its peak value that results in the copper loss to the slag in an exponential fashion [13].

In the copper smelting process, where the flow of oxygen and iron oxidation rate $\left(r_{Fe}\right)$ remain unchanged during the slag-making stage, the trajectory of matte grade over the complete batch horizon is calculated using Equation (9). Since the copper losses depend on the matte grade value, the copper loss trajectory in the slag can also be estimated as a function of time t using the results presented in [13]. This copper loss trajectory can be piece-wise linearized over the batch horizon, as shown in Figure 5.

The matte grade can be defined as the amount of non-oxidized iron present in matte. Since copper losses depend on the matte grade, as presented in Figure 5, and matte grade is defined by the non-oxidized iron present in matte, the copper losses in slag can be calculated using the amount of iron present in matte, as shown in Figure 3. Therefore, this study uses this iron in the matte to limit the copper level in the slag. This concept is deducted from the results presented in [13] and it is referred to as the copper ratio scheme.

$$\begin{array}{c}\hfill m{g}^t=m{g}^{t-1}+\frac{r_{Fe}\ast \Delta t}{100}\end{array}$$

(9)

In this framework, iron in the matte is calculated using Equation (10). Using the $M_{Fe}^t$, Equations (10)–(12) are used to estimate the optimal duration for the slag blows for which the total copper losses in the slag are at a minimum level. Trajectory $A_j^t$ is the approximation of the copper losses in the slag that depends on the non-oxidized iron in matte and parameters $B_j$ and $C_j$, which are positive real numbers. Here, j defines the number of times Equations (10)–(12) are defined in the framework, with different $B_j$ and $C_j$ values. As the iron amount in the matte decreases during the slag blow operations, trajectory $A_j^t$ starts increasing as illustrated in Figure 6 [17]. For each slag blow operation, Equations (11) and (12) determine its optimal termination point from the set of feasible points, as shown by the red points (■) in Figure 6. In this study, each optimal termination point is referred to as the copper ratio point $\left(C{u}_{ratio}^t\right)$, which represents the ratio between non-oxidized iron in matte and copper present in the slag. This simple but beneficial trade-off between the iron in matte and copper in the slag keeps the overall copper losses at a minimum level, subjected to the blister copper grade requirement.

$$\begin{array}{cc}\hfill & A_j^t=B_j-C_j\ast M_{Fe}^t\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & C{u}_{ratio}^t\ge A_j^t\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & C{u}_{ratio}^t\ge 0\hfill \end{array}$$

(12)

4.4. Batch Idle Time

In the copper smelting process, the PSC batches with shorter durations are preferred over batches that have unnecessary idle times. The prime reason for such practice is that the idle time decreases the temperature inside the PSC, thus affecting its overall performance. Therefore, this framework uses a penalty term to minimize the unnecessary idle time as shown in Equation (13). The penalty term $idl{e}^t$ has a value of one whenever any PSC operation $b_{z_i}^t$ becomes active throughout the batch horizon; otherwise, it remains at zero.

$$\begin{array}{c}\hfill \begin{array}{c}\hfill idl{e}^t=\sum _{\begin{array}{c}{z}_i\in \\ operation\end{array}}\sum _{t=1}^t{b}_{z_i}^t\end{array}\end{array}$$

(13)

4.5. Objective Function

The objective function in Equation (14) minimizes the total copper losses in the slag, unwanted elements content in the matte, and the copper ratio point. The last term of the objective function is used to penalize unnecessary idling time.

$$\begin{array}{c}\hfill \underset{Mas{s}_{cu},Mas{s}_{ele},C{u}_{ratio},idle}{min}\sum _{t=1}^{T}C{u}_{loss}^t+\sum _{t=1}^{T}Mas{s}_{ele}^t\\ \hfill +\sum _{t=1}^{T}C{u}_{ratio}^t+\sum _{t=1}^{T}idl{e}^t\end{array}$$

(14)

During the development of the mathematical model, few assumptions have been made that limit the scope of this work. Copper losses in the slag are represented by a piece-wise linear approximation and the values are taken from the literature; therefore, the selected values reflect the characteristics of this process. Another parameter that limits the performance of this framework is the choice of parameters values in the copper ratio scheme. Any unrealistic (e.g., negative) values selection may result in an unrealistic slag blow duration that may lead to higher copper losses in slag. The maximum duration value of the slag blows, which are defined by the process operator, also affect its performance. Small value selection may lead to larger copper loss, which is undesirable for this process.

4.6. Case Study

In this section, we describe a benchmark case study that was used to demonstrate the effectiveness of the proposed scheduling framework. In this case study, the PSC has the same sequence of operations as described in Figure 2. There are three loading operations, three slag blows, three slag skimming, and a single long copper blow; therefore, i = $\{1,2,3\}$. For this case study, Equations (10)–(12) are defined only once; therefore, j = $\left\{1\right\}$. The batch begins with two consecutive matte loadings, which are executed during the first loading operation. The matte in the PSC contains copper, iron, and sulfur. The proportion of those elements in the matte and process parameters were taken from the literature, and are listed in

Table 1. Framework parameters.

Parameter	Description	Value
$mg$	matte grade	68 (%)
$c_{z_i}$	matte transferred from the FSF to the PSC	20 (kg)
$ma{x}_{slagblo{w}_1}$	slag blow 1 maximum length	50 (s)
$mi{n}_{slagblo{w}_1}$	slag blow 1 minimum length	5 (s)
$ma{x}_{slagblo{w}_2}$	slag blow 2 maximum length	60 (s)
$mi{n}_{slagblo{w}_2}$	slag blow 2 minimum length	5 (s)
$slagskimmin{g}_i$	slag removal time	1 (s)
$loadin{g}_i$	loading time	1 (s)
$r_{Fe}$	iron oxidation rate	0.240 (kg/s)
$r_S$	sulfur oxidation rate	0.330 (kg/s)
$r_{slagblo{w}_1}$	copper loss rate during slag blow 1	0.103 (kg/s)
$r_{slagblo{w}_2}$	copper loss rate during slag blow 2	0.182 (kg/s)
$r_{slagblo{w}_3}$	copper loss rate during slag blow 3	0.80 (kg/s)

[17,23]. It is assumed that all loading and slag skimming operations take a single unit time and the PSC produces the blister copper with at least 98.75% matte grade. This scheduling problem is modeled in GAMS and solved with solver CPLEX 12.7 [26,27]. The computations were performed using a 2.60 GHz IntelCoreTM i7 6700HQ processor with 32 GB of RAM, running Windows 10 Enterprise, 64-bit.

To evaluate the performance of the proposed framework, five different scenarios are presented here. In scenarios 1–4, the framework was simulated with the objective as presented in Equation (14), which uses the copper ratio scheme; whereas in scenario 5, a PSC schedule is produced with a modified objective function, which is shown in Equation (15). This modified objective function produces a PSC schedule without using copper ratio scheme. Scenarios 1–4 provide the sensitivity analysis about the choice of copper ratio parameter values, whereas scenario 5 provides the novelty and importance of the copper ratio scheme in terms of copper losses. For each individual scenario, we presented the corresponding schedule that produces one batch of the blister copper, the amount of the copper losses, and the computational requirement. In the smelting process, the computational costs are not a pressing issue. However, we presented it here to provide a better sensitivity analysis of the proposed framework.

$$\begin{array}{c}\hfill \underset{Mas{s}_{cu},Mas{s}_{ele},idle}{min}\sum _{t=1}^{T}C{u}_{loss}^t+\sum _{t=1}^{T}Mas{s}_{ele}^t+\sum _{t=1}^{T}idl{e}^t\end{array}$$

(15)

Figure 7 shows that the framework has the ability to produce the schedules for all given scenarios. From

Table 2. Framework performance for different scenarios.

No.	Scheme	${\mathit{B}}_{\mathit{j}}$	${\mathit{C}}_{\mathit{j}}$	Cu Losses (kg)	Cu Saved (%)	Comp. Req. (s)
1	yes	0.1	20	18.10	21.64	109.81
2	yes	0.1	35	13.13	43.16	122.64
3	yes	0.1	50	12.60	45.45	157.34
4	yes	6	0.1	18.50	19.91	84.50
5	no	-	-	23.10	-	51.17

, it can be observed that the copper losses in scenario 5 are higher as compared to the copper losses in scenarios 1–4. Without a copper ratio scheme, the first and second slag blows terminate early and the third slag has a longer duration; hence, the copper losses are high. Consequently, the iron content in the matte for scenario 5 remains high, as shown in Figure 8. On the other hand, when the copper ratio scheme is part of the overall objective function as presented in scenarios 1–4, the amount of copper losses in the slag are reduced. The simple reason for this is that the framework finds the optimal slag blow duration. Although the framework provides a feasible schedule for scenario 5, the process operator might consider it an unreasonable schedule considering the amount of copper loss. Furthermore, shorter slag blows do not generate the required amount of heat in the PSC; thus, external resources are used to maintain the required temperature in the PSC. Therefore, the schedule produced in scenario 5 cannot be used practically in many smelting processes.

Table 2 provides a beneficial comparison between scenarios 1–4 and scenario 5 in terms of the copper that can be saved using the copper ratio scheme. Despite the fact that the framework with the copper ratio scheme requires more computational resources, it is still an optimal choice to utilize the scheme given the importance of the copper losses.

Another importance factor that affects the performance of this scheduling framework is the choice of the copper ratio parameter values. In Table 2, it is visible that, for any two given scenarios, selecting the higher value of $C_j$ as compared to $B_j$ reduces the copper losses, but increases the computational requirements. On other hand, when a lower $C_j$ value is used in comparison to the $B_j$ value, its computational requirements are reduced, but it increases the copper losses and the batch time. Hence, the process operator should select copper ratio values carefully as it affects the overall PSC scheduling and operation.

This case study shows that the proposed framework can produce schedules for the given matte. However, the framework has the capability of generating schedules for any given matte grade. It can be observed that utilization of the copper ratio scheme results in idle time generation to the schedules. Process operators who are concerned about the idle times would utilize this copper ratio scheme carefully. On the other hand, process operators who are sensitive to the copper losses would prefer the schedules provided by the framework using the copper ratio scheme.

5. Conclusions

This paper presents a linear dynamic MILP-based scheduling model for the PSC in the smelting process. The key features adopted in this formulation are the provision of a simple and linear approach for scheduling of PSC operations, minimization of the copper losses in slag, and the fulfillment of essential operational constraints that are often found in a real smelting plant.

The objective was to design linear discrete-time model for the PSC operation and apply linear techniques to keep the copper loss at a minimum level. The results of this work provide information to process operators about the effect of the copper losses on the overall schedule. Furthermore, using the proposed scheduling formulation, the operators have more command and understanding of the overall process functionality; thus, they can comfortably observe the benefits of their operational decisions. In this framework, operations, such as PSC maintenance break, start-up, and shutdown are ignored; therefore, it can be extended to more complex scenarios, and has the potential to be used for inter-PSCs scheduling.