Numerical Simulation of the Aerosol Particle Motion in Granular Filters with Solid and Porous Granules
Abstract
:1. Introduction
2. Problem Formulation and Solution Method
2.1. Filter Model
2.2. Mathematical Formulation
3. Results
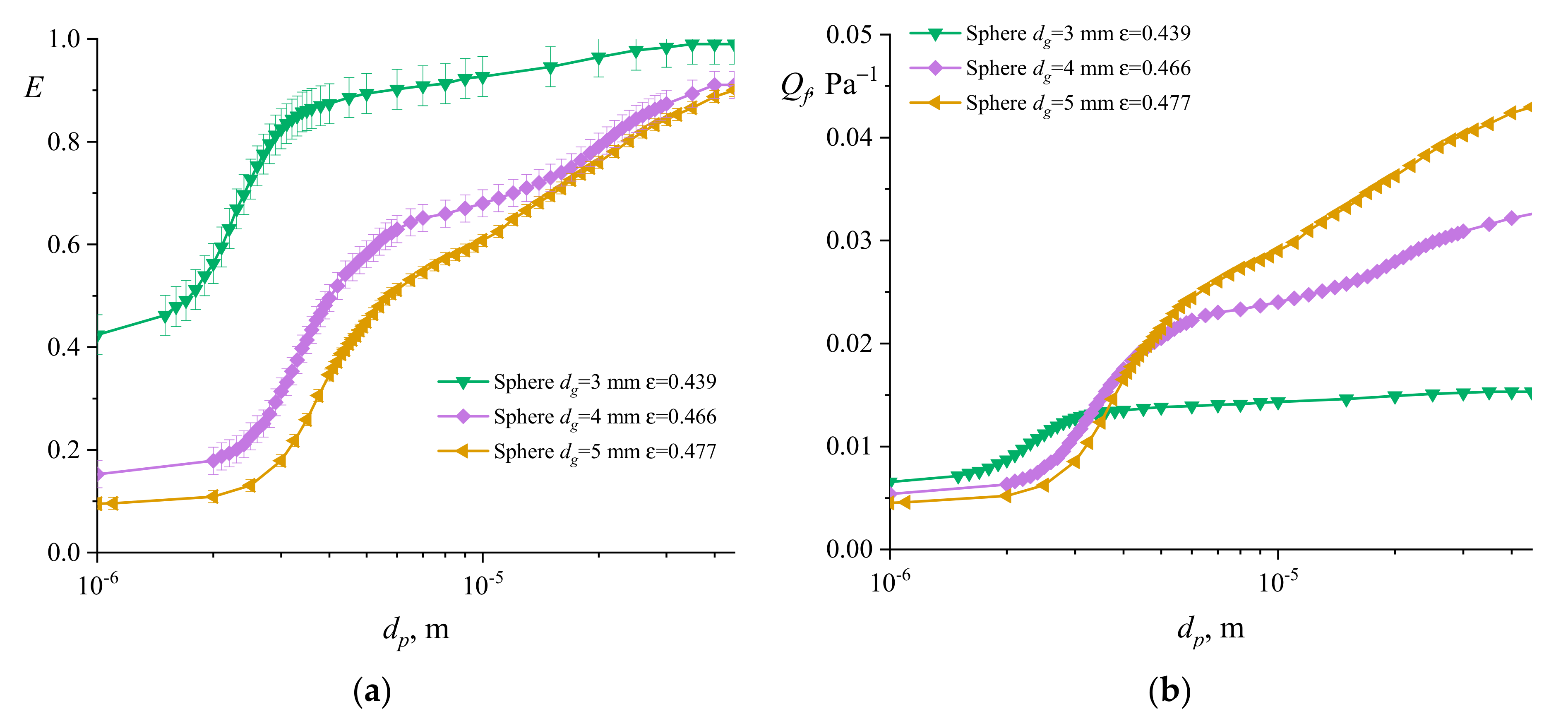
3.1. Numerical Simulation of the Aerosol Motion in a Granular Filter with Solid Spherical Granules
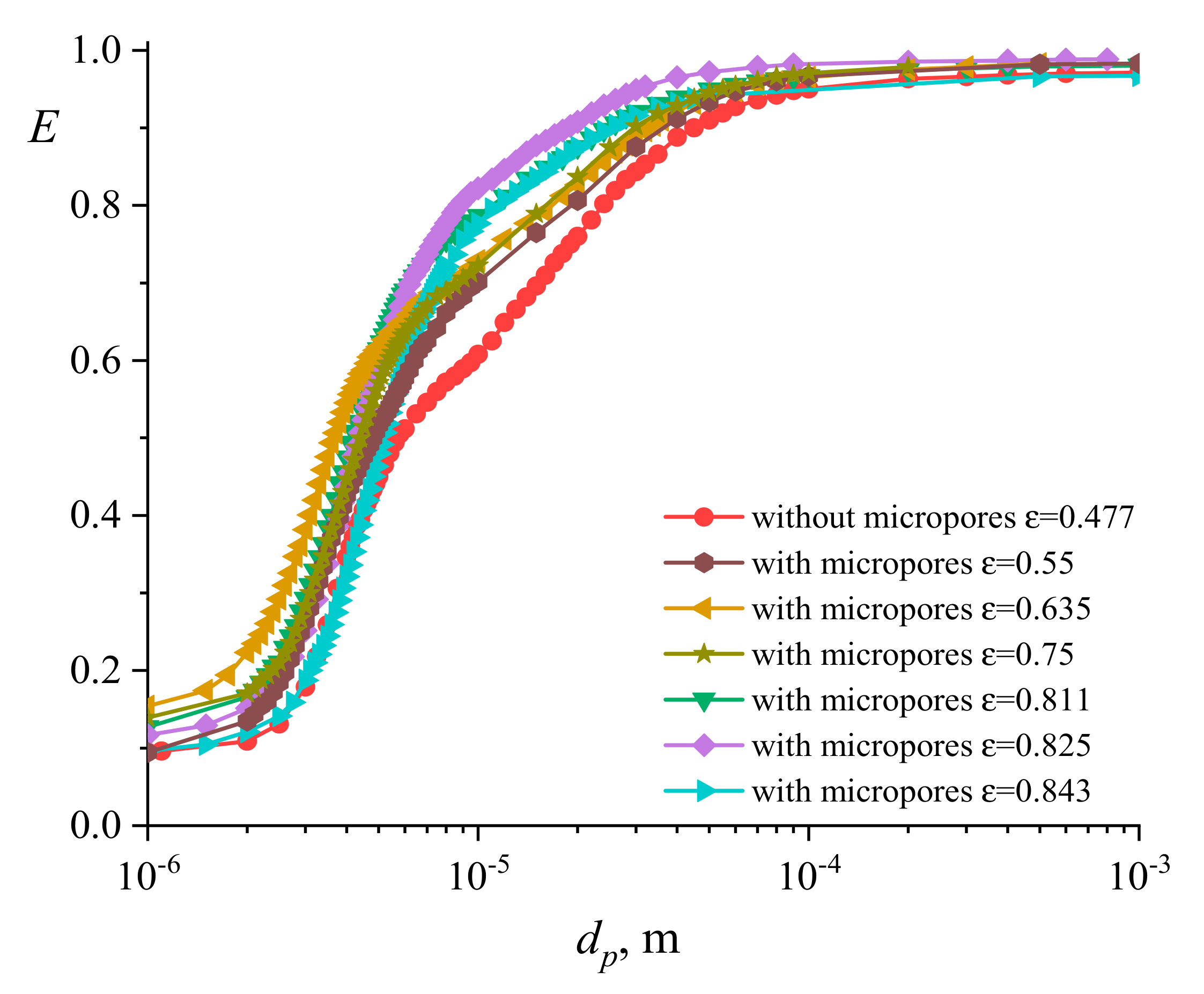
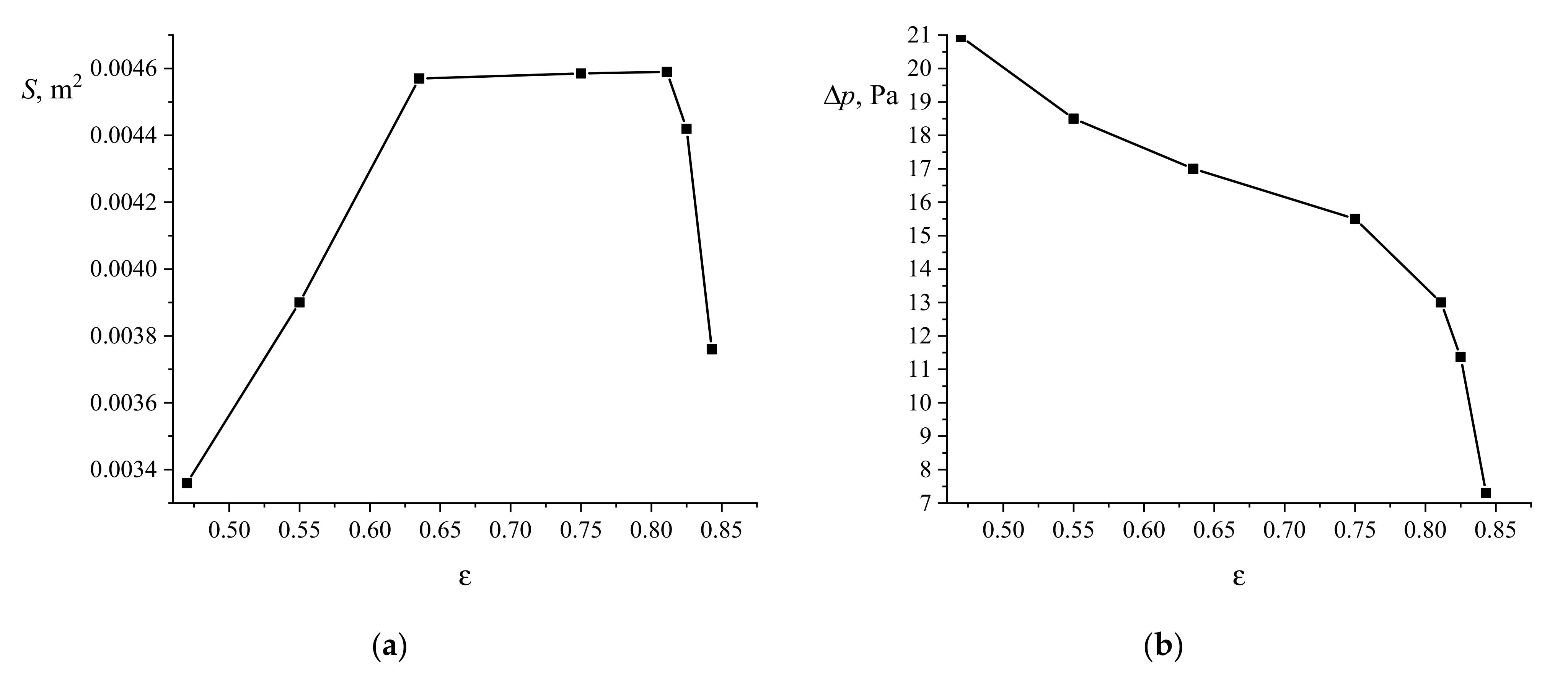
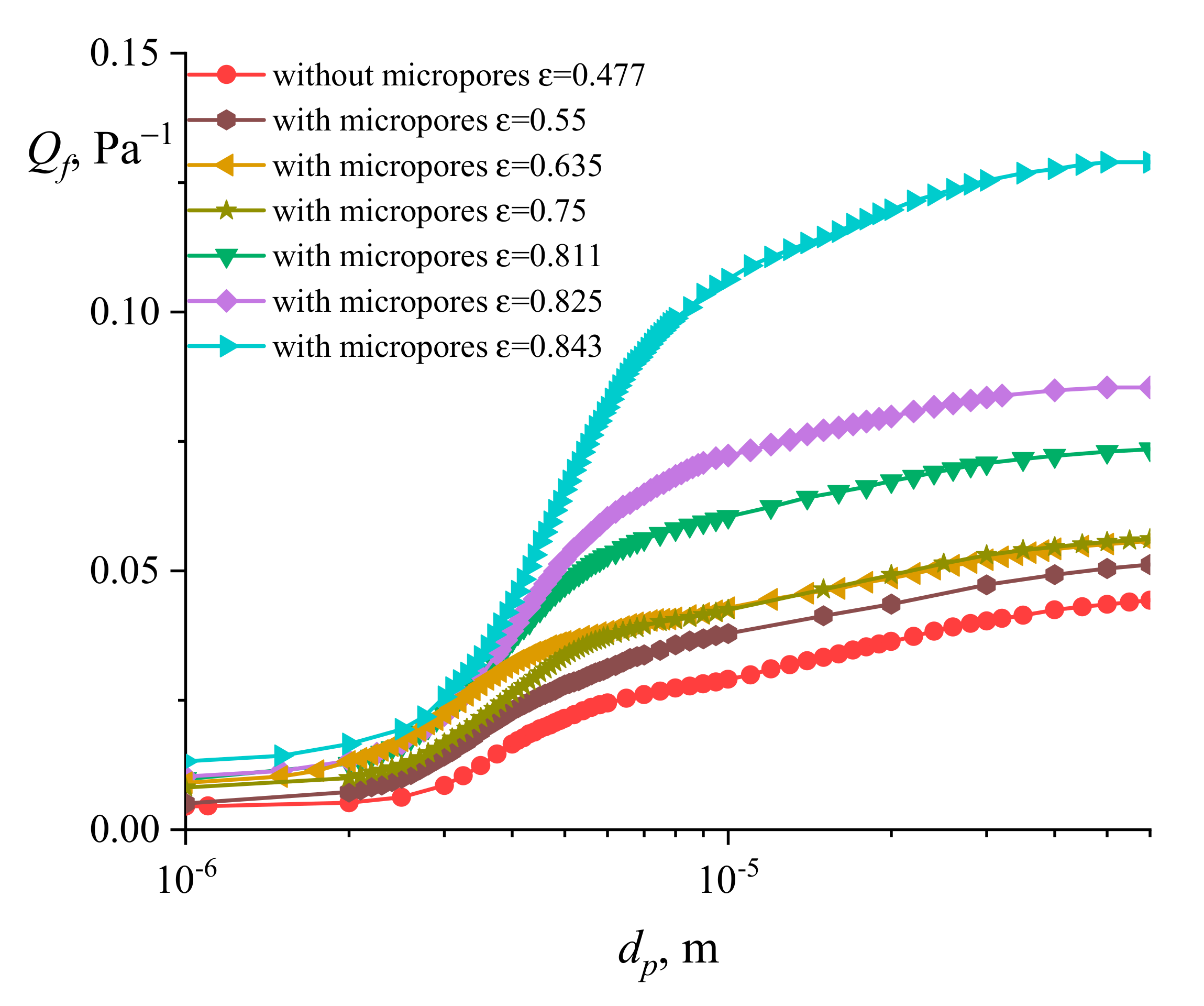
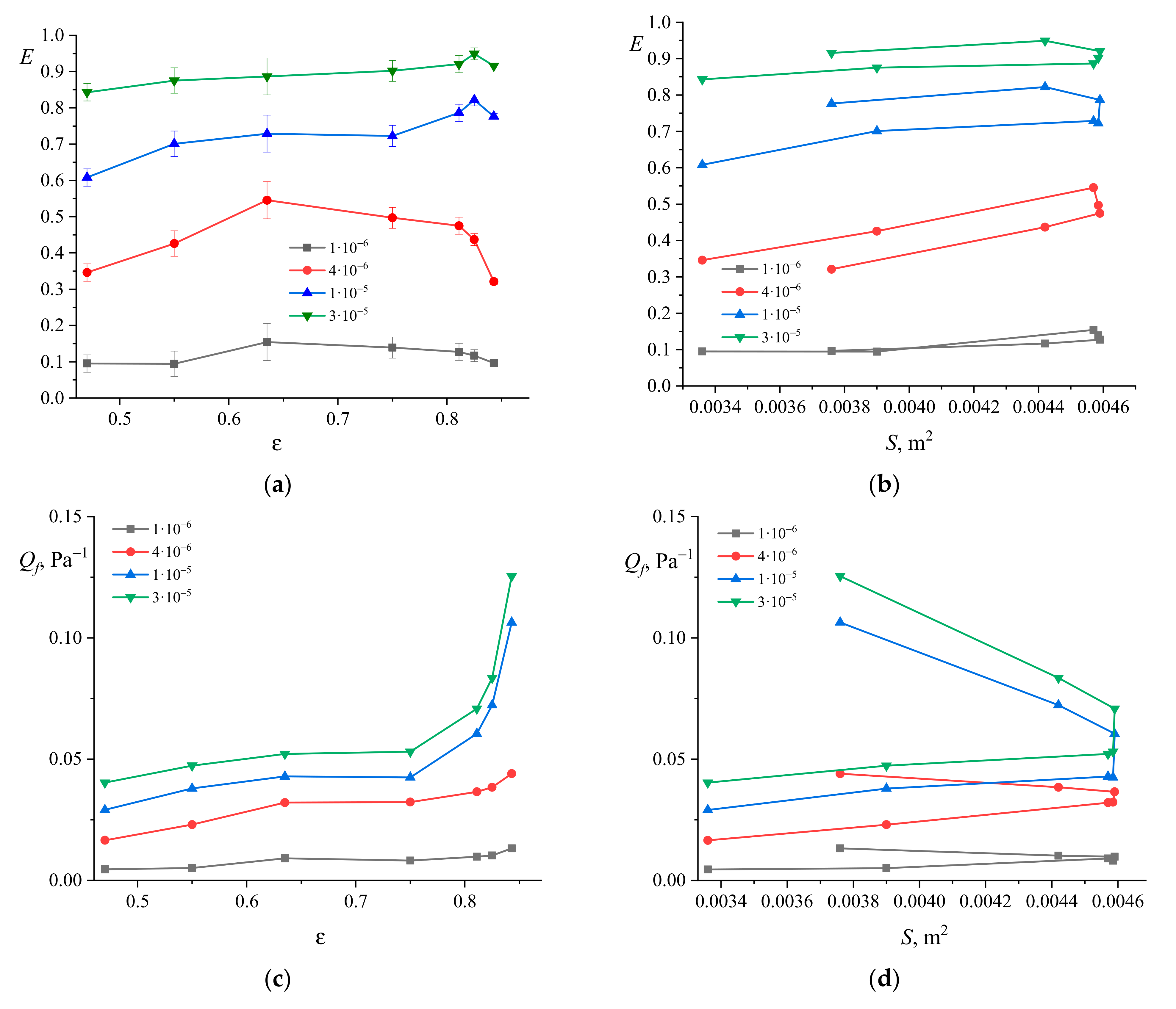
3.2. Numerical Simulation of the Aerosol Motion in a Granular Filter with Porous Spherical Granules
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jaeger, H.M.; Nagel, S.R.; Behringer, R.P. Granular solids, liquids, and gases. Rev. Mod. Phys. 1996, 68, 1259–1273. [Google Scholar] [CrossRef]
- Cai, J.; Dong, H.; Fu, W. Study on Particle Flow in Shaft Moving Beds. J. Northeast. Univ. Nat. Sci. 2007, 28, 1599–1603. [Google Scholar]
- Tien, C.; Ramarao, B.V. Macroscopic description of fixed-bed granular filtration. In Granular Filtration of Aerosols and Hydrosols; Elsevier: Amsterdam, The Netherlands, 1989; pp. 17–47. [Google Scholar]
- El-Hedok, I.A.; Whitmer, L.; Brown, R.C. The influence of granular flow rate on the performance of a moving bed granular filter. Powder Technol. 2011, 214, 69–76. [Google Scholar] [CrossRef]
- Altmann, J.; Rehfeld, D.; Träder, K.; Sperlich, A.; Jekel, M. Combination of granular activated carbon adsorption and deep-bed filtration as a single advanced wastewater treatment step for organic micropollutant and phosphorus removal. Water Res. 2016, 92, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.J.; Hsiau, S.S. A study of filtration performance in a cross-flow moving granular bed filter: The influence of gas flow uniformity. Powder Technol. 2015, 274, 20–27. [Google Scholar] [CrossRef]
- Hsu, C.J.; Hsiau, S.S.; Chen, Y.S.; Smid, J. Investigation of the gas inlet velocity distribution in a fixed granular bed filter. Adv. Powder Technol. 2010, 21, 614–622. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, X.; Zhang, J.; Ni, M.; Gao, X.; Luo, Z.; Cen, K. Granular bed filter: A promising technology for hot gas clean-up. Powder Technol. 2013, 244, 93–99. [Google Scholar] [CrossRef]
- Gutfinger, C.; Tardos, G.I. Theoretical and experimental investigation on granular bed dust filters. Atmos. Environ. 1979, 13, 853–867. [Google Scholar] [CrossRef]
- Brown, R.C.; Shi, H.; Colver, G.; Soo, S.C. Similitude study of a moving bed granular filter. Powder Technol. 2003, 138, 201–210. [Google Scholar]
- Çarpinlioğlu, M.Ö.; Özahi, E. A simplified correlation for fixed bed pressure drop. Powder Technol. 2008, 187, 94–101. [Google Scholar]
- Kuo, Y.M.; Huang, S.H.; Lin, W.Y.; Hsiao, M.F.; Chen, C.C. Filtration and loading characteristics of granular bed filters. J. Aerosol Sci. 2010, 41, 223–229. [Google Scholar] [CrossRef]
- Solovev, S.A.; Soloveva, O.V.; Popkova, O.S. Numerical simulation of the motion of aerosol particles in open cell foam materials. Russ. J. Phys. Chem. A 2018, 92, 601–604. [Google Scholar] [CrossRef]
- Zaripov, S.K.; Soloveva, O.V.; Skvortsov, E.V. Analytical model of the transport of aerosol particles in a circular hole inside a porous medium. Transp. Porous Media 2015, 107, 141–151. [Google Scholar] [CrossRef]
- Soloveva, O.V.; Solovev, S.A.; Khusainov, R.R. Evaluation of the efficiency of prefilter models using numerical simulation. J. Phys. Conf. Ser. 2019, 1399, 022059. [Google Scholar] [CrossRef]
- Soloveva, O.V.; Solovev, S.A.; Yafizov, R.R. Study of the influence of the add of micropores on filtering characteristics of high porous structures. Ecol. Ind. Russ. 2020, 24, 39–43. [Google Scholar] [CrossRef]
- Soloveva, O. Study of aerosol motion in granular and foam filters with equal porosity of the structure. Adv. Intell. Syst. Comput. 2021, 1259, 638–649. [Google Scholar]
- Soloveva, O.; Solovev, S.; Khusainov, R.; Yafizov, R. Mathematical modelling of heat transfer in open cell foam of different porosities. Adv. Intell. Syst. Comput. 2021, 1259, 371–382. [Google Scholar]
- Choi, J.H.; Choi, K.B.; Kim, P.; Shun, D.W.; Kim, S.D. The effect of temperature on particle entrainment rate in a gas fluidized bed. Powder Technol. 1997, 92, 127–133. [Google Scholar] [CrossRef]
- Wey, M.Y.; Chen, K.H.; Liu, K.Y. The effect of ash and filter media characteristics on particle filtration efficiency in fluidized bed. J. Hazard. Mater. 2005, 121, 175–181. [Google Scholar] [CrossRef]
- Liu, K.Y.; Wey, M.Y. Filtration of nano-particles by a gas–solid fluidized bed. J. Hazard. Mater. 2007, 147, 618–624. [Google Scholar] [CrossRef]
- Tian, S.R.; Yang, G.H.; Li, Z.; Shi, K.Y.; Ding, G.Z.; Hu, F.X. Cascade filtration properties of a dual-layer granular bed filter. Powder Technol. 2016, 301, 545–556. [Google Scholar] [CrossRef]
- Paenpong, C.; Pattiya, A. Filtration of fast pyrolysis char fines with a cross-flow moving-bed granular filter. Powder Technol. 2013, 245, 233–240. [Google Scholar] [CrossRef]
- Yang, G.; Zhou, J. Experimental study on a new dual-layer granular bed filter for removing particulates. J. China Univ. Min. Technol. 2007, 17, 201–204. [Google Scholar] [CrossRef]
- Yu, Y.S.; Tao, Y.B.; Ma, Z.; He, Y.L. Experimental study and optimization on filtration and fluid flow performance of a granular bed filter. Powder Technol. 2018, 333, 449–457. [Google Scholar] [CrossRef]
- Bakhshian, S.; Sahimi, M. Computer simulation of the effect of deformation on the morphology and flow properties of porous media. Phys. Rev. E 2016, 94, 042903. [Google Scholar] [CrossRef] [Green Version]
- Bakhshian, S.; Sahimi, M. Adsorption-induced swelling of porous media. Int. J. Greenh. Gas Control 2017, 57, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Guan, L.; Gu, Z.; Yuan, Z.; Yang, L.; Zhong, W.; Wu, Y.; Sun, S. Numerical study on the penetration of ash particles in a three-dimensional randomly packed granular filter. Fuel 2016, 163, 122–128. [Google Scholar] [CrossRef]
- Guan, L.; Yuan, Z.; Gu, Z.; Yang, L.; Zhong, W.; Wu, Y.; Sun, Sh.; Gu, C. Numerical simulation of ash particle deposition characteristics on the granular surface of a randomly packed granular filter. Powder Technol. 2017, 314, 78–88. [Google Scholar] [CrossRef]
- Wang, F.L.; He, Y.L.; Tang, S.Z.; Kulacki, F.A.; Tao, Y.B. Particle filtration characteristics of typical packing granular filters used in hot gas clean-up. Fuel 2018, 234, 9–19. [Google Scholar] [CrossRef]
- Wang, F.L.; He, Y.L.; Tang, S.Z.; Kulacki, F.A.; Tao, Y.B. Real-time particle filtration of granular filters for hot gas clean-up. Fuel 2019, 237, 308–319. [Google Scholar] [CrossRef]
- Chen, J.; Li, X.; Huai, X.; Wang, Y.; Zhou, J. Numerical study of collection efficiency and heat-transfer characteristics of packed granular filter. Particuology 2019, 46, 75–82. [Google Scholar] [CrossRef]
- Yang, J.; Bu, S.; Dong, Q.; Wu, J.; Wang, Q. Experimental study of flow transitions in random packed beds with low tube to particle diameter ratios. Exp. Therm. Fluid Sci. 2015, 66, 117–126. [Google Scholar] [CrossRef]
- Freund, H.; Zeiser, T.; Huber, F.; Klemm, E.; Brenner, G.; Durst, F.; Emig, G. Numerical simulations of single phase reacting flows in randomly packed fixed-bed reactors and experimental validation. Chem. Eng. Sci. 2003, 58, 903–910. [Google Scholar] [CrossRef]
- Gunjal, P.R.; Ranade, V.V. Modeling of laboratory and commercial scale hydro-processing reactors using CFD. Chem. Eng. Sci. 2007, 62, 5512–5526. [Google Scholar] [CrossRef]
- Gunjal, P.R.; Kashid, M.N.; Ranade, V.V.; Chaudhari, R.V. Hydrodynamics of trickle-bed reactors: Experiments and CFD modeling. Ind. Eng. Chem. Res. 2005, 44, 6278–6294. [Google Scholar] [CrossRef]
- Gunjal, P.R.; Ranade, V.V.; Chaudhari, R.V. Computational study of a single-phase flow in packed beds of spheres. AIChE J. 2005, 51, 365–378. [Google Scholar] [CrossRef]
- Ranade, V.V. Computational Flow Modeling for Chemical Reactor Engineering; Academic Press: San Diego, CA, USA, 2002; 452p. [Google Scholar]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Shire, T.; O’Sullivan, C. Constriction size distributions of granular filters: A numerical study. Geotechnique 2016, 66, 826–839. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Li, S. DEM simulation of wet granular-fluid flows in spouted beds: Numerical studies and experimental verifications. Powder Technol. 2017, 318, 337–349. [Google Scholar] [CrossRef]
- Kh, A.B.; Mirghasemi, A.A.; Mohammadi, S. Numerical simulation of particle breakage of angular particles using combined DEM and FEM. Powder Technol. 2011, 205, 15–29. [Google Scholar]
- Santos, D.A.; Barrozo, M.A.; Duarte, C.R.; Weigler, F.; Mellmann, J. Investigation of particle dynamics in a rotary drum by means of experiments and numerical simulations using DEM. Adv. Powder Technol. 2016, 27, 692–703. [Google Scholar] [CrossRef]
- Khan, H.J.; Mirabolghasemi, M.S.; Yang, H.; Prodanović, M.; DiCarlo, D.A.; Balhoff, M.T. Study of formation damage caused by retention of bi-dispersed particles using combined pore-scale simulations and particle flooding experiments. J. Pet. Sci. Eng. 2017, 158, 293–308. [Google Scholar] [CrossRef]
- Guo, Y.; Wassgren, C.; Ketterhagen, W.; Hancock, B.; James, B.; Curtis, J. A numerical study of granular shear flows of rod-like particles using the discrete element method. J. Fluid Mech. 2012, 713, 1–26. [Google Scholar] [CrossRef]
- He, Y.; Bayly, A.E.; Hassanpour, A.; Muller, F.; Wu, K.; Yang, D. A GPU-based coupled SPH-DEM method for particle-fluid flow with free surfaces. Powder Technol. 2018, 338, 548–562. [Google Scholar] [CrossRef]
- Guo, Y.; Curtis, J.S. Discrete element method simulations for complex granular flows. Annu. Rev. Fluid Mech. 2015, 47, 21–46. [Google Scholar] [CrossRef]
- Shams, A.; Roelofs, F.; Komen, E.M.J.; Baglietto, E. Large eddy simulation of a nuclear pebble bed configuration. Nucl. Eng. Des. 2013, 261, 10–19. [Google Scholar] [CrossRef]
- Matuttis, H.G. Simulation of the pressure distribution under a two-dimensional heap of polygonal particles. Granul. Matter 1998, 1, 83–91. [Google Scholar] [CrossRef]
- Matuttis, H.G.; Luding, S.; Herrmann, H.J. Discrete element simulations of dense packings and heaps made of spherical and non-spherical particles. Powder Technol. 2000, 109, 278–292. [Google Scholar] [CrossRef]
- Lu, G.; Third, J.R.; Müller, C.R. Discrete element models for non-spherical particle systems: From theoretical developments to applications. Chem. Eng. Sci. 2015, 127, 425–465. [Google Scholar] [CrossRef]
- Zhu, J.; Liang, Y.; Zhou, Y. The effect of the particle aspect ratio on the pressure at the bottom of sandpiles. Powder Technol. 2013, 234, 37–45. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Zou, R.P.; Pinson, D.; Yu, A.B. Angle of repose and stress distribution of sandpiles formed with ellipsoidal particles. Granul. Matter 2014, 16, 695–709. [Google Scholar] [CrossRef]
- Van Buijtenen, M.S.; Buist, K.; Deen, N.G.; Kuipers, J.A.M.; Leadbeater, T.; Parker, D.J. Numerical and experimental study on spout elevation in spout-fluidized beds. AIChE J. 2012, 58, 2524–2535. [Google Scholar] [CrossRef]
- Yu, Y.-S.; Tao, Y.-B.; He, Y.; He, Y.-L. Structure optimization of granular bed filter for industrial flue gas filtration containing coagulative particles: An experimental and numerical study. Adv. Powder Technol. 2020, 31, 2244–2256. [Google Scholar] [CrossRef]
- Wang, F.-L.; Tang, S.-Z.; He, Y.-L.; Kulacki, F.A.; Tao, Y.-B. Parameter study of filtration characteristics of granular filters for hot gas clean-up. Powder Technol. 2019, 353, 267–275. [Google Scholar] [CrossRef]
- Yu, Y.-S.; Tao, Y.-B.; Wang, F.-L.; Chen, X.; He, Y-L. Filtration performance of the granular bed filter used for industrial flue gas purification: A review of simulation and experiment. Sep. Purif. Technol. 2020, 251, 117318. [Google Scholar] [CrossRef]
- Cheng, H.; Shuku, T.; Thoeni, K.; Tempone, P.; Luding, S.; Magnanimo, V. An iterative Bayesian filtering framework for fast and automated calibration of DEM models. Comput. Methods Appl. Mech. Eng. 2019, 350, 268–294. [Google Scholar] [CrossRef]
- Benyahia, F.; O’Neill, K.E. Enhanced voidage correlations for packed beds of various particle shapes and sizes. Part. Sci. Technol. 2005, 23, 169–177. [Google Scholar] [CrossRef]
- Gosman, A.D.; Ioannides, E. Aspects of computer simulation of liquid-fuelled combustors. J. Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Tafreshi, H.V. Modeling particle filtration in disordered 2-D domains: A comparison with cell models. Sep. Purif. Technol. 2010, 74, 160–169. [Google Scholar] [CrossRef]
- Jin, X.; Yang, L.; Du, X. Modeling filtration performance of elliptical fibers with random distributions. Adv. Powder Technol. 2017, 28, 1193–1201. [Google Scholar] [CrossRef]
- Ergun, S.; Orning, A.A. Fluid flow through randomly packed columns and fluidized beds. Ind. Eng. Chem. 1949, 41, 1179–1184. [Google Scholar] [CrossRef]
- Eisfeld, B.; Schnitzlein, K. The influence of confining walls on the pressure drop in packed beds. Chem. Eng. Sci. 2001, 56, 4321–4329. [Google Scholar] [CrossRef]
- Hinds, W.C. Aerosol Technology Properties, Behavior, and Measurement of Airborne Particles; John Wiley and Sons: Hoboken, NJ, USA, 1999; 504p. [Google Scholar]
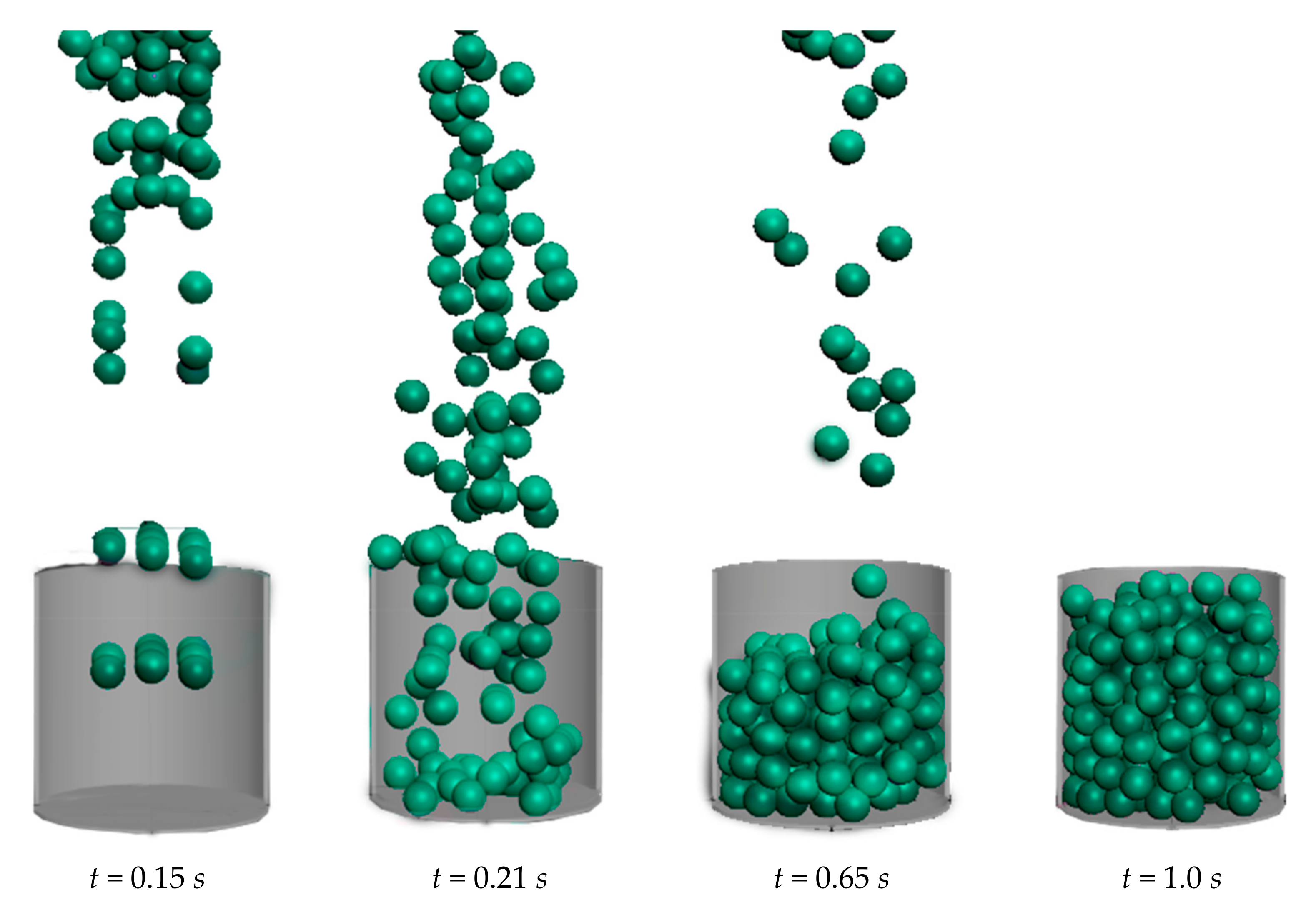
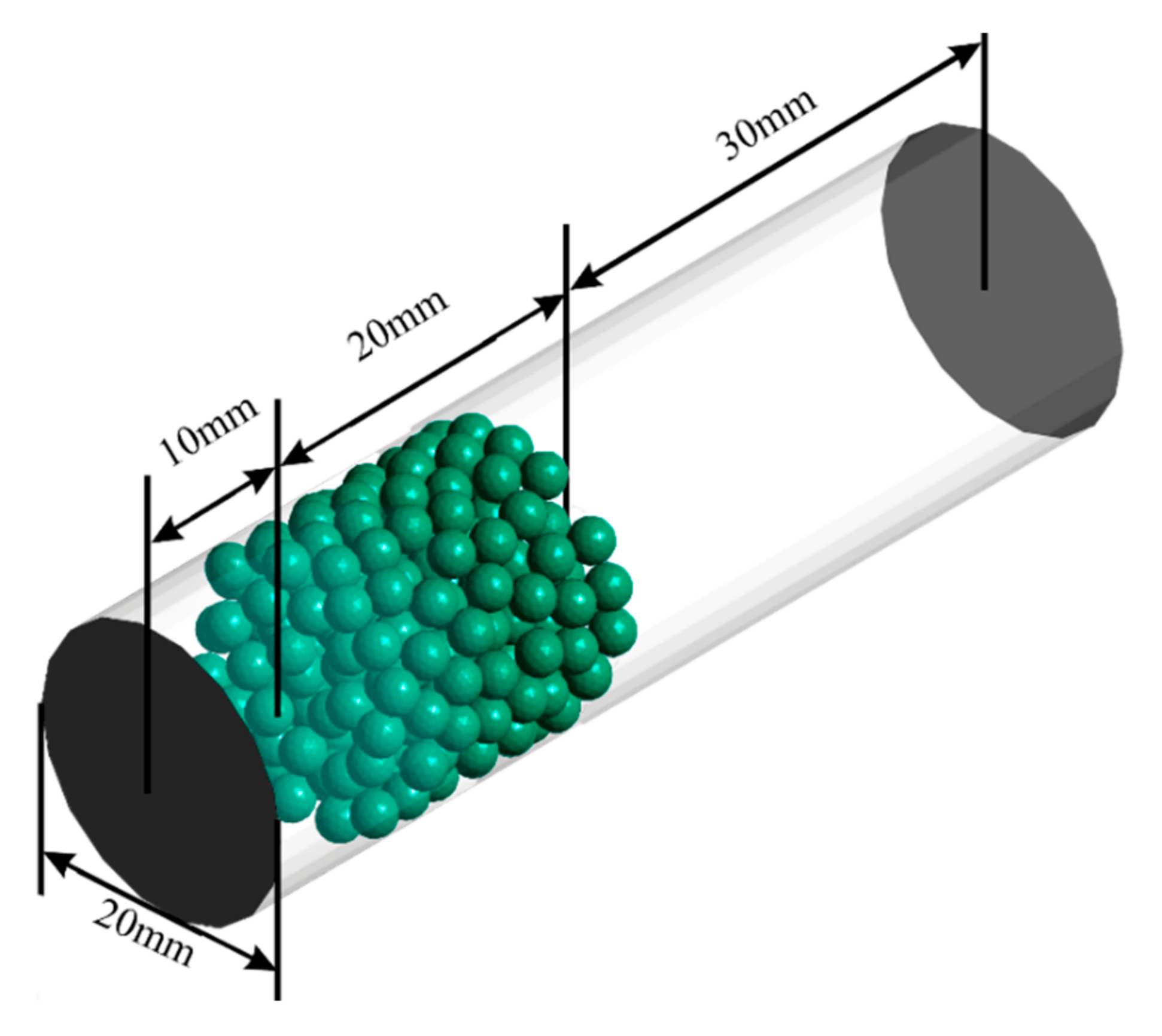

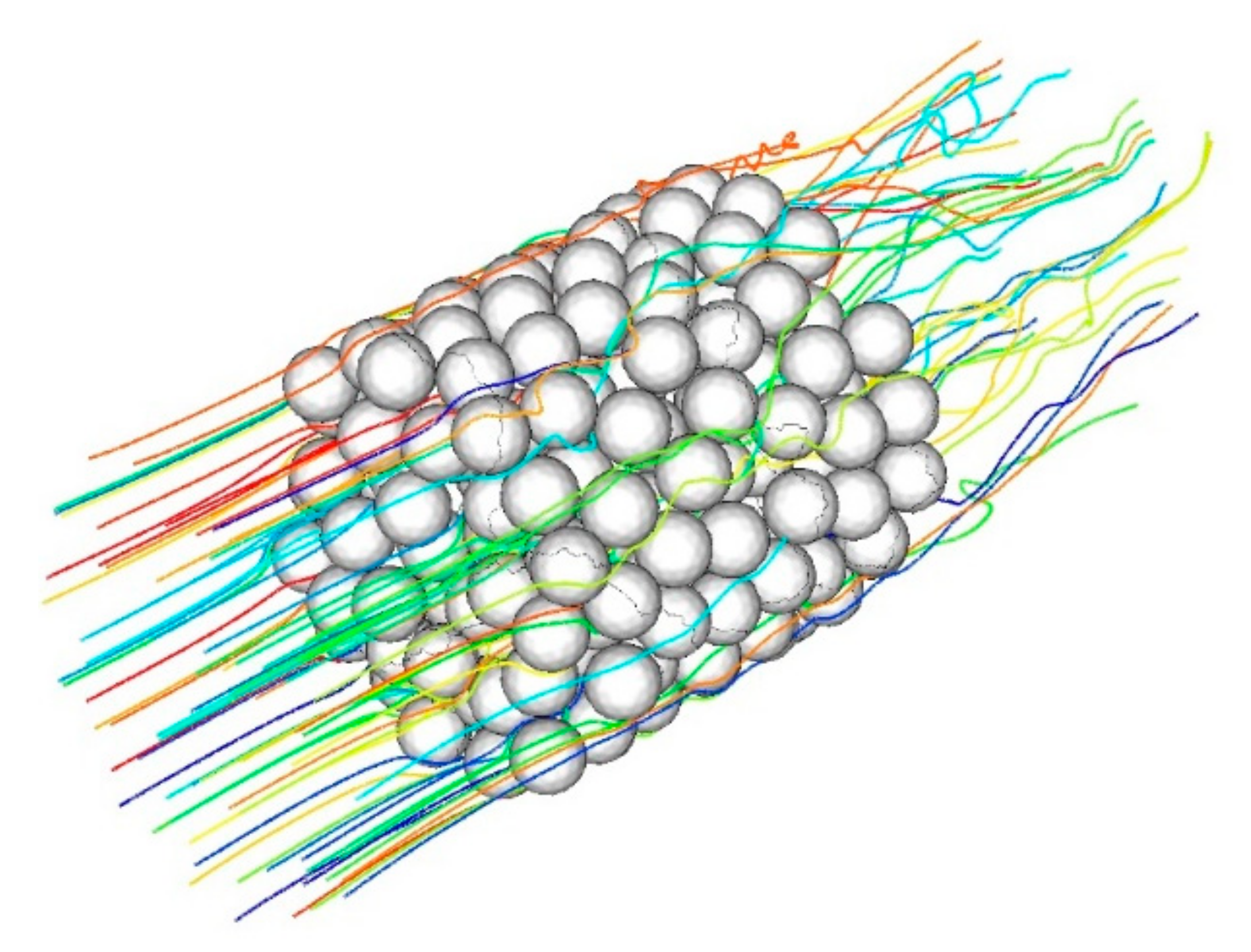
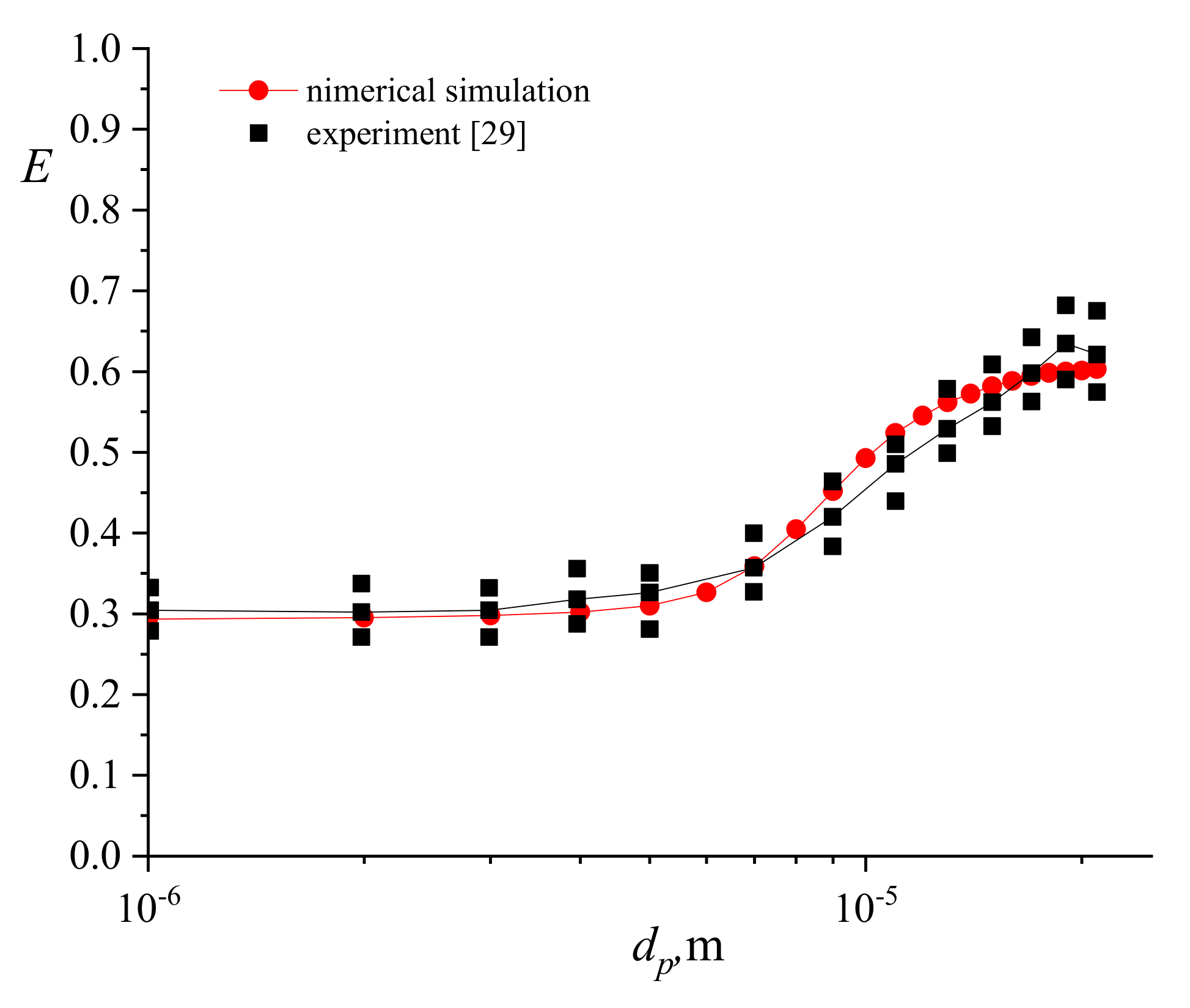

| Granule Diameter , mm | Tube to Granule Diameter Ratio | Porosity | Porosity, Calculated by the Formula (1) |
|---|---|---|---|
| 3 | 6.67 | 0.439 | 0.418 |
| 4 | 5 | 0.466 | 0.436 |
| 5 | 4 | 0.477 | 0.455 |
| Macroporosity | Microporosity | Total Porosity |
|---|---|---|
| 0.477 | 0.073 | 0.550 |
| 0.158 | 0.635 | |
| 0.273 | 0.750 | |
| 0.334 | 0.811 | |
| 0.348 | 0.825 | |
| 0.366 | 0.843 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soloveva, O.V.; Solovev, S.A.; Yafizov, R.R. Numerical Simulation of the Aerosol Particle Motion in Granular Filters with Solid and Porous Granules. Processes 2021, 9, 268. https://doi.org/10.3390/pr9020268
Soloveva OV, Solovev SA, Yafizov RR. Numerical Simulation of the Aerosol Particle Motion in Granular Filters with Solid and Porous Granules. Processes. 2021; 9(2):268. https://doi.org/10.3390/pr9020268
Chicago/Turabian StyleSoloveva, Olga V., Sergei A. Solovev, and Ruzil R. Yafizov. 2021. "Numerical Simulation of the Aerosol Particle Motion in Granular Filters with Solid and Porous Granules" Processes 9, no. 2: 268. https://doi.org/10.3390/pr9020268
APA StyleSoloveva, O. V., Solovev, S. A., & Yafizov, R. R. (2021). Numerical Simulation of the Aerosol Particle Motion in Granular Filters with Solid and Porous Granules. Processes, 9(2), 268. https://doi.org/10.3390/pr9020268








