Insights into Equilibrium and Adsorption Rate of Phenol on Activated Carbon Pellets Derived from Cigarette Butts
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of Hierarchical Activated Carbon
2.3. Chemical and Textural Characterization
2.4. CBs and Activated Carbon Leaching Test
2.5. Adsorbate
2.6. Equilibrium Experiments
2.7. Obtaining the Concentration Decay Curves
3. Results
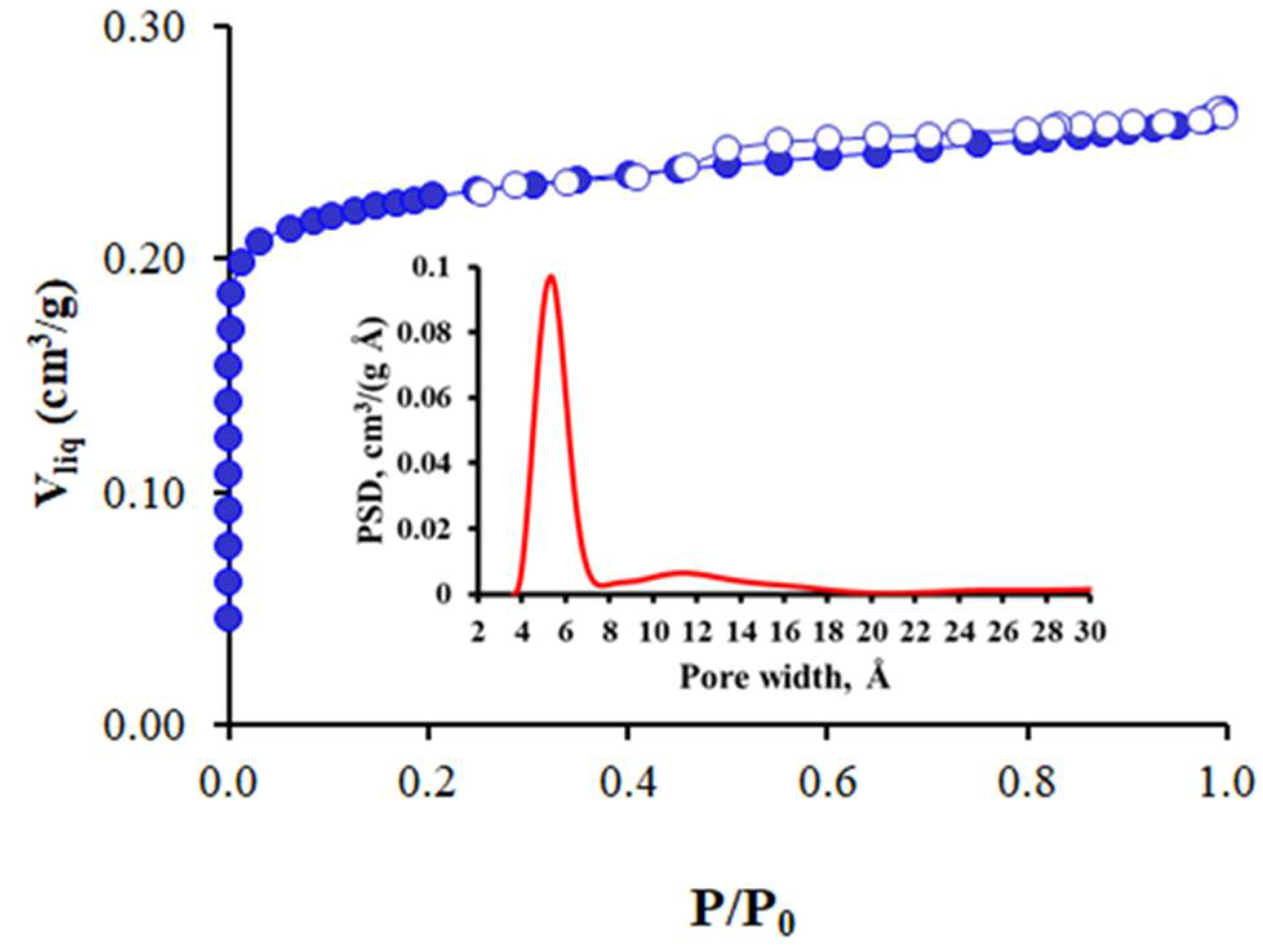
3.1. Characterization of CBs and Activated Carbon Pellets
3.2. Leaching Tests
3.3. Effect of Temperature, Type of Water, and Solution pH on Adsorption Equilibrium
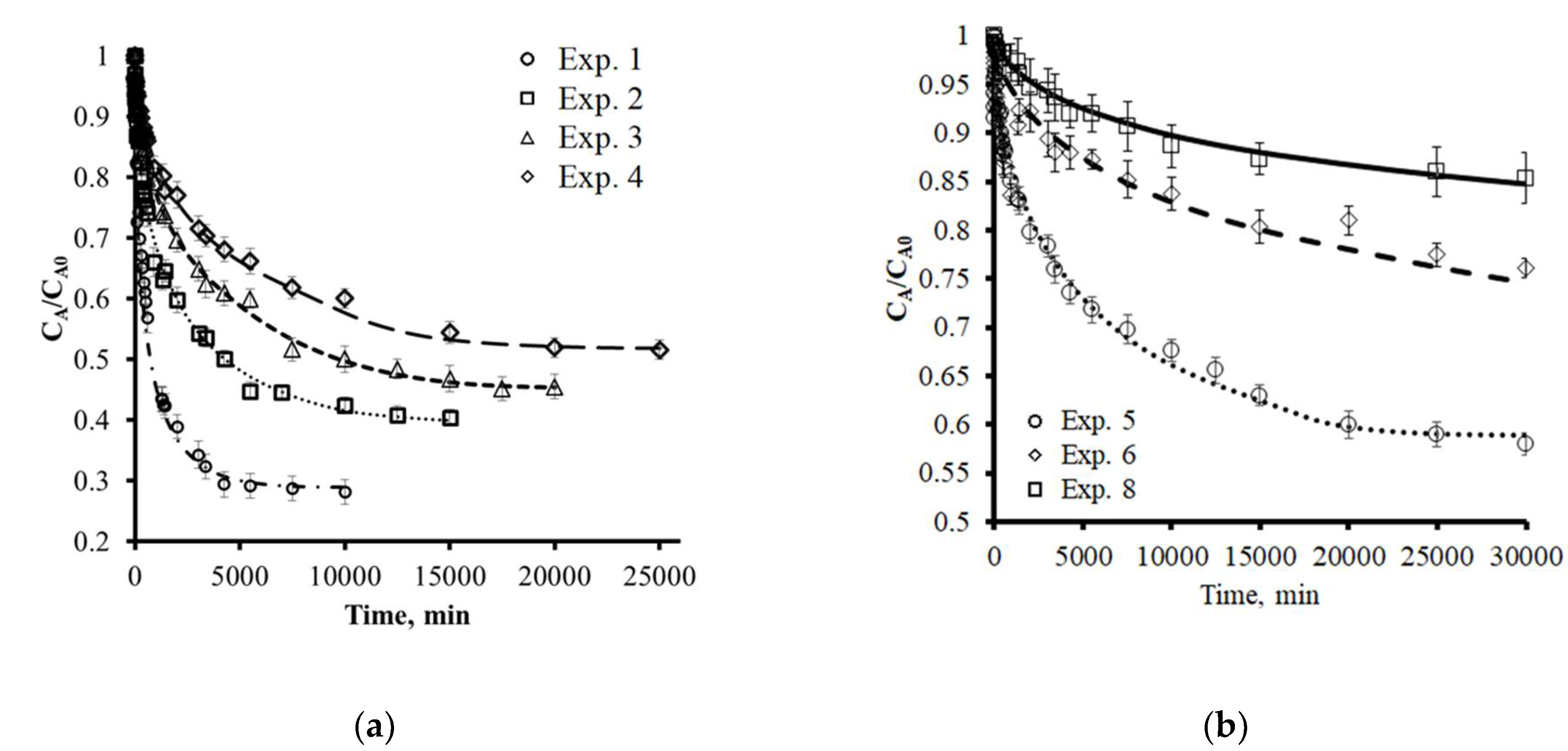
3.4. Adsorption Rate
4. Conclusions
Perspectives
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marinello, S.; Lolli, F.; Gamberini, R.; Rimini, B. A second life for cigarette butts? A review of recycling solutions. J. Hazard. Mater. 2020, 384, 121245. [Google Scholar] [CrossRef] [PubMed]
- Kurmus, H.; Mohajerani, A. The toxicity and valorization options of cigarette butts. Waste Manag. 2020, 104, 104–118. [Google Scholar] [CrossRef] [PubMed]
- Araújo, M.C.B.; Costa, M.F. A critical review of the issue of cigarette butt pollution in coastal environments. Environ. Res. 2019, 172, 137–149. [Google Scholar] [CrossRef]
- Alhokbany, N.S.; Naushad, M.; Kumar, V.; Al hatim, S.; Alshehri, S.M.; Ahamad, T. Self-nitrogen doped carbons aerogel derived from waste cigarette butts (cellulose acetate) for the adsorption of BPA: Kinetics and adsorption mechanisms. J. King Saud Univ. Sci. 2020, 32, 3351–3358. [Google Scholar] [CrossRef]
- Abu-Danso, E.; Bagheri, A.; Bhatnagar, A. Facile functionalization of cellulose from discarded cigarette butts for the removal of diclofenac from water. Carbohydr. Polym. 2019, 219, 46–55. [Google Scholar] [CrossRef]
- Aldieri, L.; Ioppolo, G.; Vinci, C.P.; Yigitcanlar, T. Waste recycling patents and environmental innovations: An economic analysis of policy instruments in the USA, Japan and Europe. Waste Manag. 2019, 95, 612–619. [Google Scholar] [CrossRef]
- Conradi, E.; Gonçalves, A.C.; Schwantes, D.; Manfrin, J.; Schiller, A.; Zimmerman, J.; Klassen, G.J.; Ziemer, G.L. Development of renewable adsorbent from cigarettes for lead removal from water. J. Environ. Chem. Eng. 2019, 7. [Google Scholar] [CrossRef]
- Lima, H.H.C.; Maniezzo, R.S.; Kupfer, V.L.; Guilherme, M.R.; Moises, M.P.; Arroyo, P.A.; Rinaldi, A.W. Hydrochars based on cigarette butts as a recycled material for the adsorption of pollutants. J. Environ. Chem. Eng. 2018, 6, 7054–7061. [Google Scholar] [CrossRef]
- Manfrin, J.; Gonçalves, A.C., Jr.; Schwantes, D.; Conradi, E., Jr.; Zimmermann, J.; Ziemer, G.L. Development of biochar and activated carbon from cigarettes wastes and their applications in Pb2+ adsorption. J. Environ. Chem. Eng. 2021, 9, 104980. [Google Scholar] [CrossRef]
- Lv, S.; Li, C.; Mi, J.; Meng, H. A functional activated carbon for efficient adsorption of phenol derived from pyrolysis of rice husk, KOH-activation and EDTA−4Na-modification. Appl. Surf. Sci. 2020, 510, 145425. [Google Scholar] [CrossRef]
- Alves, D.C.S.; Coseglio, B.B.; Pinto, L.A.A.; Cadaval, T.R.S. Development of Spirulina/chitosan foam adsorbent for phenol adsorption. J. Mol. Liq. 2020, 309, 113256. [Google Scholar] [CrossRef]
- Koochaki, C.B.; Khajavi, R.; Rashidi, A.; Mansouri, N.; Yazdanshenas, M.E. The effect of pre-swelling on the characteristics of obtained activated carbon from cigarette butts fibers. Biomass Convers. Biorefinery 2020, 10, 227–236. [Google Scholar] [CrossRef]
- Bardestani, R.; Patience, G.S.; Kaliaguine, S. Experimental methods in chemical engineering: Specific surface area and pore size distribution measurements—BET, BJH, and DFT. Can. J. Chem. Eng. 2019, 97, 2781–2791. [Google Scholar] [CrossRef]
- Bachmann, H.J.; Bucheli, T.D.; Dieguez-Alonso, A.; Fabbri, D.; Knicker, H.; Schmidt, H.P.; Ulbricht, A.; Becker, R.; Buscaroli, A.; Buerge, D.; et al. Toward the standardization of biochar analysis: The COST action TD1107 interlaboratory comparison. J. Agric. Food Chem. 2016, 64, 513–527. [Google Scholar] [CrossRef]
- Moreno-Castilla, C.; Rivera-Utrilla, J.; Carrasco-Marín, F.; López-Ramón, M.V. On the carbon dioxide and benzene adsorption on activated carbons to study their micropore structure. Langmuir 1997, 13, 5208–5209. [Google Scholar] [CrossRef]
- Landers, J.; Gor, G.Y.; Neimark, A.V. Density functional theory methods for characterization of porous materials. Colloids Surf. A Physicochem. Eng. Asp. 2013, 437, 3–32. [Google Scholar] [CrossRef]
- Boehm, H.P. Some aspects of the surface chemistry of carbon blacks and other carbons. Carbon N. Y. 1994, 32, 759–769. [Google Scholar] [CrossRef]
- Lorenc-grabowska, E. Effect of micropore size distribution on phenol adsorption on steam activated carbons. Adsorption 2016, 22, 599–607. [Google Scholar] [CrossRef] [Green Version]
- Leyva-Ramos, R.; Ocampo-Perez, R.; Mendoza-Barron, J. External mass transfer and hindered diffusion of organic compounds in the adsorption on activated carbon cloth. Chem. Eng. J. 2012, 183, 141–151. [Google Scholar] [CrossRef]
- Ocampo-Perez, R.; Leyva-Ramos, R.; Alonso-Davila, P.; Rivera-Utrilla, J.; Sanchez-Polo, M. Modeling adsorption rate of pyridine onto granular activated carbon. Chem. Eng. J. 2010, 165, 133–141. [Google Scholar] [CrossRef]
- Masoudi Soltani, S.; Yazdi, S.K.; Hosseini, S. Effects of pyrolysis conditions on the porous structure construction of mesoporous charred carbon from used cigarette filters. Appl. Nanosci. 2014, 4, 551–569. [Google Scholar] [CrossRef] [Green Version]
- Lowell, S.; Shields, J.E.; Thomas, M.A.; Thommes, M. Adsorption isotherms. In Characterization of Porous Solids and Powders: Surface Area, Pore Size and Density; Particle Technology Series; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Miao, Q.; Tang, Y.; Xu, J.; Liu, X.; Xiao, L.; Chen, Q. Activated carbon prepared from soybean straw for phenol adsorption. J. Taiwan Inst. Chem. Eng. 2013, 44, 458–465. [Google Scholar] [CrossRef]
- Lütke, S.F.; Igansi, A.V.; Pegoraro, L.; Dotto, G.L.; Pinto, L.A.A.; Cadaval, T.R.S. Preparation of activated carbon from black wattle bark waste and its application for phenol adsorption. J. Environ. Chem. Eng. 2019, 7, 103396. [Google Scholar] [CrossRef]
- Romero-Cano, L.A.; García-Rosero, H.; Gonzalez-Gutierrez, L.V.; Baldenegro-Pérez, L.A.; Carrasco-Marín, F. Functionalized adsorbents prepared from fruit peels: Equilibrium, kinetic and thermodynamic studies for copper adsorption in aqueous solution. J. Clean. Prod. 2017, 162, 195–204. [Google Scholar] [CrossRef]
- Katepalli, H.; Bikshapathi, M.; Sharma, C.S.; Verma, N.; Sharma, A. Synthesis of hierarchical fabrics by electrospinning of PAN nanofibers on activated carbon microfibers for environmental remediation applications. Chem. Eng. J. 2011, 171, 1194–1200. [Google Scholar] [CrossRef]
- Li, C.; Ma, H.; Venkateswaran, S.; Hsiao, B.S. Highly efficient and sustainable carboxylated cellulose filters for removal of cationic dyes / heavy metals ions. Chem. Eng. J. 2020, 389, 123458. [Google Scholar] [CrossRef]
- El-Hendawy, A.N.A. Variation in the FTIR spectra of a biomass under impregnation, carbonization and oxidation conditions. J. Anal. Appl. Pyrolysis 2006, 75, 159–166. [Google Scholar] [CrossRef]
- Pretsch, E.; Badertscher, M.; Buhlmann, P. Structure Determination of Organic Compounds, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 9783540938095. [Google Scholar]
- Secretaria de Salud NOM−127-SSA1−1994; 1994; pp. 73–79. Available online: http://www.salud.gob.mx/unidades/cdi/nom/127ssa14.html (accessed on 15 April 2021).
- World Health Organization (WHO). Guidelines for Drinking-Water Quality, 4th ed.; 2017; ISBN 9789241549950. Available online: https://www.who.int/publications/i/item/9789241549950 (accessed on 15 April 2021).
- Giles, C.H.; Smith, D.; Huitson, A. A general treatment and classification of the solute adsorption isotherm. I. Theoretical. J. Colloid Interface Sci. 1974, 47, 755–765. [Google Scholar] [CrossRef]
- Zhang, D.; Huo, P.; Liu, W. Behavior of phenol adsorption on thermal modified activated carbon. Chin. J. Chem. Eng. 2016, 24, 446–452. [Google Scholar] [CrossRef]
- Supong, A.; Bhomick, P.C.; Karmaker, R.; Ezung, S.L.; Jamir, L.; Sinha, U.B.; Sinha, D. Experimental and theoretical insight into the adsorption of phenol and 2,4-dinitrophenol onto Tithonia diversifolia activated carbon. Appl. Surf. Sci. 2020, 529, 147046. [Google Scholar] [CrossRef]
- Kong, X.; Gao, H.; Song, X.; Deng, Y.; Zhang, Y. Adsorption of phenol on porous carbon from Toona sinensis leaves and its mechanism. Chem. Phys. Lett. 2020, 739, 137046. [Google Scholar] [CrossRef]
- Lima, E.C.; Hosseini-Bandegharaei, A.; Moreno-Piraján, J.C.; Anastopoulos, I. A critical review of the estimation of the thermodynamic parameters on adsorption equilibria. Wrong use of equilibrium constant in the Van’t Hoof equation for calculation of thermodynamic parameters of adsorption. J. Mol. Liq. 2019, 273, 425–434. [Google Scholar] [CrossRef]
- Summers, R.S.; Haist, B.; Koehler, J.; Ritz, J.; Zimmer, G.; Sontheimer, H. The influence of background organic matter on GAC adsorption. J. Am. Water Work. Assoc. 1989, 81, 66–74. [Google Scholar] [CrossRef]
- Rodrigues, L.A.; da Silva, M.L.C.P.; Alvarez-Mendes, M.O.; dos Reis Coutinho, A.; Thim, G.P. Phenol removal from aqueous solution by activated carbon produced from avocado kernel seeds. Chem. Eng. J. 2011, 174, 49–57. [Google Scholar] [CrossRef]
- Furusawa, T.; Smith, J.M. Fluid—Particle and intraparticle mass transport rates in slurries. Ind. Eng. Chem. Fundam. 1973, 12, 197–203. [Google Scholar] [CrossRef]
- Moreno-Pérez, J.; Pauletto, P.S.; Cunha, A.M.; Bonilla-Petriciolet, Á.; Salau, N.P.G.; Dotto, G.L. Three-dimensional mass transport modeling of pharmaceuticals adsorption inside ZnAl/biochar composite. Colloids Surf. A Physicochem. Eng. Asp. 2021, 614. [Google Scholar] [CrossRef]
- Pauletto, P.S.; Moreno-Pérez, J.; Hernández-Hernández, L.E.; Bonilla-Petriciolet, A.; Dotto, G.L.; Salau, N.P.G. Novel biochar and hydrochar for the adsorption of 2-nitrophenol from aqueous solutions: An approach using the PVSDM model. Chemosphere 2021, 269. [Google Scholar] [CrossRef] [PubMed]
- Flores-Cano, J.V.; Sánchez-Polo, M.; Messoud, J.; Velo-Gala, I.; Ocampo-Pérez, R.; Rivera-Utrilla, J. Overall adsorption rate of metronidazole, dimetridazole and diatrizoate on activated carbons prepared from coffee residues and almond shells. J. Environ. Manage. 2016, 169, 116–125. [Google Scholar] [CrossRef]
- Leyva-Ramos, R.; Geankoplis, C.J. Diffusion in liquid-filled pores of activated carbon. I. Pore volume diffusion. Can. J. Chem. Eng. 1994, 72, 262–271. [Google Scholar] [CrossRef]
- Piai, L.; Dykstra, J.E.; Adishakti, M.G.; Blokland, M.; Langenhoff, A.A.M.; van der Wal, A. Diffusion of hydrophilic organic micropollutants in granular activated carbon with different pore sizes. Water Res. 2019, 162, 518–527. [Google Scholar] [CrossRef]
- Luna, F.M.T.; Oliveira Filho, A.N.; Araújo, C.C.B.; Azevedo, D.C.S.; Cavalcante, C.L. Adsorption of polycyclic aromatic hydrocarbons from heavy naphthenic oil using commercial activated carbons. 1. Fluid-Particle studies. Ind. Eng. Chem. Res. 2016, 55, 8176–8183. [Google Scholar] [CrossRef]
- Satterfield, C.N.; Colton, C.K.; Pitcher, W.H. Restricted diffusion in liquids within fine pores. AIChE J. 1973, 19, 628–635. [Google Scholar] [CrossRef]
- Bungay, P.M.; Brenner, H. The motion of a closely-fitting sphere in a fluid-filled tube. Int. J. Multiph. Flow 1973, 1, 25–56. [Google Scholar] [CrossRef]
- Leyva-Ramos, R.; Diaz-Flores, P.E.; Leyva-Ramos, J.; Femat-Flores, R.A. Kinetic modeling of pentachlorophenol adsorption from aqueous solution on activated carbon fibers. Carbon N. Y. 2007, 45, 2280–2289. [Google Scholar] [CrossRef]








| Compound | Molecular Structure | Molecular Formula | pKa | * DAB × 106 cm2 s−1 | Molecular Weight (g mol−1) | Size X, Y (nm) |
|---|---|---|---|---|---|---|
| Phenol |  | C6H6O | 9.86 | 8.1 | 94.11 | 0.43 0.57 |
| Element | Deionized Water (mg L−1) | Cigarette Butt Leaching (mg L−1) | Activated Carbon Leaching (mg L−1) |
|---|---|---|---|
| Ag | ND | <0.003 | ND |
| Al | ND | 0.121 | ND |
| As | ND | <0.010 | ND |
| B | <0.05 | <0.010 | <0.05 |
| Ba | 3.153 * | <0.010 | 5.900 * |
| Be | ND | <0.010 | ND |
| Ca | <0.05 | 0.842 | 2.139 |
| Cd | ND | <0.010 | ND |
| Co | ND | 0.023 | ND |
| Cr | ND | <0.010 | ND |
| Cu | ND | 0.062 | ND |
| Fe | ND | <0.010 | ND |
| K | 0.147 | 3.199 | 0.667 |
| Li | 3.929 * | 0.569 | 6.340 * |
| Mg | <0.05 | 0.218 | 0.101 |
| Mn | 0.830 * | <0.010 | 3.233 * |
| Mo | ND | <0.010 | ND |
| Na | <0.05 | 0.849 | 0.082 |
| Ni | ND | <0.010 | ND |
| P | ND | <0.010 | ND |
| Pb | ND | <0.010 | ND |
| Sb | ND | <0.010 | ND |
| Se | ND | <0.010 | ND |
| Si | <0.25 | <0.010 | <0.25 |
| Sn | ND | <0.010 | ND |
| Sr | 1.353 * | <0.010 | 5.526 * |
| Ti | ND | <0.010 | ND |
| Tl | ND | <0.010 | ND |
| V | ND | 0.137 | ND |
| Zn | ND | <0.010 | ND |
| Parameter | CBs Leaching | Activated Carbon Leaching | Permissible Limits | |
|---|---|---|---|---|
| NOM | WHO | |||
| pH | 5.12 | 7.8 | 6.5–8.5 | NVP |
| Color (Co/Pt) | 55.0 | Colorless | 20.0 | Colorless |
| Odor | Tabaco | Odorless | Odorless | Odorless |
| Turbidity (NTU) | 1.0 | 0.2 | 10.0 | <0.2 |
| Total hardness (mg CaCO3 L−1) | 2.0 | 2.0 | 500 | NVP |
| Ca hardness (mg CaCO3 L−1) | 2.0 | 2.0 | NVP | NVP |
| Mg hardness (mg CaCO3 L−1) | 0.0 | 0.0 | NVP | NVP |
| Chlorides (mg L−1) | 4.0 | 2.0 | 250 | NVP |
| Fluorides (mg L−1) | 0.12 | 0.10 | 1.50 | 1.50 |
| Nitrites (mg L−1) | Absent | Absent | 1.00 | 3.00 |
| Nitrates (mg L−1) | 0.11 | 0.15 | 10.0 | 50.0 |
| Sulfates (mg L−1) | 4.50 | 4.00 | 400 | NVP |
| Mesophilic Aerobic Microorganisms (UFC mL−1) | Absent | Absent | NVP | NVP |
| Total coliforms (NMP/100 mL) | Absent | - | Absent | Absent |
| Fecal coliforms (NMP/100 mL) | Absent | - | Absent | Absent |
| Total dissolved solids (mg L−1) | 10.5 | - | 1000 | NVP |
| Chlorine (mg L−1) | Absent | - | 0.10–0.50 | 5.00 |
| Temperature (°C) | Type of Water | K (L mg−1) | Ke | qm (mg g−1) | R2 |
|---|---|---|---|---|---|
| 10 | Deionized water | 0.01542 | 1451.17 | 285.11 | 0.9756 |
| 25 | Deionized water | 0.01180 | 1110.49 | 268.9 | 0.9846 |
| 40 | Deionized water | 0.00965 | 908.16 | 211.45 | 0.9563 |
| 25 | Wastewater | 0.00530 | 498.78 | 56.58 | 0.9886 |
| Activated Carbon Obtained from Different Raw Materials | T (°C) | qmax (mg g−1) | Ref. |
|---|---|---|---|
| Black wattle bark waste | 25 | 85.75 | [24] |
| Toona sinensis leaves | 25 | 325.0 | [35] |
| Tithonia diversifolia | 25 | 50.55 | [34] |
| Rise husk-KOH Rise husk-KOH/EDTA−4Na | 25 | 194.2 215.3 | [10] |
| Coconut shell | 25 | 144.9 | [33] |
| Avocado kernel seeds | 25 | 90.0 | [38] |
| Cigarette filters | 25 | 268.9 | Present study |
| Exp. Number | CA0 (mg L−1) | qe (mg g−1) | kL × 105 (cm s−1) | Dep (cm2 s−1) | τ |
|---|---|---|---|---|---|
| 1 | 102.7 | 73.79 | 3.51 | 6.10 × 10−10 | 7967 |
| 2 | 201.3 | 119.1 | 3.85 | 1.55 × 10−10 | 31,354 |
| 3 | 310.2 | 169.4 | 3.76 | 9.10 × 10−11 | 53,406 |
| 4 | 405.2 | 196.7 | 4.23 | 8.35 × 10−11 | 58,203 |
| 5 | 500.5 | 210.3 | 3.57 | 4.02 × 10−11 | 120,895 |
| 6 | 726.3 | 181.2 | 5.56 | 8.11 × 10−12 | 599,260 |
| 7 | 1017.3 | 235 | 5.47 | 6.84 × 10−12 | 710,526 |
| 8 | 1520.1 | 240 | 5.66 | 5.50 × 10−12 | 883,636 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medellín-Castillo, N.A.; Ocampo-Pérez, R.; Forgionny, A.; Labrada-Delgado, G.J.; Zárate-Guzmán, A.I.; Cruz-Briano, S.A.; Flores-Ramírez, R. Insights into Equilibrium and Adsorption Rate of Phenol on Activated Carbon Pellets Derived from Cigarette Butts. Processes 2021, 9, 934. https://doi.org/10.3390/pr9060934
Medellín-Castillo NA, Ocampo-Pérez R, Forgionny A, Labrada-Delgado GJ, Zárate-Guzmán AI, Cruz-Briano SA, Flores-Ramírez R. Insights into Equilibrium and Adsorption Rate of Phenol on Activated Carbon Pellets Derived from Cigarette Butts. Processes. 2021; 9(6):934. https://doi.org/10.3390/pr9060934
Chicago/Turabian StyleMedellín-Castillo, Nahum A., Raúl Ocampo-Pérez, Angélica Forgionny, Gladis J. Labrada-Delgado, Ana I. Zárate-Guzmán, Sergio A. Cruz-Briano, and Rogelio Flores-Ramírez. 2021. "Insights into Equilibrium and Adsorption Rate of Phenol on Activated Carbon Pellets Derived from Cigarette Butts" Processes 9, no. 6: 934. https://doi.org/10.3390/pr9060934
APA StyleMedellín-Castillo, N. A., Ocampo-Pérez, R., Forgionny, A., Labrada-Delgado, G. J., Zárate-Guzmán, A. I., Cruz-Briano, S. A., & Flores-Ramírez, R. (2021). Insights into Equilibrium and Adsorption Rate of Phenol on Activated Carbon Pellets Derived from Cigarette Butts. Processes, 9(6), 934. https://doi.org/10.3390/pr9060934







