Impact-Rubbing Dynamic Behavior of Magnetic-Liquid Double Suspension Bearing under Different Protective Bearing Forms
Abstract
:1. Introduction
2. Rotor Impact-Rubbing Model during Electromagnetic Failure
- (1)
- There is a local elastic collision between the magnetic pole and the magnetic jacket, and the deformation is elastic deformation;
- (2)
- The winding magnetic flux leakage, edge magnetic flux, eddy current loss, core material saturation, and coupling effect between magnetic poles are ignored;
- (3)
- The tiny gaps between the poles are ignored;
- (4)
- The inertial force and viscous pressure characteristics of the liquid are ignored;
- (5)
- The gravity of the inner ring of deep groove ball bearings is ignored;
- (6)
- The deep groove ball bearing is simplified into a spring damping system with mass.
2.1. Impact-Rubbing Dynamics Model of the “Rotor-Fixed Ring”
2.2. Impact-Rubbing Dynamics Model of the “Rotor-Deep Groove Ball Bearing”
2.3. Impact-Rubbing Dynamics Model of the “Rotor-Hydrostatic System”
3. Numerical Simulation of the Rotor Impact-Rubbing Process under Electromagnetic Failure
3.1. Impact-Rubbing Dynamics Behavior of the Rotor-Fixed Ring Supporting System
- Impact-rubbing behavior of the rotor under upper unit failure mode
- 2.
- Impact-rubbing behavior under upper and lower unit failure
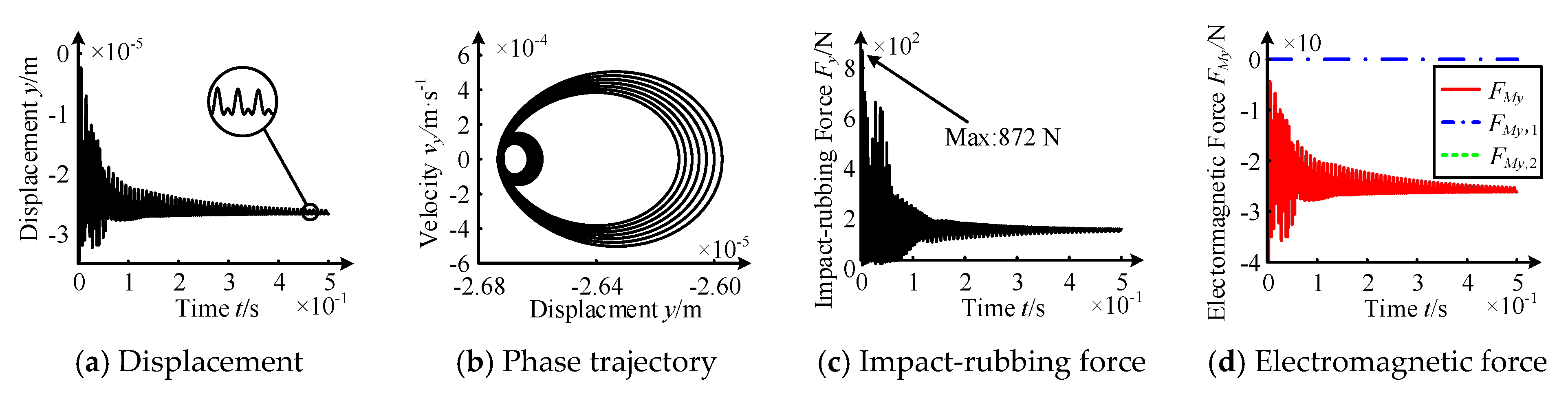
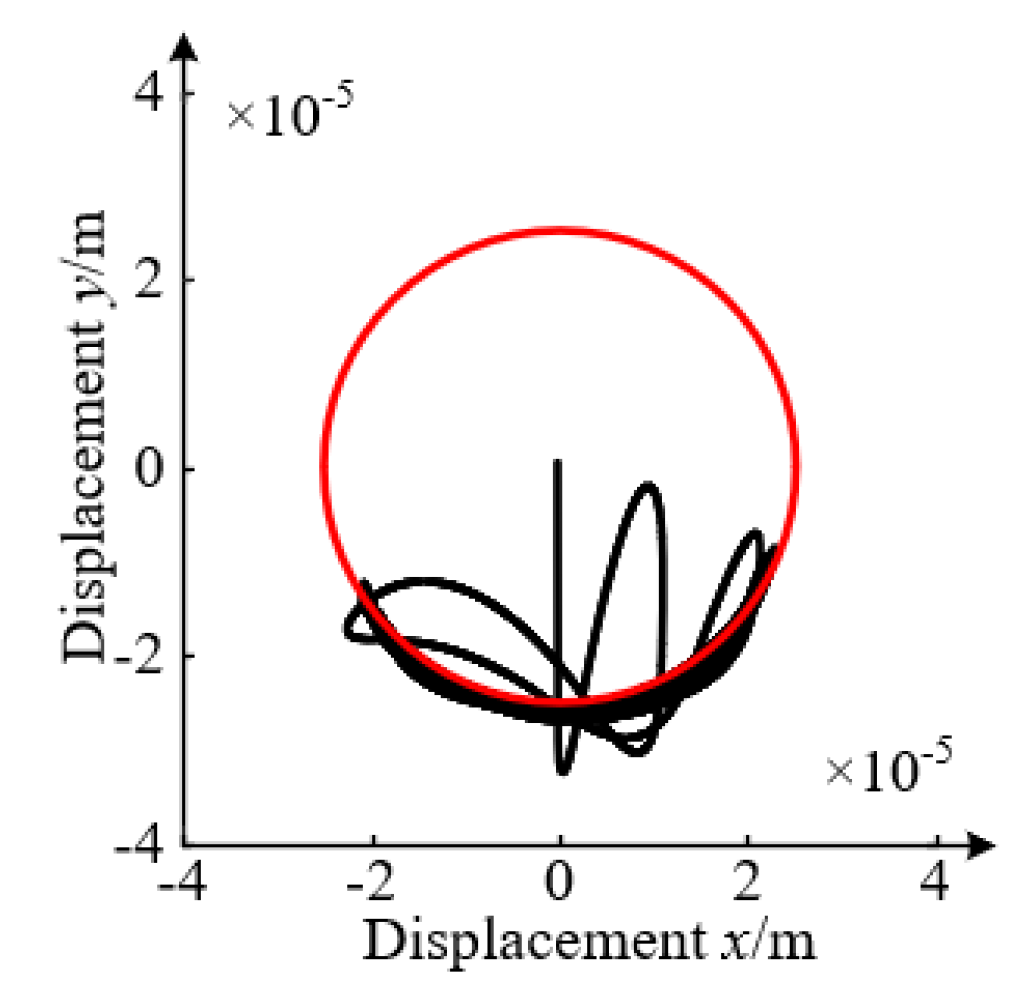
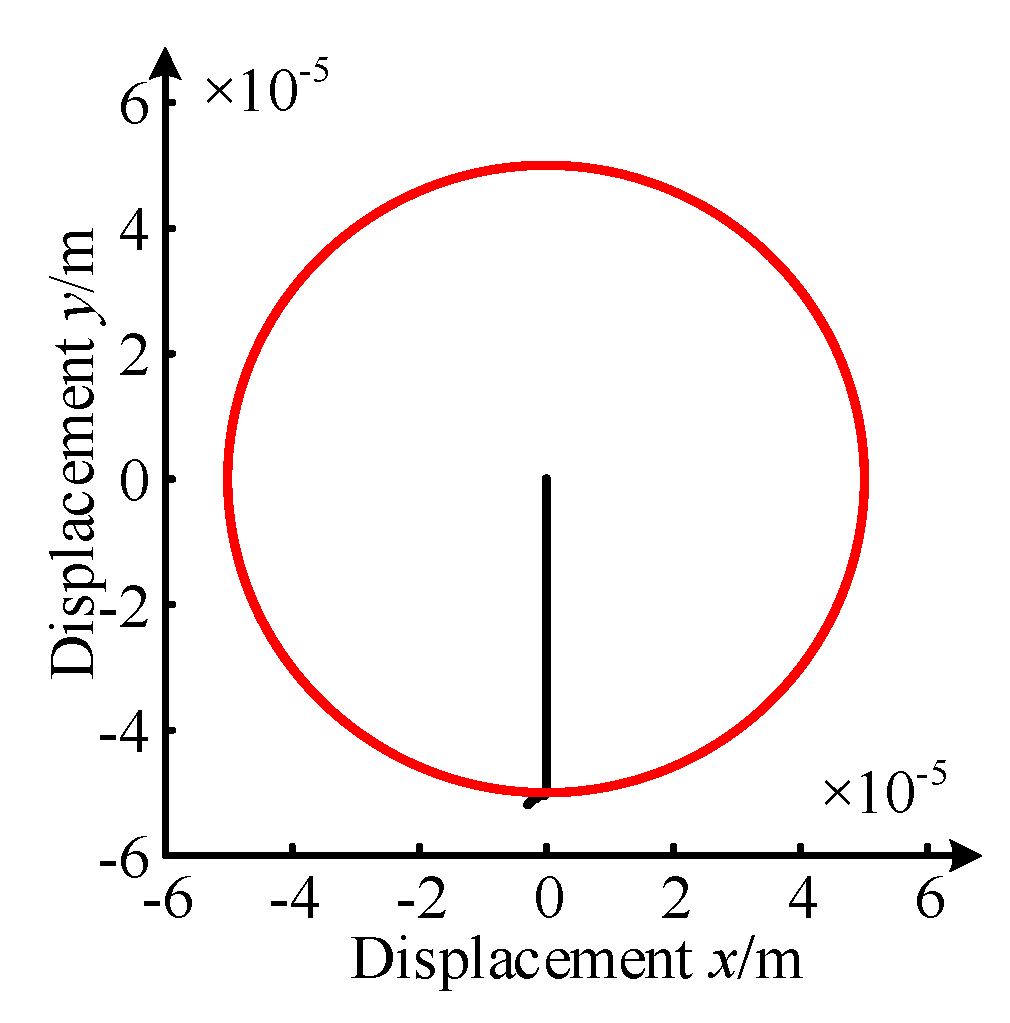
3.2. Impact-Rubbing Dynamics Behavior of the Rotor-Ball Bearings Supporting System
- Impact-rubbing behavior law under upper unit failure
- 2.
- Impact-rubbing behavior law under upper and lower unit failure
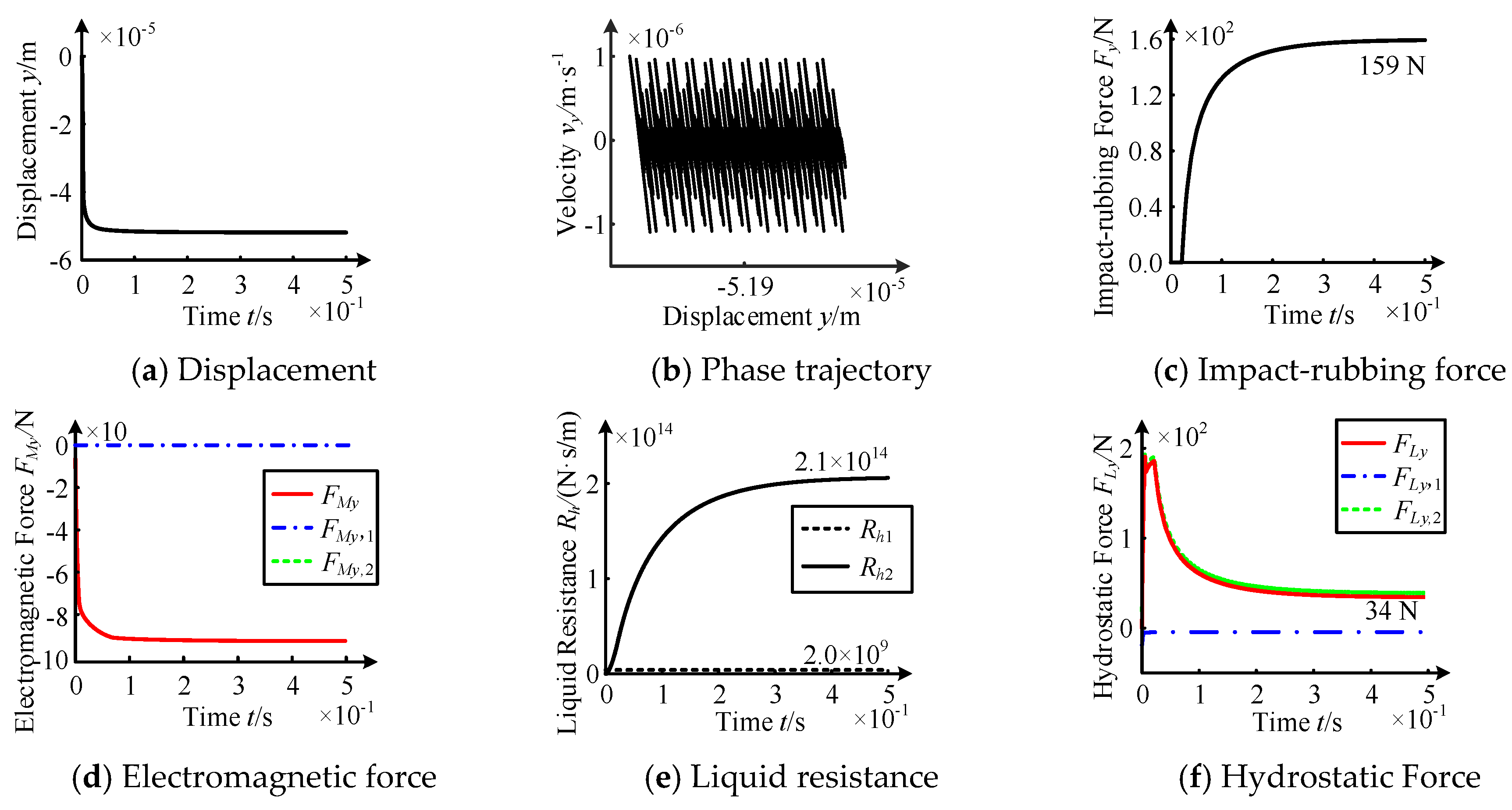
3.3. Impact-Rubbing Dynamics Behavior of the Rotor-Hydrostatic System
- Impact-rubbing behavior law under upper unit failure
- 2.
- Impact-rubbing behavior law under upper and lower unit failure.
3.4. Comparison of the Three Protection Devices in Impact-RUBBING Behavior
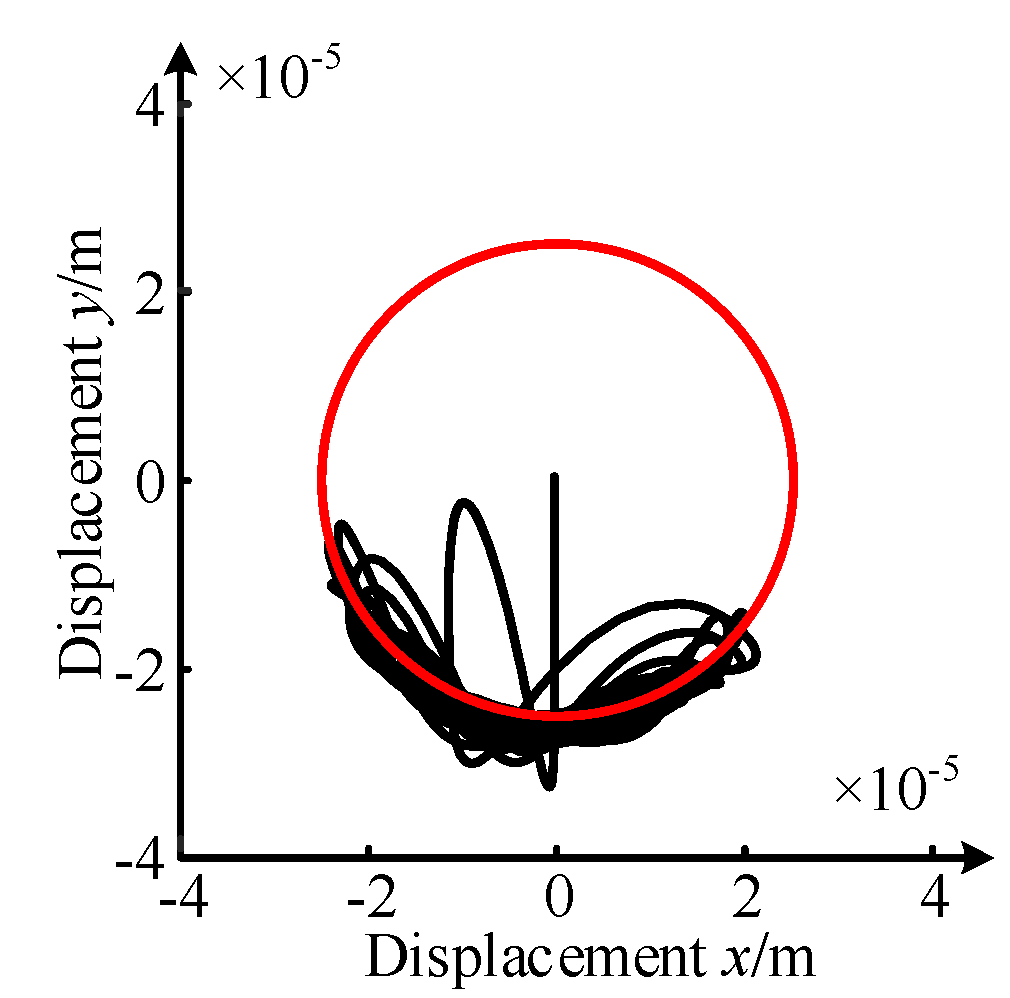
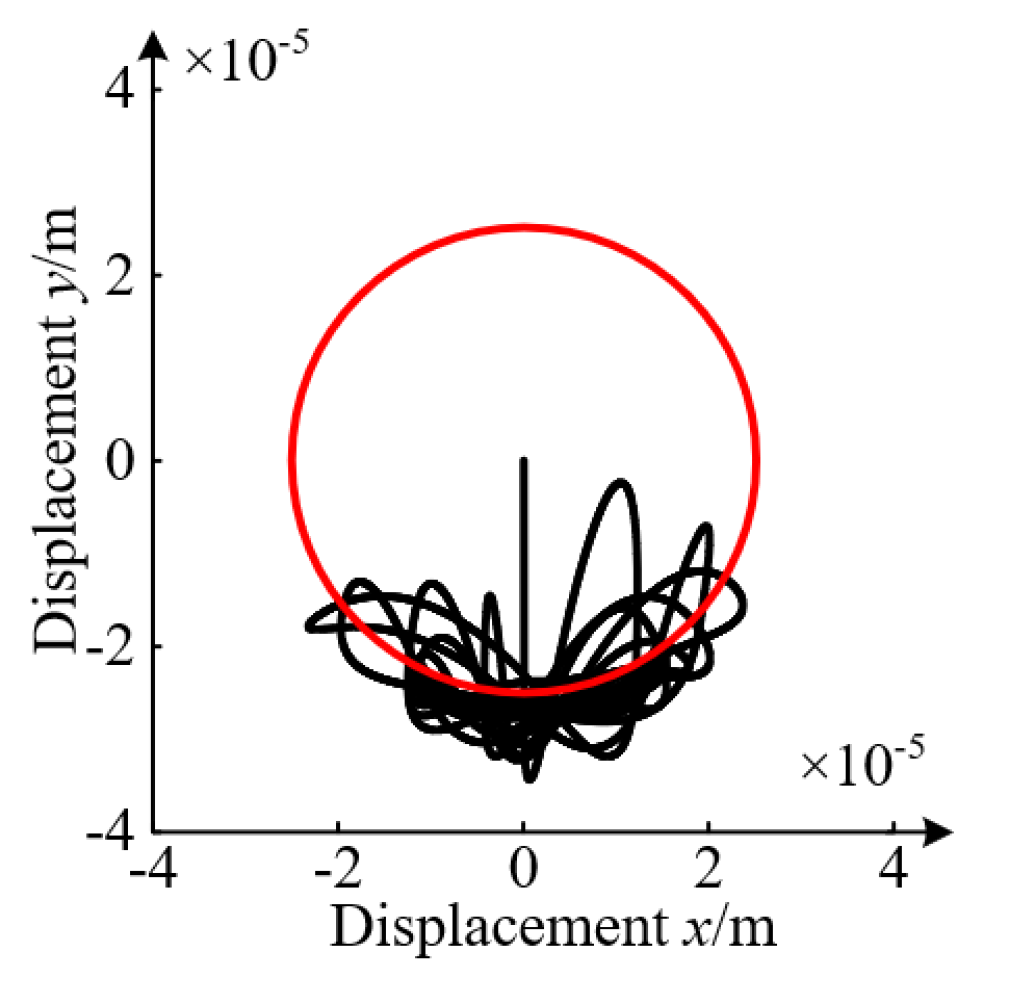
- Analysis of the impact-rubbing behavior under upper unit failure.
- 2.
- Analysis of the impact-rubbing behavior under upper and lower units.
- 3.
- Analysis of results.
4. Conclusions
- The influences of the protection devices on the bouncing time, impact-rubbing force, and impact-rubbing degree are found to be as follows: the hydrostatic system shows the best results, followed by the deep groove ball bearing and then the fixed ring.
- Compared with the fixed ring and deep groove ball bearing, the positions of the rotor impact-rubbing in the hydrostatic system are the rotor and magnetic pole, and the maximum impact-rubbing force is lower without bounce and eddy phenomena.
- Compared with the bounce time and the maximum impact-rubbing force of the rotor in the three protective devices, it can be seen that there is no bounce phenomenon of the rotor in the hydrostatic system and the maximum impact-rubbing force is greatly reduced, so the protective bear is not required to be installed in the MLDSB.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, J.H.; Yan, W.D.; Wang, Z.Q.; Gao, D.; Du, G. Study on Clearance-Rubbing Dynamic Behavior of 2-DOF Supporting System of Magnetic-Liquid Double Suspension Bearing. Processes 2020, 8, 973. [Google Scholar] [CrossRef]
- Xiong, W.L.; Hu, C.; Lang, L.; Zheng L, G. Study on the Influence of Controllable Throttle Parameters on the Characteristics of Hydrostatic Bearing. J. Mech. Eng. 2017, 22, 3354–3359. [Google Scholar]
- Zhao, J.H.; Zhang, G.J.; Cao, J.B.; Gao, D.R.; Du, G.J. Decouping Control of Single DOF Supporting System of Magnetic-Liquid Double Suspension Bearing. Mach. Tool Hydraul. 2020, 48, 1–8. [Google Scholar]
- Zu, L.; Wang, H. Design and Research of Rotor Drop Protection System Test Bench. At. Energy Sci. Technol. 2015, 49, 340–386. [Google Scholar]
- Wang, X.H.; Yang, F.F.; Zhao, Q. Dynamics Analysis of Aircraft Engine Rotor Drop after Electromagnetic Bearing Failure. Gas Turbine Test. Res. 2019, 32, 1–7. [Google Scholar]
- Jarroux, C.; Dufour, R.; Mahfoud, J.; Defoy, B.; Alban, T.; Delgado, A. Touchdown Bearing Models for Rotor-AMB Systems. J. Sound Vib. 2018, 440, 51–69. [Google Scholar] [CrossRef] [Green Version]
- Patrick, K.; Matthew, C. Dynamic Conditions to Destabilize Persistent Rotor/Touchdown Bearing Contact in AMB Systems. Mech. Eng. J. 2017, 4, 17-00005. [Google Scholar]
- Pesch, A.H.; Sawicki, J.T.; Maslen, E.H. Active Magnetic Bearing Online Levitation Recovery through μ-Synthesis Robust Control. Actuators 2017, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.L.; Gong, H.L.; Yang, G.J.; Shi, C.G. Research on Drop Recovery Control Strategy of Electromagnetic Bearing Horizontal Rotor. Fan Technol. 2020, 62, 38–45. [Google Scholar]
- Wu, G.Q.; Lu, B.; He, D.W.; Song, C.G. Influence of Protective Bearing Structure on the Spindle Dropping Trajectory of Vertical Axis Maglev Wind Turbine. Mech. Des. Res. 2018, 34, 108–110. [Google Scholar]
- Wei, P.; Wang, Y.F.; Yang, Y.; Yan, J.L. Research on the Impact Force of High Speed Suspending Rotor Dropping on the Protective Bearing. Vib. Shock. 2018, 37, 251–258. [Google Scholar]
- Yu, C.T.; Xu, L.X.; Jin, C.W. Kinematics Analysis of Protective Clearance Mechanism for Automatic Elimination of Active Magnetic Bearing System. J. Aviat. 2015, 36, 2485–2496. [Google Scholar]
- Zhu, Y.L.; Jin, C.W. Analysis of Maximum Impact Force and Thermal Characteristics of Double Layer Protective Bearings under High Speed and Heavy Duty. China Mech. Eng. 2016, 27, 25–31. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Jin, C.W.; Lian, C.Y.; Zheng, Z.Q. Dynamic Analysis of Vertical Rotor Fall into Deep Groove Ball Protective Bearing. Mech. Des. Res. 2017, 33, 72–77. [Google Scholar]
- Gosiewski, Z.; Mystowski, A. The Robust Control of Magnetic Bearings for Rotating Machinery. Solid State Phenom. 2006, 113, 125–130. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Ghayour, M.; Khanlo, H.M. Nonlinear Dynamic Analysis and Experimental Verification of a Magnetically Supported Flexible Rotor System with Auxiliary Bearings. Mech. Mach. Theory 2018, 121, 545–562. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, H.T.; Wang, Q.; Zhang, B.; Gao, D.R. Stability Analysis of Single DOF Support System of Magnetic-Liquid Double Suspension Bearing. Hydromechatron. Eng. 2019, 47, 1–7. [Google Scholar]
- Jiang, L. Research on Dynamics of Rotor Drop on Auxiliary Bearing. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2011. [Google Scholar]
- Weiss, G.; Staffans, O. Maxwell’s Equations as a Scattering Passive Linear System. SIAM J. Control. Optim. 2013, 51, 3722–3756. [Google Scholar] [CrossRef]
- Liu, T.; Sun, X.; Wu, J. Study on Extraction of Impact Vibration between Sliding Bearing and Rotor under Different Friction Condition. Lubr. Seal. 2018, 43, 67–71. [Google Scholar]
- Verma, S.; Dewan, A. Partially-Averaged Navier-Stokes (PANS) Approach for Study of Fluid Flow and Heat Transfer Characteristics in Czochralski Melt. J. Cryst. Growth 2018, 481, 56–64. [Google Scholar] [CrossRef]
- Zhao, J.H.; Liang, Y.N.; Gao, D.R. Oil Pocket’s Bearing Capacity Analysis of Liquid Hydrostatic Worktable in Gantry Moving Milling Center. Chin. J. Mech. Eng. 2014, 27, 1008–1017. [Google Scholar] [CrossRef]



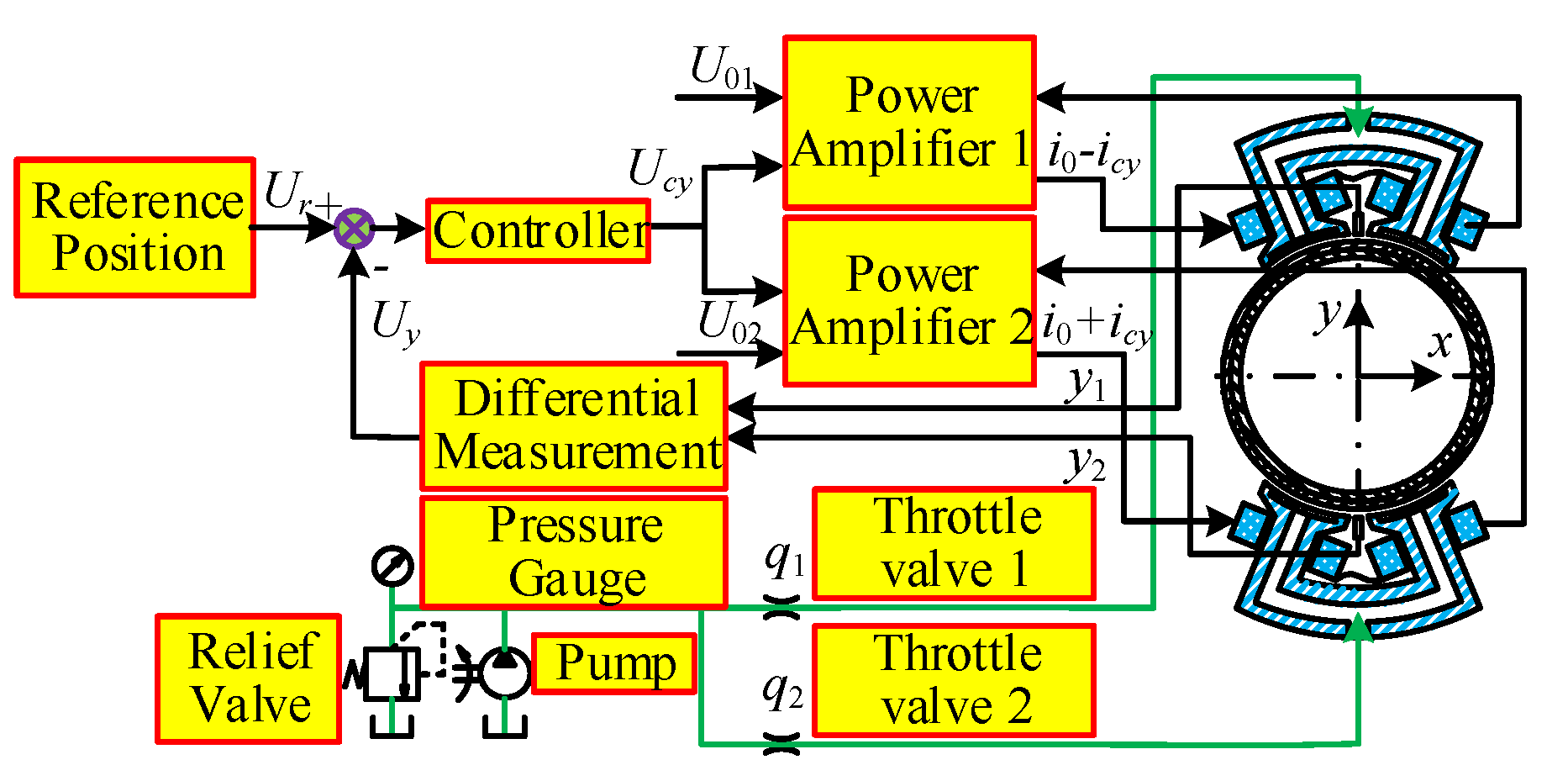


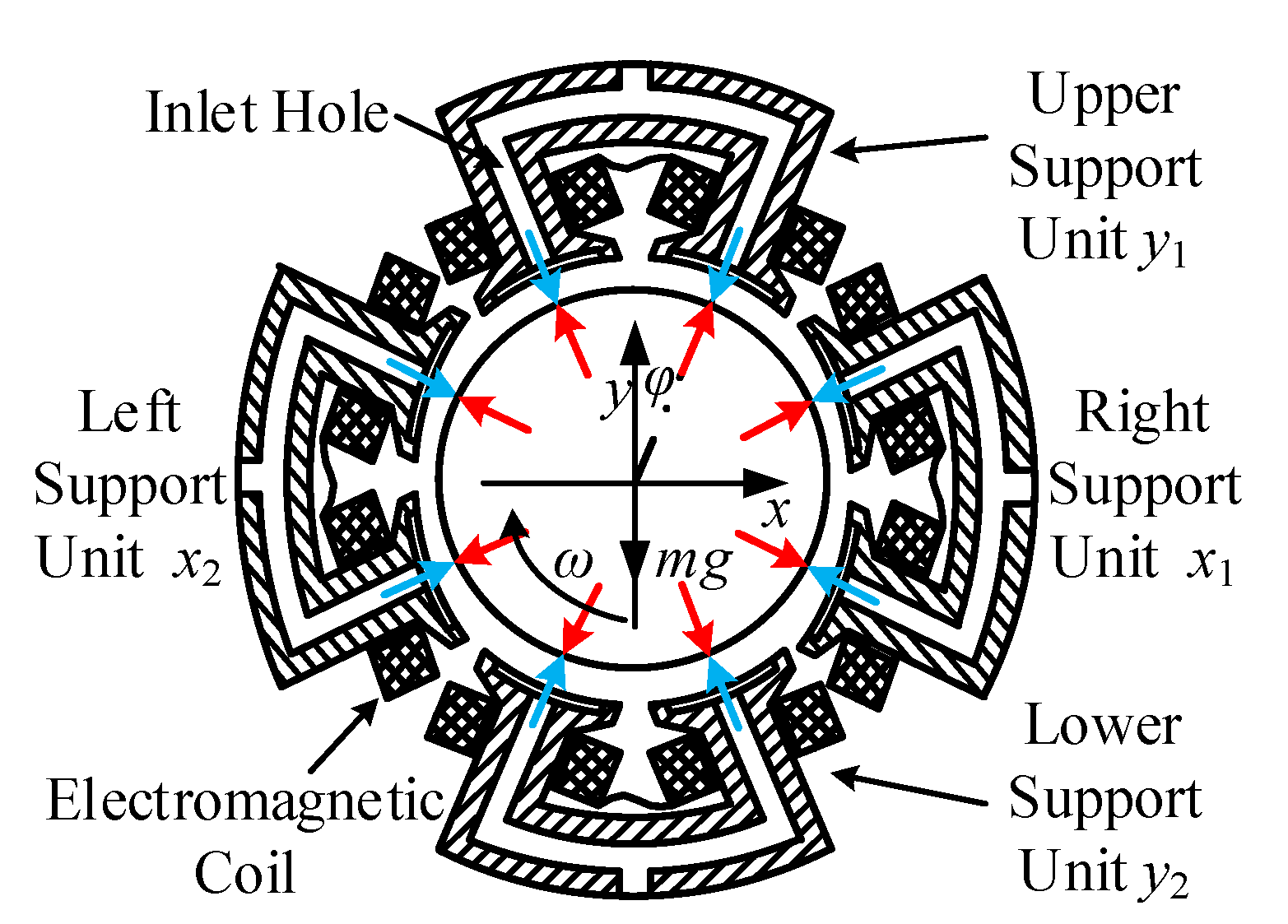






| Rotor Mass m/(kg) | Gravitational Acceleration g/(m/s2) | Rotor Radius r/(m) | Rotor Rotational Inertia J/(kg·m2) |
|---|---|---|---|
| 10 | 10 | 0.1 | 0.05 |
| Angle φ/(°) | Bias current i0/(A) | Coating thickness l/(μm) | Initial unilateral clearance h0/(μm) |
| 22.5 | 0.5 | 50 | 50 |
| Magnetic area S/(mm2) | Vacuum permeability μ0/(H/m) | Coil number N/(dimensionless) | Stator contact coefficient e1/(dimensionless) |
| 1080 | 4π × 10−7 | 50 | 10/9 |
| Stator damping c1/(N·m/s) | Stator stiffness k1/(N/m−10/9) | Stator friction coefficient f1/(dimensionless) | Inner ring unilateral clearance h1/(μm) |
| 1000 | 3.5 × 108 | 0.1 | 25 |
| Inner ring rotational inertia Jb/(kg·m2) | Inner quality mb/(kg) | Inner ring friction coefficient f2/(dimensionless) | Contact coefficient e2/(dimensionless) |
| 1 × 10−4 | 0.01 | 0.007 | 1.5 |
| Ball bearing stiffness k2/(N/m−3/2) | Ball bearing damping c2/(N·m/s) | Oil supply pressure ps/(MPa) | Extrusion area Ab/(mm2) |
| 4 × 1012 | 800 | 0.05 | 56 |
| Oil viscosity μ/(Pa·s) | Throttling ratio β/(dimensionless) | Discharge coefficient/(dimensionless) | Effective bearing area Ae/(mm2) |
| 1.3 × 10−3 | 2 | 0.71 | 416 |
| Protective Devices | Bounce Time | Eddy | Max. Impact-Rubbing Force | Impact-Rubbing Parts |
|---|---|---|---|---|
| Fixed ring | <0.07 s | yes | 880 N | rotor and fixed ring |
| Ball bearing | <0.06 s | yes | 872 N | rotor and inner ring |
| Hydrostatic system | none | none | 159 N | rotor and pole |
| Protective Devices | Bounce Time | Eddy | Max. Impact-Rubbing Force | Impact-Rubbing Parts |
|---|---|---|---|---|
| Fixed ring | <0.1 s | yes | 802 N | rotor and fixed ring |
| Ball bearing | <0.02 s | yes | 788 N | rotor and inner ring |
| Hydrostatic system | none | none | 66 N | rotor and pole |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Xing, L.; Li, S.; Yan, W.; Gao, D.; Du, G. Impact-Rubbing Dynamic Behavior of Magnetic-Liquid Double Suspension Bearing under Different Protective Bearing Forms. Processes 2021, 9, 1105. https://doi.org/10.3390/pr9071105
Zhao J, Xing L, Li S, Yan W, Gao D, Du G. Impact-Rubbing Dynamic Behavior of Magnetic-Liquid Double Suspension Bearing under Different Protective Bearing Forms. Processes. 2021; 9(7):1105. https://doi.org/10.3390/pr9071105
Chicago/Turabian StyleZhao, Jianhua, Lanchun Xing, Sheng Li, Weidong Yan, Dianrong Gao, and Guojun Du. 2021. "Impact-Rubbing Dynamic Behavior of Magnetic-Liquid Double Suspension Bearing under Different Protective Bearing Forms" Processes 9, no. 7: 1105. https://doi.org/10.3390/pr9071105
APA StyleZhao, J., Xing, L., Li, S., Yan, W., Gao, D., & Du, G. (2021). Impact-Rubbing Dynamic Behavior of Magnetic-Liquid Double Suspension Bearing under Different Protective Bearing Forms. Processes, 9(7), 1105. https://doi.org/10.3390/pr9071105





