1. Introduction
The evolutionary relationship between urban and rural areas is a global issue of urbanization, tightly attached to economic prosperity and regional sustainability [
1,
2]. Witnessing the rapid process of urbanization and industrialization for decades in China, the recent administrative promotion of rural revitalization and urban–rural integration development [
3,
4,
5] has attempted to rebalance the urban–rural divides and pursue new urbanization [
6], echoing long-term dualism, due to the biased development strategies and investments emphasizing cities over rural areas [
7,
8]. Moreover, the converging gap between urban–rural individual income and the institutional reform including unified
hukou (household registration), land use, and public resource have accelerated interactions [
9] and diminished the dichotomy between cities and the countryside. Also, highlighted by the China State Council in its
14th Five-Year Plan for Economic and Social Development and Vision 2035, an urban–rural integration development strategy has summoned bidirectional equal interlinkages between urban and rural areas to activate the latent vigor of the countryside community.
Interconnected with exchanging information, material, population, capital, knowledge and culture, cities and rural settlements are functionally shaped by the volume and direction of interactions [
10], thus determining the geographical layouts and spatial division in return. With more frequent bidirectional connections nowadays, researchers [
11,
12] have shown that urban–rural integration has also renewed the spatial configuration from distinct segmentation to spatial intersection, referring to a transformation of equal positions rather than subordinating rural areas. Therefore, identifying integrated urban–rural spatial structure is greatly significant in optimizing the coordination of spatial arrangement and revitalizing rural areas.
From the perspective of “space of flow”, [
13] networks characterized by spatial connections exceed the static territory boundaries [
14] that have constrained most traditional understandings of urban–rural spatial structures as binary and “core–periphery” (CP) [
5] in areal studies. Complex network approaches, enabling the equal involvement of cities and rural settlements as nodes with interactions as edges, tend to uncover the multiscale spatial structures of urban–rural networks and break down preconceptual urban–rural divides. The conceptualization of mesoscale [
15,
16,
17] refers to the groupings of nodes with similar positions in the network topology, as defined by their linkages, and the structural relations between these groupings, which reveal the underlying regional organization. Multiple mesoscale spatial structures, such as communities, core-peripheries, and hybrid structures [
15,
18], have been investigated in regional networks by the weighted stochastic block model (WSBM) [
16,
19,
20], offering a comprehensive understanding of function zoning and internal structures.
However, the “methodological cityism” [
21] originating in urban–rural dualism, has disproportionately impacted the conceptualization of urbanization, placing the city as the default unit of regional spatial structure analysis while neglecting the active process of “ruralization” [
2]. Due to the limitation of data availability in rural areas, most network analyses of regional spatial configuration, despite the theoretical framework of integrated relationality, have solely focused on cities, such as the World City Network (WCN) structure based on the data of APS firm distribution, airlines, and web pages [
22,
23,
24], as well as the regional city structure based on the transportation network and commuting flows [
18,
25,
26]. Nonetheless, little can be known about the linkages between urban and rural areas without considering rural nodes, and the comprehension of regional structures is biased in the absence of the rural hinterlands.
Hence, by detecting and comparing the mesoscale structure of two networks reflecting urban–urban and urban–rural daily mobility connections (i.e., the UUM and URM networks, respectively), we attempt to enrich the scant discussion of inclusive regional structures beyond the spatial binary threefold. First, we wonder about the consistency of regional mesoscale structures in comparing urban relationality and urban–rural relationality, highlighting the lack of substitutability and the intermingling of rural and urban activities in the regional integration process. Second, we discuss the theoretical role of rural areas in integrated regional systems, determining whether it interacts with the “local” urban within administrative boundaries or converges into the “global” urban center beyond territories. The discussion is barely present in the field of regional studies and policies. Third, by adopting the WSBM algorithm that relies on interactions between nodes, we consider regional mesoscale structure in a unified framework, deemphasizing predefined conceptual urban–rural divides in nodal characteristics while bridging the gap in discursive and disciplinary practices between the urban and rural geography.
In this study, we constructed a UUM network and a URM network, separately, in the Pearl River Delta (PRD) region in South China, based on aggregated daily mobility flows from massive anonymous mobile-phone signaling data. A WSBM was adopted to detect the underlying mesoscale structure in both networks to compare different spatial configurations of nodes and groupings of their roles, positions, linkages, and agglomerations. As one of China’s most urbanized and populated regions, we attempted to understand the complicated mesoscale structures for interurban and urban-rural mutual relations, clarifying different motivations and mechanisms in urban–rural interactions. Thus, three insights into the mesoscale structure yielded empirical experience for renewed urban–rural interplay and potential practical pathways to urban–rural integration.
The rest of the paper is organized as follows.
Section 2 reviews related works on regional spatial structure analysis and evolutional urban–rural relationships.
Section 3 introduces the research area and data source, while
Section 4 proposes the conceptualization of potential mesoscale structures in mobility networks and the detection approach of WSBM.
Section 5 represents the major findings of the mesoscale structure in the UUM network and the URM network.
Section 6 concludes and represents the discussion.
2. Literature Review
Regional spatial structure, which sketches out the organization of spatial entities and their interplays, has experienced a paradigm shift from static to dynamic characteristics. Based on fractal and spatial morphology, regional studies of areal attributes have distinguished various spatial configurations such as monocentric, bicentric and polycentric structures [
27,
28] in megaregions. However, such paradigms are bounded within the arbitrary administrative spatial segmentation, neglecting the accelerating mobility frequency of materials and reinforcement of internal relations [
14].
The perspective of a complex network has arisen with a transfer from concentrating on areal attributes to “flow space [
13]”, focusing on interactions between spatial entities. Network analysis investigates more than the characteristics of network space and entities composed of relations, in addition to the dynamical interacting process. Relational networks that are measured by individual behaviors such as housing migration, commuting, and traveling facilitate the bridging of the microscale of individual characteristics and the macroscale of regional patterns, thus manifesting the nature of regional spatial configuration [
29]. Zhong et al. [
30] revealed that the changing roles of local areas in the overall spatial structure of urban movement could be mined from the aggregation of smart card data. Functional linkages also assist in identifying the subdivision of functional urban regions [
31], critical city components [
32] and the evolution of urban spatial structures [
33].
Urban and rural areas, spatially separated, functionally cooperate via human economic, commercial, cultural and social behaviors, as well as material flows such as transport, logistic, capital and information. Similarly, the relationship between urban and rural areas evolves from division to integration during urbanization [
21,
34], mapping the transformation in spatial structure from the dualism of center-edge division to the intersected network, emphasizing relations.
Early theories of economic geography and regional planning, such as the location theory [
35] and Howard’s Garden Cities theory, have stated the ideas of urban–rural cooperation. However, rural areas were taken for granted as being subordinated to urban areas, calculated from the advantages in the labor force and adsorption effects from the agricultural sectors of modern industrial areas [
2,
34,
36]. The subordinate position divided the urban–rural space into a “center-edge” structure, simultaneously unbalancing investment, land use, labor-force flows, and public facilities [
7,
8].
Not until the up-speeding of mobility was the interdependency between the urban and rural substantially re-considered. Researchers have found more rapid, frequent flows between cites and countryside communities [
10,
11], with multi-directions including urban–urban, rural–rural, urban–rural and vice versa. The decaying resistance of administrative limitations on flows shifted the urban–rural spatial layouts into interconnections and integration with mutual intersection and penetration [
12]. Specifically, the megaregion concept, with its orderly flow of elements, smooth traffic, coordinated industrial division and harmonious environment, has the most potential space organization to promote free flows of urban and rural elements and construct an integrated urban–rural system [
37,
38].
Nevertheless, studies concerning urban–rural spatial structures have remained dually divided, accounting for the pre-conceptualization of urban–rural dualism and the limitation of data availability. The discussion on multiscale city networks has been in-depth, ranging from the well-known WCN research from the GaWC group on a global scale [
22] to the recent spatial optimization on a metropolitan scale [
28,
29,
39]. However, rural spatial structures have been investigated with a narrow concentration of hierarchical systems, based on the gravity model and its derivations (e.g., field models, spatial interaction models, and breaking-point formulas) [
40]. Therefore, the spatial configuration of the rural network system has been less understood, not to mention the integrated urban–rural network from a comprehensive perspective.
The PRD, located in one of the most vital strategic megaregions of China, the Great Bay Area, has been substantially concerned about its spatial layouts through intercity interactions. An array of studies [
41,
42,
43,
44] have concluded a polycentric structure of the PRD via multi-source data. However, opposite to the polycentric structure in functional space, Zhang et al. [
45] have found that the PRD represents a monocentric structure in institutional space defined by the intercity co-occurrence in the mass media, which advocates a more profound comprehension of multidimensional spatial structures of the PRD megaregion. Moreover, questions remain as to whether spatial structures derived from urban activities are representative and unbiased, and the role and mechanism the rural area, the “back-of-house”, serves in regional urban–rural systems.
Therefore, mesoscale structures, which describe the intermediate characteristics of complex networks for network abstraction [
15,
16,
17], including the grouping properties of nodes and the interplay between these groupings, offer the potential to discover latent regional structures and intrinsic mechanisms that might not be apparent at either macroscale or microscale. Zhang et al. [
18] detected a hybrid polycentric configuration of two community components, each with a core–periphery structure inside, in the Pearl River Delta of South China. Underneath the large-scale “core–periphery” structure of Western China, Yang et al. [
46] revealed a variety of network structure modes, such as dual-core, single-core, and multicore modes within the internal network of each urban agglomeration. Guimera et al. [
47] demonstrated that the multicommunity structure in the worldwide air-transportation network leads to anomalies in centrality values. Core–periphery, community, stochastic, hybrid structures, mesoscale, and variant types of mesoscale include those which have been recognized in urban networks [
15,
48,
49], identifying variant positions and roles for city agglomeration while presenting the potential for clarifying differentiated roles between the urban and rural in regional networks.
The detection of mesoscale in networks has originated from sociologists of the Social Network Analysis (SNA), who tried to find cohesive subgroups of critical social actors [
50] (pp. 345–391). With predefined schemas of complete subgraphs, corresponding algorithms such as k-cores, k-cliques, k-components, k-plex, k-club, etc., searched for the maximal sub-network that fits into the strictly-defined topological structure with k as a threshold. Recent techniques from community detection, such as graph partitioning, hierarchical clustering, modularity optimization and spectral methods, facilitate the detection of more flexible mesoscale topological structures as they search for groups of nodes that are densely connected within, and more sparsely connected between, groups. The popular Louvain algorithm [
51] relies on an iteratively greedy method to maximize a modularity score by Newman and Girvan [
52] for each community, where the modularity quantifies the quality of an assignment of nodes to communities.
Notably, the modularity optimization approach has been widely adopted in regional structure analysis [
53,
54] for its efficient calculation and assessment of the suitability of the partition. Nevertheless, only regional agglomerations were concerned, due to the constraint of the inherent presupposition of community structures in these approaches, which neglected the interactive pattern of the rest and of the other potential mesoscale structures. Similarly, the algorithms of core–periphery (CP) structure detection [
55] predefined the CP schema presentation, ruling out complex mesoscale structures.
Stochastic block models (SBM) offer a powerful alternative to a modularity approach for distinguishing multiple mesoscale structures. As a generative model, SBM splits nodes into blocks, within which all nodes are stochastically equivalent, and has been adopted robustly in various network datasets [
56,
57,
58]. A weighted stochastic block model (WSBM) was extended to capture more complicated features for weighted networks by assigning weights as covariables. Stepping beyond the “methodology determinism” issue [
15] of ruling out other potential mesoscale structures, SBM loosens the pre-definition by stochastic processes, capable of modeling multiple mesoscale structures, including disassortative, random and core–periphery structures. Additionally, the WSBM algorithm recognizes that the mesoscale structure relies on relationality rather than the semantic attributes of nodes, advancing an integrated analysis framework for various regional structures.
3. Research Area and Data
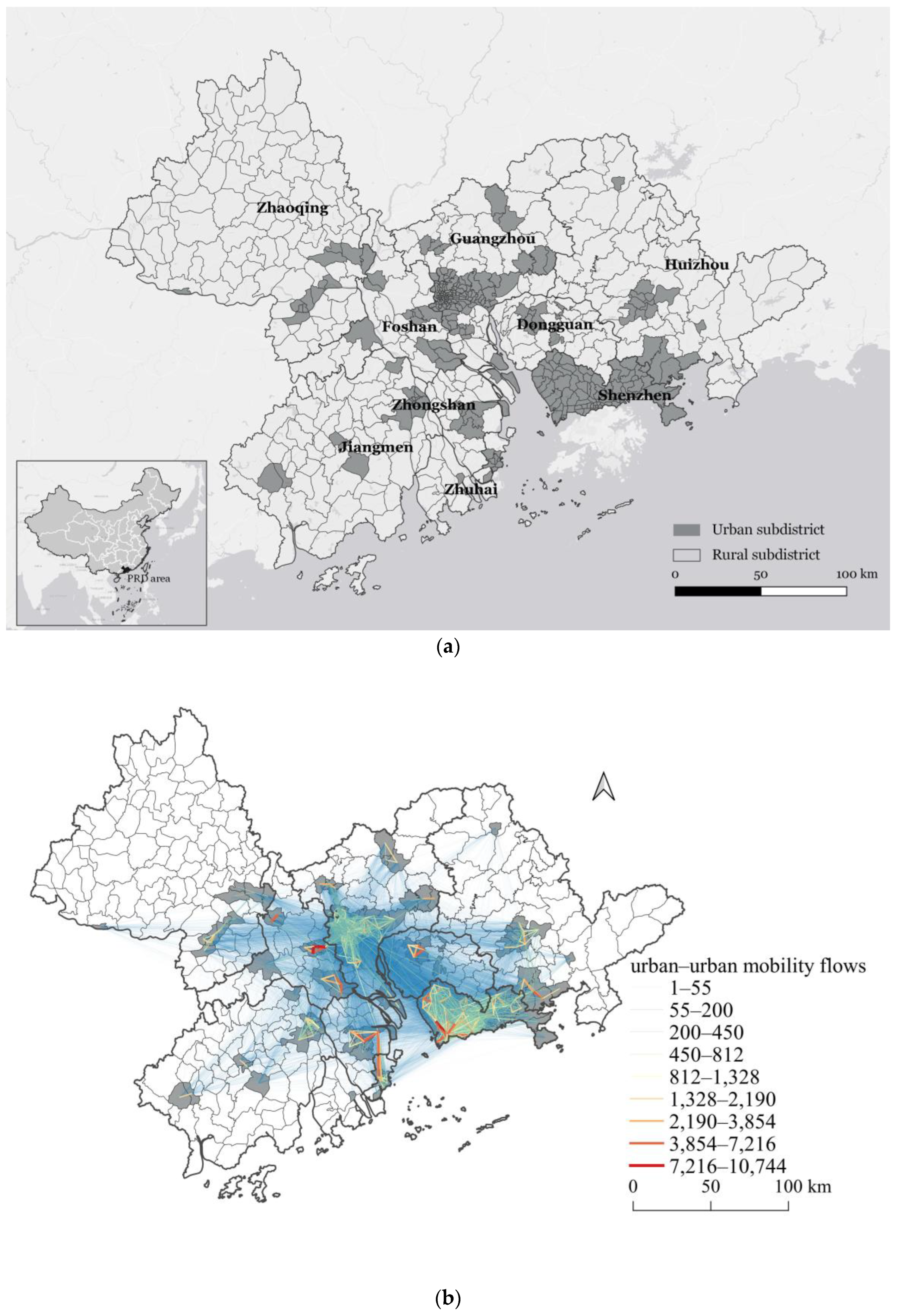
This study investigated the spatial structure of the UUM and URM networks in the PRD area in South China, which is the essential component of the Great Bay Area in the mainland, consisting of nine prefecture-level cities: Guangzhou, Shenzhen, Foshan, Dongguan, Huizhou, Zhuhai, Zhongshan, Jiangmen, and Zhaoqing. Since 2000, the PRD area has gradually won the position of a manufactural center in the global supply chain, growing into one of the most developed areas, with a premier urbanization rate and infrastructure construction intensity in China. Intensive, polycentric, urbanized spatial layouts have laid the foundation for an integrated development strategy in the PRD. Nevertheless, deep contradictions in the disorderly expansion of urbanization, the incoordination of urban–rural development and pressures on ecology have challenged its sustainable development. Hence, we attempted to clarify the underlying mesoscale structure, to aid the local government and policymakers with the insights into urban–rural interplays and integration.
The nine cities in the PRD were partitioned into 609 subdistrict-level administrative divisions for the purpose of urban/rural classification and fine-grained spatial structure detection. According to the
Statistical Compilation Rules for Administrative Division Codes and Urban-Rural Division Codes (index no. 410A03-1201-201708-0006) from the National Bureau of Statistics, we classified the urban/rural attributes of each subdistrict-level unit by the first digit of their urban/rural classification codes: 1 represented urban areas and 2 represented rural areas. We identified 324 urban subdistricts and 285 rural subdistricts in the PRD, as shown in
Figure 1a.
We used the mobile-phone-signaling dataset of April, 2018 from the China Telecom, one of China’s three leading communication carriers, to approximate the regional daily mobility connections. The dataset traced the daily trajectories of anonymous users in the PRD and included the information of estimated residence and workplace locations. To quantify the pairwise connections, we aggregated mobility flows for each pair of subdistrict-level units into 3 steps:
- (1)
Home/Workplace identification. The locations of individuals’ homes and workplaces were derived from the most frequent places that the user remained during working hours (10:30–18:00) and sleeping hours (23:00–06:00), which were provided by the dataset. In a spatial accuracy of about 500 m, according to the cell range and layout density of base stations, we dropped the locations into the subdistrict-level spatial resolution.
- (2)
Residents filtering. Considering the approximation to inter-subdistrict linkages by residents’ daily mobility, we filtered out passers-by and visitors and, extracted individuals who visited their estimated residence and workplace more than 15 days in a month as permanent residents in the PRD for further analysis. Over 12 million residents were identified, of which 24.76% resided in Guangzhou, 21.26% in Shenzhen, 14.37% in Dongguan, 13.97% in Foshan, and 22.64% in the rest.
- (3)
Flow weight aggregation. A directed mobility record was generated when a resident moved from home to workplace or from workplace to home. Directed mobility flows for each inter-subdistrict pairwise were weighted by aggregating the number of mobility records, standing for the total volume of mobility connections between the two subdistricts. Among all the mobility records, urban–rural flows accounted for 64.81% of the mobility volume, while urban–urban flows were 28.32%, constituting most of the daily mobility landscape in the PRD area. The spatial distribution of urban–urban mobility flows and urban–rural mobility flows is shown in
Figure 1b,c.
Based on aggregated mobility flows, we constructed two disparate, weighted directed mobility networks by distinguishing the urban/rural attributes of the origin subdistrict and the destination subdistrict for each flow. The urban–urban mobility (UUM) network contained 324 nodes of urban subdistricts and 104,652 links of interurban flows. The urban–rural mobility (URM) network contained 609 nodes and 92,340 links of flows originating from the urban, and ending at the rural, subdistrict (urban-to-rural) and vice versa (rural-to-urban) to represent urban–rural interactions. Notably, with the focus on the regional structure based on interactions between subdistricts, we omitted the self-loops of intra-subdistrict mobility within a minimum spatial unit, which were beyond our research scope. The categorized constructions provided pathways to investigate and compare the consistency of spatial configurations in regional urban–urban and urban–rural systems.
5. Results
Focusing on regional cooperation and urban–rural integration, we obtained the clustering optima by iterating the WSBM algorithm with the number of groups ranging from two to fifteen, separately looping twelve times. Tracing the tendency of the average marginal log-likelihood value for each partition number, we identified the optimal , corresponding to the maximum log-likelihood value. In this study, the best-fit was nine for the UUM network and eight for the URM network.
5.1. Mesoscale Structure of the UUM Network
According to the results of WSBM, nine groups of urban subdistricts were detected given the group index from one to nine. Nodes in the same group were identified with similar roles and functions in the network based on node-pair connection patterns.
Figure 3a depicts the heatmap of the inter-subdistrict adjacency matrix weighted by aggregated mobility connections of 324 urban subdistricts inside the PRD area, with columns and rows sorted by the grouping index and degree centrality within each group. By comparing the network structure in
Figure 3a with the schematic mesoscale structure (
Figure 2), a hybrid and nested mesoscale structure was deduced, based on group interactions. Three assortative communities were detected in the coarse mesoscale structure, due to the dense mobility connections on the diagonal of the matrix, which were separately labeled as
,
and
. Neither a single community structure nor a CP structure, the UUM network exhibited a gradient community structure nested with CP structures where groups #1 to #5 composed community
, groups #6 to #7 comprised community
, and group #8 independently formed community
.
To better identify inter-group and inter-community relations and their roles in the network, we compressed the subdistrict-level heatmap to group-level visualization by calculating the group average of the mobility weights.
Figure 3b, therefore, intuitively represents the concrete inter-group matrix with a vertical axis weighted by the mean of the mobility connections among subdistricts within the group.
As connections mainly lay inside communities and inter-community connections approach zero, community structures shape their functions and roles relative to isolation and independence. Therefore, comparing the aggregated volume of mobility connections among three communities in
Figure 3b, we perceived the unbalanced share of mobility flows among three distinctive communities, denoting a rather gradient community structure. Community
held the densest connections, while community
was second. The mobility weight of community
, which only contained group 9, stood at a relatively isolated and undeveloped position in the city mobility network, holding sparse linkages inside and toward other communities.
Projecting the corresponding group and subdistrict membership onto a geographical layout (
Figure 3c), the PRD area, coincidentally segmented into three externally independent, internally correlative sub-regions, represented a significant regionalization pattern. The Middle PRD region, including Guangzhou, Foshan, Zhongshan and Zhuhai, matched to community
, experiencing the most active daily human-capital exchange within the boundary. Shenzhen, Dongguan and Huizhou in the East PRD region functioned as community
, tightly connected but sparsely communicating with cities outside. Finally, Zhaoqing and Jiangmen located in the West PRD region, comprised community
, playing a subordinative, undeveloped role in the UUM network of the PRD, given the scarce exchange towards cities, both internal and external.
Specifically, the internal mesoscale structures of community and displayed a significant CP structure but held different subtle characteristics. In community , groups #1 and #2 containing subdistricts scattered across the cities of Foshan, Guangzhou and Zhongshan, served as the core role, considering their prominent inner mobility frequency dominating the exchanging network landscape. With relatively weak internal and external connections with cores, semi-cores and other peripheries, groups #4 and #5 occupied the position of peripheries. The semi-core position stood as group #3, whose inner connections were atypically dense yet showed a relatively stronger linkage to the other two peripheral groups (group #4 and #5) than did the cores (group #1 and #2). In the spatial layout, the subdistricts in the core groups constructed a mobility belt crossing the Middle PRD from north to south. Additionally, subdistricts clustered into a semi-core group located in the blank space between geographically detached core districts, played a significant role in bridging the cores and peripheries across boundaries into regional integration.
Community represented similar CP patterns as community , with group #6 positioned at the core, while groups #7 and #8 played a peripheral role. The core group consisted of the major subdistricts of Dongguan and part of Shenzhen, while the rest of Shenzhen and Huizhou comprised the peripheries. Nevertheless, the inter-linkages of the core–periphery and periphery–periphery in community had a more similar density than those in community , implying a more random and balanced connection pattern of the East PRD. Hence, the mobility flows inside the East PRD were more likely to be evenly distributed across multiple dimensions and orientations, bundling Shenzhen, Dongguan and Huizhou into an organic functional entity.
Generally, the hybrid mesoscale structure mixed with community and CP structures shed insight into the “external isolation, internal integration” landscape of the UUM network. Consistent with the community detection result from the Louvain algorithm as shown in
Figure S1a, spatial division stemming from the administrative territory was constantly maintained, limiting the free mobility of human-capital resources across the entire region. The split of Middle, East, and West PRD defined by aspatial inter-subdistrict relations proved that functional segmentation coexisted with the spatial territory, suggesting top-down integration policies. Nevertheless, spatial spillover and integration occurred within sub-regions, accompanied by various mesoscales. Driven by transport infrastructure and industrial collaboration, Middle and East PRD cities crossed the administrative boundaries and integrated into tightly related functional communities, with nuanced forms and structures. In addition to clustering and classifying, WSBM elaborated the pathway to more profound understandings of the regional spatial structure by subtly identifying multiple mesoscale forms.
5.2. Mesoscale Structure of the URM Network
The URM network was defined by the exclusive mobility flows filtered out by the urban-to-rural and rural-to-urban categories, echoing the particular concern of unified urban–rural structures with the perspective of connection and exchange. Therefore, the bipartite nature was buried inside the URM network, whose nodes could be divided into two disjoint sets, and each edge connected the nodes in two sets.
WSBM identified eight groups of subdistrict-level units in the URM network. In
Figure 4a, two communities’ bipartite structure (or disassortative community) labeled as
and
was remarkably identified in the heatmap when compared to the schematic mesoscale structure (
Figure 2), denoting the connection strength of urban–rural subdistrict pairs. Marked by few linkages within communities and massive linkages between communities, groups #1 to #5 constituted the urban community
, while groups #6 to #8 comprised the rural community
, whose membership was approximately consistent with the administrative division of urban and rural subdistricts, revealing the typical bipartite mesoscale structure in the URM network mixed with asymmetric patterns and CP hierarchies. Notably, the WSBM algorithm distinguished two distinctive communities of urban and rural nodes without any attribute characteristics, where the classical Louvain algorithms failed (
Figure S1b). Furthermore, it verified its accuracy and robustness in community detection based on inter-connections.
Differentiated by the roughly equal volumes of directed connections back and forth between two urban subdistricts in the city network, connections between the urban and rural communities of two opposite orientations in the URM network were investigated and shown to share a significant imparity in linking density. In
Figure 4b, the row index
denoted the origin of the directed linkage, while the column index
denoted the destination of the linkage. Thus,
corresponded to the average weights of connections starting from group #
and flowing into group #
. In this way, inter-group 3D blocks agglomerated in the bottom left of the axis represented rural–urban connections, while blocks agglomerated in the upper right of the axis stood for urban–rural connections.
Urban-to-rural connections were significantly denser than the other direction when comparing the average density of linkages between the two directions. More urban residents move to rural districts for work, while urban areas offered labor force and human capital supporting rural development, which was beyond our expectation. One explanation is that since populations living in urban and rural areas are disproportionate, the greater absolute number of people moving from urban to rural areas is the byproduct of unbalanced population urbanization and systematic bias rooted in mobile-phone usage between urban and rural. In addition, given the consideration of simple distinguishment between urban and rural areas by administrative division codes, the potential transformation of de facto land use [
59], driven by informal industrialization and urban sprawl occurring in rural areas, may have caused informal urbanization to be neglected by administrative division in some rural areas, leading to systematic bias.
CP mesoscale structures were detected within each community, based on pairwise group linkages. Group #6 in rural community served as the core of the URM network in the PRD, accounting for its extremely dense connections with groups #1 and #2 and group #5 in the urban community. Similarly, group #1 shared a large daily exchange of labor with groups #6 and #7, and was thus identified as the core of the urban community. Groups #2 and #7 were distinguished as the semi-cores, as they only held dense connections with specific regions mostly recognized as the cores. Group #3 stood for the semi-periphery position because it linked to various groups yet shared relatively sparse connection weights. Finally, groups #4, #5, and #8 served as the periphery, due to a weak connection to the corresponding urban/rural areas in the URM network.
In mapping the geographic layout of groupings in the URM network (
Figure 4c), we investigated the prominent circular spatial configuration. The middle layers of spatial circles, containing the urban subdistricts of the
-core group in Foshan, Zhongshan, Zhuhai, Dongguan and Huizhou and the rural subdistricts of the
-core group surrounding the regional metropolises of Guangzhou and Shenzhen, were identified as playing the most significant role in the communications between cities and the countryside. The semi-cores extended the middle layers to the inner layers of regional megacities and outer layers of the wider rural hinterland, cohering the integrated urban–rural system on the entire regional scale. Meanwhile, the peripheries that rarely contributed to the integration were subdistricts located either in geographical peripherally rural areas or at the central cores of two metropolises, Guangzhou and Shenzhen. From the mesoscale structure, we identified the fact that the urban–rural integration was dominated by key node cities and towns as well as rural (or suburban) areas near megacities by their efforts to undertake massive crossing mobility flows, breaking the obstinate dualism of pivotal urban centers and the capacious rural hinterland.
6. Discussion and Conclusions
This study contributes to the sparse discussion on the urban–rural relationship in transition and pathways to regional urban–rural integration in the sustaining urbanization process by highlighting the accurate mesoscale structures of two daily mobility networks reflecting urban–urban and urban–rural connections in the PRD region. Derived from massive mobile-phone signaling data, we weighted the mobility connections by aggregating the amount of traveling records and then built the UUM and the URM network using specific categories of connections. With the implementation of WSBM, an unbiased and unsupervised stochastic block algorithm, the distinct mesoscale structures between the two networks were identified.
In the UUM network, a gradient, community mesoscale structure nested with CP structures was investigated, and the PRD region was functionally and spatially partitioned into three externally independent, internally correlative sub-regions. The hybrid structures with multiple communities echoed the polycentric spatial configuration proposed by the
Outline Development Plan for the Great Bay Area, which was consistent with previous studies [
41,
42,
43,
44]. Due to transportation-infrastructure development, regional integration and urban agglomeration occurred [
60,
61] through dense daily mobility connections inside city communities. Nevertheless, territories strongly constrained the linkages between sub-regions, due to the top-down strategies for distinguished development orientations and the relationship of co-opetition between city communities [
62].
The URM network presented an asymmetric, bipartite, mesoscale structure mixed with CP hierarchies, in which the linkages from urban to rural areas overweighed those in the inverse direction. The URM network suggested a concentric circular global layout of multiple layers, radiating from the highly agglomerated cities to marginal, rural hinterlands. The mesoscale structure of mobility connections was consistent with the ongoing urban–rural transformation in the PRD from the perspective of land use [
12]. Suburban areas surrounding metropolises and regional key node cities, which dominated the exchange connections in the URM network, have been the spatial focus for understanding the urban–rural integration process in PRD [
11]. Their crucial roles implicate the unique impetus of the urban–rural integration process rooted in the bottom-up spillover effect and radiation impact from the core cities [
63].
Differentiations significantly distinguished that the UUM network displayed a regionalization pattern, while the diminishment of administrative boundaries in the URM network occurred on the scale of the entire PRD. The significant dissimilarity in spatial mesoscale structures between the two networks specified the rooted bias of regional studies trapped in “methodological cityism” [
21]. Rather than frozen in a pre-existing, static, undeveloped production of space, the rural areas dynamically map rural livelihood and imaginings in situ and beyond, to forge an urban–-rural relationship [
2]. Massive interactions between the urban and rural situated in the suburban area and key node cities in our result dissembled the entrenched rural–urban binary while corroborating the necessity of involvement of the rural in the regional-integration development strategy.
Moreover, few studies have discussed the issue of the theoretical urban–rural interacting model in the field of regional integration. Inferred from Thünen’s model, rural settlements would separately serve as the “back-of-house” for corresponding local urban areas within the administrative territory, leading to a “local” model. On the other side of the spectrum, a “global” model hypothesizes a monocentric/polycentric spatial pattern where all rural supply flows converge into regional central cities to build a hub-and-spoke structure. The question remains as to which scale of the urban–rural interactions would maximize the regional competitiveness and sustainability. Our findings of the concentric-circle spatial structure, where the middle layer of suburban and key node cities shared the densest interactions, suggested an intermediate scenario and a long-term tendency to cross the boundaries. Nevertheless, recent regional-integration strategies, for coordinating an urban–rural interaction system between different administrative divisions, have remained blank, and have needed further investigation in network science to guide well-aligned urban–rural and regional integration.
Therefore, our findings offer potential practical pathways and policy implications for urban–rural integration in the PRD area. First, by recognizing the differentiated spatial organization mechanism in the two networks, the integration process in the metropolises and their neighboring rural (suburban) areas should be promoted and then extended to the rural hinterlands. Second, with the measurements of a unified market construction, interconnected infrastructure development and public service sharing, the elimination of institutional barriers between the urban and the rural could further strengthen the free mobility of resources in-between them and the radiation impacts of regional core cities, accelerating the integration process. Third, key node cities such as Foshan, Zhongshan and Jiangmen play a significant role in urban connections and the urban–rural integration process, emphasizing the support for innovative and coordinated development for the node cities.
Several limitations in this study mean that the study deserves further improvements and investigation. First, the uneven usage and distribution of mobile-phone signaling data may lead to systematic bias in mesoscale detection and underestimate the active role of rural areas in the integration process. Data from other sectors such as transportation and economics, and techniques including multi-source data fusion, may help eliminate the bias. Second, a consensus WSBM workflow [
57] will further improve the consolidation of the detected mesoscale structure. And a causal inference approach [
64,
65] may enrich the causality of mesoscale structures especially for the dynamic patterns. Third, considering the high computational cost brought by the variational Bayes expectation maximization algorithm in WSBM, which limits the mesoscale analysis in a relatively small network dataset, a non-parametric WSBM approach [
20] is needed to reduce computational cost and mine the optimal regional mesoscale structure without prior input. Fourth, typical issues of urban–rural relationship, such as de facto land use in suburban neighborhoods and the urban village phenomenon in China, are neglected under the definition of administrative urban–rural division used in the study. These issues are worth discussing in the progress of urban–rural integration. Dynamic definitions of urban–rural divisions and higher-precision data on urban–rural connections are needed for further investigation of these issues.