Periodic and Axial Perturbations of Chaotic Solitons in the Realm of Complex Structured Quintic Swift-Hohenberg Equation

Abstract

This research work employs a powerful analytical method known as the Riccati Modified Extended Simple Equation Method (RMESEM) to investigate and analyse chaotic soliton solutions of the (1 + 1)-dimensional Complex Quintic Swift–Hohenberg Equation (CQSHE). This model serves to describe complex dissipative systems that produce patterns. We have found that there exist numerous chaotic soliton solutions with periodic and axial perturbations to the intended CQSHE, provided that the coefficients are constrained by certain conditions. Furthermore, by applying a sophisticated transformation, the provided transformative approach RMESEM transforms CQSHE into a set of Nonlinear Ordinary Differential Equations (NODEs). The resulting set of NODEs is then transformed into an algebraic system of equations by incorporating the extended Riccati NODE to assume a series form solution. The soliton solutions to this system of equations can be found as periodic, hyperbolic, exponential, rational-hyperbolic, and rational families of functions. A variety of 3D and contour visuals are also provided to graphically illustrate the axially and periodically perturbed dynamics of these chaotic soliton solutions and the formation of fractals. Our findings are noteworthy because they shed light on the chaotic nature of the framework we are examining, enabling us to better understand the dynamics that underlie it.

1. Introduction

The Swift–Hohenberg Equation (SHE) can be used to describe complex pattern-forming dissipative systems [1,2]. Classical examples include diverse chemical reactions [3], the Rayleigh-B-énard issue of convection in a horizontal fluid layer in the gravitational field [4,5], large-scale flows and spiral core instabilities [6], Taylor–Couette flow [7], and others. Three-level broad-area cascade lasers [8], large aspect-ratio lasers [9,10,11,12] and synchronously pumped optical parametric oscillators [13] are a few examples of applications in optics. The SHE in various forms, such as the generalized complex SHE (CSHE) [13], real SHE [14], stochastic SHE [15], and CSHE [16] have been established asymptotically in the setting of large-aperture lasers with minimum detuning across the atomic and cavity frequencies. It is also believed that oscillatory convection in binary fluids is related to this equation. Despite their apparent complexity, spatial relationships are actually made up of a limited number of spatial combinations of a few more basic localised structures that can be orderly or chaotic. The SHE is known to contain phase domains and transverse localised features [14]. These coherent structures can be thought of as either light or dark solitons. Thus, these simple localised structures and their stability are of tremendous importance to the study of any pattern-forming system [17,18,19,20].

The localised structures of the SHE bear a striking resemblance to systems represented by the complex Ginzburg–Landau equation (CGLE), which has been the subject of earlier research. Numerous studies have developed analytical solutions for the quintic and cubic CGLE [21,22,23,24]. Analytical solutions to the cubic ($1+1$)-dimensional problem characterise all potential bright and dark soliton solutions. On the other hand, the quintic problem’s soliton solutions’ limited subgroup is represented by the analytic solutions of the CGLE. Furthermore, this subclass does not contain stable soliton solutions [24]. As a result, only numerical techniques may yield conclusions that have any real value. We see that the CGLE often only has isolated solutions, i.e., they are fixed for every possible combination of equation parameters, with a few notable exceptions [24,25]. This functionality is essential to the entire collection of CGLE localised solutions. One fundamental property of dissipative systems in particular is the occurrence of isolated solutions. Ref. [26] provides the qualitative physical underpinnings of this trait. This characteristic strengthens the program’s overall viability. Since the SHE predicts dissipative systems like the CGLE, we anticipate that it will have this feature. This idea is supported in fact by preliminary computer simulations. The more complex diffraction term is the primary distinction between the CGLE and the SHE [27]. The latter is necessary to clarify the nuances of a real physical issue. However, because of their intricacy, we find it difficult to analyse the solutions. In fact, it has not been made clear in the literature as to whether any of these solutions can be found at all [8,9,10,13].

In this paper, we examine the ($1+1$)-dimensional CQSHE and offer several new chaotic soliton solutions. Prior to delving deeper, it is imperative that we differentiate between the real SHE and the highly complex structured SHE. One could consider the former to be a specific instance of the CSHE. Moreover, the true SHE cannot be logically deduced from the original equations since it is a phenomenological model [4]. On the other hand, in the long-wavelength case, the asymptotically derived complex structured SHE is rigorous. The complex structured SHE is expressed as follows in standard notation:

$$z_t=\varsigma z-(1+ic)\mid z{\mid }^{2}z+i\overline{\alpha }\Delta z-d{(\Lambda +\Delta )}^{2}z,$$

(1)

where $\overline{\alpha }$ represents the active medium’s diffraction characteristics and $\varsigma$ is the control parameter. It is possible to avoid the differential nonlinearities since they have larger orders in the long-wavelength limit, or in the limit $\Lambda ⟼0$. The diffraction term ia z in this instance is partially corrected by the wavenumber selection term ${(\Lambda +\Delta )}^{2}z$. Consequently, a perturbed cubic CGLE can be used to understand the complex organised SHE. Our main focus is the case when, in the ($1+1$)-dimensional instance, there are only x-derivatives. In physical problems, quintic nonlinearity can be just as important as cubic nonlinearity, since it governs the stability of localised solutions [28]. Sakaguchi and Brand studied the CQSHE numerically. This model is expressed as:

$$z_t=\overline{\alpha }z+\overline{\beta }\mid z{\mid }^{2}z-\gamma \mid z{\mid }^{4}z-d{(1+{\partial }_{xx})}^{2}z+if{\partial }_{xx}z,$$

(2)

In this scenario, the order parameter z, the coefficients $\overline{\alpha }={\alpha }_1+i{\alpha }_2,$ $\overline{\beta }={\beta }_1+i{\beta }_2$, ${\gamma }_1+i{\gamma }_2$, and d and f are real [27]. The original SHE, which was obtained as an order parameter equation for the start of Rayleigh–Bénard convection in a simple fluid, is given by real values of $\alpha$, $\beta$, and d, as well as by values of $\gamma$ and f. Thus, here is an alternative notation for Equation (2):

$$\begin{array}{c}\hfill i{z}_t+(f+2id)z_{xx}+id{z}_{xxxx}+({\beta }_2-i{b}_1)\mid z{\mid }^{2}z+(-{\gamma }_2+i{c}_1)\mid z{\mid }^{4}z=(-{\alpha }_2+i({\alpha }_2-d))z.\end{array}$$

(3)

An additional way to generalise this equation is:

$$z_t+\zeta z_{xx}+\delta z_{xxxx}+\epsilon \mid z{\mid }^2+\psi \mid z{\mid }^{4}z=i\eta z,$$

(4)

here, $z=z(x,t)$, $\eta$ is real and every coefficient, $\zeta ={\zeta }_1+i{\zeta }_2, \delta ={\delta }_1+i{\delta }_2, \epsilon ={\epsilon }_1+i{\epsilon }_2,$ and $\psi ={\psi }_1+i{\psi }_2$, is complex. Equation (4) can be referred to as the generalised CQSHE. Moreover, the real quintic SHE as well as the real cubic SHE can be obtained as special instances of Equation (4) by considering certain coefficients equal to 0. The specific problem determines how the variables should be interpreted. The transverse variable in optics is represented by t; the propagation distance, or cavity round-trip number, is represented by x (treated as a continuous variable); the nonlinear gain is represented by ${\epsilon }_2$ (or 2-photon absorption if negative); the second- and fourth-order diffractions are represented by ${\zeta }_1$ and ${\delta }_1$; and the difference between linear gain and loss is represented by $\delta$. The coefficients ${\delta }_2$ and ${\zeta }_2$ denote the angular spectral rise.

Several studies have shown the existence of solitons in the context of CQSHE. For instance, in their numerical studies, Sakaguchi and Brand [27] noticed specific formations that resembled solitons. It was also demonstrated that the stable hole solution for the CQSHE exists. Their findings suggest that, despite the lack of exact solutions discovered thus far, there might be some that exist. Comparatively, Maruno et al. studied analytic soliton solutions of the ($1+1$)-dimensional complex cubic and quintic SHE [29] using Painlevé analysis, the direct ansatz approach, and the Hirota multi-linear method. Finally, Crespo and Akhmediev used numerical simulations to study the single- and two-soliton solutions of the CQSHE [30]. In line with previous studies, a number of researchers have investigated the solitonic phenomena in CQSHE; however, no study has examined and evaluated periodic and axial perturbations of chaotic solitons and formations of fractals within the context of the intended model. This claim draws attention to a prominent gap in the corpus of existing research. Our paper offers a thorough analysis of the model and outlines the suggested RMESEM strategy in order to bridge this gap. Therefore, in this work, we examine the perturbing behaviour of the chaotic soliton within the context of CQSHE using the RMESEM. Furthermore, a set of contour and 3D representations are used to graphically describe the altered dynamics of different chaotic solitons. The soliton solutions we have found here can serve as a basis for further research and development.

The remainder of the paper is structured as follows: Section 2 describes the RMESEM’s analytical procedures; Section 3 deals with the CQSHE to produce new soliton solutions; Section 4 provides a visual representation of the perturbed behaviour of the chaotic solitons; Section 5 provides a summary of the findings, while an Appendix A is given in last section.

2. The Description of RMESEM

Numerous analytical techniques have been developed in the literature to investigate soliton events in nonlinear models [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48]. Although these methods significantly improve our understanding of soliton dynamics and help us link them to the models that govern occurrences, it is important to recognize that they could have limitations and certain drawbacks (e.g., the seven common errors) [49,50]. Additionally, a few of these techniques rely on the Riccati equation [51]. These methods are applicable to the analysis of soliton phenomena in nonlinear models, as the Riccati equation encompasses solitary solutions [52]. As a result, in this paper we use RMESEM, a modified version of the Simple Equation Method (SEM) which incorporates the extended Riccati equation. The SEM was first established by Kudryashov [53] and was then modified by various other researchers (such as Vitanov’s modifications to SEM [54,55,56]). Finally, the SEM was integrated with the extended Riccati and a more generalized ansatz by Xiao et al. to establish RMESEM [57]. We outline the upgraded RMESEM’s working mechanism in this section. Analysing the given NLPDE:

$$R(z,z_t,z_{y_1},z_{y_2},z{z}_{y_1},\dots )=0,$$

(5)

where $z=z(t,y_1,y_2,y_3,\dots ,y_r)$.

The procedures listed below will be used to solve Equation (5):

• Initially, $z(t,y_1,y_2,y_3,\dots ,y_r)=Z(\Omega )$, a variable-form wave transformation, is performed. $\Omega$ can be expressed in several ways. Equation (5) is transformed in this process to get the following NODE:

  $$Q(Z,Z^{\prime }Z,Z^{\prime },\dots )=0,$$

  (6)

  where $Z^{\prime }={\displaystyle \frac{dZ}{d\Omega }}$. The homogeneous balancing condition can occasionally be enforced on the NODE by applying integrating Equation (6).
• Next, we hypothesise the following series-based solution for the NODE in (6) using the solution of the extended Riccati ODE:

  $$Z(\Omega )=\sum _{j=0}^l{S}_j{\left({\displaystyle \frac{{\phi }^{\prime }(\Omega )}{\phi (\Omega )}}\right)}^j+\sum _{j=0}^{l-1}{A}_j{\left({\displaystyle \frac{{\phi }^{\prime }(\Omega )}{\phi (\Omega )}}\right)}^j·\left({\displaystyle \frac{1}{\phi (\Omega )}}\right).$$

  (7)
  In this instance, $\phi (\Omega )$ represents the solution to the resulting extended Riccati ODE, and the variables $S_j(j=0,\dots ,l)$ and $A_j(j=0,\dots ,l-1)$ represent the unknown constants that must be calculated afterwards.

  $${\phi }^{\prime }(\Omega )=p+q\phi (\Omega )+r{\left(\phi (\Omega )\right)}^2,$$

  (8)

  where $p,q$ and r are invariables.
• The highest-order derivative and the highest nonlinear component in Equation (6) can be homogeneously balanced to yield the positive integer l required in Equation (7).
• Next, when (7) is incorporated in (6) or the equation resulting from the integration of (6), all the terms of $\phi (\Omega )$ are combined into an equal ordering. An expression in terms of $\phi (\Omega )$ is produced when this procedure is used. We obtain an algebraic system of equations describing the variables $S_j(j=0,\dots ,l)$ and $A_j(j=0,\dots ,l-1)$ with additional associated parameters by setting the coefficients in this equation to zero.
• An analytical evaluation of a collection of nonlinear algebraic equations is performed through the use of MAPLE.
• Then, by computing and inserting the unknown values in Equation (7) along together with $\phi (\Omega )$ (the Equation (8) answers), analytical soliton solutions for (5) are obtained. By employing (8)’s generic solution, we can derive multiple families of soliton solutions, which are shown in

  Table 1. The particular solutions $\phi (\Omega )$ of Riccati equation in (8) and the formation of $\left({\displaystyle \frac{{\phi }^{\prime }(\Omega )}{\phi (\Omega )}}\right)$.

  S. No.	Family	Constraint(s)	$\mathit{\phi }(\mathbf{\Omega })$	$\left(\frac{{\mathit{\phi }}^{\prime }(\mathbf{\Omega })}{\mathit{\phi }(\mathbf{\Omega })}\right)$
  1	Trigonometric Solutions	$J<0,r\ne 0$
  			$-{\displaystyle \frac{q}{2r}}+{\displaystyle \frac{\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{2r}}$,	$-{\displaystyle \frac{1}{2}}{\displaystyle \frac{J\left(1+{\left(\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}^2\right)}{-q+\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}}$,
  			$-{\displaystyle \frac{q}{2r}}-{\displaystyle \frac{\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{2r}}$,	${\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(1+{\left(\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}^2\right)J}{q+\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}}$,
  			$-{\displaystyle \frac{q}{2r}}+{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)+\left(\sec \left(\sqrt{-J}\Omega \right)\right)\right)}{2r}}$,	${\displaystyle \frac{-K\left(1+\sin \left(\sqrt{-J}\Omega \right)\right)}{\cos \left(\sqrt{-J}\Omega \right)\left(-q\cos \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\sin \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\right)}}$,
  			$-{\displaystyle \frac{q}{2r}}+{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)-\left(\sec \left(\sqrt{-J}\Omega \right)\right)\right)}{2r}}$.	${\displaystyle \frac{J\left(\sin \left(\sqrt{-J}\Omega \right)-1\right)}{\cos \left(\sqrt{-J}\Omega \right)\left(-q\cos \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\sin \left(\sqrt{-J}\Omega \right)-\sqrt{-J}\right)}}$.
  2	Hyperbolic Solutions	$J>0,r\ne 0$
  			$-{\displaystyle \frac{q}{2r}}-{\displaystyle \frac{\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}{2r}}$,	$-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\left(-1+{\left(\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)\right)}^2\right)J}{q+\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}}$,
  			$-{\displaystyle \frac{q}{2r}}-{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)+i\left(\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)\right)}{2r}}$,	$-{\displaystyle \frac{J\left(-1+i\sinh \left(\sqrt{J}\Omega \right)\right)}{\cosh \left(\sqrt{J}\Omega \right)\left(q\cosh \left(\sqrt{J}\Omega \right)+\sqrt{J}\sinh \left(\sqrt{J}\Omega \right)+i\sqrt{J}\right)}}$,
  			$-{\displaystyle \frac{q}{2r}}-{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)-i\left(\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)\right)}{2r}}$,	$-{\displaystyle \frac{J\left(1+i\sinh \left(\sqrt{J}\Omega \right)\right)}{\cosh \left(\sqrt{J}\Omega \right)\left(-q\cosh \left(\sqrt{J}\Omega \right)-\sqrt{J}\sinh \left(\sqrt{J}\Omega \right)+i\sqrt{J}\right)}},$
  			$-{\displaystyle \frac{q}{2r}}-{\displaystyle \frac{\sqrt{J}\left(\coth \left(\sqrt{J}\Omega \right)+\left(\mathrm{csch}\left(\sqrt{J}\Omega \right)\right)\right)}{2r}}$.	$-{\displaystyle \frac{1}{4}}{\displaystyle \frac{J\left(2{\left(\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}^2-1\right)}{\wp \left(-2q\wp +\sqrt{J}\right)}}.$
  3	Rational Solutions
  		$J=0$	$-2{\displaystyle \frac{p\left(q\Omega +2\right)}{q^2\Omega }}$,	$-2{\displaystyle \frac{1}{\Omega \left(q\Omega +2\right)}}$,
  		$J=0$, & $q=r=0$	$\Omega p$,	${\displaystyle \frac{1}{\Omega }}$,
  		$J=0$, & $q=p=0$	$-{\displaystyle \frac{1}{\Omega r}}$.	$-{\displaystyle \frac{1}{\Omega }}$.
  4	Exponential Solutions
  		$r=0$, & $q=k$, $p=nk$	$e^{k\Omega }-n$,	${\displaystyle \frac{k{\mathrm{e}}^{k\Omega }}{{\mathrm{e}}^{k\Omega }-n}}$,
  		$p=0$, & $q=k$, $r=nk$	${\displaystyle \frac{e^{k\Omega }}{1-n{e}^{k\Omega }}}$.	$-{\displaystyle \frac{k}{-1+n{\mathrm{e}}^{k\Omega }}}$.
  5	Rational-Hyperbolic Solutions
  		$p=0$, & $q\ne 0$, $r\ne 0$	$-{\displaystyle \frac{q\tau }{r\left(\cosh \left(q\Omega \right)-\sinh \left(q\Omega \right)+\varpi \right)}}$,	${\displaystyle \frac{q\left(\sinh \left(q\Omega \right)-\cosh \left(q\Omega \right)\right)}{-\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)-\varpi }}$,
  			$-{\displaystyle \frac{q\left(\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)\right)}{r\left(\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)+\varpi \right)}}$.	${\displaystyle \frac{q\varpi }{\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)+\varpi }}$.

  :
  where $\tau ,\varpi \in \mathrm{R}$, $J=q^2-4rp$, and $\wp =\cosh \left({\displaystyle \frac{1}{4}}\sqrt{J}\Omega \right)\sinh \left({\displaystyle \frac{1}{4}}\sqrt{J}\Omega \right)$.

3. Establishing Perturbed Soliton Solutions for CQSHE

This section presents the creation of new families of soliton solutions. First, we apply the ensuing complex transformation:

$$z(x,t)=e^{i\theta }Z(\Omega );\mathrm{where}\Omega =ax+bt\mathrm{and}\theta =m_{1}x+m_{2}t.$$

(9)

The real and imaginary parts of Equation (4) are transformed into the following set of NODEs by this process:

$$\begin{array}{cc}\hfill & (-m_2-{m_1}^2\zeta +\delta {m_1}^4)Z+(a^2\zeta -6\delta a^2{m_1}^2)Z^{″}+a^4\delta Z^{\left(iv\right)}+\psi Z^2+\epsilon Z^3=0,\hfill \end{array}$$

(10)

and

$$\begin{array}{cc}\hfill & (b+2a{m}_1\zeta -4a{m_1}^3)Z^{\prime }+4a^3{m}_1\delta Z^{‴}-\eta Z=0,\hfill \end{array}$$

(11)

correspondingly. The following constraint requirements result from the NODE that was derived from the imaginary part:

$$\begin{array}{cc}\hfill & b=4a{m_1}^3-2a{m}_1\zeta ,\mathrm{and}\delta =\eta =0,\hfill \end{array}$$

(12)

which reduces the system as a whole and Equation (10) to the ensuing single NODE:

$$\begin{array}{cc}\hfill & -(m_2+{m_1}^2\zeta )Z+a^2\zeta Z^{″}+\psi Z^2+\epsilon Z^3=0.\hfill \end{array}$$

(13)

By establishing the homogeneous balancing notion between $\epsilon Z^3$ and $a^2\zeta Z^{″}$ in Equation (13), we are able to arrive at $l=1$. The following closed form solution for Equation (13) is suggested by substituting $l=1$ in Equation (7):

$$Z(\Omega )=\sum _{j=0}^1{S}_j{\left({\displaystyle \frac{{\phi }^{\prime }(\Omega )}{\phi (\Omega )}}\right)}^j+A_0\left({\displaystyle \frac{1}{\phi (\Omega )}}\right).$$

(14)

To produce an expression in $G(\Omega )$, Equation (14) is inserted into Equation (13). This is accomplished by gathering all of the terms in $G(\Omega )$ that have the same powers. The expression can be reduced to a system of nonlinear algebraic equations by setting the coefficients to zero. Using Maple, the resultant problem is solved, which gives five (5) cases of solutions given as:

Case 1.

$$\begin{array}{cc}\hfill & S_1=0,S_0={\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}},A_0=A_0,m_1=m_1,m_2={\displaystyle \frac{1}{2}}\zeta \left(-{\alpha }^{2}J-2{m_1}^2\right),\alpha =\alpha ,\zeta =\zeta ,ϵ=0,\psi =-2{\displaystyle \frac{p^2{\alpha }^2\zeta }{{A_0}^2}}.\hfill \end{array}$$

(15)

Case 2.

$$\begin{array}{cc}\hfill & S_1=S_1,S_0=S_0,A_0=A_0,m_1=m_1,m_2=0,\alpha =\alpha ,\zeta =0,ϵ=0,\psi =0.\hfill \end{array}$$

(16)

Case 3.

$$\begin{array}{cc}\hfill & S_1=S_1,S_0=-{\displaystyle \frac{1}{2}}{S}_{1}q,A_0=-S_{1}p,m_1=m_1,m_2=-{m_1}^2\zeta -{\displaystyle \frac{1}{2}}{\alpha }^2\zeta J,\alpha =\alpha ,\zeta =\zeta ,ϵ=0,\psi =-2{\displaystyle \frac{{\alpha }^2\zeta }{{S_1}^2}}.\hfill \end{array}$$

(17)

Case 4.

$$\begin{array}{cc}\hfill & S_1=0,S_0=S_0,A_0=2{\displaystyle \frac{S_{0}p}{q}},m_1=m_1,m_2=-{m_1}^2\zeta -{\displaystyle \frac{1}{2}}{\alpha }^2\zeta J,\alpha =\alpha ,\zeta =\zeta ,ϵ=0,\psi =-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\alpha }^2\zeta q^2}{{S_0}^2}}.\hfill \end{array}$$

(18)

Case 5.

$$\begin{array}{cc}\hfill & S_1=-{\displaystyle \frac{A_0}{p}},S_0={\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}},A_0=A_0,m_1=m_1,m_2=-{m_1}^2\zeta -{\displaystyle \frac{1}{2}}{\alpha }^2\zeta J,\alpha =\alpha ,\zeta =\zeta ,ϵ=0,\psi =-2{\displaystyle \frac{p^2{\alpha }^2\zeta }{{A_0}^2}}.\hfill \end{array}$$

(19)

Taking into consideration Case 1 and utilizing (9), (14) with the corresponding solution of Equation (8), we have the subsequent new families of chaotic soliton solutions for CQSHE articulated in (4):

Family 1.1:

For $J<0r\ne 0$,

$$\begin{array}{cc}\hfill z_{1,1}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill z_{1,2}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill z_{1,3}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)+\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(22)

and

$$\begin{array}{cc}\hfill z_{1,4}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)-\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}\right).\hfill \end{array}$$

(23)

Family 1.2:

For $J>0r\ne 0$,

$$\begin{array}{cc}\hfill z_{1,5}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill z_{1,6}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)+i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill z_{1,7}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)-i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(26)

and

$$\begin{array}{cc}\hfill z_{1,8}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{4}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\frac{1}{4}\sqrt{J}\Omega \right)-\coth \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(27)

Family 1.3:

For $J=0,q\ne 0$,

$$\begin{array}{cc}\hfill z_{1,9}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{A_0{q}^2\Omega }{p\left(q\Omega +2\right)}}\right).\hfill \end{array}$$

(28)

Family 1.4:

For $J=0$, in case when $r=q=0$,

$$\begin{array}{cc}\hfill z_{1,10}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+{\displaystyle \frac{A_0}{p\Omega }}\right).\hfill \end{array}$$

(29)

Family 1.5:

For $q=k$, $p=nk(n\ne 0)$ and $r=0$,

$$\begin{array}{cc}\hfill z_{1,11}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_0}{n}}+{\displaystyle \frac{A_0}{{\mathrm{e}}^{\kappa \Omega }-n}}\right).\hfill \end{array}$$

(30)

Taking into consideration Case 2 and utilizing (9), (14) with the corresponding solution of Equation (8), we have the subsequent new families of chaotic soliton solutions for CQSHE articulated in (4):

Family 2.1:

For $J<0r\ne 0$,

$$\begin{array}{cc}\hfill z_{2,1}(x,t)=& e^{i\theta }\left(S_0-{\displaystyle \frac{1}{2}}{\displaystyle \frac{S_{1}J\left(1+{\left(\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}^2\right)}{-q+\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill z_{2,2}(x,t)=& e^{i\theta }\left(S_0+{\displaystyle \frac{1}{2}}{\displaystyle \frac{S_{1}J\left(1+{\left(\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}^2\right)}{q+\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill z_{2,3}(x,t)=& e^{i\theta }(S_0-{\displaystyle \frac{S_{1}J\left(1+\sin \left(\sqrt{-J}\Omega \right)\right)}{\cos \left(\sqrt{-J}\Omega \right)\left(-q\cos \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\sin \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)+\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(33)

and

$$\begin{array}{cc}\hfill z_{2,4}(x,t)=& e^{i\theta }(S_0+{\displaystyle \frac{S_{1}J\left(\sin \left(\sqrt{-J}\Omega \right)-1\right)}{\cos \left(\sqrt{-J}\Omega \right)\left(-q\cos \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\sin \left(\sqrt{-J}\Omega \right)-\sqrt{-J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)-\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}).\hfill \end{array}$$

(34)

Family 2.2:

For $J>0r\ne 0$,

$$\begin{array}{cc}\hfill z_{2,5}(x,t)=& e^{i\theta }\left(S_0-{\displaystyle \frac{1}{2}}{\displaystyle \frac{S_{1}J\left(-1+{\left(\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)\right)}^2\right)}{q+\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill z_{2,6}(x,t)=& e^{i\theta }(S_0-{\displaystyle \frac{S_{1}J\left(-1+i\sinh \left(\sqrt{J}\Omega \right)\right)}{\cosh \left(\sqrt{J}\Omega \right)\left(q\cosh \left(\sqrt{J}\Omega \right)+\sqrt{J}\sinh \left(\sqrt{J}\Omega \right)+i\sqrt{J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)+i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill z_{2,7}(x,t)=& e^{i\theta }(S_0-{\displaystyle \frac{S_{1}J\left(1+i\sinh \left(\sqrt{J}\Omega \right)\right)}{\cosh \left(\sqrt{J}\Omega \right)\left(-q\cosh \left(\sqrt{J}\Omega \right)-\sqrt{J}\sinh \left(\sqrt{J}\Omega \right)+i\sqrt{J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)-i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(37)

and

$$\begin{array}{cc}\hfill z_{2,8}(x,t)=& e^{i\theta }(S_0+{\displaystyle \frac{1}{4}}{\displaystyle \frac{S_{1}J\left(2{\left(\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}^2-1\right)}{\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\sinh \left(\frac{1}{4}\sqrt{J}\Omega \right)\left(2q\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\sinh \left(\frac{1}{4}\sqrt{J}\Omega \right)-\sqrt{J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{4}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\frac{1}{4}\sqrt{J}\Omega \right)-\coth \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(38)

Family 2.3:

For $J=0,q\ne 0$,

$$\begin{array}{cc}\hfill z_{2,9}(x,t)=& e^{i\theta }\left(S_0-2{\displaystyle \frac{S_1}{\Omega \left(q\Omega +2\right)}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{A_0{q}^2\Omega }{p\left(q\Omega +2\right)}}\right).\hfill \end{array}$$

(39)

Family 2.4:

For $J=0$, in case when $r=q=0$,

$$\begin{array}{cc}\hfill z_{2,10}(x,t)=& e^{i\theta }\left(S_0+{\displaystyle \frac{S_1}{\Omega }}+{\displaystyle \frac{A_0}{p\Omega }}\right).\hfill \end{array}$$

(40)

Family 2.5:

For $J=0$, in case when $p=q=0$,

$$\begin{array}{cc}\hfill z_{2,11}(x,t)=& e^{i\theta }\left(S_0-{\displaystyle \frac{S_1}{\Omega }}-A_{0}r\Omega \right).\hfill \end{array}$$

(41)

Family 2.6:

For $q=k$, $p=nk(n\ne 0)$ and $r=0$,

$$\begin{array}{cc}\hfill z_{2,12}(x,t)=& e^{i\theta }\left(S_0+{\displaystyle \frac{S_1\kappa {\mathrm{e}}^{\kappa \Omega }}{{\mathrm{e}}^{\kappa \Omega }-n}}+{\displaystyle \frac{A_0}{{\mathrm{e}}^{\kappa \Omega }-n}}\right).\hfill \end{array}$$

(42)

Family 2.7:

For $q=k$, $r=nk(n\ne 0)$ and $p=0$,

$$\begin{array}{cc}\hfill z_{2,13}(x,t)=& e^{i\theta }\left(S_0-{\displaystyle \frac{S_{1}k}{-1+n{\mathrm{e}}^{k\Omega }}}+{\displaystyle \frac{A_0\left(1-n{\mathrm{e}}^{k\Omega }\right)}{{\mathrm{e}}^{k\Omega }}}\right).\hfill \end{array}$$

(43)

Family 2.8:

For $p=0$, $r\ne 0$ and $q\ne 0$,

$$\begin{array}{cc}\hfill z_{2,14}(x,t)=& e^{i\theta }\left(S_0+{\displaystyle \frac{S_{1}q\left(\sinh \left(q\Omega \right)-\cosh \left(q\Omega \right)\right)}{-\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)-\varpi }}-{\displaystyle \frac{A_{0}r\left(\cosh \left(q\Omega \right)-\sinh \left(q\Omega \right)+\varpi \right)}{\tau q}}\right),\hfill \end{array}$$

(44)

and

$$\begin{array}{cc}\hfill z_{2,15}(x,t)=& e^{i\theta }\left(S_0+{\displaystyle \frac{S_{1}q\varpi }{\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)+\varpi }}-{\displaystyle \frac{A_{0}r\left(\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)+\varpi \right)}{q\left(\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)\right)}}\right).\hfill \end{array}$$

(45)

Taking into consideration Case 3 and utilizing (9), (14) with the corresponding solution of Equation (8), we have the subsequent new families of chaotic soliton solutions for CQSHE articulated in (4):

Family 3.1:

For $J<0r\ne 0$,

$$\begin{array}{cc}\hfill z_{3,1}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{1}{2}}{S}_{1}q-{\displaystyle \frac{1}{2}}{\displaystyle \frac{S_{1}J\left(1+{\left(\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}^2\right)}{-q+\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}}-S_{1}p{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(46)

$$\begin{array}{cc}\hfill z_{3,2}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{1}{2}}{S}_{1}q+{\displaystyle \frac{1}{2}}{\displaystyle \frac{S_{1}J\left(1+{\left(\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}^2\right)}{q+\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}}-S_{1}p{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill z_{3,3}(x,t)=& e^{i\theta }(-{\displaystyle \frac{1}{2}}{S}_{1}q-{\displaystyle \frac{S_{1}J\left(1+\sin \left(\sqrt{-J}\Omega \right)\right)}{\cos \left(\sqrt{-J}\Omega \right)\left(-q\cos \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\sin \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\right)}}\hfill \\ \hfill & -S_{1}p{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)+\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(48)

and

$$\begin{array}{cc}\hfill z_{3,4}(x,t)=& e^{i\theta }(-{\displaystyle \frac{1}{2}}{S}_{1}q+{\displaystyle \frac{S_{1}J\left(\sin \left(\sqrt{-J}\Omega \right)-1\right)}{\cos \left(\sqrt{-J}\Omega \right)\left(-q\cos \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\sin \left(\sqrt{-J}\Omega \right)-\sqrt{-J}\right)}}\hfill \\ \hfill & -S_{1}p{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)-\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}).\hfill \end{array}$$

(49)

Family 3.2:

For $J>0r\ne 0$,

$$\begin{array}{cc}\hfill z_{3,5}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{1}{2}}{S}_{1}q-{\displaystyle \frac{1}{2}}{\displaystyle \frac{S_{1}J\left(-1+{\left(\tanh \left(1/2\sqrt{J}\Omega \right)\right)}^2\right)}{q+\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}}-{\displaystyle \frac{S_{1}p}{\left(-\frac{1}{2}\frac{q}{r}-\frac{1}{2}\frac{\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}{r}\right)}}\right),\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill z_{3,6}(x,t)=& e^{i\theta }(-{\displaystyle \frac{1}{2}}{S}_{1}q-{\displaystyle \frac{S_{1}J\left(-1+i\sinh \left(\sqrt{J}\Omega \right)\right)}{\cosh \left(\sqrt{J}\Omega \right)\left(q\cosh \left(\sqrt{J}\Omega \right)+\sqrt{J}\sinh \left(\sqrt{J}\Omega \right)+i\sqrt{J}\right)}}\hfill \\ \hfill & -S_{1}p{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)+i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill z_{3,7}(x,t)=& e^{i\theta }(-{\displaystyle \frac{1}{2}}{S}_{1}q-{\displaystyle \frac{S_{1}J\left(1+i\sinh \left(\sqrt{J}\Omega \right)\right)}{\cosh \left(\sqrt{J}\Omega \right)\left(-q\cosh \left(\sqrt{J}\Omega \right)-\sqrt{J}\sinh \left(\sqrt{J}\Omega \right)+i\sqrt{J}\right)}}\hfill \\ \hfill & -S_{1}p{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)-i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(52)

and

$$\begin{array}{cc}\hfill z_{3,8}(x,t)=& e^{i\theta }({\displaystyle \frac{1}{4}}{\displaystyle \frac{S_{1}J\left(2{\left(\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}^2-1\right)}{\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\sinh \left(\frac{1}{4}\sqrt{J}\Omega \right)\left(2q\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\sinh \left(\frac{1}{4}\sqrt{J}\Omega \right)-\sqrt{J}\right)}}\hfill \\ \hfill & -S_{1}p{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{4}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\frac{1}{4}\sqrt{J}\Omega \right)-\coth \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}-{\displaystyle \frac{1}{2}}{S}_{1}q),\hfill \end{array}$$

(53)

Family 3.3:

For $J=0,q\ne 0$,

$$\begin{array}{cc}\hfill z_{3,9}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{1}{2}}{S}_{1}q-2{\displaystyle \frac{S_1}{\Omega \left(q\Omega +2\right)}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{S_1{q}^2\Omega }{q\Omega +2}}\right).\hfill \end{array}$$

(54)

Family 3.4:

For $J=0$, in case when $p=q=0$,

$$\begin{array}{cc}\hfill z_{3,10}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{S_1}{\Omega }}\right).\hfill \end{array}$$

(55)

Family 3.5:

For $q=k$, $p=nk(n\ne 0)$ and $r=0$,

$$\begin{array}{cc}\hfill z_{3,11}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{1}{2}}{S}_{1}k+{\displaystyle \frac{S_1\kappa {\mathrm{e}}^{\kappa \Omega }}{{\mathrm{e}}^{\kappa \Omega }-n}}-{\displaystyle \frac{S_{1}kn}{{\mathrm{e}}^{\kappa \Omega }-n}}\right).\hfill \end{array}$$

(56)

Family 3.6:

For $q=k$, $r=nk(n\ne 0)$ and $p=0$,

$$\begin{array}{cc}\hfill z_{3,12}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{1}{2}}{S}_{1}k-{\displaystyle \frac{S_{1}k}{-1+n{\mathrm{e}}^{k\Omega }}}\right).\hfill \end{array}$$

(57)

Family 3.7:

For $p=0$, $r\ne 0$ and $q\ne 0$,

$$\begin{array}{cc}\hfill z_{3,13}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{1}{2}}{S}_{1}q+{\displaystyle \frac{S_{1}q\left(\sinh \left(q\Omega \right)-\cosh \left(q\Omega \right)\right)}{-\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)-\varpi }}\right),\hfill \end{array}$$

(58)

and

$$\begin{array}{cc}\hfill z_{3,14}(x,t)=& e^{i\theta }\left(-{\displaystyle \frac{1}{2}}{S}_{1}q+{\displaystyle \frac{S_{1}q\varpi }{\cosh \left(q\Omega \right)+\sinh \left(q\Omega \right)+\varpi }}\right).\hfill \end{array}$$

(59)

Taking into consideration Case 4 and utilizing (9), (14) with the corresponding solution of Equation (8), we have the subsequent new families of chaotic soliton solutions for CQSHE articulated in (4):

Family 4.1:

For $J<0r\ne 0$,

$$\begin{array}{cc}\hfill z_{4,1}(x,t)=& e^{i\theta }\left(S_0+2S_{0}p{q}^{-1}{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill z_{4,2}(x,t)=& e^{i\theta }\left(S_0+2S_{0}p{q}^{-1}{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(61)

$$\begin{array}{cc}\hfill z_{4,3}(x,t)=& e^{i\theta }\left(S_0+2S_{0}p{q}^{-1}{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)+\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(62)

and

$$\begin{array}{cc}\hfill z_{4,4}(x,t)=& e^{i\theta }\left(S_0+2S_{0}p{q}^{-1}{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)-\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}\right).\hfill \end{array}$$

(63)

Family 4.2:

For $J>0r\ne 0$,

$$\begin{array}{cc}\hfill z_{4,5}(x,t)=& e^{i\theta }\left(S_0+2S_{0}p{q}^{-1}{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(64)

$$\begin{array}{cc}\hfill z_{4,6}(x,t)=& e^{i\theta }\left(S_0+2S_{0}p{q}^{-1}{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)+i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill z_{4,7}(x,t)=& e^{i\theta }\left(S_0+2S_{0}p{q}^{-1}{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)-i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(66)

and

$$\begin{array}{cc}\hfill z_{4,8}(x,t)=& e^{i\theta }\left(S_0+2S_{0}p{q}^{-1}{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{4}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\frac{1}{4}\sqrt{J}\Omega \right)-\coth \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(67)

Family 4.3:

For $J=0,q\ne 0$,

$$\begin{array}{cc}\hfill z_{4,9}(x,t)=& e^{i\theta }\left(S_0-{\displaystyle \frac{S_{0}q\Omega }{q\Omega +2}}\right).\hfill \end{array}$$

(68)

Family 4.4:

For $q=k$, $p=nk(n\ne 0)$ and $r=0$,

$$\begin{array}{cc}\hfill z_{4,10}(x,t)=& e^{i\theta }\left(S_0+2{\displaystyle \frac{S_{0}n}{k\left({\mathrm{e}}^{\kappa \Omega }-n\right)}}\right).\hfill \end{array}$$

(69)

Family 4.5:

For $q=k$, $r=nk(n\ne 0)$ and $p=0$,

$$\begin{array}{cc}\hfill z_{4,11}(x,t)=& e^{i\theta }{S}_0.\hfill \end{array}$$

(70)

Taking into consideration Case 5 and utilizing (9), (14) with the corresponding solution of Equation (8), we have the subsequent new families of chaotic soliton solutions for CQSHE articulated in (4):

Family 5.1:

For $J<0r\ne 0$,

$$\begin{array}{cc}\hfill z_{5,1}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}J\left(1+{\left(\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}^2\right)}{p\left(-q+\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\tan \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(71)

$$\begin{array}{cc}\hfill z_{5,2}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}J\left(1+{\left(\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}^2\right)}{p\left(q+\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)\right)}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\cot \left(\frac{1}{2}\sqrt{-J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(72)

$$\begin{array}{cc}\hfill z_{5,3}(x,t)=& e^{i\theta }({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+{\displaystyle \frac{A_{0}J\left(1+\sin \left(\sqrt{-J}\Omega \right)\right)}{p\cos \left(\sqrt{-J}\Omega \right)\left(-q\cos \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\sin \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)+\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(73)

and

$$\begin{array}{cc}\hfill z_{5,4}(x,t)=& e^{i\theta }({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}-{\displaystyle \frac{A_{0}J\left(\sin \left(\sqrt{-J}\Omega \right)-1\right)}{p\cos \left(\sqrt{-J}\Omega \right)\left(-q\cos \left(\sqrt{-J}\Omega \right)+\sqrt{-J}\sin \left(\sqrt{-J}\Omega \right)-\sqrt{-J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{-J}\left(\tan \left(\sqrt{-J}\Omega \right)-\sec \left(\sqrt{-J}\Omega \right)\right)}{r}}\right)}^{-1}).\hfill \end{array}$$

(74)

Family 5.2:

For $J>0r\ne 0$,

$$\begin{array}{cc}\hfill z_{5,5}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}J\left(-1+{\left(\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)\right)}^2\right)}{p\left(q+\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)\right)}}+A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\tanh \left(\frac{1}{2}\sqrt{J}\Omega \right)}{r}}\right)}^{-1}\right),\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill z_{5,6}(x,t)=& e^{i\theta }({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+{\displaystyle \frac{A_{0}J\left(-1+i\sinh \left(\sqrt{J}\Omega \right)\right)}{p\cosh \left(\sqrt{J}\Omega \right)\left(q\cosh \left(\sqrt{J}\Omega \right)+\sqrt{J}\sinh \left(\sqrt{J}\Omega \right)+i\sqrt{J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)+i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(76)

$$\begin{array}{cc}\hfill z_{5,7}(x,t)=& e^{i\theta }({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+{\displaystyle \frac{A_{0}J\left(1+i\sinh \left(\sqrt{J}\Omega \right)\right)}{p\cosh \left(\sqrt{J}\Omega \right)\left(-q\cosh \left(\sqrt{J}\Omega \right)-\sqrt{J}\sinh \left(\sqrt{J}\Omega \right)+i\sqrt{J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\sqrt{J}\Omega \right)-i\mathrm{sech}\left(\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}),\hfill \end{array}$$

(77)

and

$$\begin{array}{cc}\hfill z_{5,8}(x,t)=& e^{i\theta }(-{\displaystyle \frac{1}{4}}{\displaystyle \frac{A_{0}J\left(2{\left(\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}^2-1\right)}{p\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\sinh \left(\frac{1}{4}\sqrt{J}\Omega \right)\left(2q\cosh \left(\frac{1}{4}\sqrt{J}\Omega \right)\sinh \left(\frac{1}{4}\sqrt{J}\Omega \right)-\sqrt{J}\right)}}\hfill \\ \hfill & +A_0{\left(-{\displaystyle \frac{1}{2}}{\displaystyle \frac{q}{r}}-{\displaystyle \frac{1}{4}}{\displaystyle \frac{\sqrt{J}\left(\tanh \left(\frac{1}{4}\sqrt{J}\Omega \right)-\coth \left(\frac{1}{4}\sqrt{J}\Omega \right)\right)}{r}}\right)}^{-1}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}),\hfill \end{array}$$

(78)

Family 5.3:

For $J=0,q\ne 0$,

$$\begin{array}{cc}\hfill z_{5,9}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_{0}q}{p}}+2{\displaystyle \frac{A_0}{p\Omega \left(q\Omega +2\right)}}-{\displaystyle \frac{1}{2}}{\displaystyle \frac{A_0{q}^2\Omega }{p\left(q\Omega +2\right)}}\right).\hfill \end{array}$$

(79)

Family 5.4:

For $q=k$, $p=nk(n\ne 0)$ and $r=0$,

$$\begin{array}{cc}\hfill z_{5,10}(x,t)=& e^{i\theta }\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{A_0}{n}}-{\displaystyle \frac{A_0\kappa {\mathrm{e}}^{\kappa \Omega }}{kn\left({\mathrm{e}}^{\kappa \Omega }-n\right)}}+{\displaystyle \frac{A_0}{{\mathrm{e}}^{\kappa \Omega }-n}}\right).\hfill \end{array}$$

(80)

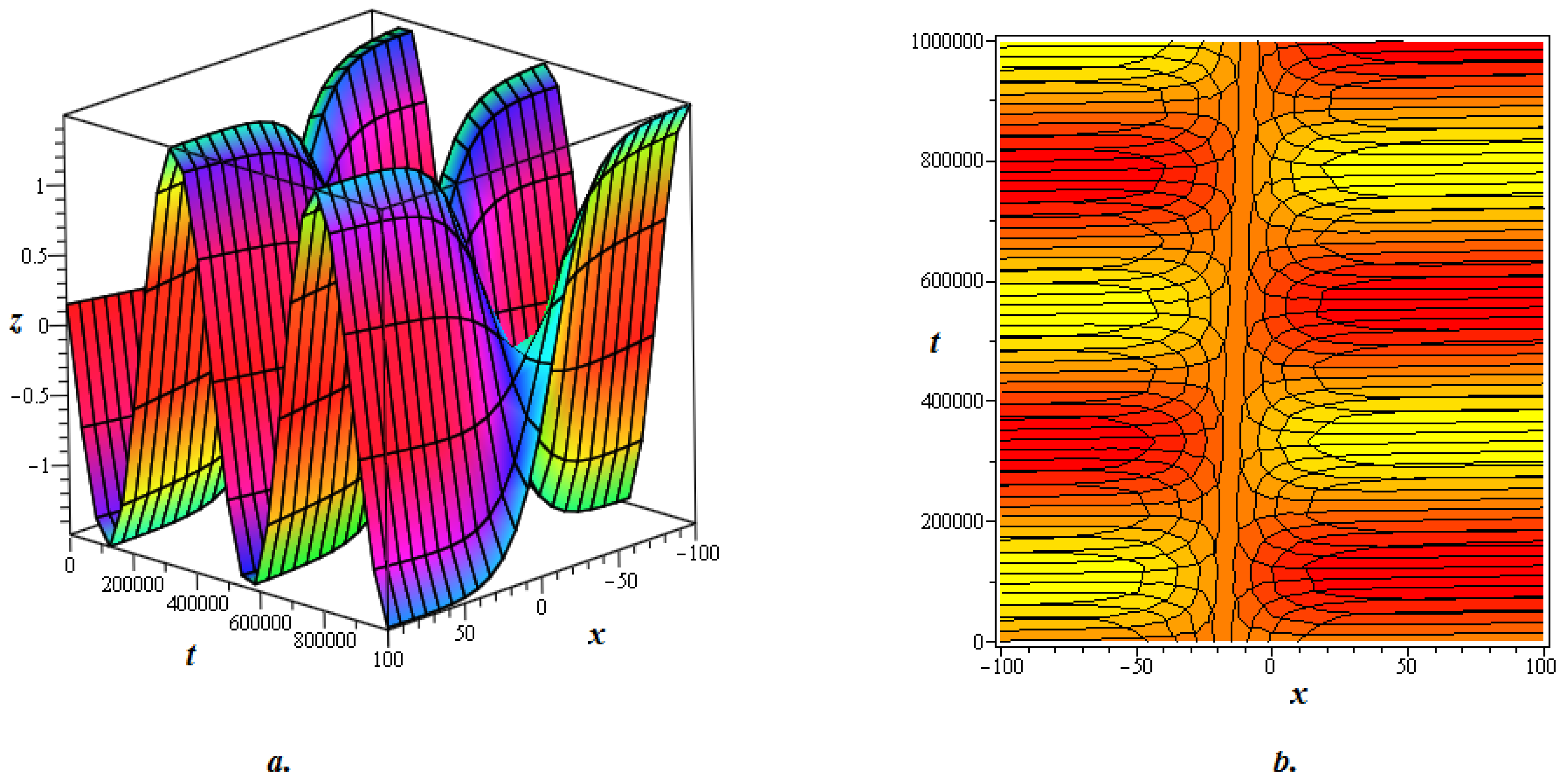
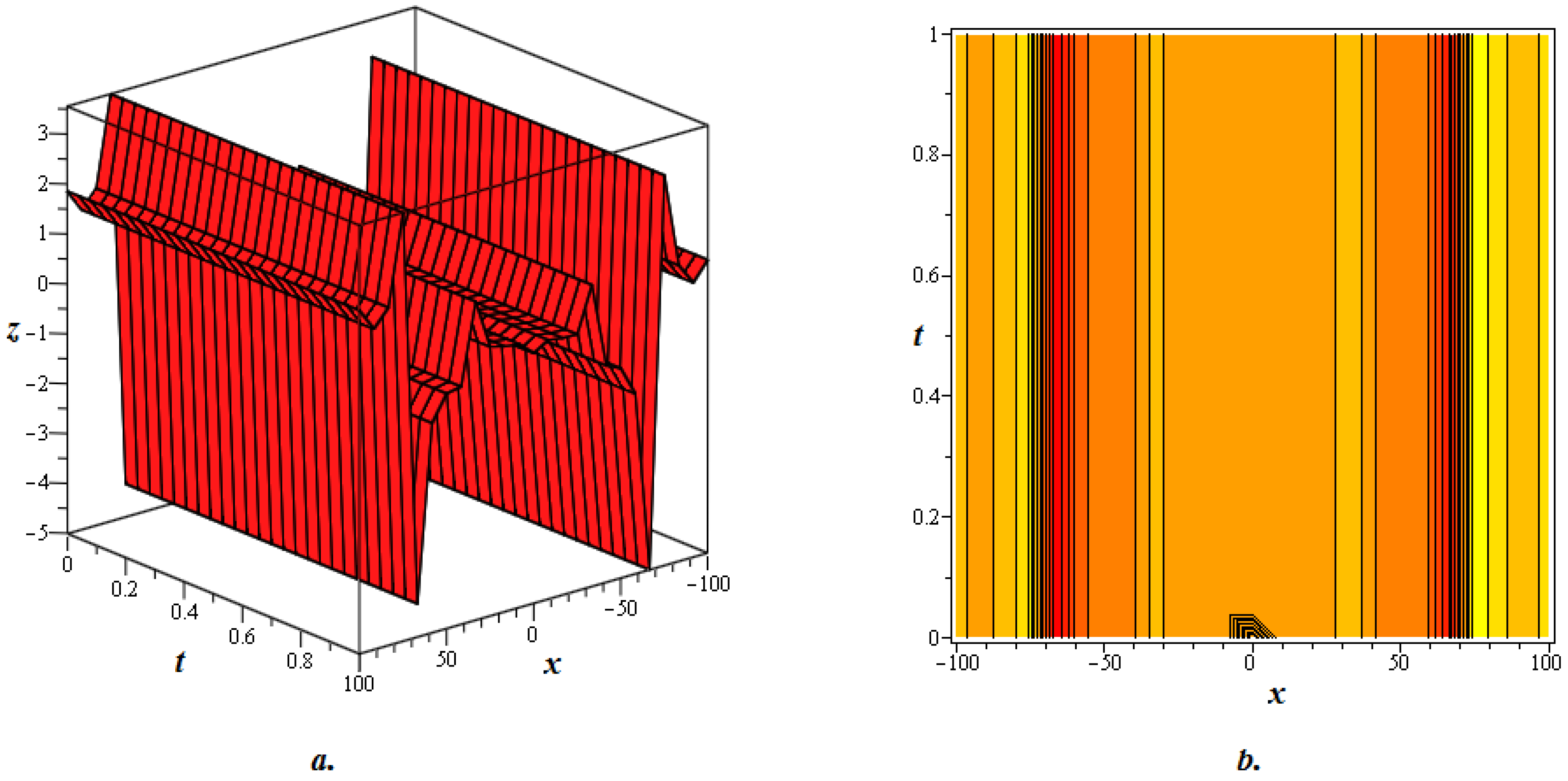
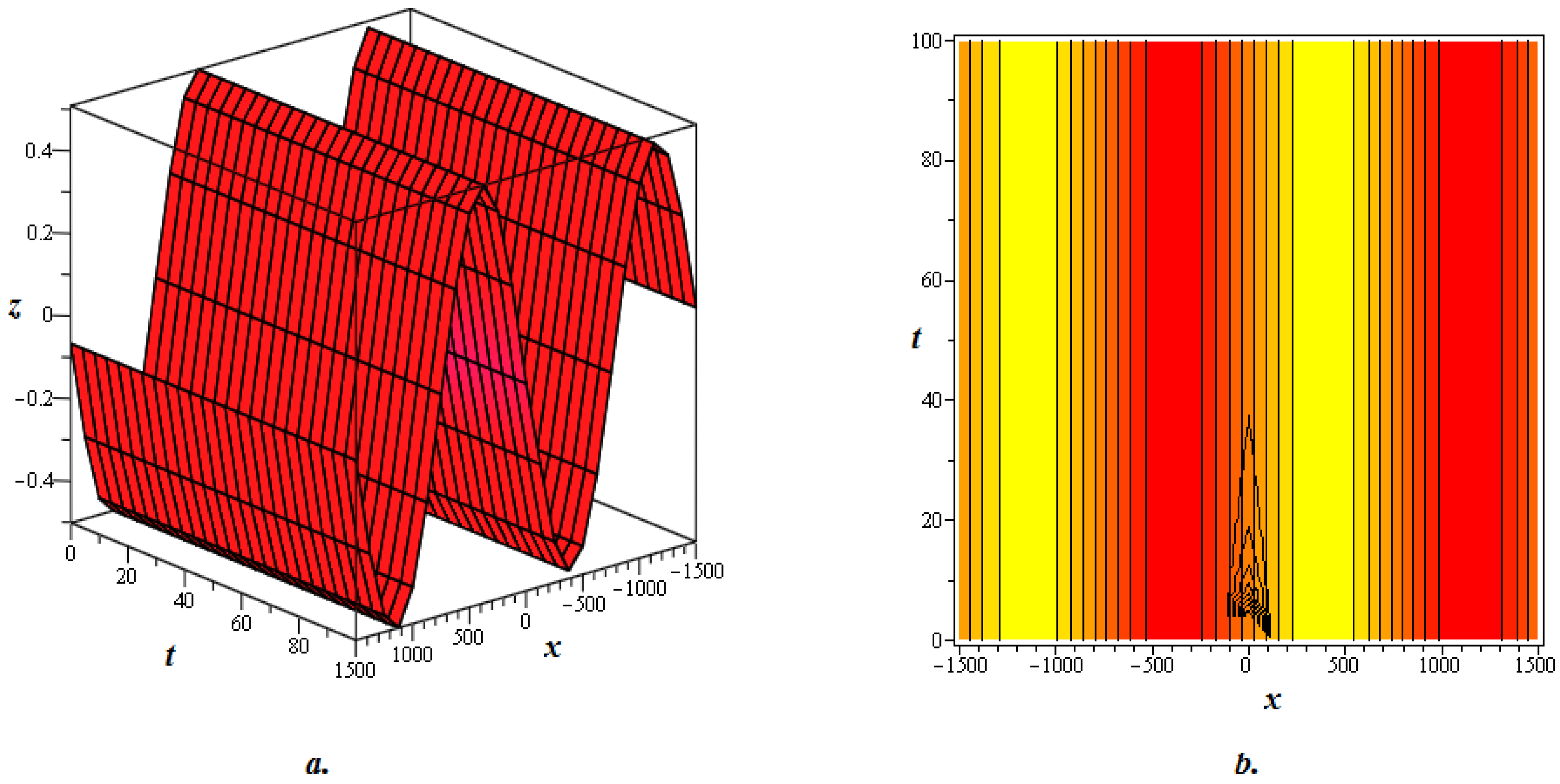
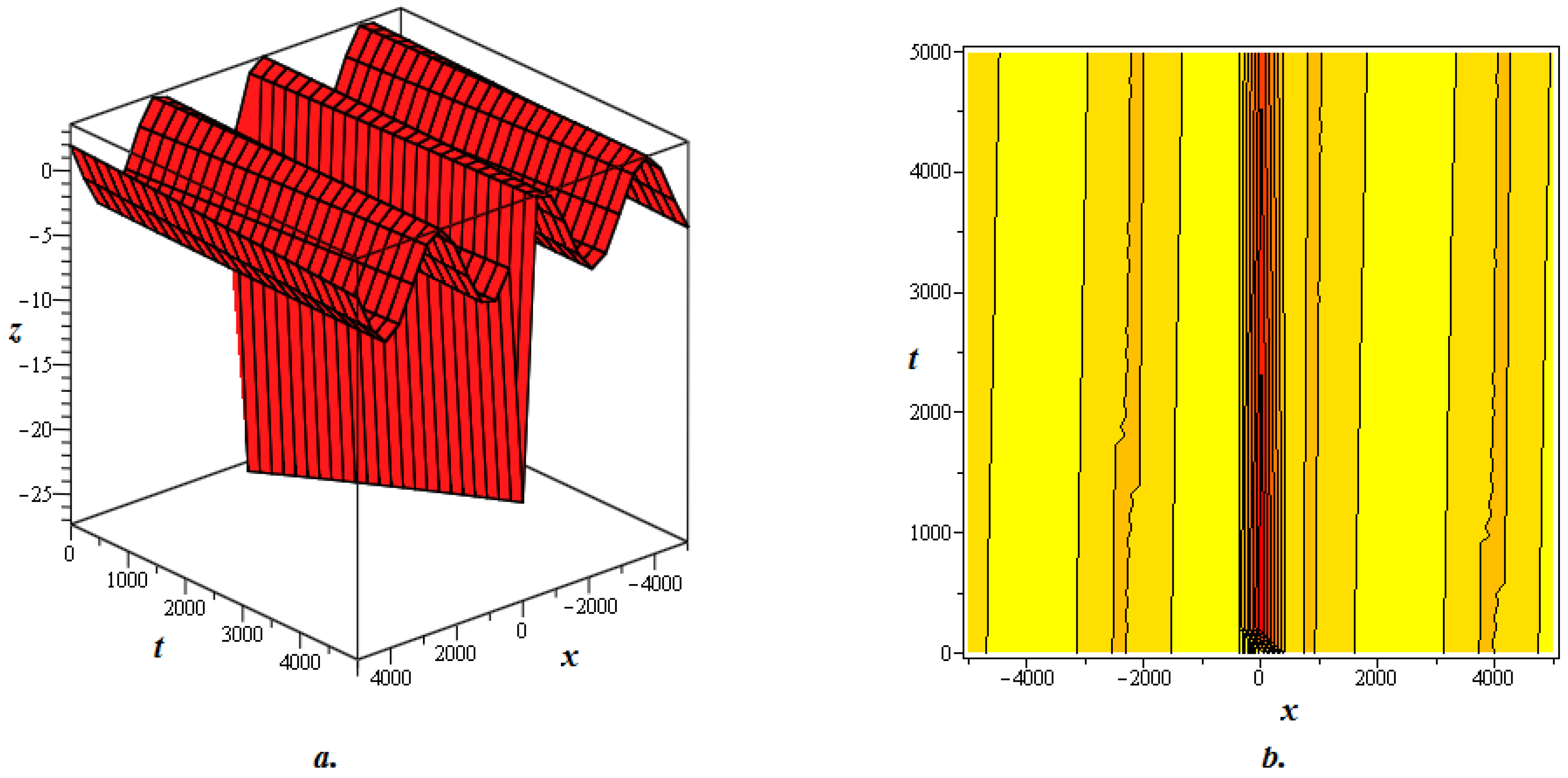
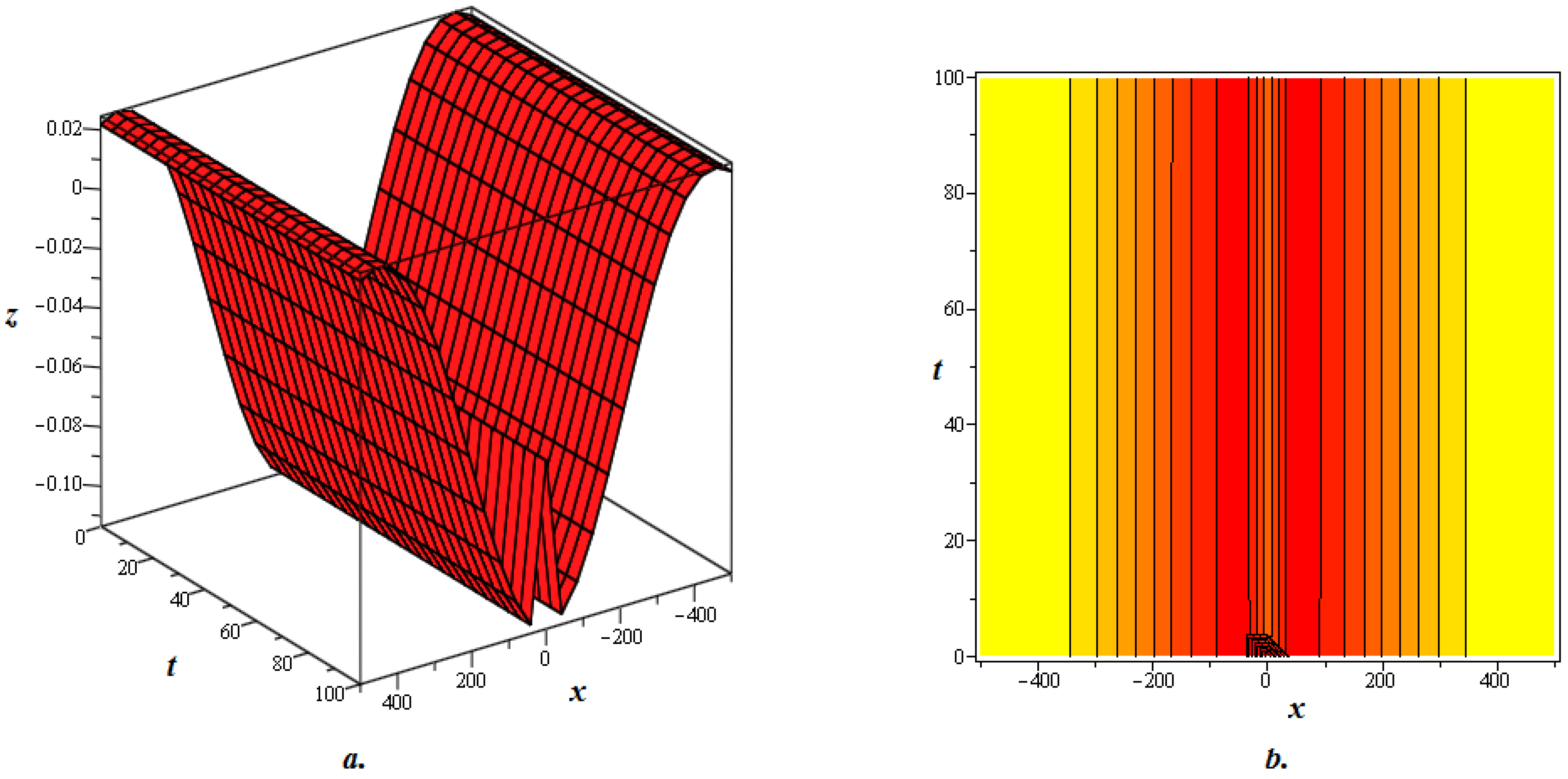
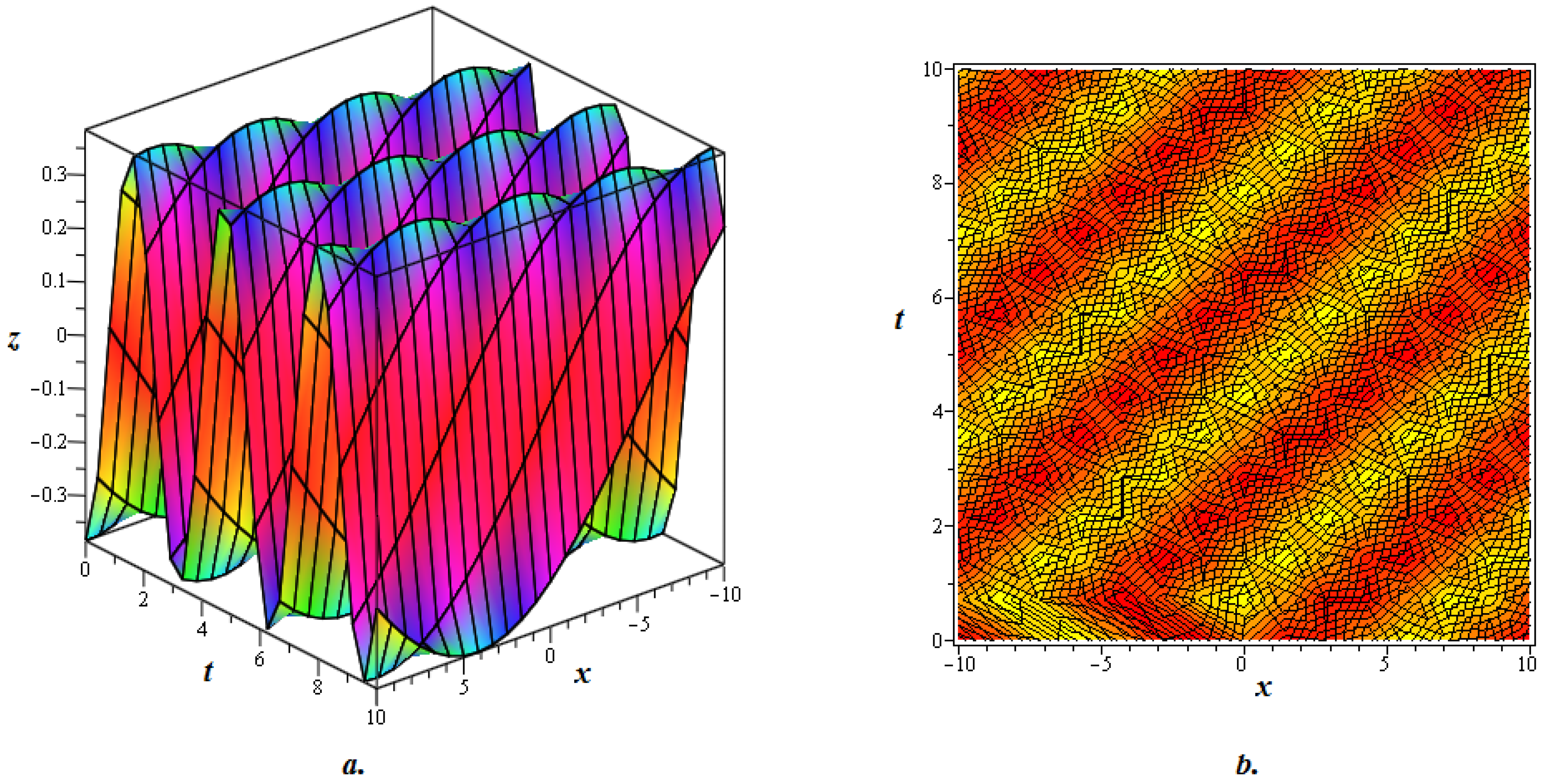
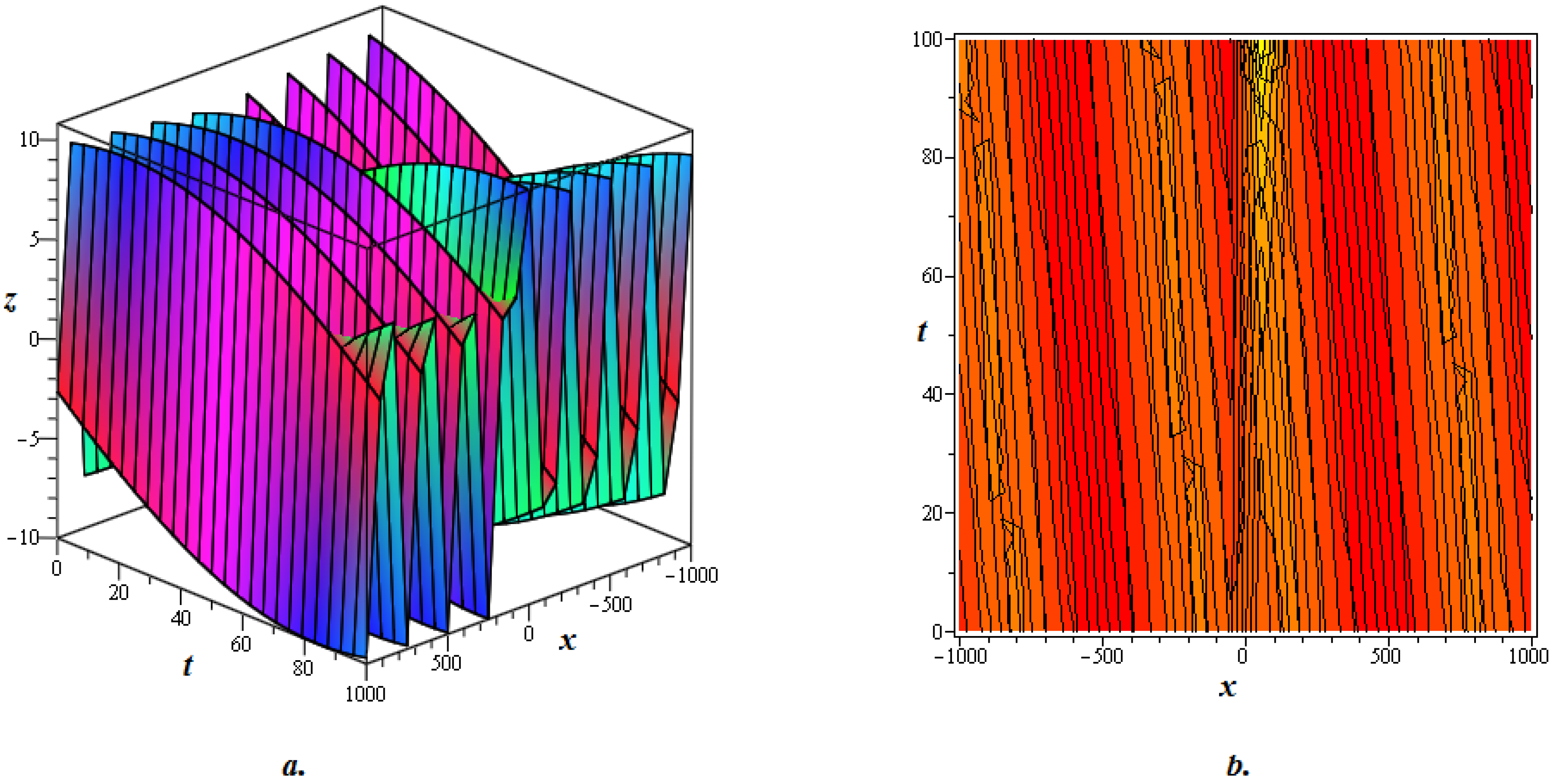
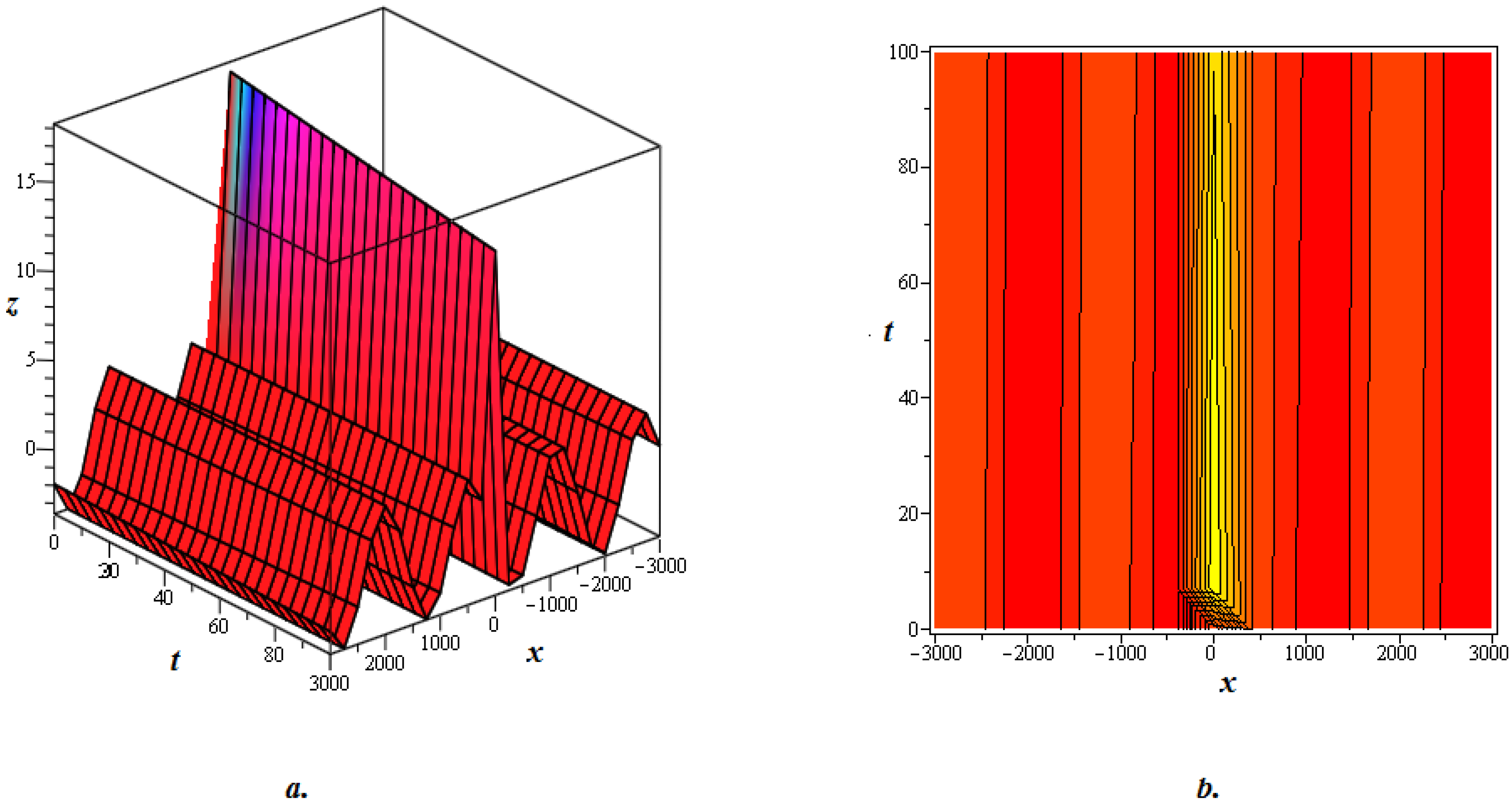
4. Graphical Discussion

A fascinating feature in the study of CQSHE is the production of soliton-exhibiting axial and periodic perturbations, which is useful in explaining complex pattern-forming dissipative structures. A soliton is a solitary, autonomous wave that keeps moving in the same direction and at the same pace. These solitons’ disruptive properties are probably caused by a number of things, including their intrinsic instability, intricate and nonlinear dynamics, and interactions with their surroundings. For example, disturbances brought about by solitons travelling through their preferred medium and forming intricate patterns that change over time could also be the consequence of solitons interacting with their environment. This is particularly valid for processes that disturb periodically. On the other hand, because CQSHE takes nonlinear dynamics and complexity into account, the soliton displays similar disruptive behaviour. Furthermore, our soliton solutions show axial and periodic perturbations, as seen in the following graphics, which lead to chaotic behavior. These perturbations cause a type of chaos by disrupting the uniformity and consistency of solitons’ trajectory. In our study the chaoticness comes from the complex framework of the CQSHE. Even in one-dimensional settings, the system’s nonlinear interactions and perturbative impacts resemble chaotic patterns. We have referred to these soliton behaviors as chaotic solitons because of their inconsistent, delicate, and unexpected nature. Moreover, the axial and periodic disturbances brought on by the interplay of numerous physical and chemical events could potentially be caused by the inherent instability of the dissipation system, as exemplified by CQSHE. Overall, our chaotic solitons can represent various phenomena, depending on the specific context, for example, topological defects, vortex structures, and soliton–soliton interjections, which lead to the formations of complex patterns. Periodic perturbations, on the other hand, can represent modulation instability, quasi-periodic patterns, and patterns doubling, which lead to the soliton breakup and formation of hierarchical, chaotic, complex and fractal patterns. A stable, constrained wave packet with both solitonic and fractal structure is called a fractal soliton. Fractal solitons are randomly formed solitons that self-replicate and exhibit intricate geometrical patterns at various sizes while moving at a steady pace. Our contour graphs show the formation of fractal structures due to the chaotic perturbations of soliton.

Moreover, we highlight the fact that the ansatz as given has a denominator which might give rise to singularities in some cases. When singularities occur, they contribute to the creation of singular solitons. Singular solitons may simulate processes like wave breaking and shock waves that have been observed in a variety of scientific settings. We have also carefully limited both amplitudes and velocities within short ranges (by assigning very small values to associated free parameters) in order to guarantee that the soliton stays confined. This keeps the solitons we covered in the study stable and prevents them from growing infinitely.

Remark 1.

Figure 1 is depicted for $z_{1,5}$ presented in (24) which exhibits the axial-periodic perturbation in the graphed chaotic fractal soliton.

Remark 2.

Figure 2 is depicted for $z_{1,11}$ presented in (30) which exhibits axially-perturbed M-shaped chaotic soliton.

Remark 3.

Figure 3 is depicted for $z_{2,1}$ presented in (31) which exhibits the axially-periodic perturbation in the graphed chaotic kink soliton.

Remark 4.

Figure 4 is depicted for $z_{2,9}$ presented in (39) which exhibits the periodic perturbation in the graphed chaotic soliton.

Remark 5.

Figure 5 is depicted for $z_{3,8}$ presented in (53) which exhibits the periodic perturbation in the graphed chaotic internal-envelope soliton.

Remark 6.

Figure 6 is depicted for $z_{3,10}$ presented in (55) which exhibits the axial perturbation in the graphed chaotic W-shaped soliton.

Remark 7.

Figure 7 is depicted for $z_{4,5}$ presented in (64) which exhibits the periodic perturbation in the graphed chaotic fractal soliton.

Remark 8.

Figure 8 is depicted for $z_{4,10}$ presented in (69) which exhibits the periodic perturbation in the graphed chaotic soliton.

Remark 9.

Figure 9 is depicted for $z_{5,2}$ presented in (72) which exhibits the periodic perturbation in the graphed chaotic internal-envelope soliton.

Remark 10.

Figure 10 is depicted for $z_{5,8}$ presented in (78) which exhibits the periodic perturbation in the graphed chaotic soliton.

5. Conclusions

In this study, we used RMESEM to examine chaotic soliton solutions of the ($1+1$)-dimensional CQSHE, which explains dissipative systems that produce complex patterns. We found that several chaotic and fractal soliton solutions with periodic and axial perturbations to the intended CQSHE exist when specific constraints are applied to the coefficients. According to RMESEM’s transformational approach, a sophisticated transformation was first used to turn CQSHE into a set of NODEs. The extended Riccati NODE was subsequently included in the resultant set of NODEs, turning it into an algebraic system of equations by assuming a series form solution. This set of equations was solved to obtain the chaotic soliton solutions in the form of rational-hyperbolic periodic, hyperbolic, exponential, and rational functional families. The perturbed dynamics of these chaotic soliton solutions and the formation of fractals were also graphically depicted using a variety of 3D and contour graphs. Our results are significant because they provide insight into the chaotic nature of the framework under investigation, helping us to comprehend its underlying dynamics. Although the RMESEM has greatly advanced our knowledge of soliton dynamics and how they are related to the models we are studying, it is crucial to recognise the method’s limitations, especially the fact that proposed method fails in cases when the highest derivative term and nonlinear component are not homogenously balanced. Despite this drawback, the current study shows that the approach used in this work is very reliable, portable, and effective for nonlinear models across a range of scientific domains.