Enhanced Discrete Wavelet Transform–Non-Local Means for Multimode Fiber Optic Vibration Signal
Abstract
:1. Introduction
2. Principle
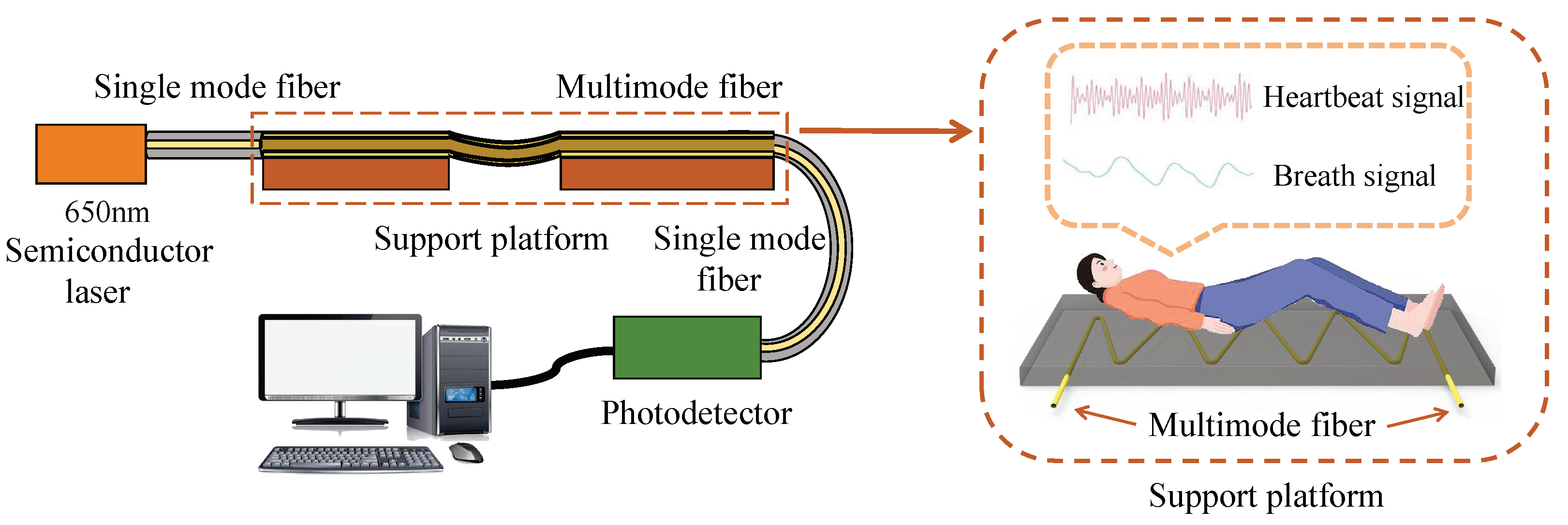
2.1. Fiber Optic Vibration Sensor
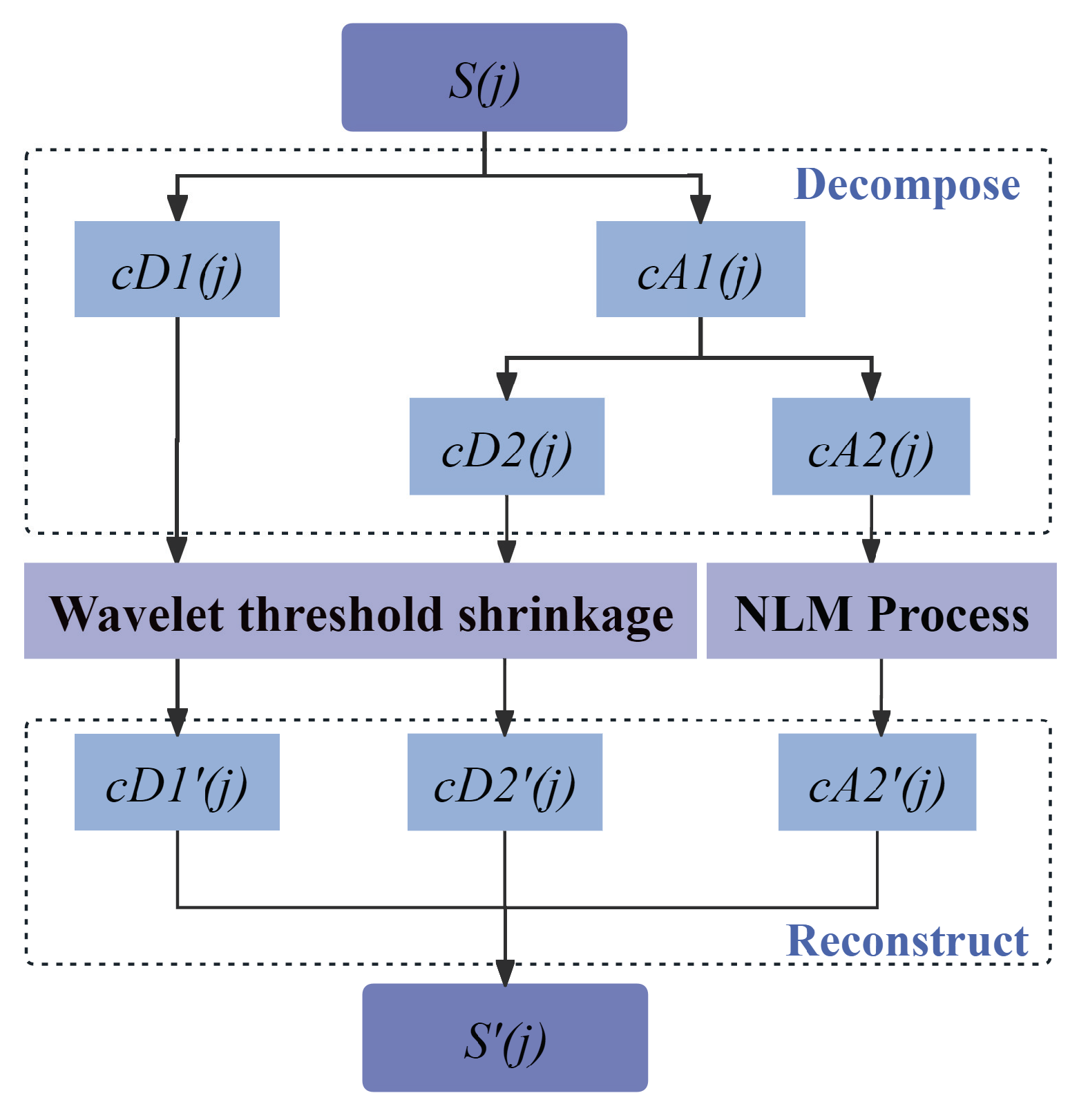
2.2. Enhanced DWT-NLM Composite Method
2.3. Objective Evaluation Metric
3. Numerical Experiment
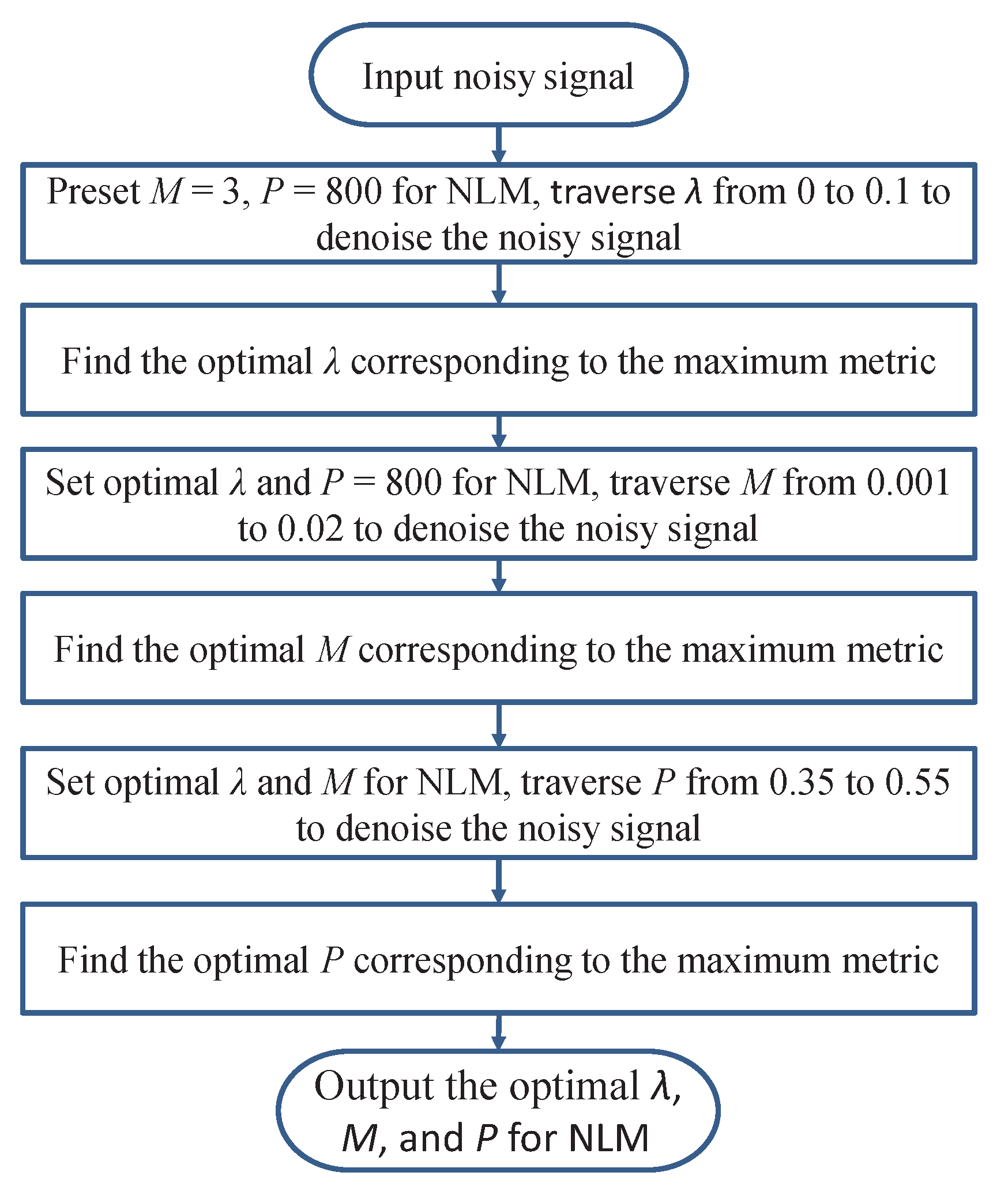
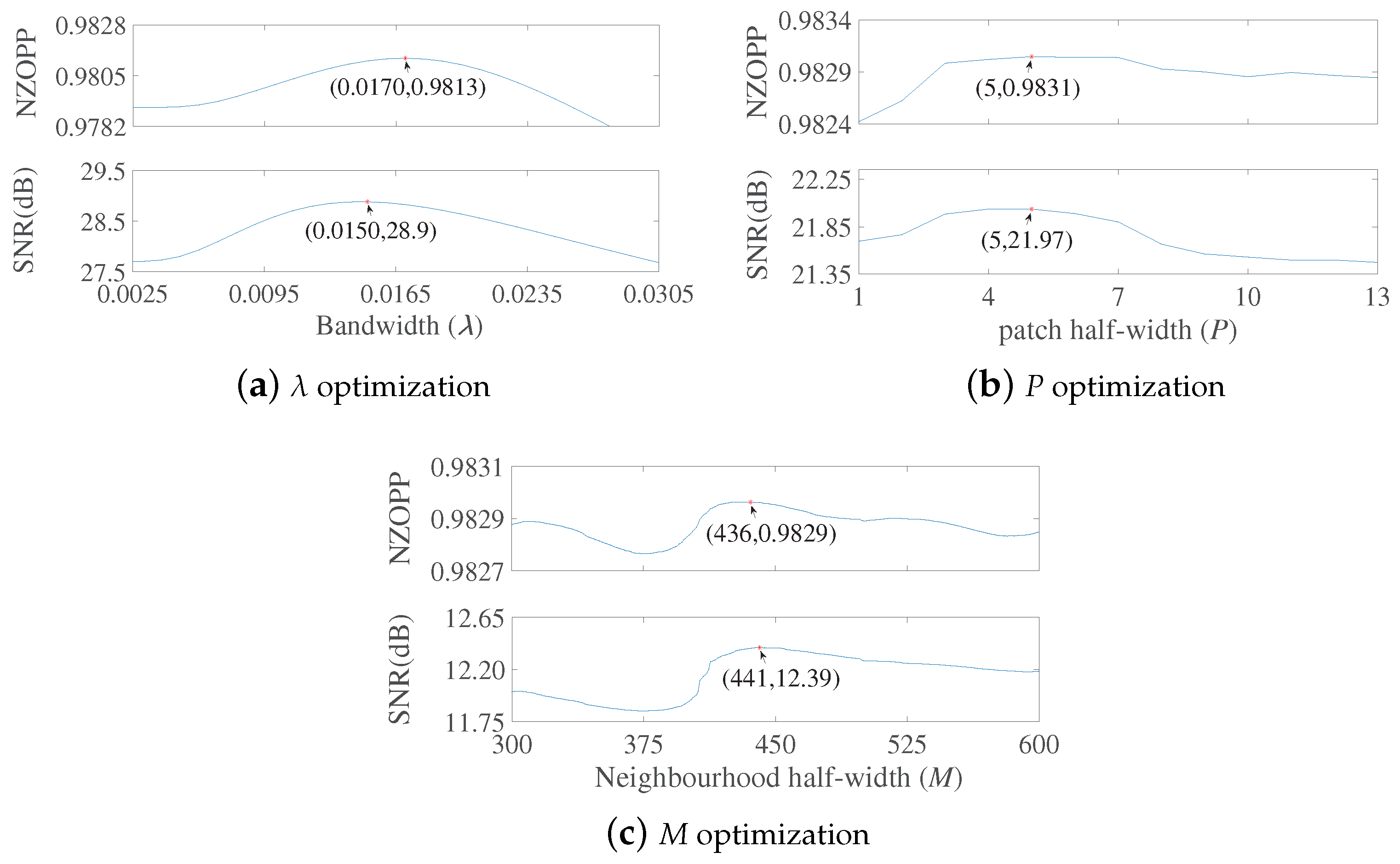
3.1. Optimizing NLM Parameter with Objective Evaluation Metric
3.2. Mimic Heartbeat Signal with AGW Noise
3.3. Measured Heartbeat Signals from Fiber Optic Vibration Sensors
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lyakhov, P.; Kiladze, M.; Lyakhova, U. System for neural network determination of atrial fibrillation on ECG signals with wavelet-based preprocessing. Appl. Sci. 2021, 11, 7213. [Google Scholar] [CrossRef]
- Fatema, K.; Montaha, S.; Rony, M.A.H.; Azam, S.; Hasan, M.Z.; Jonkman, M. A robust framework combining image processing and deep learning hybrid model to classify cardiovascular diseases using a limited number of paper-based complex ECG images. Biomedicines 2022, 10, 2835. [Google Scholar] [CrossRef] [PubMed]
- Mhamdi, L.; Dammak, O.; Cottin, F.; Dhaou, I.B. Artificial intelligence for cardiac diseases diagnosis and prediction using ECG images on embedded systems. Biomedicines 2022, 10, 2013. [Google Scholar] [CrossRef] [PubMed]
- Moshawrab, M.; Adda, M.; Bouzouane, A.; Ibrahim, H.; Raad, A. Smart wearables for the detection of cardiovascular diseases: A systematic literature review. Sensors 2023, 23, 828. [Google Scholar] [CrossRef] [PubMed]
- Fine, J.; Branan, K.L.; Rodriguez, A.J.; Boonya-Ananta, T.; Ajmal.; Ramella-Roman, J.C.; McShane, M.J.; Cote, G.L. Sources of inaccuracy in photoplethysmography for continuous cardiovascular monitoring. Biosensors 2021, 11, 126. [Google Scholar] [CrossRef] [PubMed]
- Pandey, S.K.; Janghel, R.R.; Vani, V. Patient Specific Machine Learning Models for ECG Signal Classification. Procedia Comput. Sci. 2020, 167, 2181–2190. [Google Scholar] [CrossRef]
- Aarthy, S.T.; Mazher Iqbal, J.L. A Novel Deep Learning Approach for Early Detection of Cardiovascular Diseases from ECG Signals. Med. Eng. Phys. 2024, 125, 104111. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Gu, K.; Miao, S.; Zhang, X.; Yin, Y.; Wan, C.; Yu, Y.; Hu, J.; Wang, Z.; Shan, T.; et al. Automated Detection of Cardiovascular Disease by Electrocardiogram Signal Analysis: A Deep Learning System. Cardiovasc. Diagn. Ther. 2020, 10, 227–235. [Google Scholar] [CrossRef]
- Malakouti, S.M. Heart disease classification based on ECG using machine learning models. Biomed. Signal Process. Control 2023, 84, 104796. [Google Scholar] [CrossRef]
- Rath, A.; Mishra, D.; Panda, G. Imbalanced ECG Signal-Based Heart Disease Classification Using Ensemble Machine Learning Technique. Front. Big Data 2022, 5, 1021518. [Google Scholar] [CrossRef]
- Bokma, J.; Pengel, L.; Robbers-Visser, D.; Groenink, M.; Boekholdt, S.; Bouma, B. A comparison of ECG-based home monitoring devices in adults with congenital heart disease. Eur. Heart J. 2021, 42, ehab724.1881. [Google Scholar] [CrossRef]
- Zhou, S.; AbdelWahab, A.; Sapp, J.L.; Sung, E.; Aronis, K.N.; Warren, J.W.; MacInnis, P.J.; Shah, R.; Horáček, B.M.; Berger, R.; et al. Assessment of an ECG-Based System for Localizing Ventricular Arrhythmias in Patients with Structural Heart Disease. J. Am. Heart Assoc. 2021, 10, e022217. [Google Scholar] [CrossRef]
- Guo, W.; Ma, Z.; Chen, Z.; Hua, H.; Wang, D.; Hilal, M.E.; Fu, Y.; Lu, P.; Lu, J.; Zhang, Y.; et al. Thin and soft Ti3C2Tx MXene sponge structure for highly sensitive pressure sensor assisted by deep learning. Chem. Eng. J. 2024, 485, 149659. [Google Scholar] [CrossRef]
- Ma, Z.; Hua, H.; You, C.; Ma, Z.; Guo, W.; Yang, X.; Qiu, S.; Zhao, N.; Zhang, Y.; Ho, D.; et al. FlexiPulse: A machine-learning-enabled flexible pulse sensor for cardiovascular disease diagnostics. Cell Rep. Phys. Sci. 2023, 4, 101690. [Google Scholar] [CrossRef]
- Zhang, B.; Li, J.; Zhou, J.; Chow, L.; Zhao, G.; Huang, Y.; Ma, Z.; Zhang, Q.; Yang, Y.; Yiu, C.K.; et al. A three-dimensional liquid diode for soft, integrated permeable electronics. Nature 2024, 628, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Yang, K.; Pei, Z.; Wu, Y.; Sang, S.; Zhang, Q.; Jiao, H. A highly accurate flexible sensor system for human blood pressure and heart rate monitoring based on graphene/sponge. RSC Adv. 2022, 12, 2391–2398. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. A review on flexible wearables-Recent developments in non-invasive continuous health monitoring. Sens. Actuators A Phys. 2024, 366, 114993. [Google Scholar] [CrossRef]
- Mao, P.; Li, H.; Yu, Z. A Review of Skin-Wearable Sensors for Non-Invasive Health Monitoring Applications. Sensors 2023, 23, 3673. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.U.; Rwei, A.Y.; Hourlier-Fargette, A.; Xu, S.; Lee, K.; Dunne, E.C.; Xie, Z.; Liu, C.; Carlini, A.; Kim, D.H.; et al. Skin-interfaced biosensors for advanced wireless physiological monitoring in neonatal and pediatric intensive-care units. Nat. Med. 2020, 26, 418–429. [Google Scholar] [CrossRef]
- Prieto-Avalos, G.; Cruz-Ramos, N.A.; Alor-Hernández, G.; Sánchez-Cervantes, J.L.; Rodríguez-Mazahua, L.; Guarneros-Nolasco, L.R. Wearable devices for physical monitoring of heart: A review. Biosensors 2022, 12, 292. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, J.; Zhou, Z.; Jiang, X.; Zhang, D. Fabrication of all-SiC fiber-optic pressure sensors for high-temperature applications. Sensors 2016, 16, 1660. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Geng, D.; Zhang, D.; Qin, W.; Jiang, Y. Ultrasonic vibration mill-grinding of single-crystal silicon carbide for pressure sensor diaphragms. Ceram. Int. 2018, 44, 3107–3112. [Google Scholar] [CrossRef]
- Li, J.; Jiang, Y.; Li, H.; Liang, X.; Huang, M.; Liu, D.; Zhang, D. Direct bonding of silicon carbide with hydrofluoric acid treatment for high-temperature pressure sensors. Ceram. Int. 2020, 46, 3944–3948. [Google Scholar] [CrossRef]
- Vysotskaya, N.; Will, C.; Servadei, L.; Maul, N.; Mandl, C.; Nau, M.; Harnisch, J.; Maier, A. Continuous Non-Invasive Blood Pressure Measurement Using 60 GHz-Radar—A Feasibility Study. Sensors 2023, 23, 4111. [Google Scholar] [CrossRef]
- Hussein, A.F.; Mohammed, W.R.; Musa Jaber, M.; Ibrahim Khalaf, O. An Adaptive ECG Noise Removal Process Based on Empirical Mode Decomposition (EMD). Contrast Media Mol. Imaging 2022, 2022, 3346055. [Google Scholar] [CrossRef] [PubMed]
- Boda, S.; Mahadevappa, M.; Dutta, P.K. A Hybrid Method for Removal of Power Line Interference and Baseline Wander in ECG Signals Using EMD and EWT. Biomed. Signal Process. Control 2021, 67, 102466. [Google Scholar] [CrossRef]
- Grobbelaar, M.; Phadikar, S.; Ghaderpour, E.; Struck, A.F.; Sinha, N.; Ghosh, R.; Ahmed, M.Z.I. A survey on denoising techniques of electroencephalogram signals using wavelet transform. Signals 2022, 3, 577–586. [Google Scholar] [CrossRef]
- Giorgio, A.; Guaragnella, C.; Giliberti, D.A. Improving ECG signal denoising using wavelet transform for the prediction of malignant arrhythmias. Int. J. Med. Eng. Inform. 2020, 12, 135–150. [Google Scholar] [CrossRef]
- Blanco-Velasco, M.; Weng, B.; Barner, K.E. ECG signal denoising and baseline wander correction based on the empirical mode decomposition. Comput. Biol. Med. 2008, 38, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Prashar, N.; Sood, M.; Jain, S. Design and implementation of a robust noise removal system in ECG signals using dual-tree complex wavelet transform. Biomed. Signal Process. Control 2021, 63, 102212. [Google Scholar] [CrossRef]
- Hesar, H.D.; Mohebbi, M. An Adaptive Kalman Filter Bank for ECG Denoising. IEEE J. Biomed. Health Inform. 2021, 25, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Prashar, N.; Sood, M.; Jain, S. Dual-tree complex wavelet transform technique-based optimal threshold tuning system to deliver denoised ECG signal. Trans. Inst. Meas. Control 2020, 42, 854–869. [Google Scholar] [CrossRef]
- Mohguen, W.; Bouguezel, S. Denoising the ECG signal using ensemble empirical mode decomposition. Eng. Technol. Appl. Sci. Res. 2021, 11, 7536–7541. [Google Scholar] [CrossRef]
- Gupta, V.; Mittal, M.; Mittal, V.; Gupta, A. ECG signal analysis using CWT, spectrogram and autoregressive technique. Iran J. Comput. Sci. 2021, 4, 265–280. [Google Scholar] [CrossRef]
- Jenkal, W.; Latif, R.; Laaboubi, M. ECG Signal Denoising Using an Improved Hybrid DWT-ADTF Approach. Cardiovasc. Eng. Technol. 2024, 15, 77–94. [Google Scholar] [CrossRef] [PubMed]
- Chandra, M.; Goel, P.; Anand, A.; Kar, A. Design and Analysis of Improved High-Speed Adaptive Filter Architectures for ECG Signal Denoising. Biomed. Signal Process. Control 2021, 63, 102221. [Google Scholar] [CrossRef]
- Gao, L.; Gan, Y.; Shi, J. A novel intelligent denoising method of ecg signals based on wavelet adaptive threshold and mathematical morphology. Appl. Intell. 2022, 52, 10270–10284. [Google Scholar] [CrossRef]
- Kumar, A.; Tomar, H.; Mehla, V.K.; Komaragiri, R.; Kumar, M. Stationary wavelet transform based ECG signal denoising method. ISA Trans. 2021, 114, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Yu, Q.; Yu, H. An ECG denoising method combining variational modal decomposition and wavelet soft threshold. Concurr. Comput. Pract. Exp. 2022, e7048. [Google Scholar] [CrossRef]
- Wang, J.; Sun, S.; Sun, Y. A muscle fatigue classification model based on LSTM and improved wavelet packet threshold. Sensors 2021, 21, 6369. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, P.; Yin, Y.; Wu, M.; Yu, K.; Feng, L.; Chen, W. Objective assessment of IPM denoising quality of ϕ-otdr signal. Measurement 2023, 214, 112775. [Google Scholar] [CrossRef]
- Yu, K.; Feng, L.; Chen, Y.; Wu, M.; Zhang, Y.; Zhu, P.; Chen, W.; Wu, Q.; Hao, J. Accurate Wavelet Thresholding Method for ECG Signals. Comput. Biol. Med. 2024, 169, 107835. [Google Scholar] [CrossRef] [PubMed]
- Sraitih, M.; Jabrane, Y. A denoising performance comparison based on ECG Signal Decomposition and local means filtering. Biomed. Signal Process. Control 2021, 69, 102903. [Google Scholar] [CrossRef]
- Gan, M.; Pan, H.; Chen, Y.; Pan, S. Application of the Variational Mode Decomposition (VMD) method to river tides. Estuar. Coast. Shelf Sci. 2021, 261, 107570. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, Z.; Zhang, H.; Wang, X.; Guo, Y. A short-term wind power prediction model based on CEEMD and WOA-KELM. Renew. Energy 2022, 189, 188–198. [Google Scholar] [CrossRef]
- Zhang, W.; Teng, F.; Li, J.; Zhang, Z.; Niu, L.; Zhang, D.; Song, Q.; Zhang, Z. Denoising method based on CNN-LSTM and CEEMD for LDV signals from accelerometer shock testing. Measurement 2023, 216, 112951. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Bing, P.; Liu, W.; Wang, Z.; Zhang, Z. Noise reduction in ECG signal using an effective hybrid scheme. IEEE Access 2020, 8, 160790–160801. [Google Scholar] [CrossRef]
- Dwivedi, A.K.; Ranjan, H.; Menon, A.; Periasamy, P. Noise reduction in ECG signal using combined ensemble empirical mode decomposition method with stationary wavelet transform. Circuits Syst. Signal Process. 2021, 40, 827–844. [Google Scholar] [CrossRef]
- Zhang, M.; Wei, G. An integrated EMD adaptive threshold denoising method for reduction of noise in ECG. PLoS ONE 2020, 15, e0235330. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.; Lin, H.; Li, J.; Zhang, F.; Yang, Y. ECG denoising method based on an improved VMD algorithm. IEEE Sens. J. 2022, 22, 22725–22733. [Google Scholar] [CrossRef]
- Malghan, P.G.; Hota, M.K. Grasshopper optimization algorithm based improved variational mode decomposition technique for muscle artifact removal in ECG using dynamic time warping. Biomed. Signal Process. Control 2022, 73, 103437. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, H.; Hu, M.; Jiang, A.; Zhang, L.; Xu, F.; Hao, G. An adaptive CEEMDAN thresholding denoising method optimized by nonlocal means algorithm. IEEE Trans. Instrum. Meas. 2020, 69, 6891–6903. [Google Scholar] [CrossRef]
- Chatterjee, S.; Thakur, R.S.; Yadav, R.N.; Gupta, L.; Raghuvanshi, D.K. Review of Noise Removal Techniques in ECG Signals. IET Signal Process. 2020, 14, 569–590. [Google Scholar] [CrossRef]
- Talbi, M. New approach of ECG denoising based on 1-D double-density complex DWT and SBWT. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2020, 8, 608–620. [Google Scholar] [CrossRef]
- Singh, P.; Pradhan, G. Variational Mode Decomposition Based ECG Denoising Using Non-Local Means and Wavelet Domain Filtering. Australas. Phys. Eng. Sci. Med. 2018, 41, 891–904. [Google Scholar] [CrossRef] [PubMed]
- Bhobhriya, R.; Boora, R.; Jangra, M.; Dalal, P. W-NLM: A Proficient EMG Denoising Technique. Int. J. Inf. Technol. 2023, 15, 2517–2527. [Google Scholar] [CrossRef]
- Tripathi, P.M.; Kumar, A.; Komaragiri, R.; Kumar, M. A Review on Computational Methods for Denoising and Detecting ECG Signals to Detect Cardiovascular Diseases. Arch. Comput. Methods Eng. 2022, 29, 1875–1914. [Google Scholar] [CrossRef]
- Singh, P.; Pradhan, G.; Shahnawazuddin, S. Denoising of ECG Signal by Non-Local Estimation of Approximation Coefficients in DWT. Biocybern. Biomed. Eng. 2017, 37, 599–610. [Google Scholar] [CrossRef]
- Wu, M.; Chen, Y.; Zhu, P.; Chen, W. NLM Parameter Optimization for φ-OTDR Signal. J. Light. Technol. 2022, 40, 6045–6051. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, K.; Wu, M.; Feng, L.; Zhang, Y.; Zhu, P.; Chen, W.; Hao, J. Wavelet Decomposition Layer Selection for the φ-OTDR Signal. Photonics 2024, 11, 137. [Google Scholar] [CrossRef]
- Wu, Q.; Qu, Y.; Liu, J.; Yuan, J.; Wan, S.P.; Wu, T.; He, X.D.; Liu, B.; Liu, D.; Ma, Y.; et al. Singlemode-multimode-singlemode fiber structures for sensing applications—A review. IEEE Sens. J. 2020, 21, 12734–12751. [Google Scholar] [CrossRef]
- Zhu, R.Z.; Wan, S.J.; Xiong, Y.F.; Feng, H.G.; Chen, Y.; Lu, Y.Q.; Xu, F. Magnetic field sensing based on multimode fiber specklegrams. J. Light. Technol. 2021, 39, 3614–3619. [Google Scholar] [CrossRef]
- Wang, K.; Dong, X.; Köhler, M.H.; Kienle, P.; Bian, Q.; Jakobi, M.; Koch, A.W. Advances in optical fiber sensors based on multimode interference (MMI): A review. IEEE Sens. J. 2020, 21, 132–142. [Google Scholar] [CrossRef]
- Tracey, B.H.; Miller, E.L. Nonlocal Means Denoising of ECG Signals. IEEE Trans. Biomed. Eng. 2012, 59, 2383–2386. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Shang, C.; Zhu, K.; Lu, C. Vibration Detection in Distributed Acoustic Sensor with Threshold-Based Technique: A Statistical View and Analysis. J. Light. Technol. 2021, 39, 4082–4093. [Google Scholar] [CrossRef]
- Moeyersons, J.; Morales, J.; Villa, A.; Castro, I.; Testelmans, D.; Buyse, B.; Van Hoof, C.; Willems, R.; Van Huffel, S.; Varon, C. Supervised SVM Transfer Learning for Modality-Specific Artefact Detection in ECG. Sensors 2021, 21, 662. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.; Mark, R. The Impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Nolle, F.; Badura, F.; Catlett, J.; Bowser, R.; Sketch, M. CREI-GARD, a new concept in computerized arrhythmia monitoring systems. Comput. Cardiol. 1986, 13, 515–518. [Google Scholar]
- Bousseljot, R.; Kreiseler, D.; Schnabel, A. Nutzung Der EKG-Signaldatenbank CARDIODAT Der PTB Über Das Internet. Biomed. Eng. 1995, 40, 317–318. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed]

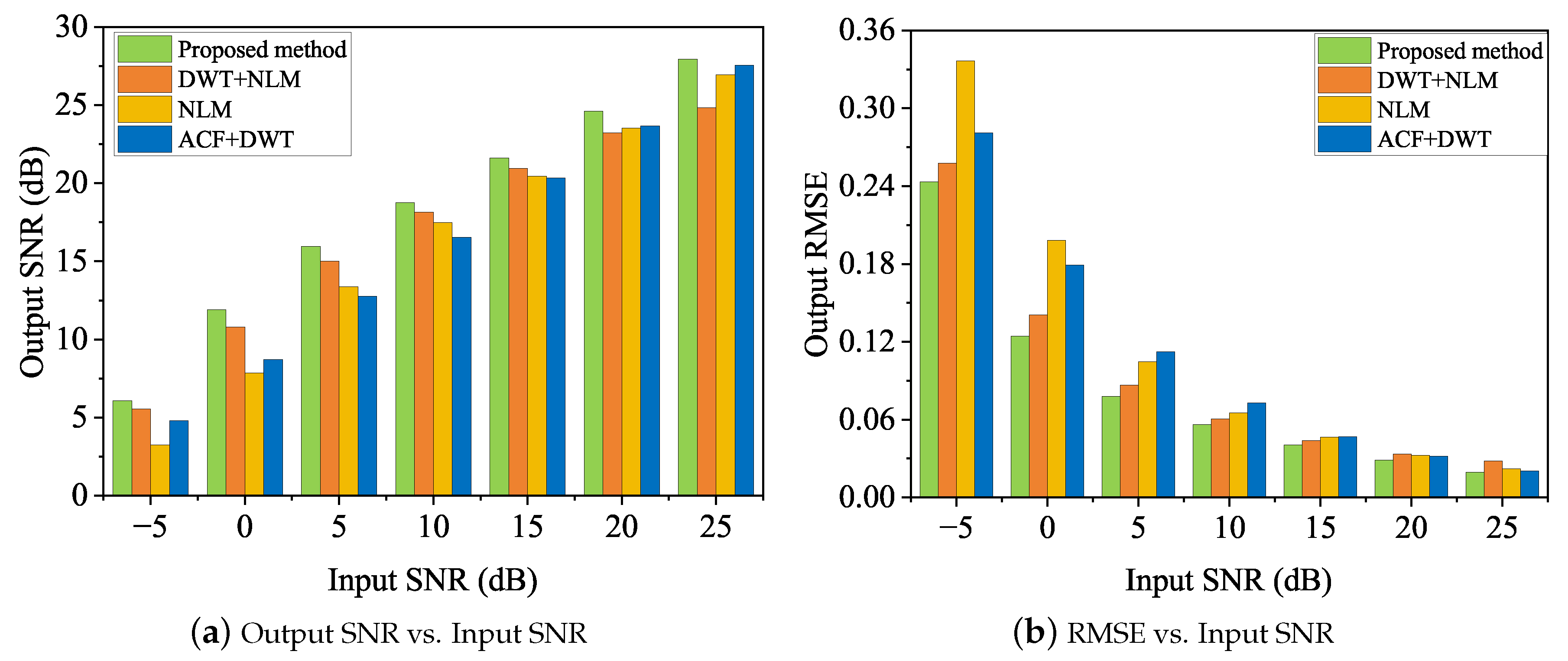
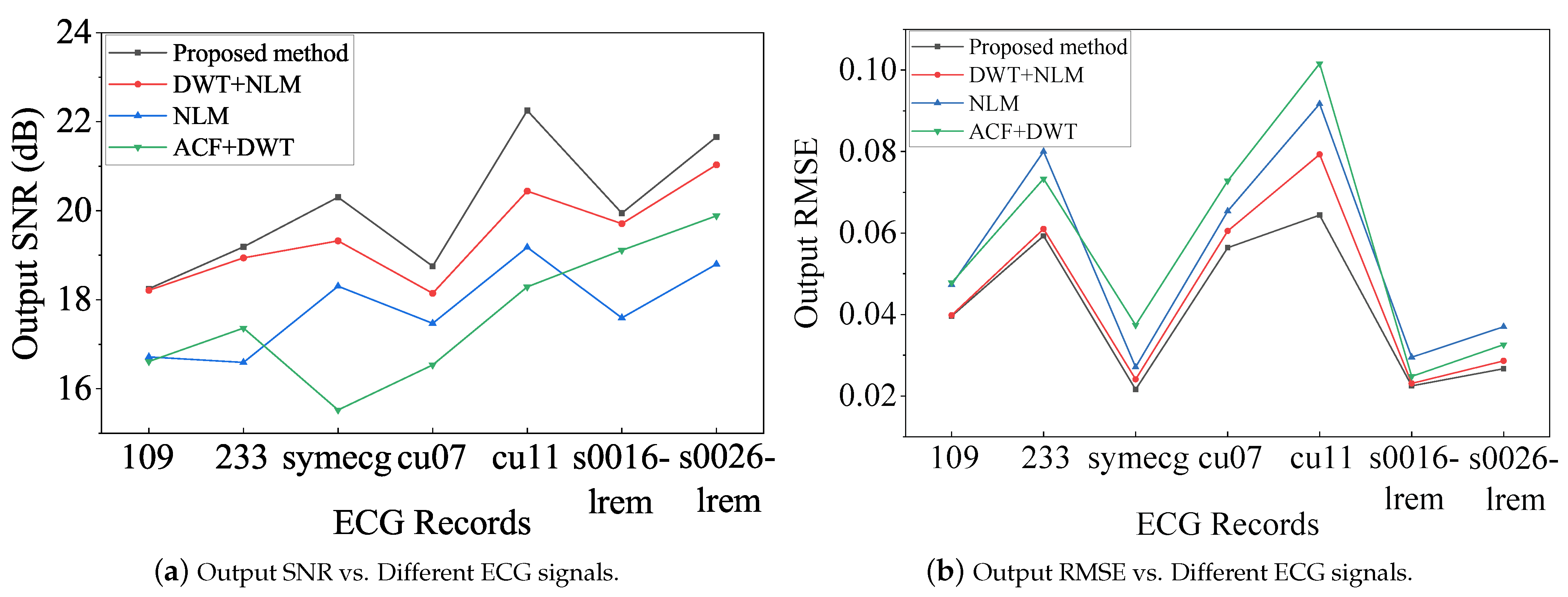
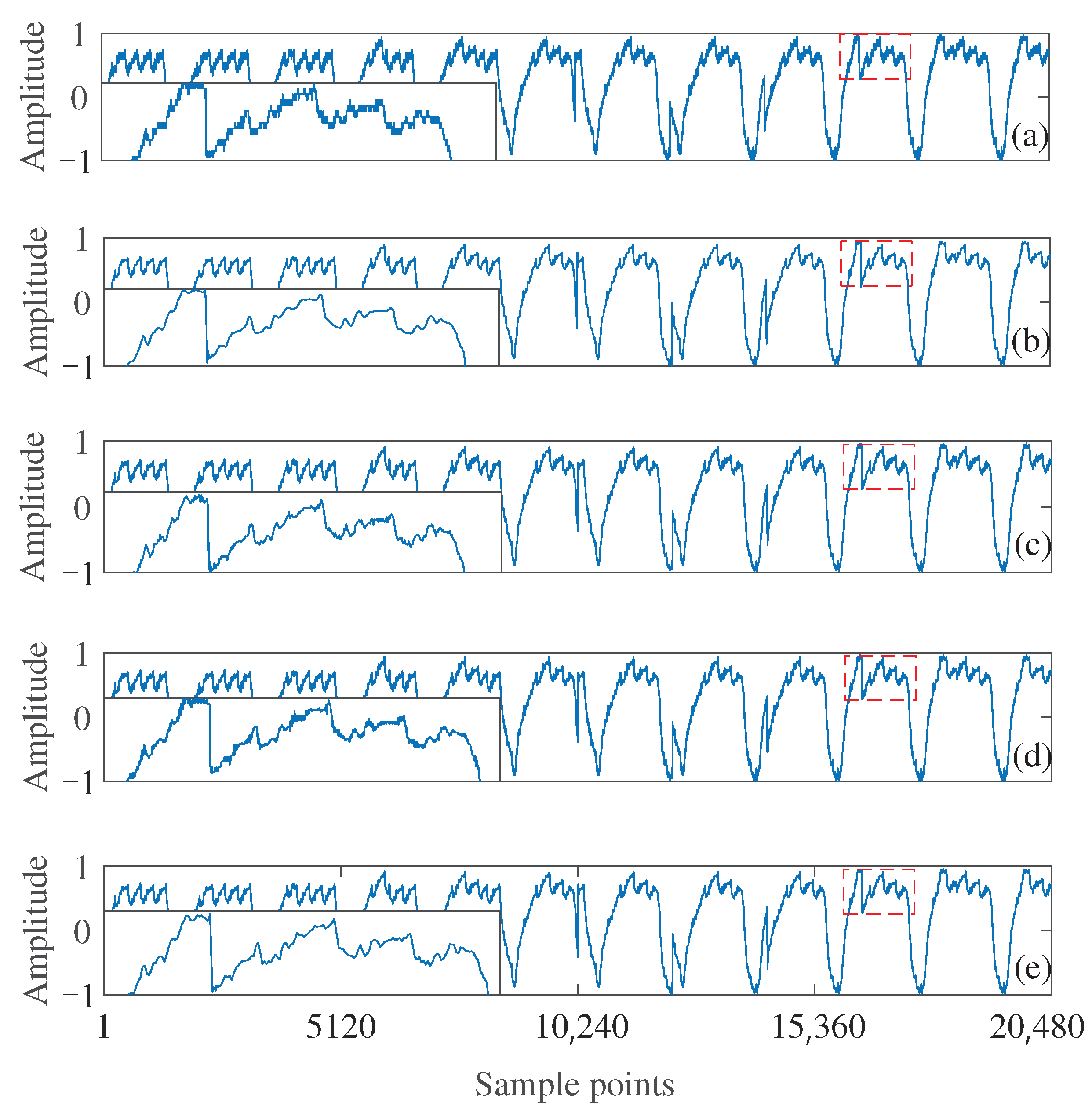
| Record | Input SNR | Proposed Method | DWT + NLM | NLM | ACF + DWT | ||||
|---|---|---|---|---|---|---|---|---|---|
| SNR | RMSE | SNR | RMSE | SNR | RMSE | SNR | RMSE | ||
| 109 | −5 | 6.6233 | 0.1511 | 6.5898 | 0.1517 | 3.9941 | 0.2045 | 6.1259 | 0.1600 |
| 0 | 11.2769 | 0.0885 | 10.6659 | 0.0949 | 7.9982 | 0.129 | 9.9449 | 0.103 | |
| 5 | 15.4440 | 0.0547 | 15.0125 | 0.0575 | 13.0431 | 0.0721 | 13.3994 | 0.0692 | |
| 10 | 18.2484 | 0.0396 | 18.2119 | 0.0398 | 16.7143 | 0.0473 | 16.6144 | 0.0478 | |
| 15 | 20.8932 | 0.0292 | 21.0628 | 0.0286 | 19.6667 | 0.0336 | 19.7731 | 0.0332 | |
| 20 | 23.6835 | 0.0212 | 23.3344 | 0.0220 | 22.8914 | 0.0232 | 22.9776 | 0.023 | |
| 25 | 26.3974 | 0.0155 | 24.8761 | 0.0185 | 26.1936 | 0.0159 | 24.7509 | 0.0187 | |
| 233 | −5 | 6.182 | 0.2655 | 6.1743 | 0.2656 | 3.2839 | 0.3701 | 5.9275 | 0.2734 |
| 0 | 11.4079 | 0.1453 | 11.4491 | 0.1446 | 8.4203 | 0.2050 | 10.2194 | 0.1667 | |
| 5 | 15.1782 | 0.0942 | 15.1495 | 0.0945 | 12.7892 | 0.1239 | 13.6163 | 0.1128 | |
| 10 | 19.1893 | 0.0593 | 18.9417 | 0.0610 | 16.5935 | 0.0800 | 17.3648 | 0.0733 | |
| 15 | 22.3322 | 0.0413 | 22.2855 | 0.0415 | 20.2585 | 0.0524 | 20.4854 | 0.0511 | |
| 20 | 26.0285 | 0.0270 | 25.2019 | 0.0297 | 23.8100 | 0.0348 | 24.8230 | 0.0310 | |
| 25 | 29.1999 | 0.0187 | 27.6468 | 0.0224 | 27.4267 | 0.0230 | 28.9878 | 0.0192 | |
| symecg | −5 | 6.7326 | 0.1028 | 6.5833 | 0.1046 | 3.1430 | 0.1554 | 3.5687 | 0.1479 |
| 0 | 12.0167 | 0.0560 | 11.8715 | 0.0569 | 8.4931 | 0.0840 | 7.3938 | 0.0953 | |
| 5 | 17.1269 | 0.0311 | 16.1246 | 0.0349 | 14.2204 | 0.0434 | 10.8810 | 0.0638 | |
| 10 | 20.3013 | 0.0216 | 19.3241 | 0.0241 | 18.3028 | 0.0271 | 15.5225 | 0.0374 | |
| 15 | 22.8914 | 0.0160 | 22.1813 | 0.0174 | 22.0242 | 0.0177 | 19.8615 | 0.0227 | |
| 20 | 25.8554 | 0.0114 | 24.3814 | 0.0135 | 25.4262 | 0.0119 | 23.0719 | 0.0157 | |
| 25 | 29.1235 | 0.0078 | 27.3772 | 0.0095 | 29.0180 | 0.0079 | 27.9403 | 0.0089 | |
| cu11m | −5 | 7.2382 | 0.3633 | 7.0867 | 0.3692 | 4.2312 | 0.5126 | 7.0593 | 0.3702 |
| 0 | 13.6470 | 0.1739 | 13.2364 | 0.1819 | 10.0258 | 0.2633 | 10.5975 | 0.2462 | |
| 5 | 18.6757 | 0.0974 | 17.2893 | 0.1140 | 15.9581 | 0.1328 | 14.4583 | 0.1579 | |
| 10 | 22.2510 | 0.0644 | 20.4426 | 0.0793 | 19.1780 | 0.0917 | 18.2890 | 0.1016 | |
| 15 | 24.9923 | 0.0470 | 24.1291 | 0.0519 | 22.4887 | 0.0626 | 22.2729 | 0.0642 | |
| 20 | 28.1655 | 0.0326 | 27.5989 | 0.0348 | 25.8905 | 0.0423 | 26.0030 | 0.0418 | |
| 25 | 31.0085 | 0.0235 | 30.5841 | 0.0247 | 29.1557 | 0.0291 | 29.7122 | 0.0273 | |
| cu07m | −5 | 6.0680 | 0.2432 | 5.5599 | 0.2578 | 3.2443 | 0.3365 | 4.8081 | 0.2810 |
| 0 | 11.8929 | 0.1245 | 10.8079 | 0.1409 | 7.8405 | 0.1983 | 8.7159 | 0.1791 | |
| 5 | 15.9500 | 0.0780 | 15.0265 | 0.0866 | 13.3721 | 0.1048 | 12.7607 | 0.1124 | |
| 10 | 18.7530 | 0.0564 | 18.1459 | 0.0605 | 17.4680 | 0.0654 | 16.5345 | 0.0728 | |
| 15 | 21.6198 | 0.0405 | 20.9517 | 0.0438 | 20.4423 | 0.0464 | 20.3314 | 0.0470 | |
| 20 | 24.6023 | 0.0288 | 23.2371 | 0.0337 | 23.5406 | 0.0325 | 23.6685 | 0.0320 | |
| 25 | 27.9255 | 0.0196 | 24.8338 | 0.0280 | 26.9331 | 0.0220 | 27.5478 | 0.0205 | |
| s0016lrem | −5 | 8.4338 | 0.0846 | 8.2942 | 0.0860 | 6.0278 | 0.1117 | 8.4383 | 0.0847 |
| 0 | 12.3234 | 0.0542 | 12.1702 | 0.0551 | 9.4621 | 0.0752 | 12.3768 | 0.0538 | |
| 5 | 16.4317 | 0.0337 | 16.0117 | 0.0354 | 13.4170 | 0.0477 | 15.8019 | 0.0363 | |
| 10 | 19.9443 | 0.0225 | 19.7073 | 0.0231 | 17.5914 | 0.0295 | 19.1118 | 0.0248 | |
| 15 | 22.8593 | 0.0161 | 22.8382 | 0.0161 | 21.1011 | 0.0197 | 22.2987 | 0.0171 | |
| 20 | 25.0637 | 0.0125 | 25.0194 | 0.0125 | 24.1383 | 0.0139 | 24.4189 | 0.0134 | |
| 25 | 28.0725 | 0.0088 | 26.6489 | 0.0104 | 27.1810 | 0.0098 | 26.9829 | 0.0100 | |
| s0026lrem | −5 | 9.4299 | 0.1090 | 8.6199 | 0.1195 | 6.4673 | 0.1532 | 9.0539 | 0.1138 |
| 0 | 13.1735 | 0.0709 | 12.5187 | 0.0763 | 9.9979 | 0.1020 | 13.1090 | 0.0713 | |
| 5 | 17.4917 | 0.0431 | 16.8151 | 0.0465 | 14.2693 | 0.0624 | 17.1589 | 0.0447 | |
| 10 | 21.6574 | 0.0267 | 21.0304 | 0.0286 | 18.7986 | 0.0370 | 19.8868 | 0.0326 | |
| 15 | 25.6682 | 0.0168 | 25.1810 | 0.0178 | 23.1156 | 0.0225 | 23.1668 | 0.0224 | |
| 20 | 29.2414 | 0.0111 | 28.8453 | 0.0116 | 27.1056 | 0.0142 | 26.8315 | 0.0147 | |
| 25 | 32.0218 | 0.0081 | 31.8264 | 0.0083 | 30.4982 | 0.0096 | 30.1870 | 0.0100 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Yu, K.; Zhang, Y.; Zhu, P.; Chen, W.; Hao, J. Enhanced Discrete Wavelet Transform–Non-Local Means for Multimode Fiber Optic Vibration Signal. Photonics 2024, 11, 645. https://doi.org/10.3390/photonics11070645
Peng Z, Yu K, Zhang Y, Zhu P, Chen W, Hao J. Enhanced Discrete Wavelet Transform–Non-Local Means for Multimode Fiber Optic Vibration Signal. Photonics. 2024; 11(7):645. https://doi.org/10.3390/photonics11070645
Chicago/Turabian StylePeng, Zixuan, Kaimin Yu, Yuanfang Zhang, Peibin Zhu, Wen Chen, and Jianzhong Hao. 2024. "Enhanced Discrete Wavelet Transform–Non-Local Means for Multimode Fiber Optic Vibration Signal" Photonics 11, no. 7: 645. https://doi.org/10.3390/photonics11070645
APA StylePeng, Z., Yu, K., Zhang, Y., Zhu, P., Chen, W., & Hao, J. (2024). Enhanced Discrete Wavelet Transform–Non-Local Means for Multimode Fiber Optic Vibration Signal. Photonics, 11(7), 645. https://doi.org/10.3390/photonics11070645






