Abstract
Having access to ideal quantum mechanical resources, the prisoners’ dilemma can be ceased. Here, we propose a distributed quantum circuit to allow spatially separated prisoners to play the prisoners’ dilemma game. Decomposing the circuit into controlled-Z and single-qubit gates only, we design a corresponding spin–photon-interaction-based physical setup within the reach of current technology. In our setup, spins are considered to be the players’ logical qubits, which can be realized via nitrogen-vacancy centers in diamond or quantum dots coupled to optical cavities, and the game is played via a flying photon realizing logic operations by interacting with the spatially separated optical cavities to which the spin qubits are coupled. We also analyze the effect of the imperfect realization of two-qubit gates on the game, and discuss the revival of the dilemma and the emergence of new Nash equilibria.
1. Introduction
Utilizing quantum-mechanical resources in game theory has been attracting considerable attention since the seminal work of Eisert et al. [1], where it was shown that the dilemma of prisoners can be ceased if quantum strategies can be implemented in an ideal setting. Another simple yet elegant example is the magic square game (MSG). While the classically achievable average winning probability in the MSG is limited to , it is possible to win every time if the players initially share entangled qubits [2]. It has also been shown that the Samaritan’s dilemma can be resolved if quantum operations are allowed, and the highest possible sum of payoffs can be achieved if entanglement is allowed [3]. As a result, in addition to super-dense coding [4,5], quantum teleportation [6,7,8,9], computation [10,11], communication [12,13] and key distribution [14,15], networking [16,17,18], metrology [19,20,21,22] and thermodynamics [23,24,25], games have appeared as an area where quantum resources can enable advantages over classical resources.
Classical game theory [26,27], and arguably quantum game theory [1], might offer great potential to advance our understanding of the quantum origins of biology [28,29] and even consciousness [30]. Because decoherence induces the transition of quantum states into classical states [31,32], analyzing not only physical models for realization of quantum games but also the impact of the imperfections of initial states, operations and measurements on the players’ payoffs appears to be of great importance in studying quantum games, which could shed light on the quantum origins of biological evolution.
The presence of quantum resources does not always guarantee an advantage over classical resources. Shimamura et al. studied classes of entangled states that cannot reproduce original classical games [33]. Considering the imperfections in preparing the initial states to play the game, Ozdemir et al. showed a critical rate at which classical strategies become more robust [34]. By deriving necessary and sufficient conditions for playing games, Ozdemir et al. showed that it is not always possible to extend a 2-player game to an N-player game by considering an N-party entangled extension of the bipartite entangled state [35]. These findings have inspired more research into games in quantum settings, taking into account physical realizations and imperfections.
Gawron et al. studied how environmental noise on the initial states affect [36], and Fialik studied how imperfect operations and measurements affect the winning probability of the MSG [37]. Ramzan and Khan showed that the MSG can be utilized for distinguishing quantum communication channels [38]. Proposing a physical setup based on distant quantum dots coupled to optical cavities, Bugu et al. studied the impact of imperfect photon–spin interactions on the winning probability [39], and Ozaydin showed that while playing the MSG with a thermal entangled state, exciting entanglement cannot always help to increase the winning probability [40].
Limited to classical resources in the prisoners’ dilemma (PD) game, players find themselves in the following dilemma, which is explained in more detail in the next section. Although they could both receive a greater payoff by cooperating, each chooses to defect and receives a lower payoff. However, if they are granted access to ideal quantum mechanical resources, they can increase their payoffs by implementing a quantum strategy, which is considered as the cease of the dilemma. This quantum advantage and the possibility of the revival of the dilemma due to imperfections in quantum resources have been attracting both experimental and theoretical attention. The game was experimentally demonstrated on a nuclear magnetic resonance (NMR) quantum computer [41]. Proposing a hybrid setup based on the quantum circuit approach and the cluster state model, Paternostro et al. studied the impact of experimental imperfections on the game [42]. Designing a linear-optics- [43] and a cavity-based system [43], Shuai et al. studied the game under noise. A three-player extension of the game was also studied in detail considering noise effects [44,45].
To play the PD game in the quantum domain, prisoners’ qubits need to be entangled. In the original circuit [1] and following proposals, to the best of our knowledge, we believe an important issue is that the prisoners’ qubits need to be under the possession of the party to implement the entangling operators. However, considering the real scenario in this particular game, where prisoners are kept in separate rooms, and in general where players should not be required to be in the same location to play an arbitrary quantum game, a distributed setup is required that allows entangling the qubits of distant players. Then, natural questions arise regarding how to transfer qubits between spatially separated players or how to realize logic operations among distant qubits.
Electronic spins and two-level atoms constituting matter qubits are good for storing, and photons traveling between sites or so-called flying photons are good for transferring quantum information [46]. Therefore, realizing interactions between matter and photonic qubits implementing logic operations plays a key role in quantum technologies. Numerous works have been reported on spatially separated systems based on atom–photon and spin–photon interactions, such as by creating entanglement among distant qubits [47,48,49], preparing large-scale multipartite entanglement [50,51], observing entanglement sudden death (ESD) in two separate Jaynes–Cummings nodes [52], manipulating separate qubits in coupled resonators [53], experimentally demonstrating the entangling gate between a flying photonic qubit and a stationary quantum dot spin qubit on a chip [54], playing the MSG with distant players [39], deterministic expansion of W states [55], and a distributed physical setup based on flying photons and atomic memories [56].
In light of these works, we chose to employ spin qubits as the logical qubits of distant players, and a flying ancillary photonic qubit to travel between players. Spin qubits can be considered as nitrogen vacancy (NV) center spins in diamond, or quantum dot spins coupled to optical cavities, each requiring specific conditions such as ultra-low temperature in the latter. When the ancillary photonic qubit is incident to the cavity, the interaction results in the implementation of a high-fidelity controlled-Z operation on the photonic and spin qubits, constituting the basic building block of our proposal along with single-qubit operations. We designed a distributed quantum circuit to play the game between spatially separated players and we decomposed the circuit into basic building blocks so that we could design a corresponding physical setup based on spin–photon interactions within the reach of current technology despite cavity leaks and spin decoherence [47,48,49].
This paper is organized as follows. In the Materials and Methods Section, first we briefly present the PD game. Next, we present how to decompose the two-qubit gates into controlled-Z () and single-qubit gates, and finally how to realize the gate via spin–photon interaction towards designing the physical setup. In the Results Section, we first present our design for the distributed quantum circuit to allow distant players to play the game. Next, we present our design for the corresponding physical setup based on spin–photon interactions each realizing a operation. Taking into account the imperfections in realizing the operation, we study the dynamics of dilemma and Nash equilibrium. Following the discussions, we present our conclusions.
2. Materials and Methods
2.1. Playing the Prisoners’ Dilemma Game
In this subsection, we briefly present how the prisoners’ dilemma game can be played with separable or entangled resources and show how the dilemma can be ceased with ideal quantum resources. Strategies of players to cooperate and to defect are assigned to two basis vectors, and , respectively. The associated strategy operators and are defined as instances of a matrix
where and . As explained in detail in ref. [1] and illustrated in Figure 1, the game starts with the initial joint state of Alice and Bob, . After applying the global operator on two qubits, Alice and Bob implement their strategies by applying single-qubit operators and on their qubits, respectively. Next, applying the global operator, qubits are finally measured to obtain the payoffs based on the final state , where the operator can be found by considering a faithful representation of the game as with . The measurement yields one of the results for Alice’s and Bob’s qubits, yielding Alice’s payoff
and Bob’s payoff is obtained by interchanging s and t. Here, the parameters are chosen as , , and , representing reward, punishment, temptation and suckers’ payoff, respectively, and . The parameter controls the entanglement of the game. The game is separable for and maximally entangled for , and Alice’s payoff is plotted in each scenario in Figure 2 on the right and left panels, respectively. In the classical game, the dominant strategy yields payoffs , while the dominant quantum strategy yields showing the advantage of ideal quantum resources.
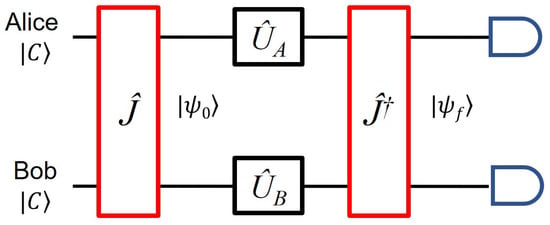
Figure 1.
The original circuit for a two-qubit circuit for playing the prisoners’ dilemma game game [1].
Figure 2.
Payoff function for Alice (left) in a separable game with and (right) in an ideal quantum game with maximal entanglement with with a ceased dilemma as presented in [1]. and are Nash equilibria in a separable and quantum game with and , respectively. Following the parametrization for and for , strategies , and correspond to , and , respectively.
2.2. Decomposition of SWAP and Gates via Spin–Photon Interactions
In the original circuit, implementation of the and gates requires qubits of both prisoners. However, in order to allow spatially separated prisoners to play the game, we design a new, three-qubit circuit by introducing an ancillary qubit. We consider matter qubits such as NV centers or quantum dot spins for the prisoners’ logical qubits, and a photon as the ancillary qubit to travel back and forth between the prisoners. As will be explained in detail in the Results section, in our design, implementing a two-qubit SWAP gate on Alice’s logical qubit and the ancillary photonic qubit is required at each visit, and we consider two-qubit and gates to be applied on the ancillary qubit and Bob’s logical qubit. In our physical setup corresponding to the circuit model, as explained the the next subsection, each spin–photon interaction between the logical and ancillary qubits implements a controlled-Z () gate. Therefore, decomposition of SWAP and into gates and single-qubit gates is required. A SWAP gate can be decomposed into three controlled-NOT (CNOT) gates, and a CNOT gate can be decomposed into one gate and two Hadamard gates.
Following the decomposition of the gate into CNOT and single-qubit gates in refs. [43,57] and denoting the single-qubit identity operator, the decomposition of the gate into and single-qubit gates can be found simply as
for , and the gate for . Note that in controlled gates, the first and second indices denote the control and target qubits, respectively, and no index implies for simplicity. Circuit models for the decomposition of SWAP and gates into and single-qubit gates are shown in Figure 3, and in the next subsection we will present how a gate can be implemented through the interaction of a photonic qubit with the optical cavity to which the logical spin qubit is coupled.
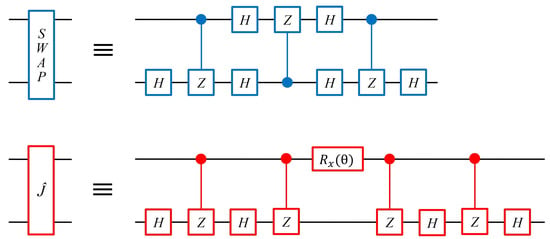
Figure 3.
(Top) Decomposing the SWAP gate into and Hadamard gates. (Bottom) Decomposing the gate into , Hadamard and gates. and gates can be implemented with and , respectively.
2.3. Implementing the Gate
In this subsection, denoting the right and left circular polarization states of the photon as and , respectively, we present how to implement a gate performing
between the electronic spin coupled to an optical cavity constituting the logical qubit of Alice or Bob, and the incident ancillary photon, as illustrated in Figure 4. As explained in [58,59,60], when the optical cavity meets the photon, assuming a weak assumption limit , adiabatically eliminating the cavity mode and neglecting the vacuum input field, the solution of the Langevin equations in the rotating frame yields the reflection coefficient for the photon
Here, and are the frequencies of the cavity field and the incident photon, respectively, is the transition frequency of the electronic energy levels, and g is the coupling strength of the NV center to the cavity. The decay rate of the NV center and the cavity are denoted as and , respectively. For the resonant condition , the reflection coefficient reduces to
When the NV center is not coupled to the optical cavity implying , the reflection coefficient in the resonant condition becomes . Due to optical Faraday rotation [59,60] and optical transition rules [48,58] as illustrated in Figure 4, an -polarized photon receives a phase shift whereas an -polarized photon receives a phase shift () depending on the spin state of the NV center , where the the arguments of the complex numbers and are denoted as and , and are approximately equal to and , respectively, for the resonant condition and a sufficiently large coupling strength, .
It is then straightforward to implement a gate as defined in Equations (4)–(7) between the incident photon and the electronic spin by placing a -phase-shifter in the reflection path of the photon [39,47,48,49,55]. Note that the implementation of single-qubit gates for both the ancillary photon and logical qubits is straightforward by using half-wave plates [61] and EM pulses [62], respectively.
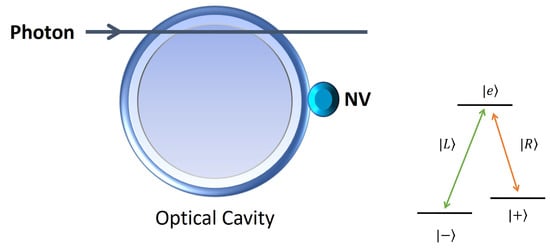
Figure 4.
(Left): A photon is introduced to an optical cavity to which an NV center is coupled. Due to the optical transition rules illustrated on the right, a operation is realized between the incident photon and the electronic spin. See the text for the details. (Right): A nitrogen-vacancy center’s -type optical transitions. The transition () is associated with the left (right) circular polarization of the photon, denoted as ().
3. Results
3.1. Distributed Quantum Circuit for Spatially Separated Players
In this subsection, we present our proposed distributed circuit to allow spatially separated prisoners to play the game. The working principle of our proposal follows. Spins coupled to optical cavities are considered to be Alice’s and Bob’s logical qubits, and when an ancillary flying photon is incident to the cavity, a gate is realized between the photonic and the spin qubits. As shown in Figure 5, the ancillary qubit is prepared in the state and sent to the cavity to which Alice’s logical spin qubit is coupled. Applying the single qubits to the photonic and spin qubit accordingly, the first SWAP gate is realized. Now, the ancillary photonic qubit is in the initial state of Alice’s qubit, and it is sent to Bob’s site. Interacting with the cavity to which Bob’s spin qubit is coupled, and with single-qubit gates applied, the gate is realized and the photonic qubit is sent back to Alice’s site for implementing the second SWAP gate. Next, to implement their choices, Alice and Bob apply single-qubit gates and defined in Equation (1), respectively. The photon is sent back to Alice’s site for implementing the third SWAP gate, then to Bob’s site for implementing the gate and finally back to Alice for implementing the last SWAP gate, which completes the procedure. The overall operation on three qubits is then
In the circuit extended to three qubits, because both Alice’s qubit and the ancillary qubit are prepared initially in the state, the first SWAP gate can be omitted for reducing the complexity. Moreover, if Alice can apply her choice operator on the ancillary photon instead of the spin qubit, the second and third SWAP gates can also be omitted. However, for the sake of generality, we do not make such assumptions and keep the SWAP gates.
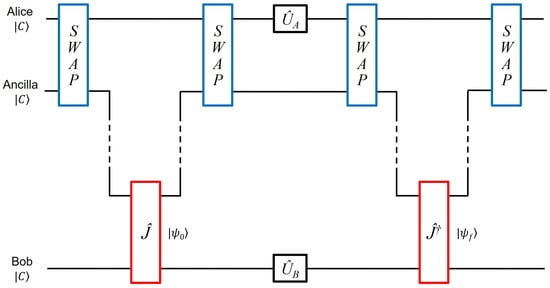
Figure 5.
In order to allow spatially separated prisoners to play the game, we design a three-qubit circuit as an extension of the original two-qubit circuit proposed in [1]. Logical qubits of Alice and Bob are considered to be spins of NV centers or quantum dots; for example, coupled to optical cavities. Alice applies a SWAP gate to the ancillary photon and her logical qubit, then sends the photon to Bob, who will apply the gate to the photon and his logical qubit, and send the photon back to Alice. She applies another SWAP gate to the photon and her logical qubit. Their spatially separated spin–qubit pair is now in the state as if the operation was applied to them, leaving the ancillary photon in its initial state. Applying single-qubit gates and corresponding to their choices, they implement the same sequence, this time with a gate.
3.2. Physical Setup Based on Spin–Photon Interactions
Although the circuit in Figure 5 can be implemented in an emerging distributed quantum computer, for experimental demonstrations in lab, we designed a corresponding setup based on spin–photon interactions. In our proposed setup is illustrated in Figure 6 where single-qubit operations and -phase-shifters are not shown for simplicity. The spin qubits of NV centers (as an example) in green and yellow colors coupled to optical cavities correspond to the logical qubits of Alice and Bob, respectively. The sequence of operations is enumerated; for example, the first two operations are “1: Swap” and “2: ”. Steps are listed as follows:
STEP 1: Swap. Applying the single-qubit operations appropriately (these are not shown in the figure and will not be mentioned in the following steps), the ancillary photon is sent to Alice’s cavity three times to implement the first SWAP operation on the photon and Alice’s NV center spin qubit. Then, the photon is sent to Bob’s site, which is shown with dashed lines in the figure.
STEP 2: . The photon is incident to Bob’s cavity four times to implement the operation, and then it is sent back to Alice.
STEP 3: Swap. The photon is incident to Alice’s cavity three times to implement the second SWAP operation, yielding , so that prisoners are now ready to apply their choice operators and .
The delay introduced in the photon’s path between STEP 3 and STEP 4 gives time to prisoners to apply their choices.
STEP 4: and . Choices are implemented by applying and to the NV center spins.
STEP 5: Swap. The photon is incident to Alice’s cavity to implement the third SWAP operation, and is then sent to Bob.
STEP 6: . The photon is incident to Bob’s cavity for the last time to implement the operation, and is then sent to Alice.
STEP 7: Swap. Implementing the last SWAP operation, the spatially separated spin qubits are now left in the final state, before the measurement yielding the payoffs.
Assuming perfect cavities, state preparations and gate realizations, this physical setup implements the original circuit in Figure 1 for playing the game, resulting in the payoff functions in Figure 2 in the separable and ideal quantum scenarios, with the dilemma ceased in the latter. However, due to experimental imperfections, the payoff functions are expected to deviate from the ideal quantum game, which will be considered in the next subsection.
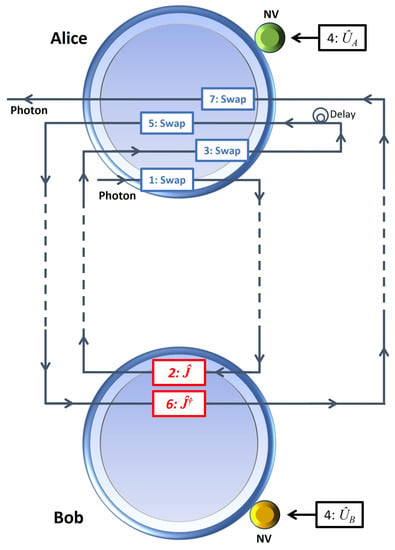
Figure 6.
Physical setup for implementing the circuit in Figure 5 for spatially separated Alice and Bob to play the prisoners’ dilemma game. Operations are applied in the enumerated order. As illustrated in Figure 3, each SWAP operation is realized by sending the photon to the cavity three times, applying a Hadamard gate to the photon and the spin before and after the interaction. and operations are realized by sending the photon to the cavity four times applying a Hadamard gate before and after the interactions, and and , respectively, in the middle.
3.3. Imperfect Realization and the Revival of the Dilemma
What makes this game separable or quantum is the parameter of the two-qubit operator. Therefore, the implementation of the two-qubit operations plays a vital role in the payoff functions. What is more, when compared to two-qubit operations, experimental imperfections in implementing single-qubit operations can be neglected. Because the two-qubit operation is the key in our designs for the implementation of , and SWAP operations, we have limited our analysis of the imperfections of implementing it. We consider that while the ideal implementation of the gate is with controlled-phase operation
nonideal implementation results in . Replacing with , we recalculate the payoffs as a function of .
We first restrict the quantum game to classical strategies with nonideal implementation of two-qubit gates. For corresponding to the ideal case, due to the restriction, payoffs appear as in a classical game, resulting in the dominant strategy . This is a Nash equilibrium because, assuming the other player’s choice is fixed, no player can be better off by changing the choice. However, as depicted in Figure 7, when becomes greater than , the payoff for (red curve) becomes greater than (orange curve). That is, assuming that Bob chooses , Alice can be better off switching from to , so the Nash equilibrium disappears. However, in extreme cases with , the initial order of payoffs is restored, resulting in the emergence of a Nash equilibrium at , implying the revival of the dilemma. Note that for , operations , and become the identity operator leaving no entanglement in the game.
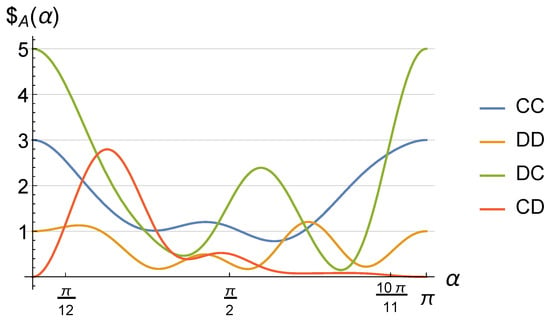
Figure 7.
Restricted to classical strategies in a quantum game, Alice’s payoff as a function of corresponding to nonideal implementation of the gate as a operation. When becomes greater than , is not the dominant strategy anymore. As approaches in the extreme case where no entanglement is left, Nash equilibrium is restored.
Having observed the cease and revival of the dilemma in the classical strategy space due to experimental imperfections, let us now analyze the case where quantum strategies are allowed. In the ideal quantum game, is a Nash equilibrium. This is because, by fixing Bob’s choice at , Alice cannot be better off by deviating from . However, in the nonideal quantum game with imperfect realization of gates, i.e., implementing with non-zero , by fixing Bob’s choice at , Alice can be better off by deviating from towards as shown in Figure 8 for . Nevertheless, new Nash equilibria appear in the band between and .
The nonideality with affects the implementation not only of the gates corresponding to the entangling operators between the players’ qubits in the original scheme, but also the SWAP gates required to allow spatially separated players to play the game in our scheme. Therefore, our simulation is not limited to considering nonideal entangling gates with , but it also covers the influence of the nonindeal gates on the distributed scheme. This shows that imperfect implementation, not only of the core gates for playing quantum games in their simplest form assuming the players are in the same room, but also gates required to design distributed versions, plays a role in determining the games’ results with dominant strategies and Nash equilibria.
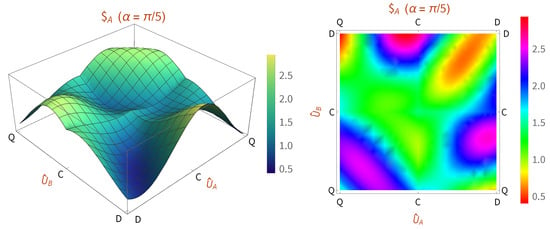
Figure 8.
(Left) Payoff function for Alice in quantum game with imperfect realization of two-qubit gate with . (Right) Density plot for better visualization. Unlike the ideal game, is not a Nash equilibrium anymore because assuming Bob plays , Alice can be better off by deviating from towards . However, new Nash equilibria appear along the band between and .
4. Discussion
Here, we have assumed the same imperfection with the value in realizing gates for implementing both SWAP gates on Alice’s site and , gates on Bob’s site, which is not strictly required in real scenarios, due to the technologies and capabilities of the players. Because the experimental imperfections on players’ sites affect the Nash equilibrium, it becomes important for each player to possess information on the experimental capabilities of other players. Therefore, as discussed also in [39], it should be considered a factor in determining whether it is a game with complete or incomplete information.
Because our main objective in this work was to propose a distributed quantum circuit and a corresponding physical setup for distant prisoners, regarding the physical imperfections, we focused on limited scenarios. For example, regarding the nonideality in realizing the gate, rather than an arbitrary imperfection, we assumed a unitary controlled-phase () gate, implying a deviation from the desired operation by , which turns out to be sufficient for observing the cease and revival of the dilemma and the change in Nash equilibrium points. However, more detailed noise scenarios might reveal further results.
Considering the nonideal implementation of logic operators highlights an important issue in quantum games. To prevent players from affecting or biasing the running of a game, each player should be able to act only by implementing the choice operators in general, and and operators in the present game, which would actually jeopardize the rationality of the game. However, in order to entangle players’ qubits in the original proposal in [1], and implementing the two-qubit operators in the circuit model in Figure 5 and corresponding physical setup in Figure 6, players can choose to deviate from the standard protocol. Thus, it would be interesting to extend the circuit model in Figure 5 by adding a trusted referee who implements the SWAP, and operators and sends the ancillary photonic qubits to players for implementing their choice operators, only.
In addition to the construction of the distributed circuit in Figure 5 per se, the idea of entangling the spin qubits belonging to spatially separated players in a specific way for playing the PD game, and the design of the physical setup in Figure 6 for implementing the distributed circuit, are the challenging steps in this work, which, to the best of our knowledge, have not been addressed yet. The entangling gate that is not simply a CNOT gate, as well as the single-qubit gates for implementing players’ choices and the impact of imperfections on players’ payoffs in our work, are specific to the PD game. Therefore, rather than a general distributed scheme, the presentation of our work is focused on the PD game.
Despite recent advances in practical quantum computers, realizing a distributed quantum computing task by transferring quantum information is yet to be achieved. However, in quantum dot systems, Bodey et al. experimentally demonstrated full SU(2) spin control with over 98% -rotation fidelity [63]. Very recently, Chan et al. reported over 96% fidelity in realizing a spin–photon entangling gate [54]. Rong et al. reported the experimental implementation of single- and two-qubit gates in NV centers at room temperature with fidelities of and , respectively [64]. The feasibility analyses in [47,48,49,55] suggest that the implementation of a high-fidelity operation on a photonic and spin qubit is possible despite realistic effects such as cavity leaks, and that the proposed physical setup is within the reach of current technology.
5. Conclusions
In the original proposal for the prisoners’ dilemma game in a quantum setting [1], two-qubit entangling operators are considered, requiring the possession of qubits of both players. Here, by designing a distributed quantum circuit, we relaxed this requirement and allowed distant players to play the game. In our circuit, each player possesses a qubit, and an ancillary qubit travels between players for realizing the game. Considering that matter qubits such as the spins of NV centers in diamond or quantum dots coupled optical cavities constitute the players’ logical qubits, and a flying photon is employed as the ancillary qubit, we also designed a spin–photon interaction-based physical setup for experimentally realizing the game between distant players. Finally, we considered the nonideal game due to imperfect realization of two-qubit gates, and analyzed the impact imperfections on the game, in particular Nash equilibrium.
Author Contributions
Conceptualization, A.A.A., F.O., V.B. and C.B.; methodology, A.A.A., F.O., V.B. and C.B.; software, A.A.A. and F.O.; validation, A.A.A., F.O. and C.B.; formal analysis, A.A.A., F.O. and C.B.; investigation, A.A.A., F.O. and C.B.; resources, A.A.A., F.O. and C.B.; data curation, A.A.A., F.O. and C.B.; writing—original draft preparation, A.A.A., F.O. and C.B.; visualization, A.A.A., F.O., V.B. and C.B.; supervision, A.A.A. and F.O.; funding acquisition, F.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Personal Research Fund of Tokyo International University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data in this study can be generated through the presented methods.
Acknowledgments
The authors thank C. Yesilyurt for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNOT | Controlled-NOT gate |
| CP | Controlled-phase gate |
| CZ | Controlled-Z gate |
| Strategy to cooperate | |
| Strategy to defect | |
| Quantum strategy | |
| ESD | Entanglement sudden death |
| MSG | Magic square game |
| NMR | Nuclear magnetic resonance |
| NV | Nitrogen vacancy |
| PD | Prisoners’ dilemma |
References
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum Games and Quantum Strategies. Phys. Rev. Lett. 1999, 83, 3077–3080. [Google Scholar] [CrossRef]
- Brassard, G.; Broadbent, A.; Tapp, A. Quantum pseudo-telepathy. Found. Phys. 2005, 35, 1877–1907. [Google Scholar] [CrossRef]
- Özdemir, S.K.; Shimamura, J.; Morikoshi, F.; Imoto, N. Dynamics of a discoordination game with classical and quantum correlations. Phys. Lett. A 2004, 333, 218–231. [Google Scholar] [CrossRef]
- Bennett, C.H.; Wiesner, S.J. Communication via one- and two-particle operators on Einstein-Podolsky-Rosen states. Phys. Rev. Lett. 1992, 69, 2881–2884. [Google Scholar] [CrossRef]
- Mattle, K.; Weinfurter, H.; Kwiat, P.G.; Zeilinger, A. Dense Coding in Experimental Quantum Communication. Phys. Rev. Lett. 1996, 76, 4656–4659. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Pirandola, S.; Eisert, J.; Weedbrook, C.; Furusawa, A.; Braunstein, S.L. Advances in quantum teleportation. Nat. Photonics 2015, 9, 641–652. [Google Scholar] [CrossRef]
- Li, K.; Kong, F.Z.; Yang, M.; Ozaydin, F.; Yang, Q.; Cao, Z.L. Generating Multi-Photon W-like States for Perfect Quantum Teleportation and Superdense Coding. Quant. Inf. Process. 2016, 15, 3137. [Google Scholar] [CrossRef]
- Im, D.G.; Lee, C.H.; Kim, Y.; Nha, H.; Kim, M.S.; Lee, S.W.; Kim, Y.H. Optimal teleportation via noisy quantum channels without additional qubit resources. NPJ Quantum Inf. 2021, 7, 86. [Google Scholar] [CrossRef]
- Woerner, S.; Egger, D.J. Quantum risk analysis. NPJ Quantum Inf. 2019, 5, 15. [Google Scholar] [CrossRef]
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.; Yard, J. Quantum Communication with Zero-Capacity Channels. Science 2008, 321, 1812–1815. [Google Scholar] [CrossRef] [PubMed]
- Hastings, M.B. Superadditivity of communication capacity using entangled inputs. Nat. Phys. 2009, 5, 255–257. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 2014, 560, 7–11. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Acín, A.; Cirac, J.I.; Lewenstein, M. Entanglement percolation in quantum networks. Nat. Phys. 2007, 3, 256–259. [Google Scholar] [CrossRef]
- Bugu, S.; Yesilyurt, C.; Ozaydin, F. Enhancing the W-State Quantum-Network-Fusion Process with a Single Fredkin Gate. Phys. Rev. A 2013, 87, 032331. [Google Scholar] [CrossRef]
- Yesilyurt, C.; Bugu, S.; Ozaydin, F.; Altintas, A.A.; Tame, M.; Yang, L.; Ozdemir, S.K. Deterministic Local Doubling of W states. J. Opt. Soc. Am. B 2016, 33, 2313. [Google Scholar] [CrossRef]
- Pezzé, L.; Smerzi, A. Entanglement, nonlinear dynamics, and the Heisenberg limit. Phys. Rev. Lett. 2009, 102, 100401. [Google Scholar] [CrossRef]
- Ozaydin, F.; Altintas, A.A. Quantum Metrology: Surpassing the shot-noise limit with Dzyaloshinskii-Moriya interaction. Sci. Rep. 2015, 5, 16360. [Google Scholar] [CrossRef]
- Ozaydin, F.; Altintas, A.A. Parameter estimation with Dzyaloshinskii–Moriya interaction under external magnetic fields. Opt. Quantum Electron. 2020, 52, 70. [Google Scholar] [CrossRef]
- Kim, Y.; Yoo, S.Y.; Kim, Y.H. Heisenberg-Limited Metrology via Weak-Value Amplification without Using Entangled Resources. Phys. Rev. Lett. 2022, 128, 040503. [Google Scholar] [CrossRef] [PubMed]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Dag, C.B.; Niedenzu, W.; Ozaydin, F.; Mustecaplıoglu, O.E.; Kurizki, G. Temperature control in dissipative cavities by entangled dimers. J. Phys. Chem. C 2019, 123, 4035–4043. [Google Scholar] [CrossRef]
- Tuncer, A.; Izadyari, M.; Dağ, C.B.; Ozaydin, F.; Müstecaplıoğlu, Ö.E. Work and heat value of bound entanglement. Quantum Inf. Process. 2019, 18, 373. [Google Scholar] [CrossRef]
- Dawkins, R.; Davis, N. The Selfish Gene; Macat Library: London, UK, 2017. [Google Scholar] [CrossRef]
- Kastampolidou, K.; Andronikos, T. A survey of evolutionary games in biology. GeNeDis 2020, 2018, 253–261. [Google Scholar] [CrossRef]
- McFadden, J.; Al-Khalili, J. The origins of quantum biology. Proc. R. Soc. A 2018, 474, 20180674. [Google Scholar] [CrossRef]
- Marais, A.; Adams, B.; Ringsmuth, A.K.; Ferretti, M.; Gruber, J.M.; Hendrikx, R.; Schuld, M.; Smith, S.L.; Sinayskiy, I.; Krüger, T.P.; et al. The future of quantum biology. J. R. Soc. Interface 2018, 15, 20180640. [Google Scholar] [CrossRef]
- Tuszynski, J.A. From quantum chemistry to quantum biology: A path toward consciousness. J. Integr. Neurosci. 2020, 19, 687–700. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence and the transition from quantum to classical—Revisited. In Quantum Decoherence; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–31. [Google Scholar] [CrossRef]
- Im, D.G.; Kim, Y.H. Decoherence-Induced Sudden Death of Entanglement and Bell Nonlocality. Photonics 2022, 9, 58. [Google Scholar] [CrossRef]
- Shimamura, J.; Özdemir, S.K.; Morikoshi, F.; Imoto, N. Entangled states that cannot reproduce original classical games in their quantum version. Phys. Lett. A 2004, 328, 20–25. [Google Scholar] [CrossRef][Green Version]
- Özdemir, S.K.; Shimamura, J.; Imoto, N. Quantum advantage does not survive in the presence of a corrupt source: Optimal strategies in simultaneous move games. Phys. Lett. A 2004, 325, 104–111. [Google Scholar] [CrossRef]
- Özdemir, S.K.; Shimamura, J.; Imoto, N. A necessary and sufficient condition to play games in quantum mechanical settings. New J. Phys. 2007, 9, 43. [Google Scholar] [CrossRef]
- Gawron, P.; Miszczak, J.; Sładkowski, J. Noise effects in quantum magic squares game. Int. J. Quantum Inf. 2008, 6, 667–673. [Google Scholar] [CrossRef]
- Fialík, I. Noise and the magic square game. Quantum Inf. Process. 2012, 11, 411–429. [Google Scholar] [CrossRef]
- Ramzan, M.; Khan, M. Distinguishing quantum channels via magic squares game. Quantum Inf. Process. 2010, 9, 667–679. [Google Scholar] [CrossRef][Green Version]
- Bugu, S.; Ozaydin, F.; Kodera, T. Surpassing the classical limit in magic square game with distant quantum dots coupled to optical cavities. Sci. Rep. 2020, 10, 22202. [Google Scholar] [CrossRef]
- Ozaydin, F. Quantum pseudo-telepathy in spin systems: The magic square game under magnetic fields and the Dzyaloshinskii–Moriya interaction. Laser Phys. 2020, 30, 025203. [Google Scholar] [CrossRef]
- Du, J.; Li, H.; Xu, X.; Shi, M.; Wu, J.; Zhou, X.; Han, R. Experimental Realization of Quantum Games on a Quantum Computer. Phys. Rev. Lett. 2002, 88, 137902. [Google Scholar] [CrossRef]
- Paternostro, M.; Tame, M.; Kim, M. Hybrid cluster state proposal for a quantum game. New J. Phys. 2005, 7, 226. [Google Scholar] [CrossRef]
- Shuai, C.; Mao-Fa, F. Linear optics implementation for quantum game under quantum noise. Chin. Phys. 2006, 15, 276–280. [Google Scholar] [CrossRef]
- Shuai, C.; Mao-Fa, F.; Xiao-Juan, Z. The effect of quantum noise on multiplayer quantum game. Chin. Phys. 2007, 16, 915–918. [Google Scholar] [CrossRef]
- Ramzan, M.; Khan, M.K. Noise effects in a three-player prisoner’s dilemma quantum game. J. Phys. A Math. Theor. 2008, 41, 435302. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Chen, Q.; Yang, W.; Feng, M.; Du, J. Entangling separate nitrogen-vacancy centers in a scalable fashion via coupling to microtoroidal resonators. Phys. Rev. A 2011, 83, 054305. [Google Scholar] [CrossRef]
- Cheng, L.Y.; Wang, H.F.; Zhang, S. Simple schemes for universal quantum gates with nitrogen-vacancy centers in diamond. J. Opt. Soc. Am. B 2013, 30, 1821–1826. [Google Scholar] [CrossRef]
- Cheng, L.Y.; Wang, H.F.; Zhang, S.; Yeon, K.H. Quantum state engineering with nitrogen-vacancy centers coupled to low-Q microresonator. Opt. Express 2013, 21, 5988–5997. [Google Scholar] [CrossRef]
- Zang, X.P.; Yang, M.; Ozaydin, F.; Song, W.; Cao, Z.L. Generating Multi-Atom Entangled W States via Light-Matter Interface Based Fusion Mechanism. Sci. Rep. 2015, 5, 16245. [Google Scholar] [CrossRef]
- Zang, X.P.; Yang, M.; Ozaydin, F.; Song, W.; Cao, Z.L. Deterministic Generation of Large Scale Atomic W States. Opt. Exp. 2015, 24, 12293. [Google Scholar] [CrossRef]
- Shen, L.T.; Shi, Z.C.; Wu, H.Z.; Yang, Z.B. Dynamics of Entanglement in Jaynes–Cummings Nodes with Nonidentical Qubit-Field Coupling Strengths. Entropy 2017, 19, 331. [Google Scholar] [CrossRef]
- Shen, L.T.; Chen, R.X.; Wu, H.Z.; Yang, Z.B. Distributed manipulation of two-qubit entanglement with coupled continuous variables. JOSA B 2015, 32, 297–302. [Google Scholar] [CrossRef]
- Chan, M.L.; Tiranov, A.; Appel, M.H.; Wang, Y.; Midolo, L.; Scholz, S.; Wieck, A.D.; Ludwig, A.; Sørensen, A.S.; Lodahl, P. On-chip spin-photon entanglement based on single-photon scattering. arXiv 2022, arXiv:2205.12844. [Google Scholar] [CrossRef]
- Ozaydin, F.; Yesilyurt, C.; Bugu, S.; Koashi, M. Deterministic preparation of W states via spin-photon interactions. Phys. Rev. A 2021, 103, 052421. [Google Scholar] [CrossRef]
- Oh, E.; Lai, X.; Wen, J.; Du, S. Distributed quantum computing with photons and atomic memories. arXiv 2022, arXiv:2207.02350. [Google Scholar] [CrossRef]
- Shuai, C.; Mao-Fa, F.; Jian-Bin, L.; Xin-Wen, W.; Xiao-Juan, Z. A scheme for implementing quantum game in cavity QED. Chin. Phys. B 2009, 18, 894–897. [Google Scholar] [CrossRef]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1995; p. xii, 351p. [Google Scholar]
- Hu, C.Y.; Young, A.; O’Brien, J.L.; Munro, W.J.; Rarity, J.G. Giant optical Faraday rotation induced by a single-electron spin in a quantum dot: Applications to entangling remote spins via a single photon. Phys. Rev. B 2008, 78, 085307. [Google Scholar] [CrossRef]
- Hu, C.Y.; Munro, W.J.; Rarity, J.G. Deterministic photon entangler using a charged quantum dot inside a microcavity. Phys. Rev. B 2008, 78, 125318. [Google Scholar] [CrossRef]
- Bartkowiak, M.; Miranowicz, A. Linear-optical implementations of the iSWAP and controlled NOT gates based on conventional detectors. J. Opt. Soc. Am. B 2010, 27, 2369–2377. [Google Scholar] [CrossRef]
- Nemoto, K.; Trupke, M.; Devitt, S.J.; Stephens, A.M.; Scharfenberger, B.; Buczak, K.; Nöbauer, T.; Everitt, M.S.; Schmiedmayer, J.; Munro, W.J. Photonic Architecture for Scalable Quantum Information Processing in Diamond. Phys. Rev. X 2014, 4, 031022. [Google Scholar] [CrossRef]
- Bodey, J.; Stockill, R.; Denning, E.; Gangloff, D.; Éthier-Majcher, G.; Jackson, D.; Clarke, E.; Hugues, M.; Gall, C.L.; Atatüre, M. Optical spin locking of a solid-state qubit. NPJ Quantum Inf. 2019, 5, 95. [Google Scholar] [CrossRef]
- Rong, X.; Geng, J.; Shi, F.; Liu, Y.; Xu, K.; Ma, W.; Kong, F.; Jiang, Z.; Wu, Y.; Du, J. Experimental fault-tolerant universal quantum gates with solid-state spins under ambient conditions. Nat. Commun. 2015, 6, 8748. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).