Modeling the Eu(III)-to-Cr(III) Energy Transfer Rates in Luminescent Bimetallic Complexes
Abstract
:1. Introduction
2. Theoretical Methodology
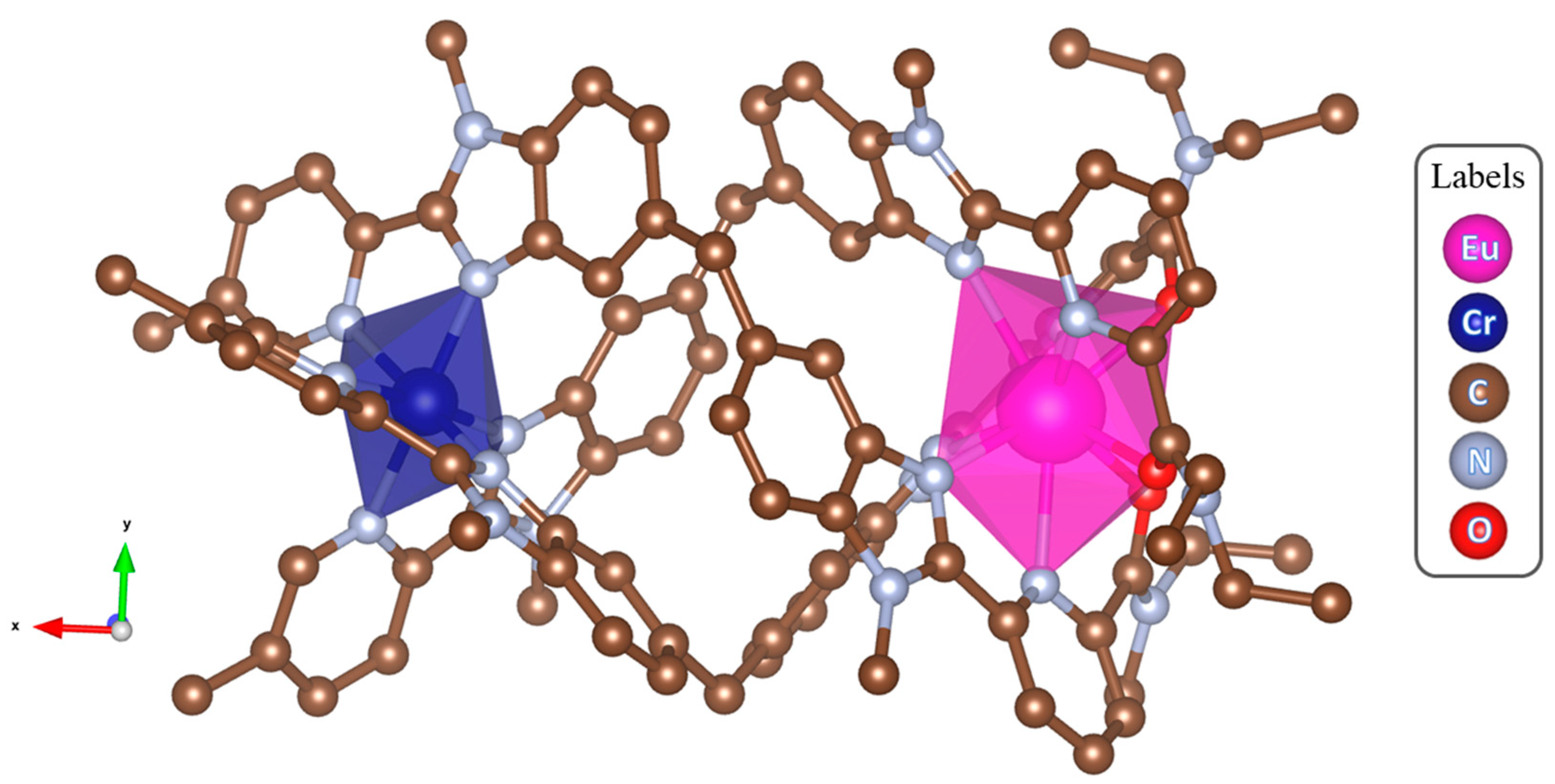
3. Selected Case
4. Results and Discussion
4.1. Multipolar Energy Transfer Rates
4.2. Exchange Energy Transfer Rates
4.3. Phonon-Assisted Energy Transfer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Bettencourt-Dias, A. Lanthanide-based emitting materials in light-emitting diodes. Dalton Trans. 2007, 22, 2229–2241. [Google Scholar] [CrossRef]
- Fang, M.; Neto, A.N.C.; Fu, L.; Ferreira, R.A.S.; deZeaBermudez, V.; Carlos, L.D. A Hybrid Materials Approach for Fabricating Efficient WLEDs Based on Di-Ureasils Doped with Carbon Dots and a Europium Complex. Adv. Mater. Technol. 2021, 7, 2100727. [Google Scholar] [CrossRef]
- Ou, X.; Qin, X.; Huang, B.; Zan, J.; Wu, Q.; Hong, Z.; Xie, L.; Bian, H.; Yi, Z.; Chen, X.; et al. High-resolution X-ray luminescence extension imaging. Nature 2021, 590, 410–415. [Google Scholar] [CrossRef]
- Neto, A.N.C.; Malta, O.L. Glowing nanocrystals enable 3D X-ray imaging. Nature 2021, 590, 396–397. [Google Scholar] [CrossRef]
- Piñol, R.; Zeler, J.; Brites, C.D.S.; Gu, Y.; Téllez, P.; Neto, A.N.C.; Da Silva, T.E.; Moreno-Loshuertos, R.; Fernandez-Silva, P.; Gallego, A.I.; et al. Real-Time Intracellular Temperature Imaging Using Lanthanide-Bearing Polymeric Micelles. Nano Lett. 2020, 20, 6466–6472. [Google Scholar] [CrossRef]
- Cotruvo, J.A. The Chemistry of Lanthanides in Biology: Recent Discoveries, Emerging Principles, and Technological Applications. ACS Central Sci. 2019, 5, 1496–1506. [Google Scholar] [CrossRef] [Green Version]
- Faulkner, S.; Blackburn, O.A. The Chemistry of Lanthanide MRI Contrast Agents. In The Chemistry of Molecular Imaging; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2014; pp. 179–197. [Google Scholar]
- Perrier, M.; Gallud, A.; Ayadi, A.; Kennouche, S.; Porredon, C.; Gary-Bobo, M.; Larionova, J.; Goze-Bac, C.; Zanca, M.; Garcia, M.; et al. Investigation of cyano-bridged coordination nanoparticles Gd3+/[Fe(CN)6]3−/d-mannitol as T1-weighted MRI contrast agents. Nanoscale 2015, 7, 11899–11903. [Google Scholar] [CrossRef]
- Ramalho, J.F.; Neto, A.N.C.; Carlos, L.D.; André, P.S.; Ferreira, R.A. Lanthanides for the new generation of optical sensing and Internet of Things. In Handbook on the Physics and Chemistry of Rare Earths; Bünzli, J.-C.G., Pecharsky, V.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 31–128. [Google Scholar] [CrossRef]
- Brites, C.D.S.; Millán, A.; Carlos, L.D. Lanthanides in Luminescent Thermometry. In Handbook on the Physics and Chemistry of Rare Earths; Bünzli, J.-C.G., Pecharsky, V.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 49, pp. 339–427. [Google Scholar]
- Salerno, E.V.; Neto, A.N.C.; Eliseeva, S.V.; Hernández-Rodríguez, M.A.; Lutter, J.C.; Lathion, T.; Kampf, J.W.; Petoud, S.; Carlos, L.D.; Pecoraro, V.L. Tunable Optical Molecular Thermometers Based on Metallacrowns. J. Am. Chem. Soc. 2022, 144, 18259–18271. [Google Scholar] [CrossRef]
- De Souza, K.M.N.; Silva, R.N.; Silva, J.A.B.; Brites, C.D.S.; Francis, B.; Ferreira, R.A.S.; Carlos, L.D.; Longo, R.L. Novel and High-Sensitive Primary and Self-Referencing Thermometers Based on the Excitation Spectra of Lanthanide Ions. Adv. Opt. Mater. 2022, 10, 2200770. [Google Scholar] [CrossRef]
- Sun, L.; Shi, L. Lanthanides: Near-Infrared Materials. In Encyclopedia of Inorganic and Bioinorganic Chemistry; John Wiley & Sons, Ltd.: Chichester, UK, 2012. [Google Scholar]
- Cho, U.; Chen, J.K. Lanthanide-Based Optical Probes of Biological Systems. Cell Chem. Biol. 2020, 27, 921–936. [Google Scholar] [CrossRef]
- Rocha, U.; Kumar, K.U.; Jacinto, C.; Villa, I.; Sanz-Rodríguez, F.; del Carmen Iglesias de la Cruz, M.; Juarranz, A.; Carrasco, E.; van Veggel, F.C.J.M.; Bovero, E.; et al. Neodymium-Doped LaF3Nanoparticles for Fluorescence Bioimaging in the Second Biological Window. Small 2013, 10, 1141–1154. [Google Scholar] [CrossRef]
- Sábio, R.M.; Santagneli, S.H.; Gressier, M.; Caiut, J.M.A.; Pazin, W.M.; Leite, I.S.; Inada, N.M.; da Silva, R.R.; Ribeiro, S.J.L.; Menu, M.-J. Luminescent nanohybrids based on silica and silylated Ru(II)—Yb(III) heterobinuclear complex: New tools for biological media analysis. Nanotechnology 2019, 31, 085709. [Google Scholar] [CrossRef]
- Ward, M.D. Transition-metal sensitised near-infrared luminescence from lanthanides in d–f heteronuclear arrays. Coord. Chem. Rev. 2007, 251, 1663–1677. [Google Scholar] [CrossRef]
- Chen, F.-F.; Chen, Z.-Q.; Bian, Z.-Q.; Huang, C.-H. Sensitized luminescence from lanthanides in d–f bimetallic complexes. Coord. Chem. Rev. 2010, 254, 991–1010. [Google Scholar] [CrossRef]
- Back, M.; Ueda, J.; Nambu, H.; Fujita, M.; Yamamoto, A.; Yoshida, H.; Tanaka, H.; Brik, M.G.; Tanabe, S. Boltzmann Thermometry in Cr3+ -Doped Ga2 O 3 Polymorphs: The Structure Matters! Adv. Opt. Mater. 2021, 9, 2100033. [Google Scholar] [CrossRef]
- Malysa, B.; Meijerink, A.; Jüstel, T. Temperature dependent Cr3+ photoluminescence in garnets of the type X3Sc2Ga3O12 (X = Lu, Y, Gd, La). J. Lumin. 2018, 202, 523–531. [Google Scholar] [CrossRef]
- Back, M.; Ueda, J.; Brik, M.G.; Tanabe, S. Pushing the Limit of Boltzmann Distribution in Cr3+-Doped CaHfO3 for Cryogenic Thermometry. ACS Appl. Mater. Interfaces 2020, 12, 38325–38332. [Google Scholar] [CrossRef]
- Back, M.; Ueda, J.; Hua, H.; Tanabe, S. Predicting the Optical Pressure Sensitivity of 2E→4A2Spin-Flip Transition in Cr3+-Doped Crystals. Chem. Mater. 2021, 33, 3379–3385. [Google Scholar] [CrossRef]
- Shen, Y.; Grinberg, M.; Barzowska, J.; Bray, K.; Hanuza, J.; Dereń, P. The effect of pressure on luminescence properties of Cr3+ ions in LiSc(WO4)2 crystals—Part I: Pressure dependent emission lineshape. J. Lumin. 2006, 116, 1–14. [Google Scholar] [CrossRef]
- Grinberg, M.; Barzowska, J.; Shen, Y.; Bray, K.; Hanuza, J.; Dereń, P. The effect of pressure on luminescence properties of Cr3+ ions in LiSc(WO4)2 crystals—Part II: Pressure- and temperature-dependent luminescence kinetics. J. Lumin. 2006, 116, 15–27. [Google Scholar] [CrossRef]
- Szymczak, M.; Woźny, P.; Runowski, M.; Pieprz, M.; Lavín, V.; Marciniak, L. Temperature invariant ratiometric luminescence manometer based on Cr3+ ions emission. Chem. Eng. J. 2023, 453, 139632. [Google Scholar] [CrossRef]
- Ward, M.D. Mechanisms of sensitization of lanthanide(III)-based luminescence in transition metal/lanthanide and anthracene/lanthanide dyads. Coord. Chem. Rev. 2010, 254, 2634–2642. [Google Scholar] [CrossRef]
- Lazarides, T.; Davies, G.M.; Adams, H.; Sabatini, C.; Barigelletti, F.; Barbieri, A.; Pope, S.J.A.; Faulkner, S.; Ward, M.D. Ligand-field excited states of hexacyanochromate and hexacyanocobaltate as sensitisers for near-infrared luminescence from Nd(III) and Yb(III) in cyanide-bridged d–f assemblies. Photochem. Photobiol. Sci. 2007, 6, 1152–1157. [Google Scholar] [CrossRef]
- Chen, F.-F.; Wei, H.-B.; Bian, Z.-Q.; Liu, Z.-W.; Ma, E.; Chen, Z.-N.; Huang, C.-H. Sensitized Near-Infrared Emission from IrIII-LnIII (Ln = Nd, Yb, Er) Bimetallic Complexes with a (N∧O)(N∧O) Bridging Ligand. Organometallics 2014, 33, 3275–3282. [Google Scholar] [CrossRef]
- Crowston, B.J.; Shipp, J.D.; Chekulaev, D.; McKenzie, L.K.; Jones, C.; Weinstein, J.A.; Meijer, A.J.H.; Bryant, H.E.; Natrajan, L.; Woodward, A.; et al. Heteronuclear d–d and d–f Ru(II)/M complexes [M = Gd(III), Yb(III), Nd(III), Zn(II) or Mn(II)] of ligands combining phenanthroline and aminocarboxylate binding sites: Combined relaxivity, cell imaging and photophysical studies. Dalton Trans. 2019, 48, 6132–6152. [Google Scholar] [CrossRef] [Green Version]
- Singaravadivel, S.; Velayudham, M.; Babu, E.; Mareeswaran, P.M.; Lu, K.-L.; Rajagopal, S. Sensitized Near-Infrared Luminescence From NdIII, YbIII and ErIII Complexes by Energy-Transfer From Ruthenium 1,3-Bis([1,10]Phenanthroline-[5,6-d]-Imidazol-2-yl)Benzene. J. Fluoresc. 2013, 23, 1167–1172. [Google Scholar] [CrossRef]
- Forster, T. Energiewanderung und Fluoreszenz. Naturwissenschaften 1946, 33, 166–175. [Google Scholar] [CrossRef]
- Dexter, D.L. A Theory of Sensitized Luminescence in Solids. J. Chem. Phys. 1953, 21, 836–850. [Google Scholar] [CrossRef]
- Lazarides, T.; Sykes, D.; Faulkner, S.; Barbieri, A.; Ward, M.D. On the Mechanism of d-f Energy Transfer in RuII/LnIIIand OsII/LnIIIDyads: Dexter-Type Energy Transfer Over a Distance of 20 Å. Chem.–A Eur. J. 2008, 14, 9389–9399. [Google Scholar] [CrossRef]
- Carneiro Neto, A.N.; Teotonio, E.E.S.; de Sá, G.F.; Brito, H.F.; Legendziewicz, J.; Carlos, L.D.; Felinto, M.C.F.C.; Gawryszewska, P.; Moura, R.T., Jr.; Longo, R.L.; et al. Modeling Intramolecular Energy Transfer in Lanthanide Chelates: A Critical Review and Recent Advances. In Handbook on the Physics and Chemistry of Rare Earths; Bünzli, J.-C.G., Pecharsky, V.K., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 56, pp. 55–162. ISBN 9780444642998. [Google Scholar]
- Shyichuk, A.; Câmara, S.S.; Weber, I.T.; Neto, A.N.C.; Nunes, L.A.; Lis, S.; Longo, R.L.; Malta, O.L. Energy transfer upconversion dynamics in YVO4:Yb3+, Er3+. J. Lumin. 2016, 170, 560–570. [Google Scholar] [CrossRef]
- Malta, O. Mechanisms of non-radiative energy transfer involving lanthanide ions revisited. J. Non-Cryst. Solids 2008, 354, 4770–4776. [Google Scholar] [CrossRef]
- Carneiro Neto, A.N.; Moura, R.T.; Shyichuk, A.; Paterlini, V.; Piccinelli, F.; Bettinelli, M.; Malta, O.L. Theoretical and Experimental Investigation of the Tb3+ → Eu3+ Energy Transfer Mechanisms in Cubic A3Tb0.90Eu0.10(PO4)3 (A = Sr, Ba) Materials. J. Phys. Chem. C 2020, 124, 10105–10116. [Google Scholar] [CrossRef]
- Trannoy, V.; Neto, A.N.C.; Brites, C.D.S.; Carlos, L.D.; Serier-Brault, H. Engineering of Mixed Eu3+/Tb3+ Metal-Organic Frameworks Luminescent Thermometers with Tunable Sensitivity. Adv. Opt. Mater. 2021, 9, 2001938. [Google Scholar] [CrossRef]
- Malta, O. Ligand—Rare-earth ion energy transfer in coordination compounds. A theoretical approach. J. Lumin. 1997, 71, 229–236. [Google Scholar] [CrossRef]
- E Silva, F.R.; Malta, O. Calculation of the ligand–lanthanide ion energy transfer rate in coordination compounds: Contributions of exchange interactions. J. Alloys Compd. 1997, 250, 427–430. [Google Scholar] [CrossRef]
- Neto, A.N.C.; Moura, R.T.; Malta, O.L. On the mechanisms of non-radiative energy transfer between lanthanide ions: Centrosymmetric systems. J. Lumin. 2019, 210, 342–347. [Google Scholar] [CrossRef]
- Gomez, G.E.; Marin, R.; Neto, A.N.C.; Botas, A.M.P.; Ovens, J.; Kitos, A.A.; Bernini, M.C.; Carlos, L.D.; Soler-Illia, G.J.A.A.; Murugesu, M. Tunable energy transfer process in heterometallic MOFs materials based on 2,6-naphtalenedicarboxylate: Solid-state lighting and near-infrared luminescence thermometry. Chem. Mater. 2020, 32, 7458–7468. [Google Scholar] [CrossRef]
- Neto, A.N.C.; Mamontova, E.; Botas, A.M.P.; Brites, C.D.S.; Ferreira, R.A.S.; Rouquette, J.; Guari, Y.; Larionova, J.; Long, J.; Carlos, L.D. Rationalizing the Thermal Response of Dual-Center Molecular Thermometers: The Example of an Eu/Tb Coordination Complex. Adv. Opt. Mater. 2021, 10, 2101870. [Google Scholar] [CrossRef]
- Lyubov, D.M.; Neto, A.N.C.; Fayoumi, A.; Lyssenko, K.A.; Korshunov, V.M.; Taydakov, I.V.; Salles, F.; Guari, Y.; Larionova, J.; Carlos, L.D.; et al. Employing three-blade propeller lanthanide complexes as molecular luminescent thermometers: Study of temperature sensing through a concerted experimental/theory approach. J. Mater. Chem. C 2022, 10, 7176–7188. [Google Scholar] [CrossRef]
- Ramalho, J.F.C.B.; Dias, L.M.S.; Fu, L.; Botas, A.M.P.; Carlos, L.D.; Neto, A.N.C.; André, P.S.; Ferreira, R.A.S. Customized Luminescent Multiplexed Quick-Response Codes as Reliable Temperature Mobile Optical Sensors for eHealth and Internet of Things. Adv. Photonics Res. 2021, 3, 2100206. [Google Scholar] [CrossRef]
- Cantuel, M.; Bernardinelli, G.; Imbert, D.; Bünzli, J.-C.G.; Hopfgartner, G.; Piguet, C. A kinetically inert and optically active CrIII partner in thermodynamically self-assembled heterodimetallic non-covalent d–f podates. J. Chem. Soc. Dalton Trans. 2002, 9, 1929–1940. [Google Scholar] [CrossRef] [Green Version]
- Carnall, W.T.; Crosswhite, H.; Crosswhite, H.M. Energy Level Structure and Transition Probabilities in the Spectra of the Trivalent Lanthanides in LaF₃; Argonne: Lemont, IL, USA, 1978. [Google Scholar]
- Edvardsson, S.; Klintenberg, M. Role of the electrostatic model in calculating rare-earth crystal-field parameters. J. Alloys Compd. 1998, 275, 230–233. [Google Scholar] [CrossRef]
- Silver, B.L. Irreducible Tensor Methods; ACADEMIC PRESS, INC.: London, UK, 1976; ISBN 0-12-643650-9. [Google Scholar]
- Judd, B.R. Operator Techniques in Atomic Spectroscopy; McGraw-Hill Book Company: New York, NY, USA, 1998; ISBN 9780691604275. [Google Scholar]
- Neto, A.N.C.; Moura, R.T., Jr. Overlap integrals and excitation energies calculations in trivalent lanthanides 4f orbitals in pairs Ln-L (L = Ln, N, O, F, P, S, Cl, Se, Br, and I). Chem. Phys. Lett. 2020, 757, 137884. [Google Scholar] [CrossRef]
- Moura, R.T., Jr.; Neto, A.N.C.; Aguiar, E.C.; Santos-Jr., C.V.; de Lima, E.M.; Faustino, W.M.; Teotonio, E.E.; Brito, H.F.; Felinto, M.C.; Ferreira, R.A.; et al. (INVITED) JOYSpectra: A web platform for luminescence of lanthanides. Opt. Mater. X 2021, 11, 100080. [Google Scholar] [CrossRef]
- Carneiro Neto, A.N.; Moura, R.T., Jr.; Coelho, J.A.A.; Silva-Junior, M.E.; Costa, J.L.; Malta, O.L.; Longo, R.L. A Tutorial Review on the Nonradiative Energy Transfer Rates between Lanthanide Ions. Chin. J. Lumin. 2022, 43, 20. [Google Scholar] [CrossRef]
- Miyakawa, T.; Dexter, D.L. Phonon Sidebands, Multiphonon Relaxation of Excited States, and Phonon-Assisted Energy Transfer between Ions in Solids. Phys. Rev. B 1970, 1, 2961–2969. [Google Scholar] [CrossRef]
- Golesorkhi, B.; Taarit, I.; Bolvin, H.; Nozary, H.; Jiménez, J.-R.; Besnard, C.; Guénée, L.; Fürstenberg, A.; Piguet, C. Molecular light-upconversion: We have had a problem! When excited state absorption (ESA) overcomes energy transfer upconversion (ETU) in Cr(III)/Er(III) complexes. Dalton Trans. 2021, 50, 7955–7968. [Google Scholar] [CrossRef]
- Rohatgi, A. WebPlotDigitizer 2021. Available online: https://automeris.io/WebPlotDigitizer/ (accessed on 6 September 2022).
- Judd, B.R. Optical Absorption Intensities of Rare-Earth Ions. Phys. Rev. 1962, 127, 750–761. [Google Scholar] [CrossRef]
- Ofelt, G.S. Intensities of Crystal Spectra of Rare-Earth Ions. J. Chem. Phys. 1962, 37, 511–520. [Google Scholar] [CrossRef]
- Smentek, L.; Ke¸dziorski, A. Efficiency of the energy transfer in lanthanide-organic chelates; spectral overlap integral. J. Lumin. 2010, 130, 1154–1159. [Google Scholar] [CrossRef]
- Milos, M.; Kairouani, S.; Rabaste, S.; Hauser, A. Energy migration within the 2E state of Cr3+. Coord. Chem. Rev. 2008, 252, 2540–2551. [Google Scholar] [CrossRef] [Green Version]
- Dexpert-Ghys, J.; Auzel, F. Existence of cooperative absorption lines for Yb–(OH,OD) pairs: Absolute oscillator strengths. J. Chem. Phys. 1984, 80, 4003–4012. [Google Scholar] [CrossRef]
- Donega, C.D.M.; Meijerink, A.; Blasse, G. Vibronic transition probabilities in the excitation spectra of the Pr3+ion. J. Physics: Condens. Matter 1992, 4, 8889–8902. [Google Scholar] [CrossRef]
- Yamada, N.; Shionoya, S.; Kushida, T. Phonon-Assisted Energy Transfer between Trivalent Rare Earth Ions. J. Phys. Soc. Jpn. 1972, 32, 1577–1586. [Google Scholar] [CrossRef]
- Fonger, W.; Struck, C. Unified model of energy transfer for arbitrary Franck-Condon offset and temperature. J. Lumin. 1978, 17, 241–261. [Google Scholar] [CrossRef]
- Auzel, F.; De Sa’, G.; de Azevedo, W. An example of concentration sensitive electron-phonon coupling in {(C4H9)4N}3 EuxY1−x(NCS)6 and a new hypothesis for self-quenching. J. Lumin. 1980, 21, 187–192. [Google Scholar] [CrossRef]
- Blasse, G. Luminescence of inorganic solids: From isolated centres to concentrated systems. Prog. Solid State Chem. 1988, 18, 79–171. [Google Scholar] [CrossRef]
- Nie, W.; Boulon, G.; Monteil, A. Vibronic levels and zero-phonon lines of Cr3+—doped yttrium aluminium garnet (Y3Al5O12). J. Phys. 1989, 50, 3309–3315. [Google Scholar] [CrossRef]
- Silverstein, R.M.; Webster, F.X.; Kieml, D.J. Spectrometric Identification of Organic Compounds, 7th ed.; John Wiley & Sons: New York, NY, USA, 2005; ISBN 0-471-39362-2. [Google Scholar]
- Reinhard, C.; Güdel, H.U. High-Resolution Optical Spectroscopy of Na3[Ln(dpa)3]·13H2O with Ln = Er3+, Tm3+, Yb3+. Inorg. Chem. 2002, 41, 1048–1055. [Google Scholar] [CrossRef]
- Costa, I.F.; Blois, L.; Carneiro Neto, A.N.; Teotonio, E.E.S.; Brito, H.F.; Carlos, L.D.; Felinto, M.C.F.C.; Moura, R.T., Jr.; Longo, R.L.; Faustino, W.M.; et al. Reinterpreting the Judd–Ofelt Parameters Based on Recent Theoretical Advances. In Luminescent Materials: Fundamentals and Applications; Brik, M.G., Srivastava, A.M., Eds.; De Gruyter: Berlin, Germany, 2023; pp. 19–62. [Google Scholar]




| Pathway | Donor | Aceptor | (cm−1) | (erg−1) | (s−1) | (s−1) | (s−1) |
|---|---|---|---|---|---|---|---|
| 1 | 5D0 → 7F2 | 2E ← 4A2 | 2748 | 1 × 10−11 | 1 × 10−22 | 3 × 10−20 | 3 × 10−20 |
| 2 | 5D0 → 7F4 | 2E ← 4A2 | 982 | 7 × 109 | 4 × 10−2 | 3 × 10−3 | 4 × 10−2 |
| 3 | 5D0 → 7F6 | 2E ← 4A2 | −1032 | 2 × 107 | 3 × 10−5 | 5 × 10−10 | 3 × 10−5 |
| 4 | 5D0 → 7F2 | 2T1 ← 4A2 | 2026 | 2 × 106 | 7 × 10−6 | 3 × 10−3 | 3 × 10−3 |
| 5 | 5D0 → 7F4 | 2T1 ← 4A2 | 260 | 4 × 1012 | 20 | 1 | 21 |
| 6 | 5D0 → 7F6 | 2T1 ← 4A2 | −1754 | 2 × 104 | 1 × 10−8 | 2 × 10−13 | 1 × 10−8 |
| 21 | |||||||
| Pathway | Donor | (cm−1) | (erg−1) | (s−1) | (s−1) | (s−1) |
|---|---|---|---|---|---|---|
| 1 | 5D0 → 7F2 | 2239 | 4 × 1010 | 4 × 10−1 | 98 | 98 |
| 2 | 5D0 → 7F4 | 470 | 2 × 1012 | 11 | 8 × 10−1 | 11 |
| 3 | 5D0 → 7F6 | −1541 | 2 × 108 | 2 × 10−4 | 4 × 10−9 | 2 × 10−4 |
| 109 | ||||||
| 0.01 | 0.85 | 4.1 | 3.4 | 927.6 | 931.0 |
| 0.01 | 0.90 | 4.3 | 3.6 | 987.9 | 991.5 |
| 0.01 | 0.95 | 4.6 | 3.8 | 1046.8 | 1050.6 |
| 0.01 | 1.00 | 4.8 | 4.0 | 1101.2 | 1105.2 |
| 0.04 | 0.85 | 4.2 | 3.5 | 964.1 | 967.6 |
| 0.04 | 0.90 | 4.5 | 3.8 | 1023.0 | 1026.8 |
| 0.04 | 0.95 | 4.7 | 4.0 | 1079.4 | 1083.4 |
| 0.04 | 1.00 | 4.9 | 4.2 | 1133.0 | 1137.2 |
| 0.08 | 0.85 | 4.4 | 3.7 | 1011.4 | 1015.1 |
| 0.08 | 0.90 | 4.7 | 3.9 | 1068.3 | 1072.2 |
| 0.08 | 0.95 | 4.9 | 4.1 | 1122.5 | 1126.6 |
| 0.08 | 1.00 | 5.1 | 4.3 | 1174.0 | 1178.3 |
| 0.10 | 0.85 | 4.5 | 3.8 | 1034.5 | 1038.3 |
| 0.10 | 0.90 | 4.8 | 4.0 | 1090.3 | 1094.3 |
| 0.10 | 0.95 | 5.0 | 4.2 | 1143.4 | 1147.6 |
| 0.10 | 1.00 | 5.2 | 4.4 | 1193.7 | 1198.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coelho, J.A.A.; Moura, R.T., Jr.; Longo, R.L.; Malta, O.L.; Carneiro Neto, A.N. Modeling the Eu(III)-to-Cr(III) Energy Transfer Rates in Luminescent Bimetallic Complexes. Inorganics 2023, 11, 38. https://doi.org/10.3390/inorganics11010038
Coelho JAA, Moura RT Jr., Longo RL, Malta OL, Carneiro Neto AN. Modeling the Eu(III)-to-Cr(III) Energy Transfer Rates in Luminescent Bimetallic Complexes. Inorganics. 2023; 11(1):38. https://doi.org/10.3390/inorganics11010038
Chicago/Turabian StyleCoelho, Jorge A. A., Renaldo T. Moura, Jr., Ricardo L. Longo, Oscar L. Malta, and Albano N. Carneiro Neto. 2023. "Modeling the Eu(III)-to-Cr(III) Energy Transfer Rates in Luminescent Bimetallic Complexes" Inorganics 11, no. 1: 38. https://doi.org/10.3390/inorganics11010038
APA StyleCoelho, J. A. A., Moura, R. T., Jr., Longo, R. L., Malta, O. L., & Carneiro Neto, A. N. (2023). Modeling the Eu(III)-to-Cr(III) Energy Transfer Rates in Luminescent Bimetallic Complexes. Inorganics, 11(1), 38. https://doi.org/10.3390/inorganics11010038








