Switching the Local Symmetry from D5h to D4h for Single-Molecule Magnets by Non-Coordinating Solvents
Abstract
:1. Introduction
2. Results and Discussion
2.1. Synthesis of 1–2
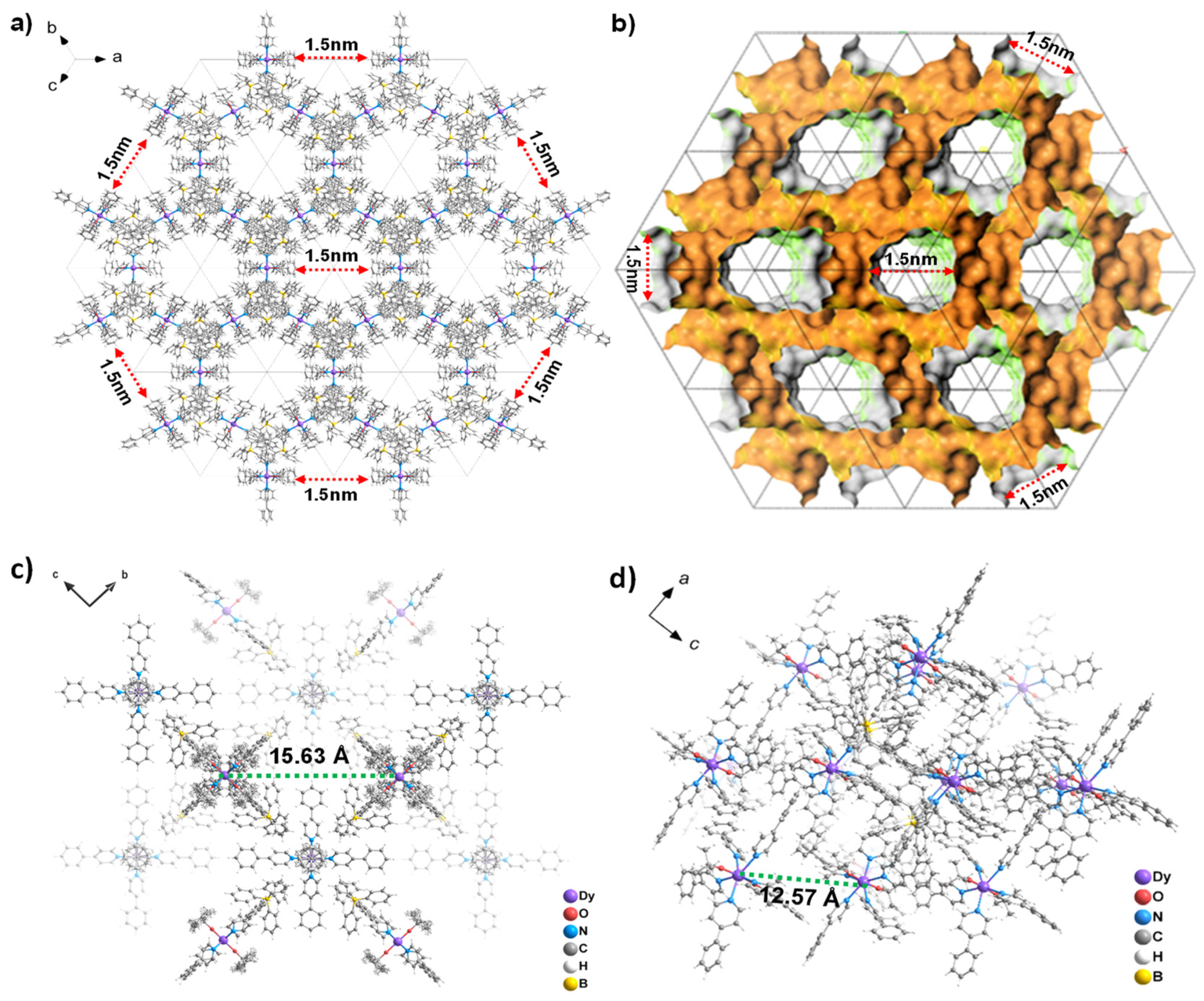
2.2. Single Crystal Structure
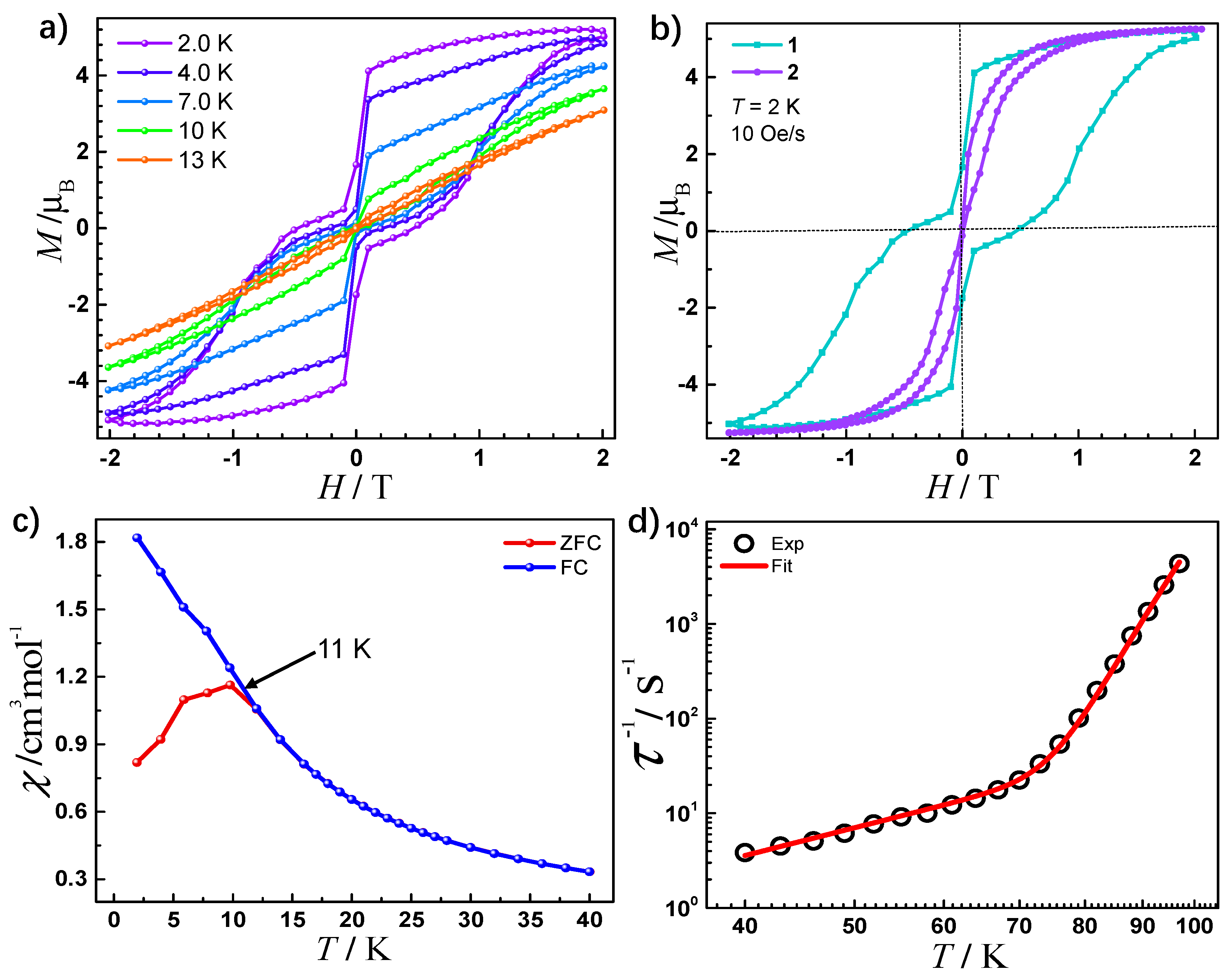
2.3. Magnetic Properties
2.4. Ab initio Calculation
3. Materials and Methods
3.1. Synthesis
3.2. X-ray Crystallography Data
3.3. Magnetic Properties
3.4. Electronic Structure Calculations
3.5. DFT Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular Magnetic Hysteresis at 60 Kelvin in Dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Jin, P.-B.; Zhai, Y.-Q.; Yu, K.-X.; Winpenny, R.E.P.; Zheng, Y.-Z. Dysprosiacarboranes as Organometallic Single-Molecule Magnets. Angew. Chem. Int. Ed. 2020, 59, 9350–9354. [Google Scholar] [CrossRef]
- Canaj, A.B.; Dey, S.; Martí, E.R.; Wilson, C.; Rajaraman, G.; Murrie, M. Insight into D6h Symmetry: Targeting Strong Axiality in Stable Dysprosium(III) Hexagonal Bipyramidal Single-Ion Magnets. Angew. Chem. Int. Ed. 2019, 58, 14146–14151. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Li, Q.-W.; Wu, S.-G.; Chen, Y.-C.; Wan, R.-C.; Huang, G.-Z.; Liu, Y.; Liu, J.-L.; Reta, D.; Giansiracusa, M.J.; et al. Opening Magnetic Hysteresis by Axial Ferromagnetic Coupling: From Mono-Decker to Double-Decker Metallacrown. Angew. Chem. Int. Ed. 2021, 60, 5299–5306. [Google Scholar] [CrossRef]
- Ding, X.-L.; Zhai, Y.-Q.; Han, T.; Chen, W.-P.; Ding, Y.-S.; Zheng, Y.-Z. A Local D4h Symmetric Dysprosium(III) Single-Molecule Magnet with an Energy Barrier Exceeding 2000 K. Chem. Eur. J. 2021, 27, 2623–2627. [Google Scholar] [CrossRef]
- Pedersen, K.S.; Ariciu, A.M.; McAdams, S.; Weihe, H.; Bendix, J.; Tuna, F.; Piligkos, S. Toward Molecular 4f Single-Ion Magnet Qubits. J. Am. Chem. Soc. 2016, 138, 5801–5804. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, B.-W.; Bian, Y.; Gao, S.; Jiang, J. Single-Molecule Magnetism of Tetrapyrrole Lanthanide Compounds with Sandwich Multiple-Decker Structures. Coord. Chem. Rev. 2016, 306, 195–216. [Google Scholar] [CrossRef]
- Gould, C.A.; McClain, K.R.; Yu, J.M.; Groshens, T.J.; Furche, F.; Harvey, B.G.; Long, J.R. Synthesis and Magnetism of Neutral, Linear Metallocene Complexes of Terbium (II) and Dysprosium (II). J. Am. Chem. Soc. 2019, 141, 12967–12973. [Google Scholar] [CrossRef] [PubMed]
- Moutet, J.; Schleinitz, J.; Droitte, L.L.; Tricoire, M.; Pointillart, F.; Gendron, F.; Simler, T.; Clavaguéra, C.; Guennic, B.L.; Cador, O.; et al. Bis-Cyclooctatetraenyl Thulium (II): Highly Reducing Lanthanide Sandwich Single-Molecule Magnets. Angew. Chem. Int. Ed. 2021, 133, 6107–6111. [Google Scholar] [CrossRef]
- Meihaus, K.R.; Long, J.R. Magnetic Blocking at 10 K and a Dipolar-Mediated Avalanche in Salts of the Bis(η8-Cyclooctatetraenide) Complex [Er(COT)2]−. J. Am. Chem. Soc. 2013, 135, 17952–17957. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, Y.-C.; Jia, J.-H.; Liu, J.-L.; Vieru, V.; Ungur, L.; Chibotaru, L.F.; Lan, Y.; Wernsdorfer, W.; Gao, S.; et al. A Stable Pentagonal Bipyramidal Dy (III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K. J. Am. Chem. Soc. 2016, 138, 5441–5450. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Liu, J.-L.; Ungur, L.; Liu, J.; Li, Q.-W.; Wang, L.-F.; Ni, Z.-P.; Chibotaru, L.F.; Chen, X.-M.; Tong, M.-L. Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy (III) Single-Ion Magnets. J. Am. Chem. Soc. 2016, 138, 2829–2837. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.-X.; Kragskow, J.G.C.; Ding, Y.-S.; Zhai, Y.-Q.; Reta, D.; Chilton, N.F.; Zheng, Y.-Z. Enhancing Magnetic Hysteresis in Single-Molecule Magnets by Ligand Functionalization. Chem 2020, 6, 1777–1793. [Google Scholar] [CrossRef]
- Ding, Y.-S.; Chilton, N.F.; Winpenny, R.E.P.; Zheng, Y.-Z. On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium (III) Single-Molecule Magnet. Angew. Chem. Int. Ed. 2016, 55, 16071–16074. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. Magnetic Hysteresis up to 80 Kelvin in a Dysprosium Metallocene Single-Molecule Magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef] [Green Version]
- Shao, L.; Hua, B.; Hu, X.-Q.; Stalla, D.; Kelley, S.P.; Atwood, J.L. Construction of Polymeric Metal–Organic Nanocapsule Networks via Supramolecular Coordination-Driven Self-Assembly. J. Am. Chem. Soc. 2020, 142, 7270–7275. [Google Scholar] [CrossRef]
- Forgan, R.S. Modulated Self-Assembly of Metal–Organic Frameworks. Chem. Sci. 2020, 11, 4546–4562. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, Y.-J.; Hu, J.-X.; Han, S.-D.; Pan, J.; Li, J.-H.; Wang, G.-M. Manipulating on/off Single-Molecule Magnet Behavior in a Dy (III)-Based Photochromic Complex. J. Am. Chem. Soc. 2020, 142, 2682–2689. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Zheng, Y.-Z.; Lin, W.-Q.; Ungur, L.; Wernsdorfer, W.; Chibotaru, L.F.; Tong, M.-L. Switching the Anisotropy Barrier of a Single-Ion Magnet by Symmetry Change from Quasi-D5h to Quasi-Oh. Chem. Sci. 2013, 4, 3310–3316. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Tong, M.-L. Symmetry Strategies for High Performance Lanthanide-Based Single-Molecule Magnets. Chem. Soc. Rev. 2018, 47, 2431–2453. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, L.; Wang, C.; Xue, S.; Lin, S.Y.; Tang, J. Equatorially Coordinated Lanthanide Single Ion Magnets. J. Am. Chem. Soc. 2014, 136, 4484–4487. [Google Scholar] [CrossRef]
- Wu, S.-G.; Ruan, Z.-Y.; Huang, G.-Z.; Wernsdorfer, W.; Chen, X.-M.; Tong, M.-L. Field-Induced Oscillation of Magnetization Blocking Barrier in a Holmium Metallacrown Single-Molecule Magnet. Angew. Chem. Int. Ed. 2021, 7, 982–992. [Google Scholar]
- Li, S.; Wang, Z.-Y.; Gao, G.-G.; Li, B.; Luo, P.; Kong, Y.-J.; Liu, H.; Zang, S.-Q. Smart Transformation of a Polyhedral Oligomeric Silsesquioxane Shell Controlled by Thiolate Silver (I) Nanocluster Core in Cluster@ Clusters Dendrimers. Angew. Chem. Int. Ed. 2018, 57, 12775–12779. [Google Scholar] [CrossRef] [PubMed]
- Miao, L.-P.; Qi, Q.; Zhang, W. Solvent-Induced Structural Transformation and Luminescence Response in a Dumbbell-Shaped Crystalline Molecular Rotor. Inorg. Chem. 2021, 60, 3149–3155. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.-L.; Yao, L.-Y.; Yam, V.W.-W. Concentration and Solvation-Induced Reversible Structural Transformation and Assembly of Polynuclear Gold (I) Sulfido Complexes. J. Am. Chem. Soc. 2020, 142, 11560–11568. [Google Scholar] [CrossRef]
- Alvarez, S. Distortion Pathways Of Transition Metal Coordination Polyhedra Induced By Chelating Topology. Chem. Rev. 2015, 115, 13447–13483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Canaj, A.B.; Dey, S.; Wilson, C.; Céspedes, O.; Rajaraman, G.; Murrie, M. Engineering Macrocyclic High Performance Pentagonal Bipyramidal Dy(III) Single-Ion Magnets. Chem. Commun. 2020, 56, 12037–12040. [Google Scholar] [CrossRef] [PubMed]
- Aravena, D.; Ruiz, E. Spin Dynamics in Single-Molecule Magnets and Molecular Qubits. Dalton Trans. 2020, 49, 9916–9928. [Google Scholar] [CrossRef]
- Galván, I.F.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef] [PubMed]
- Roos, B.O.; Lindh, R.; Malmqvist, P.Å.; Veryazov, V.; Widmark, P.O. Main Group Atoms and Dimers Studied with a New Relativistic ANO Basis Set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Malmqvist, P.A.; Roos, B.O.; Schimmelpfennig, B. The restricted active space (RAS) state interaction approach with spin–orbit coupling. Chem. Phys. Lett. 2002, 357, 230–240. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.Å.; Veryazov, V.; Widmark, P.O. New relativistic ANO basis sets for actinide atoms. Chem. Phys. Lett. 2005, 409, 295–299. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868, Erratum in 1997, 78, 1396. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Lanza, G.; Fragalà, I.L. A relativistic effective core potential ab initio study of molecular geometries and vibrational frequencies of lanthanide trihalides LnX3 (Ln = Gd, Lu; X = F, Cl). Chem. Phys. Lett. 1996, 255, 341–346. [Google Scholar] [CrossRef]
- Aebersold, L.E.; Yuwono, S.H.; Schoendorff, G.; Wilson, A.K. Efficacy of Density Functionals and Relativistic Effective Core Potentials for Lanthanide-Containing Species: The Ln54 Molecule Set. J. Chem. Theory Comput. 2017, 13, 2831–2839. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.-L.; Luo, Q.-C.; Zhai, Y.-Q.; Zhang, Q.; Tian, L.; Zhang, X.; Ke, C.; Zhang, X.-F.; Lv, Y.; Zheng, Y.-Z. Switching the Local Symmetry from D5h to D4h for Single-Molecule Magnets by Non-Coordinating Solvents. Inorganics 2021, 9, 64. https://doi.org/10.3390/inorganics9080064
Ding X-L, Luo Q-C, Zhai Y-Q, Zhang Q, Tian L, Zhang X, Ke C, Zhang X-F, Lv Y, Zheng Y-Z. Switching the Local Symmetry from D5h to D4h for Single-Molecule Magnets by Non-Coordinating Solvents. Inorganics. 2021; 9(8):64. https://doi.org/10.3390/inorganics9080064
Chicago/Turabian StyleDing, Xia-Li, Qian-Cheng Luo, Yuan-Qi Zhai, Qian Zhang, Lei Tian, Xinliang Zhang, Chao Ke, Xu-Feng Zhang, Yi Lv, and Yan-Zhen Zheng. 2021. "Switching the Local Symmetry from D5h to D4h for Single-Molecule Magnets by Non-Coordinating Solvents" Inorganics 9, no. 8: 64. https://doi.org/10.3390/inorganics9080064
APA StyleDing, X.-L., Luo, Q.-C., Zhai, Y.-Q., Zhang, Q., Tian, L., Zhang, X., Ke, C., Zhang, X.-F., Lv, Y., & Zheng, Y.-Z. (2021). Switching the Local Symmetry from D5h to D4h for Single-Molecule Magnets by Non-Coordinating Solvents. Inorganics, 9(8), 64. https://doi.org/10.3390/inorganics9080064







