An Integrated Model of Heat Transfer in Meat Products during Multistage Operations
Abstract
:1. Introduction
2. Modelling of Heat Transfer during the Processing of Smoked–Salted Loin Pork
2.1. Process Description and Model Formulation
2.2. Heat Transfer Equations
2.2.1. Governing Equation
2.2.2. Boundary Condition
2.2.3. Initial Condition and Thermo-Physical Properties
2.3. Model Solution
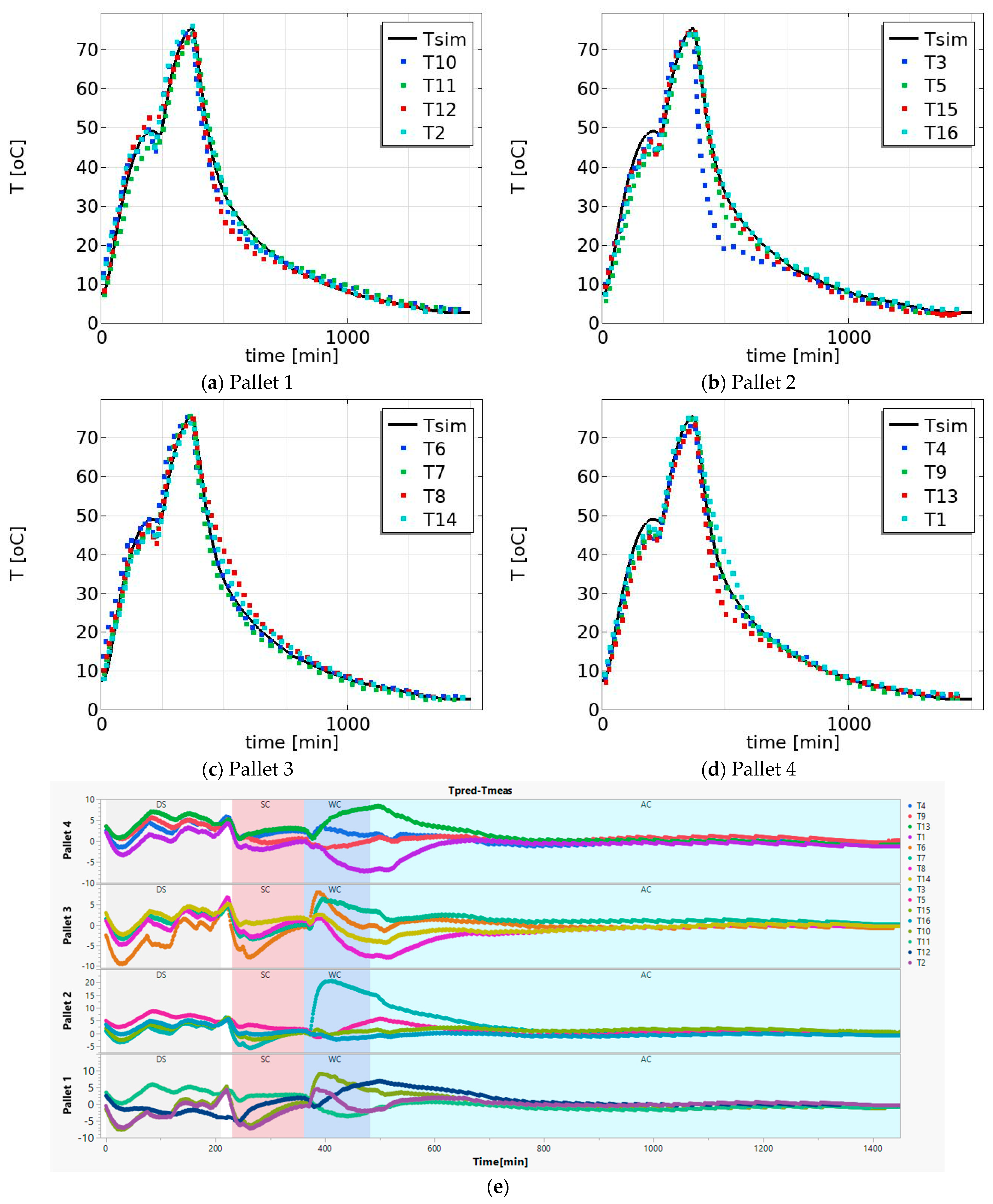
2.4. Experimental Data and Model Validation
3. Results
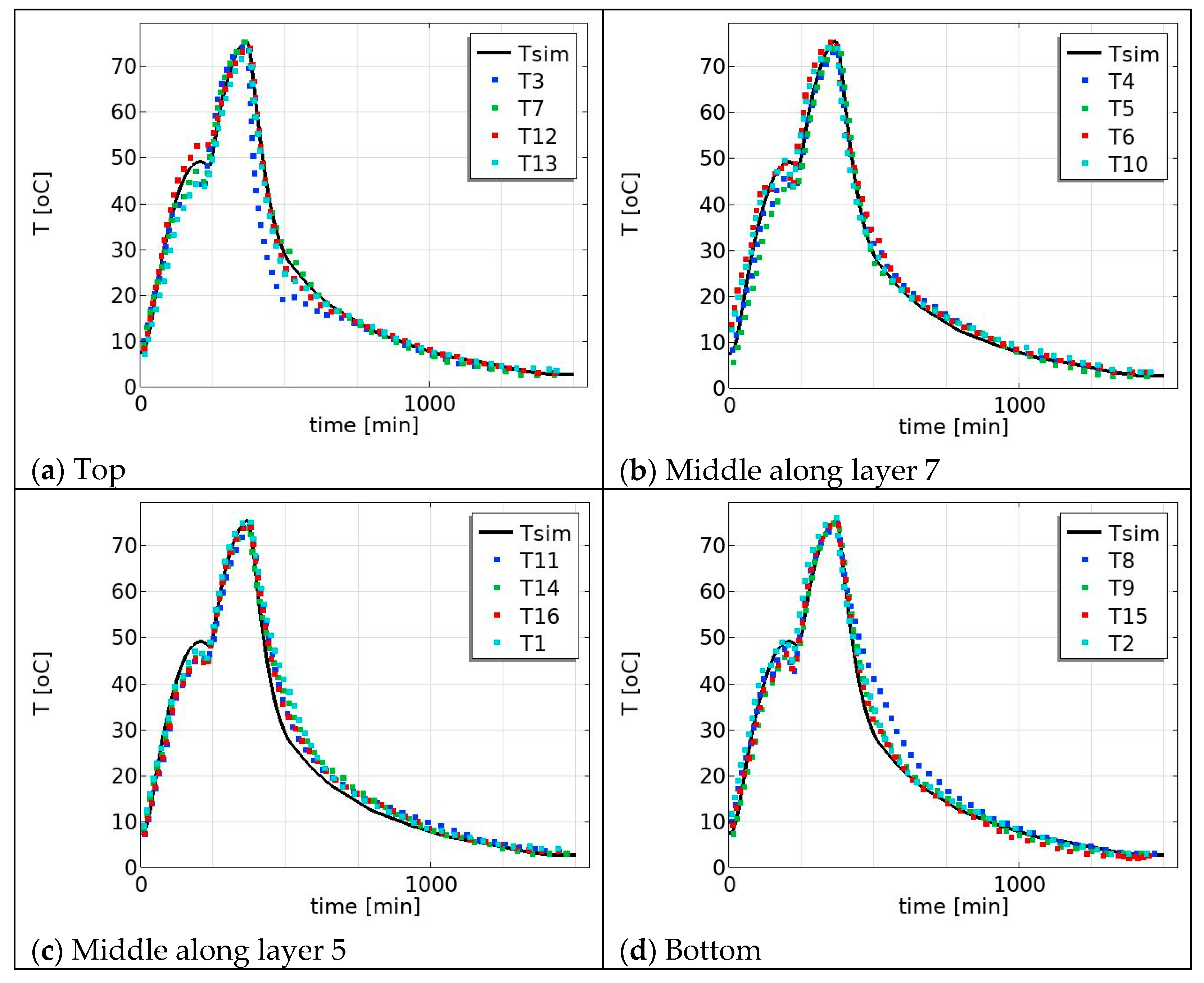
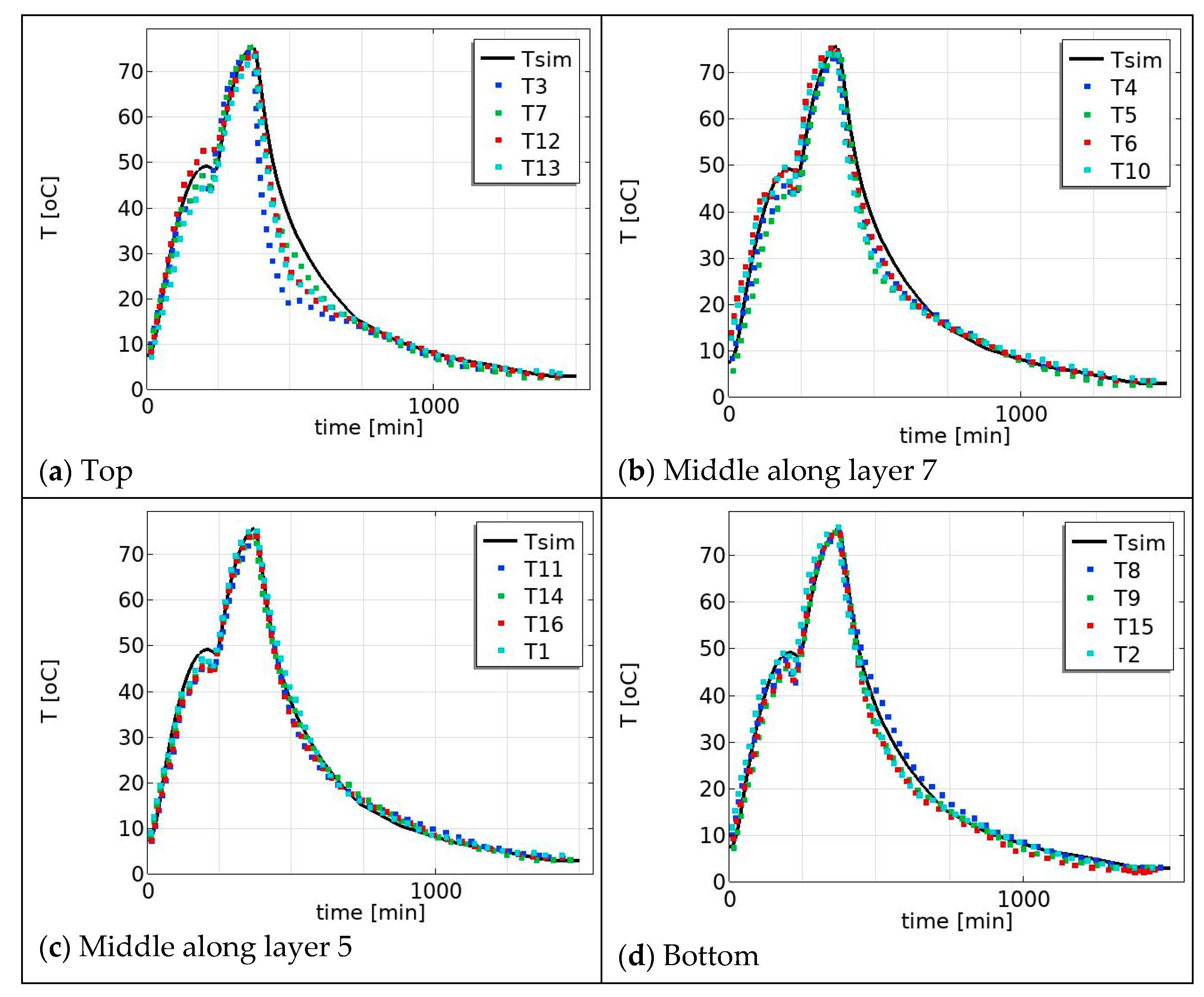
3.1. Temperature Profiles: Average, Maximum, and Minimum Temperature Profile
3.2. Model Validation and Effect of Position on the Temperature Profile
4. Conclusions and Perspective
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bejerholm, C.; Aaslyng, M.D. The influence of cooking technique and core temperature on results of a sensory analysis of pork—Depending on the raw meat quality. Food Qual. Prefer. 2004, 15, 19–30. [Google Scholar] [CrossRef]
- Amézquita, A.; Weller, C.L.; Wang, L.; Thippareddi, H.; Burson, D.E. Development of an integrated model for heat transfer and dynamic growth of Clostridium perfringens during the cooling of cooked boneless ham. Int. J. Food Microbiol. 2005, 101, 123–144. [Google Scholar] [CrossRef]
- Bottani, E.; Volpi, A. An analytical model for cooking automation in industrial steam ovens. J. Food Eng. 2009, 90, 153–160. [Google Scholar] [CrossRef]
- Hu, Z.; Sun, D.W. CFD simulation of heat and moisture transfer for predicting cooling rate and weight loss of cooked ham during air-blast chilling process. J. Food Eng. 2000, 46, 189–197. [Google Scholar] [CrossRef]
- Llave, Y.; Suzuki, A.; Fukuoka, M.; Umiuchi, E.; Sakai, N. Migration of smoke components into pork loin ham during processing and storage. J. Food Eng. 2015, 166, 221–229. [Google Scholar] [CrossRef]
- Sun, D.-W.; Hu, Z. CFD predicting the effects of various parameters on core temperature and weight loss profiles of cooked meat during vacuum cooling. Comput. Electron. Agric. 2002, 34, 111–127. [Google Scholar] [CrossRef]
- Hoang, D.K.; Lovatt, S.J.; Olatunji, J.R.; Carson, J.K. Validated numerical model of heat transfer in the forced air freezing of bulk packed whole chickens. Int. J. Refrig. 2020, 118, 93–103. [Google Scholar] [CrossRef]
- Chan, S.S.; Feyissa, A.H.; Jessen, F.; Roth, B.; Jakobsen, A.N.; Lerfall, J. Modelling water and salt diffusion of cold-smoked Atlantic salmon initially immersed in refrigerated seawater versus on ice. J. Food Eng. 2022, 312, 110747. [Google Scholar] [CrossRef]
- Cotrim, W.D.S.; Coimbra, J.C.; Cotrim, K.C.F. Modeling and simulation of broiler carcass precooling by computational fluid dynamics. J. Food Process Eng. 2021, 44, e13693. [Google Scholar] [CrossRef]
- Chen, H.; Marks, B.P.; Murphy, R.Y. Modeling coupled heat and mass transfer for convection cooking of chicken patties. J. Food Eng. 1999, 42, 139–146. [Google Scholar] [CrossRef]
- Oroszvari, B.K.; Bayod, E.; Sjöholm, I.; Tornberg, E. The mechanisms controlling heat and mass transfer on frying of beefburgers. III. Mass transfer evolution during frying. J. Food Eng. 2006, 76, 169–178. [Google Scholar] [CrossRef]
- Singh, R.P.; Pan, Z.; Vijayan, J. Use of predictive modelling in hamburger cooking. Food Aust. 1997, 49, 526–531. [Google Scholar]
- Van Der Sman, R.G.M. Soft condensed matter perspective on moisture transport in cooking meat. AICHE J. 2007, 53, 2986–2995. [Google Scholar] [CrossRef]
- Feyissa, A.H.; Gernaey, K.V.; Ashokkumar, S.; Adler-Nissen, J. Modelling of coupled heat and mass transfer during a contact baking process. J. Food Eng. 2011, 106, 228–235. [Google Scholar] [CrossRef]
- Feyissa, A.H.; Gernaey, K.V.; Adler-Nissen, J. Uncertainty and sensitivity analysis: Mathematical model of coupled heat and mass transfer for a contact baking process. J. Food Eng. 2012, 109, 281–290. [Google Scholar] [CrossRef]
- Feyissa, A.H.; Gernaey, K.V.; Adler-Nissen, J. 3D modelling of coupled mass and heat transfer of a convection-oven roasting process. Meat Sci. 2013, 93, 810–820. [Google Scholar] [CrossRef]
- Lemus-Mondaca, R.A.; Vega-Galvez, A.; Moraga, N.O. Computational Simulation and Developments Applied to Food Thermal Processing. Food Eng. Rev. 2011, 3, 121–135. [Google Scholar] [CrossRef]
- Schillaci, E.; Gràcia, A.; Capellas, M.; Rigola, J. Numerical modeling and experimental validation of meat burgers and vegetarian patties cooking process with an innovative IR laser system. J. Food Process Eng. 2022, 45, e14097. [Google Scholar] [CrossRef]
- Szpicer, A.; Wierzbicka, A.; Półtorak, A. Optimization of beef heat treatment using CFD simulation: Modeling of protein denaturation degree. J. Food Process Eng. 2022, 45, e14014. [Google Scholar] [CrossRef]
- Bird, R.B.; Sterwart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley and Sons, Inc.: New York, NY, USA, 2001; Volume 2. [Google Scholar]
- Carson, J.K.; Willix, J.; North, M.F. Measurements of heat transfer coefficients within convection ovens. J. Food Eng. 2006, 72, 293–301. [Google Scholar] [CrossRef]
- Rabeler, F.; Feyissa, A.H. Modelling the transport phenomena and texture changes of chicken breast meat during the roasting in a convective oven. J. Food Eng. 2018, 237, 60–68. [Google Scholar] [CrossRef]
- Huang, S.R.; Yang, J.I.; Lee, Y.C. Interactions of heat and mass transfer in steam reheating of starchy foods. J. Food Eng. 2013, 114, 174–182. [Google Scholar] [CrossRef]
- Nesvadba, P. Thermal properties of unfrozen foods. In Engineering Properties of Foods; Rao, M.A., Rizvi, S.H., Datta, A.K., Ahmed, J., Eds.; CRC Press: Boca Raton, FL, USA, 2014; Volume 4, pp. 223–245. [Google Scholar]
- Feyissa, A.H.; Christensen, M.G.; Pedersen, S.J.; Hickman, M.; Adler-Nissen, J. Studying fluid-to-particle heat transfer coefficients in vessel cooking processes using potatoes as measuring devices. J. Food Eng. 2015, 163, 71–78. [Google Scholar] [CrossRef]
- Ilhan, D.; Ashwini, K. Fluid flow and its modeling using computational fluid dynamics. In Handbook of Food and Bioprocess Modeling Techniques; CRC Press: Boca Raton, FL, USA, 2006; pp. 41–83. [Google Scholar]
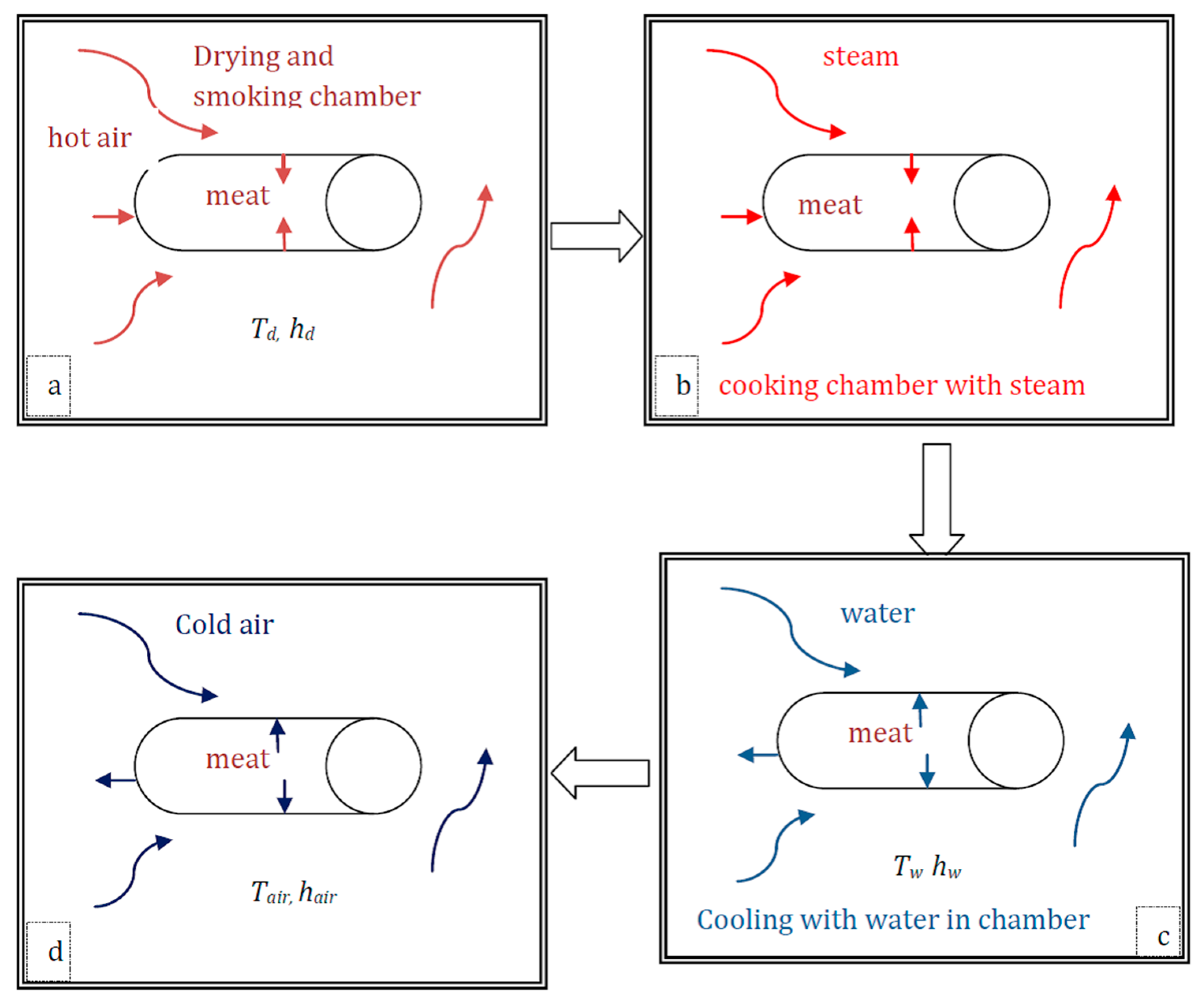
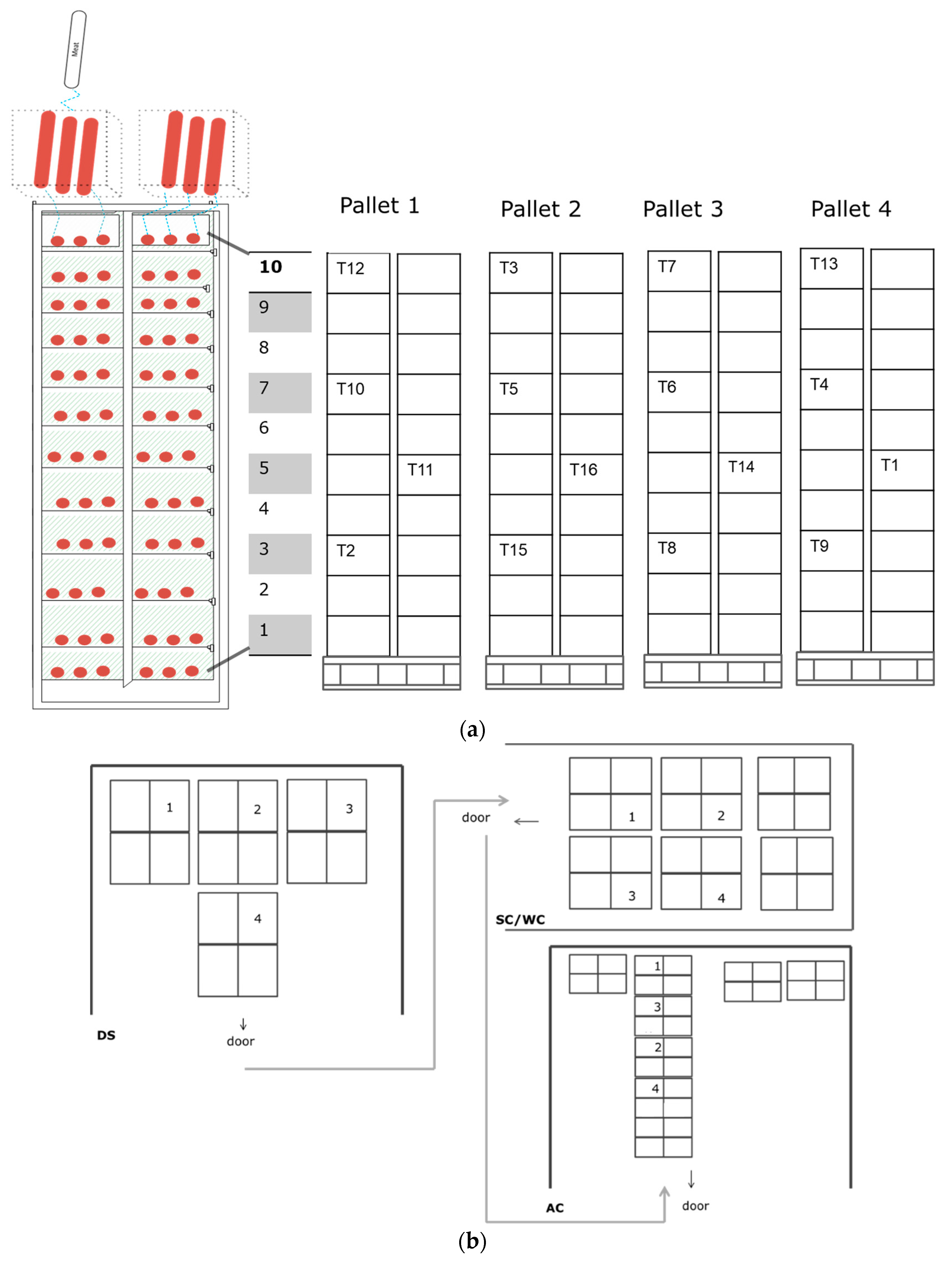
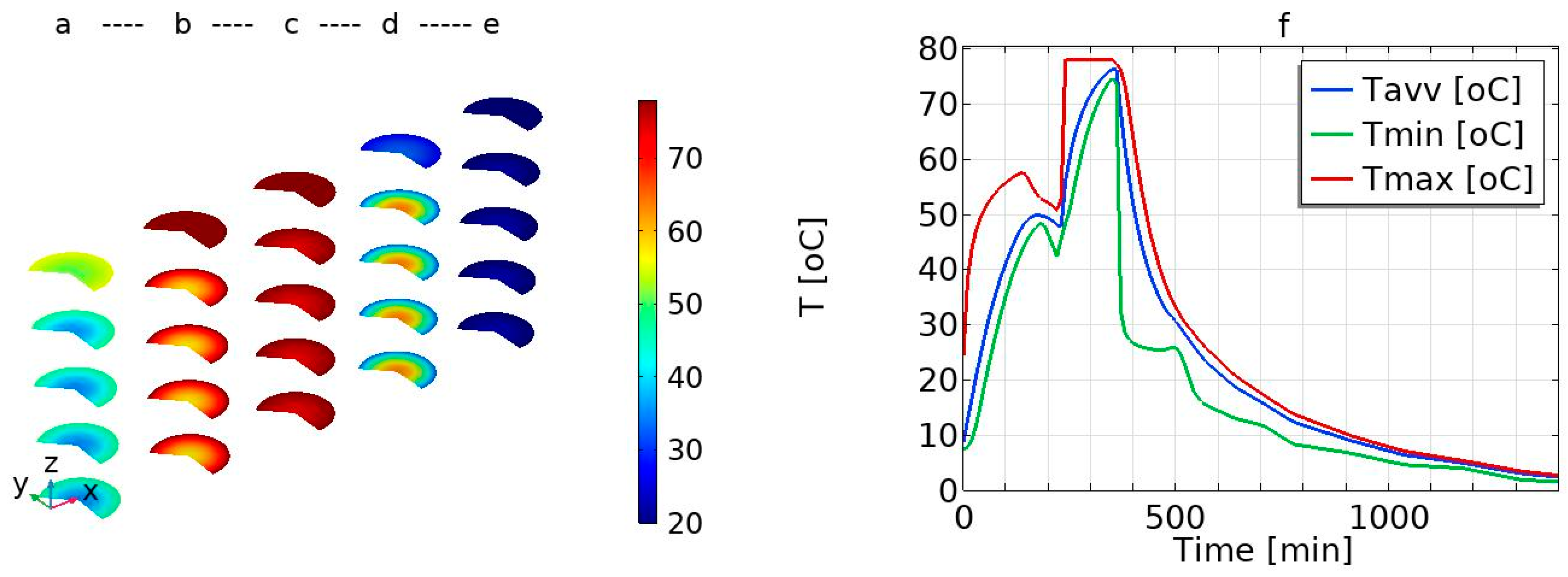
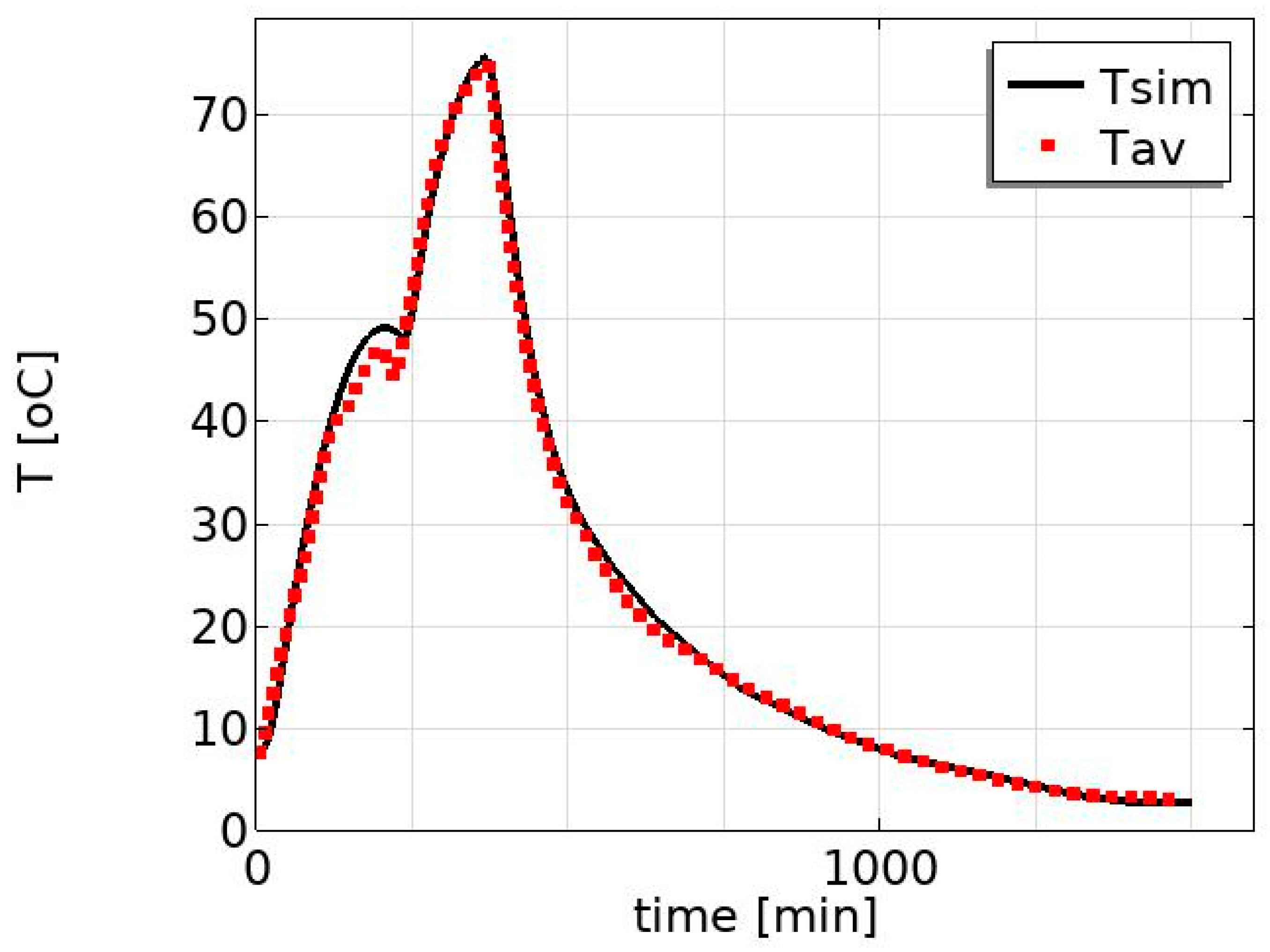
| Parameter | Value [Unit] | Description | Source |
|---|---|---|---|
| D | 0.085 [m] | Diameter of the product | This study (measured) |
| L | 0.54 [m] | Length of the product | This study (measured) |
| tds | 12,600 [s] | Total time for the drying–smoking process (td + tsmoke) | This study (measured) |
| hd | 20 [W/(m2K)] | Heat transfer coefficient during drying and smoking process | [21,22] |
| Td | 333.15 [K] | The temperature of the air during the drying process | This study (measured) |
| Tsmoke | 318.15 [K] | Process temperature during the smoking process | This study (measured) |
| hsmoke | hd | Heat transfer coefficient during the smoking process | Assumed the same as during drying |
| tst | 7920 [s] | Time for the steam-cooking process | This study (measured) |
| hst | 2000 [W/(m2K)] | Heat transfer coefficient during the steam-cooking process | [23] |
| Tst | 351.15 [K] | The steam temperature during the steam-cooking | This study (set+) |
| tw | 7200 [s] | Time for the water-cooling process | This study (measured) |
| hw | 80 [W/(m2K)] | Heat transfer coefficient for the water-cooling process | This study (estimated using measured data, Section 2.3)) |
| Tw | 298.15 [K] | Water temperature during the water-cooling process | This study (measured) |
| tair | 54,000 [s] | Time for the air-cooling process | This study (measured) |
| hair | 12 [W/(m2K)] | Heat transfer coefficient during the air-cooling process | This study (estimated using measured data, Section 2.3) |
| Tair | 276.15 [K] | Air temperature during the air-cooling process | This study (measured) |
| To | 280.65 [K] | The initial temperature of the product | This study (measured) |
| ttrans1 | 1200 [s] | Transfer time (transferring the product from DS to SC) | This study (measured) |
| ttrans2 | 1200 [s] | Transfer time (transferring the product from SC to AC) | This study (measured) |
| Tamb | 298.15 [K] | The ambient air temperature during the transfer time | This study (measured) |
| hamb | 8 [W/(m2K)] | Heat transfer coefficient during the transfer time | [14] |
| ρm | ** 1064.5 [kg/m3] | The density of the product | Estimated from composition [3,16,24] |
| cpm | , ** 3535.5 [J/(K kg)], | Specific heat capacity of the product | Estimated from composition [3,16,24] |
| km | ** 0.47 [W/(m K)] | Thermal conductivity of the product | Estimated from composition [16,25] |
| T3 | T4 | T5 | T6 | T7 | T8 | T9 | T10 | T11 * | |
|---|---|---|---|---|---|---|---|---|---|
| R2 | 0.938 | 0.997 | 0.989 | 0.985 | 0.994 | 0.987 | 0.996 | 0.982 | 0.992 |
| RMSE | 5.945 | 1.697 | 2.895 | 2.653 | 2.013 | 2.672 | 1.639 | 2.881 | 2.047 |
| T12 | T13 | T14 | T15 | T16 | T1 | T2 | Tav | ||
| R2 | 0.987 | 0.989 | 0.994 | 0.996 | 0.995 | 0.991 | 0.991 | 0.997 | |
| RMSE | 2.495 | 3.244 | 1.751 | 1.773 | 1.590 | 2.263 | 2.152 | 1.260 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feyissa, A.H.; Frosch, S. An Integrated Model of Heat Transfer in Meat Products during Multistage Operations. Foods 2023, 12, 3369. https://doi.org/10.3390/foods12183369
Feyissa AH, Frosch S. An Integrated Model of Heat Transfer in Meat Products during Multistage Operations. Foods. 2023; 12(18):3369. https://doi.org/10.3390/foods12183369
Chicago/Turabian StyleFeyissa, Aberham Hailu, and Stina Frosch. 2023. "An Integrated Model of Heat Transfer in Meat Products during Multistage Operations" Foods 12, no. 18: 3369. https://doi.org/10.3390/foods12183369
APA StyleFeyissa, A. H., & Frosch, S. (2023). An Integrated Model of Heat Transfer in Meat Products during Multistage Operations. Foods, 12(18), 3369. https://doi.org/10.3390/foods12183369





