Dielectric Properties and Dipole Moment of Edible Oils Subjected to ‘Frying’ Thermal Treatment
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Methods
2.2.1. Specific Absorption Coefficient at 232 and 268 nm
2.2.2. Refractive Index
2.2.3. Density
2.2.4. Saponification Value
2.2.5. Dielectric Properties
2.3. Mathematical Models for the Interpretation of the Dielectric Spectra
2.3.1. Corach and Coworkers Model
2.3.2. Cole–Cole model
2.3.3. Power Law Models
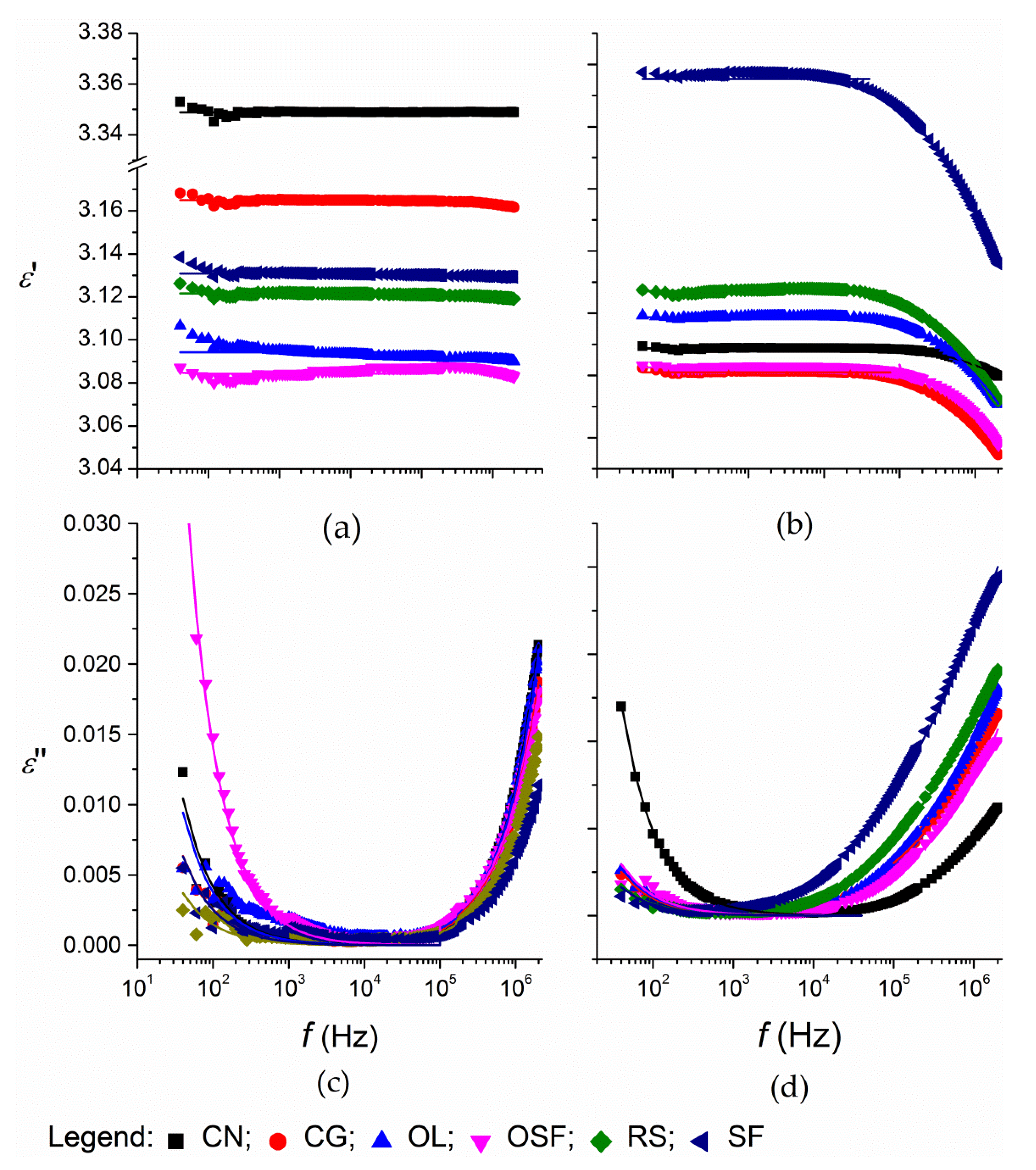
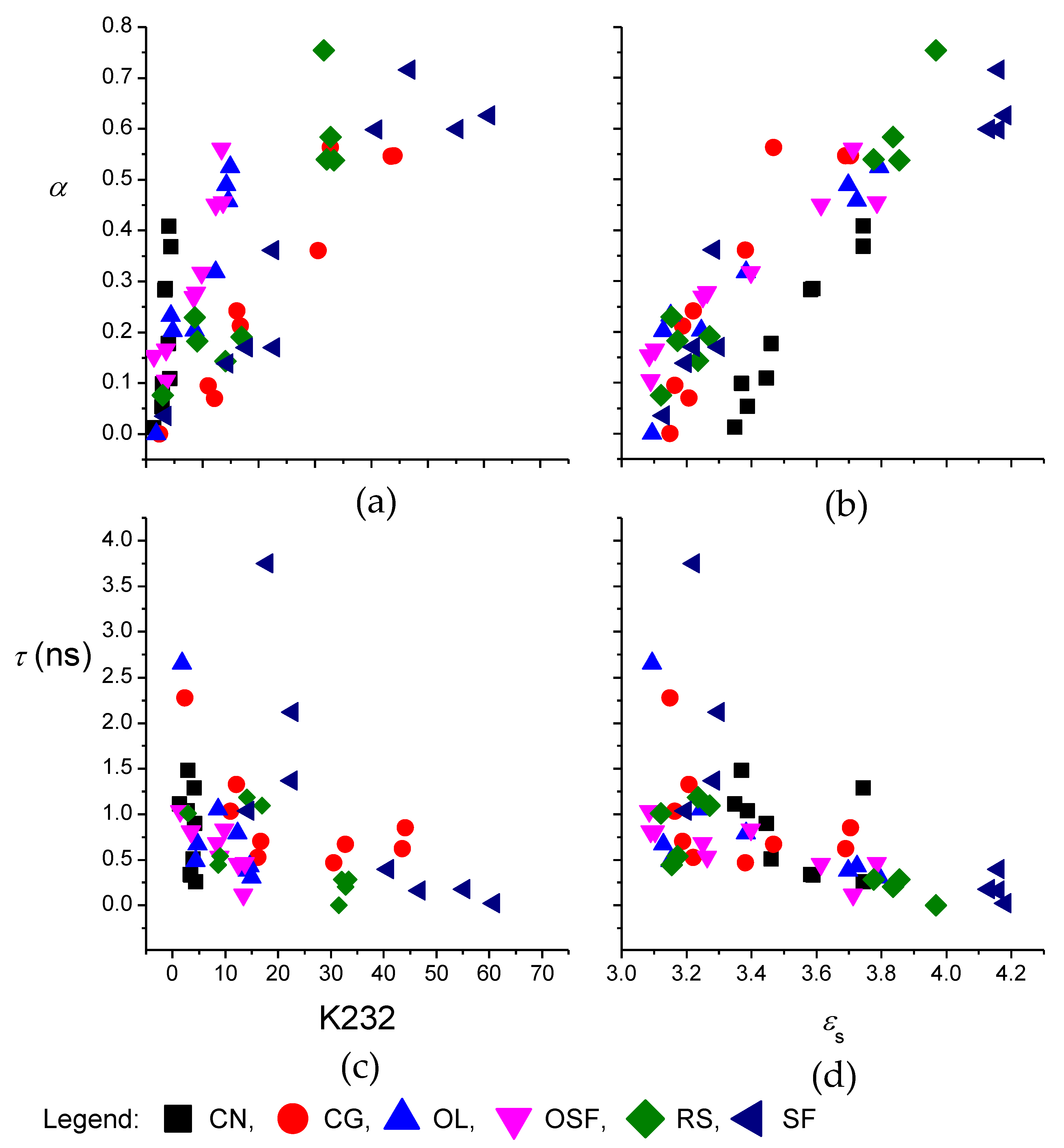
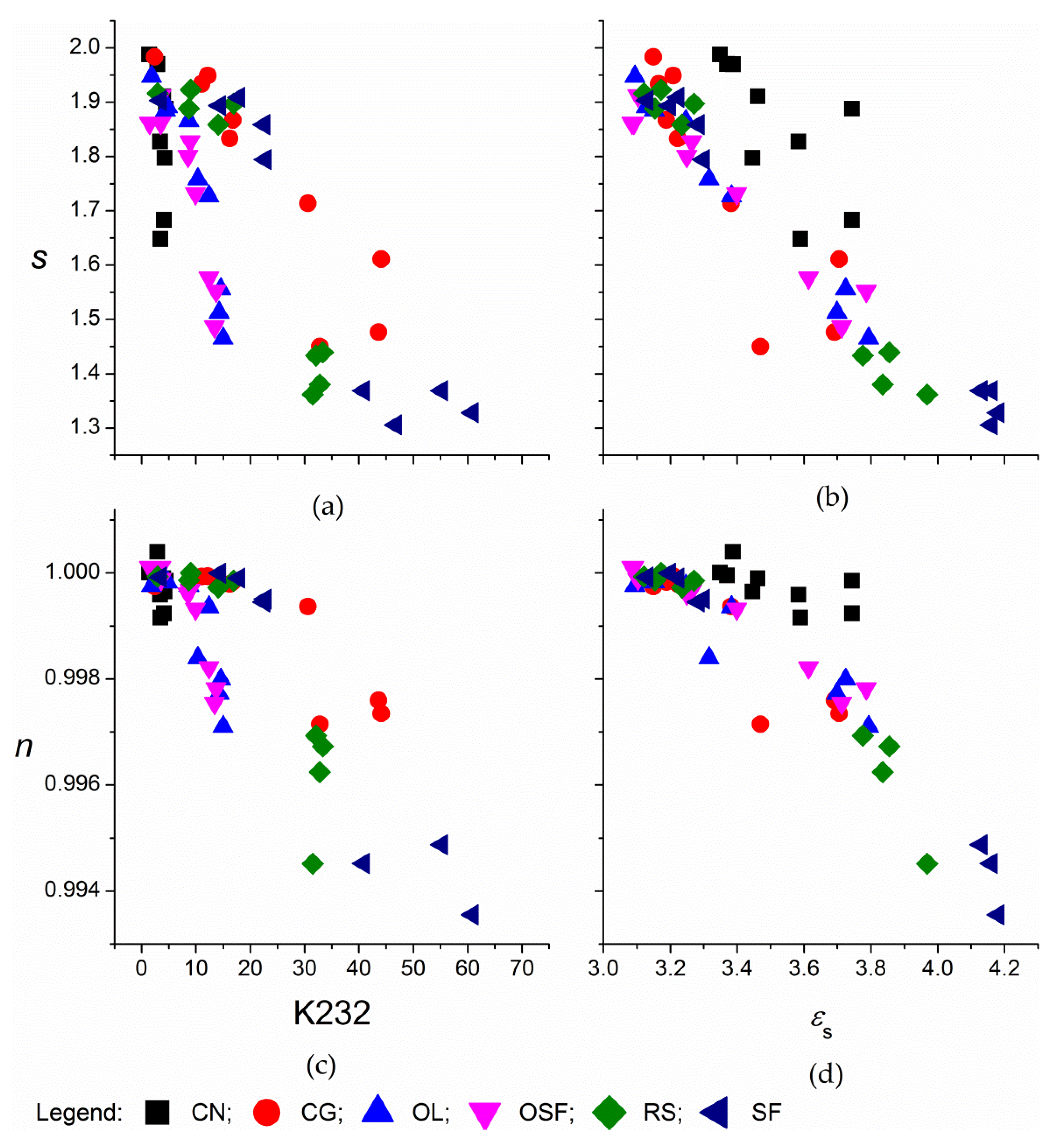
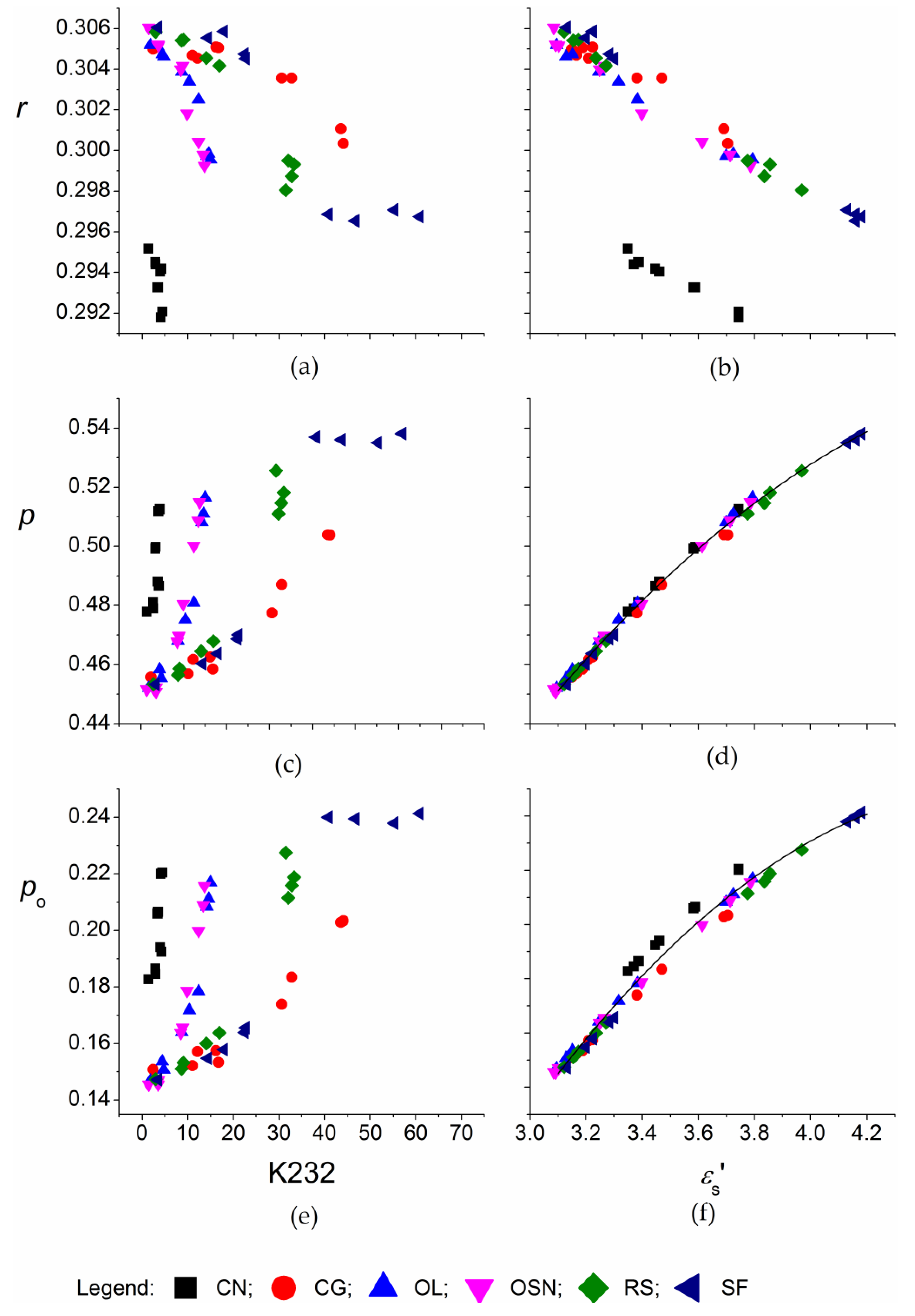
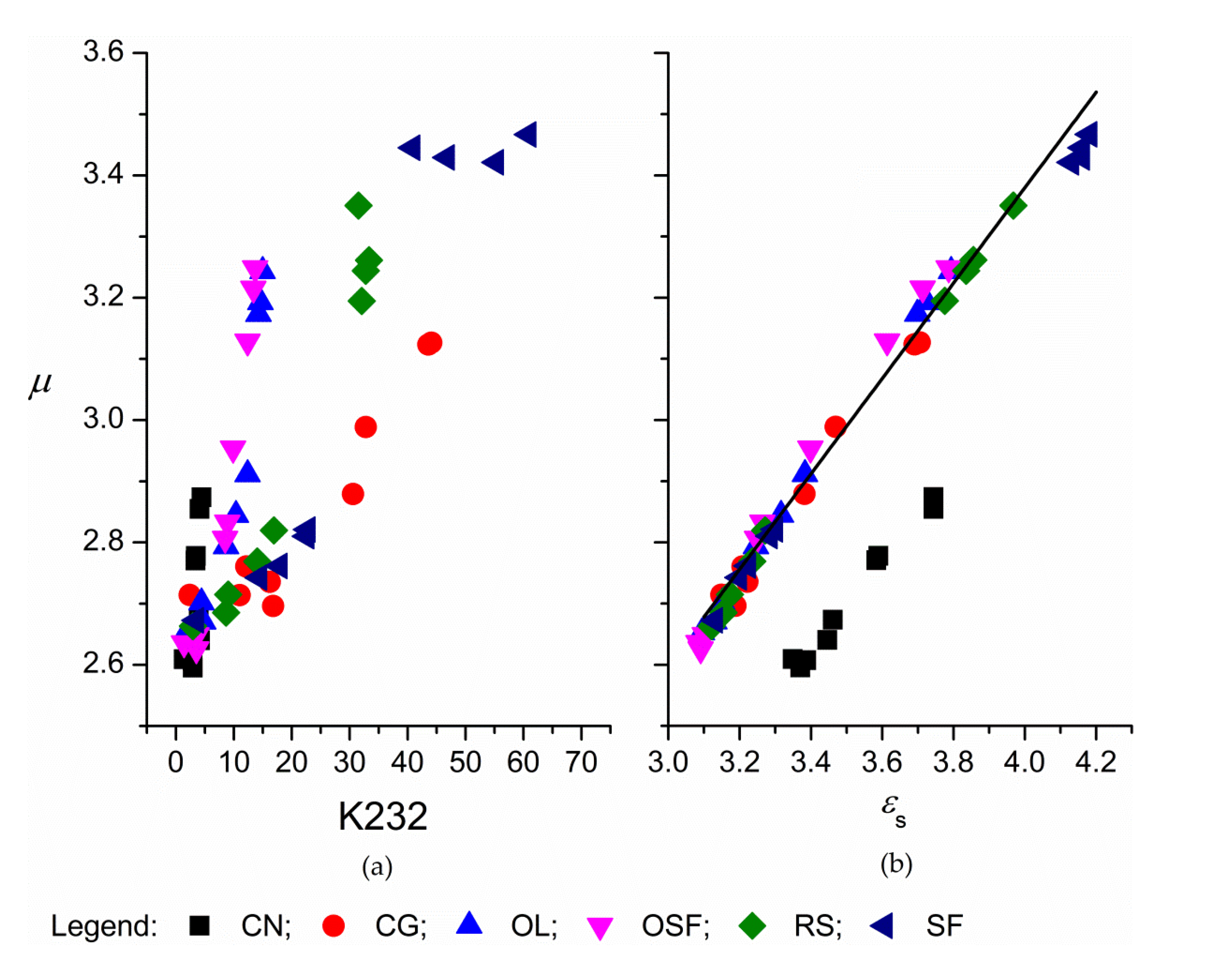
3. Results and Discussion
3.1. Corach and Coworkers Model
3.2. Cole–Cole Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Fatty Acid Composition—Analytical Procedure
| Edible Oil | Fatty Acid Composition (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| C10:0 | C12:0 | C14:0 | C16:0 | C18:0 | C18:1 | C18:2 | C18:3 | |
| Coconut | 7.89 ± 0.85 | 40.0 ± 0.92 | 15.99 ± 0.34 | 8.25 ± 0.14 | 2.34 ± 0.04 | 5.94 ± 0.10 | 1.31 ± 0.02 | 0.040 ± 0.005 |
| Corn germ | nd | nd | 0.12 ± 0.02 | 9.93 ± 0.05 | 1.43 ±0.01 | 27.22 ± 0.15 | 48.21 ± 0.26 | 0.97 ± 0.04 |
| Olive | nd | nd | 0.009 ± 0.001 | 11.33 ± 0.01 | 2.56 ± 0.01 | 69.81 ± 0.02 | 6.74 ± 0.01 | 0.68 ± 0.02 |
| Rapeseed | nd | nd | 0.048 ± 0.006 | 4.46 ± 0.07 | 1.26 ± 0.04 | 53.93 ± 0.25 | 21.05 ± 0.06 | 6.45 ± 0.01 |
| Sunflower | nd | nd | 0.073 ± 0.001 | 5.56 ± 0.02 | 2.60 ± 0.01 | 25.87 ± 0.13 | 53.09 ± 0.25 | 0.301 ± 0.001 |
| Sunflower: high oleic | nd | nd | 0.152 ± 0.002 | 3.90 ± 0.02 | 2.09 ± 0.03 | 75.81 ± 0.33 | 8.10 ± 0.03 | 0.205 ± 0.003 |
References
- Akoh, C.C.; Min, D.B. Chemistry and Properties. In Food Lipids: Chemistry, Nutrition and Biotechnology; Akoh, C.C., Min, D.B., Eds.; Dekker: New York, NY, USA, 2002; pp. 192–238. [Google Scholar]
- Gunstone, F.D. Vegetable Oils in Food Technology: Composition, Properties and Uses, 2nd ed.; Blackwell Publishing: Cambridge, UK, 2011; ISBN 9781588297167. [Google Scholar]
- Vidrih, R.; Vidakovič, S.; Abramovič, H. Biochemical parameters and oxidative resistance to thermal treatment of refined and unrefined vegetable edible oils. Czech J. Food Sci. 2010, 28, 376–384. [Google Scholar] [CrossRef]
- Chantzos, N.V.; Georgiou, C.A. Monitoring lipid oxidation events at frying temperatures through radical scavenging assays. Chem. Ind. Chem. Eng. Q. 2007, 13, 163–166. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Wang, Y.; Cao, P.; Liu, Y. Effects of frying oils’ fatty acids profile on the formation of polar lipids components and their retention in French fries over deep-frying process. Food Chem. 2017, 237, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wu, G.; Yang, F.; Meng, L.; Huang, J.; Zhang, H.; Jin, Q.; Wang, X. Influence of fried food and oil type on the distribution of polar compounds in discarded oil during restaurant deep frying. Food Chem. 2019, 272, 12–17. [Google Scholar] [CrossRef]
- Filip, S.; Hribar, J.; Vidrih, R. Influence of natural antioxidants on the formation of trans-fatty-acid isomers during heat treatment of sunflower oil. Eur. J. Lipid Sci. Technol. 2011, 113, 224–230. [Google Scholar] [CrossRef]
- Matthäus, B. Oxidation of edible oils. In Oxidation in Foods and Beverages and Antioxidant Applications; Decker, E.A., Ed.; Woodhead Publishing: Cambridge, UK, 2010; pp. 183–238. [Google Scholar]
- Arya, S.S.; Ramanujam, S.; Vijayaraghavan, P.K. Refractive index as an objective method for evaluation of rancidity in edible oils and fats. J. Am. Oil Chem. Soc. 1969, 46, 28–30. [Google Scholar] [CrossRef]
- Kalogianni, E.P.; Karapantsios, T.D.; Miller, R. Effect of repeated frying on the viscosity, density and dynamic interfacial tension of palm and olive oil. J. Food Eng. 2011, 105, 169–179. [Google Scholar] [CrossRef]
- Ayoola, A.A.; Adeeyo, O.A.; Efeovbokhan, V.E.; Mosugu, A.T. Degradation of oil during frying and its effect on biodiesel production. Int. J. Res. Eng. Technol. 2016, 5, 68–73. [Google Scholar] [CrossRef]
- Zribi, A.; Jabeur, H.; Aladedunye, F.; Rebai, A.; Matthäus, B.; Bouaziz, M. Monitoring of quality and stability characteristics and fatty acid compositions of refined olive and seed oils during repeated pan and deep-frying using GC, FT-NIRS and chemometrics. J. Agric. Food Chem. 2014, 62, 10357–10367. [Google Scholar] [CrossRef]
- Guillén, M.D.; Uriarte, P.S. A very simple, fast, and non-destructive approach to predict the time at which edible oils submitted to high temperature reach the established limits of safety. Food Chem. 2011, 127, 802–806. [Google Scholar] [CrossRef]
- Ahmadi, E.; Mosaferi, M.; Nikniaz, L.; Tabrizi, J.S.; Asghari Jafarabadi, M.; Safari, G.; Bargar, M. Frying oils quality control: Necessity for new approach of supervision. Br. Food J. 2018, 120, 490–498. [Google Scholar] [CrossRef]
- Rubalya Valantina, S.; Phebee Angeline, D.R.; Uma, S.; Jeya Prakash, B.G. Estimation of dielectric constant of oil solution in the quality analysis of heated vegetable oil. J. Mol. Liq. 2017, 238, 136–144. [Google Scholar] [CrossRef]
- Rubalya Valantina, S.; Uma, S.; Jeya Prakash, B.G.; Phebee Angeline, D.R.; Alfred Maxwell, A.; Aravindhan, R. Modelling, characterization and quality analysis of heated oil using electric moment and chemical properties. J. Food Sci. Technol. 2019, 56, 571–579. [Google Scholar] [CrossRef]
- Sonkamble, A.A.; Sonsale, R.P.; Kanshette, M.S.; Kabara, K.B.; Wananje, K.H.; Kumbharkhane, A.C.; Sarode, A.V. Relaxation dynamics and thermophysical properties of vegetable oils using time-domain reflectometry. Eur. Biophys. J. 2017, 46, 283–291. [Google Scholar] [CrossRef] [PubMed]
- Prevc, T.; Cigić, B.; Vidrih, R.; Poklar Ulrih, N.; Šegatin, N. Correlation of basic oil quality indices and electrical properties of model vegetable oil systems. J. Agric. Food Chem. 2013, 61, 11356–11362. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, K.S.; He, Y.J. Quality evaluation of frying oil deterioration by dielectric spectroscopy. J. Food Eng. 2016, 180, 69–76. [Google Scholar] [CrossRef]
- Paquot, C.; Hautfenne, A. Standard Methods for the Analysis of Oils, Fats and Derivatives; 7st Supple International Union of Pure and Applied Chemistry Commission on Oils; Blackwell: Oxford, UK, 1987; pp. 712–782. [Google Scholar]
- Polak, T.; Polak, A.; Ulrih Poklar, N.; Šegatin, N. Electrical admittance and dielectric properties of whipping cream. J. Food Eng. 2020, 278. [Google Scholar] [CrossRef]
- Agilent Technologies. Agilent 16452A Liquid Test Fixture—Operation and Service Manual; Agilent Technologies Japan, LTD.: Kobe, Japan, 2000. [Google Scholar]
- Raicu, V.; Feldman, Y. Dielectric Relaxation in Biological Systems; Blackwell: Oxford, UK, 2015; pp. 33–81. [Google Scholar]
- Corach, J.; Sorichetti, P.A.; Romano, S.D. Electrical properties of vegetable oils between 20 Hz and 2 MHz. Int. J. Hydrogen Energy 2014, 39, 8754–8758. [Google Scholar] [CrossRef]
- Feldman, Y.; Gusev, Y.A.; Vasilyeva, M.A. Dielectric Relaxation Phenomena in Complex Materials; Kazan University: Kazan, Russia, 2012. [Google Scholar]
- Dielectric Relaxation Phenomena in Complex Systems. Available online: https://kpfu.ru/docs/F789845537/Dielectric_Relaxation_Phenomena_in_Complex_Systems.pdf (accessed on 12 November 2014).
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Chawla, M.; Shekhawat, N.; Aggarwal, S.; Sharma, A.; Nair, K.G.M. Cole-cole analysis and electrical conduction mechanism of N+ implanted polycarbonate. J. Appl. Phys. 2014, 115, 184104. [Google Scholar] [CrossRef]
- Raju, G.G. Dielectric loss and relaxation—I. In Dielectrics in Electric Fields, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Lawton, B.A.; Pethig, R. Determining the fat content of milk and cream using AC conductivity measurements. Meas. Sci. Technol. 1993, 4, 38–41. [Google Scholar] [CrossRef]
- Tuncer, E.; Serdyuk, Y.V.; Gubanski, S.M. Dielectric mixtures: Electrical properties and modeling. IEEE Trans. Dielectr. Electr. Insul. 2002, 9, 809–828. [Google Scholar] [CrossRef]
- Mabrook, M.F.; Darbyshire, A.M.; Petty, M.C. Quality control of dairy products using single frequency admittance measurements. Meas. Sci. Technol. 2006, 17, 275–280. [Google Scholar] [CrossRef]
- Wei, Y.Z.; Sridhar, S. A new graphical representation for dielectric data. J. Chem. Phys. 1993, 99, 3119–3124. [Google Scholar] [CrossRef]
- Aouaichia, M.; Bouamrane, R. Modeling and analysis of the dielectric properties of composite materials using large random RC networks. arXiv 2017, arXiv:1709.08381, 1–7. [Google Scholar]
- Inoue, C.; Hagura, Y.; Ishikawa, M.; Suzuki, K. The dielectric property of soybean oil in deep-fat frying and the effect of frequency. J. Food Sci. 2002, 67, 1126–1129. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, A.; Tarsikka, P.S. Interrelationship between viscosity and electrical properties for edible oils. J. Food Sci. Technol. 2013, 50, 549–554. [Google Scholar] [CrossRef]
- Tsonos, C. Comments on frequency dependent AC conductivity in polymeric materials at low frequency regime. Curr. Appl. Phys. 2019, 19, 491–497. [Google Scholar] [CrossRef]
- Goual, L.; Firoozabadi, A. Measuring asphaltenes and resins, and dipole moment in petroleum fluids. AIChE J. 2002, 48, 2646–2663. [Google Scholar] [CrossRef]
- Kao, K.C. Dielectiric Phenomena in Solids; Elsevier Academic Press: San Diego, CA, USA, 2004. [Google Scholar]
- Barot, V.B.; Andher, S.S. Application of some available formulas of specific refraction for edible oils. Res. J. Phys. Sci. 2015, 3, 1–3. [Google Scholar]
- Rudan-Tasič, D.; Klofutar, C. Characteristics of vegetable oils of some Slovene manufacturers. Acta Chim. Slov. 1999, 46, 511–521. [Google Scholar]
- Caldwell, B.P.; Payne, H.F. Dielectric Constant and Effective Dipole Moment of Drying Oils. Ind. Eng. Chem. 1941, 33, 954–960. [Google Scholar] [CrossRef]
- Tels, M.; Kruidenier, A.J.; Boelhouwer, C.; Waterman, H.I. The specific refraction of fatty oils. J. Am. Oil Chem. Soc. 1958, 35, 163–166. [Google Scholar] [CrossRef]
| Edible Oil | K232 | K268 | Saponification Value (mg/g) | Refractive Index nD | Density d/(g/cm3) | Dielectric Constant a εs | Conductivity σ0/(nS/m) |
|---|---|---|---|---|---|---|---|
| Coconut | 1.39 | 0.12 | 252.2 | 1.45480 | 0.91884 | 3.3488 ± 0.0001 | 0.023 ± 0.001 |
| 2.87 | 0.31 | 258.9 | 1.45500 | 0.92126 | 3.3873 ± 0.0001 | 0.046 ± 0.001 | |
| 2.94 | 0.32 | 258.0 | 1.45496 | 0.92155 | 3.3702 ± 0.0002 | 0.037 ± 0.004 | |
| 3.97 | 0.46 | 258.3 | 1.45540 | 0.92343 | 3.4614 ± 0.0001 | 0.080 ± 0.001 | |
| 4.21 | 0.44 | 262.1 | 1.45544 | 0.92306 | 3.4462 ± 0.0001 | 0.081 ± 0.001 | |
| 3.40 | 0.62 | 258.8 | 1.45596 | 0.92685 | 3.5834 ± 0.0001 | 0.180 ± 0.001 | |
| 3.47 | 0.63 | 258.4 | 1.45598 | 0.92688 | 3.5895 ± 0.0001 | 0.268 ± 0.001 | |
| 4.10 | 1.11 | 265.3 | 1.45694 | 0.93326 | 3.7437 ± 0.0002 | 0.270 ± 0.003 | |
| 4.43 | 1.25 | 262.2 | 1.45678 | 0.93210 | 3.7440 ± 0.0002 | 0.291 ± 0.002 | |
| Corn-germ | 2.4 | 1.55 | 186.8 | 1.47054 | 0.91569 | 3.1491 ± 0.0001 | 0.024 ± 0.001 |
| 11.0 | 3.83 | 189.0 | 1.47107 | 0.91749 | 3.1653 ± 0.0003 | 0.021 ± 0.003 | |
| 12.2 | 4.23 | 189.5 | 1.47121 | 0.91818 | 3.2082 ± 0.0001 | 0.030 ± 0.002 | |
| 16.2 | 6.09 | 193.5 | 1.47323 | 0.91986 | 3.2222 ± 0.0001 | 0.023 ± 0.001 | |
| 16.8 | 5.72 | 193.3 | 1.47322 | 0.91996 | 3.1882 ± 0.0001 | 0.031 ± 0.001 | |
| 30.6 | 7.32 | 196.3 | 1.47464 | 0.92688 | 3.3819 ± 0.0001 | 0.034 ± 0.002 | |
| 32.8 | 7.77 | 194.2 | 1.47473 | 0.92702 | 3.4695 ± 0.0003 | 0.032 ± 0.004 | |
| 43.6 | 9.87 | 201.3 | 1.47694 | 0.93841 | 3.6909 ± 0.0005 | 0.058 ± 0.008 | |
| 44.1 | 9.97 | 201.9 | 1.47723 | 0.94114 | 3.7050 ± 0.0006 | 0.056 ± 0.010 | |
| Olive | 1.8 | 0.15 | 189.6 | 1.46709 | 0.90935 | 3.0944 ± 0.0002 | 0.021 ± 0.003 |
| 4.4 | 0.93 | 192.4 | 1.46740 | 0.91121 | 3.1518 ± 0.0001 | 0.035 ± 0.001 | |
| 4.7 | 0.98 | 192.7 | 1.46743 | 0.91160 | 3.1290 ± 0.0001 | 0.033 ± 0.001 | |
| 8.7 | 1.12 | 194.2 | 1.46808 | 0.91493 | 3.2462 ± 0.0001 | 0.037 ± 0.001 | |
| 10.4 | 1.22 | 197.6 | 1.46840 | 0.91694 | 3.3161 ± 0.0001 | 0.044 ± 0.001 | |
| 12.4 | 1.40 | 197.4 | 1.46905 | 0.92069 | 3.3834 ± 0.0001 | 0.036 ± 0.002 | |
| 14.6 | 2.04 | 202.0 | 1.47054 | 0.93144 | 3.7249 ± 0.0004 | 0.049 ± 0.007 | |
| 14.2 | 2.46 | 201.1 | 1.47066 | 0.93196 | 3.6984 ± 0.0007 | 0.050 ± 0.009 | |
| 15.0 | 2.49 | 202.5 | 1.47126 | 0.93354 | 3.7932 ± 0.0007 | 0.061 ± 0.010 | |
| Rapeseed | 2.9 | 0.80 | 189.2 | 1.47096 | 0.91388 | 3.1215 ± 0.0001 | 0.014 ± 0.001 |
| 8.7 | 2.27 | 191.3 | 1.47134 | 0.91575 | 3.1546 ± 0.0001 | 0.008 ± 0.001 | |
| 9.0 | 2.38 | 190.2 | 1.47145 | 0.91581 | 3.1729 ± 0.0001 | 0.010 ± 0.001 | |
| 14.1 | 3.36 | 192.2 | 1.47180 | 0.91913 | 3.2354 ± 0.0001 | 0.012 ± 0.001 | |
| 16.9 | 3.44 | 190.6 | 1.47212 | 0.92082 | 3.2715 ± 0.0001 | 0.011 ± 0.001 | |
| 31.5 | 6.23 | 202.6 | 1.47597 | 0.94629 | 3.9681 ± 0.0012 | 0.055 ± 0.017 | |
| 33.3 | 6.33 | 203.1 | 1.47536 | 0.94120 | 3.8557 ± 0.0001 | 0.052 ± 0.012 | |
| 32.1 | 5.59 | 202.8 | 1.47526 | 0.94045 | 3.7755 ± 0.0001 | 0.054 ± 0.012 | |
| 32.8 | 6.15 | 202.0 | 1.47602 | 0.94419 | 3.8355 ± 0.0011 | 0.050 ± 0.016 | |
| Sunflower | 3.5 | 2.06 | 187.7 | 1.47275 | 0.91618 | 3.1309 ± 0.0001 | 0.014 ± 0.001 |
| 14.4 | 3.51 | 188.7 | 1.47335 | 0.91870 | 3.1983 ± 0.0001 | 0.005 ± 0.001 | |
| 17.9 | 3.87 | 190.3 | 1.47349 | 0.91798 | 3.2238 ± 0.0001 | 0.003 ± 0.001 | |
| 22.8 | 4.11 | 192.9 | 1.47410 | 0.92305 | 3.2996 ± 0.0003 | 0.044 ± 0.005 | |
| 22.5 | 4.08 | 192.1 | 1.47414 | 0.92244 | 3.2847 ± 0.0001 | 0.015 ± 0.002 | |
| 40.8 | 9.12 | 206.4 | 1.47918 | 0.95553 | 4.1602 ± 0.0017 | 0.035 ± 0.014 | |
| 55.3 | 9.12 | 206.7 | 1.47892 | 0.95439 | 4.1301 ± 0.0016 | 0.034 ± 0.013 | |
| 46.8 | 10.35 | 207.8 | 1.47948 | 0.95709 | 4.1604 ± 0.0015 | 0.047 ± 0.025 | |
| 55.3 | 11.98 | 205.4 | 1.47948 | 0.95641 | 4.1810 ± 0.0014 | 0.036 ± 0.018 | |
| Sunflower: | 1.4 | 0.49 | 190.1 | 1.46776 | 0.90790 | 3.0849 ± 0.0001 | 0.078 ± 0.002 |
| high oleic | 3.5 | 0.87 | 191.6 | 1.46816 | 0.91107 | 3.0905 ± 0.0001 | 0.075 ± 0.001 |
| 3.6 | 0.82 | 190.6 | 1.46815 | 0.91115 | 3.1028 ± 0.0001 | 0.075 ± 0.002 | |
| 8.5 | 0.85 | 192.2 | 1.46898 | 0.91607 | 3.2494 ± 0.0001 | 0.075 ± 0.001 | |
| 8.9 | 0.91 | 191.0 | 1.46894 | 0.91550 | 3.2638 ± 0.0001 | 0.077 ± 0.001 | |
| 9.9 | 0.93 | 192.4 | 1.47014 | 0.92465 | 3.3986 ± 0.0002 | 0.053 ± 0.002 | |
| 13.7 | 1.82 | 200.5 | 1.47164 | 0.93513 | 3.7861 ± 0.0005 | 0.049 ± 0.007 | |
| 12.4 | 1.25 | 196.4 | 1.47119 | 0.93070 | 3.6136 ± 0.0004 | 0.043 ± 0.006 | |
| 13.4 | 1.41 | 196.7 | 1.47167 | 0.93348 | 3.7132 ± 0.0005 | 0.042 ± 0.008 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šegatin, N.; Pajk Žontar, T.; Poklar Ulrih, N. Dielectric Properties and Dipole Moment of Edible Oils Subjected to ‘Frying’ Thermal Treatment. Foods 2020, 9, 900. https://doi.org/10.3390/foods9070900
Šegatin N, Pajk Žontar T, Poklar Ulrih N. Dielectric Properties and Dipole Moment of Edible Oils Subjected to ‘Frying’ Thermal Treatment. Foods. 2020; 9(7):900. https://doi.org/10.3390/foods9070900
Chicago/Turabian StyleŠegatin, Nataša, Tanja Pajk Žontar, and Nataša Poklar Ulrih. 2020. "Dielectric Properties and Dipole Moment of Edible Oils Subjected to ‘Frying’ Thermal Treatment" Foods 9, no. 7: 900. https://doi.org/10.3390/foods9070900
APA StyleŠegatin, N., Pajk Žontar, T., & Poklar Ulrih, N. (2020). Dielectric Properties and Dipole Moment of Edible Oils Subjected to ‘Frying’ Thermal Treatment. Foods, 9(7), 900. https://doi.org/10.3390/foods9070900






