Study on Spatial Effects of Influencing Factors and Zoning Strategies for PM2.5 and CO2 Synergistic Reduction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Evaluation Index for PM2.5 and CO2 Reductions
2.3. Multiscale Geographically Weighted Regression
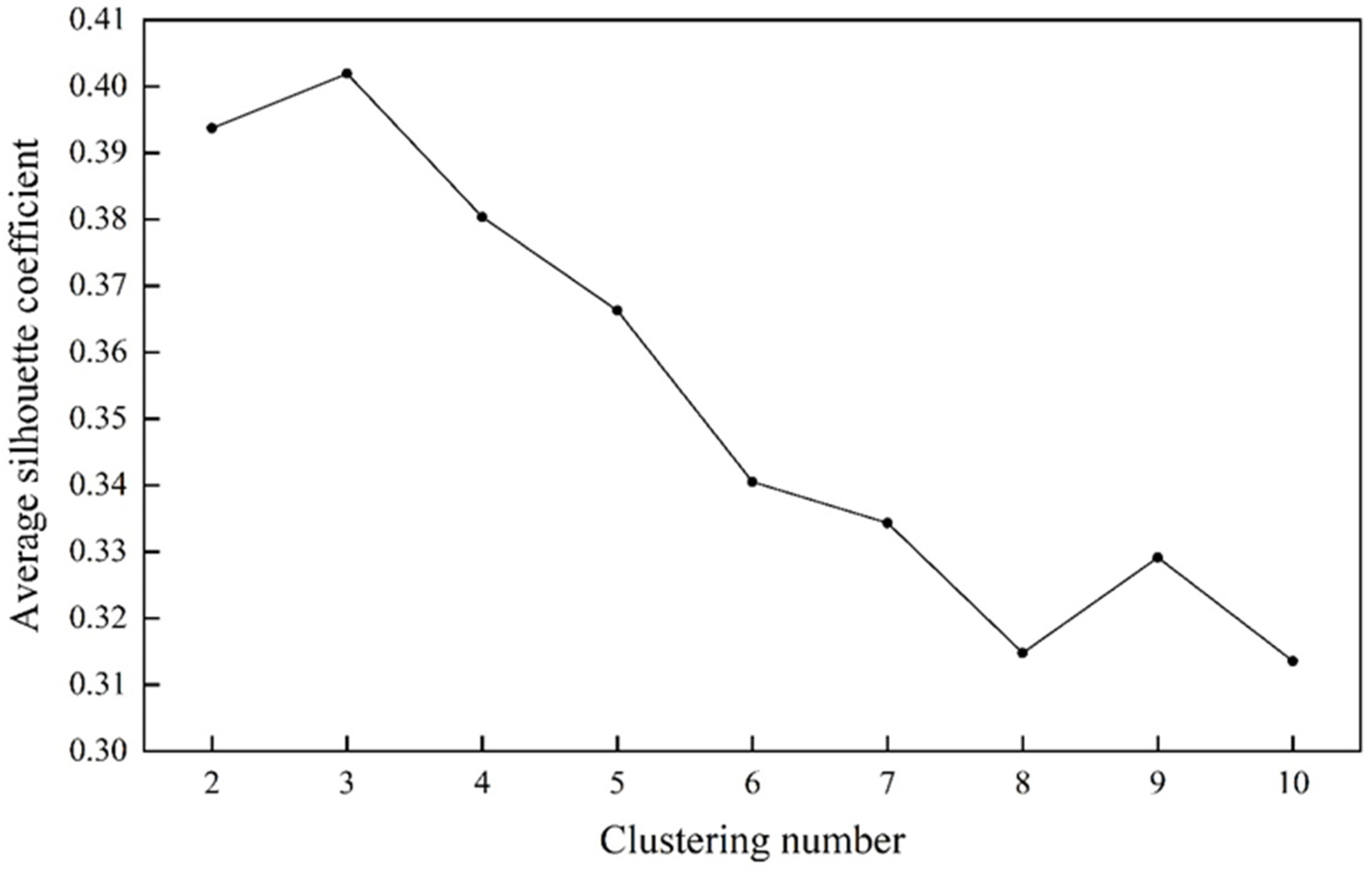
2.4. K-Means Clustering
3. Results
3.1. Spatial Characteristics of Reduction Indexes
3.2. Spatial Characteristics of Coefficients in MGWR
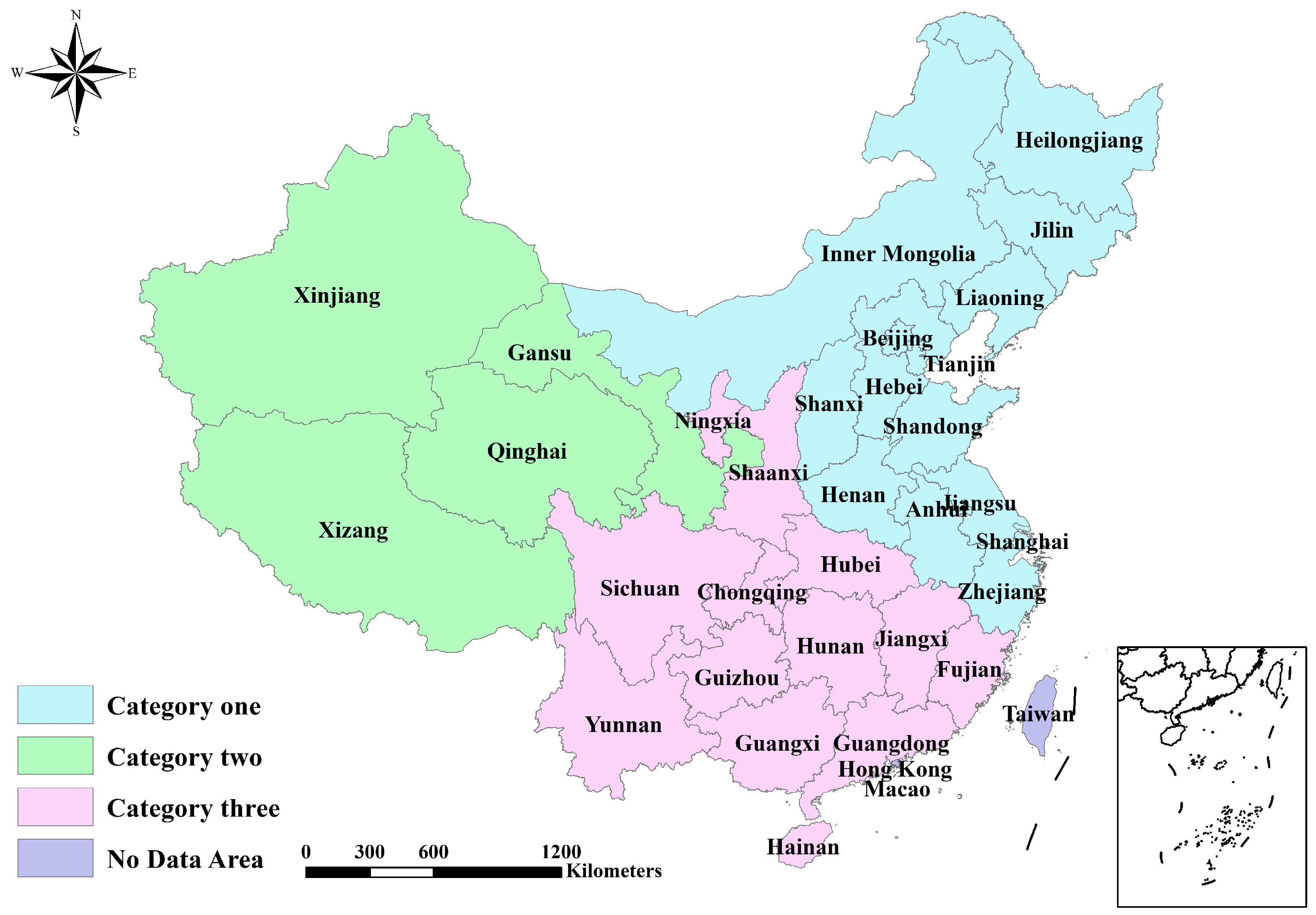
3.3. Clustering and Zoning of Provinces
4. Discussion
4.1. Analysis of Influencing Factors and Their Spatial Effects
4.2. Zoning Features and Policy Implications
4.3. Research Limitations and Future Prospects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, F.; Xie, Y.; Zhou, D. Air pollution’s impact on the settlement intention of domestic migrants: Evidence from China. Environ. Impact Assess. Rev. 2022, 95, 106761. [Google Scholar] [CrossRef]
- Wang, K.-L.; Xu, R.-Y.; Jiang, W.; Liu, Y. Impact of National Industrial Relocation Demonstration Zones (NIRDZs) policy on urban carbon emissions in China. Environ. Impact Assess. Rev. 2023, 102, 107165. [Google Scholar] [CrossRef]
- Shi, Q.; Zheng, B.; Zheng, Y.; Tong, D.; Liu, Y.; Ma, H.; Hong, C.; Geng, G.; Guan, D.; He, K.; et al. Co-benefits of CO2 emission reduction from China’s clean air actions between 2013–2020. Nat. Commun. 2022, 13, 5061. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Niu, Y.; Li, M.; Yu, Q.; Chen, W. Spatial structure and carbon emission of urban agglomerations: Spatiotemporal characteristics and driving forces. Sustain. Cities Soc. 2022, 78, 103600. [Google Scholar] [CrossRef]
- Xian, B.; Xu, Y.; Chen, W.; Wang, Y.; Qiu, L. Co-benefits of policies to reduce air pollution and carbon emissions in China. Environ. Impact Assess. Rev. 2024, 104, 107301. [Google Scholar] [CrossRef]
- Zhang, Q.; Yin, Z.; Lu, X.; Gong, J.; Lei, Y.; Cai, B.; Cai, C.; Chai, Q.; Chen, H.; Dai, H.; et al. Synergetic roadmap of carbon neutrality and clean air for China. Environ. Sci. Ecotechnol. 2023, 16, 100280. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Yang, X.; Zhu, J.; Jiang, P.; Lin, H.; Cai, Z.; Huang, H.; Long, J. Synergic emissions reduction effect of China’s “Air Pollution Prevention and Control Action Plan”: Benefits and efficiency. Sci. Total Environ. 2022, 847, 157564. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Tan, Z.; Wang, J.; Zhang, L.; He, X.; Mu, S. Spatial and temporal evolution of synergizing the reduction of pollution and carbon emissions and examination on comprehensive pilot effects–evidence from the national eco-industrial demonstration parks in China. Environ. Impact Assess. Rev. 2023, 101, 107147. [Google Scholar] [CrossRef]
- Portugal-Pereira, J.; Koberle, A.; Lucena, A.F.P.; Rochedo, P.R.R.; Império, M.; Carsalade, A.M.; Schaeffer, R.; Rafaj, P. Interactions between global climate change strategies and local air pollution: Lessons learnt from the expansion of the power sector in Brazil. Clim. Chang. 2018, 148, 293–309. [Google Scholar] [CrossRef]
- Jiao, J.; Huang, Y.; Liao, C. Co-benefits of reducing CO2 and air pollutant emissions in the urban transport sector: A case of Guangzhou. Energy Sustain. Dev. 2020, 59, 131–143. [Google Scholar] [CrossRef]
- Wei, X.; Tong, Q.; Magill, I.; Vithayasrichareon, P.; Betz, R. Evaluation of potential co-benefits of air pollution control and climate mitigation policies for China’s electricity sector. Energ. Econ. 2020, 92, 104917. [Google Scholar] [CrossRef]
- Mao, X.; Zeng, A.; Hu, T.; Zhou, J.; Xing, Y.; Liu, S. Co-control of local air pollutants and CO2 in the Chinese iron and steel industry. Environ. Sci. Technol. 2013, 47, 12002–12010. [Google Scholar] [CrossRef] [PubMed]
- Adila, A.; Jiang, P. Synergy and co-benefits of reducing CO2 and air pollutant emissions by promoting electric vehicles—A case of Shanghai. Energy Sustain. Dev. 2020, 55, 181–189. [Google Scholar]
- Chen, Y.; Zhao, Z.; Yi, W.; Hong, J.; Zhang, B. Has China achieved synergistic reduction of carbon emissions and air pollution? Evidence from 283 Chinese cities. Environ. Impact Assess. Rev. 2023, 103, 107277. [Google Scholar] [CrossRef]
- Lu, Z.; Huang, L.; Liu, J.; Zhou, Y.; Chen, M.; Hu, J. Carbon dioxide mitigation co-benefit analysis of energy-related measures in the Air Pollution Prevention and Control Action Plan in the Jing-Jin-Ji region of China. Resour. Conserv. Recycl. X 2019, 1, 100006. [Google Scholar] [CrossRef]
- Xue, B.; Ma, Z.; Geng, Y.; Heck, P.; Ren, W.; Tobias, M.; Maas, A.; Jiang, P.; Puppim de Oliveira, J.A.; Fujita, T. A life cycle co-benefits assessment of wind power in China. Renew. Sustain. Energy Rev. 2015, 41, 338–346. [Google Scholar] [CrossRef]
- Dong, H.; Dai, H.; Dong, L.; Fujita, T.; Geng, Y.; Klimont, Z.; Inoue, T.; Bunya, S.; Fujii, M.; Masui, T. Pursuing air pollutant co-benefits of CO2 mitigation in China: A provincial leveled analysis. Appl. Energy 2015, 144, 165–174. [Google Scholar] [CrossRef]
- Liu, F.; Klimont, Z.; Zhang, Q.; Cofala, J.; Zhao, L.; Huo, H.; Nguyen, B.; Schöpp, W.; Sander, R.; Zheng, B.; et al. Integrating mitigation of air pollutants and greenhouse gases in Chinese cities: Development of GAINS-City model for Beijing. J. Clean. Prod. 2013, 58, 25–33. [Google Scholar] [CrossRef]
- Hernández, K.D.; Fajardo, O.A. Estimation of industrial emissions in a Latin American megacity under power matrix scenarios projected to the year 2050 implementing the LEAP model. J. Clean. Prod. 2021, 303, 126921. [Google Scholar] [CrossRef]
- Kuylenstierna, J.C.I.; Heaps, C.G.; Ahmed, T.; Vallack, H.W.; Hicks, W.K.; Ashmore, M.R.; Malley, C.S.; Wang, G.; Lefèvre, E.N.; Anenberg, S.C.; et al. Development of the Low Emissions Analysis Platform—Integrated Benefits Calculator (LEAP-IBC) tool to assess air quality and climate co-benefits: Application for Bangladesh. Environ. Int. 2020, 145, 106155. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Ma, X.; Chen, B.; Shang, Y.; Song, M. Challenges toward carbon neutrality in China: Strategies and countermeasures. Resour. Conserv. Recycl. 2022, 176, 105959. [Google Scholar] [CrossRef]
- She, Q.; Cao, S.; Zhang, S.; Zhang, J.; Zhu, H.; Bao, J.; Meng, X.; Liu, M.; Liu, Y. The impacts of comprehensive urbanization on PM2.5 concentrations in the Yangtze River Delta, China. Ecol. Indic. 2021, 132, 108337. [Google Scholar] [CrossRef]
- Kılkış, Ş.; Krajačić, G.; Duić, N.; Rosen, M.A.; Al-Nimr, M.d.A. Advances in integration of energy, water and environment systems towards climate neutrality for sustainable development. Energy Convers. Manag. 2020, 225, 113410. [Google Scholar] [CrossRef]
- Jia, Z.; Lin, B. How to achieve the first step of the carbon-neutrality 2060 target in China: The coal substitution perspective. Energy 2021, 233, 121179. [Google Scholar] [CrossRef]
- Fu, Z.; Li, R. The contributions of socioeconomic indicators to global PM2.5 based on the hybrid method of spatial econometric model and geographical and temporal weighted regression. Sci. Total Environ. 2020, 703, 135481. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, F.; Tang, Z.; Tang, J. Predictions and driving factors of production-based CO2 emissions in Beijing, China. Sustain. Cities Soc. 2020, 53, 101909. [Google Scholar] [CrossRef]
- Zhu, L.; Hao, Y.; Lu, Z.-N.; Wu, H.; Ran, Q. Do economic activities cause air pollution? Evidence from China’s major cities. Sustain. Cities Soc. 2019, 49, 101593. [Google Scholar] [CrossRef]
- Jiang, F.; Chen, B.; Li, P.; Jiang, J.; Zhang, Q.; Wang, J.; Deng, J. Spatio-temporal evolution and influencing factors of synergizing the reduction of pollution and carbon emissions—Utilizing multi-source remote sensing data and GTWR model. Environ. Res. 2023, 229, 115775. [Google Scholar] [CrossRef] [PubMed]
- Yi, H.; Zhao, L.; Qian, Y.; Zhou, L.; Yang, P. How to achieve synergy between carbon dioxide mitigation and air pollution control? Evidence from China. Sustain. Cities Soc. 2022, 78, 103609. [Google Scholar] [CrossRef]
- Hu, J. Synergistic effect of pollution reduction and carbon emission mitigation in the digital economy. J. Environ. Manag. 2023, 337, 117755. [Google Scholar] [CrossRef] [PubMed]
- Makov, T.; Meshulam, T.; Cansoy, M.; Shepon, A.; Schor, J.B. Digital food sharing and food insecurity in the COVID-19 era. Resour. Conserv. Recycl. 2023, 189, 106735. [Google Scholar] [CrossRef] [PubMed]
- Holzmann, P.; Gregori, P. The promise of digital technologies for sustainable entrepreneurship: A systematic literature review and research agenda. Int. J. Inf. Manag. 2023, 68, 102593. [Google Scholar] [CrossRef]
- Gao, X.; Liu, N.; Hua, Y. Environmental Protection Tax Law on the synergy of pollution reduction and carbon reduction in China: Evidence from a panel data of 107 cities. Sustain. Prod. Consum. 2022, 33, 425–437. [Google Scholar] [CrossRef]
- Li, M.; Zhang, D.; Li, C.-T.; Mulvaney, K.M.; Selin, N.E.; Karplus, V.J. Air quality co-benefits of carbon pricing in China. Nat. Clim. Chang. 2018, 8, 398–403. [Google Scholar] [CrossRef]
- Li, Z.; Bai, T.; Tang, C. How does the low-carbon city pilot policy affect the synergistic governance efficiency of carbon and smog? Quasi-experimental evidence from China. J. Clean. Prod. 2022, 373, 133809. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically weighted regression: A natural evolution of the expansion method for spatial data analysis. Environ. Plann. A Econ. Space 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Mansour, S.; Al Kindi, A.; Al-Said, A.; Al-Said, A.; Atkinson, P. Sociodemographic determinants of COVID-19 incidence rates in Oman: Geospatial modelling using multiscale geographically weighted regression (MGWR). Sustain. Cities Soc. 2021, 65, 102627. [Google Scholar] [CrossRef] [PubMed]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, F.; Zhang, H.; Dong, J. Mechanisms of non-stationary influence of urban form on the diurnal thermal environment based on machine learning and MGWR analysis. Sustain. Cities Soc. 2024, 101, 105194. [Google Scholar] [CrossRef]
- Hering, L.; Poncet, S. Environmental policy and exports: Evidence from Chinese cities. J. Environ. Econ. Manag. 2014, 68, 296–318. [Google Scholar] [CrossRef]
- Zhai, H.; Yao, J.; Wang, G.; Tang, X. Study of the effect of vegetation on reducing atmospheric pollution particles. Remote Sens. 2022, 14, 1255. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, W.; Shi, H. Regional environmental efficiency in China: Analysis based on a regional slack-based measure with environmental undesirable outputs. Ecol. Indic. 2016, 71, 218–228. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, W.; Wang, J.; Yang, F.; Jiang, H. Regional low-carbon economy efficiency in China: Analysis based on the Super-SBM model with CO2 emissions. J. Clean. Prod. 2017, 163, 202–211. [Google Scholar] [CrossRef]
- Jia, Z.; Cai, Y.; Chen, Y.; Zeng, W. Regionalization of water environmental carrying capacity for supporting the sustainable water resources management and development in China. Resour. Conserv. Recycl. 2018, 134, 282–293. [Google Scholar] [CrossRef]

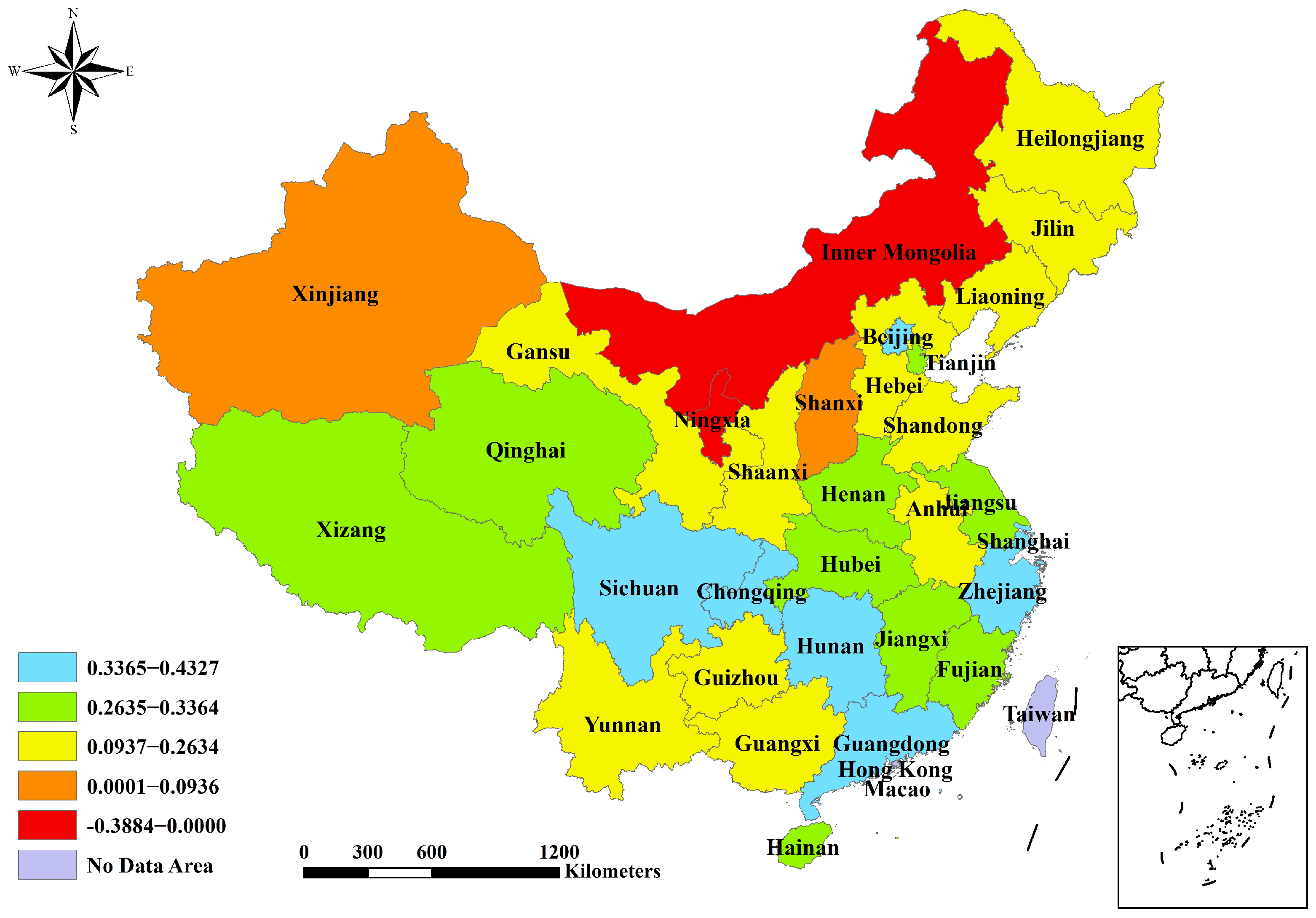
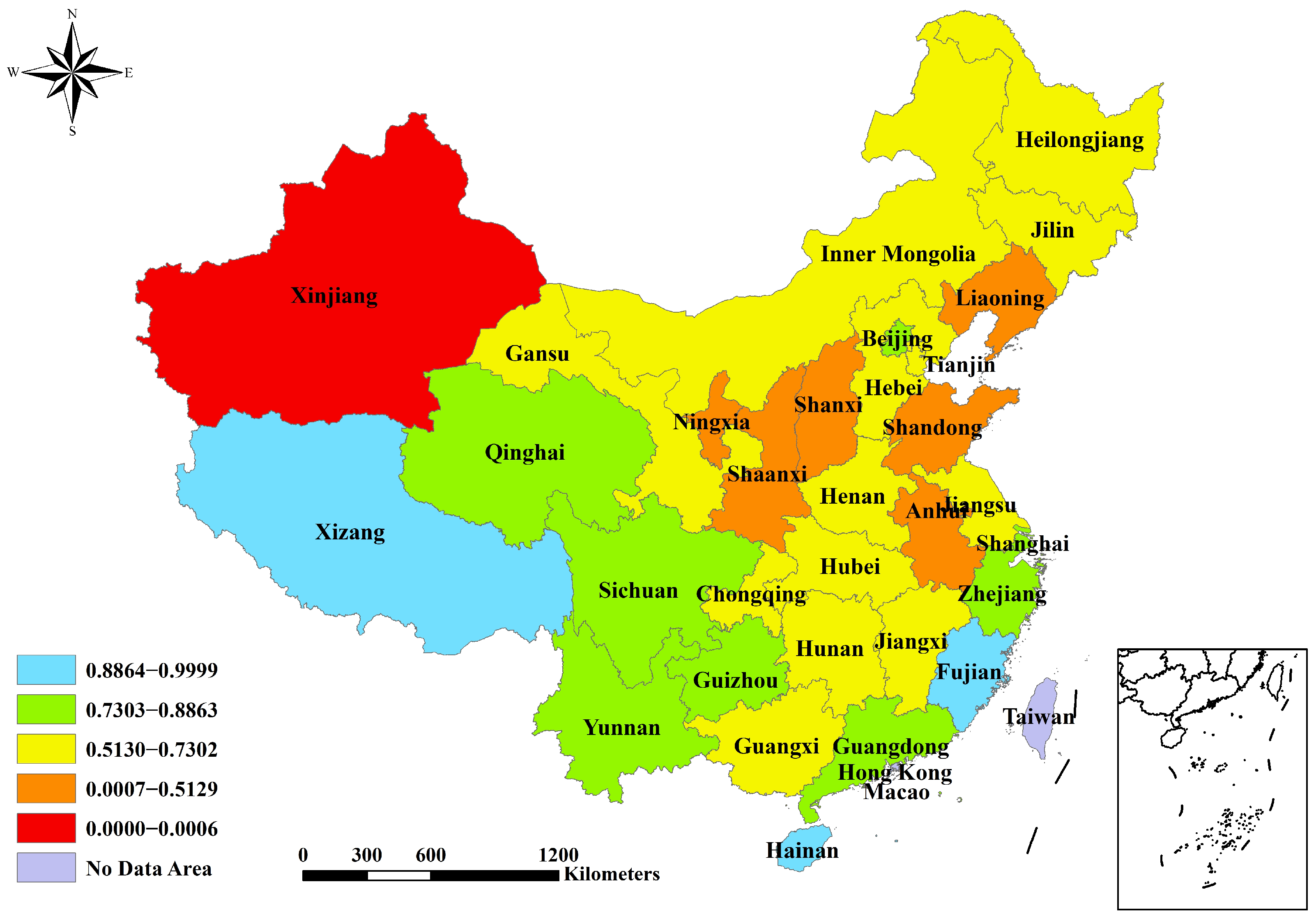

| Province | EIPC | ||
|---|---|---|---|
| Beijing | 0.6605 | 0.4327 | 0.7904 |
| Tianjin | 0.5300 | 0.3364 | 0.6562 |
| Hebei | 0.6113 | 0.1506 | 0.6584 |
| Shanxi | 0.3606 | 0.0936 | 0.3967 |
| Inner Mongolia | 0.6098 | −0.0811 | 0.5858 |
| Liaoning | 0.3454 | 0.1966 | 0.4256 |
| Jilin | 0.5822 | 0.2624 | 0.6710 |
| Heilongjiang | 0.5740 | 0.2189 | 0.6482 |
| Shanghai | 0.6794 | 0.3848 | 0.7883 |
| Jiangsu | 0.5363 | 0.3307 | 0.6590 |
| Zhejiang | 0.7799 | 0.3532 | 0.8515 |
| Anhui | 0.3954 | 0.2522 | 0.4997 |
| Fujian | 0.8724 | 0.3249 | 0.9120 |
| Jiangxi | 0.6252 | 0.2989 | 0.7194 |
| Shandong | 0.3494 | 0.2634 | 0.4610 |
| Henan | 0.4785 | 0.3177 | 0.6047 |
| Hubei | 0.5522 | 0.3300 | 0.6717 |
| Hunan | 0.4253 | 0.3485 | 0.5729 |
| Guangdong | 0.8002 | 0.3674 | 0.8685 |
| Guangxi | 0.6613 | 0.2397 | 0.7302 |
| Hainan | 0.9820 | 0.3174 | 0.9877 |
| Chongqing | 0.5416 | 0.3533 | 0.6726 |
| Sichuan | 0.6730 | 0.3531 | 0.7740 |
| Guizhou | 0.7849 | 0.2572 | 0.8353 |
| Yunnan | 0.7389 | 0.2510 | 0.7972 |
| Xizang | 0.9999 | 0.3347 | 0.9999 |
| Shaanxi | 0.4152 | 0.2403 | 0.5129 |
| Gansu | 0.6817 | 0.1421 | 0.7198 |
| Qinghai | 0.8453 | 0.2822 | 0.8863 |
| Ningxia | 0.3973 | −0.3884 | 0.2776 |
| Xinjiang | 0.0005 | 0.0293 | 0.0006 |
| Diagnostic Information | OLS | GWR | MGWR |
|---|---|---|---|
| AICc | 82.605 | 82.390 | 76.671 |
| R2 | 0.778 | 0.807 | 0.928 |
| Adj. R2 | 0.667 | 0.684 | 0.857 |
| Variable | Maximum | Minimum | Mean | Standard Deviation |
|---|---|---|---|---|
| ACL | 0.5692 | 0.5682 | 0.5686 | 0.0002 |
| TRL | −0.4233 | −0.4248 | −0.4241 | 0.0003 |
| NDVI | 1.1436 | 1.1422 | 1.1429 | 0.0003 |
| FCR | 0.8499 | 0.8475 | 0.8490 | 0.0005 |
| SVF | 0.2160 | 0.1803 | 0.1972 | 0.0083 |
| GDP | −0.1266 | −0.1290 | −0.1279 | 0.0006 |
| PTI | 0.1715 | 0.1706 | 0.1709 | 0.0001 |
| ERE | 1.2097 | 0.2507 | 0.5887 | 0.2110 |
| ENP | −0.0158 | −0.6201 | −0.1100 | 0.1231 |
| NED | 0.1603 | 0.1592 | 0.1598 | 0.0002 |
| Variable | OLS | GWR | MGWR | |||
|---|---|---|---|---|---|---|
| β | p-Value | β (Mean) | p-Value (Mean) | β (Mean) | p-Value (Mean) | |
| ACL | 0.398 | 0.070 *** | 0.405 | 0.062 *** | 0.569 | 0.001 * |
| TRL | −0.371 | 0.044 ** | −0.370 | 0.043 ** | −0.424 | 0.001 * |
| NDVI | 0.961 | 0.008 * | 0.967 | 0.009 * | 1.143 | 0.000 * |
| FCR | 0.880 | 0.003 * | 0.873 | 0.004 * | 0.849 | 0.000 * |
| SVF | 0.277 | 0.054 *** | 0.273 | 0.056 *** | 0.197 | 0.073 *** |
| GDP | −0.137 | 0.434 | −0.133 | 0.430 | −0.128 | 0.281 |
| PTI | 0.196 | 0.147 | 0.191 | 0.148 | 0.171 | 0.062 *** |
| ERE | 0.786 | 0.000 * | 0.762 | 0.000 * | 0.589 | 0.005 * |
| ENP | −0.041 | 0.095 *** | −0.032 | 0.080 *** | −0.061 | 0.058 *** |
| NED | 0.180 | 0.356 | 0.177 | 0.348 | 0.160 | 0.255 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Z.; Sun, S.; Zhao, D.; Bo, Y.; Wang, Z. Study on Spatial Effects of Influencing Factors and Zoning Strategies for PM2.5 and CO2 Synergistic Reduction. Toxics 2024, 12, 498. https://doi.org/10.3390/toxics12070498
Jia Z, Sun S, Zhao D, Bo Y, Wang Z. Study on Spatial Effects of Influencing Factors and Zoning Strategies for PM2.5 and CO2 Synergistic Reduction. Toxics. 2024; 12(7):498. https://doi.org/10.3390/toxics12070498
Chicago/Turabian StyleJia, Zimu, Shida Sun, Deming Zhao, Yu Bo, and Zifa Wang. 2024. "Study on Spatial Effects of Influencing Factors and Zoning Strategies for PM2.5 and CO2 Synergistic Reduction" Toxics 12, no. 7: 498. https://doi.org/10.3390/toxics12070498
APA StyleJia, Z., Sun, S., Zhao, D., Bo, Y., & Wang, Z. (2024). Study on Spatial Effects of Influencing Factors and Zoning Strategies for PM2.5 and CO2 Synergistic Reduction. Toxics, 12(7), 498. https://doi.org/10.3390/toxics12070498







