Simplified Approach to Predict Food Safety through the Maximum Specific Bacterial Growth Rate as Function of Extrinsic and Intrinsic Parameters

Abstract

Currently, we assist the emergence of sensors and low-cost information and communication technologies applied to food products, in order to improve food safety and quality along the food chain. Thus, it is relevant to implement predictive mathematical modeling tools in order to predict changes in the food quality and allow decision-making for expiration dates. To perform that, the Baranyi and Roberts model and the online tool Combined Database for Predictive Microbiology (Combase) were used to determine the factors that define the growth of different bacteria. These factors applied to the equation that determines the maximum specific growth rate establish a relation between the bacterial growth and the intrinsic and extrinsic factors that define the bacteria environment. These models may be programmed in low-cost wireless biochemical sensor devices applied to packaging and food supply chains to promote food safety and quality through real time traceability.

1. Introduction

The validity periods presented in the traditional labels of perishable products are described as the period during which a stored product remains safe and retains the desired properties and qualities for consumption [1,2]. Usually, one of two types of validity periods are applied: one is the expiration date that limits the period of time for which perishable food remains safe for human consumption; the other is “consumption before” that indicates the estimated time for consumption during which the food will be able to maintain its nutritional properties if it is preserved in the recommended conditions [2].

However, sometimes deviations occur that alter the desired conditions of perishable foods preservation and maintenance, compromising the quality of the products. When this happens, differences result between the actual remaining useful life and with the shelf-life described in the label. For this reason, many countries require regulations so that food has an indication of appropriate durability on the packaging in order to indicate the supposed end of its useful life. Therefore, with the determination through traditional methods of the expiration date, it is not possible to determine the useful life of a product when it has been adulterated [1].

The current world’s digitalization brings several benefits to food supply chains and to the consumer. New technologies based on biochemical sensors and low-cost information and communication technologies (ICT), mostly focusing on Internet of Things (IoT), can be applied to solve old paradigms and mitigate inefficiencies. Particularly, it can be applied to food product traceability, promoting better planning and coordination among the different stages of the supply chain, in terms of the product’s remaining shelf life, and supply and demand of fresh food [3]. These technologies have been integrated in packaging, developing the concept of intelligent or smart packaging [4]. This package is able to provide additional real time data besides the current regular information available such as origin, validity date, organization, nutritional composition, among others. It may inform and/or advise producers, retailers, or consumers about the product traceability considering routes, extrinsic parameters e.g., temperature (T), relative humidity (RH) and atmosphere and intrinsic parameters, e.g., water activity (a_w), hydrogen potential (pH), oxidation-reduction potential, chemical composition and biological structure of the food as well as its anti-microbial substances, microbial development, among others [5].

Intelligent packaging can provide information concerning food quality, safety and the history of a product during transport and storage, through the six main functions of intelligent packaging: monitoring, detecting, sensing, recording, tracking and communicating [6].

In this sense, the development and implementation of predictive mathematical modeling tools is an effective way to predict changes in food quality and enable decision-making regarding shelf life [1,7]. These models can be integrated as decisive data information for a better functioning of several sensors and indicators in intelligent food packaging. In smart packaging, indicators are usually applied, which are devices that can determine the presence or absence, the extent of the reaction between two or more substances or the concentration of a particular substance. This information is transmitted to the user through an irreversible and visible color change [8,9,10]. On the other hand, sensors are electronic devices or tools that can detect, quantify and convert a signal to an electrical signal using transducers. Most sensors are composed of two parts: the first one can detect the presence, activity, composition or concentration of certain chemical or physical analytes, such as pH, humidity, color and biological compounds. Physical or chemical information is also converted by the sensor into a form of energy that can be measured by the second component, the transducer [9,10]. These two concepts are often confused and alternately applied to smart packaging, since the indicator refers to a colorimetric sensor normally consisting of a chemical sensor or a biosensor [11]. Some types of sensors used in intelligent packaging are physical sensors, chemical sensors, gas sensors and biosensors. Smart packaging with a sensor that monitors the packaged food product and its environment throughout the supply chain is really helpful and important in ensuring the food quality and safety for end consumers [12].

There is a growing diversity of strategies available in the food industry to improve product quality and reduce food waste, as it is a reality that exists worldwide. This waste is also due to the food damage along all the food chain, from the producer until the final consumer, to the point when the food security is compromised [13]. To talk about food security, it is necessary to know what causes the food deterioration and make them unhealthy, as well as the conditions it happens [7]. The answer is the bacterial growth in the food. Each bacteria grows at a different rhythm and under different conditions [7] depending on intrinsic and extrinsic factors. Despite all factors contributing to bacterial growth, temperature, pH and water activity, are considered to be the most influent [14], and can be directly used in the mathematical models.

The experimental study of bacterial growth allowed biologists to create a growth curve [15]. In 1993, Baranyi and, in 1994, Baranyi and Roberts, created a model able to represent that growth curve, which is showed in Equation (1) [16,17].

$$\begin{array}{c}y\left(t\right)=y_0+{\mu }_{max}t+\frac{1}{{\mu }_{max}}\ln \left(e^{-vt}+e^{-h_0}-e^{-vt-h_0}\right)+\dots \\ \dots -\frac{1}{m}\ln \left(1+\frac{e^{m{\mu }_{max}t+\frac{1}{{\mu }_{max}}\ln \left(e^{-vt}+e^{-h_0}-e^{-vt-h_0}\right)}-1}{e^{m\left(y_{max}-y_0\right)}}\right)\end{array}$$

(1)

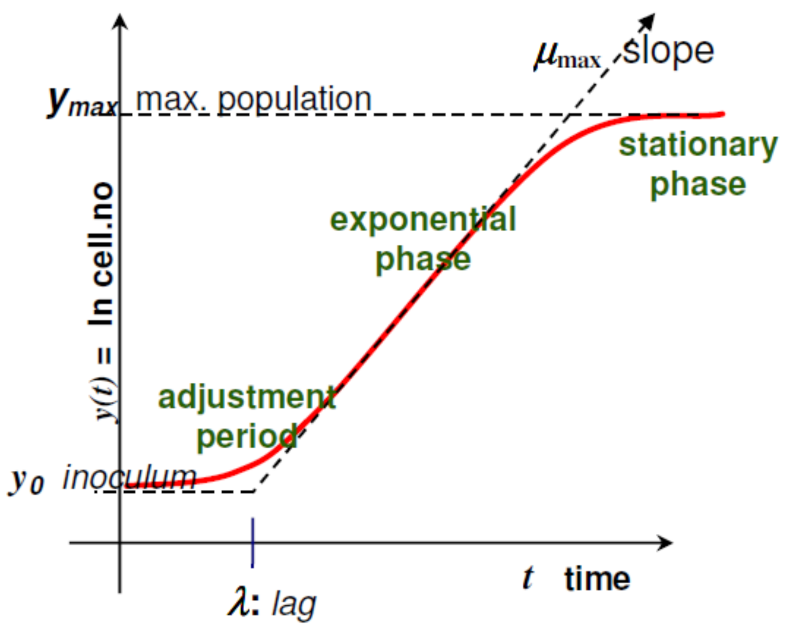
The relation between this model variables and the microbial growth curve can be visualized in Figure 1 and is explained in detail [18,19]:

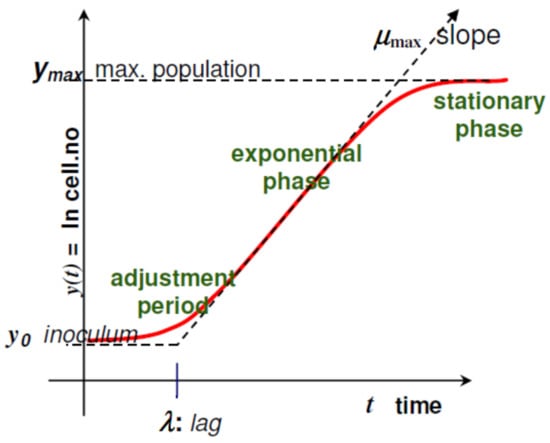
Figure 1. Relation between the growth curve and the Baranyi and Roberts model variables (Reprinted from ref. [19]).

• $y\left(t\right)$ is the same as $\ln \left(x\left(t\right)\right)$ where $x\left(t\right)$ is the number of colony-forming unit (CFU)/g;
• $y_0$ is the initial value of CFU/g (scaled logarithmically) and its value derived from Tables 1–6 is shown as result in Table 7;
• $y_{max}$ is the maximum value of CFU/g (scaled logarithmically) and its value is also defined in Table 7;
• µmax is the maximum specific growth rate and its value is affected by intrinsic and extrinsic factors;
• $h_0$ is a constant defined by $h_0=-\ln \left({\propto }_0\right)$, where ${\propto }_0$ is the physiological state; It is also related with $\lambda$ (lag phase), where $\lambda =\frac{h_0}{{\mu }_{max}}$;
• $m$ is the parameter that define the curvature between the exponential and stationary phase;
• $n_c$ is the parameter that define the curvature between the initial and exponential phase through the equation $n_c=\frac{v}{{\mu }_{max}}$;
• $t$ is the time since the beginning of the bacteria growth.

As stated above, new technologies applied to the packaging and food supply chain to promote food safety and quality through real time traceability need to engage low cost, effective biochemical sensors and ICT. In this case, it is intended to apply predictive mathematical models of bacterial growth according to temperature, pH and water activity as a freshness sensor or indicator. Thus, the freshness sensor can be defined as a device that has the ability to feel the freshness of the food related to the environment inside or outside the packaging and inform about the food quality and safety. There are diverse commercially available sensors and indicators for freshness monitoring of food packaging, such as Freshtag^® (COX Technologies), Sensorq^® (DSM NV and Food Quality Sensor International), among others [11].

However, the computational requirements to predict bacterial growth curves that can be used to predict food safety and quality are substantial for the system requisites.

In this context, the maximum specific growth rate, µ_max, represents, in the bacterial growth curve, how intrinsic and extrinsic factors affect the bacterial development, being manifested in distinct ways for each bacteria.

Of the various models that relate µ_max with temperature (T), pH and water activity (a_w), the Masana & Baranyi model will be used, presented in Equation (2) [20]:

$$\begin{array}{c}\ln \left({\mu }_{max}\right)=a_0+a_1·T+a_2·\mathrm{pH}+a_3·b_w+a_4·T·\mathrm{pH}+\dots \\ \dots +a_5·T·b_w+a_6·\mathrm{pH}·b_w+a_7·T^2+a_8·{\mathrm{pH}}^2+a_9·b_w{}^2\end{array}$$

(2)

where a_i are the coefficients to be estimated, T and pH are respectively the values of temperature (°C) and pH, and b_w is calculated through [21]:

$$b_w=\sqrt{1-a_w}$$

(3)

The Equation (2) applied in Equation (1) allows to have the parameters that define intrinsic and extrinsic factors in Baranyi and Roberts model.

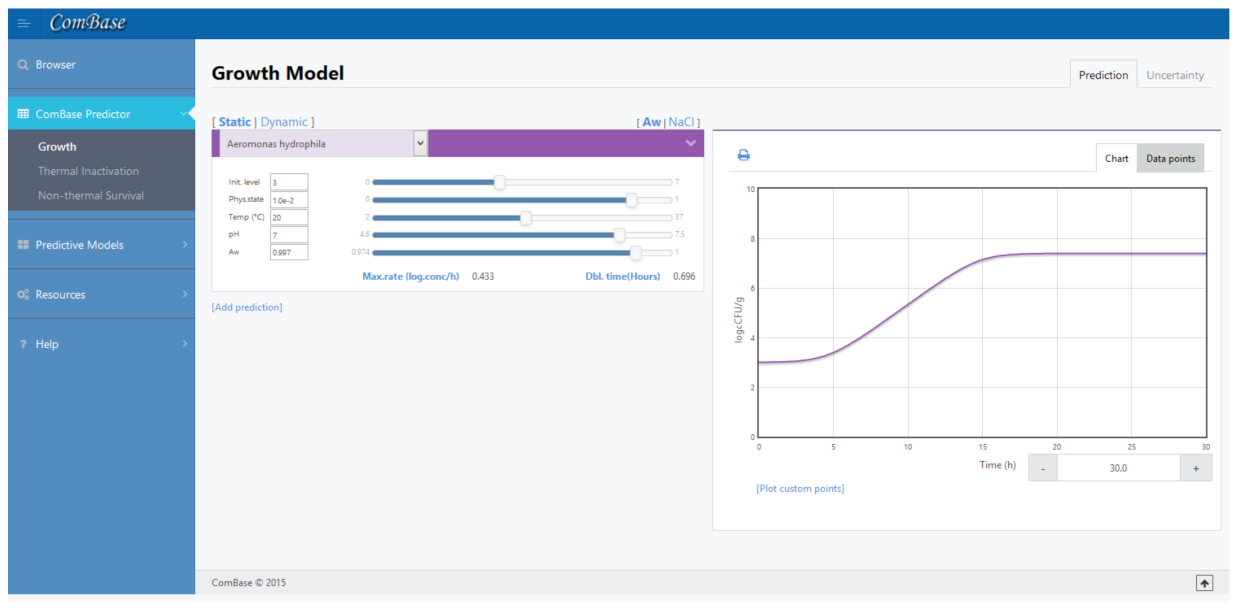
Online tool Combase Predictor [22] uses the link of these two equations to present the growth curve of a previous selected bacteria when subjected to environment conditions previously defined by the user. This interface, defined in Figure 2, also presents the value of ${\mathit{\mu }}_{max}$, that allows to estimate the coefficients of Equation (2).

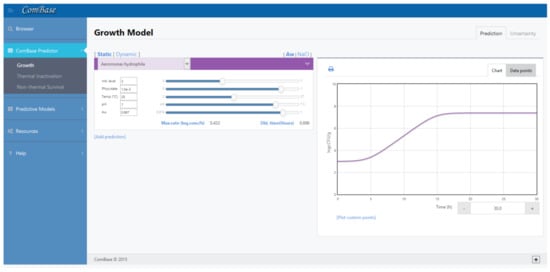
Figure 2. Example of ComBase Predictor (available online in www.ComBase.com, accessed on 3 March 2021).

ComBase is a highly useful tool, with over 60,000 records, to understand safer ways of producing and storing foods. These data were obtained from scientific literature and produced by diverse institutions. Each data record allows users know how bacteria populations change for a particular combination of environmental factors, and, thus, gives predictions from models based on selected data as a function of environmental factors such as temperature, pH and water activity.

Thus, the paper describes a simplified approach to predict food safety through the maximum specific bacterial growth rate as a function of extrinsic and intrinsic parameters. The model coefficients developed in this paper allow for the use of bacterial growth curve models to predict food safety in low-cost computational requirements devices, contributing in this sense to the development of technologies that improve food systems.

2. Materials and Methods

To estimate a_i values, will be used the online tool available in www.ComBase.com (accessed on 3 March 2021). This way will only be considered some bacteria presented on the referred tool:

• Aeromonas hydrophila;
• Bacillus cereus;
• Bacillus licheniformis;
• Bacillus subtilis;
• Clostridium botulinum;
• Clostridium perfringens;
• Escherichia coli;
• Listeria monocytogenes;
• Salmonella;
• Shigella flexneri;
• Staphylococcus aureus;
• Yersinia enterocolitica;
• Brochothrix thermosphacta;
• Pseudomonas.

Interventional studies involving animals or humans, and other studies that require ethical approval, must list the authority that provided approval and the corresponding ethical approval code.

2.1. Determination of the Maximum Specific Growth Rate

The coefficients ai varies from 0 to 9 and are used in Equation (2). These coefficients will be estimated for the calculation of the value of the maximum specific growth rate for any temperature, pH and aw for any bacteria. Thus, to determine the maximum specific growth rate to each bacteria is necessary to get the values of these coefficients of Equation (2), as will be described below. To do that, the value of maximum specific growth rate obtained in the referred online tool is used, together with the values of temperature, pH and water activity that give origin to that value of µ_max.

2.2. Calculation of Coefficients

Once the experimental procedure of calculation is the same for all the bacteria, is used only as one example of demonstration. Thus, the values of a_i to the Brochothrix thermosphacta bacteria will be estimated. To do that, with Combase, Table 1 with different combinations of values of temperature, pH and a_w (and b_w) is constructed and, after, with those conditions the maximum specific growth rate is verified.

Table 1. Maximum specific growth rate to different values of temperature (T), pH and water activity (a_w), to the bacteria Brochothrix thermosphacta.

Input
T [°C]	pH	aw	µmax
1	5.50	0.950	0.012
1	6.25	0.975	0.027
1	7.00	0.95	0.011
15	5.50	1.000	0.132
15	6.25	1.000	0.247
30	5.50	0.950	0.028
30	6.25	0.950	0.061
30	7.00	0.950	0.066
30	7.00	0.975	0.145
30	7.00	1.000	0.313

From those values, Table 2 is constructed, where are presented the a_i. factors. This table will be used as a matrix, Matrix A, with 10 rows and 10 columns. Another matrix, Matrix B, with 10 rows and 1 column, is made with the values of ln(µ_max), which also included in Table 2.

Table 2. Matrix A and Matrix B to the bacteria Brochothrix thermosphacta, using the values of Table 1.

Matrix A										Matrix B
	T	pH	bw	T·pH	T·bw	pH.bw	T2	pH2	bw2	ln(µmax)
1	1	5.50	0.223607	5.50	0.2236068	1.229837388	1	30.2500	0.050	−4.42285
1	1	6.25	0.158114	6.25	0.1581139	0.988211769	1	39.0625	0.025	−3.61192
1	1	7.00	0.223607	7.00	0.2236068	1.565247584	1	49.0000	0.050	−4.50986
1	15	5.50	0	82.5	0	0	225	30.2500	0	−2.02495
1	15	6.25	0	93.75	0	0	225	39.0625	0	−1.39837
1	30	5.50	0.223607	165.00	6.7082039	1.229837388	900	30.2500	0.050	−3.57555
1	30	6.25	0.223607	187.5	6.7082039	1.397542486	900	39.0625	0.050	−2.79688
1	30	7.00	0.223607	210.00	6.7082039	1.565247584	900	49.0000	0.050	−2.71810
1	30	7.00	0.158114	210.00	4.7434165	1.106797181	900	49.0000	0.025	−1.93102
1	30	7.00	0	210.00	0	0	900	49.0000	0	−1.16155

Using a linear equations system, these matrices will be used to calculate the coefficients a₀ to a₉, through the Equation (4).

$$\left[A\right]·\left[a_i\right]=\left[B\right]$$

(4)

That represents a system with 10 equations and 10 unknowns, from which is possible to obtain the values presented in Table 3. These are the estimated values that when applied in Equation (2) permit the calculation of the value of the maximum specific growth rate for any temperature, pH and a_w for any bacteria, in this case for the Brochothrix thermosphacta. Once all these values start to be calculated with an estimation, when compared with Combase Predictor there is a small error associated. Table 4 represents that error for randomly obtained environments.

Table 3. Value of a_i to the bacteria Brochothrix thermosphacta, using the values of Table 1.

ai	Value
a0	−28.3244
a1	0.0976
a2	7.8197
a3	8.0746
a4	0.0217
a5	−0.1346
a6	−0.5496
a7	−0.0051
a8	−0.6221
a9	−31.9812

Table 4. Calculation errors of µ_max using estimated values of a_i.

Input				µmax
T [°C]	pH	aw	µmax	µmax (estimated)	Absolute Error	Relative Error
4.65	5.7	0.960	0.031	0.0313837	3.837 × 10−4	1.2%
17.00	6.8	0.962	0.129	0.1302418	12.418 × 10−4	1.0%
28.00	6.5	0.990	0.257	0.2611274	41.274 × 10−4	1.6%
1.50	6.5	0.990	0.036	0.0360317	0.317 × 10−4	0.1%
1.50	5.8	0.960	0.020	0.0199184	0.816 × 10−4	0.4%
3.50	6.0	0.990	0.051	0.0520164	10.164 × 10−4	2.0%
5.40	6.0	0.997	0.074	0.0746830	6.83 × 10−4	0.9%
20.00	7.0	0.997	0.323	0.3226309	3.691 × 10−4	0.1%
3.00	5.9	0.960	0.027	0.0271576	1.576 × 10−4	0.6%
10.00	6.8	0.960	0.070	0.0702477	2.477 × 10−4	0.4%
23.00	6.0	0.962	0.114	0.1167338	27.338 × 10−4	2.4%

Using the values that would generate the smaller error when estimating a_i coefficients, Table 5 was formulated, which contains these coefficients to the bacteria.

Table 5. Coefficients to determine the maximum specific growth rate to each bacteria.

Microorganism	ai
	a0	a1	a2	a3	a4	a5	a6	a7	a8	a9
Aeromonas hydrophila	−28.0530	0.2469	7.2505	3.1783	0.0067	−0.0561	1.3009	−0.0054	−0.5609	−125.5860
Bacillus cereus	−2.7330	0.1622	−0.8614	1.5969	0.0122	−0.1831	1.2199	−0.0025	0.0720	−59.3343
Bacillus licheniformis	−29.1238	0.4592	6.4417	−12.1128	−0.0053	0.0649	2.7058	−0.0055	−0.4889	−54.4646
Bacillus subtilis	−20.5091	0.2066	4.7178	2.1808	0.0075	0.0456	−1.1555	−0.0025	−0.3835	19.8195
Clostridium botulinum	−32.7539	0.4803	7.6414	26.4667	0	−0.0939	−1.0452	−0.0096	−0.5609	−163.932
Clostridium perfringens	−7.4775	0.2831	0.0580	8.6498	0.0068	0.1154	2.3642	−0.0042	−0.0195	−153.4672
Escherichia coli	−20.3231	0.4115	4.1261	2.2349	0.0002	−0.2249	−0.0415	−0.0060	−0.3162	−31.9882
Listeria monocytogenes	−18.2070	0.2029	3.9028	6.0167	0.0024	0.0408	−0.1241	−0.0028	−0.2886	−43.1797
Salmonella	−12.9739	0.3529	1.8967	6.4026	−0.0048	0.0224	−0.0118	−0.0043	−0.1336	−62.1296
Shigella flexneri	−17.2012	0.4993	1.7936	21.6882	−0.0044	0.3454	−0.5534	−0.0065	−0.1091	−182.8641
Staphylococcus aureus	−18.4275	0.3267	3.8293	−4.5893	0.0029	0.1031	0.9995	−0.0050	−0.3105	−25.0405
Yersinia enterocolitica	−15.3130	0.2159	3.2613	4.7524	−0.0118	0.1356	0.4380	−0.0016	−0.2312	−93.5564
Brochothrix thermosphacta	−28.3244	0.0976	7.8197	8.0746	0.0217	−0.1346	−0.5496	−0.0051	−0.6221	−31.9812
Pseudomonas	−14.0267	0.1571	3.2135	0.4892	0.0005	−0.0371	2.9697	−0.0021	−0.2671	−117.0019

Using the values obtained, Table 6 includes the relative error provided by those values, when subjected to different environments randomly chosen. These errors are divided into:

Table 6. Relative errors in the calculation of µ_max using estimated values of a_i.

Microorganism	Relative Error, er				Total Number of Tests
	er < 5%	5% < er < 10%	10% < er < 15%	er > 15%
Aeromonas hydrophila	45%	23%	7%	25%	60
Bacillus cereus	64%	19%	14%	3%	36
Bacillus licheniformis	62%	24%	10%	5%	21
Bacillus subtilis	100%	0%	0%	0%	21
Clostridium botulinum	86%	10%	5%	0%	21
Clostridium perfringens	95%	5%	0%	0%	20
Escherichia coli	80%	10%	10%	0%	20
Listeria monocytogenes	64%	27%	9%	0%	22
Salmonella	83%	4%	8%	4%	24
Shigella flexneri	86%	5%	10%	0%	21
Staphylococcus aureus	62%	14%	24%	0%	21
Yersinia enterocolitica	76%	14%	5%	5%	21
Brochothrix thermosphacta	100%	0%	0%	0%	21
Pseudomonas	95%	5%	0%	0%	20

• Relative error below 5%, e_r < 5%;
• Relative error between 5% and 10%, 5% < e_r < 10%;
• Relative error between 10% and 15%, 10% < e_r < 15%;
• Relative error above 15%, e_r > 15%.

The values presented in Table 6 corresponds to the number (in percentage) of tests that fit between the limits referred.

2.3. Graphic Generating

Table 5 allows to determine the value of µ_max in order of the intrinsic and extrinsic factors that define a specific bacterial growth environment. This way it is possible to analyze how the temperature, pH and water activity affects the maximum specific growth rate. Since there are no graphics that represent this, a code in MatLab was created that presents a tridimensional graphic with the predictive value of µ_max when changing the three parameters referred. Because is only possible to build graphics until 3 variables, and in this case there is a requirement to see the changes in four parameters, the temperature and the pH were represented in the axes x and y and µ_max in z. To represent how a_w changing affects the maximum specific growth rate, the graphic with the lowest value of a_w was constructed. Then, this value was increased and built the graphic, in the same figure, to this new value. This process was repeated until the maximum value of a_w is reached. This way it is possible to visualize the changing of the four variables in the same graphic. As a complement, a graphic was also created that represents the maximum value of µ_max obtained to each value of a_w. In this figure is also represented the maximum specific growth rate value for the studied bacteria and the conditions that make it happen.

3. Results

Despite all bacteria following the same development model, their growth can be very different from each other. This is due to the alteration of the environment where they exist. Below, these differences will be analyzed to the 14 bacteria considered in this study, and some representative graphics that define them. It is important to emphasize that the graphs are not all with the same conformation and direction of axes (T and pH) in order to improve the visualization and perception of all three-dimensional variables.

Since each factor has a different minimum and maximum value for each bacteria, Equation (5) is used, in order to simplify the process of comparing bacteria, where X can be the temperature or the pH.

$$X_{\%}{}_{opt}=\frac{X_{opt}-X_{min}}{X_{max}-X_{min}}·100$$

(5)

3.1. Aeromonas hydrophila

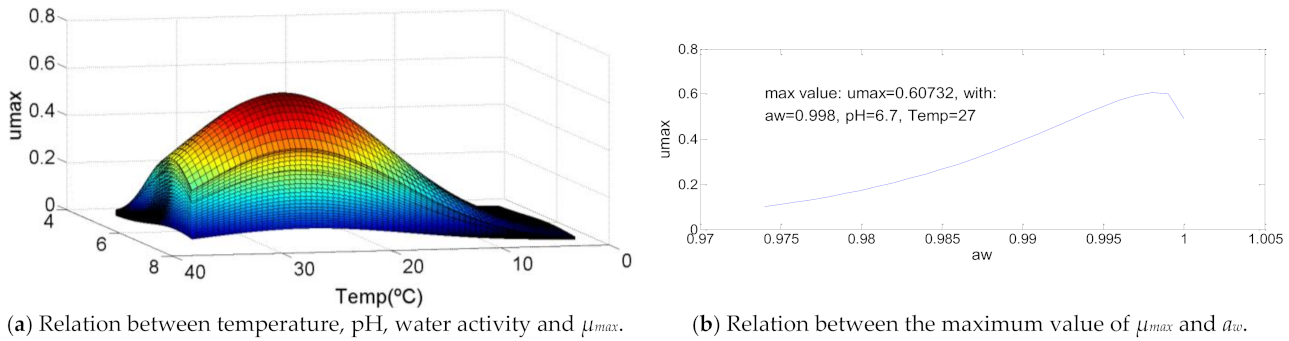
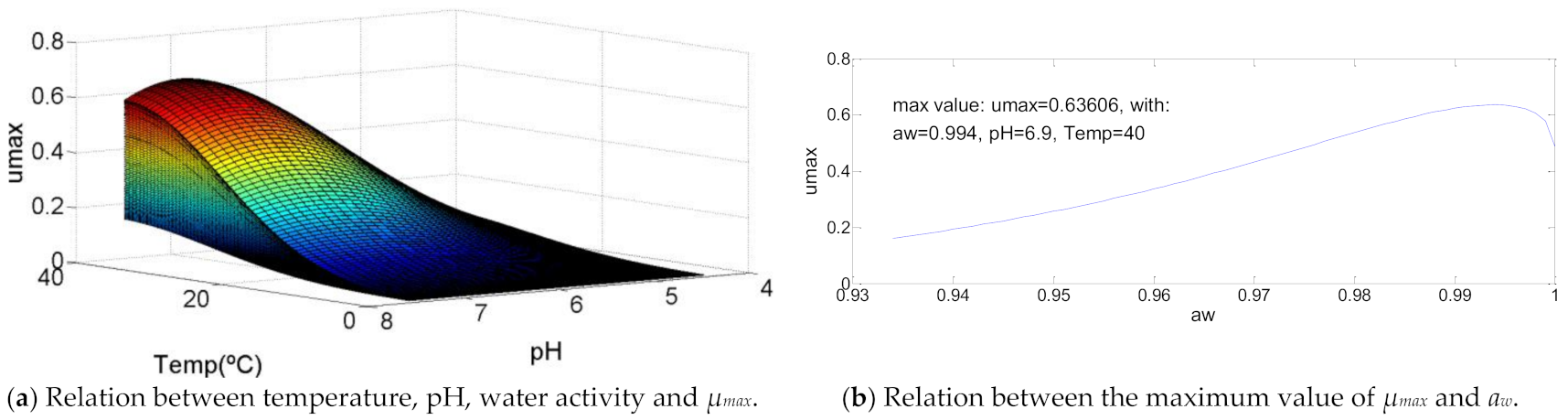
Figure 3 represents the most usual growth curve between the analyzed bacteria. This growth is characterized by a maximum point of growth with a temperature between 70% and 80% of the bacteria temperature range in which it grows, a pH between 65% and 75% of the bacteria pH range of development and a water activity of approximately 90%. For this bacteria those values are 71.4% (T = 34 °C), 72.4% (pH = 7.4) and 92.3% (a_w = 0.999), respectively. The decrease of temperature causes a quit decrease in µ_max value, the same that happens for pH and water activity, but, in this last case, not so abruptly. The maximum value of µ_max = 0.6.

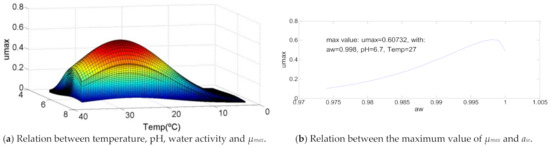
Figure 3. Influence of intrinsic and extrinsic factors in the maximum specific growth rate of Aeromonas hydrophila.

3.2. Bacillus cereus

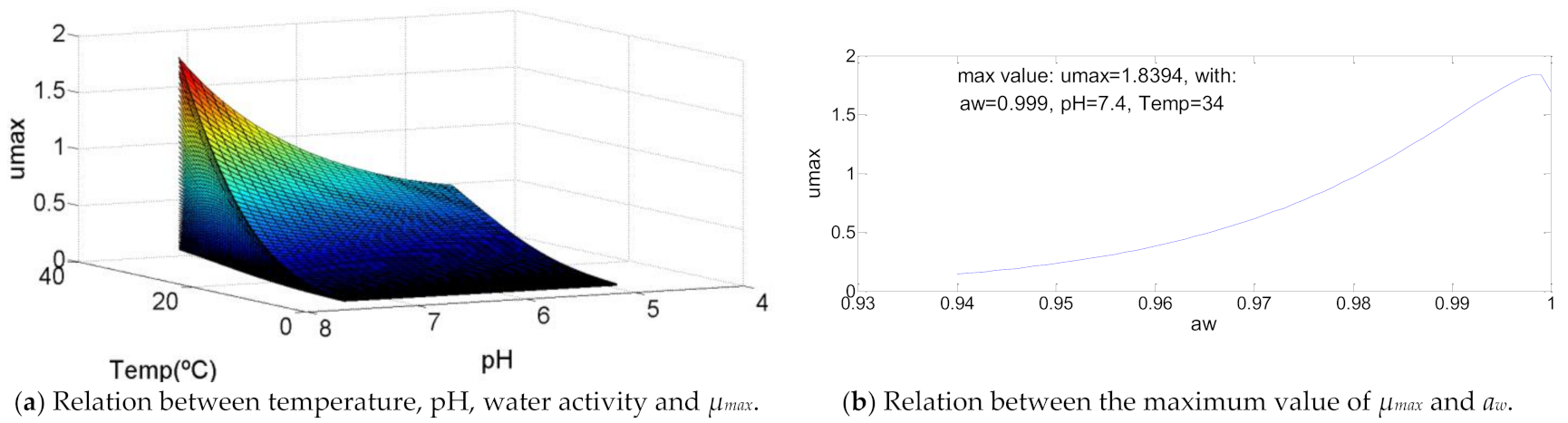
The way the temperature, pH and a_w affect this bacteria growth is different to all the others analyzed. To Bacillus cereus as represented in Figure 4, the maximum specific growth rate is maximum to the maximum value of temperature and pH, meanwhile for water activity only decreases when its value is greater than a_w = 0.999, which can be ignored in a practical situation. The maximum µ_max = 1.8 log(CFU/g)/h, which is the greatest between the microorganisms analyzed. It is also relevant to mention that the values for µ_max are relatively low (about 0.5 log(CFU/g)/h) while the temperature is lower than 25 °C, pH below 5.5 and a_w until 0.97. A small increase of these values triggers a quit increase of the maximum specific growth rate.

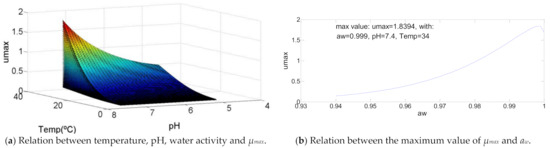
Figure 4. Influence of intrinsic and extrinsic factors in the maximum specific growth rate of Bacillus cereus.

3.3. Bacillus licheniformis

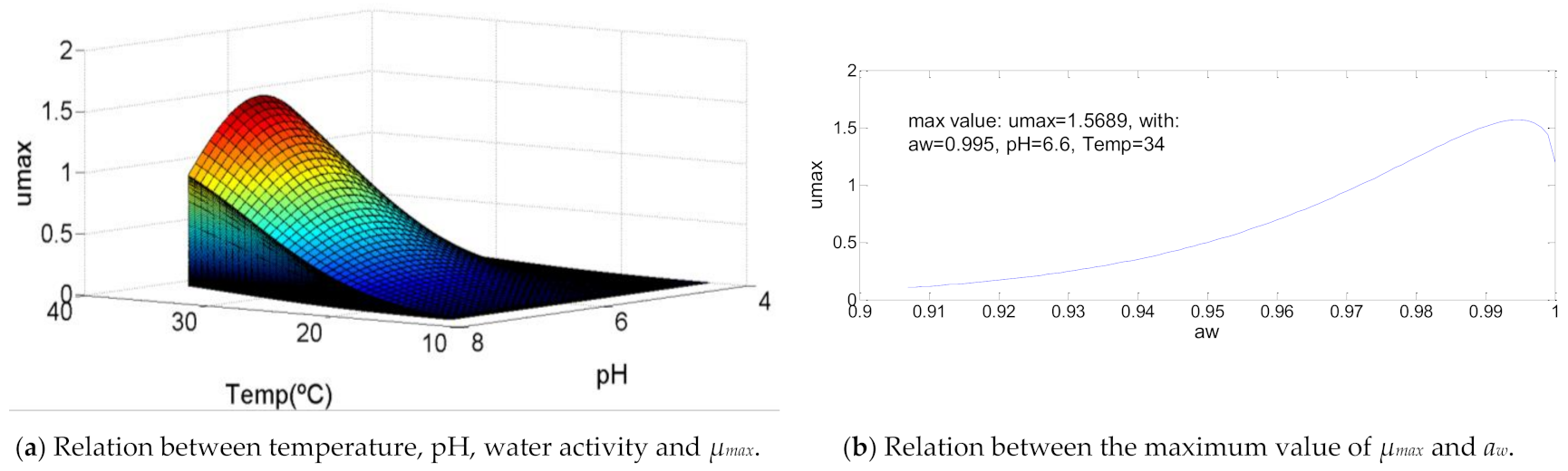
As shown in Figure 5, this bacteria curve reveals a growth of µ_max similar to the one presented for Aeromonas hydrophila. The main difference is that while in the first case the maximum specific growth rate increases until 73% of the temperature value range of growth, in this case the maximum value happens to the maximum value of temperature (T = 34 °C). The values to pH and water activity to get the maximum value of µ_max are pH = 6.6 and a_w = 0.995, respectively, which is between the same range defined in the first bacteria commented, with values of 72% and 94%.

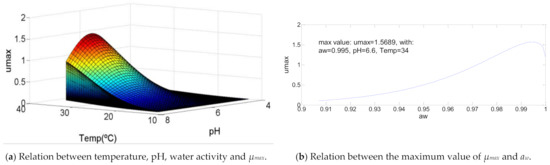
Figure 5. Influence of intrinsic and extrinsic factors in the maximum specific growth rate of Bacillus licheniformis.

3.4. Bacillus subtilis

Of the 14 bacteria studied, Bacillus subtilis has a unique property. Despite all the others, which in high values of the water activity means an increase of µ_max, in Bacillus subtilis the reaction is the opposite. The optimal growth condition is achieved with a_w = 0.933, and, after that point, the maximum specific growth rate decreases with the rise of a_w and increases again only between 0.993 and 1, thus not being relevant. While the rise of the temperature value creates an increase in µ_max, the pH simply does this until half of the range of growth of this bacteria, which causes a decrease with the same rhythm.

3.5. Clostridium botulinum

As referred in the description of Aeromonas hydrophila, this kind of curve is assigned with diverse bacteria, and this is one of them. The percentage value of the range of growth of Clostridium botulinum that causes a maximum value of µ_max are in the range defined previously: 78% (T = 24.5 °C), 70% (pH = 6.8) and 88% (a_w = 0.997) respectively for the range of values of temperature, pH and water activity.

3.6. Clostridium perfringens

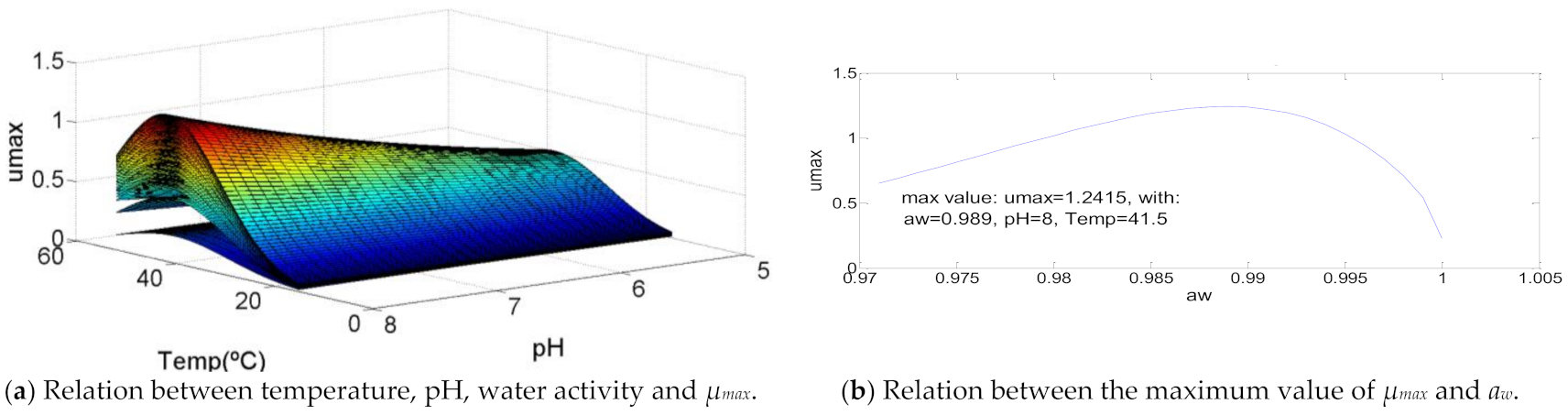
This bacterium has several characteristics different from the others. Regarding the temperature, it is possible to see that an increase of its value causes an increase in µ_max which becomes bigger as it approaches the maximum temperature range of growth, T = 41.5 °C. When this value is achieved, the decrease of µ_max, caused by the rise of the temperature, happens at a slow pace. However, pH is mainly responsible for the odd curve created. While, in the other bacteria, the increase of pH causes a greater raise of µ_max until the optimal value of pH is reached, for Clostridium perfringens, the rise of pH causes the same increase of µ_max along all the range of growth. Therefore, the pH value that causes the maximum value of µ_max = 8. Water activity also has a distinct growth curve, since its minimum value corresponds to a specific growth rate value of 0.6, which increases with the increase of a_w until a_w = 0.989, that represents the maximum µ_max = 1.24. These characteristics are described in Figure 6.

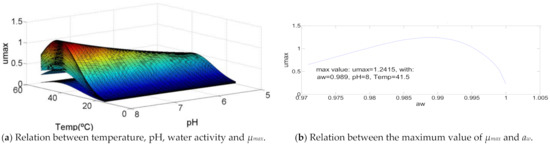
Figure 6. Influence of intrinsic and extrinsic factors in the maximum specific growth rate of Clostridium perfringens.

3.7. Escherichia coli

The influence of the temperature and pH in this bacterium is identical to the cases of Aeromonas hydrophila and Clostridium botulinum, wherein the percentages are in the range defined for that kind of curve (Figure 7). In this case, the maximum value of µ_max occurs with temperature at 76% (T = 34.5 °C) of its range of growth and 66.7% (pH = 6.5) of the same range of pH. The maximum µ_max is obtained with the maximum value of water activity, this is, a_w = 1, Escherichia coli being the only bacteria where this happens.

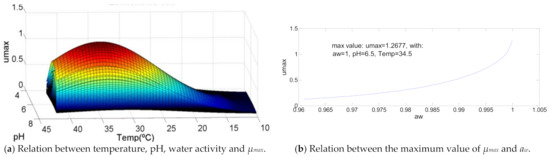
Figure 7. Influence of intrinsic and extrinsic factors in the maximum specific growth rate of Escherichia coli.

3.8. Listeria monocytogenes

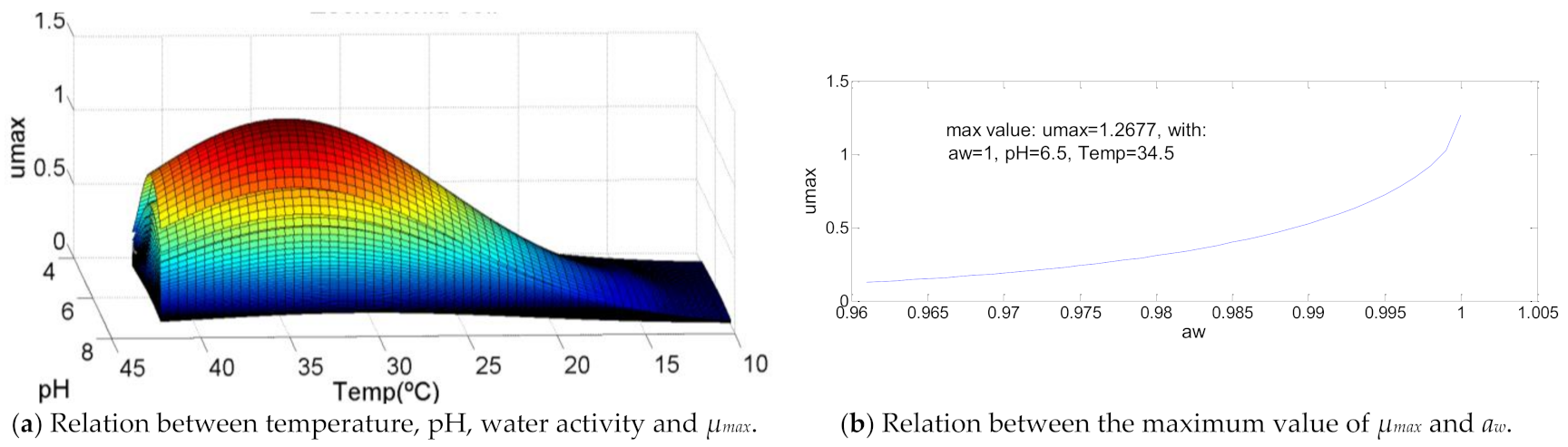
Listeria monocytogenes presents a similar curve with Aeromonas hydrophila, however the difference of the optimal temperature value has to be equal to its maximum value (T = 40 °C). As shown in Figure 8, The values of pH and water activity for which µ_max is maximum, are, respectively, pH = 6.9 and a_w = 0.994 that, in percentage, represents 80% and 90% of its correspondent range of growth.

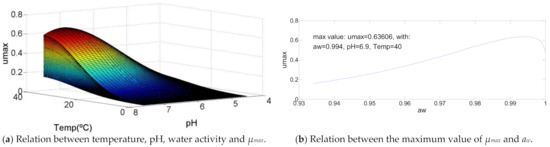
Figure 8. Influence of intrinsic and extrinsic factors in the maximum specific growth rate of Listeria monocytogenes.

3.9. Salmonella

This bacterium is similar with the previous, except in the µ_max value, where Listeria monocytogenes achieved a maximum value of µ_max = 0.63 and Salmonella went beyond 0.93. This value is reached with both temperature (T = 37.5 °C) and water activity at a_w = 90% of its range of growth, while the optimal pH = 6.4 happens around 70%.

3.10. Shigella flexneri

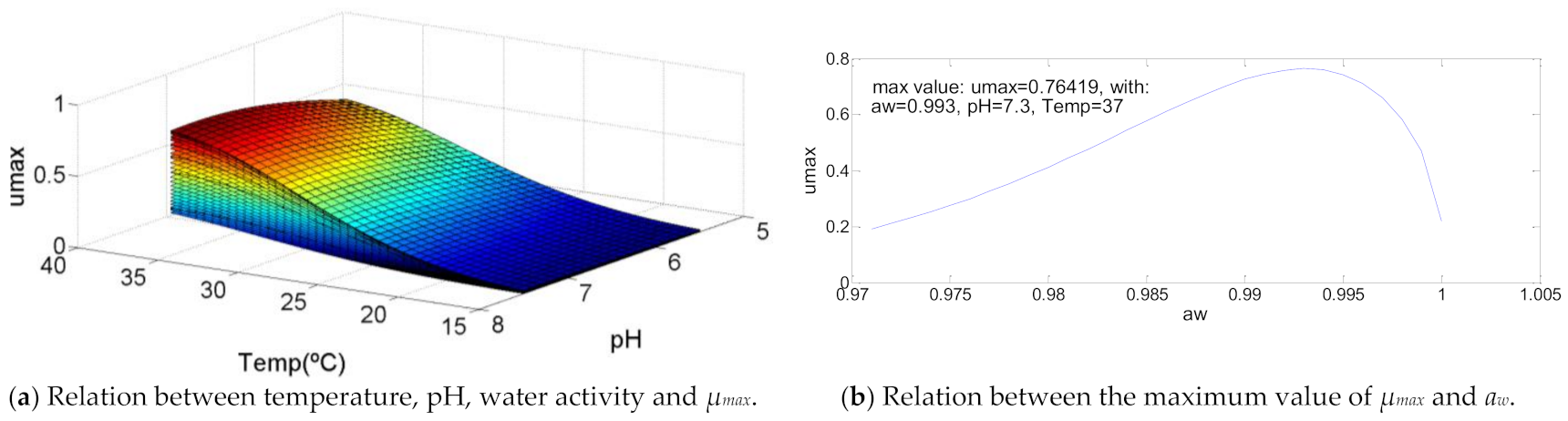
Shigella flexneri growth curve (Figure 9) represents a direct and constant relation between the increase of the temperature and the increase of the maximum specific growth rate, which achieves it maximum value with the maximum temperature, T = 37 °C. The increase of the pH value represents a tiny increase (about 25%) in µ_max value that justifies the growth curve shape. Water activity almost has a symmetrical growth curve, once the minimum value of µ_max is achieved to a_w,min, but also to a_w,max, where a_w = 0.993 represents the maximum value of µ_max = 0.76.

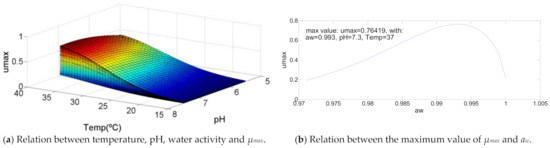
Figure 9. Influence of intrinsic and extrinsic factors in the maximum specific growth rate of Shigella flexneri.

3.11. Staphylococcus aureus

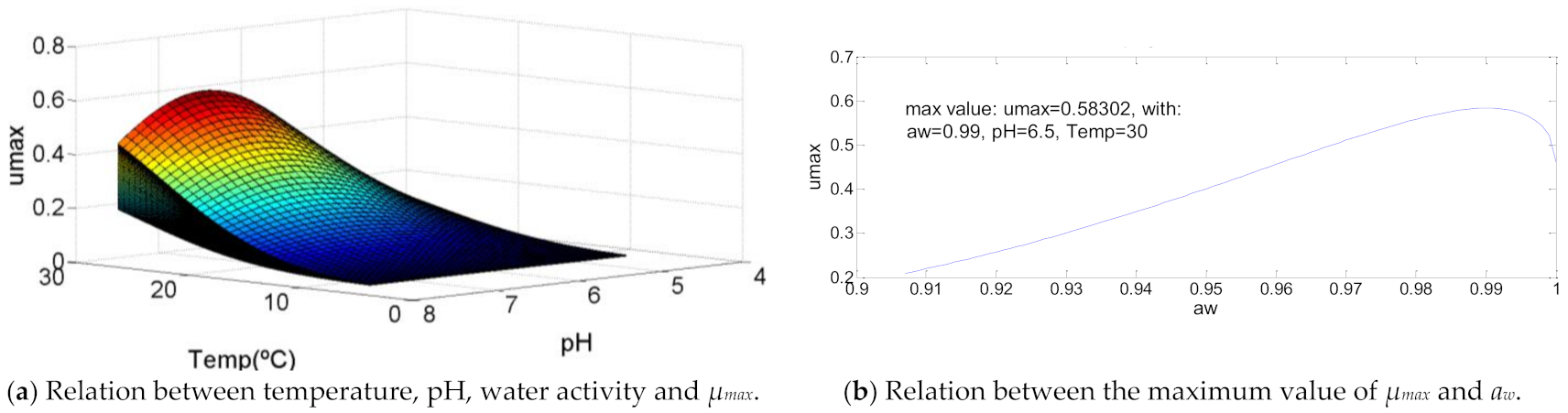
Staphylococcus aureus has a growth curve like some graphics already defined, as shown in Figure 10. It is characterized by an optimal temperature equal to the maximum temperature, an optimal pH = 60% of its growth range and a_w between 80% and 90% of water activity growth range. In this specific case, these percentages are respectively 67.7% (pH = 6.5) and 89% (a_w = 0.99), that, with a temperature of 30 °C, result in µ_max = 0.58.

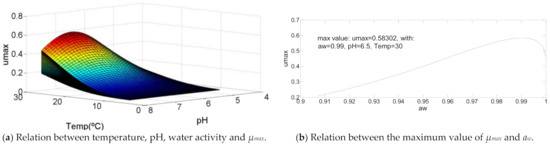
Figure 10. Influence of intrinsic and extrinsic factors in the maximum specific growth rate of Staphylococcus aureus.

3.12. Yersinia enterocolitica

The growth of this bacteria is similar to the graphic of Staphylococcus aureus, only with differences in the percentage of temperature, pH and water activity growth range, which are 100% for temperature, T = 37 °C, 64% for pH = 6.2 and 90% for water activity, a_w = 0.996. The value of µ_max for these parameters is equal to 0.66.

3.13. Brochothrix thermosphacta

The microorganism Brochothrix thermosphacta is, once more, one of the bacteria related with Aeromonas hydrophila because of their similar growth curve. However, it is important to refer the value of a_w for which µ_max is maximum, because of its proximity to the maximum value (a_w = 0.999). Both values of temperature and pH are close to 80% (T = 23.5 °C; pH = 6.7) of their growth range and contribute to a maximum µ_max = 0.38.

3.14. Pseudomonas

A growth curve identical to the one of Pseudomonas is already described in Staphylococcus aureus graphic. Just like Yersinia enterocolitica, µ_max is maximum when the temperature achieves its maximum value (T = 20 °C), while pH is around 60% (pH = 6.5) of its growth range and the water activity is slightly lower than the other bacteria, 82% (a_w = 0.993). The largest value of µ_max = 0.28 is the lowest between the bacteria analyzed.

4. Discussion

Despite many recent advances in food safety and quality, there is still an existential challenge and, therefore, a gap for novel opportunities in which the current technologies available can be improved in order to have versatile, fast, simple, portable, robust and multivariate levels of detection of food contaminants and different analytes matrices [23]. Therefore, after the individualized study of the 14 bacteria, it is possible to verify that despite the values of each factor considered—temperature, pH and water activity—having different minimum, maximum and optimal values, as well as different maximum values of µ_max, between bacteria, they can be put together in groups defined by their growth curve relation of these 4 parameters.

The bacteria Aeromonas hydrophila, Brochothrix thermosphacta, Clostridium botulinum and Escherichia coli are characterized by T_%opt = [70%, 80%] and pH_%opt = [65%, 80%] and are put together in one group. The other group is composed of bacteria where T_%opt = T_max, this is, T_%opt = 100% and pH_%opt = [50%, 70%]. This occurs in bacteria like Bacillus licheniformis, Bacillus subtilis, Staphylococcus aureus, Yersinia enterocolitica and Pseudomonas.

Listeria monocytogenes and Salmonella are some of the cases where there is a join of the groups presented. On one hand, T_%opt is bigger than 90%, on the other, pH_%opt has bigger values than the ones considered in the second group, pH_%opt = [70%, 80%]. One example of this category is the bacteria Shigella flexneri, which maintains the value of T_%opt = 100% but has pH_%opt > 90%. Bacillus cereus is an extreme case of the last example, once T_%opt = pH_%opt = 100%. Beyond this microorganism, Clostridium perfringens also presents a unique case where T_%opt = 70%, like the first group, but with pH_%opt = 100%.

Concerning the water activity influence seen in previous graphics, it is possible to relate the increase of water activity with the approach of maximum value of µ_max. With the particular case of Escherichia coli, where the increase happens until the water activity maximum value, in all of the others the growth of a_w represents an increase of µ_max but only until a certain value. The increase after that value represents a decrease of the maximum specific growth rate. That value will be denoted as a_w,opt. The different water activity limits are due to the diverse mechanisms of water movements between bacteria and their environment. This conditions the way different microorganisms deal with osmotic stress, that is, the impossibility of absorbing more water into the cells, and, thus, becoming unable to grow. In Table 7 all the values obtained with this study are presented, represented as minimum, maximum and optimal values of the temperature, pH and water activity for each bacteria, and also the values of initial, final and infective dose of CFU/g for each microorganism already described [22,24].

Table 7. Minimum, maximum and optimal parameters to bacterial growth.

Microorganism	Tmin [°C]	Topt [°C]	Tmax [°C]	pHmin	pHopt	pHmax	aw,min	aw,opt	aw,max	µmax,opt	Initial Colony [UFC/g]	Infective Colony [UFC/g]	Final Colony [UFC/g]
Aeromonas hydrophila	2.0	27-0	37.0	4.6	6.7	7.5	0.974	0.998	1	0.60732	103	>105	107.39
Bacillus cereus	5.0	34-0	34.0	4.9	7.4	7.4	0.94	0.999	1	1.83940	101	>105	107.61
Bacillus licheniformis	13.0	34.0	34.0	4	6.6	7.6	0.907	0.995	1	1.56890	103	>105	107.83
Bacillus subtilis	10.0	34.0	34.0	4.3	6.1	7.8	0.933	0.933	1	1.17800	101	>105	107.83
Clostridium botulinum	4.0	24.5	30.0	5.1	6.8	7.5	0.974	0.997	1	0.75511	100	>104	107.04
Clostridium perfringens	15.0	41.5	52.0	5.0	8.0	8.0	0.971	0.989	1	1.24150	101	>106	107.61
Escherichia coli	10.0	34.5	42.0	4.5	6.5	7.5	0.961	1	1	1.26770	102	>106	108.7
Listeria monocytogenes	1.0	40.0	40.0	4.4	6.9	7.5	0.934	0.994	1	0.63606	101	>102	108.52
Salmonella	7.0	37.5	40.0	3.9	6.4	7.4	0.973	0.997	1	0.93591	102	>105	108.52
Shigella flexneri	15.0	37.0	37.0	5.5	7.3	7.5	0.971	0.993	1	0.76419	100	>102	108.78
Staphylococcus aureus	7.5	30.0	30.0	4.4	6.5	7.5	0.907	0.99	1	0.58302	101	>105	108.09
Yersinia enterocolitica	−1.0	37.0	37.0	4.4	6.2	7.2	0.957	0.996	1	0.66226	102	>107	108.3
Brochothrix thermosphacta	0.0	23.5	30.0	5.5	6.7	7.0	0.950	0.999	1	0.38374	102	>107	107.83
Pseudomonas	0.0	20.0	20.0	5.0	6.5	7.4	0.961	0.993	1	0.27746	102	>107	108.26

5. Conclusions

With growing consumer demand for food safety and security, several commercial sensors for smart packaging have been developed, however these require more research for their integration in food packaging and, still, it is necessary to overcome the obstacles for the commercial application of sensors on a large scale.

Thus, special attention is required, and extensive research efforts must be applied due to the potentially dangerous effects of chemical and biological components of sensors in food packaging. Therefore, the integration of such devices in the food industry is not an easy ordeal as the sensor components cannot be placed directly in contact with the food. In addition, it is necessary to evaluate their propensity to migrate to food content, in order to avoid interference in the texture, flavor, or taste of food.

That said, the application of mathematical predictive models to biochemical sensors represents an increasing challenge for sensor technologies applied to smart packaging. In this work a simplified approach to predict the food safety through the maximum specific bacterial growth rate as function of extrinsic and intrinsic parameters was described.

After the study of Baranyi and Roberts model, as well as the study of the variables that define it, it is possible to understand the relation between the bacterial growth curve and the intrinsic and extrinsic factors of the environment in which the bacteria develops. It is represented by the maximum specific growth rate (µ_max). Through the Massana and Baranyi model, that allows the calculation of the referred growth rate, and the data provided in Combase Predictor, the coefficients that define the bacterial growth were estimated. Obtaining the value of these coefficients was possible to create tridimensional graphics that represent the relation between four parameters—temperature, pH, water activity and maximum specific growth rate—and conclude that the 14 bacteria studied can be divided in different groups characterized by the way that µ_max is affected by the described factors.

The four groups were elaborated according to the similarities of the parameters that influence the bacterial growth, that is, mainly according to the optimal conditions of temperature, pH and water activity. Aeromonas hydrophila, Brochothrix thermosphacta, Clostridium botulinum and Escherichia coli composed the first one. The second group is formed by Bacillus licheniformis, Bacillus subtilis, Staphylococcus aureus, Yersinia enterocolitica and Pseudomonas. Another group is composed of Listeria monocytogenes, Salmonella and Shigella flexneri, and at last, the fourth group is constituted by unique and extreme cases such as Bacillus cereus and Clostridium perfringens.

Therefore, with these mathematical models it was possible to categorize some bacteria according to their different bacterial growth. In addition, they also allow to evaluate the conditions of temperature, pH and water activity that affect the development of these bacteria. Thus, it is possible to predict food security with regard to bacterial development, since this is one of the main promoters in food corruption. This study can then be applied as a predictive model for diverse food preservation, maintenance and packaging systems.