Structural Identifiability and Observability of Microbial Community Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Definitions
2.2. Analysis Methods
| Algorithm 1: Probabilistic algorithm to test local algebraic observability in polynomial time |
| Preprocesing Construct a straight-line program encoding the variational system with and the expressions used during its integration. Specialization Specialisation of the parameters, , and the inputs, Power Series Solution Computation of the power series solution of at order with a specialised value for the states Jacobian computation Evaluation of on the previous results, giving the coefficients of the Jacobian matrix Rank computation Calculation of the matrix rank and transcendence degree if transcendence degree = 0 then | System is algebraically observable else | Determine which variable or variables are not observable. end |
3. Models
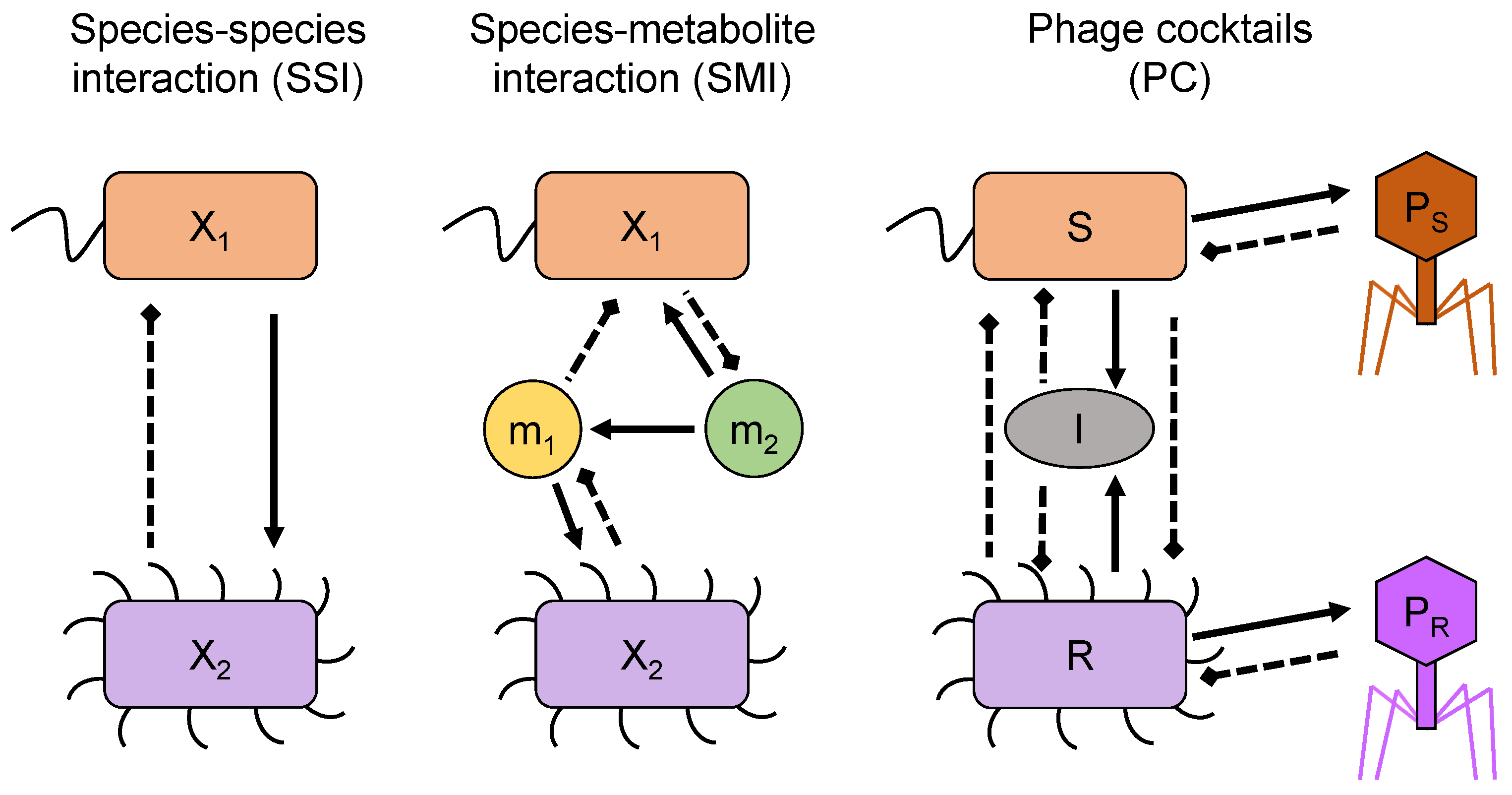
3.1. Species–Species Interaction Models (SSI)
3.1.1. Generalized Lotka–Volterra Models (gLV)
3.1.2. Composite Lotka–Volterra Models (cLV)
3.2. Species–Metabolite Interaction Models (SMI)
3.2.1. Quadratic Species–Metabolite Interaction Models (QSMI)
3.2.2. SMI Models with Simple Monod Growth Kinetics (MSMI)
3.3. A Phage Cocktail Model (PC)
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ODE | Ordinary Differential Equation |
| SIO | Structural Identifiability and Observability |
| gLV | generalized Lotka–Volterra |
| SLI | Structurally Locally Identifiable |
| SU | Structurally Unidentifiable |
| SSI | Species–Species Interaction |
| SMI | Species–Metabolite Interaction |
| QSMI | Quadratic Species–Metabolite Interaction |
| MSMI | SMI model with Monod growth kinetics |
| cLV | composite Lotka–Volterra |
| PC | Phage Cocktail |
References
- Distefano, J. Dynamic Systems Biology Modeling and Simulation; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Villaverde, A.F. Observability and structural identifiability of nonlinear biological systems. Complexity 2019, 2019. [Google Scholar] [CrossRef]
- Wieland, F.G.; Hauber, A.L.; Rosenblatt, M.; Tönsing, C.; Timmer, J. On structural and practical identifiability. Curr. Opin. Syst. Biol. 2021, 25, 60–69. [Google Scholar] [CrossRef]
- Hermann, R.; Krener, A. Nonlinear controllability and observability. IEEE Trans. Autom. Control 1977, 22, 728–740. [Google Scholar] [CrossRef]
- Rey Barreiro, X.; Villaverde, A.F. Benchmarking tools for a priori identifiability analysis. Bioinformatics 2023, 39, btab065. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, J.A.; Jansson, J.K.; Knight, R. The Earth Microbiome project: Successes and aspirations. BMC Biol. 2014, 12, 1–4. [Google Scholar] [CrossRef]
- Angulo, M.T.; Moog, C.H.; Liu, Y.Y. A theoretical framework for controlling complex microbial communities. Nat. Commun. 2019, 10, 1–12. [Google Scholar] [CrossRef]
- Treloar, N.J.; Fedorec, A.J.; Ingalls, B.; Barnes, C.P. Deep reinforcement learning for the control of microbial co-cultures in bioreactors. PLoS Comput. Biol. 2020, 16, e1007783. [Google Scholar] [CrossRef]
- Salzano, D.; Fiore, D.; di Bernardo, M. Ratiometric control of cell phenotypes in monostrain microbial consortia. J. R. Soc. Interface 2022, 19, 20220335. [Google Scholar] [CrossRef]
- Larsen, P.; Hamada, Y.; Gilbert, J. Modeling microbial communities: Current, developing, and future technologies for predicting microbial community interaction. J. Biotechnol. 2012, 160, 17–24. [Google Scholar] [CrossRef]
- Coyte, K.Z.; Schluter, J.; Foster, K.R. The ecology of the microbiome: Networks, competition, and stability. Science 2015, 350, 663–666. [Google Scholar] [CrossRef]
- Clokie, M.R.; Millard, A.D.; Letarov, A.V.; Heaphy, S. Phages in nature. Bacteriophage 2011, 1, 31–45. [Google Scholar] [CrossRef] [PubMed]
- Stein, R.R.; Bucci, V.; Toussaint, N.C.; Buffie, C.G.; Rätsch, G.; Pamer, E.G.; Sander, C.; Xavier, J.B. Ecological modeling from time-series inference: Insight into dynamics and stability of intestinal microbiota. PLoS Comput. Biol. 2013, 9, e1003388. [Google Scholar] [CrossRef] [PubMed]
- Joseph, T.A.; Shenhav, L.; Xavier, J.B.; Halperin, E.; Pe’er, I. Compositional Lotka-Volterra describes microbial dynamics in the simplex. PLoS Comput. Biol. 2020, 16, e1007917. [Google Scholar] [CrossRef]
- Brunner, J.D.; Chia, N. Metabolite-mediated modelling of microbial community dynamics captures emergent behaviour more effectively than species–species modelling. J. R. Soc. Interface 2019, 16, 20190423. [Google Scholar] [CrossRef] [PubMed]
- Fridman, Y.; Wang, Z.; Maslov, S.; Goyal, A. Fine-scale diversity of microbial communities due to satellite niches in boom and bust environments. PLoS Comput. Biol. 2022, 18, e1010244. [Google Scholar] [CrossRef]
- Remien, C.H.; Eckwright, M.J.; Ridenhour, B.J. Structural identifiability of the generalized Lotka–Volterra model for microbiome studies. R. Soc. Open Sci. 2021, 8, 201378. [Google Scholar] [CrossRef]
- Massonis, G.; Banga, J.R.; Villaverde, A.F. Structural identifiability and observability of compartmental models of the COVID-19 pandemic. Annu. Rev. Control 2021, 51, 441–459. [Google Scholar] [CrossRef]
- Villaverde, A.F.; Tsiantis, N.; Banga, J.R. Full observability and estimation of unknown inputs, states and parameters of nonlinear biological models. J. R. Soc. Interface 2019, 16, 20190043. [Google Scholar] [CrossRef]
- Tunali, E.; Tarn, T.J. New results for identifiability of nonlinear systems. IEEE Trans. Autom. Control 1987, 32, 146–154. [Google Scholar] [CrossRef]
- Sedoglavic, A. A probabilistic algorithm to test local algebraic observability in polynomial time. J. Symb. Comput. 2002, 33, 735–755. [Google Scholar] [CrossRef]
- Díaz-Seoane, S.; Rey Barreiro, X.; Villaverde, A.F. STRIKE-GOLDD 4.0: User-friendly, efficient analysis of structural identifiability and observability. Bioinformatics 2023, 39, btac748. [Google Scholar] [CrossRef]
- Maes, K.; Chatzis, M.; Lombaert, G. Observability of nonlinear systems with unmeasured inputs. Mech. Syst. Signal Process. 2019, 130, 378–394. [Google Scholar] [CrossRef]
- Martinelli, A. Nonlinear unknown input observability and unknown input reconstruction: The general analytical solution. Inf. Fusion 2022, 85, 23–51. [Google Scholar] [CrossRef]
- Gloor, G.B.; Macklaim, J.M.; Pawlowsky-Glahn, V.; Egozcue, J.J. Microbiome datasets are compositional: And this is not optional. Front. Microbiol. 2017, 8, 2224. [Google Scholar] [CrossRef]
- Greenacre, M.; Martínez-Álvaro, M.; Blasco, A. Compositional data analysis of microbiome and any-omics datasets: A validation of the additive logratio transformation. Front. Microbiol. 2021, 12, 727398. [Google Scholar] [CrossRef] [PubMed]
- Leclerc, Q.J.; Wildfire, J.; Gupta, A.; Lindsay, J.A.; Knight, G.M. Growth-Dependent Predation and Generalized Transduction of Antimicrobial Resistance by Bacteriophage. Msystems 2022, 7, e00135-22. [Google Scholar] [CrossRef] [PubMed]
- Leclerc, Q.J.; Lindsay, J.A.; Knight, G.M. Modelling the synergistic effect of bacteriophage and antibiotics on bacteria: Killers and drivers of resistance evolution. PLoS Comput. Biol. 2022, 18, e1010746. [Google Scholar] [CrossRef]
- Li, G.; Leung, C.Y.; Wardi, Y.; Debarbieux, L.; Weitz, J.S. Optimizing the timing and composition of therapeutic phage cocktails: A control-theoretic approach. Bull. Math. Biol. 2020, 82, 1–29. [Google Scholar] [CrossRef]
| x | y | Id | Non-Id | Obs | Non-Obs |
|---|---|---|---|---|---|
| , | , | all | - | all | - |
| , | |||||
| RM | - | ||||
| , , | , , | all | - | all | - |
| , | , , | , | |||
| , | , | , | |||
| RM | - |
| x | u | y | Id | Non-Id | Obs | Non-Obs |
|---|---|---|---|---|---|---|
| - | - | all | all | - | ||
| , | all | - | ||||
| , | - | , | - | all | all | - |
| , | , | all | - |
| x | y | Id | Non-Id | Obs | Non-Obs |
|---|---|---|---|---|---|
| , , | , | , , , | , | all | - |
| , | , , , | , | , | ||
| , , , | , | , | |||
| , | , , , | ||||
| , | , , , | , | |||
| , , , | , | , , , | , | all | - |
| , , | , , , | , | , , | ||
| , | , , , | , | , | , | |
| , , , | , | , , | |||
| , | , , , | ||||
| , | , | , , , | , | , | |
| , | , , , | , , | |||
| , , , | , | , , , , , | , , | all | - |
| , | , , , , , | , , , | , | ||
| , , , | , | ||||
| , | , , , , | , , , | , | ||
| , | , , , | , , , , | , | , | |
| , , , | , , , , | , | |||
| , | , , , | ||||
| , | , , , | , | |||
| , , , , | , | , , , , , | , , | all | - |
| , , | , , , , , , , | , , , , , | , , | ||
| , | , , , , , | , , , , | , | , | |
| , , , | , | ||||
| , | , , , | , , , | , | ||
| , , | , , , | , , , | , , | , | |
| , | , , , | , , , | , | , , | |
| , , , | , , , | , | |||
| , | , , , | ||||
| , | , | , , , | , | , | |
| , | , , , | , , |
| x | y | Id | Non-Id | Obs | Non-Obs |
|---|---|---|---|---|---|
| , , | , | , , , , , | , | all | - |
| , | , , , , , | , , , , | , | ||
| , , | , , , , | , | |||
| , , | , , , , | ||||
| , , | , , , , , | , | |||
| , , , | , | , , , , , , , | , , | all | - |
| , | , , , , , , , | , , , , , | , | ||
| , , , , | , , , , , | ||||
| , | , , , , , , | , , , , , , | , | ||
| , | , , , , , , | , , , , , , , , , , , | , | , | |
| , , , | , , , , , , , | , | |||
| , , | , , , , | ||||
| , , | , , , , , | , | |||
| , , , , | , | , , , , , , , | , , | all | - |
| , , | , , , , , , , , , , | , , , , , | , , | ||
| , | , , , , , , , | , , , , , , , , | , | , | |
| , , , , | , , , , , | ||||
| , | , , , , , , | , , , , , , | , | ||
| , , | , , , , , , , , , | , , , , , , , , , , , | , , | , | |
| , | , , , , , , | , , , , , , , , , , , , | , | , , | |
| , , , | , , , , , , , | , | |||
| , , | , , , , | ||||
| , | , , , | , , , , , | , | , | |
| , , | , , , , , , | , , |
| x | y | Id | Non-Id | Obs | Non-Obs |
|---|---|---|---|---|---|
| I, S, R, , | I | all | - | all | - |
| S, R, , | r, , m, , , , , , , , | E, | S, R, , | I | |
| S, R | r, , m, , , , , , , , | E, | S, R, , | I | |
| , | r, , m, , , , , , , , | E, | S, R, , | I | |
| , , , , | Any | all | - | all | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Seoane, S.; Sellán, E.; Villaverde, A.F. Structural Identifiability and Observability of Microbial Community Models. Bioengineering 2023, 10, 483. https://doi.org/10.3390/bioengineering10040483
Díaz-Seoane S, Sellán E, Villaverde AF. Structural Identifiability and Observability of Microbial Community Models. Bioengineering. 2023; 10(4):483. https://doi.org/10.3390/bioengineering10040483
Chicago/Turabian StyleDíaz-Seoane, Sandra, Elena Sellán, and Alejandro F. Villaverde. 2023. "Structural Identifiability and Observability of Microbial Community Models" Bioengineering 10, no. 4: 483. https://doi.org/10.3390/bioengineering10040483
APA StyleDíaz-Seoane, S., Sellán, E., & Villaverde, A. F. (2023). Structural Identifiability and Observability of Microbial Community Models. Bioengineering, 10(4), 483. https://doi.org/10.3390/bioengineering10040483









