Electric Field Characteristics of Rotating Permanent Magnet Stimulation
Abstract
:1. Introduction
2. Methods
2.1. Simulations and Solver
2.2. Magnet Configuration
2.3. E-Field Measurements
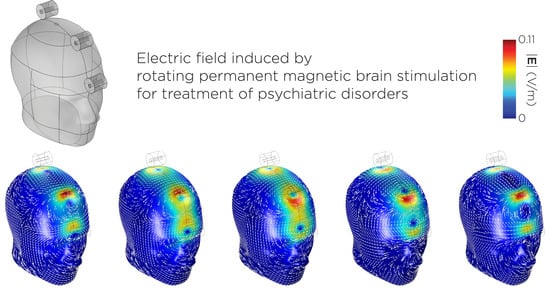
3. Results
3.1. Simulations
3.2. Experimental Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cohen, S.L.; Bikson, M.; Badran, B.W.; George, M.S. A visual and narrative timeline of US FDA milestones for Transcranial Magnetic Stimulation (TMS) devices. Brain Stimul. 2022, 15, 73–75. [Google Scholar] [CrossRef]
- Rizvi, S.; Khan, A.M. Use of transcranial magnetic stimulation for depression. Cureus 2019, 11, e4736. [Google Scholar] [CrossRef]
- Phillips, J.W.; Jin, Y. Systems and Methods for Neuro-EEG Synchronization Therapy. U.S. Patent 8961386B2, 24 February 2015. [Google Scholar]
- Watterson, P.A. Device Including Moving Magnet Configurations. U.S. Patent 20140163305A1, 12 June 2014. [Google Scholar]
- Helekar, S.A.; Voss, H.U. Method and apparatus for providing trancranial magnetic stimulation (TMS) to a individual. U.S. Patent 10398907B2, 3 September 2019. [Google Scholar]
- Leuchter, A.F.; Cook, I.A.; Jin, Y.; Phillips, B. The relationship between brain oscillatory activity and therapeutic effectiveness of transcranial magnetic stimulation in the treatment of major depressive disorder. Front. Hum. Neurosci. 2013, 7, 37. [Google Scholar] [CrossRef]
- Leuchter, A.F.; Cook, I.A.; Feifel, D.; Goethe, J.W.; Husain, M.; Carpenter, L.L.; Thase, M.E.; Krystal, A.D.; Philip, N.S.; Bhati, M.T.; et al. Efficacy and safety of low-field synchronized transcranial magnetic stimulation (sTMS) for treatment of major depression. Brain Stimul. 2015, 8, 787–794. [Google Scholar] [CrossRef]
- Philip, N.S.; Leuchter, A.F.; Cook, I.A.; Massaro, J.; Goethe, J.W.; Carpenter, L.L. Predictors of response to synchronized transcranial magnetic stimulation for major depressive disorder. Depress. Anxiety 2019, 36, 278–285. [Google Scholar] [CrossRef]
- Jin, Y.; Phillips, B. A pilot study of the use of EEG-based synchronized transcranial magnetic stimulation (sTMS) for treatment of major depression. BMC Psychiatry 2014, 14, 13. [Google Scholar] [CrossRef]
- Cook, I.A.; Wilson, A.C.; Corlier, J.; Leuchter, A.F. Brain activity and clinical outcomes in adults with depression treated with synchronized transcranial magnetic stimulation: An exploratory study. Neuromodulation 2019, 22, 894–897. [Google Scholar] [CrossRef]
- Phillips, J.W.; Jin, Y. Devices and Methods of Low Frequency Magnetic Stimulation Therapy. U.S. Patent 9649502B2, 16 May 2017. [Google Scholar]
- Philip, N.S.; Aiken, E.E.; Kelley, M.E.; Burch, W.; Waterman, L.; Holtzheimer, P.E. Synchronized transcranial magnetic stimulation for posttraumatic stress disorder and comorbid major depression. Brain Stimul. 2019, 12, 1335–1337. [Google Scholar] [CrossRef] [PubMed]
- Helekar, S.A.; Voss, H.U. Transcranial brain stimulation with rapidly spinning high-field permanent magnets. IEEE Access 2016, 4, 2520–2528. [Google Scholar] [CrossRef]
- Helekar, S.A.; Convento, S.; Nguyen, L.; John, B.S.; Patel, A.; Yau, J.M.; Voss, H.U. The strength and spread of the electric field induced by transcranial rotating permanent magnet stimulation in comparison with conventional transcranial magnetic stimulation. J. Neurosci. Methods 2018, 309, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Khavari, R.; Tran, K.; Helekar, S.A.; Shi, Z.; Karmonik, C.; Rajab, H.; John, B.; Jalali, A.; Boone, T. Noninvasive, individualized cortical modulation using transcranial rotating permanent magnet stimulator for voiding dysfunction in women with multiple sclerosis: A pilot trial. J. Urol. 2022, 207, 657–668. [Google Scholar] [CrossRef]
- Greene, E.; Thonhoff, J.; John, B.S.; Rosenfield, D.B.; Helekar, S.A. Multifocal noninvasive magnetic stimulation of the primary motor cortex in yype 1 myotonic dystrophy - a proof of concept pilot study. J. Neuromuscul. Dis. 2021, 8, 963–972. [Google Scholar] [CrossRef]
- Jang, Y.; Tran, K.; Shi, Z.; Christof, K.; Choksi, D.; Salazar, B.H.; Lincoln, J.A.; Khavari, R. Predictors for outcomes of noninvasive, individualized transcranial magnetic neuromodulation in multiple sclerosis women with neurogenic voiding dysfunction. Continence 2022, 4, 100517. [Google Scholar] [CrossRef]
- Tran, K.; Shi, Z.; Karmonik, C.; John, B.; Rajab, H.; Helekar, S.A.; Boone, T.; Khavari, R. Therapeutic effects of non-invasive, individualized, transcranial neuromodulation treatment for voiding dysfunction in multiple sclerosis patients: Study protocol for a pilot clinical trial. Pilot Feasibility Stud. 2021, 7, 83. [Google Scholar] [CrossRef]
- Wide-Bore Low-Frequency Magnetic Spinner for Non-Contact E-Field Generation in a Tissue via Faraday’s Law of Induction. Available online: https://www.nevaelectromagnetics.com/wide-bore-low-freq-generator-type1 (accessed on 24 December 2023).
- Watterson, P.A.; Nicholson, G.M. Nerve-muscle activation by rotating permanent magnet configurations. J. Physiol. 2016, 594, 1799–1819. [Google Scholar] [CrossRef]
- Heller, L.; van Hulsteyn, D.B. Brain stimulation using electromagnetic sources: Theoretical aspects. Biophys. J. 1992, 63, 129–138. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef] [PubMed]
- Gabriel, S.; Lau, R.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef] [PubMed]
- Temperature and Neodymium Magnets. Available online: https://www.kjmagnetics.com/blog.asp?p=temperature-and-neodymium-magnets (accessed on 10 January 2023).
- Rotating Machinery 3D Tutorial. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.models.acdc.rotating_machinery_3d_tutorial/models.acdc.rotating_machinery_3d_tutorial.pdf (accessed on 15 February 2022).
- Glover, P.M.; Bowtell, R. Measurement of electric fields due to time-varying magnetic field gradients using dipole probes. Phys. Med. Biol. 2007, 52, 5119–5130. [Google Scholar] [CrossRef] [PubMed]
- Ramon, C.; Garguilo, P.; Fridgeirsson, E.A.; Haueisen, J. Changes in scalp potentials and spatial smoothing effects of inclusion of dura layer in human head models for EEG simulations. Front. Neuroeng. 2014, 7, 32. [Google Scholar] [CrossRef] [PubMed]
- Sauerheber, R.; Heinz, B. Temperature effects on conductivity of seawater and physiologic saline, mechanism and significance. Chem. Sci. J. 2015, 6, 1000109. [Google Scholar] [CrossRef]
- Smith, J.E.; Peterchev, A.V. Electric field measurement of two commercial active/sham coils for transcranial magnetic stimulation. J. Neural. Eng. 2018, 15, 054001. [Google Scholar] [CrossRef]
- Deng, Z.D.; Lisanby, S.H.; Peterchev, A.V. Electric field depth–focality tradeoff in transcranial magnetic stimulation: Simulation comparison of 50 coil designs. Brain Stimul. 2013, 6, 1–13. [Google Scholar] [CrossRef]
- Rohan, M.L.; Yamamoto, R.T.; Ravichandran, C.T.; Cayetano, K.R.; Morales, O.G.; Olson, D.P.; Vitaliano, G.; Paul, S.M.; Cohen, B.M. Rapid mood-elevating effects to low field magnetic stimulation in depression. Biol. Psychiatry 2014, 76, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Miranda, P.C.; Mekonnen, A.; Salvador, R.; Ruffini, G. The electric field in the cortex during transcranial current stimulation. Neuroimage 2013, 70, 48–58. [Google Scholar] [CrossRef] [PubMed]
- Guidetti, M.; Arlotti, M.; Bocci, T.; Bianchi, A.M.; Parazzini, M.; Ferrucci, R.; Priori, A. Electric fields induced in the brain by transcranial electric stimulation: A review of in vivo recordings. Biomedicines 2022, 10, 2333. [Google Scholar] [CrossRef]
- Grehl, S.; Martina, D.; Goyenvalle, C.; Deng, Z.D.; Rodger, J.; Sherrard, R.M. In vitro magnetic stimulation: A simple stimulation device to deliver defined low intensity electromagnetic fields. Front. Neural. Circuits 2016, 10, 85. [Google Scholar] [CrossRef] [PubMed]
- Moretti, J.; Terstege, D.J.; Poh, E.Z.; Epp, J.R.; Rodger, J. Low intensity repetitive transcranial magnetic stimulation modulates brain-wide functional connectivity to promote anti-correlated c-Fos expression. Sci. Rep. 2022, 12, 20571. [Google Scholar] [CrossRef] [PubMed]
- Dufor, T.; Grehl, S.; Tang, A.D.; Doulazmi, M.; Traoré, M.; Debray, N.; Dubacq, C.; Deng, Z.D.; Mariani, J.; Lohof, A.M.; et al. Neural circuit repair by low-intensity magnetic stimulation requires cellular magnetoreceptors and specific stimulation patterns. Sci. Adv. 2019, 5, eaav9847. [Google Scholar] [CrossRef] [PubMed]
- Makowiecki, K.; Garrett, A.; Harvey, A.R.; Rodger, J. Low-intensity repetitive transcranial magnetic stimulation requires concurrent visual system activity to modulate visual evoked potentials in adult mice. Sci. Rep. 2018, 8, 5792. [Google Scholar] [CrossRef] [PubMed]
- Brunel, N.; van Rossum, M.C.W. Quantitative investigations of electrical nerve excitation treated as polarization. Biol. Cybern. 2007, 97, 341–349. [Google Scholar] [CrossRef] [PubMed]
- Moliadze, V.; Atalay, D.; Antal, A.; Paulus, W. Close to threshold transcranial electrical stimulation preferentially activates inhibitory networks before switching to excitation with higher intensities. Brain Stimul. 2012, 5, 505–511. [Google Scholar] [CrossRef] [PubMed]
- Numssen, O.; Zier, A.L.; Thielscher, A.; Hartwigsen, G.; Knösche, T.R.; Weise, K. Efficient high-resolution TMS mapping of the human motor cortex by nonlinear regression. Neuroimage 2021, 245, 118654. [Google Scholar] [CrossRef] [PubMed]
- Thielscher, A.; Opitz, A.; Windhoff, M. Impact of the gyral geometry on the electric field induced by transcranial magnetic stimulation. Neuroimage 2011, 54, 234–243. [Google Scholar] [CrossRef]
- Colella, M.; Paffi, A.; De Santis, V.; Apollonio, F.; Liberti, M. Effect of skin conductivity on the electric field induced by transcranial stimulation techniques in different head models. Phys. Med. Biol. 2021, 66, 035010. [Google Scholar] [CrossRef]












| Model | Dimensions (cm) | Magnetization Direction | Br (T) | Rotational Frequency (rps) | Maximum (mT) | Maximum (V/m) |
|---|---|---|---|---|---|---|
| A | Axial | 1.48 | 350 | 94.1 | 0.52 | |
| B | Diametrical | 1.32 | 10 | 334.8 | 0.098 | |
| C | 2 segments , | Diametrical, multipole | 1.48 | 10 | 462.8 | 0.13 |
| D | 2 segments , | Diametrical, multipole | 1.48 | 10 | 209.8 | 0.13 |
| E | 2 segments , | Axial, multipole | 1.48 | 10 | 134.1 | 0.025 |
| F | 4 segments , | Axial, multipole | 1.48 | 10 | 2 | 0.13 |
| G | 4 segments , | Radial, multipole | 1.48 | 10 | 353.7 | 0.23 |
| H | 8 segments , | Radial, multipole | 1.48 | 10 | 350.6 | 0.14 |
| I | Diametrical | 1.32 | 10 | 354.7 | 0.11 | |
| J | 12 layers | Axial | 1.48 | 13.3 | 2.5 | 0.0092 |
| Configuration | Measured Rotational/Pulse Frequency (rps, Hz) | Measured Maximum (V/m) | Simulated Maximum (V/m) |
|---|---|---|---|
| Model A | 349.9 | 0.39 | 0.52 |
| Model B | 10.1 | 0.082 | 0.098 |
| TMS | 3448 | 401.5 | 370 [29] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robins, P.L.; Makaroff, S.N.; Dib, M.; Lisanby, S.H.; Deng, Z.-D. Electric Field Characteristics of Rotating Permanent Magnet Stimulation. Bioengineering 2024, 11, 258. https://doi.org/10.3390/bioengineering11030258
Robins PL, Makaroff SN, Dib M, Lisanby SH, Deng Z-D. Electric Field Characteristics of Rotating Permanent Magnet Stimulation. Bioengineering. 2024; 11(3):258. https://doi.org/10.3390/bioengineering11030258
Chicago/Turabian StyleRobins, Pei L., Sergey N. Makaroff, Michael Dib, Sarah H. Lisanby, and Zhi-De Deng. 2024. "Electric Field Characteristics of Rotating Permanent Magnet Stimulation" Bioengineering 11, no. 3: 258. https://doi.org/10.3390/bioengineering11030258
APA StyleRobins, P. L., Makaroff, S. N., Dib, M., Lisanby, S. H., & Deng, Z.-D. (2024). Electric Field Characteristics of Rotating Permanent Magnet Stimulation. Bioengineering, 11(3), 258. https://doi.org/10.3390/bioengineering11030258