The Stiffness of the Ascending Aorta Has a Direct Impact on Left Ventricular Function: An In Silico Model
Abstract
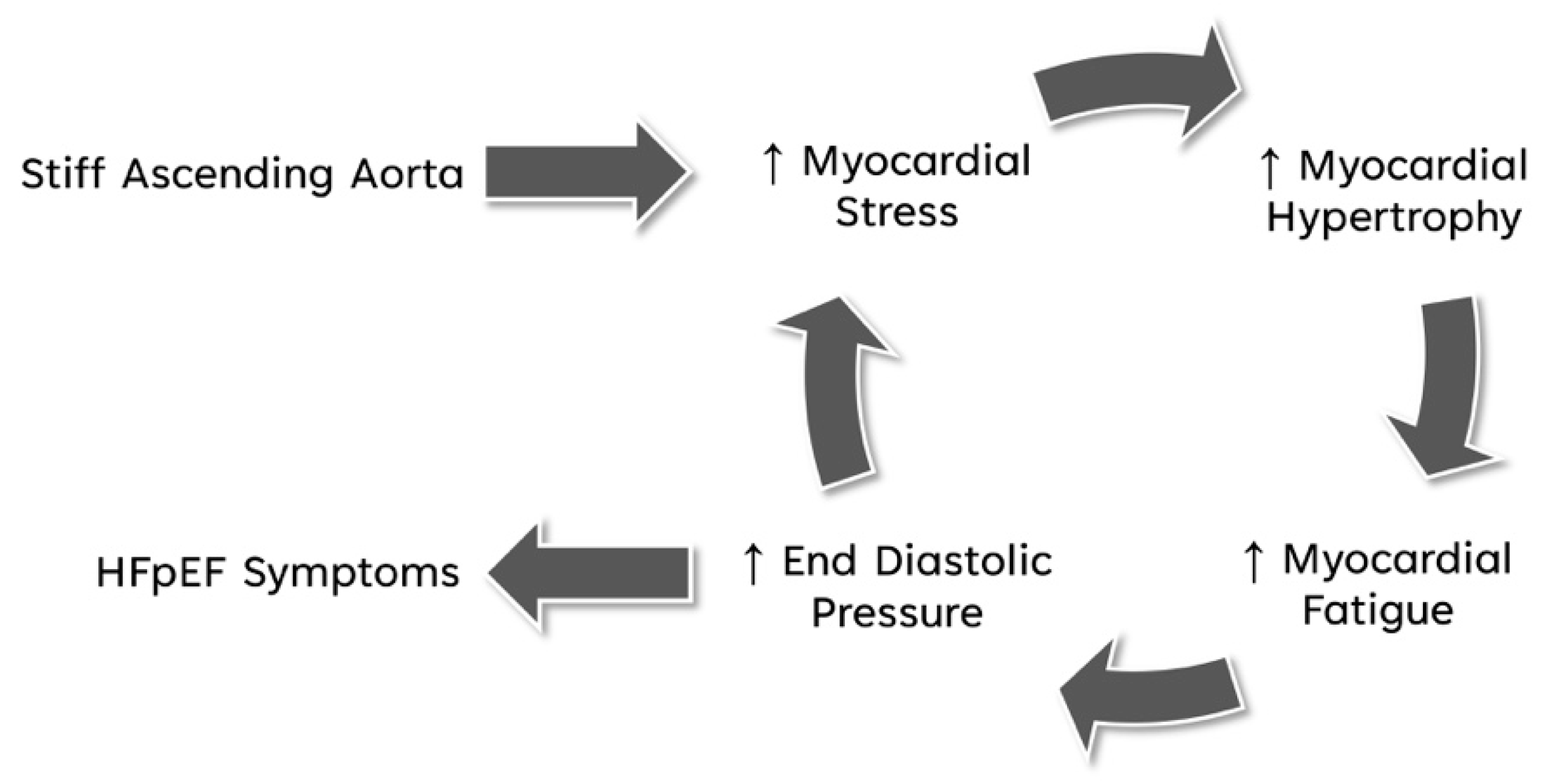
:1. Introduction
2. Methods
Computational Model
3. Results
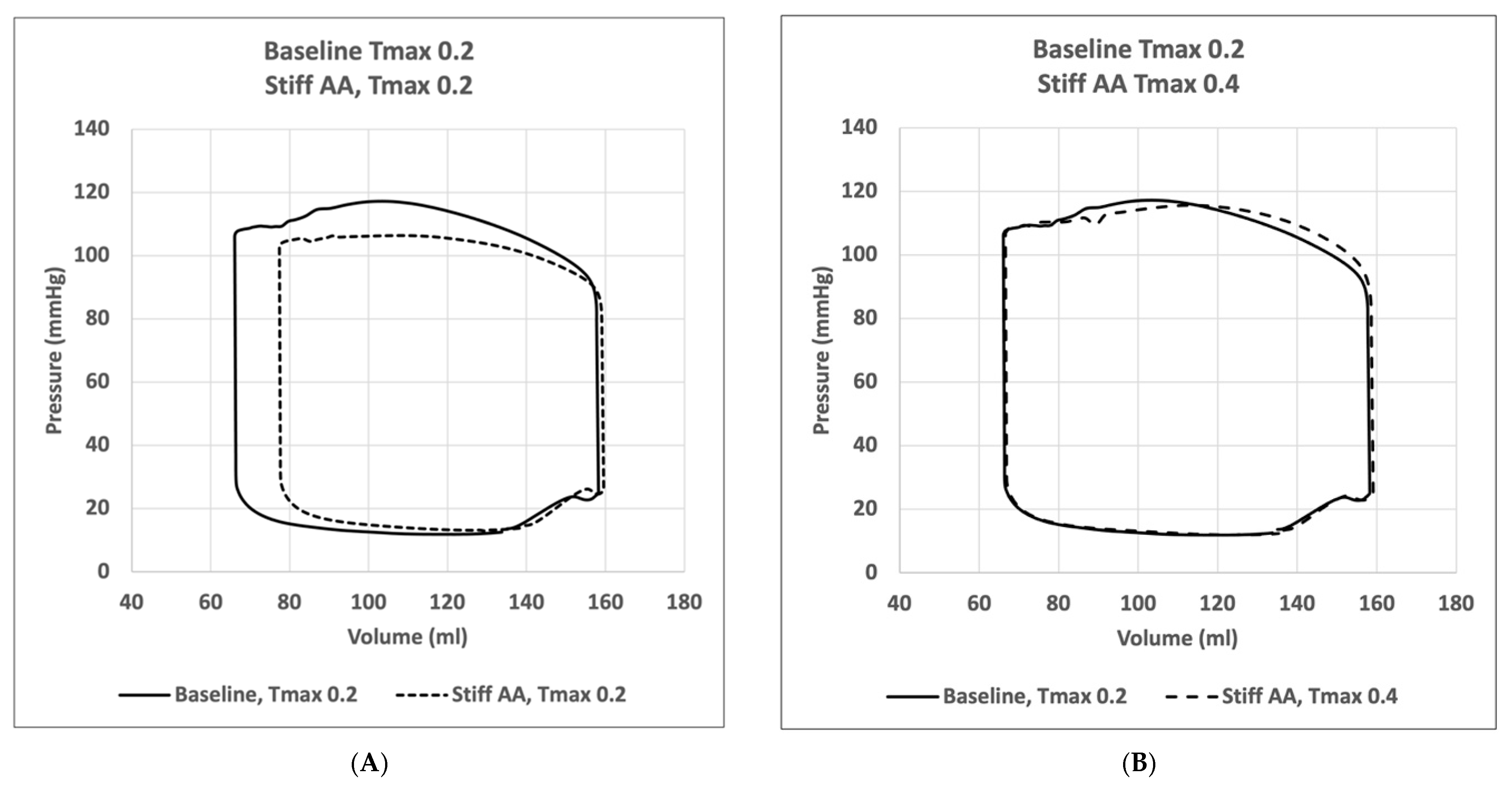
3.1. Baseline Simulation
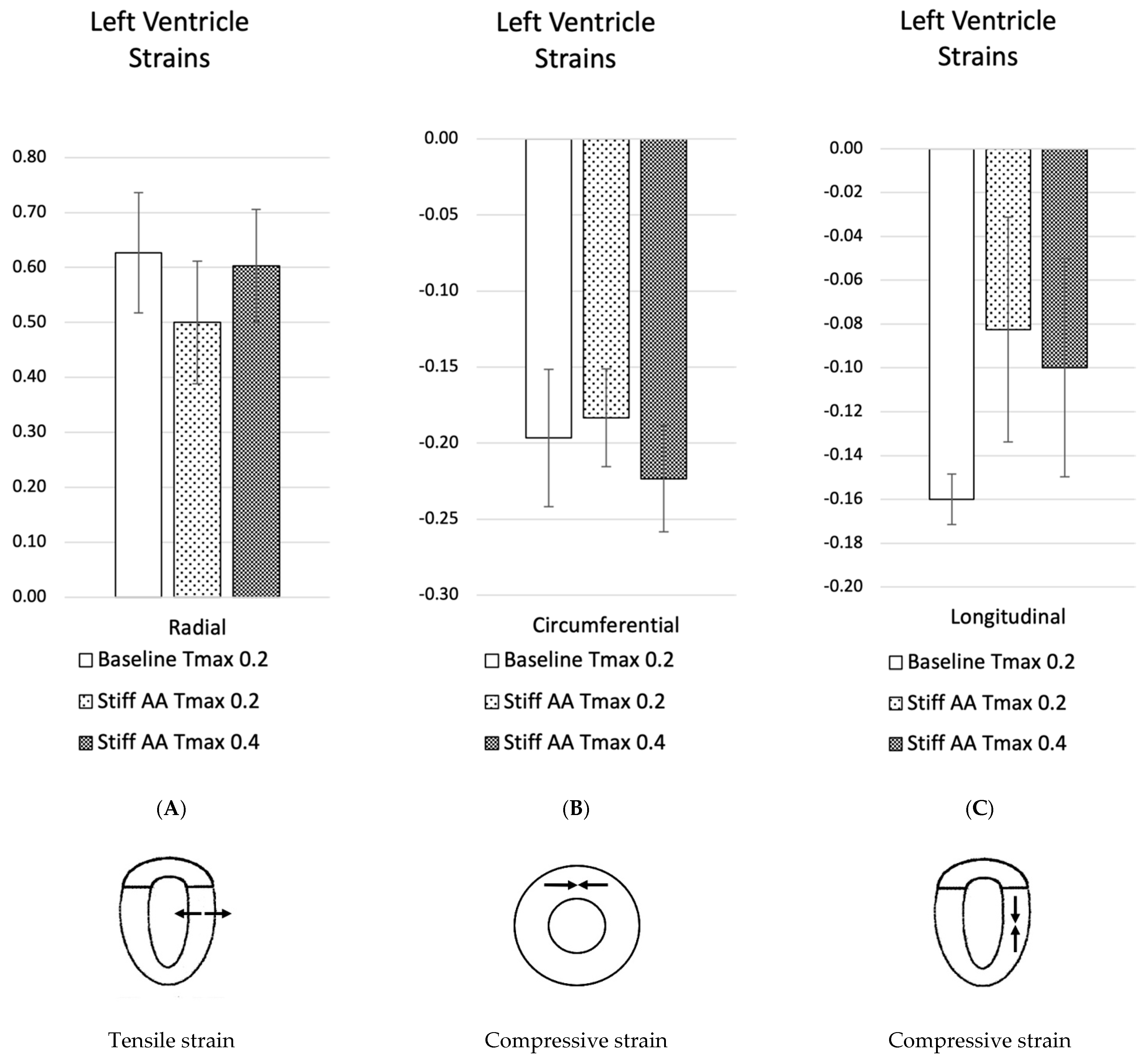
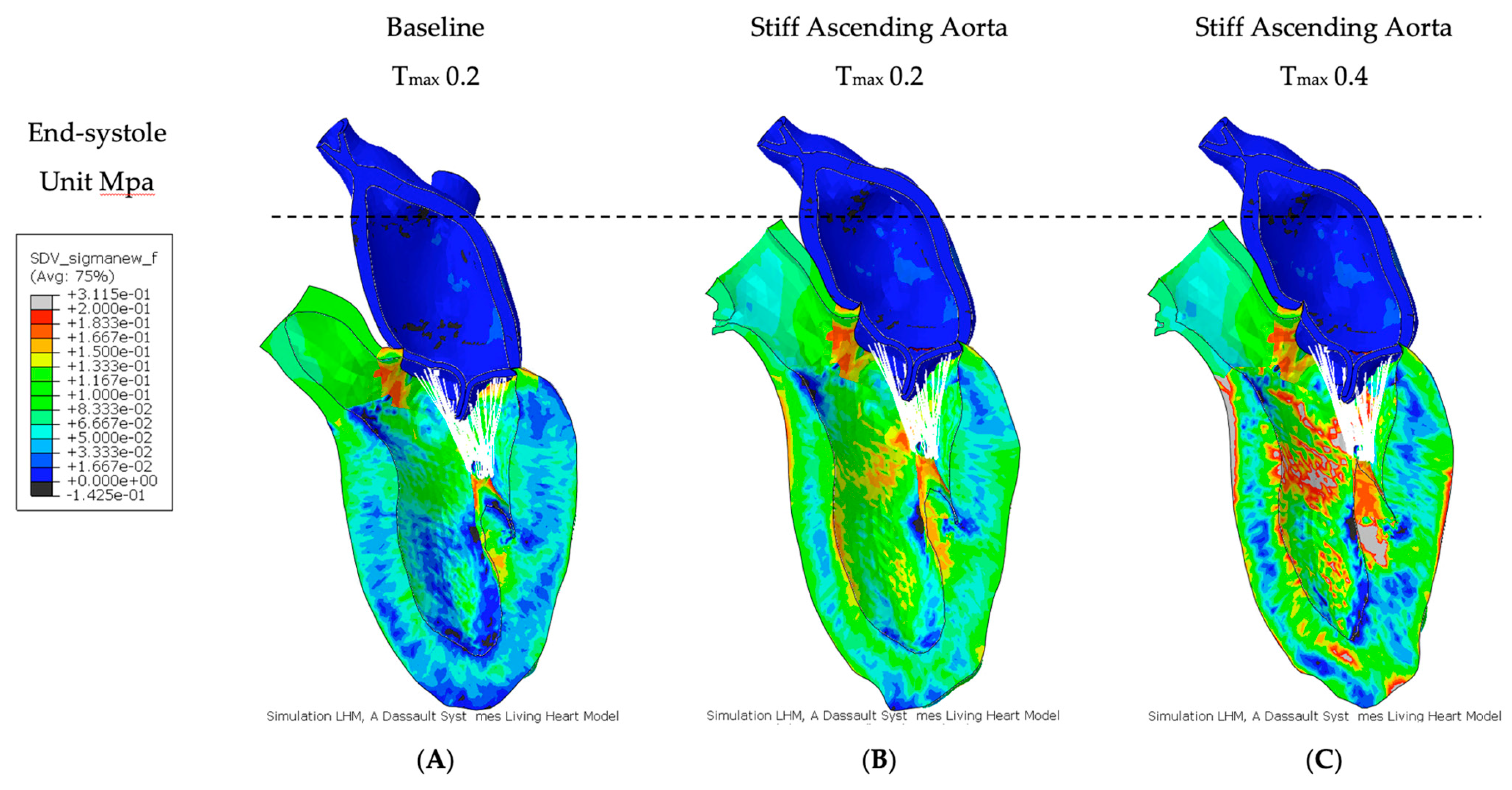
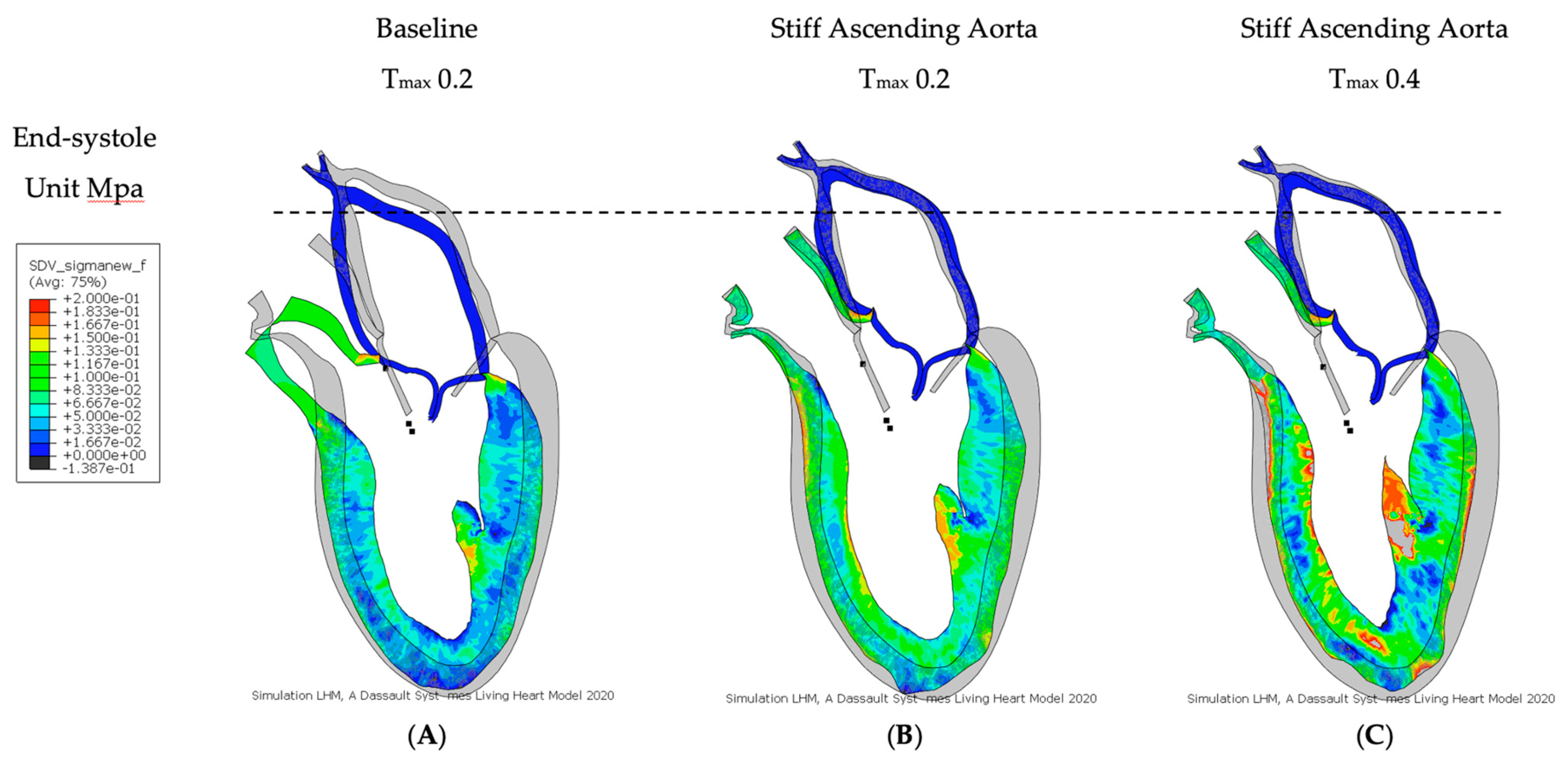
3.2. Effect of Baseline Contractility with a Stiff Ascending Aorta
3.3. Effect of Increasing Myocardial Contractility with a Stiff Ascending Aorta
4. Discussion
5. Limitation of Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buckberg, G.; Mahajan, A.; Saleh, S.; Hoffman, J.I.; Coghlan, C. Structure and function relationships of the helical ventricular myocardial band. J. Thorac. Cardiovasc. Surg. 2008, 136, 578–589.e11. [Google Scholar] [CrossRef] [PubMed]
- Plonek, T.; Rylski, B.; Nawrocki, P.; Beyersdorf, F.; Jasinski, M.; Kuliczkowski, W. Systolic stretching of the ascending aorta. Arch. Med. Sci. 2021, 17, 25–30. [Google Scholar] [CrossRef]
- Carlsson, M.; Ugander, M.; Mosen, H.; Buhre, T.; Arheden, H. Atrioventricular plane displacement is the major contributor to left ventricular pumping in healthy adults, athletes, and patients with dilated cardiomyopathy. Am. J. Physiol. Heart Circ. Physiol. 2007, 292, H1452–H1459. [Google Scholar] [CrossRef] [PubMed]
- Plonek, T.; Berezowski, M.; Kurcz, J.; Podgorski, P.; Sasiadek, M.; Rylski, B.; Mysiak, A.; Jasinski, M. The evaluation of the aortic annulus displacement during cardiac cycle using magnetic resonance imaging. BMC Cardiovasc. Disord. 2018, 18, 154. [Google Scholar] [CrossRef] [PubMed]
- Bell, V.; McCabe, E.L.; Larson, M.G.; Rong, J.; Merz, A.A.; Osypiuk, E.; Lehman, B.T.; Stantchev, P.; Aragam, J.; Benjamin, E.J.; et al. Relations between aortic stiffness and left ventricular mechanical function in the community. J. Am. Heart Assoc. 2017, 6, e004903. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, M.; Ugander, M.; Heiberg, E.; Arheden, H. The quantitative relationship between longitudinal and radial function in left, right, and total heart pumping in humans. Am. J. Physiol. Heart Circ. Physiol. 2007, 293, H636–H644. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.T.; Wenzelburger, F.; Lee, E.; Heatlie, G.; Leyva, F.; Patel, K.; Frenneaux, M.; Sanderson, J.E. The pathophysiology of heart failure with normal ejection fraction: Exercise echocardiography reveals complex abnormalities of both systolic and diastolic ventricular function involving torsion, untwist, and longitudinal motion. J. Am. Coll. Cardiol. 2009, 54, 36–46. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, M.; Hay, I.; Fetics, B.; Kass, D.A. Combined ventricular systolic and arterial stiffening in patients with heart failure and preserved ejection fraction: Implications for systolic and diastolic reserve limitations. Circulation 2003, 107, 714–720. [Google Scholar] [CrossRef] [PubMed]
- Shah, A.M.; Claggett, B.; Sweitzer, N.K.; Shah, S.J.; Anand, I.S.; Liu, L.; Pitt, B.; Pfeffer, M.A.; Solomon, S.D. Prognostic importance of impaired systolic function in heart failure with preserved ejection fraction and the impact of spironolactone. Circulation 2015, 132, 402–414. [Google Scholar] [CrossRef]
- Karagodin, I.; Aba-Omer, O.; Sparapani, R.; Strande, J.L. Aortic stiffening precedes onset of heart failure with preserved ejection fraction in patients with asymptomatic diastolic dysfunction. BMC Cardiovasc. Disord. 2017, 17, 62. [Google Scholar] [CrossRef]
- Yip, G.; Wang, M.; Zhang, Y.; Fung, J.W.; Ho, P.Y.; Sanderson, J.E. Left ventricular long axis function in diastolic heart failure is reduced in both diastole and systole: Time for a redefinition? Heart 2002, 87, 121–125. [Google Scholar] [CrossRef] [PubMed]
- DeVore, A.D.; McNulty, S.; Alenezi, F.; Ersboll, M.; Vader, J.M.; Oh, J.K.; Lin, G.; Redfield, M.M.; Lewis, G.; Semigran, M.J.; et al. Impaired left ventricular global longitudinal strain in patients with heart failure with preserved ejection fraction: Insights from the relax trial. Eur. J. Heart Fail. 2017, 19, 893–900. [Google Scholar] [CrossRef] [PubMed]
- Morris, D.A.; Boldt, L.H.; Eichstadt, H.; Ozcelik, C.; Haverkamp, W. Myocardial systolic and diastolic performance derived by 2-dimensional speckle tracking echocardiography in heart failure with normal left ventricular ejection fraction. Circ. Heart Fail. 2012, 5, 610–620. [Google Scholar] [CrossRef] [PubMed]
- Kohn, J.C.; Lampi, M.C.; Reinhart-King, C.A. Age-related vascular stiffening: Causes and consequences. Front. Genet. 2015, 6, 112. [Google Scholar] [CrossRef] [PubMed]
- Chow, B.; Rabkin, S.W. The relationship between arterial stiffness and heart failure with preserved ejection fraction: A systemic meta-analysis. Heart Fail. Rev. 2015, 20, 291–303. [Google Scholar] [CrossRef]
- Hundley, W.G.; Kitzman, D.W.; Morgan, T.M.; Hamilton, C.A.; Darty, S.N.; Stewart, K.P.; Herrington, D.M.; Link, K.M.; Little, W.C. Cardiac cycle-dependent changes in aortic area and distensibility are reduced in older patients with isolated diastolic heart failure and correlate with exercise intolerance. J. Am. Coll. Cardiol. 2001, 38, 796–802. [Google Scholar] [CrossRef] [PubMed]
- Desai, A.S.; Mitchell, G.F.; Fang, J.C.; Creager, M.A. Central aortic stiffness is increased in patients with heart failure and preserved ejection fraction. J. Card. Fail. 2009, 15, 658–664. [Google Scholar] [CrossRef] [PubMed]
- Baillargeon, B.; Rebelo, N.; Fox, D.D.; Taylor, R.L.; Kuhl, E. The living heart project: A robust and integrative simulator for human heart function. Eur. J. Mech. A Solids 2014, 48, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Wisneski, A.D.; Wang, Y.; Cutugno, S.; Pasta, S.; Stroh, A.; Yao, J.; Nguyen, T.C.; Mahadevan, V.S.; Guccione, J.M. Left ventricle biomechanics of low-flow, low-gradient aortic stenosis: A patient-specific computational model. Front. Physiol. 2022, 13, 848011. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. Constitutive modelling of passive myocardium: A structurally based framework for material characterization. Philos. Trans. A Math. Phys. Eng. Sci. 2009, 367, 3445–3475. [Google Scholar] [CrossRef]
- Sommer, G.; Schriefl, A.J.; Andra, M.; Sacherer, M.; Viertler, C.; Wolinski, H.; Holzapfel, G.A. Biomechanical properties and microstructure of human ventricular myocardium. Acta Biomater. 2015, 24, 172–192. [Google Scholar] [CrossRef] [PubMed]
- Klotz, S.; Hay, I.; Dickstein, M.L.; Yi, G.H.; Wang, J.; Maurer, M.S.; Kass, D.A.; Burkhoff, D. Single-beat estimation of end-diastolic pressure-volume relationship: A novel method with potential for noninvasive application. Am. J. Physiol. Heart Circ. Physiol. 2006, 291, H403–H412. [Google Scholar] [CrossRef] [PubMed]
- Guccione, J.M.; Waldman, L.K.; McCulloch, A.D. Mechanics of active contraction in cardiac muscle: Part ii--cylindrical models of the systolic left ventricle. J. Biomech. Eng. 1993, 115, 82–90. [Google Scholar] [CrossRef] [PubMed]
- Sack, K.L.; Baillargeon, B.; Acevedo-Bolton, G.; Genet, M.; Rebelo, N.; Kuhl, E.; Klein, L.; Weiselthaler, G.M.; Burkhoff, D.; Franz, T.; et al. Partial lvad restores ventricular outputs and normalizes lv but not rv stress distributions in the acutely failing heart in silico. Int. J. Artif. Organs 2016, 39, 421–430. [Google Scholar] [CrossRef] [PubMed]
- Walker, J.C.; Ratcliffe, M.B.; Zhang, P.; Wallace, A.W.; Fata, B.; Hsu, E.W.; Saloner, D.; Guccione, J.M. Mri-based finite-element analysis of left ventricular aneurysm. Am. J. Physiol. Heart Circ. Physiol. 2005, 289, H692–H700. [Google Scholar] [CrossRef]
- Strocchi, M.; Gsell, M.A.F.; Augustin, C.M.; Razeghi, O.; Roney, C.H.; Prassl, A.J.; Vigmond, E.J.; Behar, J.M.; Gould, J.S.; Rinaldi, C.A.; et al. Simulating ventricular systolic motion in a four-chamber heart model with spatially varying robin boundary conditions to model the effect of the pericardium. J. Biomech. 2020, 101, 109645. [Google Scholar] [CrossRef]
- Pagoulatou, S.Z.; Ferraro, M.; Trachet, B.; Bikia, V.; Rovas, G.; Crowe, L.A.; Vallee, J.P.; Adamopoulos, D.; Stergiopulos, N. The effect of the elongation of the proximal aorta on the estimation of the aortic wall distensibility. Biomech. Model. Mechanobiol. 2021, 20, 107–119. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.C.; Lugo-Olivieri, C.H.; McVeigh, E.R.; Zerhouni, E.A. Three-dimensional systolic strain patterns in the normal human left ventricle: Characterization with tagged mr imaging. Radiology 2000, 214, 453–466. [Google Scholar] [CrossRef] [PubMed]
- Bell, V.; Mitchell, W.A.; Sigurethsson, S.; Westenberg, J.J.; Gotal, J.D.; Torjesen, A.A.; Aspelund, T.; Launer, L.J.; de Roos, A.; Gudnason, V.; et al. Longitudinal and circumferential strain of the proximal aorta. J. Am. Heart Assoc. 2014, 3, e001536. [Google Scholar] [CrossRef]
- Goetz, W.A.; Lim, H.S.; Lansac, E.; Saber, H.A.; Pekar, F.; Weber, P.A.; Duran, C.M. Anterior mitral basal ‘stay’ chords are essential for left ventricular geometry and function. J. Heart Valve Dis. 2005, 14, 195–202, (discussion 202–193). [Google Scholar]
- Oishi, Y.; Miyoshi, H.; Mizuguchi, Y.; Iuchi, A.; Nagase, N.; Oki, T. Aortic stiffness is strikingly increased with age ≥ 50 years in clinically normal individuals and preclinical patients with cardiovascular risk factors: Assessment by the new technique of 2d strain echocardiography. J. Cardiol. 2011, 57, 354–359. [Google Scholar] [CrossRef]
- Wuyts, F.L.; Vanhuyse, V.J.; Langewouters, G.J.; Decraemer, W.F.; Raman, E.R.; Buyle, S. Elastic properties of human aortas in relation to age and atherosclerosis: A structural model. Phys. Med. Biol. 1995, 40, 1577–1597. [Google Scholar] [CrossRef]
- Safar, M.E.; Levy, B.I.; Struijker-Boudier, H. Current perspectives on arterial stiffness and pulse pressure in hypertension and cardiovascular diseases. Circulation 2003, 107, 2864–2869. [Google Scholar] [CrossRef] [PubMed]
- Zieman, S.J.; Melenovsky, V.; Kass, D.A. Mechanisms, pathophysiology, and therapy of arterial stiffness. Arterioscler. Thromb. Vasc. Biol. 2005, 25, 932–943. [Google Scholar] [CrossRef]
- Gillebert, T.C.; De Buyzere, M.L. Hfpef, diastolic suction, and exercise. JACC Cardiovasc. Imaging 2012, 5, 871–873. [Google Scholar] [CrossRef] [PubMed]
- Yotti, R.; Bermejo, J.; Antoranz, J.C.; Desco, M.M.; Cortina, C.; Rojo-Alvarez, J.L.; Allue, C.; Martin, L.; Moreno, M.; Serrano, J.A.; et al. A noninvasive method for assessing impaired diastolic suction in patients with dilated cardiomyopathy. Circulation 2005, 112, 2921–2929. [Google Scholar] [CrossRef]
- Kelly, R.P.; Tunin, R.; Kass, D.A. Effect of reduced aortic compliance on cardiac efficiency and contractile function of in situ canine left ventricle. Circ. Res. 1992, 71, 490–502. [Google Scholar] [CrossRef]
- Ali, D.; Tran, P.; Ennis, S.; Powell, R.; McGuire, S.; McGregor, G.; Kimani, P.K.; Weickert, M.O.; Miller, M.A.; Cappuccio, F.P.; et al. Rising arterial stiffness with accumulating comorbidities associates with heart failure with preserved ejection fraction. ESC Heart Fail. 2023, 10, 2487–2498. [Google Scholar] [CrossRef] [PubMed]
- Lyle, M.A.; Brozovich, F.V. Hfpef, a disease of the vasculature: A closer look at the other half. Mayo Clin. Proc. 2018, 93, 1305–1314. [Google Scholar] [CrossRef]
- Tran, P.; Banerjee, P. Myocardial fatigue at a glance. Curr. Heart Fail. Rep. 2023, 20, 191–193. [Google Scholar] [CrossRef]
- Tran, P.; Maddock, H.; Banerjee, P. Myocardial fatigue: A mechano-energetic concept in heart failure. Curr. Cardiol. Rep. 2022, 24, 711–730. [Google Scholar] [CrossRef] [PubMed]
- Sundberg, C.W.; Fitts, R.H. Bioenergetic basis of skeletal muscle fatigue. Curr. Opin. Physiol. 2019, 10, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Lemon, D.D.; Papst, P.J.; Joly, K.; Plato, C.F.; McKinsey, T.A. A high-performance liquid chromatography assay for quantification of cardiac myosin heavy chain isoform protein expression. Anal. Biochem. 2011, 408, 132–135. [Google Scholar] [CrossRef] [PubMed]
- McDonald, K.S.; Hanft, L.M.; Robinett, J.C.; Guglin, M.; Campbell, K.S. Regulation of myofilament contractile function in human donor and failing hearts. Front. Physiol. 2020, 11, 468. [Google Scholar] [CrossRef] [PubMed]
- Tran, P.; Linekar, A.; Dandekar, U.; Barker, T.; Balasubramanian, S.; Bhaskara-Pillai, J.; Shelley, S.; Maddock, H.; Banerjee, P. Profiling the biomechanical responses to workload on the human myocyte to explore the concept of myocardial fatigue and reversibility: Rationale and design of the power heart failure study. J. Cardiovasc. Transl. Res. 2024, 17, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Daou, D.; Gillette, T.G.; Hill, J.A. Inflammatory mechanisms in heart failure with preserved ejection fraction. Physiology 2023, 38, 217–230. [Google Scholar] [CrossRef]
- Frangogiannis, N.G. Cardiac fibrosis. Cardiovasc. Res. 2021, 117, 1450–1488. [Google Scholar] [CrossRef]
- Garg, P.; Assadi, H.; Jones, R.; Chan, W.B.; Metherall, P.; Thomas, R.; van der Geest, R.; Swift, A.J.; Al-Mohammad, A. Left ventricular fibrosis and hypertrophy are associated with mortality in heart failure with preserved ejection fraction. Sci. Rep. 2021, 11, 617. [Google Scholar] [CrossRef]


| Passive Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a (MPa) | b | af (MPa) | bf | as (MPa) | bs | afs (MPa) | bfs | Calibration Data | ||
| Atrium | 1.0 × 10−3 | 3.1 | 4.7 × 10−3 | 1.2 × 10+1 | 2.7 × 10−3 | 9.1 | 9.0 × 10−7 | 6.7 × 10−4 | Sommer [21], Klotz [22] | |
| Ventricle | 3.9 × 10−4 | 3.7 | 1.9 × 10−3 | 1.4 × 10+1 | 1.1 × 10−3 | 1.1 × 10+1 | 3.6 × 10−7 | 7.8 × 10−4 | Sommer [21], Klotz [22] | |
| Active Parameters | ||||||||||
| t0 (s) | m (s/mm) | b (s) | l0 (mm) | B (1/mm) | Ca0_max (mM) | Ca0 (mM) | Tmax (Mpa) | Lr (mm) | Reference | |
| Atrium | 0.05 | 1048.9 | −1.5 | 0.00158 | 4750 | 4.35 | 4.35 | 0.1 | 0.00185 | Sack [24], Guccione [23] |
| Ventricle | 0.35 | 950 | −1.5 | 0.00158 | 4750 | 4.35 | 4.35 | 0.2 | 0.00185 | Sack [24], Guccione [23] |
| EDP | EDV | ESP | ESV | SVed-es | SW | |
|---|---|---|---|---|---|---|
| (mmHg) | (mL) | (mmHg) | (mL) | (mL) | (Joule) | |
| Baseline Tmax 0.2 | 11.85 | 158.30 | 117.10 | 66.10 | 92.20 | 8747.50 |
| Stiff AA Tmax 0.2 | 12.86 | 159.60 | 106.40 | 77.40 | 82.20 | 7084.50 |
| Stiff AA increased contractility Tmax 0.4 | 11.94 | 159.09 | 115.62 | 66.63 | 92.46 | 8794.81 |
| Baseline vs. stiff AA Tmax 0.2 vs. Tmax 0.2 | 1.01 | 1.30 | −10.70 | 11.30 | −10.00 | −1663.00 |
| Baseline vs. stiff AA Tmax 0.2 vs. Tmax 0.2 (%) | 8.52% | 0.82% | −9.14% | 17.10% | −10.85% | −19.01% |
| Baseline vs. stiff AA Tmax 0.2 vs. Tmax 0.4 | 0.09 | 0.79 | −1.48 | 0.53 | 0.26 | 47.31 |
| Baseline vs. stiff AA Tmax 0.2 vs. Tmax 0.4 (%) | 0.74% | 0.50% | −1.26% | 0.80% | 0.28% | 0.54% |
| Average Strain | Radial | Circumferential | Longitudinal |
|---|---|---|---|
| Baseline Tmax 0.2 | 0.63 ± 0.11 | −0.20 ± 0.05 | −0.16 ± 0.01 |
| Stiff AA Tmax 0.2 | 0.50 ± 0.11 | −0.18 ± 0.03 | −0.08 ± 0.05 |
| Stiff AA Tmax 0.4 | 0.60 ± 0.10 | −0.22 ± 0.04 | −0.10 ± 0.05 |
| Baseline Tmax 0.2 vs. stiff AA Tmax 0.2 | −0.13 ± 0.02 | 0.01 ± 0.02 | 0.08 ± 0.06 |
| Baseline Tmax 0.2 vs. stiff AA Tmax 0.2 (%) | −20.21 ± 2.39% | −6.78 ± 10.86% | −48.44 ± 36.88% |
| Baseline Tmax 0.2 vs. stiff AA Tmax 0.4 | −0.02 ± 0.06 | 0.03 ± 0.01 | 0.06 ± 0.06 |
| Baseline Tmax 0.2 vs. stiff AA Tmax 0.4 (%) | −3.72 ± 8.78% | +13.56 ± 6.10% | −37.50 ± 35.00% |
| Longitudinal Strain | Septal | Anterior | Lateral | Posterior |
|---|---|---|---|---|
| Baseline Tmax 0.2 | −0.17 | −0.17 | −0.15 | −0.15 |
| Stiff AA Tmax 0.2 | −0.01 | −0.10 | −0.13 | −0.09 |
| Stiff AA Tmax 0.4 | −0.03 | −0.13 | −0.14 | −0.10 |
| Baseline Tmax 0.2 vs. Stiff AA Tmax 0.2 | 0.16 | 0.07 | 0.02 | 0.06 |
| Baseline Tmax 0.2 vs. Stiff AA Tmax 0.2 (%) | −94.12% | −41.18% | −13.33% | −40.00% |
| Baseline Tmax 0.2 vs. stiff AA Tmax 0.4 | 0.14 | 0.04 | 0.01 | 0.05 |
| Baseline Tmax 0.2 vs. stiff AA Tmax 0.4 (%) | −82.35% | −23.53% | −6.67% | −33.33% |
| Stress | Baseline | Stiff AA | Stiff AA |
|---|---|---|---|
| Tmax 0.2 | Tmax 0.2 | Tmax 0.4 | |
| Baseline—Stroke Volume | Reduced—Stroke Volume | Recovered—Stroke Volume | |
| (MPa) | 0.056 ± 0.036 | 0.076 ± 0.042 | 0.090 ± 0.071 |
| vs. baseline | 36.98 ± 42.91% | 61.76 ± 88.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goetz, W.A.; Yao, J.; Brener, M.; Puri, R.; Swaans, M.; Schopka, S.; Wiesner, S.; Creutzenberg, M.; Sievert, H.; Kassab, G.S. The Stiffness of the Ascending Aorta Has a Direct Impact on Left Ventricular Function: An In Silico Model. Bioengineering 2024, 11, 603. https://doi.org/10.3390/bioengineering11060603
Goetz WA, Yao J, Brener M, Puri R, Swaans M, Schopka S, Wiesner S, Creutzenberg M, Sievert H, Kassab GS. The Stiffness of the Ascending Aorta Has a Direct Impact on Left Ventricular Function: An In Silico Model. Bioengineering. 2024; 11(6):603. https://doi.org/10.3390/bioengineering11060603
Chicago/Turabian StyleGoetz, Wolfgang Anton, Jiang Yao, Michael Brener, Rishi Puri, Martin Swaans, Simon Schopka, Sigrid Wiesner, Marcus Creutzenberg, Horst Sievert, and Ghassan S. Kassab. 2024. "The Stiffness of the Ascending Aorta Has a Direct Impact on Left Ventricular Function: An In Silico Model" Bioengineering 11, no. 6: 603. https://doi.org/10.3390/bioengineering11060603
APA StyleGoetz, W. A., Yao, J., Brener, M., Puri, R., Swaans, M., Schopka, S., Wiesner, S., Creutzenberg, M., Sievert, H., & Kassab, G. S. (2024). The Stiffness of the Ascending Aorta Has a Direct Impact on Left Ventricular Function: An In Silico Model. Bioengineering, 11(6), 603. https://doi.org/10.3390/bioengineering11060603








