A Muscle-Driven Spine Model for Predictive Simulations in the Design of Spinal Implants and Lumbar Orthoses
Abstract
1. Introduction
2. Materials and Methods
- [i]
- First MLS model manipulation during runtime,
- [ii]
- activation of the Tacking Controller and all boundary conditions including gravity, with subsequent 2° flexion and 2° extension of the thorax (spinal settling phase),
- [iii]
- second MLS model manipulation during runtime,
- [iv]
- changing the body posture,
- [v]
- application of external manipulators and loads,
- [vi]
- evaluation of model responses once static equilibrium was reached.
2.1. Spinal Instrumentation
| Used for Scenario | Moment in Nm | Follower Load in N | References |
|---|---|---|---|
| 1 | 3.75 | [89] | |
| 1 | 6.60 | [36,90] | |
| 1 | 250 | [36,90] | |
| 2 | 10.0 | 200 | [91] |
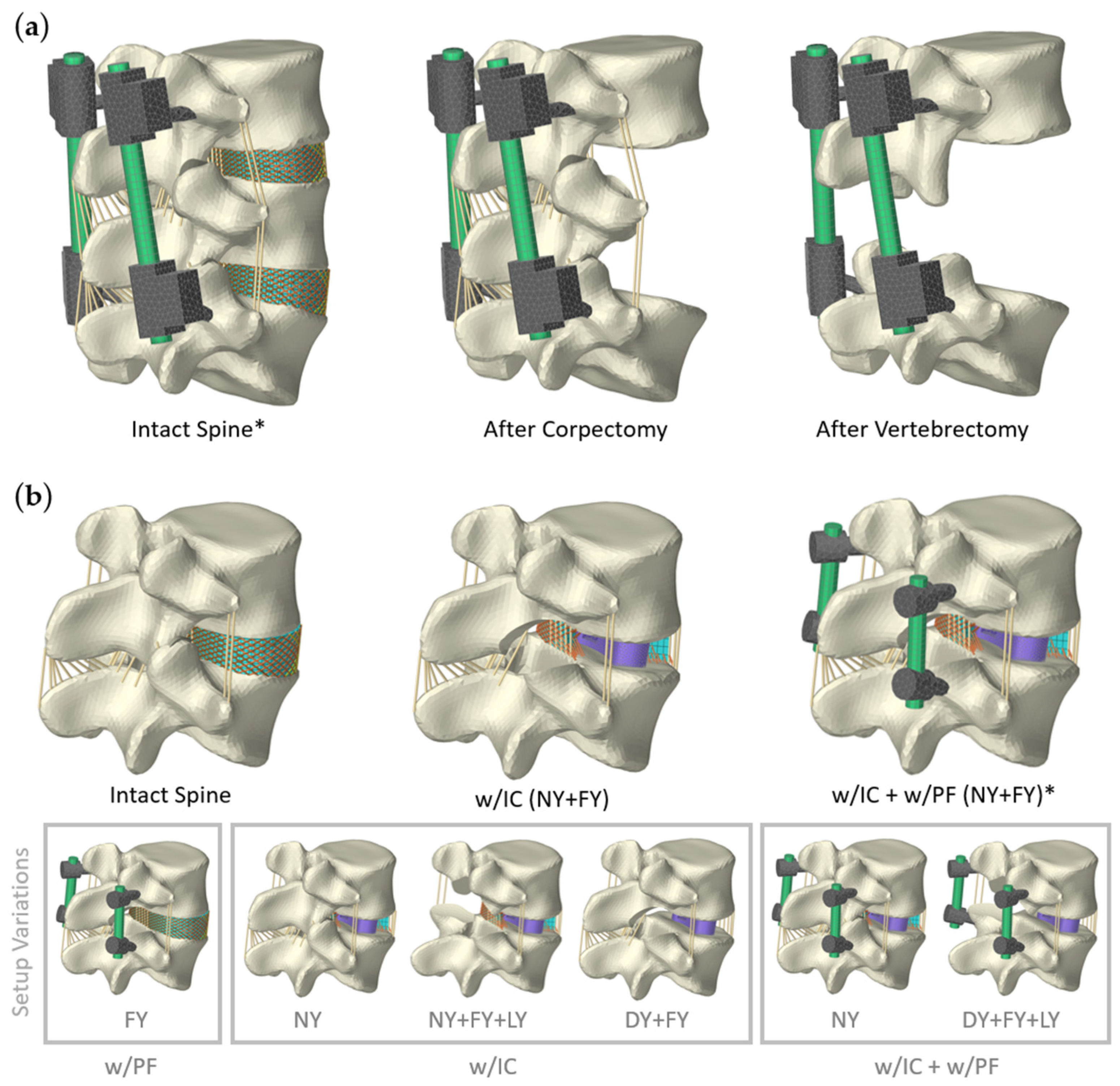
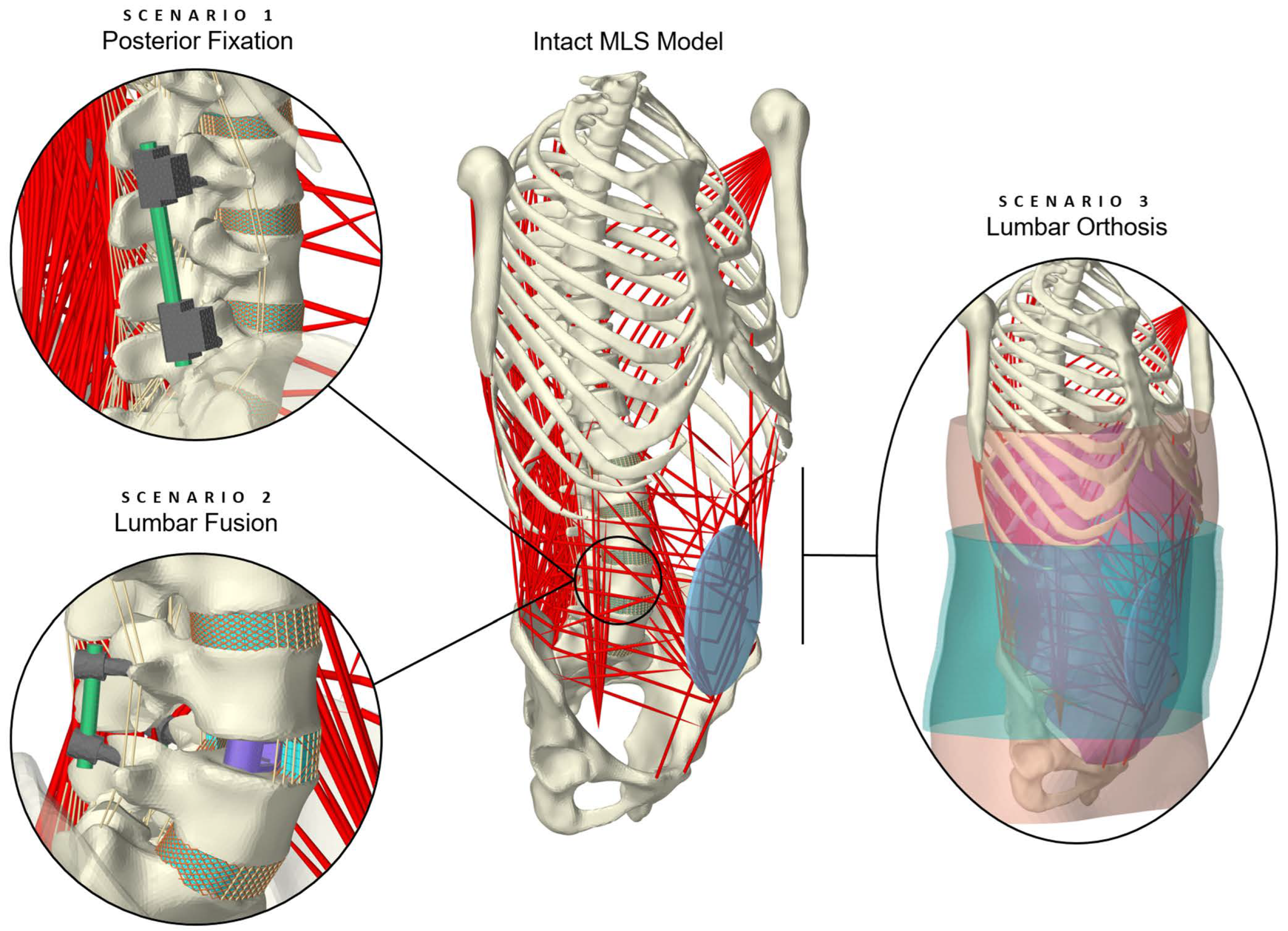
2.1.1. Scenario 1: Posterior Fixation
2.1.2. Scenario 2: Lumbar Fusion
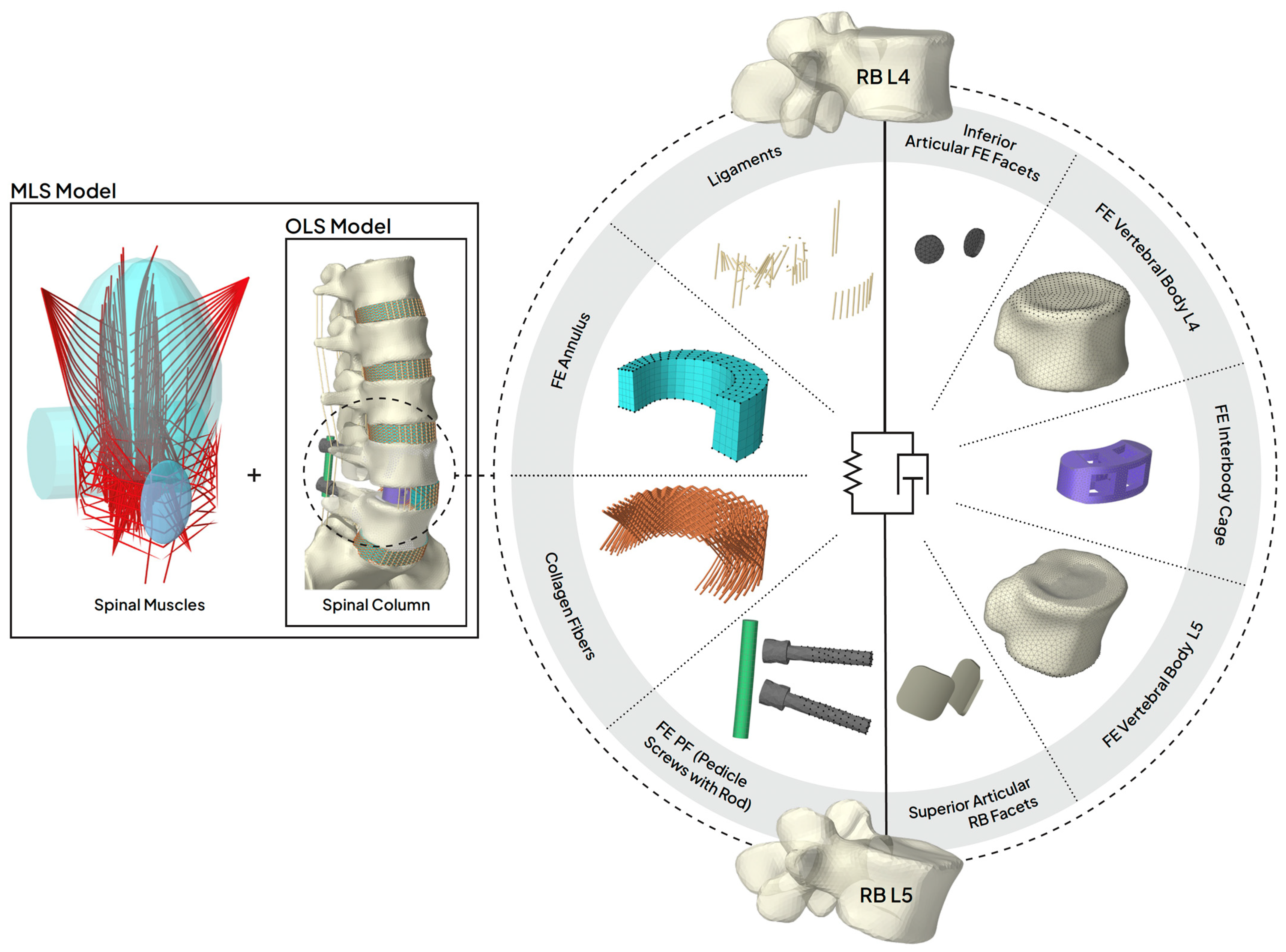

2.2. Scenario 3: Lumbar Orthosis
3. Results
3.1. Scenario 1: Posterior Fixation
3.2. Scenario 2: Lumbar Fusion
3.3. Scenario 3: Lumbar Orthosis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CY | Corpectomy |
| DY | Discectomy |
| IC | Interbody cage |
| IT | Intact spine |
| FE | Finite element |
| FY | Facetectomy |
| HU | Hounsfield unit |
| IDP | Intradiscal pressure |
| LY | Laminectomy |
| OLS | Osteoligamentous lumbosacral spine |
| MB | Multibody |
| MLS | Musculoskeletal lumbosacral spine |
| PF | Posterior fixation |
| PLIF | Posterior lumbar interbody fusion |
| ROM | Range of motion |
| TLIF | Transforaminal lumbar interbody fusion |
| VY | Vertebrectomy |
Appendix A
References
- GBD 2021 Low Back Pain Collaborators. Global, regional, and national burden of low back pain, 1990–2020, its attributable risk factors, and projections to 2050: A systematic analysis of the Global Burden of Disease Study 2021. Lancet Rheumatol. 2023, 5, e316–e329. [Google Scholar] [CrossRef] [PubMed]
- GBD 2019 Diseases and Injuries Collaborators. Global burden of 369 diseases and injuries in 204 countries and territories, 1990–2019: A systematic analysis for the Global Burden of Disease Study 2019. Lancet 2020, 396, 1204–1222. [Google Scholar] [CrossRef] [PubMed]
- Andersson, G.B.J. Epidemiology of low back pain. Acta Orthop. Scand. 1998, 69, 28–31. [Google Scholar] [CrossRef]
- Kliner, K.; Rennert, D.; Richter, M. (Eds.) BKK Gesundheitsatlas 2019; MWV Medizinisch Wisschenschaftliche Verlagsgesellschaft: Berlin, Germany, 2019; ISBN 978-3-95466-443-6. [Google Scholar]
- Setchell, J.; Costa, N.; Ferreira, M.L.; Hodges, P.W. What decreases low back pain? A qualitative study of patient perspectives. Scand. J. Pain 2019, 19, 597–603. [Google Scholar] [CrossRef] [PubMed]
- Matheve, T.; Hodges, P.W.; Danneels, L. The Role of Back Muscle Dysfunctions in Chronic Low Back Pain: State-of-the-Art and Clinical Implications. J. Clin. Med. 2023, 12, 5510. [Google Scholar] [CrossRef]
- Duthey, B. Background Paper 6.24 Low Back Pain; WHO: Geneva, Switzerland, 2013. [Google Scholar]
- Lee, S.-B.; Yoon, J.; Park, S.-J.; Chae, D.-S. Expandable Cages for Lumbar Interbody Fusion: A Narrative Review. J. Clin. Med. 2024, 13, 2889. [Google Scholar] [CrossRef] [PubMed]
- Chou, R.; Deyo, R.; Friedly, J.; Skelly, A.; Hashimoto, R.; Weimer, M.; Fu, R.; Dana, T.; Kraegel, P.; Griffin, J.; et al. Nonpharmacologic Therapies for Low Back Pain: A Systematic Review for an American College of Physicians Clinical Practice Guideline. Ann. Intern. Med. 2017, 166, 493–505. [Google Scholar] [CrossRef]
- Mayer, F.; Arampatzis, A.; Banzer, W.; Platen, P.; Schneider, C. (Eds.) Rückenschmerz und Sport: Evidenzbasierte Prävention und Therapie aus dem Forschungsprojekt “RanRücken”, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2024; ISBN 978-3-662-63253-6. [Google Scholar]
- La Barbera, L. Fixation and Fusion. In Biomechanics of the Spine: Basic Concepts, Spinal Disorders and Treatments, 1st ed.; Galbusera, F., Wilke, H.-J., Eds.; Academic Press: London, UK, 2018; Chapter 17; pp. 301–327. ISBN 0128128526. [Google Scholar]
- Wilke, H.-J.; Wenger, K.; Claes, L.E. Testing criteria for spinal implants: Recommendations for the standardization of in vitro stability testing of spinal implants. Eur. Spine J. 1998, 7, 148–154. [Google Scholar] [CrossRef]
- Phan, K.; Mobbs, R.J. Evolution of Design of Interbody Cages for Anterior Lumbar Interbody Fusion. Orthop. Surg. 2016, 8, 270–277. [Google Scholar] [CrossRef]
- Jellema, P.; van Tulder, M.W.; van Poppel, M.N.M.; Nachemson, A.L.; Bouter, L.M. Lumbar supports for prevention and treatment of low back pain: A systematic review within the framework of the Cochrane Back Review Group. Spine 2001, 26, 377–386. [Google Scholar] [CrossRef]
- Cholewicki, J.; Juluru, K.; Radebold, A.; Panjabi, M.M.; McGill, S.M. Lumbar spine stability can be augmented with an abdominal belt and/or increased intra-abdominal pressure. Eur. Spine J. Off. Publ. Eur. Spine Soc. Eur. Spinal Deform. Soc. Eur. Sect. Cerv. Spine Res. Soc. 1999, 8, 388–395. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.D.; Michael, J.W.; Fisk, J.R. AAOS Atlas of Orthoses and Assistive Devices, 4th ed.; Mosby/Elsevier: Philadelphia, PA, USA, 2008; ISBN 0323076319. [Google Scholar]
- Anderson, C.W.; Redford, J.B. Orthotic treatment for injuries and diseases of the spinal column. Phys. Med. Rehabil. State Art Rev. 2000, 14, 471–484. [Google Scholar]
- Lei, W.; Yan, Y. (Eds.) Internal Fixation of the Spine: Principles and Practice; Springer: Berlin/Heidelberg, Germany, 2021; ISBN 978-981-16-1562-7. [Google Scholar]
- Mobbs, R.J.; Phan, K.; Malham, G.; Seex, K.; Rao, P.J. Lumbar interbody fusion: Techniques, indications and comparison of interbody fusion options including PLIF, TLIF, MI-TLIF, OLIF/ATP, LLIF and ALIF. J. Spine Surg. 2015, 1, 2–18. [Google Scholar] [CrossRef]
- Evans, J.H. Biomechanics of lumbar fusion. Clin. Orthop. Relat. Res. 1985, 38–46. [Google Scholar] [CrossRef]
- Campbell, R.C.; Mobbs, R.J.; Lu, V.M.; Xu, J.; Rao, P.J.; Phan, K. Posterolateral Fusion Versus Interbody Fusion for Degenerative Spondylolisthesis: Systematic Review and Meta-Analysis. Glob. Spine J. 2017, 7, 482–490. [Google Scholar] [CrossRef] [PubMed]
- Oxland, T.R.; Lund, T. Biomechanics of stand-alone cages and cages in combination with posterior fixation: A literature review. Eur. Spine J. 2000, 9 (Suppl. S1), S95–S101. [Google Scholar] [CrossRef]
- Schwab, F.; Patel, A.; Ungar, B.; Farcy, J.-P.; Lafage, V. Adult spinal deformity-postoperative standing imbalance: How much can you tolerate? An overview of key parameters in assessing alignment and planning corrective surgery. Spine 2010, 35, 2224–2231. [Google Scholar] [CrossRef] [PubMed]
- White, A.A.; Panjabi, M.M. Clinical Biomechanics of the Spine, 2nd ed.; Lippincott: Philadelphia, PA, USA, 1990; ISBN 0397507208. [Google Scholar]
- Bender, B.; Gericke, K. Pahl/Beitz Konstruktionslehre; Springer: Berlin/Heidelberg, Germany, 2021; ISBN 978-3-662-57302-0. [Google Scholar]
- La Barbera, L.; Galbusera, F.; Wilke, H.-J.; Villa, T.M.T. Preclinical evaluation of posterior spine stabilization devices: Can the current standards represent basic everyday life activities? Eur. Spine J. 2016, 25, 2909–2918. [Google Scholar] [CrossRef]
- Augat, P.; Hast, M.W.; Schemitsch, G.; Heyland, M.; Trepczynski, A.; Borgiani, E.; Russow, G.; Märdian, S.; Duda, G.N.; Hollensteiner, M.; et al. Biomechanical models: Key considerations in study design. OTA Int. 2021, 4, e099. [Google Scholar] [CrossRef]
- Galbusera, F.; Wilke, H.-J. (Eds.) Biomechanics of the Spine: Basic Concepts, Spinal Disorders and Treatments, 1st ed.; Academic Press: London, UK, 2018; ISBN 0128128526. [Google Scholar]
- Knapik, G.G.; Mendel, E.; Bourekas, E.; Marras, W.S. Computational lumbar spine models: A literature review. Clin. Biomech. 2022, 100, 105816. [Google Scholar] [CrossRef]
- Wilke, H.-J.; Heuer, F.; Schmidt, H. Prospective design delineation and subsequent in vitro evaluation of a new posterior dynamic stabilization system. Spine 2009, 34, 255–261. [Google Scholar] [CrossRef]
- Wechsler, I.; Wolf, A.; Shanbhag, J.; Leyendecker, S.; Eskofier, B.M.; Koelewijn, A.D.; Wartzack, S.; Miehling, J. Bridging the sim2real gap. Investigating deviations between experimental motion measurements and musculoskeletal simulation results—A systematic review. Front. Bioeng. Biotechnol. 2024, 12, 1386874. [Google Scholar] [CrossRef] [PubMed]
- Viceconti, M. Biomechanics-based in silico medicine: The manifesto of a new science. J. Biomech. 2015, 48, 193–194. [Google Scholar] [CrossRef]
- Nispel, K.; Lerchl, T.; Senner, V.; Kirschke, J.S. Recent Advances in Coupled MBS and FEM Models of the Spine—A Review. Bioengineering 2023, 10, 315. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wu, Z. Recent advancement in finite element analysis of spinal interbody cages: A review. Front. Bioeng. Biotechnol. 2023, 11, 1041973. [Google Scholar] [CrossRef]
- Loenen, A.C.Y.; Noailly, J.; Ito, K.; Willems, P.C.; Arts, J.J.; van Rietbergen, B. Patient-Specific Variations in Local Strain Patterns on the Surface of a Trussed Titanium Interbody Cage. Front. Bioeng. Biotechnol. 2021, 9, 750246. [Google Scholar] [CrossRef] [PubMed]
- Rohlmann, A.; Bergmann, G.; Graichen, F.; Weber, U. Comparison of loads on internal spinal fixation devices measured in vitro and in vivo. Med. Eng. Phys. 1997, 19, 539–546. [Google Scholar] [CrossRef]
- Wilke, H.-J.; Rohlmann, A.; Neller, S.; Graichen, F.; Claes, L.E.; Bergmann, G. ISSLS prize winner: A novel approach to determine trunk muscle forces during flexion and extension: A comparison of data from an in vitro experiment and in vivo measurements. Spine 2003, 28, 2585–2593. [Google Scholar] [CrossRef]
- Rohlmann, A.; Zander, T.; Rao, M.; Bergmann, G. Realistic loading conditions for upper body bending. J. Biomech. 2009, 42, 884–890. [Google Scholar] [CrossRef]
- Abbasi-Ghiri, A.; Ebrahimkhani, M.; Arjmand, N. Novel force–displacement control passive finite element models of the spine to simulate intact and pathological conditions; comparisons with traditional passive and detailed musculoskeletal models. J. Biomech. 2022, 141, 111173. [Google Scholar] [CrossRef]
- Fang, G.; Lin, Y.; Wu, J.; Cui, W.; Zhang, S.; Guo, L.; Sang, H.; Huang, W. Biomechanical Comparison of Stand-Alone and Bilateral Pedicle Screw Fixation for Oblique Lumbar Interbody Fusion Surgery-A Finite Element Analysis. World Neurosurg. 2020, 141, e204–e212. [Google Scholar] [CrossRef]
- Cegoñino, J.; Calvo-Echenique, A.; Pérez-del Palomar, A. Influence of different fusion techniques in lumbar spine over the adjacent segments: A 3D finite element study. J. Orthop. Res. 2015, 33, 993–1000. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhu, W. The path to deliver the most realistic follower load for a lumbar spine in standing posture: A finite element study. J. Biomech. Eng. 2019, 141, 031010. [Google Scholar] [CrossRef] [PubMed]
- Rajaee, M.A.; Arjmand, N.; Shirazi-Adl, A. A novel coupled musculoskeletal finite element model of the spine—Critical evaluation of trunk models in some tasks. J. Biomech. 2021, 119, 110331. [Google Scholar] [CrossRef]
- Ebrahimkhani, M.; Arjmand, N.; Shirazi-Adl, A. Adjacent segments biomechanics following lumbar fusion surgery: A musculoskeletal finite element model study. Eur. Spine J. 2022, 31, 1630–1639. [Google Scholar] [CrossRef]
- Ledet, E.H.; Liddle, B.; Kradinova, K.; Harper, S. Smart implants in orthopedic surgery, improving patient outcomes: A review. Innov. Entrep. Health 2018, 5, 41–51. [Google Scholar] [CrossRef]
- Rohlmann, A.; Bergmann, G.; Graichen, F.; Mayer, H.M. Influence of muscle forces on loads in internal spinal fixation devices. Spine 1998, 23, 537–542. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.; Reitmaier, S. Modelle zur Vorhersage von Kräften und der Belastung der Wirbelsäule. In Rückenschmerz und Sport: Evidenzbasierte Prävention und Therapie aus dem Forschungsprojekt “RanRücken”, 1st ed.; Mayer, F., Arampatzis, A., Banzer, W., Platen, P., Schneider, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2024; pp. 121–139. ISBN 978-3-662-63253-6. [Google Scholar]
- Azari, F.; Arjmand, N.; Shirazi-Adl, A.; Rahimi-Moghaddam, T. A combined passive and active musculoskeletal model study to estimate L4-L5 load sharing. J. Biomech. 2018, 70, 157–165. [Google Scholar] [CrossRef]
- Favier, C.D.; McGregor, A.H.; Phillips, A.T.M. Maintaining Bone Health in the Lumbar Spine: Routine Activities Alone Are Not Enough. Front. Bioeng. Biotechnol. 2021, 9, 661837. [Google Scholar] [CrossRef]
- Bernier, E.; Driscoll, M. Numerical investigation of intra-abdominal pressure and spinal load-sharing upon the application of an abdominal belt. J. Biomech. 2023, 161, 111863. [Google Scholar] [CrossRef]
- Zander, T.; Rohlmann, A.; Calisse, J.; Bergmann, G. Estimation of muscle forces in the lumbar spine during upper-body inclination. Clin. Biomech. 2001, 16 (Suppl. S1), S73–S80. [Google Scholar] [CrossRef]
- Khoddam-Khorasani, P.; Arjmand, N.; Shirazi-Adl, A. Trunk Hybrid Passive-Active Musculoskeletal Modeling to Determine the Detailed T12-S1 Response Under In Vivo Loads. Ann. Biomed. Eng. 2018, 46, 1830–1843. [Google Scholar] [CrossRef]
- Rohlmann, A.; Bergmann, G.; Graichen, F. Loads on an internal spinal fixation device during walking. J. Biomech. 1997, 30, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Panico, M.; Bassani, T.; Villa, T.M.T.; Galbusera, F. The Simulation of Muscles Forces Increases the Stresses in Lumbar Fixation Implants with Respect to Pure Moment Loading. Front. Bioeng. Biotechnol. 2021, 9, 745703. [Google Scholar] [CrossRef] [PubMed]
- Wilke, H.-J.; Wolf, S.; Claes, L.E.; Arand, M.; Wiesend, A. Stability increase of the lumbar spine with different muscle groups. A biomechanical in vitro study. Spine 1995, 20, 192–198. [Google Scholar] [CrossRef]
- Ghezelbash, F.; Shahvarpour, A.; Larivière, C.; Shirazi-Adl, A. Evaluating stability of human spine in static tasks: A combined in vivo-computational study. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 1156–1168. [Google Scholar] [CrossRef]
- Panjabi, M.M. The stabilizing system of the spine. Part I. Function, dysfunction, adaptation, and enhancement. J. Spinal Disord. 1992, 5, 383–389; discussion 397. [Google Scholar] [CrossRef]
- Oxland, T.R. Fundamental biomechanics of the spine--What we have learned in the past 25 years and future directions. J. Biomech. 2016, 49, 817–832. [Google Scholar] [CrossRef] [PubMed]
- Gardner-Morse, M.G.; Stokes, I.A.; Laible, J.P. Role of muscles in lumbar spine stability in maximum extension efforts. J. Orthop. Res. 1995, 13, 802–808. [Google Scholar] [CrossRef]
- Cholewicki, J.; Lee, A.S.; Peter Reeves, N.; Morrisette, D.C. Comparison of trunk stiffness provided by different design characteristics of lumbosacral orthoses. Clin. Biomech. 2010, 25, 110–114. [Google Scholar] [CrossRef]
- Cholewicki, J. The effects of lumbosacral orthoses on spine stability: What changes in EMG can be expected? J. Orthop. Res. 2004, 22, 1150–1155. [Google Scholar] [CrossRef] [PubMed]
- Holzinger, T.; Cazzola, D.; Sagl, B. Development, calibration and validation of impact-specific cervical spine models: A novel approach using hybrid multibody and finite-element methods. Comput. Methods Programs Biomed. 2024, 108430. [Google Scholar] [CrossRef]
- Stavness, I.; Lloyd, J.E.; Payan, Y.; Fels, S. Coupled hard-soft tissue simulation with contact and constraints applied to jaw-tongue-hyoid dynamics. Int. J. Numer. Meth. Biomed. Eng. 2011, 27, 367–390. [Google Scholar] [CrossRef]
- Erdemir, A.; McLean, S.; Herzog, W.; van den Bogert, A.J. Model-based estimation of muscle forces exerted during movements. Clin. Biomech. 2007, 22, 131–154. [Google Scholar] [CrossRef] [PubMed]
- Meszaros-Beller, L.; Hammer, M.; Schmitt, S.; Pivonka, P. Effect of neglecting passive spinal structures: A quantitative investigation using the forward-dynamics and inverse-dynamics musculoskeletal approach. Front. Physiol. 2023, 14, 1135531. [Google Scholar] [CrossRef]
- van den Bogert, A.J.; Blana, D.; Heinrich, D. Implicit methods for efficient musculoskeletal simulation and optimal control. Procedia IUTAM 2011, 2, 297–316. [Google Scholar] [CrossRef]
- Liu, T.; Khalaf, K.; Naserkhaki, S.; El-Rich, M. Load-sharing in the lumbosacral spine in neutral standing & flexed postures—A combined finite element and inverse static study. J. Biomech. 2018, 70, 43–50. [Google Scholar] [CrossRef]
- Honegger, J.D.; Actis, J.A.; Gates, D.H.; Silverman, A.K.; Munson, A.H.; Petrella, A.J. Development of a multiscale model of the human lumbar spine for investigation of tissue loads in people with and without a transtibial amputation during sit-to-stand. Biomech. Model. Mechanobiol. 2021, 20, 339–358. [Google Scholar] [CrossRef]
- Kumaran, Y.; Shah, A.; Katragadda, A.; Padgaonkar, A.; Zavatsky, J.; McGuire, R.; Serhan, H.; Elgafy, H.; Goel, V.K. Iatrogenic muscle damage in transforaminal lumbar interbody fusion and adjacent segment degeneration: A comparative finite element analysis of open and minimally invasive surgeries. Eur. Spine J. 2021, 30, 2622–2630. [Google Scholar] [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef]
- Ignasiak, D.; Turner, A.W. Corrigendum to ‘A novel method for prediction of postoperative global sagittal alignment based on full-body musculoskeletal modeling and posture optimization’ [J. Biomech. (2019) https://doi.org/10.1016/j.jbiomech.2019.109324]. J. Biomech. 2020, 102, 109672. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Miehling, J.; Wartzack, S. Challenges in interaction modelling with digital human models—A systematic literature review of interaction modelling approaches. Ergonomics 2020, 63, 1442–1458. [Google Scholar] [CrossRef]
- Neumann, M.; Bender, B. Challenges in the Development of Biomechatronic Systems. In Design Methodology for Future Products; Springer: Cham, Switzerland, 2022; pp. 105–122. [Google Scholar]
- Remus, R.; Selkmann, S.; Lipphaus, A.; Neumann, M.; Bender, B. Muscle-driven forward dynamic active hybrid model of the lumbosacral spine: Combined FEM and multibody simulation. Front. Bioeng. Biotechnol. 2023, 11, 1223007. [Google Scholar] [CrossRef]
- Remus, R.; Lipphaus, A.; Neumann, M.; Bender, B. Calibration and validation of a novel hybrid model of the lumbosacral spine in ArtiSynth-The passive structures. PLoS ONE 2021, 16, e0250456. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, J.E.; Stavness, I.; Fels, S. ArtiSynth: A fast interactive biomechanical modeling toolkit combining multibody and finite element simulation. In Soft Tissue Biomechanical Modeling for Computer Assisted Surgery; Payan, Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 355–394. ISBN 978-3-642-29014-5. [Google Scholar]
- Stavness, I.; Hannam, A.G.; Lloyd, J.E.; Fels, S. Predicting muscle patterns for hemimandibulectomy models. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 483–491. [Google Scholar] [CrossRef] [PubMed]
- Stavness, I.; Lloyd, J.E.; Fels, S. Automatic prediction of tongue muscle activations using a finite element model. J. Biomech. 2012, 45. [Google Scholar] [CrossRef]
- Been, E.; Kalichman, L. Lumbar lordosis. Spine J. 2014, 14, 87–97. [Google Scholar] [CrossRef]
- Galbusera, F.; Bellini, C.M.; Anasetti, F.; Ciavarro, C.; Lovi, A.; Brayda-Bruno, M. Rigid and flexible spinal stabilization devices: A biomechanical comparison. Med. Eng. Phys. 2011, 33, 490–496. [Google Scholar] [CrossRef]
- Turbucz, M.; Pokorni, A.J.; Szőke, G.; Hoffer, Z.; Kiss, R.M.; Lazary, A.; Eltes, P.E. Development and Validation of Two Intact Lumbar Spine Finite Element Models for In Silico Investigations: Comparison of the Bone Modelling Approaches. Appl. Sci. 2022, 12, 10256. [Google Scholar] [CrossRef]
- Behr, M.; Thollon, L.; Arnoux, P.-J.; Serre, T.; Berdah, S.V.; Baque, P.; Brunet, C. 3D reconstruction of the diaphragm for virtual traumatology. Surg. Radiol. Anat. 2006, 28, 235–240. [Google Scholar] [CrossRef]
- Pato, M.P.M.; Santos, N.J.G.; Areias, P.; Pires, E.B.; de Carvalho, M.; Pinto, S.; Lopes, D.S. Finite element studies of the mechanical behaviour of the diaphragm in normal and pathological cases. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 505–513. [Google Scholar] [CrossRef] [PubMed]
- Villa, T.M.T.; La Barbera, L.; Galbusera, F. Comparative analysis of international standards for the fatigue testing of posterior spinal fixation systems. Spine J. 2014, 14, 695–704. [Google Scholar] [CrossRef] [PubMed]
- Remus, R.; Sure, C.; Selkmann, S.; Uttich, E.; Bender, B. Soft tissue material properties based on human abdominal in vivo macro-indenter measurements. Front. Bioeng. Biotechnol. 2024, 12, 1384062. [Google Scholar] [CrossRef]
- Renner, S.M.; Natarajan, R.N.; Patwardhan, A.G.; Havey, R.M.; Voronov, L.I.; Guo, B.Y.; Andersson, G.B.J.; An, H.S. Novel model to analyze the effect of a large compressive follower pre-load on range of motions in a lumbar spine. J. Biomech. 2007, 40, 1326–1332. [Google Scholar] [CrossRef] [PubMed]
- Dreischarf, M.; Zander, T.; Bergmann, G.; Rohlmann, A. A non-optimized follower load path may cause considerable intervertebral rotations. J. Biomech. 2010, 43, 2625–2628. [Google Scholar] [CrossRef]
- Volkheimer, D.; Malakoutian, M.; Oxland, T.R.; Wilke, H.-J. Limitations of current in vitro test protocols for investigation of instrumented adjacent segment biomechanics: Critical analysis of the literature. Eur. Spine J. 2015, 24, 1882–1892. [Google Scholar] [CrossRef]
- Wilke, H.-J.; Rohlmann, A.; Neller, S.; Schultheiss, M.; Bergmann, G.; Graichen, F.; Claes, L.E. Is it possible to simulate physiologic loading conditions by applying pure moments? A comparison of in vivo and in vitro load components in an internal fixator. Spine 2001, 26, 636–642. [Google Scholar] [CrossRef]
- Rohlmann, A.; Riley, L.H.; Bergmann, G.; Graichen, F. In vitro load measurement using an instrumented spinal fixation device. Med. Eng. Phys. 1996, 18, 485–488. [Google Scholar] [CrossRef]
- Lund, T.; Oxland, T.R.; Jost, B.; Cripton, P.; Grassmann, S.; Etter, C.; Nolte, L.P. Interbody cage stabilisation in the lumbar spine: Biomechanical evaluation of cage design, posterior instrumentation and bone density. J. Bone Jt. Surgery. Br. Vol. 1998, 80, 351–359. [Google Scholar] [CrossRef]
- Dick, W. Internal Fixation of Thoracic and Lumbar Spine Fractures; H. Huber: Toronto, ON, Canada; Lewiston, NY, USA, 1989; ISBN 978-0920887301. [Google Scholar]
- Rohlmann, A.; Bergmann, G.; Graichen, F. Loads on internal spinal fixators measured in different body positions. Eur. Spine J. 1999, 8, 354–359. [Google Scholar] [CrossRef]
- Rohlmann, A.; Bergmann, G.; Graichen, F. A spinal fixation device for in vivo load measurement. J. Biomech. 1994, 27, 961–967. [Google Scholar] [CrossRef]
- Rohlmann, A.; Eick, O.; Bergmann, G.; Graichen, F. In vitro-Messung der Belastung mit instrumentierten Wirbel-Fixateur interne. Z. Orthop. Ihre Grenzgeb. 1995, 133, 136–140. [Google Scholar] [CrossRef]
- Spitzer, V.; Ackerman, M.J.; Scherzinger, A.L.; Whitlock, D. The visible human male: A technical report. J. Am. Med. Inform. Assoc. 1996, 3, 118–130. [Google Scholar] [CrossRef] [PubMed]
- Taddei, F.; Schileo, E.; Helgason, B.; Cristofolini, L.; Viceconti, M. The material mapping strategy influences the accuracy of CT-based finite element models of bones: An evaluation against experimental measurements. Med. Eng. Phys. 2007, 29, 973–979. [Google Scholar] [CrossRef] [PubMed]
- Schileo, E.; Balistreri, L.; Grassi, L.; Cristofolini, L.; Taddei, F. To what extent can linear finite element models of human femora predict failure under stance and fall loading configurations? J. Biomech. 2014, 47, 3531–3538. [Google Scholar] [CrossRef] [PubMed]
- Ashjaee, N.; Kalajahi, S.M.H.; Johnston, J.D. QCT-FE modeling of the proximal tibia: Effect of mapping strategy on convergence time and model accuracy. Med. Eng. Phys. 2021, 88, 41–46. [Google Scholar] [CrossRef]
- Panjabi, M.M. Clinical spinal instability and low back pain. J. Electromyogr. Kinesiol. 2003, 13, 371–379. [Google Scholar] [CrossRef]
- Shirazi-Adl, A.; Dammak, M.; Paiement, G. Experimental determination of friction characteristics at the trabecular bone/porous-coated metal interface in cementless implants. J. Biomed. Mater. Res. 1993, 27, 167–175. [Google Scholar] [CrossRef]
- Galbusera, F.; Schmidt, H.; Wilke, H.-J. Lumbar interbody fusion: A parametric investigation of a novel cage design with and without posterior instrumentation. Eur. Spine J. 2012, 21, 455–462. [Google Scholar] [CrossRef][Green Version]
- Fels, S.; Vogt, F.; van den Doel, K.; Lloyd, J.E.; Stavness, I.; Vatikiotis-Bateson, E. ArtiSynth: A Biomechanical Simulation Platform for the Vocal Tract and Upper Airway. Technical Report. Available online: https://www.cs.ubc.ca/sites/default/files/tr/2006/TR-2006-10_0.pdf (accessed on 3 March 2025).
- Kimura, S.; Steinbach, G.C.; Watenpaugh, D.E.; Hargens, A.R. Lumbar spine disc height and curvature responses to an axial load generated by a compression device compatible with magnetic resonance imaging. Spine 2001, 26, 2596–2600. [Google Scholar] [CrossRef]
- Stavness, I.; Sánchez, C.A.; Lloyd, J.E.; Ho, A.; Wang, J.; Fels, S.; Huang, D. Unified skinning of rigid and deformable models for anatomical simulations. In Proceedings of the SIGGRAPH Asia 2014 Technical Briefs, Shenzhen, China, 3–6 December 2014; ACM: New York, NY, USA, 2014; pp. 1–4, ISBN 9781450328951. [Google Scholar]
- Lloyd, J.E.; Sánchez, C.A.; Widing, E.; Stavness, I.; Fels, S.; Niroomandi, S.; Perrier, A.; Payan, Y.; Perrier, P. New Techniques for Combined FEM-Multibody Anatomical Simulation. In New Developments on Computational Methods and Imaging in Biomechanics and Biomedical Engineering; Springer: Cham, Switzerland, 2019; pp. 75–92. [Google Scholar]
- Nesme, M.; Faure, F.; Payan, Y. Accurate interactive animation of deformable models at arbitrary resolution. Int. J. Image Graph. 2010, 10, 175–202. [Google Scholar] [CrossRef]
- Snedeker, J.G.; Barnstuble, B.B.; Iaizzo, P.A.; Farshad, M.; Niederer, P.; Schmidlin, F.R. A comprehensive renal injury concept based on a validated finite element model of the human abdomen. J. Trauma 2007, 62, 1240–1249. [Google Scholar] [CrossRef]
- Todros, S.; de Cesare, N.; Concheri, G.; Natali, A.N.; Pavan, P.G. Numerical modelling of abdominal wall mechanics: The role of muscular contraction and intra-abdominal pressure. J. Mech. Behav. Biomed. Mater. 2020, 103, 103578. [Google Scholar] [CrossRef]
- Simo, J.C.; Taylor, R.L. Quasi-incompressible finite elasticity in principal stretches. Continuum basis and numerical algorithms. Appl. Mech. Eng. 1991, 85, 273–310. [Google Scholar] [CrossRef]
- Lohr, M.J.; Sugerman, G.P.; Kakaletsis, S.; Lejeune, E.; Rausch, M.K. An introduction to the Ogden model in biomechanics: Benefits, implementation tools and limitations. Philos. Trans. A Math. Phys. Eng. Sci. 2022, 380, 20210365. [Google Scholar] [CrossRef]
- Lalwani, L.K.; Govindagoudar, M.B.; Singh, P.K.; Sharma, M.; Chaudhry, D. The role of diaphragmatic thickness measurement in weaning prediction and its comparison with rapid shallow breathing index: A single-center experience. Acute Crit. Care 2022, 37, 347–354. [Google Scholar] [CrossRef]
- Netter, F.H. Atlas of Human Anatomy, 7th ed.; Elsevier: Philadelphia, PA, USA, 2017; ISBN 9780323547048. [Google Scholar]
- Petrofsky, J.S.; McLellan, K.; Prowse, M.; Bains, G.; Berk, L.; Lee, S. The effect of body fat, aging, and diabetes on vertical and shear pressure in and under a waist belt and its effect on skin blood flow. Diabetes Technol. Ther. 2010, 12, 153–160. [Google Scholar] [CrossRef]
- Périé, D.; Aubin, C.E.; Lacroix, M.; Lafon, Y.; Labelle, H. Biomechanical modelling of orthotic treatment of the scoliotic spine including a detailed representation of the brace-torso interface. Med. Biol. Eng. Comput. 2004, 42, 339–344. [Google Scholar] [CrossRef]
- Nachemson, A.L.; Morris, J.M. In Vivo Measurements of Intradiscal Pressure: Discometry, a method for the determination of pressure in the lower lumbar disc. J. Bone Jt. Surg. Am. 1964, 46, 1077–1092. [Google Scholar] [CrossRef]
- Molimard, J.; Bonnaire, R.; Han, W.S.; Convert, R.; Calmels, P. In-silico pre-clinical trials are made possible by a new simple and comprehensive lumbar belt mechanical model based on the Law of Laplace including support deformation and adhesion effects. PLoS ONE 2019, 14, e0212681. [Google Scholar] [CrossRef] [PubMed]
- Larivière, C.; Shahvarpour, A.; Gravel, C.; Gauvin, M.; Jean, A.-M.; Viau, A.; Mecheri, H. Revisiting the effect of manipulating lumbar stability with load magnitudes and positions: The effect of sex on trunk muscle activation. J. Electromyogr. Kinesiol. 2019, 46, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Heuer, F.; Schmidt, H.; Klezl, Z.; Claes, L.E.; Wilke, H.-J. Stepwise reduction of functional spinal structures increase range of motion and change lordosis angle. J. Biomech. 2007, 40, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Fantigrossi, A.; Galbusera, F.; Raimondi, M.T.; Sassi, M.; Fornari, M. Biomechanical analysis of cages for posterior lumbar interbody fusion. Med. Eng. Phys. 2007, 29, 101–109. [Google Scholar] [CrossRef]
- Calvo-Echenique, A.; Cegoñino, J.; Del Perez Palomar, A. Is there any advantage of using stand-alone cages? A numerical approach. Biomed. Eng. Online 2019, 18, 63. [Google Scholar] [CrossRef]
- Nibu, K.; Panjabi, M.M.; Oxland, T.R.; Cholewicki, J. Intervertebral disc distraction with a laparoscopic anterior spinal fusion system. Eur. Spine J. 1998, 7, 142–147. [Google Scholar] [CrossRef][Green Version]
- Panjabi, M.M. Hybrid multidirectional test method to evaluate spinal adjacent-level effects. Clin. Biomech. 2007, 22, 257–265. [Google Scholar] [CrossRef]
- Lin, S.-C.; Tsai, W.-C.; Wu, S.-S.; Chen, P.-Q. Radiological and Mathematical Studies Regarding the Effects of Spinal Fixation on Kinematics and Mechanics at the Parafixed Segments. J. Mech. 2010, 26, 413–422. [Google Scholar] [CrossRef]
- Rohlmann, A.; Bauer, L.; Zander, T.; Bergmann, G.; Wilke, H.-J. Determination of trunk muscle forces for flexion and extension by using a validated finite element model of the lumbar spine and measured in vivo data. J. Biomech. 2006, 39, 981–989. [Google Scholar] [CrossRef]
- Zander, T.; Rohlmann, A.; Klöckner, C.; Bergmann, G. Comparison of the mechanical behavior of the lumbar spine following mono- and bisegmental stabilization. Clin. Biomech. 2002, 17, 439–445. [Google Scholar] [CrossRef]
- Sato, K.; Kikuchi, S.; Yonezawa, T. In vivo intradiscal pressure measurement in healthy individuals and in patients with ongoing back problems. Spine 1999, 24, 2468–2474. [Google Scholar] [CrossRef]
- Wilke, H.-J.; Neef, P.; Hinz, B.; Seidel, H.; Claes, L.E. Intradiscal pressure together with anthropometric data—A data set for the validation of models. Clin. Biomech. 2001, 16, 111–126. [Google Scholar] [CrossRef]
- Takahashi, I.; Kikuchi, S.; Sato, K.; Sato, N. Mechanical load of the lumbar spine during forward bending motion of the trunk-a biomechanical study. Spine 2006, 31, 18–23. [Google Scholar] [CrossRef] [PubMed]
- Bonnaire, R. Caractérisation Mécanique des Orthèses: Application aux Ceintures de Soutien Lombaire Dans le Cadre de la Lombalgie. Doctoral Dissertation, Ecole des Mines de Saint-Étienne, Saint-Étienne, France, 2015. [Google Scholar]
- Morris, J.M.; Lucas, D.; Bresler, B. Role of the Trunk in Stability of the Spine. J. Bone Jt. Surg. 1961, 43, 327–351. [Google Scholar] [CrossRef]
- El Bojairami, I.; Jacobson, N.; Driscoll, M. Development and evaluation of a numerical spine model comprising intra-abdominal pressure for use in assessing physiological changes on abdominal compliance and spinal stability. Clin. Biomech. 2022, 97, 105689. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, M.J.; Marras, W.S. The effect of lumbar back support tension on trunk muscle activity. Clin. Biomech. 2000, 15, 292–294. [Google Scholar] [CrossRef]
- van Poppel, M.N.M.; de Looze, M.P.; Koes, B.W.; Smid, T.; Bouter, L.M. Mechanisms of action of lumbar supports: A systematic review. Spine 2000, 25, 2103–2113. [Google Scholar] [CrossRef]
- Nispel, K.; Lerchl, T.; Gruber, G.; Möller, H.; Graf, R.; Senner, V.; Kirschke, J.S. From MRI to FEM: An automated pipeline for biomechanical simulations of vertebrae and intervertebral discs. Front. Bioeng. Biotechnol. 2025, 12, 1485115. [Google Scholar] [CrossRef]
- Möller, H.; Graf, R.; Schmitt, J.; Keinert, B.; Schön, H.; Atad, M.; Sekuboyina, A.; Streckenbach, F.; Kofler, F.; Kroencke, T.; et al. SPINEPS-automatic whole spine segmentation of T2-weighted MR images using a two-phase approach to multi-class semantic and instance segmentation. Eur. Radiol. 2024, 35, 1178–1189. [Google Scholar] [CrossRef]
- Liu, T.; El-Rich, M. Subject-specific trunk segmental masses prediction for musculoskeletal models using artificial neural networks. Med. Biol. Eng. Comput. 2024, 62, 2757–2768. [Google Scholar] [CrossRef]
- Lewandowski, A. Issues in Model Validation; Angewandte Systemanalyse; IIASA: Laxenburg, Austria, 1982; pp. 1–29. [Google Scholar]
- Kia, M.; Stylianou, A.P.; Guess, T.M. Evaluation of a musculoskeletal model with prosthetic knee through six experimental gait trials. Med. Eng. Phys. 2014, 36, 335–344. [Google Scholar] [CrossRef][Green Version]
- Ignasiak, D.; Ferguson, S.J.; Arjmand, N. A rigid thorax assumption affects model loading predictions at the upper but not lower lumbar levels. J. Biomech. 2016, 49, 3074–3078. [Google Scholar] [CrossRef] [PubMed]
- Hodges, P.W.; Ferreira, P.H.; Ferreira, M.L. Chapter 14—Lumbar Spine: Treatment of Motor Control Disorders. In Pathology and Intervention in Musculoskeletal Rehabilitation, 2nd ed.; Magee, D.J., Zachazewski, J.E., Quillen, W.S., Manske, R.C., Eds.; Elsevier Health Sciences: Amsterdam, The Netherlands, 2015; pp. 520–560. ISBN 978-0-323-31072-7. [Google Scholar]
- Malakoutian, M.; Sánchez, C.A.; Brown, S.H.M.; Street, J.; Fels, S.; Oxland, T.R. Biomechanical Properties of Paraspinal Muscles Influence Spinal Loading-A Musculoskeletal Simulation Study. Front. Bioeng. Biotechnol. 2022, 10, 852201. [Google Scholar] [CrossRef] [PubMed]
- Rupp, T.K.; Ehlers, W.; Karajan, N.; Günther, M.; Schmitt, S. A forward dynamics simulation of human lumbar spine flexion predicting the load sharing of intervertebral discs, ligaments, and muscles. Biomech. Model. Mechanobiol. 2015, 14, 1081–1105. [Google Scholar] [CrossRef] [PubMed]
- Rohlmann, A.; Zander, T.; Bergmann, G.; Boustani, H.N. Optimal stiffness of a pedicle-screw-based motion preservation implant for the lumbar spine. Eur. Spine J. 2012, 21, 666–673. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kettler, A.; Rohlmann, F.; Ring, C.; Mack, C.; Wilke, H.-J. Do early stages of lumbar intervertebral disc degeneration really cause instability? Evaluation of an in vitro database. Eur. Spine J. 2011, 20, 578–584. [Google Scholar] [CrossRef]
- McNally, D.S.; Adams, M.A. Internal intervertebral disc mechanics as revealed by stress profilometry. Spine 1992, 17, 66–73. [Google Scholar] [CrossRef]
- La Barbera, L.; Galbusera, F.; Villa, T.M.T.; Costa, F.; Wilke, H.-J. ASTM F1717 standard for the preclinical evaluation of posterior spinal fixators: Can we improve it? Proc. Inst. Mech. Eng. H 2014, 228, 1014–1026. [Google Scholar] [CrossRef]
- Chen, C.-S.; Chen, W.-J.; Cheng, C.-K.; Jao, S.-H.E.; Chueh, S.-C.; Wang, C.-C. Failure analysis of broken pedicle screws on spinal instrumentation. Med. Eng. Phys. 2005, 27, 487–496. [Google Scholar] [CrossRef]
- Cho, W.; Wu, C.; Mehbod, A.A.; Transfeldt, E.E. Comparison of cage designs for transforaminal lumbar interbody fusion: A biomechanical study. Clin. Biomech. 2008, 23, 979–985. [Google Scholar] [CrossRef]
- Calvo-Echenique, A.; Cegoñino, J.; Chueca, R.; Pérez-del Palomar, A. Stand-alone lumbar cage subsidence: A biomechanical sensitivity study of cage design and placement. Comput. Methods Programs Biomed. 2018, 162, 211–219. [Google Scholar] [CrossRef]
- Reinshagen, C.; Ruess, D.; Walcott, B.P.; Molcanyi, M.; Goldbrunner, R.; Rieger, B. A novel minimally invasive technique for lumbar decompression, realignment, and navigated interbody fusion. J. Clin. Neurosci. 2015, 22, 1484–1490. [Google Scholar] [CrossRef] [PubMed]
- Pao, J.-L. Biportal Endoscopic Transforaminal Lumbar Interbody Fusion Using Double Cages: Surgical Techniques and Treatment Outcomes. Neurospine 2023, 20, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Bonnaire, R.; Woo-Suck, H.; Calmels, P.; Convert, R.; Molimard, J. Parametric Study of Lumbar Belts in the Case of Low Back Pain: Effect of Patients’ Specific Characteristics. In Computational Biomechanics for Medicine: Personalisation, Validation and Therapy; Nash, M.P., Nielsen, P.M.F., Wittek, A., Miller, K., Joldes, G.R., Eds.; Springer: Cham, Switzerland, 2020; pp. 43–59. ISBN 303015923X. [Google Scholar]
- Guo, J.; Guo, W.; Ren, G. Embodiment of intra-abdominal pressure in a flexible multibody model of the trunk and the spinal unloading effects during static lifting tasks. Biomech. Model. Mechanobiol. 2021, 20, 1599–1626. [Google Scholar] [CrossRef]
- Hodges, P.W.; Cresswell, A.G.; Daggfeldt, K.; Thorstensson, A. In vivo measurement of the effect of intra-abdominal pressure on the human spine. J. Biomech. 2001, 34, 347–353. [Google Scholar] [CrossRef]
- Spadoni, S.; Todros, S.; Pavan, P.G. Numerical modeling of the abdominal wall biomechanics and experimental analysis for model validation. Front. Bioeng. Biotechnol. 2024, 12, 1472509. [Google Scholar] [CrossRef]
- Jourdan, A.; Rapacchi, S.; Guye, M.; Bendahan, D.; Masson, C.; Bège, T. Dynamic-MRI quantification of abdominal wall motion and deformation during breathing and muscular contraction. Comput. Methods Programs Biomed. 2022, 217, 106667. [Google Scholar] [CrossRef] [PubMed]
- Cholewicki, J.; Ivancic, P.C.; Radebold, A. Can increased intra-abdominal pressure in humans be decoupled from trunk muscle co-contraction during steady state isometric exertions? Eur. J. Appl. Physiol. 2002, 87, 127–133. [Google Scholar] [CrossRef]
- Miyamoto, K.; Iinuma, N.; Ueki, S.; Shimizu, K. Effects of abdominal belts on the cross-sectional shape of the trunk during intense contraction of the trunk muscles observed by computer tomography. Clin. Biomech. 2008, 23, 1220–1226. [Google Scholar] [CrossRef]
- Sánchez, C.A.; Li, Z.; Hannam, A.G.; Abolmaesumi, P.; Agur, A.; Fels, S. Constructing Detailed Subject-Specific Model of the Human Masseter. In Imaging for Patient-Customized Simulations and Systems for Point-of-Care Ultrasound: International Workshops, BIVPCS 2017 and POCUS 2017, Held in Conjunction with MICCAI 2017, Québec City, QC, Canada, September 14, 2017, Proceedings; Cardoso, M.J., Arbel, T., Tavares, J., Aylward, S., Li, S., Boctor, E., Fichtinger, G., Cleary, K., Freeman, B., Kohli, L., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 52–60. ISBN 9783319675527. [Google Scholar]
- Jourdan, A.; Dhume, R.; Guérin, E.; Siegel, A.; Le Ruyet, A.; Palmer, M. Numerical investigation of a finite element abdominal wall model during breathing and muscular contraction. Comput. Methods Programs Biomed. 2024, 244, 107985. [Google Scholar] [CrossRef]
- Miyamoto, K.; Iinuma, N.; Maeda, M.; Wada, E.; Shimizu, K. Effects of abdominal belts on intra-abdominal pressure, intramuscular pressure in the erector spinae muscles and myoelectrical activities of trunk muscles. Clin. Biomech. 1999, 14, 79–87. [Google Scholar] [CrossRef]
- Tuong, N.H.; Dansereau, J.; Maurais, G.; Herrera, R. Three-dimensional evaluation of lumbar orthosis effects on spinal behavior. J. Rehabil. Res. Dev. 1998, 35, 34–42. [Google Scholar] [PubMed]
- Thoumie, P.; Drape, J.-L.; Aymard, C.; Bedoiseau, M. Effects of a lumbar support on spine posture and motion assessed by electrogoniometer and continuous recording. Clin. Biomech. 1998, 13, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Ivancic, P.C.; Cholewicki, J.; Radebold, A. Effects of the abdominal belt on muscle-generated spinal stability and L4/L5 joint compression force. Ergonomics 2002, 45, 501–513. [Google Scholar] [CrossRef]
- Jegede, K.A.; Miller, C.P.; Bible, J.E.; Whang, P.G.; Grauer, J.N. The effects of three different types of orthoses on the range of motion of the lumbar spine during 15 activities of daily living. Spine 2011, 36, 2346–2353. [Google Scholar] [CrossRef]
- Granata, K.P.; Marras, W.S.; Davis, K.G. Biomechanical assessment of lifting dynamics, muscle activity and spinal loads while using three different styles of lifting belt. Clin. Biomech. 1997, 12, 107–115. [Google Scholar] [CrossRef]
- Lloyd, J.E.; Roewer-Després, F.; Stavness, I. Muscle Path Wrapping on Arbitrary Surfaces. IEEE Trans. Biomed. Eng. 2021, 68, 628–638. [Google Scholar] [CrossRef]
- Millard, M.; Uchida, T.; Seth, A.; Delp, S.L. Flexing computational muscle: Modeling and simulation of musculotendon dynamics. J. Biomech. Eng. 2013, 135, 21005. [Google Scholar] [CrossRef] [PubMed]
- Sagl, B.; Dickerson, C.R.; Stavness, I. Fast Forward-Dynamics Tracking Simulation: Application to Upper Limb and Shoulder Modeling. IEEE Trans. Biomed. Eng. 2019, 66, 335–342. [Google Scholar] [CrossRef]
- Byrne, R.M.; Aiyangar, A.K.; Zhang, X. Sensitivity of musculoskeletal model-based lumbar spinal loading estimates to type of kinematic input and passive stiffness properties. J. Biomech. 2020, 102, 109659. [Google Scholar] [CrossRef]
- Meszaros-Beller, L.; Hammer, M.; Riede, J.M.; Pivonka, P.; Little, J.P.; Schmitt, S. Effects of geometric individualisation of a human spine model on load sharing: Neuro-musculoskeletal simulation reveals significant differences in ligament and muscle contribution. Biomech. Model. Mechanobiol. 2023, 22, 669–694. [Google Scholar] [CrossRef]
- Lerchl, T.; Nispel, K.; Baum, T.; Bodden, J.; Senner, V.; Kirschke, J.S. Multibody Models of the Thoracolumbar Spine: A Review on Applications, Limitations, and Challenges. Bioengineering 2023, 10, 202. [Google Scholar] [CrossRef] [PubMed]
- Breen, A.; de Carvalho, D.; Funabashi, M.; Kawchuk, G.; Pagé, I.; Wong, A.Y.L.; Breen, A. A Reference Database of Standardised Continuous Lumbar Intervertebral Motion Analysis for Conducting Patient-Specific Comparisons. Front. Bioeng. Biotechnol. 2021, 9, 745837. [Google Scholar] [CrossRef] [PubMed]
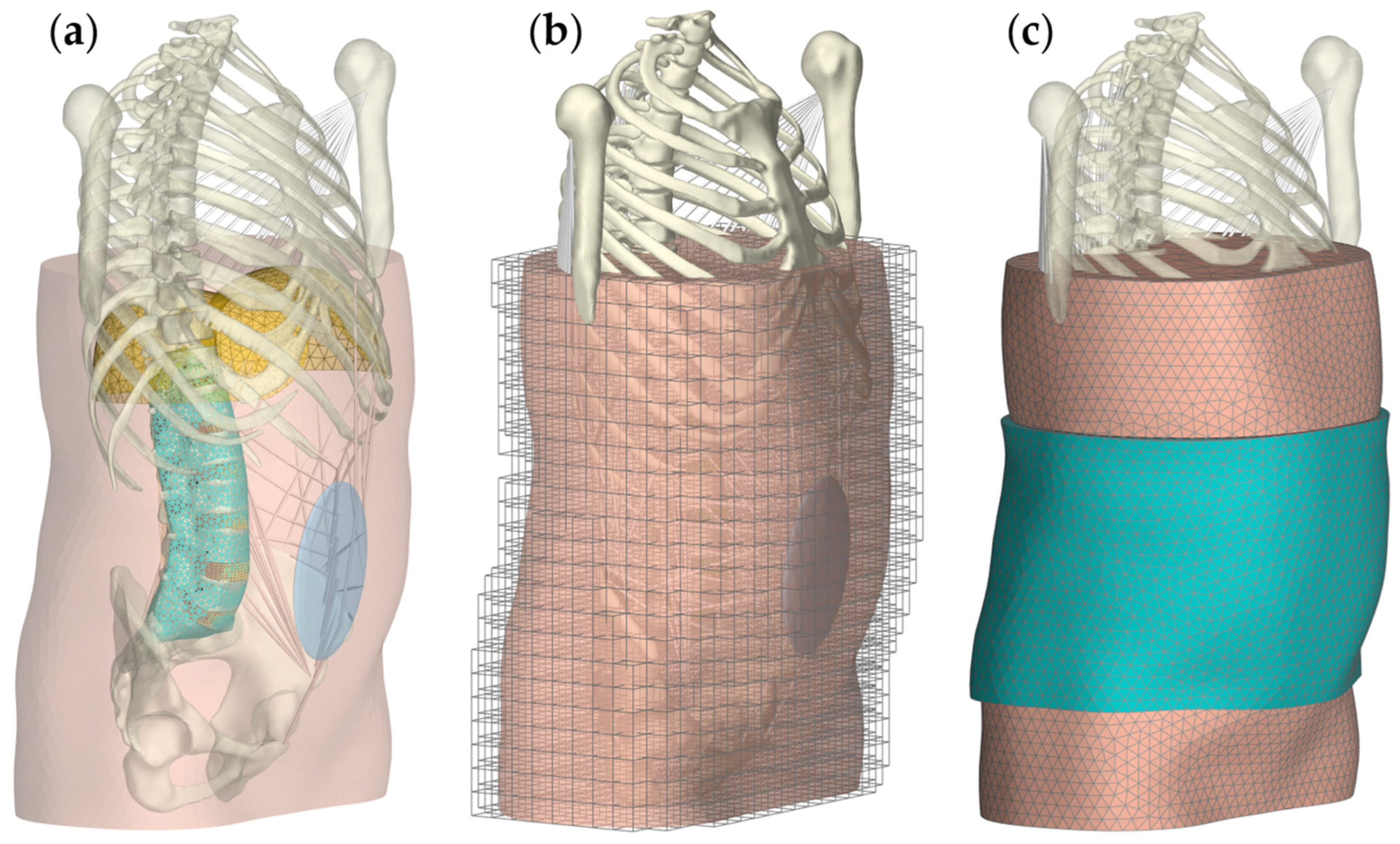
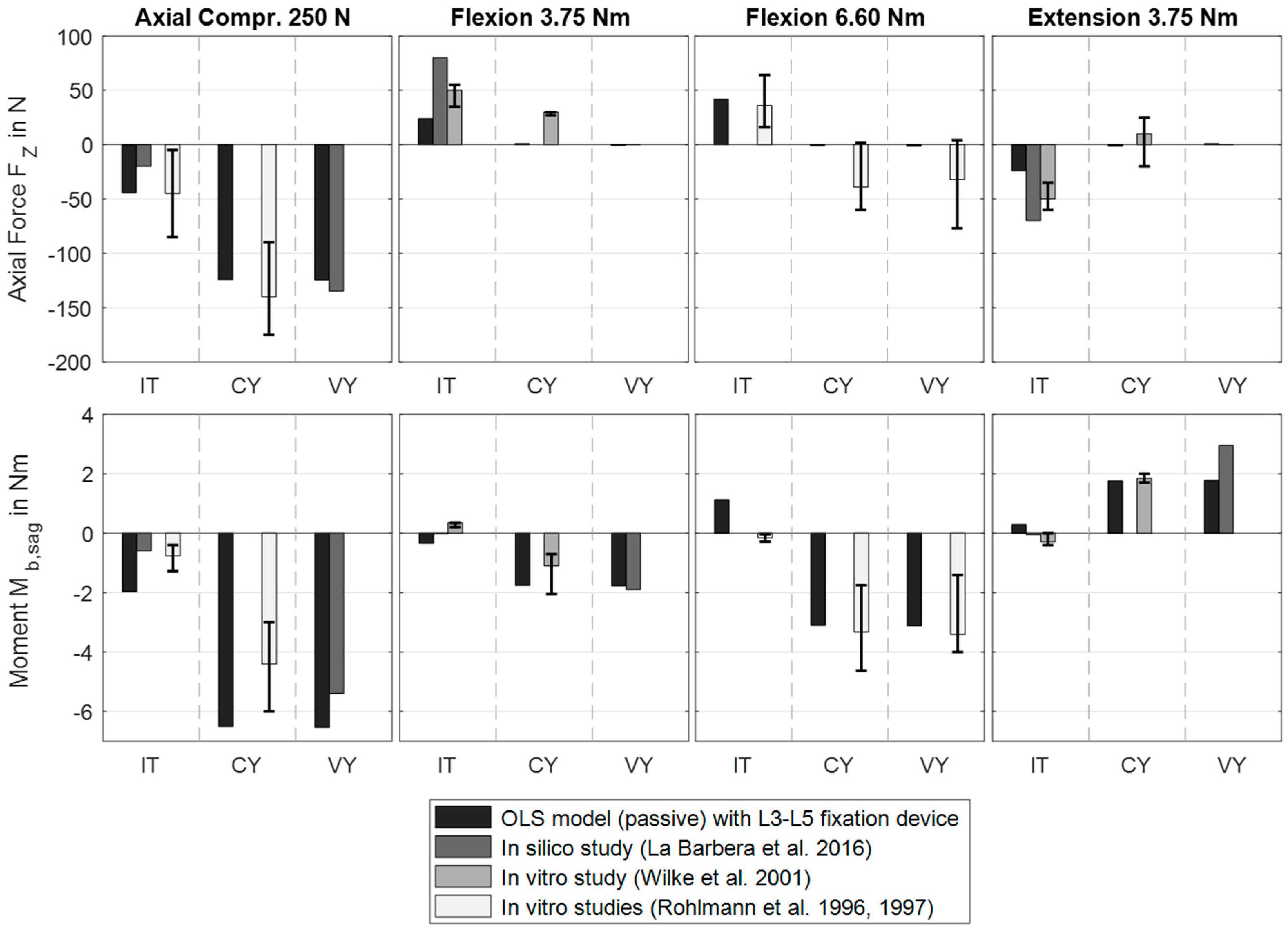

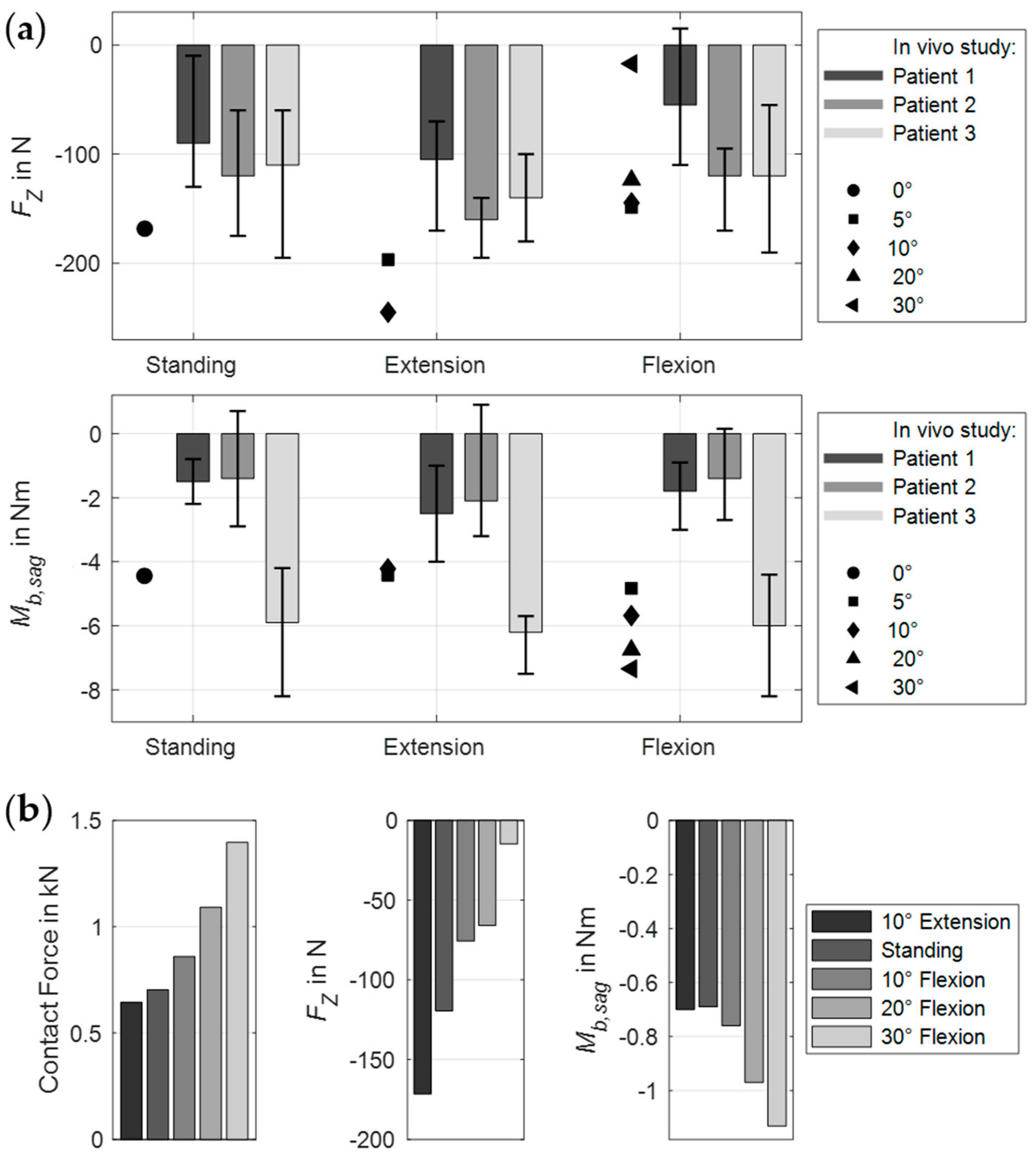
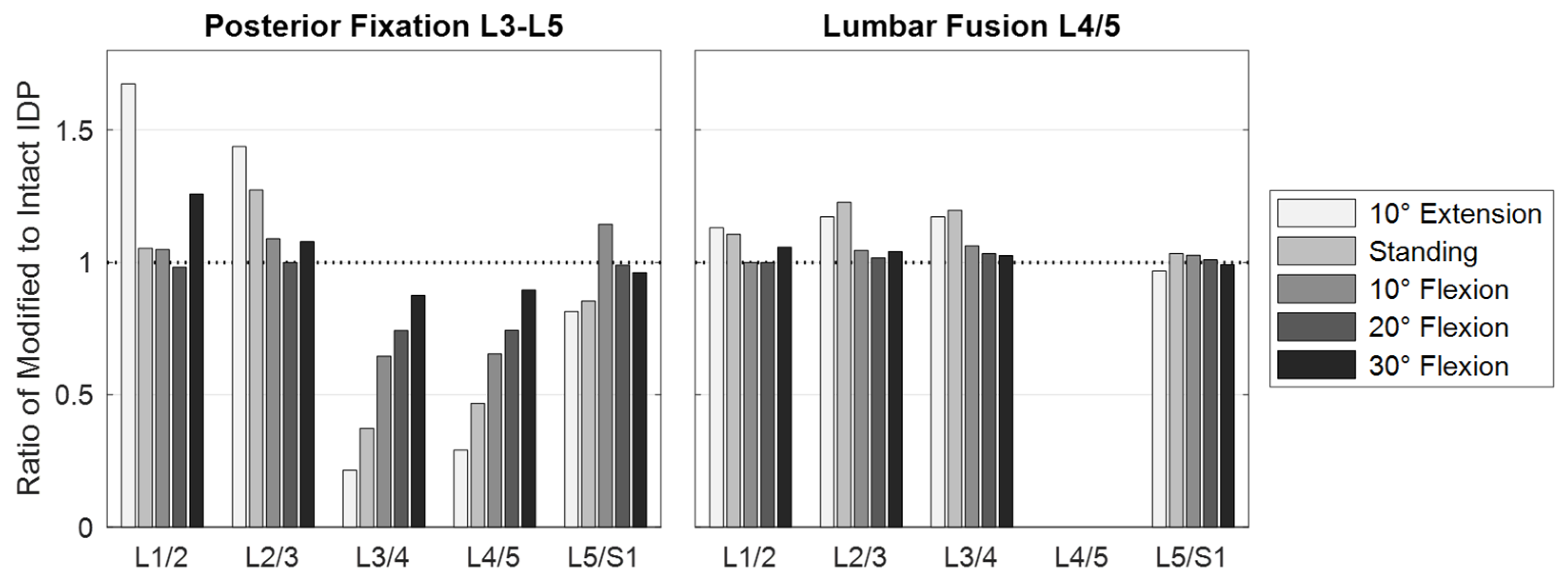



| Component | Material Properties | References | |
|---|---|---|---|
| Young’s Modulus | Poisson’s Ratio | ||
| Bone (cancellous and cortical) | 0.1 … 12 GPa | 0.30 | [34,80,81] |
| Diaphragm muscle tissue | 5.32 MPa | 0.33 | [82] |
| Diaphragm tendon tissue | 33 MPa | 0.33 | [82,83] |
| Implants (Ti6Al4V alloy) | 110 GPa | 0.30 | [80,84] |
| Lumbar belt fabric | 3 MPa | 0.49 | [50] |
| c | m | ||
| Abdominal and pelvic cavity region | 7 kPa | 17 | [85] |
| Abdominal wall region | 10 … 19 kPa | 19 … 22 | [85] |
| Posterior muscle region | 25 … 100 kPa | 19 … 23 | [85] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Remus, R.; Lipphaus, A.; Ritter, M.; Neumann, M.; Bender, B. A Muscle-Driven Spine Model for Predictive Simulations in the Design of Spinal Implants and Lumbar Orthoses. Bioengineering 2025, 12, 263. https://doi.org/10.3390/bioengineering12030263
Remus R, Lipphaus A, Ritter M, Neumann M, Bender B. A Muscle-Driven Spine Model for Predictive Simulations in the Design of Spinal Implants and Lumbar Orthoses. Bioengineering. 2025; 12(3):263. https://doi.org/10.3390/bioengineering12030263
Chicago/Turabian StyleRemus, Robin, Andreas Lipphaus, Marisa Ritter, Marc Neumann, and Beate Bender. 2025. "A Muscle-Driven Spine Model for Predictive Simulations in the Design of Spinal Implants and Lumbar Orthoses" Bioengineering 12, no. 3: 263. https://doi.org/10.3390/bioengineering12030263
APA StyleRemus, R., Lipphaus, A., Ritter, M., Neumann, M., & Bender, B. (2025). A Muscle-Driven Spine Model for Predictive Simulations in the Design of Spinal Implants and Lumbar Orthoses. Bioengineering, 12(3), 263. https://doi.org/10.3390/bioengineering12030263







