Modeling Techniques and Boundary Conditions in Abdominal Aortic Aneurysm Analysis: Latest Developments in Simulation and Integration of Machine Learning and Data-Driven Approaches
Abstract
1. Introduction
2. Computational Techniques for AAA Simulations
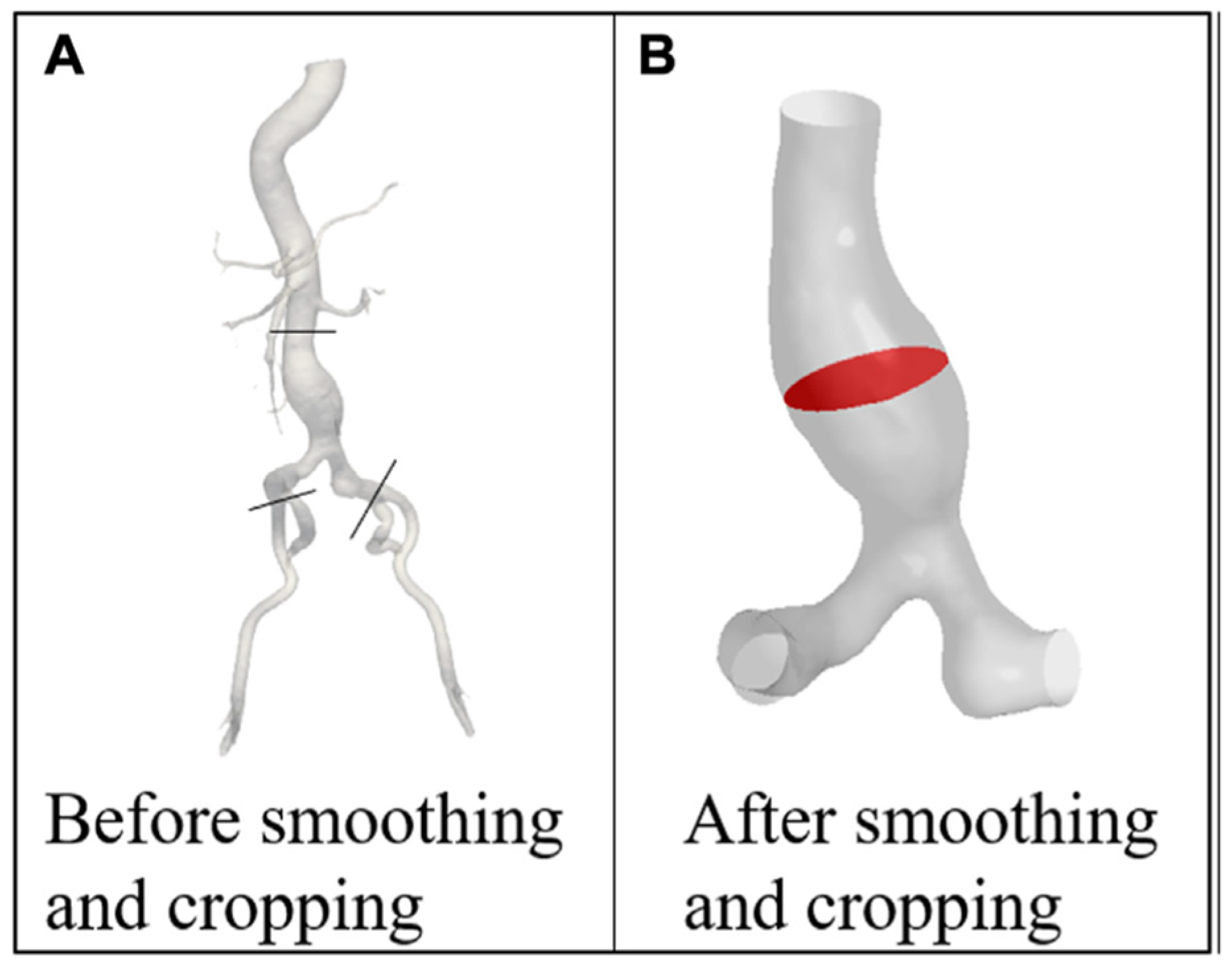
2.1. Patient-Specific Modeling Approaches
2.2. Analysis of the Fluid Domain
Constitutive Models for Blood
2.3. Analysis of Solid Domain
2.3.1. Constitutive Models for AAA Wall
2.3.2. Hyperelastic and Isotropic Models
Mooney–Rivlin Model
Yeoh Model
2.3.3. Hyperelastic and Anisotropic Models
2.3.4. Constitutive Models for ILT
2.4. Coupling of Solid and Fluid Domains: Fluid–Structure Interaction (FSI)
3. Modeling Boundary Conditions in Fluid Domain
3.1. Inlet BCs
3.2. Outlet BCs
3.2.1. Prescribed Outlet Pressure
3.2.2. Flow-Split Method
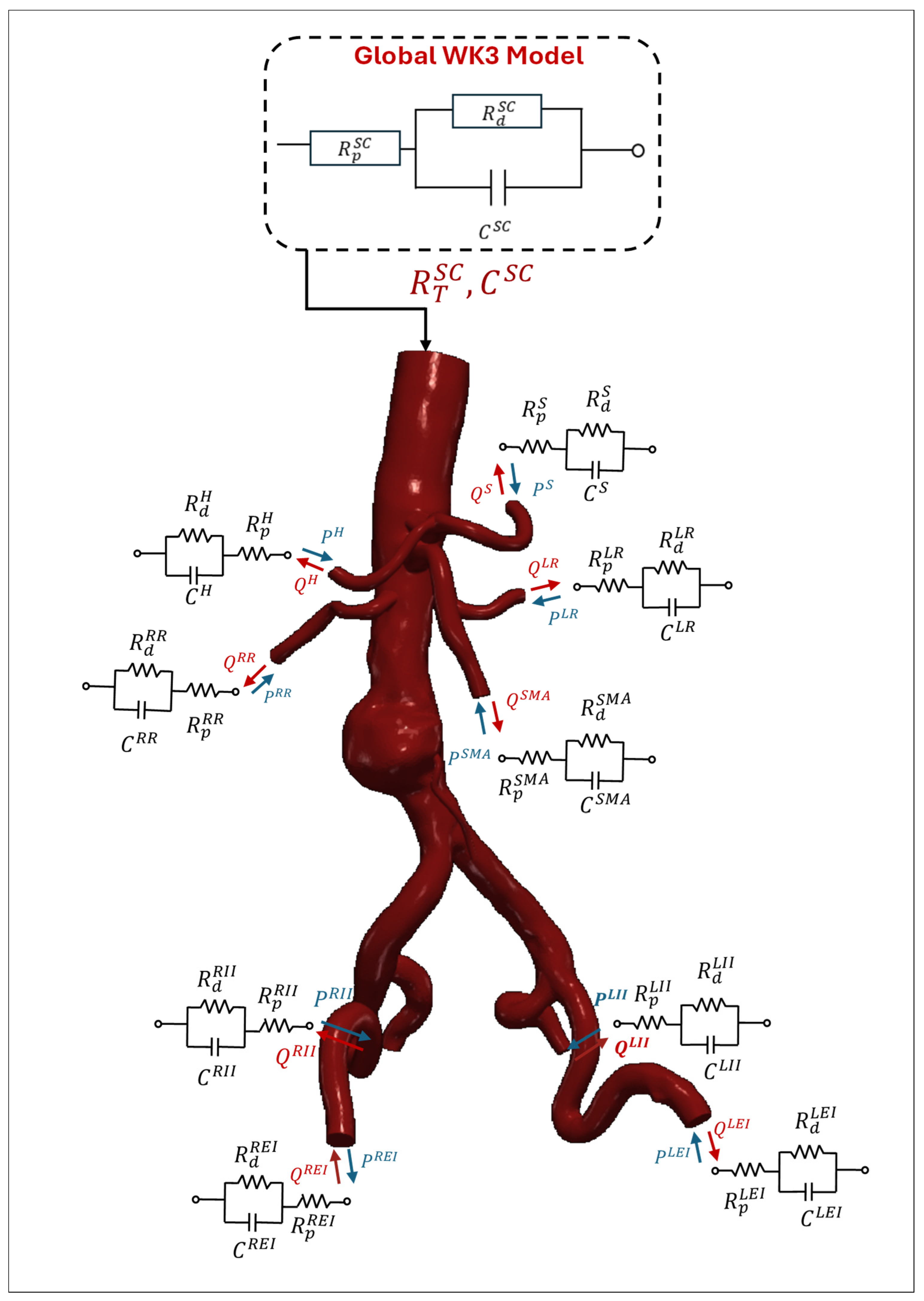
3.2.3. Lumped Parameter Model
3.2.4. Resistance BC
4. Modeling Boundary Conditions in Solid Domain
4.1. Inlet and Outlet of the Wall
4.2. External Wall Boundary
4.3. FSI Boundary: Coupling Solid and Fluid Domains
5. Important Post-Processing Indices
6. Recent Findings
7. Potential for Integrating AI and ML in AAA Research
Applications of AI and ML in AAA Flow Simulations
8. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAA | Abdominal aortic aneurysm |
| ILT | Intraluminal thrombus |
| CFDs | Computational fluid dynamics |
| FEA | Finite element analysis |
| FSI | Fluid–structure interaction |
| BC | Boundary condition |
| WK2 | 2-element Windkessel model |
| WK3 | 3-element Windkessel model |
| WK4 | 4-element Windkessel model |
| RC | 2-element Windkessel model |
| RCR | 3-element Windkessel model |
| RLC | 4-element Windkessel model |
| RCR | 3-element Windkessel model |
| WSS | Wall shear stress |
| TAWSS | Time-averaged wall shear stress |
| OSI | Oscillatory shear index |
| ECAP | Endothelial cell activation potential |
| RRT | Relative residence time |
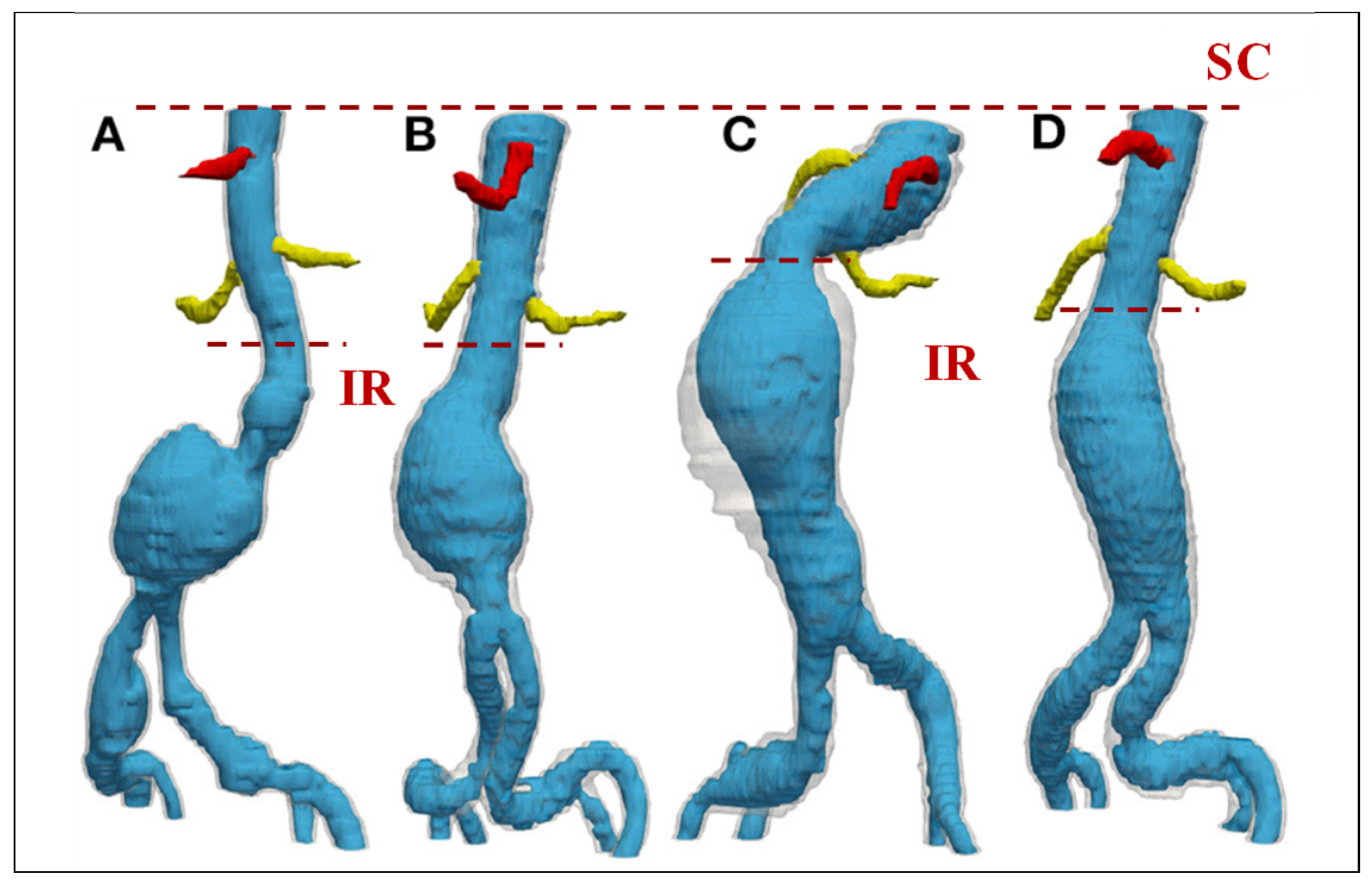
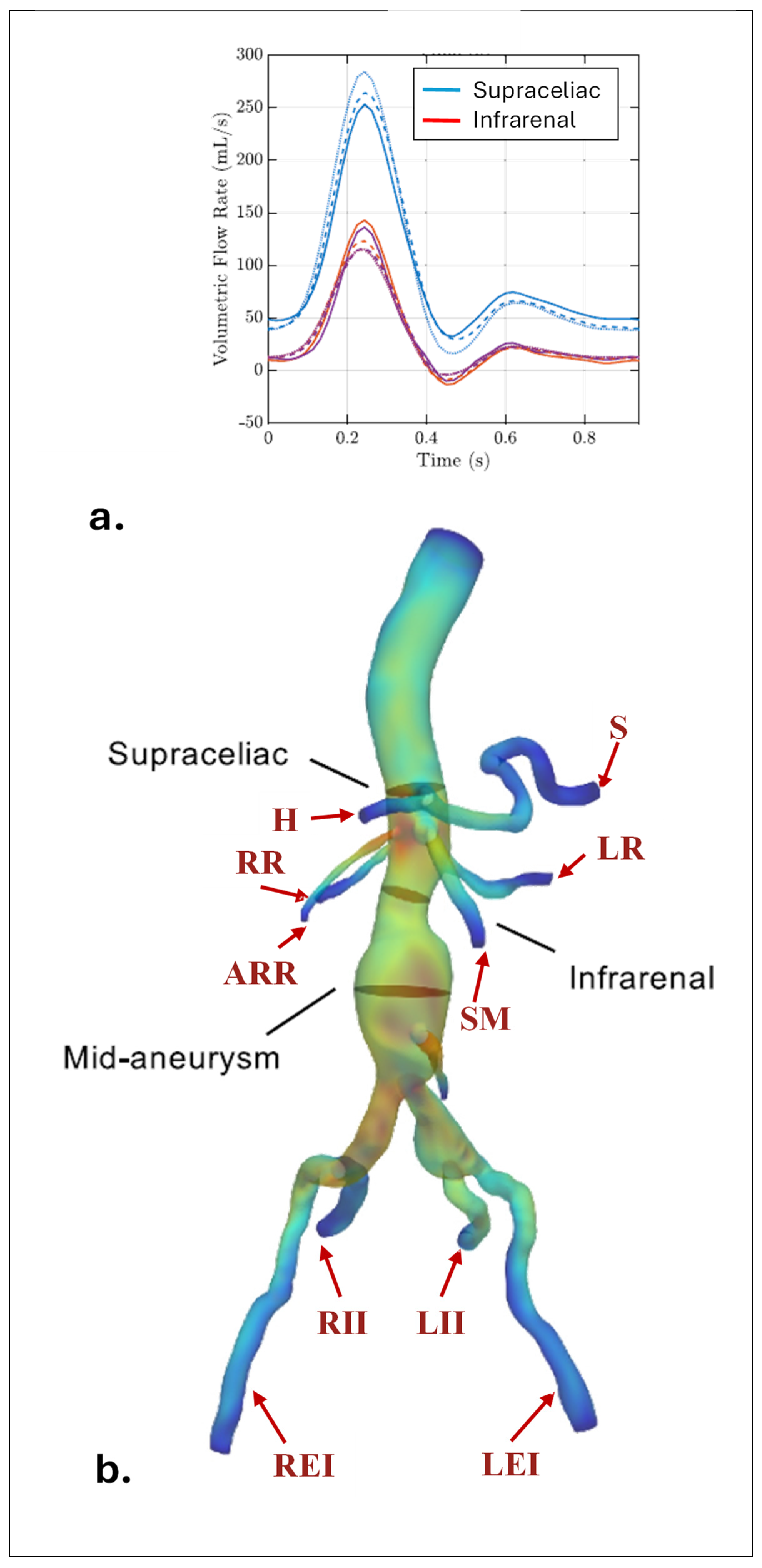
| IR | Infrarenal region |
| SC | Supraceliac region |
| CT | Celiac trunk branch |
| H | Hepatic |
| SM | Superior mesenteric |
| LR | Left renal |
| RR | Right renal |
| ARR | Accessory renal |
| LEI | Left external iliac |
| REI | Right external iliac |
| LII | Left internal iliac |
| RII | Right internal iliac |
| ML | Machine learning |
| DL | Deep learning |
Appendix A
Appendix B
| Global WK3 | ||
|---|---|---|
Appendix C
References
- Lech, C.; Swaminathan, A. Abdominal Aortic Emergencies. Emerg. Med. Clin. North. Am. 2017, 35, 847–867. [Google Scholar] [CrossRef] [PubMed]
- Sakalihasan, N.; Michel, J.B.; Katsargyris, A.; Kuivaniemi, H.; Defraigne, J.O.; Nchimi, A.; Powell, J.T.; Yoshimura, K.; Hultgren, R. Abdominal Aortic Aneurysms. Nat. Rev. Dis. Primers 2018, 4, 34. [Google Scholar] [CrossRef] [PubMed]
- Dua, M.M.; Dalman, R.L. Hemodynamic Influences on Abdominal Aortic Aneurysm Disease: Application of Biomechanics to Aneurysm Pathophysiology. Vasc. Pharmacol. 2010, 53, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Darling, R.C.; Messina, C.R.; Brewster, D.C.; Ottinger, L.W. Autopsy Study of Unoperated Abdominal Aortic Aneurysms. The Case for Early Resection. Circulation 1977, 56 (Suppl. 3), II161-4. [Google Scholar]
- Wang, X.; Ghayesh, M.H.; Kotousov, A.; Zander, A.C.; Amabili, M.; Dawson, J.A.; Psaltis, P.J. Biomechanics of Abdominal Aortic Aneurysm in the Framework of Windkessel Effect and Fully-Developed Inflow Velocity via Two-Way Non-Linear FSI. Int. J. Non Linear Mech. 2023, 157, 104517. [Google Scholar] [CrossRef]
- Weintraub, N.L. Understanding Abdominal Aortic Aneurysm. N. Engl. J. Med. 2009, 361, 1114–1116. [Google Scholar] [CrossRef]
- Soudah, E.; Ng, E.Y.K.; Loong, T.H.; Bordone, M.; Pua, U.; Narayanan, S. CFD Modelling of Abdominal Aortic Aneurysm on Hemodynamic Loads Using a Realistic Geometry with CT. Comput. Math. Methods Med. 2013, 2013, 472564. [Google Scholar] [CrossRef]
- Saphirstein, R.J.; Morgan, K.G. The Contribution of Vascular Smooth Muscle to Aortic Stiffness across Length Scales. Microcirculation 2014, 21, 201–207. [Google Scholar] [CrossRef]
- Boyd, A.J.; Kuhn, D.C.S.; Lozowy, R.J.; Kulbisky, G.P. Low Wall Shear Stress Predominates at Sites of Abdominal Aortic Aneurysm Rupture. J. Vasc. Surg. 2016, 63, 1613–1619. [Google Scholar] [CrossRef]
- Scotti, C.M.; Shkolnik, A.D.; Muluk, S.C.; Finol, E.A. Fluid-Structure Interaction in Abdominal Aortic Aneurysms: Effects of Asymmetry and Wall Thickness. Biomed. Eng. Online 2005, 4, 64. [Google Scholar] [CrossRef]
- Wolters, B.J.B.M.; Rutten, M.C.M.; Schurink, G.W.H.; Kose, U.; De Hart, J.; Van De Vosse, F.N. A Patient-Specific Computational Model of Fluid-Structure Interaction in Abdominal Aortic Aneurysms. Med. Eng. Phys. 2005, 27, 871–883. [Google Scholar] [CrossRef] [PubMed]
- Papaharilaou, Y.; Ekaterinaris, J.A.; Manousaki, E.; Katsamouris, A.N. A Decoupled Fluid Structure Approach for Estimating Wall Stress in Abdominal Aortic Aneurysms. J. Biomech. 2007, 40, 367–377. [Google Scholar] [CrossRef] [PubMed]
- Chandra, S.; Raut, S.S.; Jana, A.; Biederman, R.W.; Doyle, M.; Muluk, S.C.; Finol, E.A. Fluid-Structure Interaction Modeling of Abdominal Aortic Aneurysms: The Impact of Patient-Specific Inflow Conditions and Fluid/Solid Coupling. J. Biomech. Eng. 2013, 135, 081001. [Google Scholar] [CrossRef]
- Rengarajan, B.; Wu, W.; Wiedner, C.; Ko, D.; Muluk, S.C.; Eskandari, M.K.; Menon, P.G.; Finol, E.A. A Comparative Classification Analysis of Abdominal Aortic Aneurysms by Machine Learning Algorithms. Ann. Biomed. Eng. 2020, 48, 1419–1429. [Google Scholar] [CrossRef]
- Vorp, D.A. Biomechanics of Abdominal Aortic Aneurysm. J. Biomech. 2007, 40, 1887–1902. [Google Scholar] [CrossRef]
- Blanco, P.J.; Watanabe, S.M.; Dari, E.A.; Passos, M.A.R.F.; Feijoo, R.A. Blood Flow Distribution in an Anatomically Detailed Arterial Network Model: Criteria and Algorithms. Biomech. Model. Mechanobiol. 2014, 13, 1303–1330. [Google Scholar] [CrossRef]
- Xiao, N.; Alastruey, J.; Figueroa, C.A. A Systematic Comparison between 1-D and 3-D Hemodynamics in Compliant Arterial Models. Int. J. Numer. Method. Biomed. Eng. 2014, 30, 204–231. [Google Scholar] [CrossRef]
- Zhou, S.; Xu, L.; Hao, L.; Xiao, H.; Yao, Y.; Qi, L.; Yao, Y. A Review on Low-Dimensional Physics-Based Models of Systemic Arteries: Application to Estimation of Central Aortic Pressure. Biomed. Eng. Online 2019, 18, 41. [Google Scholar] [CrossRef]
- Mirramezani, M.; Shadden, S.C. Distributed Lumped Parameter Modeling of Blood Flow in Compliant Vessels. J. Biomech. 2022, 140, 111161. [Google Scholar] [CrossRef]
- Zakerzadeh, R.; Cupac, T.; Dorfner, N.; Guy, A. Coupled Hemodynamics and Oxygen Diffusion in Abdominal Aortic Aneurysm: A Computational Sensitivity Study. Cardiovasc. Eng. Technol. 2021, 12, 166–182. [Google Scholar] [CrossRef]
- Ramazanli, B.; Sert, C.; Yavuz, M.M. Effect of Inlet Velocity Profile and Entrance Length on Abdominal Aortic Aneurysm Hemodynamics Simulations. J. Therm. Sci. Technol. 2023, 43, 159–174. [Google Scholar] [CrossRef]
- Xiao, N.; Humphrey, J.D.; Figueroa, C.A. Multi-Scale Computational Model of Three-Dimensional Hemodynamics within a Deformable Full-Body Arterial Network. J. Comput. Phys. 2013, 244, 22–40. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.J.; Qin, S.; Chen, R.; Cai, X.C. A Parallel Domain Decomposition Method for Large Eddy Simulation of Blood Flow in Human Artery with Resistive Boundary Condition. Comput. Fluids 2022, 232, 105201. [Google Scholar] [CrossRef]
- Grinberg, L.; Karniadakis, G.E. Outflow Boundary Conditions for Arterial Networks with Multiple Outlets. Ann. Biomed. Eng. 2008, 36, 1496–1514. [Google Scholar] [CrossRef]
- Liu, H.; Liang, F.; Wong, J.; Fujiwara, T.; Ye, W.; Tsubota, K.; Sugawara, M. Multi-Scale Modeling of Hemodynamics in the Cardiovascular System. Acta Mech. Sin. 2015, 31, 446–464. [Google Scholar] [CrossRef]
- Sughimoto, K.; Takahara, Y.; Mogi, K.; Yamazaki, K.; Tsubota, K.; Liang, F.; Liu, H. Blood Flow Dynamic Improvement with Aneurysm Repair Detected by a Patient-Specific Model of Multiple Aortic Aneurysms. Heart Vessel. 2014, 29, 404–412. [Google Scholar] [CrossRef]
- Olufsen, M.S. Structured Tree Outflow Condition for Blood Flow in Larger Systemic Arteries. Am. J. Physiol. 1999, 276, 257–268. [Google Scholar] [CrossRef]
- Alastruey, J.; Khir, A.W.; Matthys, K.S.; Segers, P.; Sherwin, S.J.; Verdonck, P.R.; Parker, K.H.; Peiró, J. Pulse Wave Propagation in a Model Human Arterial Network: Assessment of 1-D Visco-Elastic Simulations against in Vitro Measurements. J. Biomech. 2011, 44, 2250–2258. [Google Scholar] [CrossRef]
- Formaggia, L.; Lamponi, D.; Quarteroni, A. One-Dimensional Models for Blood Flow in Arteries. J. Eng. Math. 2003, 47, 251–276. [Google Scholar] [CrossRef]
- Olufsen, M.S.; Peskin, C.S.; Kim, W.Y.; Pedersen, E.M.; Nadim, A.; Larsen, J. Numerical Simulation and Experimental Validation of Blood Flow in Arteries with Structured-Tree Outflow Conditions. Ann. Biomed. Eng. 2000, 28, 1281–1299. [Google Scholar] [CrossRef]
- Morris, P.D.; Narracott, A.; Von Tengg-Kobligk, H.; Alejandro, D.; Soto, S.; Hsiao, S.; Lungu, A.; Evans, P.; Bressloff, N.W.; Lawford, P.V.; et al. Computational Fluid Dynamics Modelling in Cardiovascular Medicine. Heart 2015, 102, 18–28. [Google Scholar] [CrossRef] [PubMed]
- Salman, H.E.; Ramazanli, B.; Yavuz, M.M.; Yalcin, H.C. Biomechanical Investigation of Disturbed Hemodynamics-Induced Tissue Degeneration in Abdominal Aortic Aneurysms Using Computational and Experimental Techniques. Front. Bioeng. Biotechnol. 2019, 7, 111. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.A.; Figueroa, C.A. Patient-Specific Modeling of Cardiovascular Mechanics. Annu. Rev. Biomed. Eng. 2009, 11, 109–134. [Google Scholar] [CrossRef]
- Les, A.S.; Yeung, J.J.; Schultz, G.M.; Herfkens, R.J.; Dalman, R.L.; Taylor, C.A. Supraceliac and Infrarenal Aortic Flow in Patients with Abdominal Aortic Aneurysms: Mean Flows, Waveforms, and Allometric Scaling Relationships. Cardiovasc. Eng. Technol. 2010, 1, 39–51. [Google Scholar] [CrossRef]
- Les, A.S.; Shadden, S.C.; Figueroa, C.A.; Park, J.M.; Tedesco, M.M.; Herfkens, R.J.; Dalman, R.L.; Taylor, C.A. Quantification of Hemodynamics in Abdominal Aortic Aneurysms during Rest and Exercise Using Magnetic Resonance Imaging and Computational Fluid Dynamics. Ann. Biomed. Eng. 2010, 38, 1288–1313. [Google Scholar] [CrossRef]
- Di Achille, P.; Tellides, G.; Figueroa, C.A.; Humphrey, J.D. A Haemodynamic Predictor of Intraluminal Thrombus Formation in Abdominal Aortic Aneurysms. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20140163. [Google Scholar] [CrossRef]
- Fonken, J.H.C.; Maas, E.J.; Nievergeld, A.H.M.; van Sambeek, M.R.H.M.; van de Vosse, F.N.; Lopata, R.G.P. Ultrasound-Based Fluid-Structure Interaction Modeling of Abdominal Aortic Aneurysms Incorporating Pre-Stress. Front. Physiol. 2021, 12, 717593. [Google Scholar] [CrossRef]
- Owen, B.; Lowe, C.; Ashton, N.; Mandal, P.; Rogers, S.; Wein, W.; McCollum, C.; Revell, A. Computational Hemodynamics of Abdominal Aortic Aneurysms: Three-Dimensional Ultrasound versus Computed Tomography. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2016, 230, 201–210. [Google Scholar] [CrossRef]
- Qiu, Y.; Yuan, D.; Wang, Y.; Wen, J.; Zheng, T. Hemodynamic Investigation of a Patient-Specific Abdominal Aortic Aneurysm with Iliac Artery Tortuosity. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 824–833. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, Y.; Fan, Y.; Peng, L.; Liu, R.; Zhao, J.; Yuan, D.; Zheng, T. Role of Intraluminal Thrombus in Abdominal Aortic Aneurysm Ruptures: A Hemodynamic Point of View. Med. Phys. 2019, 46, 4263–4275. [Google Scholar] [CrossRef]
- Teng, B.; Zhou, Z.; Zhao, Y.; Wang, Z. Combined Curvature and Wall Shear Stress Analysis of Abdominal Aortic Aneurysm: An Analysis of Rupture Risk Factors. Cardiovasc. Intervent Radiol. 2022, 45, 752–760. [Google Scholar] [CrossRef] [PubMed]
- Mei, Y.; Xu, H.; Ma, W.; Li, Z.; Yang, R.; Yuan, H.; Peng, Y.; Wu, M.; Chen, Z.; Guo, W.; et al. Retrograde Branched Extension Limb Assembling Stent of Pararenal Abdominal Aortic Aneurysm: A Longitudinal Hemodynamic Analysis for Stent Graft Migration. Int. J. Numer. Method. Biomed. Eng. 2020, 36, e3394. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Li, J.; Qin, S.; Guo, W.; Chen, R. Hemodynamic Simulation of Aneurysmal Aorta Using a Parallel Algorithm and a Flow-Rate Based Resistance Splitting Method. Comput. Electr. Eng. 2022, 104, 108440. [Google Scholar] [CrossRef]
- Dzieciuchowicz, Ł.; Krzyżański, R.; Nowak, A. Use of Intravascular Ultrasound in Endovascular Repair of Abdominal Aortic Aneurysm. Postep. W Kardiol. Interwencyjnej 2020, 16, 202–205. [Google Scholar] [CrossRef]
- Van Rooij, W.J.; Sprengers, M.E.; De Gast, A.N.; Peluso, J.P.P.; Sluzewski, M. 3D Rotational Angiography: The New Gold Standard in the Detection of Additional Intracranial Aneurysms. Am. J. Neuroradiol. 2008, 29, 976–979. [Google Scholar] [CrossRef]
- Mai, D.V.C.; Drami, I.; Pring, E.T.; Gould, L.E.; Lung, P.; Popuri, K.; Chow, V.; Beg, M.F.; Athanasiou, T.; Jenkins, J.T. A Systematic Review of Automated Segmentation of 3D Computed-Tomography Scans for Volumetric Body Composition Analysis. J. Cachexia Sarcopenia Muscle 2023, 14, 1973–1986. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Bhalerao, M.; Thakur, S. Brain Tumor Segmentation Based on 3D Residual U-Net. In Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2020; Volume 11993 LNCS, pp. 218–225. [Google Scholar] [CrossRef]
- Mu, N.; Lyu, Z.; Rezaeitaleshmahalleh, M.; Tang, J.; Jiang, J. An Attention Residual U-Net with Differential Preprocessing and Geometric Postprocessing: Learning How to Segment Vasculature Including Intracranial Aneurysms. Med. Image Anal. 2023, 84, 102697. [Google Scholar] [CrossRef]
- Mu, N.; Lyu, Z.; Rezaeitaleshmahalleh, M.; Zhang, X.; Rasmussen, T.; McBane, R.; Jiang, J. Automatic Segmentation of Abdominal Aortic Aneurysms from CT Angiography Using a Context-Aware Cascaded U-Net. Comput. Biol. Med. 2023, 158, 106569. [Google Scholar] [CrossRef]
- Chung, T.K.; Liang, N.L.; Vorp, D.A. Artificial Intelligence Framework to Predict Wall Stress in Abdominal Aortic Aneurysm. Appl. Eng. Sci. 2022, 10, 100104. [Google Scholar] [CrossRef]
- Lan, I.S.; Liu, J.; Yang, W.; Marsden, A.L. Numerical Investigation of Abdominal Aortic Aneurysm Hemodynamics Using the Reduced Unified Continuum Formulation for Vascular Fluid-Structure Interaction. Forces Mech. 2022, 7, 100089. [Google Scholar] [CrossRef]
- Peng, C.; He, W.; Huang, X.; Ma, J.; Yuan, T.; Shi, Y.; Wang, S. The Study on the Impact of AAA Wall Motion on the Hemodynamics Based on 4D CT Image Data. Front. Bioeng. Biotechnol. 2023, 11, 1103905. [Google Scholar] [CrossRef] [PubMed]
- Arslan, A.C.; Salman, H.E. Effect of Intraluminal Thrombus Burden on the Risk of Abdominal Aortic Aneurysm Rupture. J. Cardiovasc. Dev. Dis. 2023, 10, 233. [Google Scholar] [CrossRef] [PubMed]
- Brambila-Solórzano, A.; Méndez-Lavielle, F.; Naude, J.L.; Martínez-Sánchez, G.J.; García-Rebolledo, A.; Hernández, B.; Escobar-del Pozo, C. Influence of Blood Rheology and Turbulence Models in the Numerical Simulation of Aneurysms. Bioengineering 2023, 10, 1170. [Google Scholar] [CrossRef]
- Drewe, C.J.; Parker, L.P.; Kelsey, L.J.; Norman, P.E.; Powell, J.T.; Doyle, B.J. Haemodynamics and Stresses in Abdominal Aortic Aneurysms: A Fluid-Structure Interaction Study into the Effect of Proximal Neck and Iliac Bifurcation Angle. J. Biomech. 2017, 60, 150–156. [Google Scholar] [CrossRef]
- Jayendiran, R.; Nour, B.; Ruimi, A. Computational Analysis of Nitinol Stent-Graft for Endovascular Aortic Repair (EVAR) of Abdominal Aortic Aneurysm (AAA): Crimping, Sealing and Fluid-Structure Interaction (FSI). Int. J. Cardiol. 2020, 304, 164–171. [Google Scholar] [CrossRef]
- Kaewchoothong, N.; Algabri, Y.A.; Assawalertsakul, T.; Nuntadusit, C.; Chatpun, S. Computational Study of Abdominal Aortic Aneurysms with Severely Angulated Neck Based on Transient Hemodynamics Using an Idealized Model. Appl. Sci. 2022, 12, 2113. [Google Scholar] [CrossRef]
- Moradicheghamahi, J. The Role of Wall Mechanics in the Hemodynamics of a Realistic Abdominal Aortic Aneurysm: A Fluid-Structure Interaction Study. J. Eng. 2024, 2024, 3280563. [Google Scholar] [CrossRef]
- Piccinelli, M.; Vergara, C.; Antiga, L.; Forzenigo, L.; Biondetti, P.; Domanin, M. Impact of Hemodynamics on Lumen Boundary Displacements in Abdominal Aortic Aneurysms by Means of Dynamic Computed Tomography and Computational Fluid Dynamics. Biomech. Model. Mechanobiol. 2013, 12, 1263–1276. [Google Scholar] [CrossRef]
- Suh, G.Y.; Les, A.S.; Tenforde, A.S.; Shadden, S.C.; Spilker, R.L.; Yeung, J.J.; Cheng, C.P.; Herfkens, R.J.; Dalman, R.L.; Taylor, C.A. Quantification of Particle Residence Time in Abdominal Aortic Aneurysms Using Magnetic Resonance Imaging and Computational Fluid Dynamics. Ann. Biomed. Eng. 2011, 39, 864–883. [Google Scholar] [CrossRef]
- Suh, G.Y.; Les, A.S.; Tenforde, A.S.; Shadden, S.C.; Spilker, R.L.; Yeung, J.J.; Cheng, C.P.; Herfkens, R.J.; Dalman, R.L.; Taylor, C.A. Hemodynamic Changes Quantified in Abdominal Aortic Aneurysms with Increasing Exercise Intensity Using MR Exercise Imaging and Image-Based Computational Fluid Dynamics. Ann. Biomed. Eng. 2011, 39, 2186–2202. [Google Scholar] [CrossRef] [PubMed]
- Abdolmanafi, A.; Forneris, A.; Moore, R.D.; Di Martino, E.S. Deep-Learning Method for Fully Automatic Segmentation of the Abdominal Aortic Aneurysm from Computed Tomography Imaging. Front. Cardiovasc. Med. 2023, 9, 1040053. [Google Scholar] [CrossRef] [PubMed]
- Bologna, E.; Dinoto, E.; Di Simone, F.; Pecoraro, F.; Ragusa, S.; Siciliano, K.; Zingales, M. Computational Fluid Dynamics (CFD) and Finite Element Analysis (FEM) of a Customized Stent-Graft for Endovascular (EVAR) Treatment of Abdominal Aortic Aneurism (AAA). Appl. Sci. 2023, 13, 5712. [Google Scholar] [CrossRef]
- Al-Jumaily, A.M.; Embong, A.H.; AL-Rawi, M.; Mahadevan, G.; Sugita, S. Aneurysm Rupture Prediction Based on Strain Energy-CFD Modelling. Bioengineering 2023, 10, 1231. [Google Scholar] [CrossRef]
- Scotti, C.M.; Finol, E.A. Compliant Biomechanics of Abdominal Aortic Aneurysms: A Fluid-Structure Interaction Study. Comput. Struct. 2007, 85, 1097–1113. [Google Scholar] [CrossRef]
- Scotti, C.M.; Jimenez, J.; Muluk, S.C.; Finol, E.A. Wall Stress and Flow Dynamics in Abdominal Aortic Aneurysms: Finite Element Analysis vs. Fluid-Structure Interaction. Comput. Methods Biomech. Biomed. Eng. 2008, 11, 301–322. [Google Scholar] [CrossRef]
- Torii, R.; Oshima, M.; Kobayashi, T.; Takagi, K.; Tezduyar, T.E. Numerical Investigation of the Effect of Hypertensive Blood Pressure on Cerebral Aneurysm—Dependence of the Effect on the Aneurysm Shape. Int. J. Numer. Methods Fluids 2007, 54, 995–1009. [Google Scholar] [CrossRef]
- Torii, R.; Oshima, M.; Kobayashi, T.; Takagi, K.; Tezduyar, T.E. Computer Modeling of Cardiovascular Fluid-Structure Interactions with the Deforming-Spatial-Domain/Stabilized Space-Time Formulation. Comput. Methods Appl. Mech. Eng. 2006, 195, 1885–1895. [Google Scholar] [CrossRef]
- Arzani, A.; Shadden, S.C. Characterizations and Correlations of Wall Shear Stress in Aneurysmal Flow. J. Biomech. Eng. 2016, 138, 014503. [Google Scholar] [CrossRef]
- Bessonov, N.; Sequeira, A.; Simakov, S.; Vassilevskii, Y.; Volpert, V. Methods of Blood Flow Modelling. Math. Model. Nat. Phenom. 2016, 11, 1–25. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Mirafzal, I.; Rahbary, A.; Shamloo, A.; Naseri, T. Optimization of Nano-Microparticle Size and Shape on Wall-Interaction: A Human Case Study on an Abdominal Aortic Aneurysm. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2236166. [Google Scholar] [CrossRef]
- Arzani, A. Accounting for Residence-Time in Blood Rheology Models: Do We Really Need Non-Newtonian Blood Flow Modelling in Large Arteries? J. R. Soc. Interface 2018, 15, 20180486. [Google Scholar] [CrossRef] [PubMed]
- Biasetti, J.; Hussain, F.; Christian Gasser, T. Blood Flow and Coherent Vortices in the Normal and Aneurysmatic Aortas: A Fluid Dynamical Approach to Intraluminal Thrombus Formation. J. R. Soc. Interface 2011, 8, 1449–1461. [Google Scholar] [CrossRef]
- Bilgi, C.; Atalik, K. Numerical Investigation of the Effects Ofblood Rheology and Wall Elasticity in Abdominal Aortic Aneurysm under Pulsatile Flow Conditions. Biorheology 2019, 56, 51–71. [Google Scholar] [CrossRef]
- Marrero, V.L.; Tichy, J.A.; Sahni, O.; Jansen, K.E. Numerical Study of Purely Viscous Non-Newtonian Flow in an Abdominal Aortic Aneurysm. J. Biomech. Eng. 2014, 136, 101001. [Google Scholar] [CrossRef]
- Childress, E.M.; Kleinstreuer, C. Impact of Fluid-Structure Interaction on Direct Tumor-Targeting in a Representative Hepatic Artery System. Ann. Biomed. Eng. 2014, 42, 461–474. [Google Scholar] [CrossRef]
- Razavi, A.; Shirani, E.; Sadeghi, M.R. Numerical Simulation of Blood Pulsatile Flow in a Stenosed Carotid Artery Using Different Rheological Models. J. Biomech. 2011, 44, 2021–2030. [Google Scholar] [CrossRef]
- Morbiducci, U.; Ponzini, R.; Gallo, D.; Bignardi, C.; Rizzo, G. Inflow Boundary Conditions for Image-Based Computational Hemodynamics: Impact of Idealized versus Measured Velocity Profiles in the Human Aorta. J. Biomech. 2013, 46, 102–109. [Google Scholar] [CrossRef]
- Mendieta, J.B.; Fontanarosa, D.; Wang, J.; Paritala, P.K.; McGahan, T.; Lloyd, T.; Li, Z. The Importance of Blood Rheology in Patient-Specific Computational Fluid Dynamics Simulation of Stenotic Carotid Arteries. Biomech. Model. Mechanobiol. 2020, 19, 1477–1490. [Google Scholar] [CrossRef]
- Karimi, S.; Dabagh, M.; Vasava, P.; Dadvar, M.; Dabir, B.; Jalali, P. Effect of Rheological Models on the Hemodynamics within Human Aorta: CFD Study on CT Image-Based Geometry. J. Nonnewton Fluid Mech. 2014, 207, 42–52. [Google Scholar] [CrossRef]
- Faraji, A.; Sahebi, M.; SalavatiDezfouli, S. Numerical Investigation of Different Viscosity Models on Pulsatile Blood Flow of Thoracic Aortic Aneurysm (TAA) in a Patient-Specific Model. Comput. Methods Biomech. Biomed. Eng. 2023, 26, 986–998. [Google Scholar] [CrossRef] [PubMed]
- Skiadopoulos, A.; Neofytou, P.; Housiadas, C. Comparison of Blood Rheological Models in Patient Specific Cardiovascular System Simulations. J. Hydrodyn. B 2017, 29, 293–304. [Google Scholar] [CrossRef]
- Cho, Y.I.; Kensey, K.R. Effects of the Non-Newtonian Viscosity of Blood on Flows in a Diseased Arterial Vessel. Part 1: Steady Flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef] [PubMed]
- Leuprecht, A.; Perktold, K. Computer Simulation of Non-Newtonian Effects on Blood Flow in Large Arteries. Comput. Methods Biomech. Biomed. Eng. 2001, 4, 149–163. [Google Scholar] [CrossRef]
- Quemada, D. Rheology of Concentrated Disperse Systems III. General Features of the Proposed Non-Newtonian Model. Comparison with Experimental Data. Rheol. Acta 1978, 17, 643–653. [Google Scholar] [CrossRef]
- Bilgi, C.; Atalık, K. Effects of Blood Viscoelasticity on Pulsatile Hemodynamics in Arterial Aneurysms. J. Nonnewton Fluid Mech. 2020, 279, 104263. [Google Scholar] [CrossRef]
- Bodnár, T.; Sequeira, A.; Prosi, M. On the Shear-Thinning and Viscoelastic Effects of Blood Flow under Various Flow Rates. Appl. Math. Comput. 2011, 217, 5055–5067. [Google Scholar] [CrossRef]
- Guranov, I.; Ćoćić, A.; Lečić, M. Numerical Studies of Viscoelastic Flow Using the Software OpenFOAM. PAMM 2013, 13, 591–592. [Google Scholar] [CrossRef]
- Habla, F.; Tan, M.W.; Haßlberger, J.; Hinrichsen, O. Numerical Simulation of the Viscoelastic Flow in a Three-Dimensional Lid-Driven Cavity Using the Log-Conformation Reformulation in OpenFOAM®. J. Nonnewton Fluid Mech. 2014, 212, 47–62. [Google Scholar] [CrossRef]
- Elhanafy, A.; Guaily, A.; Elsaid, A. Numerical Simulation of Oldroyd-B Fluid with Application to Hemodynamics. Adv. Mech. Eng. 2019, 11, 1687814019852844. [Google Scholar] [CrossRef]
- Wang, X.; Carpenter, H.J.; Ghayesh, M.H.; Kotousov, A.; Zander, A.C.; Amabili, M.; Psaltis, P.J. A Review on the Biomechanical Behaviour of the Aorta. J. Mech. Behav. Biomed. Mater. 2023, 144, 105922. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Ogden, R.W. Constitutive Modelling of Arteries. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 1551–1597. [Google Scholar] [CrossRef]
- Humphrey, J.D.; Holzapfel, G.A. Mechanics, Mechanobiology, and Modeling of Human Abdominal Aorta and Aneurysms. J. Biomech. 2012, 45, 805–814. [Google Scholar] [CrossRef]
- Tong, J.; Holzapfel, G.A. Structure, Mechanics, and Histology of Intraluminal Thrombi in Abdominal Aortic Aneurysms. Ann. Biomed. Eng. 2015, 43, 1488–1501. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Raghavan, M.L.; Vorp, D.A. Toward a Biomechanical Tool to Evaluate Rupture Potential of Abdominal Aortic Aneurysm: Identi"cation of a "nite Strain Constitutive Model and Evaluation of Its Applicability. J. Biomech. 2000, 33, 475–482. [Google Scholar] [CrossRef]
- Di Martino, E.S.; Guadagni, G.; Fumero, A.; Ballerini, G.; Spirito, R.; Biglioli, P.; Redaelli, A. Fluid-Structure Interaction within Realistic Three-Dimensional Models of the Aneurysmatic Aorta as a Guidance to Assess the Risk of Rupture of the Aneurysm. Med. Eng. Phys. 2001, 23, 647–655. [Google Scholar] [CrossRef]
- Salman, H.E.; Yalcin, H.C. Computational Investigation of the Effect of Wall Thickness on Rupture Risk in Abdominal Aortic Aneurysms. J. Appl. Fluid Mech. 2021, 14, 499–513. [Google Scholar] [CrossRef]
- Javadzadegan, A.; Fakhim, B.; Behnia, M.; Behnia, M. Fluid-Structure Interaction Investigation of Spiral Flow in a Model of Abdominal Aortic Aneurysm. Eur. J. Mech. B/Fluids 2014, 46, 109–117. [Google Scholar] [CrossRef]
- Khanafer, K.; Berguer, R. Fluid-Structure Interaction Analysis of Turbulent Pulsatile Flow within a Layered Aortic Wall as Related to Aortic Dissection. J. Biomech. 2009, 42, 2642–2648. [Google Scholar] [CrossRef]
- Gao, F.; Ueda, H.; Gang, L.; Okada, H. Fluid Structure Interaction Simulation in Three-Layered Aortic Aneurysm Model under Pulsatile Flow: Comparison of Wrapping and Stenting. J. Biomech. 2013, 46, 1335–1342. [Google Scholar] [CrossRef]
- Simsek, F.G.; Kwon, Y.W. Investigation of Material Modeling in Fluid–Structure Interaction Analysis of an Idealized Three-Layered Abdominal Aorta: Aneurysm Initiation and Fully Developed Aneurysms. J. Biol. Phys. 2015, 41, 173–201. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, A.; Zheng, Q.; Li, P.; Wang, Y.; He, L.; Xue, Y.; Chen, W.; Wu, X.; Zhao, Y.; et al. The Biomechanical Effects of Different Membrane Layer Structures and Material Constitutive Modeling on Patient-Specific Cerebral Aneurysms. Front. Bioeng. Biotechnol. 2023, 11, 1323266. [Google Scholar] [CrossRef]
- Gasser, T.C.; Miller, C.; Polzer, S.; Roy, J. A Quarter of a Century Biomechanical Rupture Risk Assessment of Abdominal Aortic Aneurysms. Achievements, Clinical Relevance, and Ongoing Developments. Int. J. Numer. Method. Biomed. Eng. 2023, 39, e3587. [Google Scholar] [CrossRef]
- Bluestein, D.; Dumont, K.; De Beule, M.; Ricotta, J.; Impellizzeri, P.; Verhegghe, B.; Verdonck, P. Intraluminal Thrombus and Risk of Rupture in Patient Specific Abdominal Aortic Aneurysm—FSI Modelling. Comput. Methods Biomech. Biomed. Eng. 2009, 12, 73–81. [Google Scholar] [CrossRef]
- Lin, S.; Han, X.; Bi, Y.; Ju, S.; Gu, L. Fluid-Structure Interaction in Abdominal Aortic Aneurysm: Effect of Modeling Techniques. Biomed. Res. Int. 2017, 2017, 7023078. [Google Scholar] [CrossRef]
- Stevens, R.R.F.; Grytsan, A.; Biasetti, J.; Roy, J.; Liljeqvist, M.L.; Christian Gasser, T. Biomechanical Changes during Abdominal Aortic Aneurysm Growth. PLoS ONE 2017, 12, e0187421. [Google Scholar] [CrossRef]
- Balzani, D.; Heinlein, A.; Klawonn, A.; Rheinbach, O.; Schröder, J. Comparison of Arterial Wall Models in Fluid–Structure Interaction Simulations. Comput. Mech. 2023, 72, 949–965. [Google Scholar] [CrossRef]
- Józsa, T.I.; Paál, G. Boundary Conditions for Flow Simulations of Abdominal Aortic Aneurysms. Int. J. Heat. Fluid Flow. 2014, 50, 342–351. [Google Scholar] [CrossRef]
- Keramati, H.; Birgersson, E.; Ho, J.P.; Kim, S.; Chua, K.J.; Leo, H.L. The Effect of the Entry and Re-Entry Size in the Aortic Dissection: A Two-Way Fluid–Structure Interaction Simulation. Biomech. Model. Mechanobiol. 2020, 19, 2643–2656. [Google Scholar] [CrossRef]
- Vande Geest, J.P.; Wang, D.H.J.; Wisniewski, S.R.; Makaroun, M.S.; Vorp, D.A. Towards A Noninvasive Method for Determination of Patient-Specific Wall Strength Distribution in Abdominal Aortic Aneurysms. Ann. Biomed. Eng. 2006, 34, 1098–1106. [Google Scholar] [CrossRef]
- Vande Geest, J.P.; Sacks, M.S.; Vorp, D.A. A Planar Biaxial Constitutive Relation for the Luminal Layer of Intra-Luminal Thrombus in Abdominal Aortic Aneurysms. J. Biomech. 2006, 39, 2347–2354. [Google Scholar] [CrossRef]
- Raut, S.S.; Jana, A.; De Oliveira, V.; Muluk, S.C.; Finol, E.A. The Effect of Uncertainty in Vascular Wall Material Properties on Abdominal Aortic Aneurysm Wall Mechanics. In Computational Biomechanics for Medicine: Fundamental Science and Patient-Specific Applications; Springer New York: New York, NY, USA, 2014; Volume 9781493907458, pp. 69–86. [Google Scholar] [CrossRef]
- Polzer, S.; Gasser, T.C. Biomechanical Rupture Risk Assessment of Abdominal Aortic Aneurysms Based on a Novel Probabilistic Rupture Risk Index. J. R. Soc. Interface 2015, 12, 20150852. [Google Scholar] [CrossRef]
- Federico, S.; Grillo, A.; Giaquinta, G.; Herzog, W. Convex Fung-Type Potentials for Biological Tissues. Meccanica 2008, 43, 279–288. [Google Scholar] [CrossRef]
- Gasser, T.C.; Ogden, R.W.; Holzapfel, G.A. Hyperelastic Modelling of Arterial Layers with Distributed Collagen Fibre Orientations. J. R. Soc. Interface 2006, 3, 15–35. [Google Scholar] [CrossRef]
- Chuong, C.J.; Fung, Y.C. Three-Dimensional Stress Distribution in Arteries. J. Biomech. Eng. 1983, 105, 268–274. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C. A Viscoelastic Model for Fiber-Reinforced Composites at Finite Strains: Continuum Basis, Computational Aspects and Applications. Comput. Methods Appl. Mech. Eng. 2001, 190, 4379–4403. [Google Scholar] [CrossRef]
- Choi, H.S.; Vito, R.P. Two-Dimensional Stress-Strain Relationship for Canine Pericardium. J. Biomech. Eng. 1990, 112, 153–159. [Google Scholar] [CrossRef]
- Di Martino, E.S.; Vorp, D.A. Effect of Variation in Intraluminal Thrombus Constitutive Properties on Abdominal Aortic Aneurysm Wall Stress. Ann. Biomed. Eng. 2003, 31, 804–809. [Google Scholar] [CrossRef]
- Xenos, M.; Labropoulos, N.; Rambhia, S.; Alemu, Y.; Einav, S.; Tassiopoulos, A.; Sakalihasan, N.; Bluestein, D. Progression of Abdominal Aortic Aneurysm Towards Rupture: Refining Clinical Risk Assessment Using a Fully Coupled Fluid–Structure Interaction Method. Ann. Biomed. Eng. 2015, 43, 139–153. [Google Scholar] [CrossRef]
- De Borst, R.; Nithiarasu, P.; Tezduyar, T.E.; Yagawa, G.; Zohdi, T. Computational Fluid-Structure Interaction Wiley Series in Computational Mechanics Series Advisors; Wiley Series in Computational Echanicsa; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Reymond, P.; Crosetto, P.; Deparis, S.; Quarteroni, A.; Stergiopulos, N. Physiological Simulation of Blood Flow in the Aorta: Comparison of Hemodynamic Indices as Predicted by 3-D FSI, 3-D Rigid Wall and 1-D Models. Med. Eng. Phys. 2013, 35, 784–791. [Google Scholar] [CrossRef]
- Crosetto, P.; Reymond, P.; Deparis, S.; Kontaxakis, D.; Stergiopulos, N.; Quarteroni, A. Fluid-Structure Interaction Simulation of Aortic Blood Flow. Comput. Fluids 2011, 43, 46–57. [Google Scholar] [CrossRef]
- Takizawa, K.; Christopher, J.; Tezduyar, T.E.; Sathe, S. Space-Time Finite Element Computation of Arterial Fluid-Structure Interactions with Patient-Specific Data. Int. J. Numer. Method. Biomed. Eng. 2010, 26, 101–116. [Google Scholar] [CrossRef]
- Donea, J.; Giuliani, S.; Halleux, J.P. An Arbitrary Lagrangian-Eulerian Finite Element Method for Transient Dynamic Fluid-Structure Interactions. Comput. Methods Appl. Mech. Eng. 1982, 33, 689–723. [Google Scholar] [CrossRef]
- Pirola, S.; Cheng, Z.; Jarral, O.A.; O’Regan, D.P.; Pepper, J.R.; Athanasiou, T.; Xu, X.Y. On the Choice of Outlet Boundary Conditions for Patient-Specific Analysis of Aortic Flow Using Computational Fluid Dynamics. J. Biomech. 2017, 60, 15–21. [Google Scholar] [CrossRef]
- Mariotti, A.; Boccadifuoco, A.; Celi, S.; Salvetti, M.V. Hemodynamics and Stresses in Numerical Simulations of the Thoracic Aorta: Stochastic Sensitivity Analysis to Inlet Flow-Rate Waveform. Comput. Fluids 2021, 230, 105123. [Google Scholar] [CrossRef]
- Kim, H.J.; Vignon-Clementel, I.E.; Figueroa, C.A.; Ladisa, J.F.; Jansen, K.E.; Feinstein, J.A.; Taylor, C.A. On Coupling a Lumped Parameter Heart Model and a Three-Dimensional Finite Element Aorta Model. Ann. Biomed. Eng. 2009, 37, 2153–2169. [Google Scholar] [CrossRef]
- Bonfanti, M.; Franzetti, G.; Maritati, G.; Homer-Vanniasinkam, S.; Balabani, S.; Díaz-Zuccarini, V. Patient-Specific Haemodynamic Simulations of Complex Aortic Dissections Informed by Commonly Available Clinical Datasets. Med. Eng. Phys. 2019, 71, 45–55. [Google Scholar] [CrossRef]
- Formaggia, L.; Lamponi, D.; Tuveri, M.; Veneziani, A. Numerical Modeling of 1D Arterial Networks Coupled with a Lumped Parameters Description of the Heart. Comput. Methods Biomech. Biomed. Eng. 2006, 9, 273–288. [Google Scholar] [CrossRef]
- Alastruey, J.; Xiao, N.; Fok, H.; Schaeffter, T.; Figueroa, C.A. On the Impact of Modelling Assumptions in Multi-Scale, Subject-Specific Models of Aortic Haemodynamics. J. R. Soc. Interface 2016, 13, 20160073. [Google Scholar] [CrossRef]
- van ’t Veer, M.; Buth, J.; Merkx, M.; Tonino, P.; van den Bosch, H.; Pijls, N.; van de Vosse, F. Biomechanical Properties of Abdominal Aortic Aneurysms Assessed by Simultaneously Measured Pressure and Volume Changes in Humans. J. Vasc. Surg. 2008, 48, 1401–1407. [Google Scholar] [CrossRef]
- Youssefi, P.; Gomez, A.; Arthurs, C.; Sharma, R.; Jahangiri, M.; Figueroa, C.A. Impact of Patient-Specific Inflow Velocity Profile on Hemodynamics of the Thoracic Aorta. J. Biomech. Eng. 2018, 140, 011002. [Google Scholar] [CrossRef]
- Cheng, Z.; Kidher, E.; Jarral, O.A.; O’Regan, D.P.; Wood, N.B.; Athanasiou, T.; Xu, X.Y. Assessment of Hemodynamic Conditions in the Aorta Following Root Replacement with Composite Valve-Conduit Graft. Ann. Biomed. Eng. 2016, 44, 1392–1404. [Google Scholar] [CrossRef][Green Version]
- Pirola, S.; Guo, B.; Menichini, C.; Saitta, S.; Fu, W.; Dong, Z.; Xu, X.Y. 4-D Flow Mri-Based Computational Analysis of Blood Flow in Patient-Specific Aortic Dissection. IEEE Trans. Biomed. Eng. 2019, 66, 3411–3419. [Google Scholar] [CrossRef]
- Markl, M.; Schnell, S.; Wu, C.; Bollache, E.; Jarvis, K.; Barker, A.J.; Robinson, J.D.; Rigsby, C.K. Advanced Flow MRI: Emerging Techniques and Applications. Clin. Radiol. 2016, 71, 779–795. [Google Scholar] [CrossRef]
- Lodi Rizzini, M.; Gallo, D.; De Nisco, G.; D’Ascenzo, F.; Chiastra, C.; Bocchino, P.P.; Piroli, F.; De Ferrari, G.M.; Morbiducci, U. Does the Inflow Velocity Profile Influence Physiologically Relevant Flow Patterns in Computational Hemodynamic Models of Left Anterior Descending Coronary Artery? Med. Eng. Phys. 2020, 82, 58–69. [Google Scholar] [CrossRef]
- Armour, C.H.; Guo, B.; Pirola, S.; Saitta, S.; Liu, Y.; Dong, Z.; Xu, X.Y. The Influence of Inlet Velocity Profile on Predicted Flow in Type B Aortic Dissection. Biomech. Model. Mechanobiol. 2021, 20, 481–490. [Google Scholar] [CrossRef]
- Chen, X.; Zhuang, J.; Wu, Y. The Effect of Womersley Number and Particle Radius on the Accumulation of Lipoproteins in the Human Aorta. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 571–584. [Google Scholar] [CrossRef]
- Bit, A.; Alblawi, A.; Chattopadhyay, H.; Quais, Q.A.; Benim, A.C.; Rahimi-Gorji, M.; Do, H.T. Three Dimensional Numerical Analysis of Hemodynamic of Stenosed Artery Considering Realistic Outlet Boundary Conditions. Comput. Methods Programs Biomed. 2020, 185, 105163. [Google Scholar] [CrossRef]
- Colciago, C.M.; Deparis, S.; Domanin, M.; Riccobene, C.; Schenone, E.; Quarteroni, A. Analysis of Morphological and Haemodynamical Indexes in Abdominal Aortic Aneurysms as Preliminary Indicators of Intraluminal Thrombus Deposition. Biomech. Model. Mechanobiol. 2020, 19, 1035–1053. [Google Scholar] [CrossRef]
- Arzani, A.; Suh, G.Y.; Dalman, R.L.; Shadden, S.C. A Longitudinal Comparison of Hemodynamics and Intraluminal Thrombus Deposition in Abdominal Aortic Aneurysms. Am. J. Physiol. Heart Circ. Physiol. 2014, 307, H1786–H1795. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, S.; Anupindi, K.; Patnaik, B.S.V. Influence of Wall Shear Stress and Geometry on the Lumen Surface Concentration of Low Density Lipoprotein in a Model Abdominal Aortic Aneurysm. Phys. Fluids 2019, 31, 011901. [Google Scholar] [CrossRef]
- Hardman, D.; Semple, S.I.; Richards, J.M.J.; Hoskins, P.R. Comparison of Patient-Specific Inlet Boundary Conditions in the Numerical Modelling of Blood Flow in Abdominal Aortic Aneurysm Disease. Int. J. Numer. Method. Biomed. Eng. 2013, 29, 165–178. [Google Scholar] [CrossRef] [PubMed]
- Lozowy, R.J.; Kuhn, D.C.S.; Ducas, A.A.; Boyd, A.J. The Relationship Between Pulsatile Flow Impingement and Intraluminal Thrombus Deposition in Abdominal Aortic Aneurysms. Cardiovasc. Eng. Technol. 2017, 8, 57–69. [Google Scholar] [CrossRef]
- Wei, Z.A.; Huddleston, C.; Trusty, P.M.; Singh-Gryzbon, S.; Fogel, M.A.; Veneziani, A.; Yoganathan, A.P. Analysis of Inlet Velocity Profiles in Numerical Assessment of Fontan Hemodynamics. Ann. Biomed. Eng. 2019, 47, 2258–2270. [Google Scholar] [CrossRef]
- Womersley, J.R. Method for the Calculation of Velocity, Rate of Flow and Viscous Drag in Arteries When the Pressure Gradient Is Known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef]
- Campbell, I.C.; Ries, J.; Dhawan, S.S.; Quyyumi, A.A.; Taylor, W.R.; Oshinski, J.N. Effect of Inlet Velocity Profiles on Patient-Specific Computational Fluid Dynamics Simulations of the Carotid Bifurcation. J. Biomech. Eng. 2012, 134, 051001. [Google Scholar] [CrossRef]
- Impiombato, A.N.; La Civita, G.; Orlandi, F.; Franceschini Zinani, F.S.; Oliveira Rocha, L.A.; Biserni, C. A Simple Transient Poiseuille-Based Approach to Mimic the Womersley Function and to Model Pulsatile Blood Flow. Dynamics 2021, 1, 9–17. [Google Scholar] [CrossRef]
- Madhavan, S.; Kemmerling, E.M.C. The Effect of Inlet and Outlet Boundary Conditions in Image-Based CFD Modeling of Aortic Flow. Biomed. Eng. Online 2018, 17, 66. [Google Scholar] [CrossRef]
- Li, Z.; Mao, W. A Fast Approach to Estimating Windkessel Model Parameters for Patient-Specific Multi-Scale CFD Simulations of Aortic Flow. Comput. Fluids 2023, 259, 105894. [Google Scholar] [CrossRef]
- Javadzadegan, A.; Simmons, A.; Behnia, M.; Barber, T. Computational Modelling of Abdominal Aortic Aneurysms: Effect of Suprarenal vs Infrarenal Positions. Eur. J. Mech. B/Fluids 2017, 61, 112–124. [Google Scholar] [CrossRef]
- Von Spiczak, J.; Crelier, G.; Giese, D.; Kozerke, S.; Maintz, D.; Bunck, A.C. Quantitative Analysis of Vortical Blood Flow in the Thoracic Aorta Using 4D Phase Contrast MRI. PLoS ONE 2015, 10, e0139025. [Google Scholar] [CrossRef] [PubMed]
- Stonebridge, P.; Thompson, A.; Dick, J.; Hunter, G.; Chudek, J.A.; Houston, J.; Belch, J. Non Spiral and Spiral (Helical) Flow Patterns in Stenoses. In Vitro Observations Using Spin and Gradient Echo Magnetic Resonance Imaging (MRI) and Computational Fluid Dynamic Modeling. Int. Angiol. 2004, 23, 276–283. [Google Scholar] [PubMed]
- Vignon-Clementel, I.E.; Alberto Figueroa, C.; Jansen, K.E.; Taylor, C.A. Outflow Boundary Conditions for Three-Dimensional Finite Element Modeling of Blood Flow and Pressure in Arteries. Comput. Methods Appl. Mech. Eng. 2006, 195, 3776–3796. [Google Scholar] [CrossRef]
- Vignon-Clementel, I.E.; Figueroa, C.A.; Jansen, K.E.; Taylor, C.A. Outflow Boundary Conditions for 3D Simulations of Non-Periodic Blood Flow and Pressure Fields in Deformable Arteries. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 625–640. [Google Scholar] [CrossRef]
- Gallo, D.; De Santis, G.; Negri, F.; Tresoldi, D.; Ponzini, R.; Massai, D.; Deriu, M.A.; Segers, P.; Verhegghe, B.; Rizzo, G.; et al. On the Use of in Vivo Measured Flow Rates as Boundary Conditions for Image-Based Hemodynamic Models of the Human Aorta: Implications for Indicators of Abnormal Flow. Ann. Biomed. Eng. 2012, 40, 729–741. [Google Scholar] [CrossRef]
- O’Rourke, M.J.; McCullough, J.P.; Kelly, S. An Investigation of the Relationship between Hemodynamics and Thrombus Deposition within Patient-Specific Models of Abdominal Aortic Aneurysm. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2012, 226, 548–564. [Google Scholar] [CrossRef]
- O’Rourke, M.J.; McCullough, J.P. An Investigation of the Flow Field within Patient-Specific Models of an Abdominal Aortic Aneurysm under Steady Inflow Conditions. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2010, 224, 971–988. [Google Scholar] [CrossRef]
- Raptis, A.; Xenos, M.; Dimas, S.; Giannoukas, A.; Labropoulos, N.; Bluestein, D.; Matsagkas, M.I. Effect of Macroscale Formation of Intraluminal Thrombus on Blood Flow in Abdominal Aortic Aneurysms. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 84–92. [Google Scholar] [CrossRef]
- Arzani, A.; Gambaruto, A.M.; Chen, G.; Shadden, S.C. Wall Shear Stress Exposure Time: A Lagrangian Measure of near-Wall Stagnation and Concentration in Cardiovascular Flows. Biomech. Model. Mechanobiol. 2017, 16, 787–803. [Google Scholar] [CrossRef]
- Belkacemi, D.; Tahar Abbes, M.; Al-Rawi, M.; Al-Jumaily, A.M.; Bachene, S.; Laribi, B. Intraluminal Thrombus Characteristics in AAA Patients: Non-Invasive Diagnosis Using CFD. Bioengineering 2023, 10, 540. [Google Scholar] [CrossRef] [PubMed]
- Casciaro, M.E.; Dottori, J.; El-Batti, S.; Alsac, J.M.; Mousseaux, E.; Larrabide, I.; Craiem, D. Effects on Aortoiliac Fluid Dynamics After Endovascular Sealing of Abdominal Aneurysms. Vasc. Endovasc. Surg. 2018, 52, 621–628. [Google Scholar] [CrossRef] [PubMed]
- Dottori, J.; Casciaro, M.; Craiem, D.; El-Batti, S.; Mousseaux, E.; Alsac, J.M.; Larrabide, I. Regional Assessment of Vascular Morphology and Hemodynamics: Methodology and Evaluation for Abdominal Aortic Aneurysms after Endovascular Repair. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 1060–1070. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez-Urquijo, M.; de Zamacona, R.G.; Mendoza, A.K.M.; Iribarren, M.Z.; Ibarra, E.G.; Bencomo, M.D.M.; Fabiani, M.A. 3D Modeling of Blood Flow in Simulated Abdominal Aortic Aneurysm. Vasc. Endovascular Surg. 2021, 55, 677–683. [Google Scholar] [CrossRef]
- Hansen, K.B.; Shadden, S.C. A Reduced-Dimensional Model for near-Wall Transport in Cardiovascular Flows. Biomech. Model. Mechanobiol. 2016, 15, 713–722. [Google Scholar] [CrossRef]
- McClarty, D.B.; Kuhn, D.C.S.; Boyd, A.J. Hemodynamic Changes in an Actively Rupturing Abdominal Aortic Aneurysm. J. Vasc. Res. 2021, 58, 172–179. [Google Scholar] [CrossRef]
- Rezaeitaleshmahalleh, M.; Lyu, Z.; Mu, N.; Zhang, X.; Rasmussen, T.E.; McBane, R.D.; Jiang, J. Characterization of Small Abdominal Aortic Aneurysms’ Growth Status Using Spatial Pattern Analysis of Aneurismal Hemodynamics. Sci. Rep. 2023, 13, 13832. [Google Scholar] [CrossRef]
- Qiu, Y.; Yuan, D.; Wen, J.; Fan, Y.; Zheng, T. Numerical Identification of the Rupture Locations in Patient-Specific Abdominal Aortic Aneurysmsusing Hemodynamic Parameters. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 1–12. [Google Scholar] [CrossRef]
- Poelma, C.; Watton, P.N.; Ventikos, Y. Transitional Flow in Aneurysms and the Computation of Haemodynamic Parameters. J. R. Soc. Interface 2015, 12, 20141394. [Google Scholar] [CrossRef]
- Qiu, Y.; Wang, J.; Zhao, J.; Wang, T.; Zheng, T.; Yuan, D. Association Between Blood Flow Pattern and Rupture Risk of Abdominal Aortic Aneurysm Based on Computational Fluid Dynamics. Eur. J. Vasc. Endovasc. Surg. 2022, 64, 155–164. [Google Scholar] [CrossRef]
- Zambrano, B.A.; Gharahi, H.; Lim, C.Y.; Jaberi, F.A.; Choi, J.; Lee, W.; Baek, S. Association of Intraluminal Thrombus, Hemodynamic Forces, and Abdominal Aortic Aneurysm Expansion Using Longitudinal CT Images. Ann. Biomed. Eng. 2016, 44, 1502–1514. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Xiong, J.; Chen, Z.; Deng, X.; Xu, Z.; Sun, A.; Fan, Y. Gender Differences of Morphological and Hemodynamic Characteristics of Abdominal Aortic Aneurysm. Biol. Sex. Differ. 2020, 11, 41. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Kleinstreuer, C. Fluid-Structure Interaction Effects on Sac-Blood Pressure and Wall Stress in a Stented Aneurysm. J. Biomech. Eng. 2005, 127, 662–671. [Google Scholar] [CrossRef] [PubMed]
- Biasetti, J.; Gasser, T.C.; Auer, M.; Hedin, U.; Labruto, F. Hemodynamics of the Normal Aorta Compared to Fusiform and Saccular Abdominal Aortic Aneurysms with Emphasis on a Potential Thrombus Formation Mechanism. Ann. Biomed. Eng. 2010, 38, 380–390. [Google Scholar] [CrossRef]
- Ene, F.; Delassus, P.; Morris, L. The Influence of Computational Assumptions on Analysing Abdominal Aortic Aneurysm Haemodynamics. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 768–780. [Google Scholar] [CrossRef]
- Arzani, A.; Dyverfeldt, P.; Ebbers, T.; Shadden, S.C. In Vivo Validation of Numerical Prediction for Turbulence Intensity in an Aortic Coarctation. Ann. Biomed. Eng. 2012, 40, 860–870. [Google Scholar] [CrossRef]
- Reymond, P.; Merenda, F.; Perren, F.; Rü, D.; Stergiopulos, N. Validation of a One-Dimensional Model of the Systemic Arterial Tree. Am. J. Physiol. Heart Circ. Physiol. 2009, 297, 208–222. [Google Scholar] [CrossRef]
- Sherman, T.F. On Connecting Large Vessels to Small The Meaning of Murray’s Law. J. Gen. Physiol. 1981, 78, 431–453. [Google Scholar] [CrossRef]
- Painter, P.R.; Edén, P.; Bengtsson, H.U. Pulsatile Blood Flow, Shear Force, Energy Dissipation and Murray’s Law. Theor. Biol. Med. Model. 2006, 3, 31. [Google Scholar] [CrossRef]
- Murray, C.D. The Physiological Principle of Minimum Work. Proc. Natl. Acad. Sci. USA 1926, 12, 207–214. [Google Scholar] [CrossRef]
- Boccadifuoco, A.; Mariotti, A.; Celi, S.; Martini, N.; Salvetti, M.V. Impact of Uncertainties in Outflow Boundary Conditions on the Predictions of Hemodynamic Simulations of Ascending Thoracic Aortic Aneurysms. Comput. Fluids 2018, 165, 96–115. [Google Scholar] [CrossRef]
- Qin, S.; Chen, R.; Wu, B.; Shiu, W.S.; Cai, X.C. Numerical Simulation of Blood Flows in Patient-Specific Abdominal Aorta with Primary Organs. Biomech. Model. Mechanobiol. 2021, 20, 909–924. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.; Wu, B.; Shiu, W.S.; Yan, Z.; Chen, R.; Cai, X.C. Efficient Parallel Simulation of Hemodynamics in Patient-Specific Abdominal Aorta with Aneurysm. Comput. Biol. Med. 2021, 136, 104652. [Google Scholar] [CrossRef] [PubMed]
- Lo, S.C.Y.; McCullough, J.W.S.; Coveney, P.V. Parametric Analysis of an Efficient Boundary Condition to Control Outlet Flow Rates in Large Arterial Networks. Sci. Rep. 2022, 12, 19092. [Google Scholar] [CrossRef]
- Caballero, A.D.; Laín, S. A Review on Computational Fluid Dynamics Modelling in Human Thoracic Aorta. Cardiovasc. Eng. Technol. 2013, 4, 103–130. [Google Scholar] [CrossRef]
- Arbia, G.; Vignon-Clementel, I.; Hsia, T.Y.; Gerbeau, J.-F.; Arbia, G.; Vignon-Clementel, I.E.; Hsia, T.-Y.; Gerbeau, J.-F. Modified Navier-Stokes Equations for the Outflow Boundary Conditions in Hemodynamics. Eur. J. Me-Chanics-B/Fluids 2016, 60, 175–188. [Google Scholar] [CrossRef]
- Ladisa, J.F.; Alberto Figueroa, C.; Vignon-Clementel, I.E.; Jin Kim, H.; Xiao, N.; Ellwein, L.M.; Chan, F.P.; Feinstein, J.A.; Taylor, C.A. Computational Simulations for Aortic Coarctation: Representative Results from a Sampling of Patients. J. Biomech. Eng. 2011, 133, 091008. [Google Scholar] [CrossRef]
- Stergiopulos, N.; Westerhof, B.E.; Westerhof, N. Total Arterial Inertance as the Fourth Element of the Windkessel Model. Am. J. Physiol.-Heart Circ. Physiol. 1999, 276, H81–H88. [Google Scholar] [CrossRef]
- Westerhof, N.; Lankhaar, J.W.; Westerhof, B.E. The Arterial Windkessel. Med. Biol. Eng. Comput. 2009, 47, 131–141. [Google Scholar] [CrossRef]
- Lo, S.C.Y.; McCullough, J.W.S.; Xue, X.; Coveney, P.V. Uncertainty Quantification of the Impact of Peripheral Arterial Disease on Abdominal Aortic Aneurysms in Blood Flow Simulations. J. R. Soc. Interface 2024, 21, 20230656. [Google Scholar] [CrossRef]
- Kung, E.O.; Les, A.S.; Medina, F.; Wicker, R.B.; Mcconneil, M.V.; Taylor, C.A. In Vitro Validation of Finite-Element Model of AAA Hemodynamics Incorporating Realistic Outlet Boundary Conditions. J. Biomech. Eng. 2011, 133, 041003. [Google Scholar] [CrossRef] [PubMed]
- Taebi, A.; Pillai, R.M.; Roudsari, B.S.; Vu, C.T.; Roncali, E. Computational Modeling of the Liver Arterial Blood Flow for Microsphere Therapy: Effect of Boundary Conditions. Bioengineering 2020, 7, 64. [Google Scholar] [CrossRef] [PubMed]
- Alimohammadi, M.; Agu, O.; Balabani, S.; Díaz-Zuccarini, V. Development of a Patient-Specific Simulation Tool to Analyse Aortic Dissections: Assessment of Mixed Patient-Specific Flow and Pressure Boundary Conditions. Med. Eng. Phys. 2014, 36, 275–284. [Google Scholar] [CrossRef] [PubMed]
- Jonášová, A.; Vimmr, J. On the Relevance of Boundary Conditions and Viscosity Models in Blood Flow Simulations in Patient-Specific Aorto-Coronary Bypass Models. Int. J. Numer. Method. Biomed. Eng. 2021, 37, e3439. [Google Scholar] [CrossRef] [PubMed]
- Romarowski, R.M.; Lefieux, A.; Morganti, S.; Veneziani, A.; Auricchio, F. Patient-Specific CFD Modelling in the Thoracic Aorta with PC-MRI–Based Boundary Conditions: A Least-Square Three-Element Windkessel Approach. Int. J. Numer. Method. Biomed. Eng. 2018, 34, e3134. [Google Scholar] [CrossRef]
- Joly, F.; Soulez, G.; Lessard, S.; Kauffmann, C.; Vignon-Clementel, I. A Cohort Longitudinal Study Identifies Morphology and Hemodynamics Predictors of Abdominal Aortic Aneurysm Growth. Ann. Biomed. Eng. 2020, 48, 606–623. [Google Scholar] [CrossRef]
- Joly, F.; Soulez, G.; Garcia, D.; Lessard, S.; Kauffmann, C. Flow Stagnation Volume and Abdominal Aortic Aneurysm Growth: Insights from Patient-Specific Computational Fluid Dynamics of Lagrangian-Coherent Structures. Comput. Biol. Med. 2018, 92, 98–109. [Google Scholar] [CrossRef]
- Capellini, K.; Gasparotti, E.; Cella, U.; Costa, E.; Fanni, B.M.; Groth, C.; Porziani, S.; Biancolini, M.E.; Celi, S. A Novel Formulation for the Study of the Ascending Aortic Fluid Dynamics with in Vivo Data. Med. Eng. Phys. 2022, 91, 68–78. [Google Scholar] [CrossRef]
- Martínez, A.; Hoeijmakers, M.; Geronzi, L.; Morgenthaler, V.; Tomasi, J.; Rochette, M.; Biancolini, M.E. Effect of Turbulence and Viscosity Models on Wall Shear Stress Derived Biomarkers for Aorta Simulations. Comput. Biol. Med. 2023, 167, 107603. [Google Scholar] [CrossRef]
- Stokes, C.; Bonfanti, M.; Li, Z.; Xiong, J.; Chen, D.; Balabani, S.; Díaz-Zuccarini, V. A Novel MRI-Based Data Fusion Methodology for Efficient, Personalised, Compliant Simulations of Aortic Haemodynamics. J. Biomech. 2021, 129, 110793. [Google Scholar] [CrossRef]
- Fonken, J.; Maas, E.; Nievergeld, A.; van Sambeek, M.; van de Vosse, F.; Lopata, R. The Impact of a Limited Field-of-View on Computed Hemodynamics in Abdominal Aortic Aneurysms: Evaluating the Feasibility of Completing Ultrasound Segmentations with Parametric Geometries. Ann. Biomed. Eng. 2023, 51, 1296–1309. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Li, D.; Wu, P.; Li, X.; Zheng, T. A Two-Fluid Blood Stasis Model for False Lumen Thrombosis after Type B Dissection Repair. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 1499–1508. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Xiang, G.; Du, G.; Li, X.; Wu, P.; Du, X. A Hemodynamic Analysis of Fenestrated Physician-Modified Endograft Repair for Complicated Aortic Dissections Involving the Visceral Arteries. Comput. Methods Programs Biomed. 2023, 242, 107785. [Google Scholar] [CrossRef] [PubMed]
- Stokes, C.; Haupt, F.; Becker, D.; Muthurangu, V.; von Tengg-Kobligk, H.; Balabani, S.; Díaz-Zuccarini, V. The Influence of Minor Aortic Branches in Patient-Specific Flow Simulations of Type-B Aortic Dissection. Ann. Biomed. Eng. 2023, 51, 1627–1644. [Google Scholar] [CrossRef]
- Kandail, H.; Hamady, M.; Xu, X.Y. Effect of a Flared Renal Stent on the Performance of Fenestrated Stent-Grafts at Rest and Exercise Conditions. J. Endovasc. Ther. 2016, 23, 809–820. [Google Scholar] [CrossRef]
- Xu, H.; Piccinelli, M.; Leshnower, B.G.; Lefieux, A.; Taylor, W.R.; Veneziani, A. Coupled Morphological–Hemodynamic Computational Analysis of Type B Aortic Dissection: A Longitudinal Study. Ann. Biomed. Eng. 2018, 46, 927–939. [Google Scholar] [CrossRef]
- Pant, S.; Fabrèges, B.; Gerbeau, J.F.; Vignon-Clementel, I.E. A Methodological Paradigm for Patient-Specific Multi-Scale CFD Simulations: From Clinical Measurements to Parameter Estimates for Individual Analysis. Int. J. Numer. Method. Biomed. Eng. 2014, 30, 1614–1648. [Google Scholar] [CrossRef]
- Spilker, R.L.; Taylor, C.A. Tuning Multidomain Hemodynamic Simulations to Match Physiological Measurements. Ann. Biomed. Eng. 2010, 38, 2635–2648. [Google Scholar] [CrossRef]
- Di Achille, P.; Tellides, G.; Humphrey, J.D. Hemodynamics-Driven Deposition of Intraluminal Thrombus in Abdominal Aortic Aneurysms. Int. J. Numer. Method. Biomed. Eng. 2017, 33, e2828. [Google Scholar] [CrossRef]
- Kelsey, L.J.; Powell, J.T.; Norman, P.E.; Miller, K.; Doyle, B.J. A Comparison of Hemodynamic Metrics and Intraluminal Thrombus Burden in a Common Iliac Artery Aneurysm. Int. J. Numer. Method. Biomed. Eng. 2017, 33, e2821. [Google Scholar] [CrossRef]
- Feher, J. Multiscale, Multiphysics and Reduced Order Modelling Techniques for Hemodynamics. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2019. [Google Scholar]
- Schenkel, T.; Halliday, I. Continuum Scale Non Newtonian Particle Transport Model for Hæmorheology. Mathematics 2021, 9, 2100. [Google Scholar] [CrossRef]
- Saha, S.C.; Francis, I.; Saha, G.; Huang, X.; Molla, M.M. Hemodynamic Insights into Abdominal Aortic Aneurysms: Bridging the Knowledge Gap for Improved Patient Care. Fluids 2024, 9, 50. [Google Scholar] [CrossRef]
- Menichini, C.; Xu, X.Y. Mathematical Modeling of Thrombus Formation in Idealized Models of Aortic Dissection: Initial Findings and Potential Applications. J. Math. Biol. 2016, 73, 1205–1226. [Google Scholar] [CrossRef]
- Wu, J.; Shadden, S.C. Coupled Simulation of Hemodynamics and Vascular Growth and Remodeling in a Subject-Specific Geometry. Ann. Biomed. Eng. 2015, 43, 1543–1554. [Google Scholar] [CrossRef]
- Vignon, I.E.; Taylor, C.A. Outflow Boundary Conditions for One-Dimensional Finite Element Modeling of Blood Flow and Pressure Waves in Arteries. Wave Motion 2004, 39, 361–374. [Google Scholar] [CrossRef]
- Tang, D.; Yang, C.; Zheng, J.; Woodard, P.K.; Saffitz, J.E.; Sicard, G.A.; Pilgram, T.K.; Yuan, C. Quantifying Effects of Plaque Structure and Material Properties on Stress Distributions in Human Atherosclerotic Plaques Using 3D FSI Models. J. Biomech. Eng. 2005, 127, 1185–1194. [Google Scholar] [CrossRef]
- Hinnen, J.W.; Koning, O.H.J.; Visser, M.J.T.; Van Bockel, H.J. Effect of Intraluminal Thrombus on Pressure Transmission in the Abdominal Aortic Aneurysm. J. Vasc. Surg. 2005, 42, 1176–1182. [Google Scholar] [CrossRef]
- Moireau, P.; Bertoglio, C.; Xiao, N.; Figueroa, C.A.; Taylor, C.A.; Chapelle, D.; Gerbeau, J.-F. Sequential Identification of Boundary Support Parameters in a Fluid-Structure Vascular Model Using Patient Image Data. Biomech. Model. Mechanobiol. 2013, 12, 475–496. [Google Scholar] [CrossRef]
- Moireau, P.; Xiao, N.; Astorino, M.; Figueroa, C.A.; Chapelle, D.; Taylor, C.A.; Gerbeau, J.-F. External Tissue Support and Fluid–Structure Simulation in Blood Flows. Biomech. Model. Mechanobiol. 2012, 11, 1–18. [Google Scholar] [CrossRef]
- DA SILVA, M.L.F.; Gonçalves, S.D.F.; Haniel, J.; Lucas, T.C.; Huebner, R. Comparative Study between 1-Way and 2-Way Coupled Fluid-Structure Interaction in Numerical Simulation of Aortic Arch Aneurysms. An. Acad. Bras. Cienc. 2023, 95, e20210859. [Google Scholar] [CrossRef]
- Pinto, S.I.S.; Campos, J.B.L.M. Numerical Study of Wall Shear Stress-Based Descriptors in the Human Left Coronary Artery. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 1443–1455. [Google Scholar] [CrossRef] [PubMed]
- Mutlu, O.; Salman, H.E.; Al-Thani, H.; El-Menyar, A.; Qidwai, U.A.; Yalcin, H.C. How Does Hemodynamics Affect Rupture Tissue Mechanics in Abdominal Aortic Aneurysm: Focus on Wall Shear Stress Derived Parameters, Time-Averaged Wall Shear Stress, Oscillatory Shear Index, Endothelial Cell Activation Potential, and Relative Residence Time. Comput. Biol. Med. 2023, 154, 106609. [Google Scholar] [CrossRef] [PubMed]
- Saqr, K.M.; Rashad, S.; Tupin, S.; Niizuma, K.; Hassan, T.; Tominaga, T.; Ohta, M. What Does Computational Fluid Dynamics Tell Us about Intracranial Aneurysms? A Meta-Analysis and Critical Review. J. Cereb. Blood Flow Metab. 2020, 40, 1021–1039. [Google Scholar] [CrossRef] [PubMed]
- Zambrano, B.A.; Gharahi, H.; Lim, C.Y.; Lee, W.; Baek, S. Association of Vortical Structures and Hemodynamic Parameters for Regional Thrombus Accumulation in Abdominal Aortic Aneurysms. Int. J. Numer. Method. Biomed. Eng. 2022, 38, e3555. [Google Scholar] [CrossRef]
- Epps, B. Review of Vortex Identification Methods. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; AIAA SciTech Forum. American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- Chen, Q.; Zhong, Q.; Qi, M.; Wang, X. Comparison of Vortex Identification Criteria for Planar Velocity Fields in Wall Turbulence. Phys. Fluids 2015, 27, 085101. [Google Scholar] [CrossRef]
- Liu, C.; Gao, Y.; Tian, S.; Dong, X. Rortex—A New Vortex Vector Definition and Vorticity Tensor and Vector Decompositions. Phys. Fluids 2018, 30, 035103. [Google Scholar] [CrossRef]
- Fillinger, M.F.; Marra, S.P.; Raghavan, M.L.; Kennedy, F.E. Prediction of Rupture Risk in Abdominal Aortic Aneurysm during Observation: Wall Stress versus Diameter. J. Vasc. Surg. 2003, 37, 724–732. [Google Scholar] [CrossRef]
- Özcan, C.; Kocatürk, Ö.; Işlak, C.; Öztürk, C. Integrated Particle Image Velocimetry and Fluid–Structure Interaction Analysis for Patient-Specific Abdominal Aortic Aneurysm Studies. Biomed. Eng. Online 2023, 22, 113. [Google Scholar] [CrossRef]
- Rissland, P.; Alemu, Y.; Einav, S.; Ricotta, J.; Bluestein, D. Abdominal Aortic Aneurysm Risk of Rupture: Patient-Specific FSI Simulations Using Anisotropic Model. J. Biomech. Eng. 2009, 131, 031001. [Google Scholar] [CrossRef]
- Wang, X.; Li, X. A Fluid-Structure Interaction-Based Numerical Investigation on the Evolution of Stress, Strength and Rupture Potential of an Abdominal Aortic Aneurysm. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 1032–1039. [Google Scholar] [CrossRef]
- Canchi, T.; Saxena, A.; Ng, E.; Pwee, E.C.; Narayanan, S. Application of Fluid Structure Interaction Methods to Estimate the Mechanics of Rupture in Asian Abdominal Aortic Aneurysms. Bionanoscience 2018, 8, 1035–1044. [Google Scholar] [CrossRef]
- Mesri, Y.; Niazmand, H.; Deyranlou, A. Numerical Study on Fluid-Structure Interaction in a Patient-Specific Abdominal Aortic Aneurysm for Evaluating Wall Heterogeneity and Material Model Effects on Its Rupture. J. Appl. Fluid Mech. 2017, 10, 1699–1709. [Google Scholar] [CrossRef]
- Raghavan, M.; Kratzbergö, J.; Simão Da Silva, E. Heterogeneous, Variable Wall-Thickness Modeling of a Ruptured Abdominal Aortic Aneurysm. In Proceedings of the ASME International Mechanical Engineering Conference, Anaheim, CA, USA, 13–19 November 2004. [Google Scholar]
- Raut, S.S.; Jana, A.; De Oliveira, V.; Muluk, S.C.; Finol, E.A. The Importance of Patient-Specific Regionally Varying Wall Thickness in Abdominal Aortic Aneurysm Biomechanics. J. Biomech. Eng. 2013, 135, 081010. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, A.; Berg, N.; Prahl Wittberg, L. Pulsatile Aortic Blood Flow—A Critical Assessment of Boundary Conditions. J. Eng. Sci. Med. Diagn. Ther. 2021, 4, 011002. [Google Scholar] [CrossRef]
- Varble, N.; Kono, K.; Rajabzadeh-Oghaz, H.; Meng, H. Rupture Resemblance Models May Correlate to Growth Rates of Intracranial Aneurysms: Preliminary Results. World Neurosurg. 2018, 110, e794–e805. [Google Scholar] [CrossRef]
- Varshney, M.; Farooqi, M.H.; Usmani, A.Y. Quantifying Hemodynamics within an Aneurysm Exposed to Prolonged Exercise Levels. Comput. Methods Programs Biomed. 2020, 184, 105124. [Google Scholar] [CrossRef]
- Zhan, J.M.; Lu, T.D.; Yang, Z.Y.; Hu, W.Q.; Su, W. Influence of the Flow Field and Vortex Structure of Patient-Specific Abdominal Aortic Aneurysm with Intraluminal Thrombus on the Arterial Wall. Eng. Appl. Comput. Fluid Mech. 2022, 16, 2100–2122. [Google Scholar] [CrossRef]
- Domingos, P. A Few Useful Things to Know about Machine Learning. Commun. of the ACM. 2012, 55, 78–87. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A Deep Learning Approach to Estimate Stress Distribution: A Fast and Accurate Surrogate of Finite-Element Analysis. J. R. Soc. Interface 2018, 15, 20170844. [Google Scholar] [CrossRef]
- Taye, M.M. Understanding of Machine Learning with Deep Learning: Architectures, Workflow, Applications and Future Directions. Computers 2023, 12, 91. [Google Scholar] [CrossRef]
- Larochelle, H.; Bengio, Y.; Louradour, J.; Ca, L.U. Exploring Strategies for Training Deep Neural Networks Pascal Lamblin. J. Mach. Learn. Res. 2009, 1, 1–40. [Google Scholar]
- O’Shea, K.; Nash, R. An Introduction to Convolutional Neural Networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Basha, S.H.S.; Dubey, S.R.; Pulabaigari, V.; Mukherjee, S. Impact of Fully Connected Layers on Performance of Convolutional Neural Networks for Image Classification. Neurocomputing 2020, 378, 112–119. [Google Scholar] [CrossRef]
- Aloysius, N.; Geetha, M. A Review on Deep Convolutional Neural Networks. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 6–8 April 2017; pp. 588–592. [Google Scholar] [CrossRef]
- Hasan, M.; Ullah, S.; Khan, M.J.; Khurshid, K. Comparative Analysis of SVM, Ann and Cnn for Classifying Vegetation Species Using Hyperspectral Thermal Infrared Data. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives; International Society for Photogrammetry and Remote Sensing: Baton Rouge, LA, USA, 2019; Volume 42, pp. 1861–1868. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6999–7019. [Google Scholar] [CrossRef]
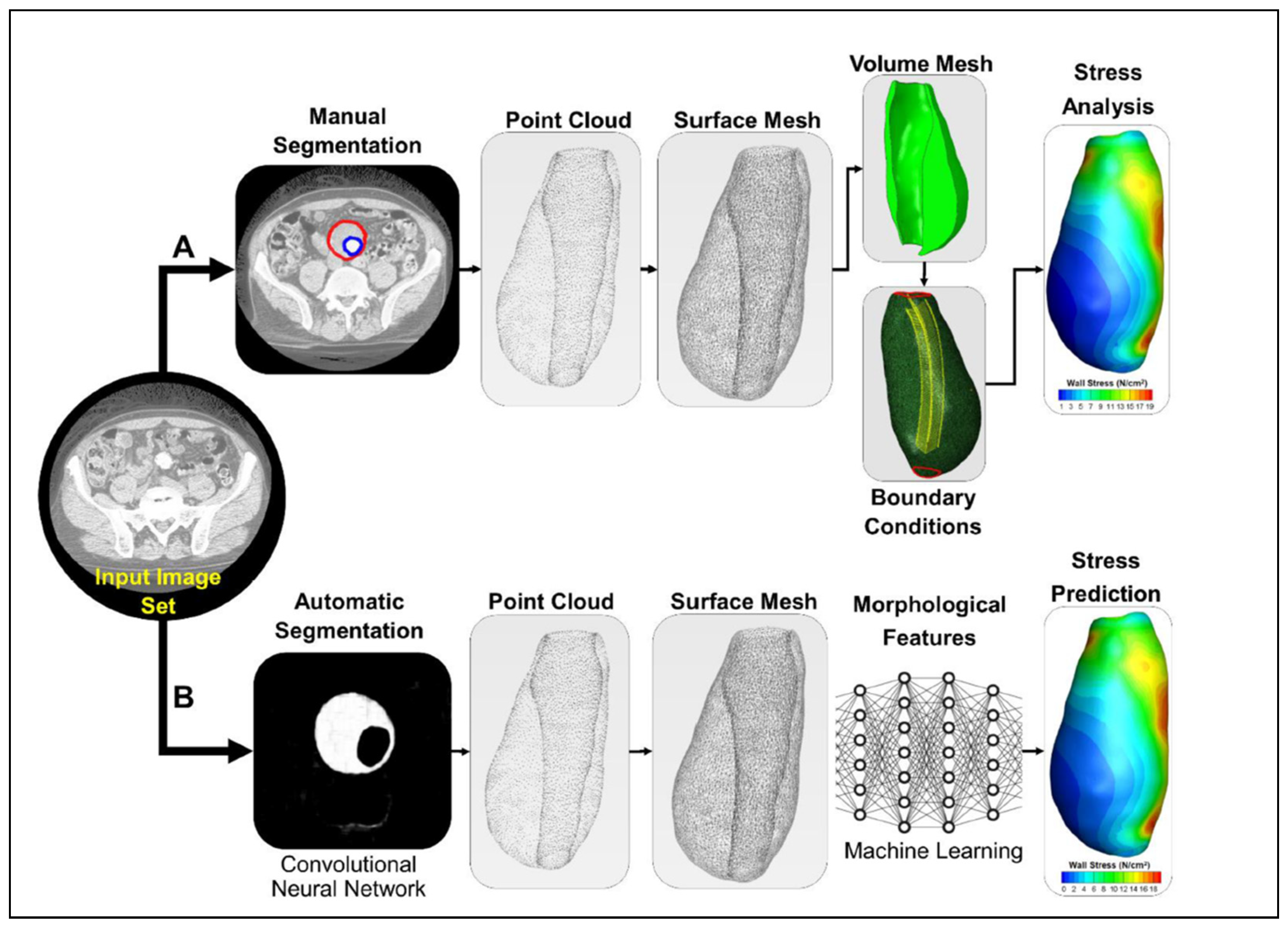
- Lyu, Z.; King, K.; Rezaeitaleshmahalleh, M.; Pienta, D.; Mu, N.; Zhao, C.; Zhou, W.; Jiang, J. Deep-Learning-Based Image Segmentation for Image-Based Computational Hemodynamic Analysis of Abdominal Aortic Aneurysms: A Comparison Study. Biomed. Phys. Eng. Express 2023, 9, 067001. [Google Scholar] [CrossRef]
- López-Linares, K.; Aranjuelo, N.; Kabongo, L.; Maclair, G.; Lete, N.; Ceresa, M.; García-Familiar, A.; Macía, I.; González Ballester, M.A. Fully Automatic Detection and Segmentation of Abdominal Aortic Thrombus in Post-Operative CTA Images Using Deep Convolutional Neural Networks. Med. Image Anal. 2018, 46, 202–214. [Google Scholar] [CrossRef]
- Liang, L.; Mao, W.; Sun, W. A Feasibility Study of Deep Learning for Predicting Hemodynamics of Human Thoracic Aorta. J. Biomech. 2020, 99, 109544. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Martin, C.; Elefteriades, J.A.; Sun, W. A Machine Learning Approach to Investigate the Relationship between Shape Features and Numerically Predicted Risk of Ascending Aortic Aneurysm. Biomech. Model. Mechanobiol. 2017, 16, 1519–1533. [Google Scholar] [CrossRef]
- Rościszewski, P.; Krzywaniak, A.; Iserte, S.; Rojek, K.; Gepner, P. Optimizing Throughput of Seq2Seq Model Training on the IPU Platform for AI-Accelerated CFD Simulations. Future Gener. Comput. Syst. 2023, 147, 149–162. [Google Scholar] [CrossRef]
- Feiger, B.; Gounley, J.; Adler, D.; Leopold, J.A.; Draeger, E.W.; Chaudhury, R.; Ryan, J.; Pathangey, G.; Winarta, K.; Frakes, D.; et al. Accelerating Massively Parallel Hemodynamic Models of Coarctation of the Aorta Using Neural Networks. Sci. Rep. 2020, 10, 9508. [Google Scholar] [CrossRef] [PubMed]
- Hahn, L.D.; Baeumler, K.; Hsiao, A. Artificial Intelligence and Machine Learning in Aortic Disease. Curr. Opin. Cardiol. 2021, 36, 695–703. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Jiang, Z.; Zambrano, B.A.; Jang, Y.; Baek, S.; Yoo, S.; Chang, H.-J. Deep Learning on Multiphysical Features and Hemodynamic Modeling for Abdominal Aortic Aneurysm Growth Prediction. IEEE Trans. Med. Imaging 2023, 42, 196–208. [Google Scholar] [CrossRef] [PubMed]
- Choi, E.; Bahadori, M.T.; Schuetz, A.; Stewart, W.F.; Sun, J. Doctor AI: Predicting Clinical Events via Recurrent Neural Networks. In Proceedings of the Machine Learning for Healthcare Conference, Los Angeles, CA, USA, 19–20 August 2016. [Google Scholar]
- Mushtaq, S.; Singh, O. Convolution Neural Networks for Disease Prediction: Applications and Challenges. Scalable Comput. Pract. Exp. 2024, 25, 615–636. [Google Scholar] [CrossRef]
- Jiang, Z.; Do, H.N.; Choi, J.; Lee, W.; Baek, S. A Deep Learning Approach to Predict Abdominal Aortic Aneurysm Expansion Using Longitudinal Data. Front. Phys. 2020, 7, 235. [Google Scholar] [CrossRef]
- Soudah, E.; Rodriguez, J.F.; Lopez, R. Mechanical Stress in Abdominal Aortic Aneurysms Using Artificial Neural Networks. J. Mech. Med. Biol. 2014, 15, 1550029. [Google Scholar] [CrossRef]
- Thamsen, B.; Yevtushenko, P.; Gundelwein, L.; Lamecker, H.; Kühne, T.; Goubergrits, L. Unsupervised Learning and Statistical Shape Modeling of the Morphometry and Hemodynamics of Coarctation of the Aorta. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2020, Lima, Peru, 4–8 October 2020. [Google Scholar] [CrossRef]
- Jiang, Z.; Choi, J.; Baek, S. Machine Learning Approaches to Surrogate Multifidelity Growth and Remodeling Models for Efficient Abdominal Aortic Aneurysmal Applications. Comput. Biol. Med. 2021, 133, 104394. [Google Scholar] [CrossRef]
- Barrera-Naranjo, A.; Marin-Castrillon, D.M.; Decourselle, T.; Lin, S.; Leclerc, S.; Morgant, M.C.; Bernard, C.; De Oliveira, S.; Boucher, A.; Presles, B.; et al. Segmentation of 4D Flow MRI: Comparison between 3D Deep Learning and Velocity-Based Level Sets. J. Imaging 2023, 9, 123. [Google Scholar] [CrossRef]
- Ferdian, E.; Marlevi, D.; Schollenberger, J.; Aristova, M.; Edelman, E.R.; Schnell, S.; Figueroa, C.A.; Nordsletten, D.A.; Young, A.A. Cerebrovascular Super-Resolution 4D Flow MRI—Sequential Combination of Resolution Enhancement by Deep Learning and Physics-Informed Image Processing to Non-Invasively Quantify Intracranial Velocity, Flow, and Relative Pressure. Med. Image Anal. 2023, 88, 102831. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine Learning and Deep Learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Kodenko, M.R.; Vasilev, Y.A.; Vladzymyrskyy, A.V.; Omelyanskaya, O.V.; Leonov, D.V.; Blokhin, I.A.; Novik, V.P.; Kulberg, N.S.; Samorodov, A.V.; Mokienko, O.A.; et al. Diagnostic Accuracy of AI for Opportunistic Screening of Abdominal Aortic Aneurysm in CT: A Systematic Review and Narrative Synthesis. Diagnostics. 2022, 12, 3197. [Google Scholar] [CrossRef] [PubMed]
- Abbas, G.H.; Khouri, E.; Pouwels, S. Artificial Intelligence-Based Predictive Modeling for Aortic Aneurysms. Cureus 2025, 17, e79662. [Google Scholar] [CrossRef] [PubMed]
- Chung, T.K.; Gueldner, P.H.; Aloziem, O.U.; Liang, N.L.; Vorp, D.A. An Artificial Intelligence Based Abdominal Aortic Aneurysm Prognosis Classifier to Predict Patient Outcomes. Sci. Rep. 2024, 14, 3390. [Google Scholar] [CrossRef] [PubMed]
- Kampaktsis, P.N.; Emfietzoglou, M.; Al Shehhi, A.; Fasoula, N.A.; Bakogiannis, C.; Mouselimis, D.; Tsarouchas, A.; Vassilikos, V.P.; Kallmayer, M.; Eckstein, H.H.; et al. Artificial Intelligence in Atherosclerotic Disease: Applications and Trends. Front. Cardiovasc. Med. 2023, 9, 949454. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, H.; Chen, S.; Li, S.S.; Lu, M.; Alhamoud, K.; Mun, J.; Grau, C.; Jung, M.; Gameiro, R.; et al. Medical Hallucinations in Foundation Models and Their Impact on Healthcare. medRxiv 2025. [Google Scholar] [CrossRef]
- Stergiou, Y.G.; Kanaris, A.G.; Mouza, A.A.; Paras, S.V. Fluid-Structure Interaction in Abdominal Aortic Aneurysms: Effect of Haematocrit. Fluids 2019, 4, 11. [Google Scholar] [CrossRef]
- Shibeshi, S.S.; Collins, W.E. The Rheology of Blood Flow in a Branced Arterial System. Appl. Rheol. 2005, 15, 398–405. [Google Scholar] [CrossRef]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T.M. Mechanisms for Generating Coherent Packets of Hairpin Vortices in Channel Flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the Identification of a Vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]







| Boundary | ||
|---|---|---|
| Inlet | ||
| Outlet | ||
| FSI Interface | ||
| External Wall | ||
| Artery Branch | Flow Split |
|---|---|
| BC Model | Accuracy | Computational Cost | Clinical Relevance |
|---|---|---|---|
| Uniform and Parabolic Inlet Profiles | (L) Does not capture patient-specific flow variations and pulsatile nature of blood flow | (L) Not costly | (L) Simplified models may not reflect realistic hemodynamics |
| Womersley Inlet Profile | (H) Captures pulsatile nature of blood flow | (M) Requires analytical computation of velocity distribution | (M) Common in cardiovascular studies but may not reflect patient-specific hemodynamics |
| 4D Flow MRI-based Inlet | (VH) Patient-specific and time-dependent | (VH) Computationally expensive and data-intensive | (H) Clinically relevant, but limited availability due to imaging constraints |
| Prescribed Pressure Outlet | (M) Assumes static or average pressure conditions | (L) Simple to implement and computationally efficient | (M) Common in AAA studies but does not reflect accurate wave propagation characteristics of vessels |
| 3-Element Windkessel (WK3) Outlet | (H) Models vascular resistance, compliance and pressure reflections | (H) Requires parameter tuning and iterative solutions | (H) Clinically relevant when patient-specific parameters are available |
| FSI with Elastic Wall | (H) Captures wall deformation and ILT effects | (VH) Requires coupling between CFDs and FEA, increasing computational time | (H) Improves stress predictions but difficult to integrate clinically |
| FSI with Hyperelastic and Anisotropic Wall | (VH) Most realistic representation of arterial wall and ILT mechanics | (EH) Very expensive especially for large-scale studies | (H) Needed for advanced biomechanical analysis, but not practical for routine clinical use |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramazanli, B.; Yagmur, O.; Sarioglu, E.C.; Salman, H.E. Modeling Techniques and Boundary Conditions in Abdominal Aortic Aneurysm Analysis: Latest Developments in Simulation and Integration of Machine Learning and Data-Driven Approaches. Bioengineering 2025, 12, 437. https://doi.org/10.3390/bioengineering12050437
Ramazanli B, Yagmur O, Sarioglu EC, Salman HE. Modeling Techniques and Boundary Conditions in Abdominal Aortic Aneurysm Analysis: Latest Developments in Simulation and Integration of Machine Learning and Data-Driven Approaches. Bioengineering. 2025; 12(5):437. https://doi.org/10.3390/bioengineering12050437
Chicago/Turabian StyleRamazanli, Burcu, Oyku Yagmur, Efe Cesur Sarioglu, and Huseyin Enes Salman. 2025. "Modeling Techniques and Boundary Conditions in Abdominal Aortic Aneurysm Analysis: Latest Developments in Simulation and Integration of Machine Learning and Data-Driven Approaches" Bioengineering 12, no. 5: 437. https://doi.org/10.3390/bioengineering12050437
APA StyleRamazanli, B., Yagmur, O., Sarioglu, E. C., & Salman, H. E. (2025). Modeling Techniques and Boundary Conditions in Abdominal Aortic Aneurysm Analysis: Latest Developments in Simulation and Integration of Machine Learning and Data-Driven Approaches. Bioengineering, 12(5), 437. https://doi.org/10.3390/bioengineering12050437







