Darcy–Brinkman Model for Ternary Dusty Nanofluid Flow across Stretching/Shrinking Surface with Suction/Injection

Abstract

Understanding of dusty fluids for different Brinkman numbers in porous media is limited. This study examines the Darcy–Brinkman model for two-dimensional magneto-hydrodynamic fluid flow across permeable stretching/shrinking surfaces with heat transfer. Water was considered as a conventional base fluid in which the copper (Cu), silver (Ag), and titanium dioxide ($Ti{O}_2$) nanoparticles were submerged in a preparation of a ternary dusty nanofluid. The governing nonlinear partial differential equations are converted to ordinary differential equations through suitable similarity conversions. Under radiation and mass transpiration, analytical solutions for stretching sheets/shrinking sheets are obtained. Several parameters are investigated, including the magnetic field, Darcy–Brinkman model, solution domain, and inverse Darcy number. The outcomes of the present article reveal that increasing the Brinkman number and inverse Darcy number decreases the velocity of the fluid and dusty phase. Increasing the magnetic field decreases the momentum of the boundary layer. Ternary dusty nanofluids have significantly improved the heat transmission process for manufacturing with applications in engineering, and biological and physical sciences. The findings of this study demonstrate that the ternary nanofluid phase’s heat and mass transpiration performance is better than the dusty phase’s performance.

1. Introduction

The Darcy–Brinkman model with magneto-hydrodynamics (MHD) has many applications in paint sparing, research on air pollution, capillary blood flow, and vehicle and factory emissions of smoke and other pollutants; dusty fluids contain fine dust particles. The laminar boundary layer flow of an electrically conducting dusty fluid across a stretching/shrinking sheet has drawn the attention of many researchers. For example, Saffaman et al. [1] studied stability solutions of dusty fluid flow. Modeling the flow and heat of a two-phase dusty fluid across deteriorating isothermal boundaries was investigated by Turkyilmazoglu et al. [2]. Farooq et al. [3] investigated the influence of thermal radiation on the laminar fluid flow of dust-containing ternary nanofluid across permeable stretched sheets. Jalil et al. [4] and Datta et al. [5] explored an accurate solution to the dusty fluid flow problems in the MHD boundary layer across a shrunken sheet with fluid flowing across an infinitely flat surface.

Crane et al. [6] studied flow over a stretching sheet. Flow on a continuously stretched sheet with heat transfer was investigated by Carragher et al. [7]. A reduction in temperature over a stretched sheet with constant heat flux was studied by Dutta et al. [8]. In another study, Pradhan et al. [9] investigated the Marangoni convection and radiation effects on ternary nanofluid flow in a permeable media with mass transfer. An investigation on the heat transfer and viscous dissipation over stretched sheets and around the stagnation point was carried out by Aly et al. [10]. Sheu et al. [11] explored a layer of porous material saturated with a nanofluid that exhibited thermal instability.

The Brinkman ratio is a crucial parameter in controlling heat conduction. Increasing the Brinkman parameter causes the temperature to rise because of the slower heat transfer in viscous dissipation. Many researchers have explored the effect of the Brinkman ratio on fluid flow; for example, Pop et al. [12] studied the Brinkman concept for flow across a circular cylinder contained in a permeable material. The thermal conveyance model for sinusoidally oscillating Brinkman-type nanofluids containing carbon nanotubes was examined by Jie et al. [13]. Hsu et al. [14] studied a Brinkman model for spontaneous convection in a permeable material around a vertical flat surface with a semi-infinite height. This work was extended by Sachhin et al. [15] and Adun et al. [16], exploring the Brinkman model’s effect on heat-transfer-enhanced porous stretched sheets with non-Newtonian fluid flow, and they also reviewed the synthesis stability and thermophysical characteristics.

Sarwar et al. [17] studied ternary nanoparticles in a magneto-hydrodynamics non-Newtonian fluid flow for heat and mass transpiration. The effects of radiation on a ternary nanofluid flow in a porous media with heat and mass transfer were examined by Mahabaleshwar et al. [18], while Sahoo et al. [19] and Adnan et al. [20] examined the novel correlation to measure the viscosity of ternary hybrid nanofluid and analyzed the heat transfer efficiency for TNF flow in a radiated channel under various conditions. Nagamgari et al. [21] studied the volume percentage of dusty particles with nanofluid flow in magneto-hydrodynamics across a stretched surface, with Sneha et al. [22] carrying out an investigation on the Darcy–Brinkman equation for heat transport and mass transpiration in a hybrid dusty nanofluid flow, while thermal management of curved solid conductive panels linked with various nanofluid cooling methods was investigated by Selimefendigil et al. [23].

Hayat et al. [24] and Roy et al. [25] studied copper and silver water nanofluids using nonlinear thermal radiation and magneto-hydrodynamics dusty hybrid nanofluid flows and heat transmission across a contracting sheet. Furthermore, the dynamics of a heated convective surface with magnetic flux density and partial slip in asymmetric flow over a stretched sheet was examined by Animasun et al. [26]. Ariel et al. [27] and Jalili et al. [28] investigated the heat transmission in a polar system in a cylinder-shaped magnetic field. Nawaz et al. [29] studied the asymmetric MHD flow of a Casson fluid with varying thermal conductivity. Following the above work, Sachhin et al. [30] investigated the analytical solution of a Casson fluid flow across a stretched surface. Finally, several other studies regarding stretching surfaces under thermal radiation and mass transfer have been published [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46].

Although the extrusion and cooling of dusty-fluid processes have various practical and scientific applications, the mass transpiration in the boundary layer of ternary dusty nanofluids has yet to be adequately studied as an analytical technique applicable to permeable media. The originality of this investigation concerns the influence of radiation and a heat source/sink on ternary dusty nanofluid water flow with heat transfer across permeable stretching/shrinking surfaces. The motivation is to combine dusty particles with the ternary nanofluid in the framework of momentum and temperature equations to derive an analytic solution. The analytic solution is important for supporting nanofluid computational research [47,48,49,50,51]. The non-dimensional governing equations are obtained using suitable similarity transformations over various boundaries [52,53,54]. The results of the current study impact several scientific and industrial applications.

Considering the findings and research gaps identified by previous studies and the associated impact on applications, the magnetic field and the Darcy–Brinkman model on ternary dusty nanofluid flow across permeable stretching/shrinking surfaces are investigated. The results of this study contribute to improving the understanding of ternary nanoliquids under MHD and different Brinkman ratios. A similarity transformation is used to reduce the governing equations of the problem into a system of nonlinear ordinary differential equations. The paper presents the analytical solution of the momentum equations and discusses the results of the porous medium, MHD, and volume fraction. The findings of this paper are applicable in the development of efficient fuel cells and the polymer industry, concerning stretching/shrinking sheets.

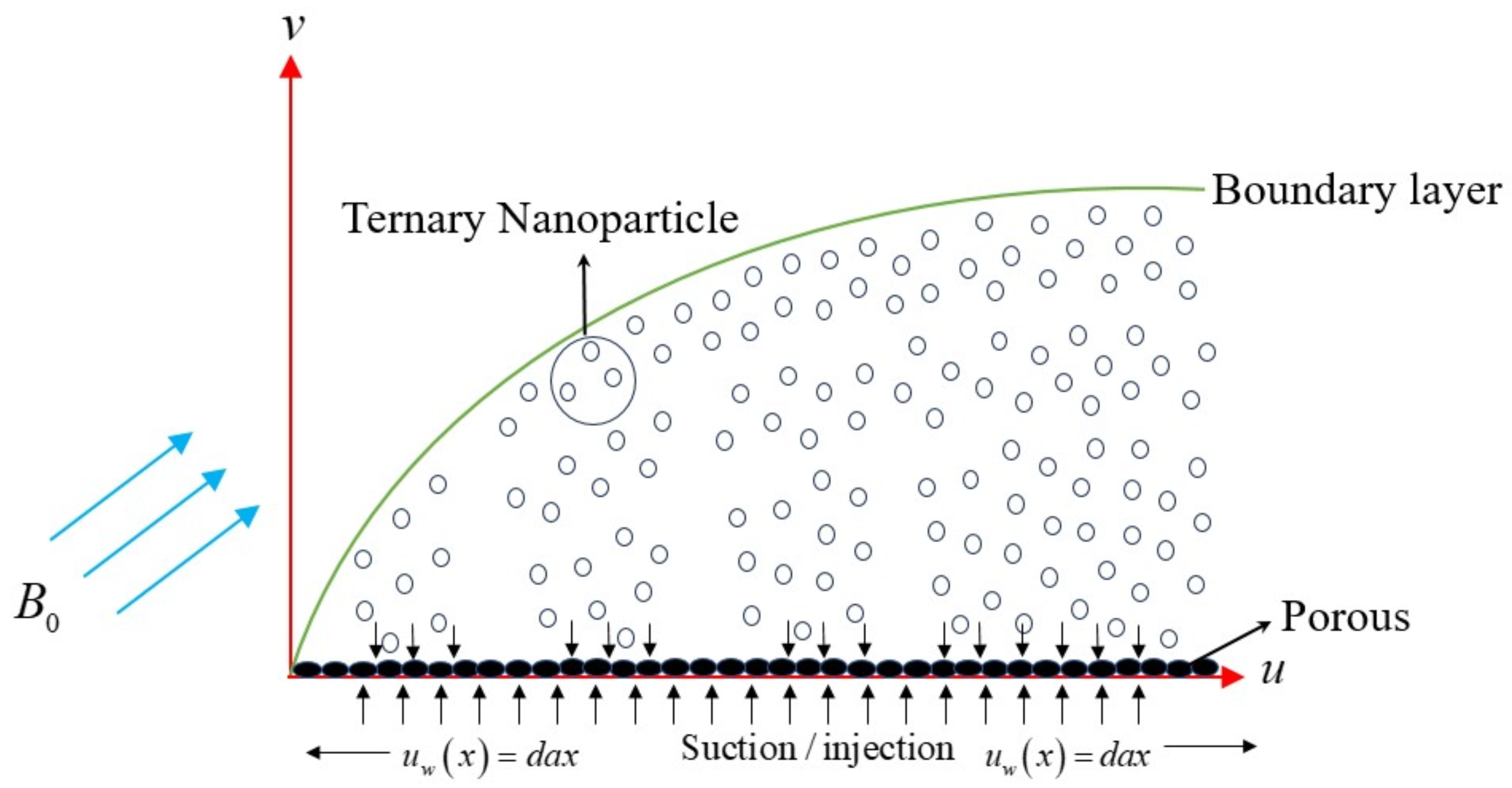
2. Mathematical Formulation

Consider the steady two-dimensional, incompressible, viscous, laminar flow of a ternary dusty nanofluid across a permeable stretching/shrinking surface. The surface is parallel to the x-axis and normal to the y-axis (Figure 1); the stretching/shrinking sheet is parallel to the y-axis, and the momentum of the fluid flow is assumed as $U_w\left(x\right)=dax$. The added ternary nanoparticles are copper (Cu), silver (Ag), and titanium dioxide $\left(Ti{O}_2\right)$, with water as the base fluid.

Assumptions in the Mathematical Equations Describing the Physical Model

• The fluid phase and nanoparticles are in the thermal equilibrium state.
• Water is considered a conventional base fluid in which the copper (Cu), silver (Ag), and titanium dioxide ($Ti{O}_2$) nanoparticles are submerged in the preparation of a ternary dusty nanofluid.
• An inclined magnetic field is introduced.
• No chemical reactions take place in the fluid layer.
• There is negligible viscous dissipation.
• The nanofluid is incompressible; Newtonian and laminar flow are considered.
• The Darcy–Brinkman model is examined.
• The fluid flow is generated by stretching/shrinking the sheet, and there is no pressure gradient affecting the fluid, i.e., $\nabla p=0$.
• Finally, steady flow is considered, i.e., $\frac{\mathsf{\partial }u}{\mathsf{\partial }t}=0$.
• A stretching velocity, $u=dax$, is also introduced.

A. 

Governing equations

The boundary layer flow [2,3,22] is described by the following equations:

a. 

Fluid phase:

• Continuity equation:

  $$\frac{\mathsf{\partial }u}{\mathsf{\partial }x}+\frac{\mathsf{\partial }v}{\mathsf{\partial }y}=0,$$

  (1)
• Momentum equation:

  $$\begin{array}{c}u\frac{\mathsf{\partial }u}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }u}{\mathsf{\partial }y}=\frac{{\mu }_{eff}}{{\rho }_{tnf}}\frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{y}^2}+\frac{L_{1}N}{{\rho }_{tnf}}\left(u_p-u\right)-\frac{{\sigma }_{tnf}}{{\rho }_{tnf}}Si{n}^2\left(\tau \right)B_0^{2}u\hfill \\ -\frac{{\mu }_{tnf}}{k_1{\rho }_{tnf}}u,\hfill \end{array}$$

  (2)
• Temperature equation:

  $$\begin{array}{c}u\frac{\mathsf{\partial }T}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }T}{\mathsf{\partial }y}=\frac{{\kappa }_{tnf}}{{\left(\rho C_p\right)}_{tnf}}\frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{y}^2}+\frac{{\rho }_p{c}_m}{{\left(\rho C_p\right)}_{tnf}{\tau }_T}\left(T_p-T\right)\hfill \\ +\frac{{\rho }_p}{{\left(\rho C_p\right)}_{tnf}{\tau }_v}{\left(u_p-u\right)}^2+\frac{Q_0\left(T-T_{\infty }\right)}{{\left(\rho C_p\right)}_{tnf}}-\frac{1}{{\left(\rho C_p\right)}_{tnf}}\frac{\mathsf{\partial }{q}_r}{\mathsf{\partial }y},\hfill \end{array}$$

  (3)

b. 

Dusty phase:

• Continuity equation:

  $$\frac{\mathsf{\partial }{u}_p}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{v}_p}{\mathsf{\partial }y}=0,$$

  (4)
• Momentum equation:

  $$u_p\frac{\mathsf{\partial }{u}_p}{\mathsf{\partial }x}+v_p\frac{\mathsf{\partial }{u}_p}{\mathsf{\partial }y}=\frac{L_1}{m}\left(u-u_p\right),$$

  (5)
• Temperature equation:

  $$u_p\frac{\mathsf{\partial }{T}_p}{\mathsf{\partial }x}+v_p\frac{\mathsf{\partial }{T}_p}{\mathsf{\partial }y}=-\frac{{\rho }_p{c}_m}{{\tau }_T}\left(T_p-T\right).$$

  (6)

The imposed boundary conditions (BCs) include the fluid and dusty phases [2,22], given as

$$u=u_w\left(x\right)=ax,\mathrm{v}={\mathrm{v}}_w,T=T_w\left(x\right)=T_{\infty }+b{x}^2,\mathrm{at}y=0,$$

(7)

$$u\to 0,{\mathrm{v}}_p\to \mathrm{v},T\to T_{\infty },T_p\to T_{\infty },\mathrm{as}y\to \infty ,$$

(8)

Similar to previous studies [2], here, $u,v,u_p$, and $v_p$ are the velocity components of a fluid and dusty fluid phase along the x- and y-directions, respectively; the dusty and fluid phase temperatures are Tp and T; $\mu$ is the dynamic viscosity; $\rho$ is the effective density; $\kappa$ is the thermal conductivity; b is a parameter that is b > 0 for heated and b < 0 for cooled plate; $\sigma$ is the electrical conductivity; $C_p$ and $C_m$ are the specific heat coefficients; ${\tau }_T$ is the heat equilibrium time; ${\mathit{L}}_1$ is the Stokes drag/resistance term; $\nu$ is the kinematic viscosity of nanoparticles N; $k_1$ is the flow permeability; and ${\tau }_v=\frac{m}{L_1}$ is a relaxation time parameter, where m denotes the mass of dusty particles [2].

B. 

Similarity variables introduced to convert governing PDEs to ODEs [2,22]

$$\left.\begin{array}{c}u=ax{f}_{\eta }\left(\eta \right),v=-\sqrt{a{\nu }_f}f\left(\eta \right),\eta =\sqrt{\frac{a}{{\nu }_f}}y,\hfill \\ u_p=ax{F}_{\eta }\left(\eta \right),{\nu }_p=\sqrt{a{\nu }_f}F\left(\eta \right),\hfill \\ \theta =\frac{T-T_{\infty }}{T_w-T_{\infty }},\mathrm{\Phi }=\frac{Tp-T_{\infty }}{T_w-T_{\infty }},\hfill \end{array}\right\}$$

(9)

where F and f denote stream functions of the dusty and fluid phases, $\eta$ denotes the similarity variable, a > 0 is a constant, and the wall mass transfer velocity is given by $v_w=-\sqrt{{\nu }_{f}a}S$. We employ the Rosseland approximation for the value of the radiative heat flux, given by [33]

$$q_r=-\frac{4\sigma \ast }{3k\ast }\frac{\mathsf{\partial }{T}^4}{\mathsf{\partial }y},$$

(10)

where ${\sigma }^{\ast }$ denotes the Stefan–Boltzmann constant, and ${\kappa }^{\ast }$ is the mean absorption. We expand the above equation by a Taylor expansion, neglecting the higher-order terms, as a linear function of temperature [33]:

$$T^4\cong 4T_{\infty }^3-3T_{\infty }^4.$$

(11)

Equations (9) and (10) yield

$$\frac{\mathsf{\partial }{q}_r}{\mathsf{\partial }y}=-\frac{16\sigma \ast T_{\infty }^3}{3k\ast }\frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{y}^2}.$$

(12)

Combining Equations (11) and (3) gives

$$\begin{array}{c}u\frac{\mathsf{\partial }T}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }T}{\mathsf{\partial }y}=\frac{{\kappa }_{tnf}}{{\left(\rho C_p\right)}_{tnf}}\frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{y}^2}+\frac{{\rho }_p{c}_m}{{\left(\rho C_p\right)}_{tnf}{\tau }_T}\hfill \\ \left(T_p-T\right)+\frac{{\rho }_p}{{\left(\rho C_p\right)}_{tnf}{\tau }_v}{\left(u_p-u\right)}^2+\frac{Q_0\left(T-T_{\infty }\right)}{{\left(\rho C_p\right)}_{tnf}}\hfill \\ -\frac{1}{{\left(\rho C_p\right)}_{tnf}}\frac{16\sigma \ast T_{\infty }^3}{3k\ast }\frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{y}^2}.\hfill \end{array}$$

(13)

• Using the similarity transformation, Equations (2), (3), (5), and (6) can be written as

  c. 

  Fluid phase:

  $$\begin{array}{c}\frac{\mathrm{\Lambda }}{\mathit{\varphi }}{f}_{\eta \eta \eta }\left(\eta \right)+A_2\left[f_{\eta }{\left(\eta \right)}^2+f\left(\eta \right)f_{\eta \eta }\left(\eta \right)\right]\hfill \\ +l\beta \left[F_{\eta }\left(\eta \right)-f_{\eta }\left(\eta \right)\right]-\left(A_{1}D{a}^{-1}+A_{3}Si{n}^2\left(\tau \right)M\right)f_{\eta }\left(\eta \right)=0.\hfill \end{array}$$

  (14)

  $$\begin{array}{c}\left(\frac{A_4}{\mathrm{\varphi }}+Nr\right){\theta }_{\eta \eta }\left(\eta \right)+Pr{A}_5\left[\begin{array}{c}f\left(\eta \right){\theta }_{\eta }\left(\eta \right)\hfill \\ -2f_{\eta }\left(\eta \right)\theta \left(\eta \right)\hfill \end{array}\right]+\hfill \\ l{\beta }_T\gamma \left[\mathrm{\Phi }\left(\eta \right)-\theta \left(\eta \right)\right]+l{\beta }_T\gamma PrEc{\left[F_{\eta }\left(\eta \right)-f_{\eta }\left(\eta \right)\right]}^2\hfill \\ +\frac{Ni}{A_5}\theta \left(\eta \right)=0.\hfill \end{array}$$

  (15)

  d. 

  Dusty phase:

  $$F_{\eta }{\left(\eta \right)}^2-F\left(\eta \right)F_{\eta \eta }\left(\eta \right)+\beta \left[F_{\eta }\left(\eta \right)-f_{\eta }\left(\eta \right)\right]=0,$$

  (16)

  $$2F_{\eta }\left(\eta \right)\mathrm{\Phi }\left(\eta \right)-F\left(\eta \right){\mathrm{\Phi }}_{\eta }\left(\eta \right)+{\beta }_T\left[\mathrm{\Phi }\left(\eta \right)-\theta \left(\eta \right)\right]=0.$$

  (17)

The modified boundary conditions are [2,3]

$$f=S,f_{\eta }\left(\eta \right)=d,\theta \left(\eta \right)=1,\mathrm{at}\eta =0,$$

(18)

$$\begin{array}{c}{f}_{\eta }\left(\eta \right)\to 0,F_{\eta }\left(\eta \right)\to 0,F=f,\hfill \\ \theta \to 0,\mathrm{\Phi }\to 0,\mathrm{as}\eta \to \infty ,\hfill \end{array}$$

(19)

where $A_1=\frac{{\mu }_{tnf}}{{\mu }_f}$, $A_2=\frac{{\rho }_{tnf}}{{\rho }_f}$, $A_3=\frac{{\sigma }_{tnf}}{{\sigma }_f}$, $A_4=\frac{{\kappa }_{tnf}}{{\kappa }_f}$, and $A_5=\frac{{\left(\rho C_p\right)}_{tnf}}{{\left(\rho C_p\right)}_f}$ are constant terms; $l=\frac{{\rho }_p}{\rho }$ denotes the mass number of dust particles; ${\rho }_p=Nm$ denotes the particle-phase density, fluid–particle interaction parameter denoted as $\beta =\frac{1}{a{\tau }_v}$. The Prandtl number is given by $Pr=\frac{\mu C_p}{k_f}$. S is the mass suction/injection parameter; the particular heat coefficient is $\gamma =\frac{c_m}{c_p}$; the temperature of the fluid interaction component is ${\beta }_T=\frac{1}{a{\tau }_T}$; the Eckert number is denoted as $Ec=\frac{a^2}{b{C}_p}$; the inverse Darcy number is $D{a}^{-1}=\frac{{\nu }_f}{k_{1}a}$; the radiation parameter is $Nr=\frac{16\sigma \ast T_{\infty }^3}{3k\ast {\kappa }_f}$; and the heat source/sink parameter is given by $Ni=\frac{Q_0}{a{\rho }_f}$, where d denotes a stretching/shrinking parameter.

3. Analytic Solution for Velocity Equations for Fluid- and Dusty-Phase Flow

Using the above boundary conditions, the exponential forms of solutions lead to exact solutions to Equations (13) and (14) as follows [2,3]:

$$\begin{array}{c}f\left(\eta \right)=S+d\left[\frac{1-exp\left(-\lambda \eta \right)}{\lambda }\right]\hfill \\ F\left(\eta \right)=S+d\left[\frac{1-\alpha exp\left(-\lambda \eta \right)}{\lambda }\right]\hfill \end{array}$$

(20)

where $\lambda >0$, and $\alpha$ denotes the stretching speed of dust particles. Differentiating Equation (18) for the fluid phase, Equation (13), yields

$$\frac{\mathrm{\Lambda }}{\mathit{\varphi }}{\lambda }^2+A_{2}S\lambda +A_{2}d+l\beta \left(\alpha -1\right)-A_{1}D{a}^{-1}-A_{3}Si{n}^2\left(\tau \right)M=0.$$

(21)

The momentum equation for the dusty phase is

$$\beta -S\alpha \lambda -d\alpha -\beta \alpha =0.$$

(22)

Solving Equation (22) gives

$$\alpha =\frac{\beta }{\beta +S\lambda +d},$$

(23)

we substitute Equation (21) into Equation (19); the cubic equation is obtained:

$${\xi }_1{\lambda }^3+{\xi }_2{\lambda }^2+{\xi }_3\lambda +{\xi }_4=0,$$

(24)

The roots of the above algebraic equation are

$$\begin{array}{c}{\lambda }_1=\frac{-\frac{{\xi }_2}{3{\xi }_1}-\left(2^{1/3}\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)\right)}{3{\xi }_1{\left(z+\sqrt{4{\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)}^3+{\left(z\right)}^2}\right)}^{1/3}}\hfill \\ +\frac{1}{32^{1/3}{\xi }_1}{\left(z+\sqrt{4{\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)}^3+{\left(z\right)}^2}\right)}^{1/3}\hfill \end{array},$$

(25)

$$\begin{array}{c}{\lambda }_2=\frac{-\frac{{\xi }_2}{3{\xi }_1}+\left((1+i\sqrt{3})\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)\right)}{3{\xi }_1{2}^{1/3}{\left(z+\sqrt{4{\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)}^3+{\left(a\right)}^2}\right)}^{1/3}}\hfill \\ -\frac{1}{6{\xi }_1{2}^{1/3}}(1+i\sqrt{3}){\left(z+\sqrt{4{\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)}^3+{\left(z\right)}^2}\right)}^{1/3}\hfill \end{array},$$

(26)

$$\begin{array}{c}{\lambda }_3=\frac{-\frac{{\xi }_2}{3{\xi }_1}-\left((1+i\sqrt{3})\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)\right)}{3{\xi }_1{2}^{1/3}{\left(z+\sqrt{4{\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)}^3+{\left(a\right)}^2}\right)}^{1/3}}\hfill \\ -\frac{1}{6{\xi }_1{2}^{1/3}}(1-i\sqrt{3}){\left(z+\sqrt{4{\left(-{\xi }_2^2+3{\xi }_1{\xi }_3\right)}^3+{\left(z\right)}^2}\right)}^{1/3}\hfill \end{array},$$

(27)

for simplification $\left(-2{\xi }_2^3+9{\xi }_1{\xi }_2{\xi }_3-27{\xi }_1^2{\xi }_4\right)$ is defined by z, where

$$\left.\begin{array}{c}{\xi }_1=\frac{\mathrm{\Lambda }}{\mathit{\varphi }}S,\hfill \\ {\xi }_2=\left(\frac{\mathrm{\Lambda }}{\mathit{\varphi }}d+\frac{\mathrm{\Lambda }}{\mathit{\varphi }}\beta +A_2{S}^2\right),\hfill \\ {\xi }_3=\left(\begin{array}{c}{A}_{2}Sd+A_{2}S\beta +A_{2}Sd\hfill \\ -l\beta S-A_{1}D{a}^{-1}S-A_{3}MSi{n}^2\left(\tau \right)S\hfill \end{array}\right),\hfill \\ {\xi }_4=\left(\begin{array}{c}{A}_2{d}^2+A_{2}d\beta -l\beta d-A_{1}D{a}^{-1}d\hfill \\ -A_{1}D{a}^{-1}\beta -A_{3}MSi{n}^2\left(\tau \right)d-A_{3}MSi{n}^2\left(\tau \right)\beta \hfill \end{array}\right),\hfill \end{array}\right\}.$$

(28)

The wall shear can be calculated from Equation (20) with the values of $\lambda$ and $\alpha$ [2,3]:

$$\left.{\left(\frac{d^{2}f}{d{\eta }^2}\right)}_{\eta =0}=-d\lambda \mathrm{and}{\left(\frac{d^{2}F}{d{\eta }^2}\right)}_{\eta =0}=-\alpha d\lambda .\right\}$$

(29)

4. Analytic Solution for Temperature Equations for Fluid- and Dusty-Phase Flow

By using boundary conditions, we can write specific forms for solutions of the fluid and dusty phases of temperature, Equations (15) and (16), as follows [2,3]:

$$\left.\theta \left(\eta \right)=exp\left[-2\lambda \eta \right]\mathrm{and}\mathrm{\Phi }\left(\eta \right)=\phi exp\left[-2\lambda \eta \right],\right\}$$

(30)

differentiating the above equations and substituting into the energy Equations (15) and (16) leads to the polynomial equations

$$\begin{array}{c}2dPr{A}_5+2\left[PrS{A}_5-2\lambda \left(\frac{A_4}{\mathit{\varphi }}+Nr\right)\right]\lambda \hfill \\ -d^{2}Ecl{\left(\alpha -1\right)}^2-l{\beta }_T\gamma Pr\left(\phi -1\right)-\frac{Ni}{A_4}=0\hfill \end{array},$$

(31)

$$2d\phi +2S\phi \lambda +{\beta }_T\left(\phi -1\right)=0.$$

(32)

After simplifying Equation (29), the following value of $\phi$ is obtained:

$$\phi =\frac{{\beta }_T}{{\beta }_T+\left(2d+2S\lambda \right)}.$$

(33)

The efficient heat exchange of the fluid and dusty phase are obtained as follows as [2,3]

$${\left(\frac{d\theta }{d\eta }\right)}_{\eta =0}=2\lambda ,\mathrm{and}{\left(\frac{d\mathrm{\Phi }}{d\eta }\right)}_{\eta =0}=-2\phi \lambda .$$

(34)

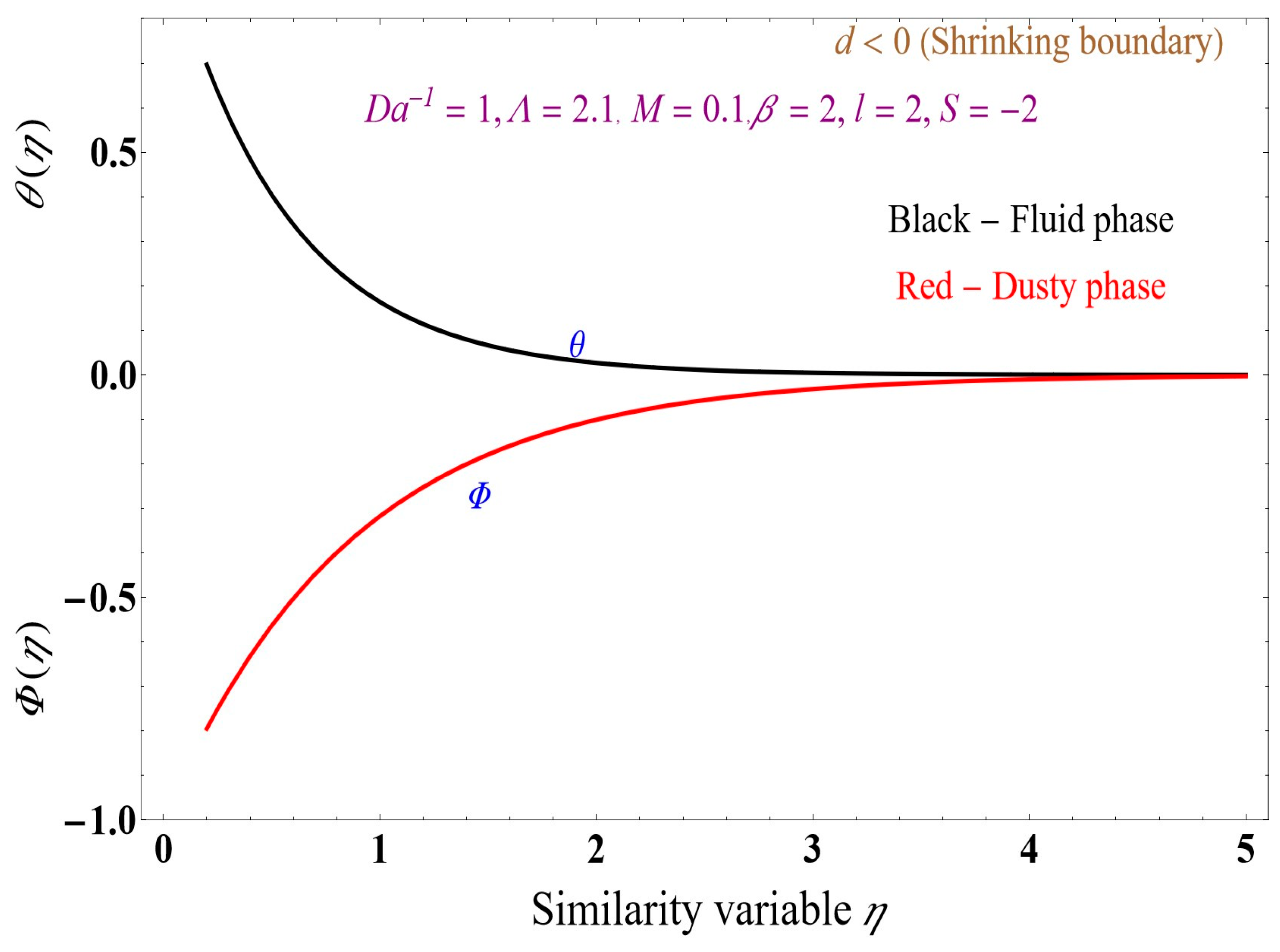
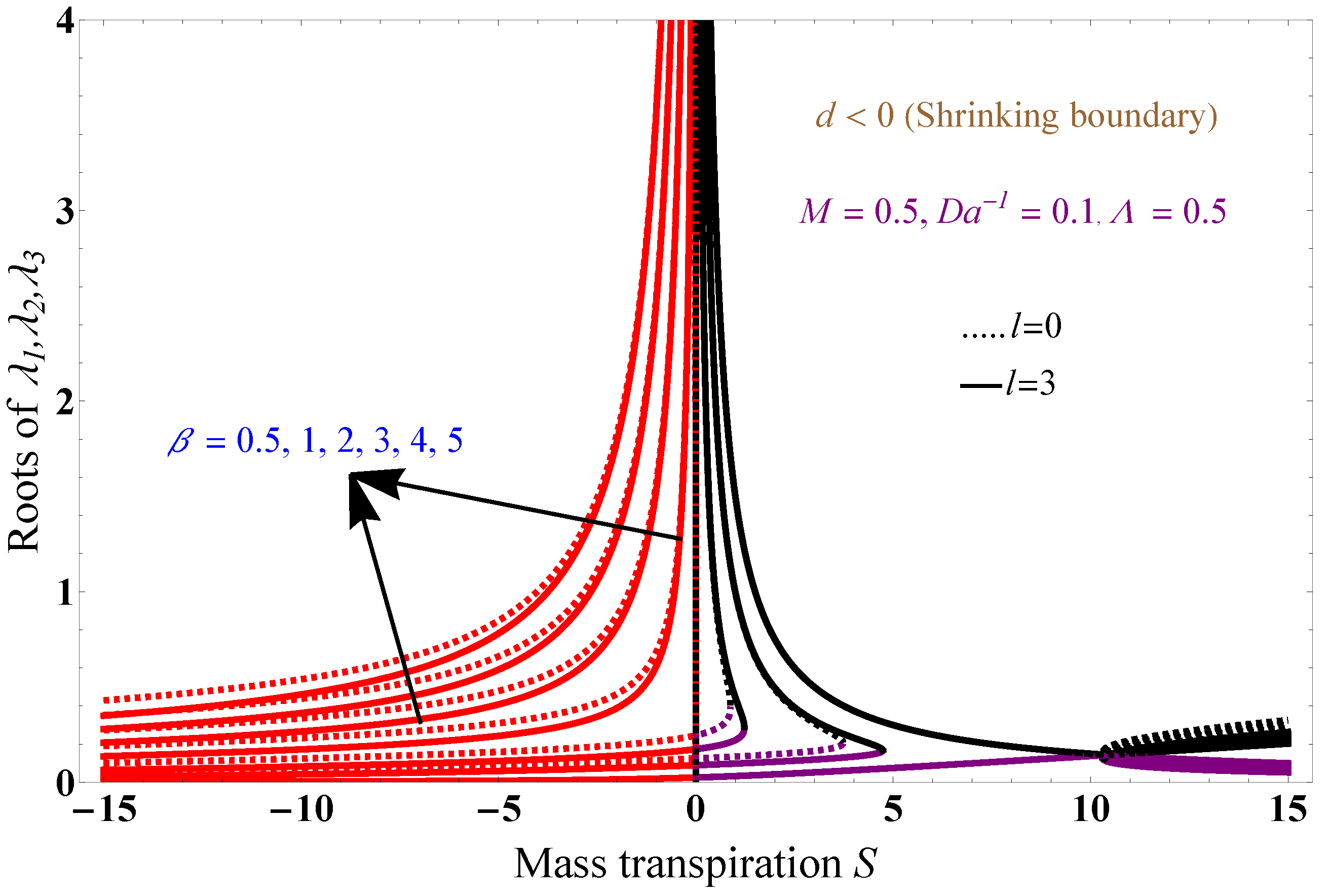
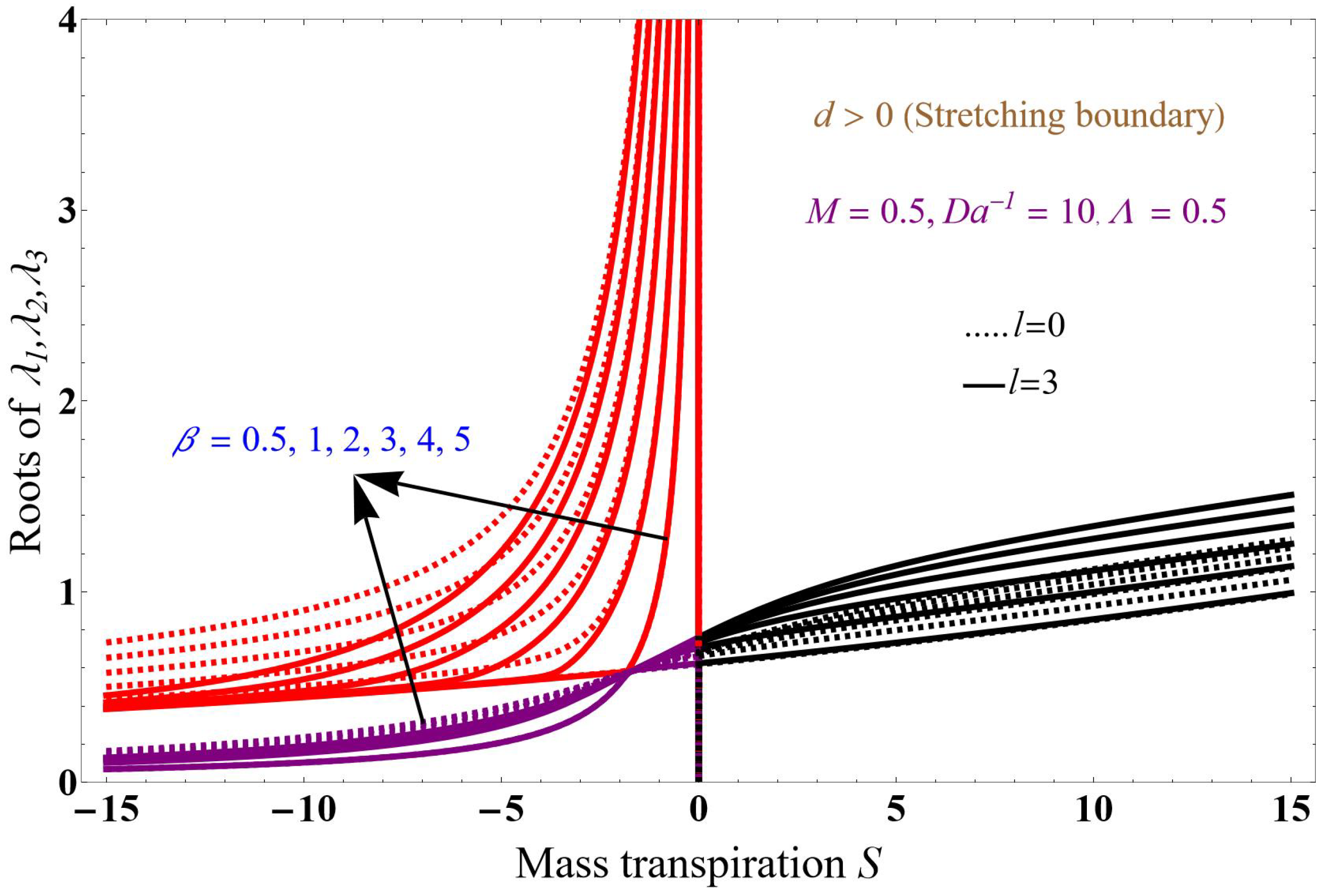
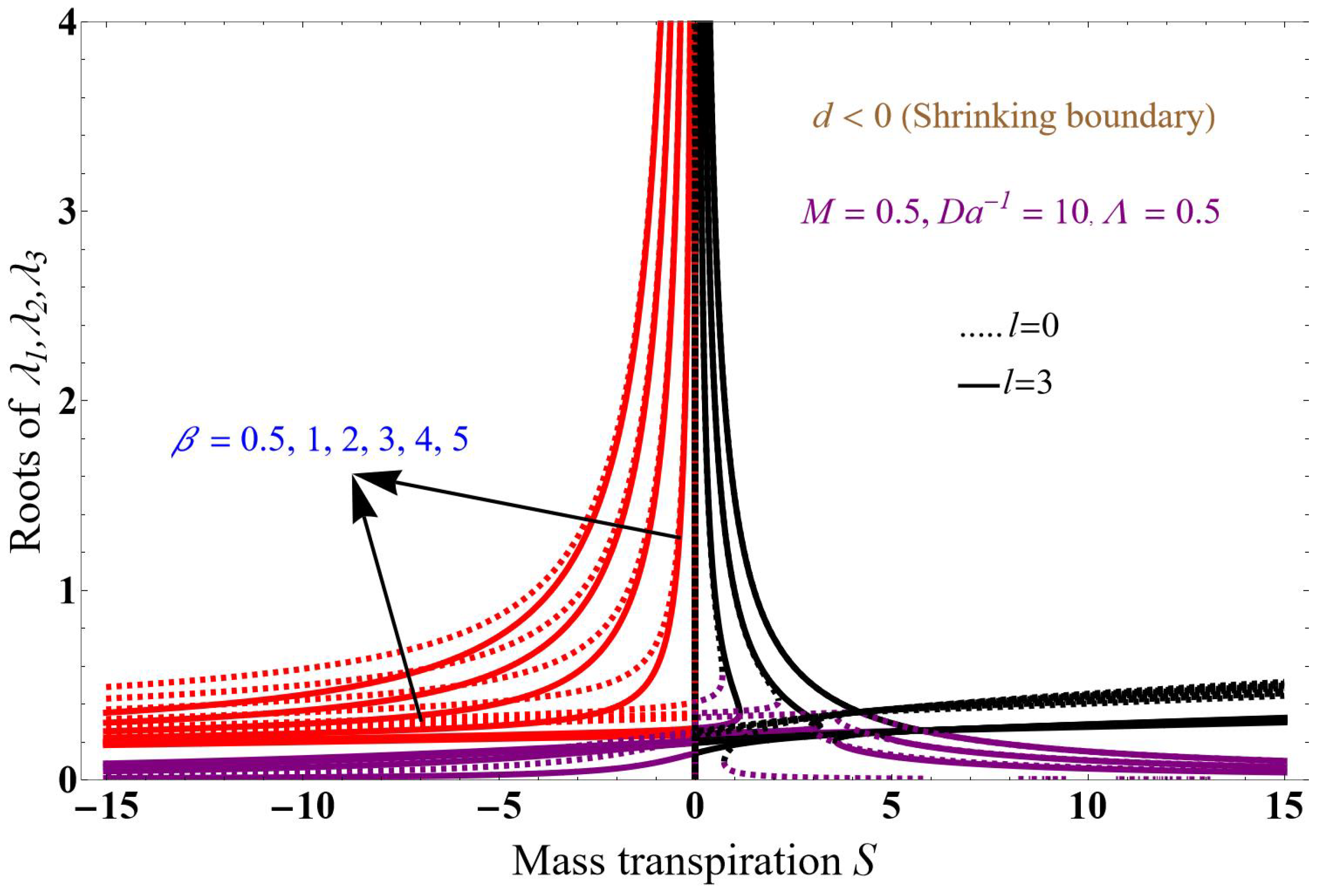
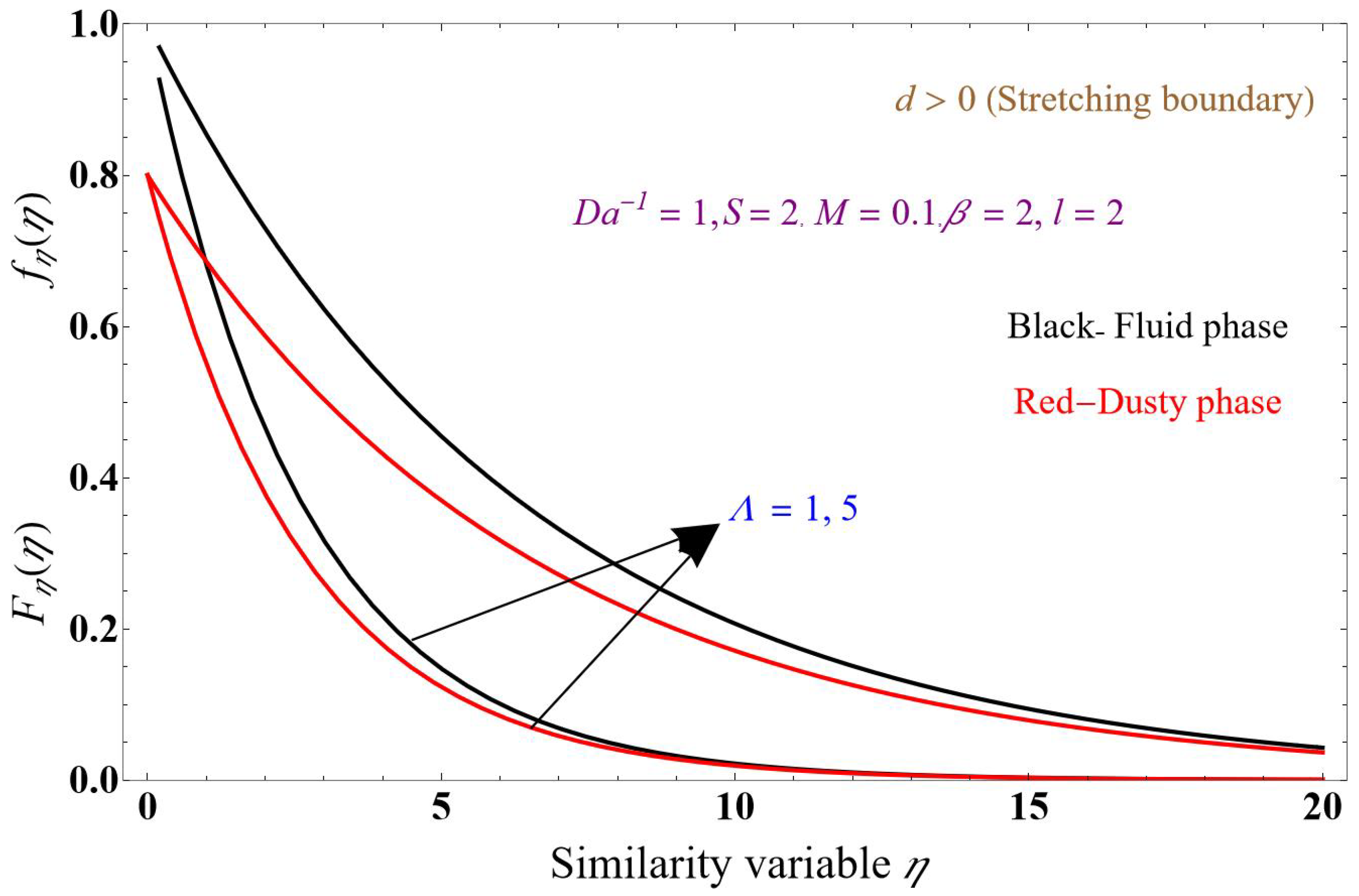
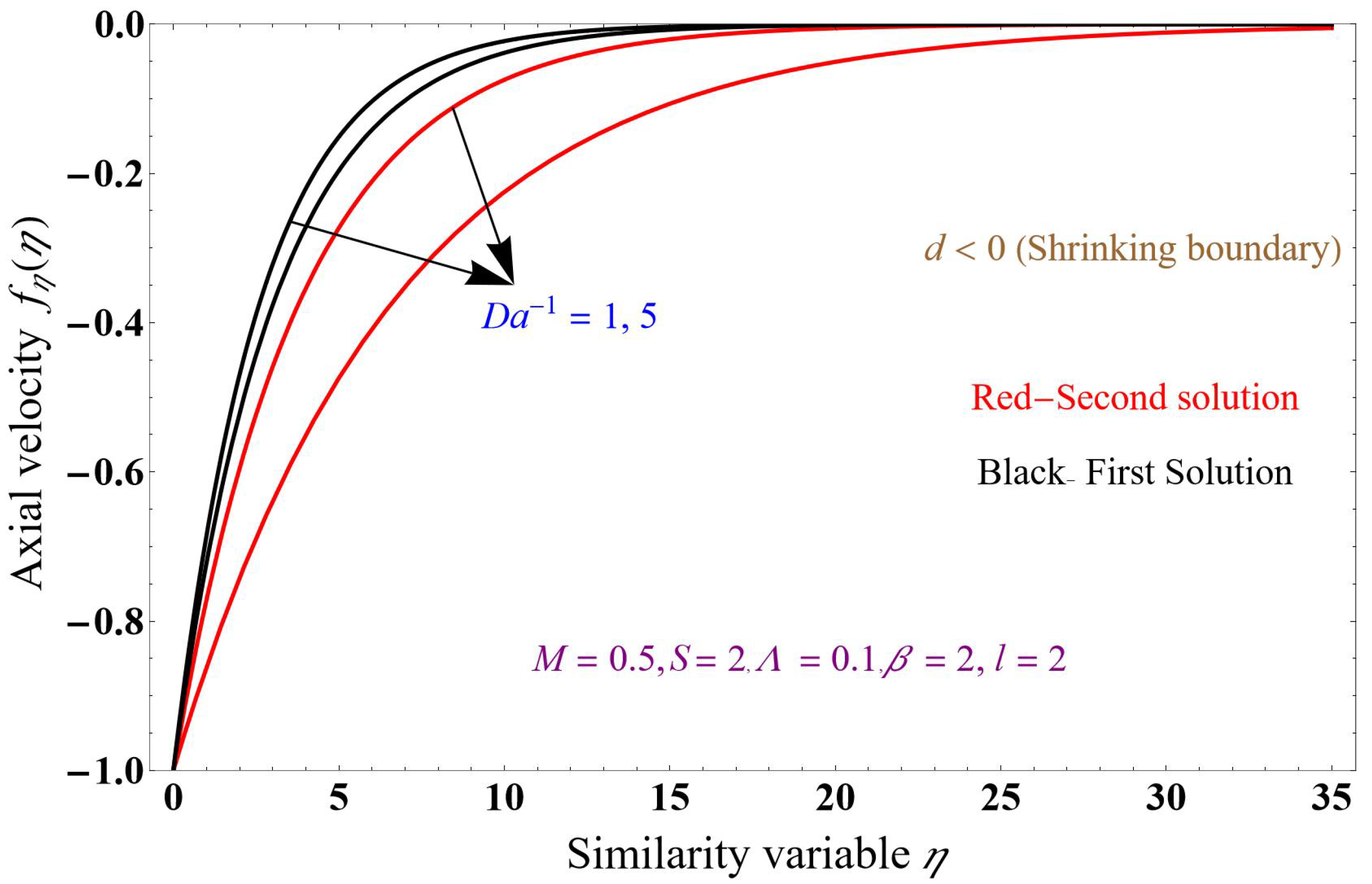
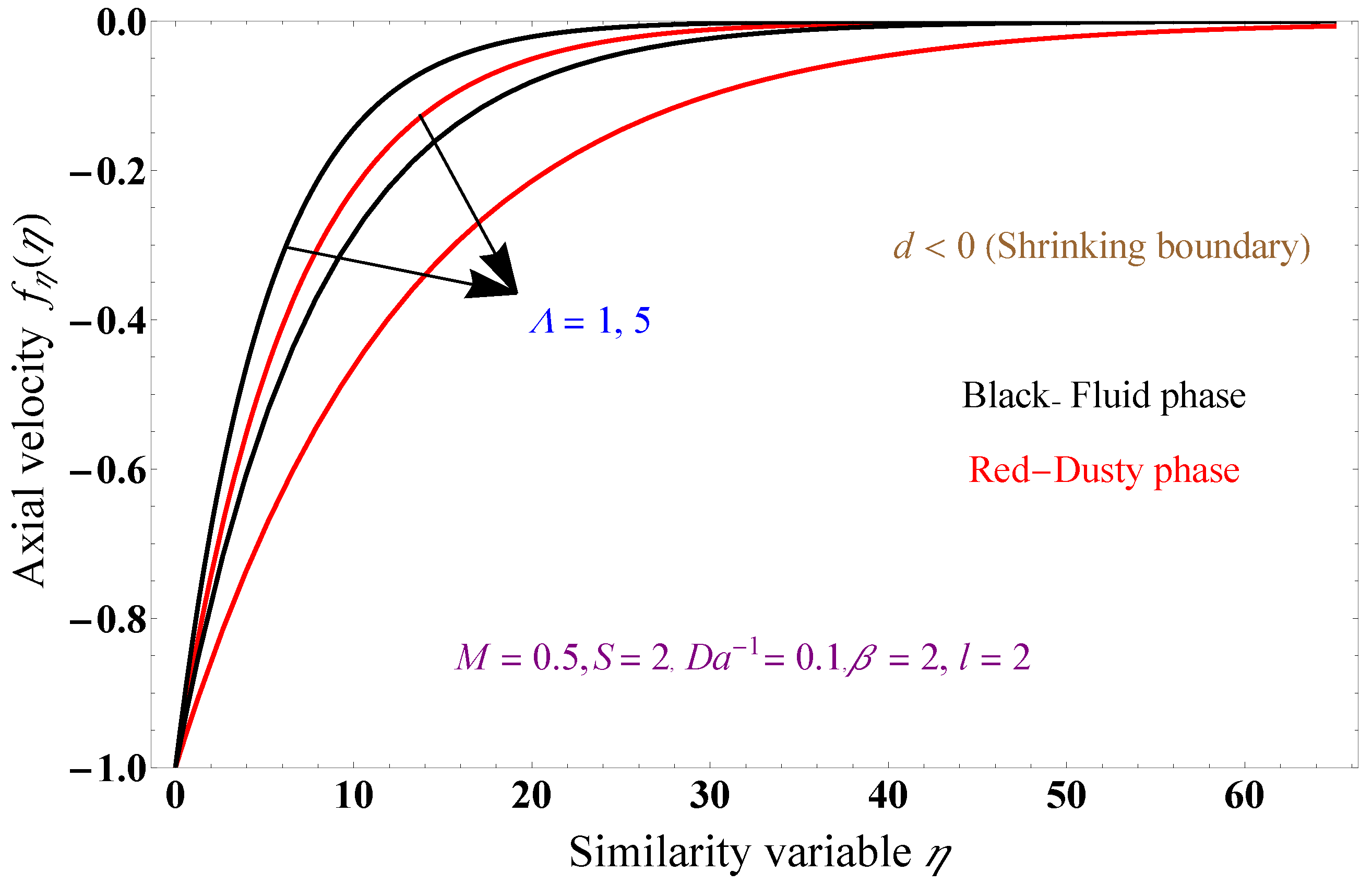
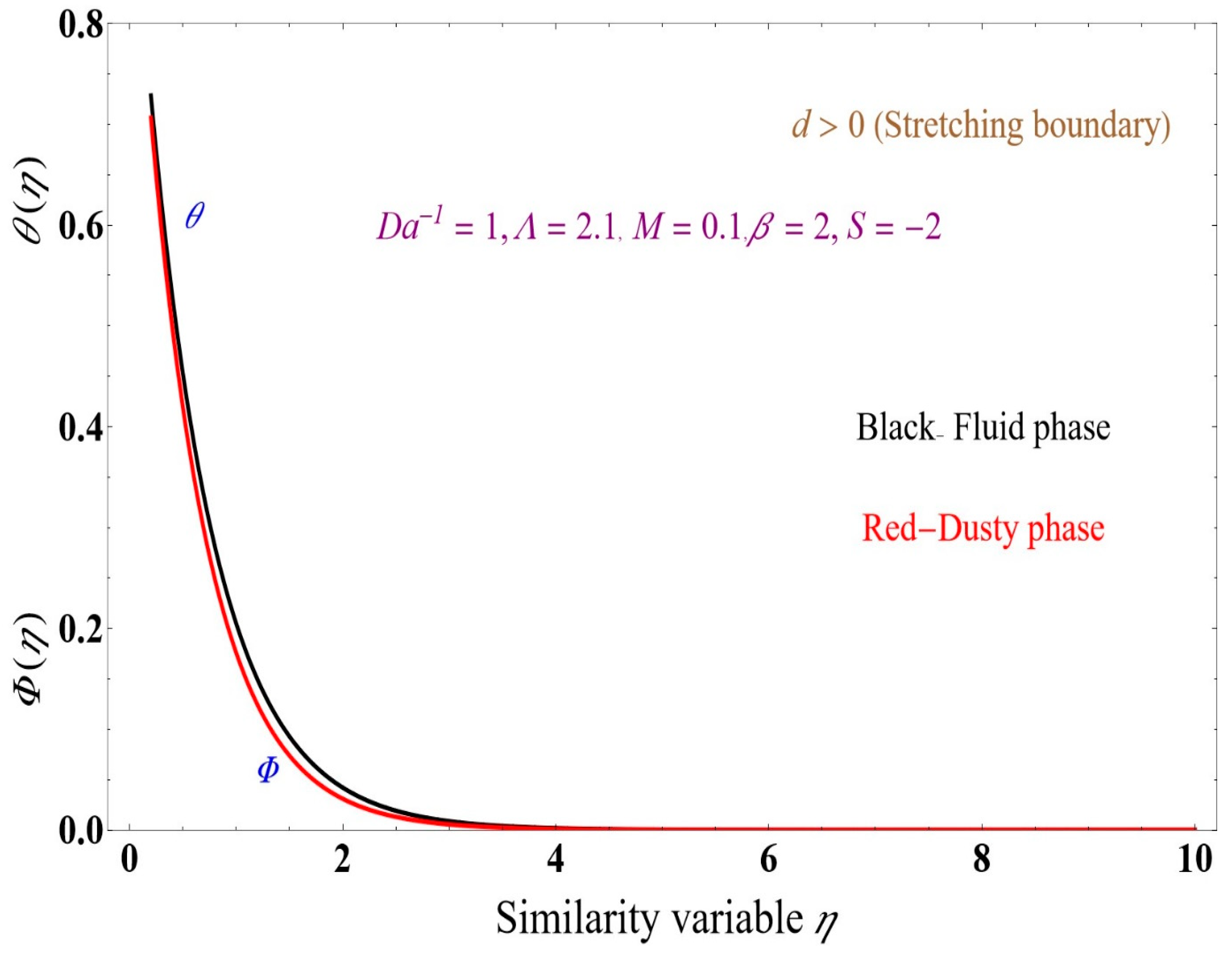
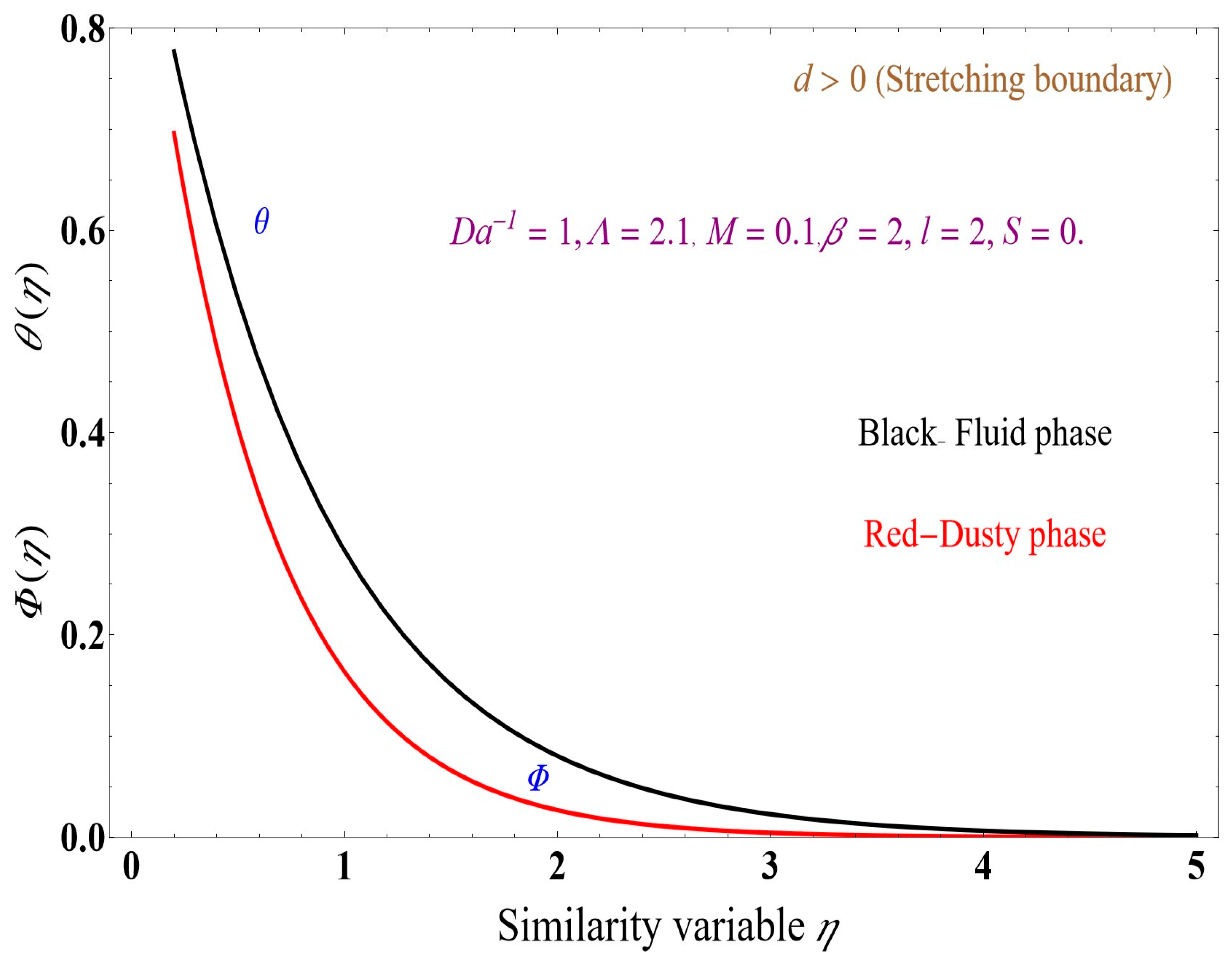
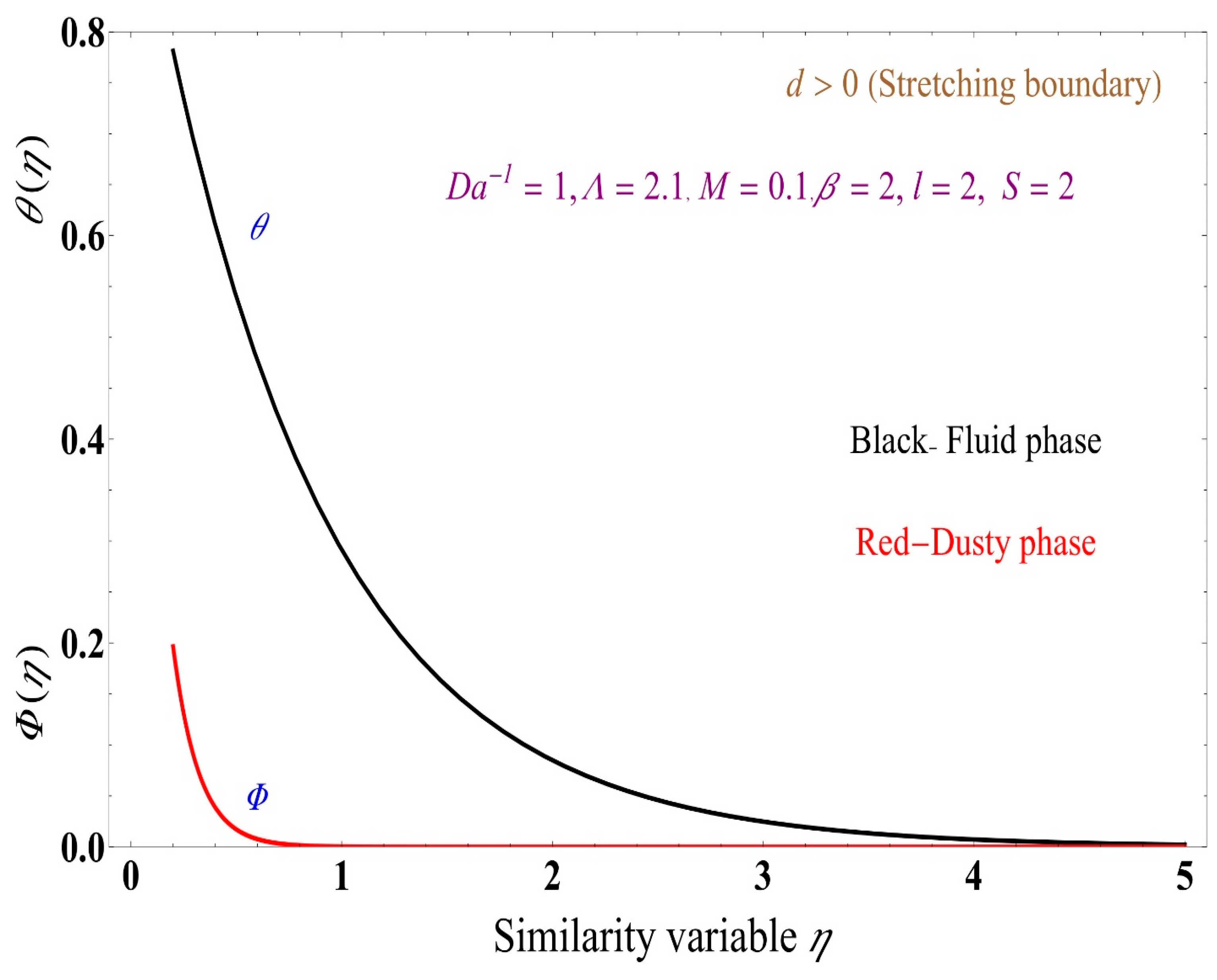
5. Results and Discussion

The present study focuses on the Darcy–Brinkman model in conjunction with a magnetic field over a two-phase ternary nanofluid with dusty particles flowing across stretching/shrinking boundaries and under the influence of thermal radiation and a heat source/sink. The governing equations are converted to coupled ODEs via similarity transformations, and exact solutions for the momentum and temperature equations are obtained for the fluid and dusty phases. The Prandtl number for water, Pr, is considered to be 6.2. The range of parameters used are as follows: Brinkman number $0.1⩽\mathrm{\Lambda }⩽5$, mass suction/injection $0.1⩽S⩽5$, stretching/shrinking parameter $-2⩽d⩽2$, magnetic field parameter $0.5⩽M⩽10$, inverse Darcy number $0.5⩽D{a}^{-1}⩽10$, $0.1⩽l⩽5$, and volume fraction $0.1⩽\mathrm{\varphi }<0.3$. The application of the model concerns the parameters shown in Table 1. Note that past investigations served as the limiting case of the present work:

• Absence of heat source/sink, and the presence of hybrid nanoparticles: limiting case is the results of Sneha et al. [22].
• Absence of magnetic field, heat source/sink, Brinkman ratio: limiting case is the results of Farooq et al. [3].
• Absence of magnetic field, heat source/sink, Brinkman ratio, volume fraction: limiting case is the results of Turkyilmazoglu et al. [2].
  In the following sections, we will show the results of the analytic solution for a range of parameters.

  e. 

  The ternary nanoparticles’ thermophysical properties [17,37,39]

Viscosity of the ternary nanofluids stated as [17]:

$${\mu }_{tnf}=\frac{1}{{\left(1-{\mathit{\varphi }}_{Ag}\right)}^{2.5}{\left(1-{\mathit{\varphi }}_{Cu}\right)}^{2.5}{\left(1-{\mathit{\varphi }}_{Ti{O}_2}\right)}^{2.5}}.$$

(35)

Density of the ternary nanofluids stated as [17,39]:

$$\begin{array}{c}\frac{{\rho }_{tnf}}{{\rho }_f}=\left(1-{\mathit{\varphi }}_{Ag}\right)\left\{\left(1-{\mathit{\varphi }}_{Cu}\right)\left[\begin{array}{c}\left(1-{\mathit{\varphi }}_{Ti{O}_2}\right)\hfill \\ +{\mathit{\varphi }}_{Ti{O}_2}\frac{{\rho }_{Ti{O}_2}}{{\rho }_f}\hfill \end{array}\right]+{\mathit{\varphi }}_{Cu}\frac{{\rho }_{Cu}}{{\rho }_f}\right\}\hfill \\ +{\mathit{\varphi }}_{Ag}\frac{{\rho }_{Ag}}{{\rho }_f}.\hfill \end{array}$$

(36)

Thermal capacity of the ternary nanofluids stated as [37]:

$$\frac{{\left(\rho C_p\right)}_{tnf}}{{\left(\rho C_p\right)}_f}=\left(1-{\mathit{\varphi }}_{Ag}\right)\left\{\begin{array}{c}\left(1-{\mathit{\varphi }}_{Cu}\right)\times \hfill \\ \left[\begin{array}{c}\left(1-{\mathit{\varphi }}_{Ti{O}_2}\right)\hfill \\ +{\mathit{\varphi }}_{Ti{O}_2}\frac{{\left(\rho C_p\right)}_{Ti{O}_2}}{{\left(\rho C_p\right)}_f}\hfill \end{array}\right]\hfill \\ +{\mathit{\varphi }}_{Cu}\frac{{\left(\rho C_p\right)}_{Cu}}{{\left(\rho C_p\right)}_f}\hfill \end{array}\right\}+{\mathit{\varphi }}_{Ag}\frac{{\left(\rho C_p\right)}_{Ag}}{{\left(\rho C_p\right)}_f}.$$

(37)

The nanoparticles’ effects on the thermal conductivities in a ternary nanofluid [17] are described by the following set of equations:

$$\left.\begin{array}{c}\frac{{\kappa }_{tnf}}{{\kappa }_{hnf}}=\frac{{\kappa }_{Ag}+2{\kappa }_{hnf}-2{\mathit{\varphi }}_{Ag}\left({\kappa }_{hnf}-{\kappa }_{Ag}\right)}{{\kappa }_{Ag}+2{\kappa }_{hnf}+{\mathit{\varphi }}_{Ag}\left({\kappa }_{hnf}-{\kappa }_{Ag}\right)},\hfill \\ \frac{{\kappa }_{hnf}}{{\kappa }_{nf}}=\frac{{\kappa }_{Cu}+2{\kappa }_{nf}-2{\mathit{\varphi }}_{Cu}\left({\kappa }_{nf}-{\kappa }_{Cu}\right)}{{\kappa }_{Cu}+2{\kappa }_{nf}+{\mathit{\varphi }}_{Cu}\left({\kappa }_{nf}-{\kappa }_{Cu}\right)},\hfill \\ \frac{{\kappa }_{nf}}{{\kappa }_f}=\frac{{\kappa }_{Ti{O}_2}+2{\kappa }_f-2{\mathit{\varphi }}_{Ti{O}_2}\left({\kappa }_f-{\kappa }_{Ti{O}_2}\right)}{{\kappa }_{Ti{O}_2}+2{\kappa }_f+{\mathit{\varphi }}_{Ti{O}_2}\left({\kappa }_f-{\kappa }_{Ti{O}_2}\right)}.\hfill \end{array}\right\}$$

(38)

• The electrical conductivities are given by

  $$\left.\begin{array}{c}\frac{{\sigma }_{tnf}}{{\sigma }_{hnf}}=1+\frac{3\left(\frac{{\sigma }_{Ag}}{{\sigma }_{hnf}}-1\right){\mathit{\varphi }}_{Ag}}{\left(\frac{{\sigma }_{Ag}}{{\sigma }_{hnf}}+2\right)-\left(\frac{{\sigma }_{Ag}}{{\sigma }_{hnf}}-1\right){\mathit{\varphi }}_{Ag}},\hfill \\ \frac{{\sigma }_{hnf}}{{\sigma }_{nf}}=1+\frac{3\left(\frac{{\sigma }_{Cu}}{{\sigma }_{nf}}-1\right){\mathit{\varphi }}_{Cu}}{\left(\frac{{\sigma }_{Cu}}{{\sigma }_{nf}}+2\right)-\left(\frac{{\sigma }_{Cu}}{{\sigma }_{nf}}-1\right){\mathit{\varphi }}_{Cu}},\hfill \\ \frac{{\sigma }_{nf}}{{\sigma }_f}=1+\frac{3\left(\frac{{\sigma }_{Ti{O}_2}}{{\sigma }_f}-1\right){\mathit{\varphi }}_{Ti{O}_2}}{\left(\frac{{\sigma }_{Ti{O}_2}}{{\sigma }_f}+2\right)-\left(\frac{{\sigma }_{Ti{O}_2}}{{\sigma }_f}-1\right){\mathit{\varphi }}_{Ti{O}_2}}.\hfill \end{array}\right\}$$

  (39)

  f. 

  Thermophysical properties of ternary nanofluid [17]:

  Properties	$H_{2}O$	$Ag$	Cu	$Ti{O}_2$
  $\rho$ $\left({\mathrm{kgm}}^{-3}\right)$	997.1	10,500	8993	4250
  $Cp\left({\mathrm{Jkg}}^{-1}{\mathrm{K}}^{-1}\right)$	4179	235	385	12,686.2
  $k\left({\mathrm{kgms}}^{-3}{\mathrm{K}}^{-1}\right)$	0.613	429	401	8.95
  $\sigma \left({\Omega }^{-1}{\mathrm{m}}^{-1}\right)$	$0.05$	${3.6\times 10}^7$	${59.6\times 10}^6$	${2.6\times 10}^6$

Figure 2 and Figure 3 show the solution concerning mass transpiration for a magnetic field of 0.5, an inverse Darcy parameter of 0.1, a Brinkman number of 0.5, and various values of $\beta$. The results are obtained for two different values of mass number l: mass number l = 0 (dotted lines) and mass number l = 3 (solid lines). Black solid and dotted lines correspond to ${\lambda }_1$; red solid and dotted lines correspond to ${\lambda }_2$; purple solid and dotted lines correspond to ${\lambda }_3$ roots. All three solutions are in the positive x-axis. The free-stream velocity remains the same on the stretching surface and differs on the shrinking surface. The boundary layer increases as the $\beta$ increases, which leads to the relaxation time becoming very small, and increasing $\beta$ leads to a greater fluid-phase thickness than the thickness related to the dusty phase.

Figure 4 and Figure 5 show the solution concerning mass transpiration. The black solid and dotted lines correspond to ${\lambda }_1$, red solid and dotted lines correspond to ${\lambda }_2$, and purple solid and dotted lines correspond to ${\lambda }_3$ roots, with a magnetic field of 0.5, inverse Darcy parameter of 10, Brinkman number of 0.5, and variation in $\beta$. Figure 4 is obtained when stretching the boundary (d = 2), and Figure 5 when shrinking the boundary (d = −1.2) for two different values of mass number l, where the mass number is l = 0 (dotted lines) and l = 3 (solid lines); all three solutions are in the positive x-axis.

Increasing the value of porous media and $\beta$ leads to resisting the fluid flow and decreases the boundary layer thickness. The flow paths for the flow of the fluid are restricted due to improvement in the permeable factor, which exhibits frictional and drag forces on the fluid flow. Increasing the $\beta$ values decreases the boundary layer thickness for stretching and shrinking boundaries. At specific points, the results reveal similar orientations for different values of the mass number.

Figure 6 and Figure 7 show the solution concerning mass transpiration, a magnetic field of 10, inverse Darcy parameter of 1, Brinkman number of 0.5, and variation in $\beta$. Figure 6 concerns the stretching boundary, d = 2, and Figure 7 the shrinking, d = −1.2, for two different values of the mass number l: 0 (dotted lines) and 3 (solid lines). Similar notation to Figure 6 applies to Figure 7, which elucidates the effect of the higher value of a magnetic field on the solution $\beta$ for both stretching/shrinking boundaries. The imposed magnetic field produces a kind of drag or resistive force and encourages the resistive Lorentz force which is present in an electrically conducting fluid. This force results in resistance to the fluid particle’s momentum, which raises the fluid-phase stretching sheet, significantly retards the transport phenomenon, and consequently decreases the boundary layer thickness.

Figure 8, Figure 9 and Figure 10 show the dusty- and fluid-phase velocity profile plots concerning similarity variables, where the red lines denote the dusty phase and the black lines represent the fluid phase for a stretching boundary. Figure 8 corresponds to inverse Darcy numbers 0, 5. This condition will restrict the flow of both phases. Due to the permeable factor, which imposes frictional and drag forces on the liquid, the following values are used for the various parameters: the magnetic field is 1, the mass suction is 2, the Brinkman number is 0.1, the mass number is 2, and the fluid particle interaction parameter is 2. When increasing the inverse Darcy number, both fluid phases and the velocity profile decrease, and the fluid phase is more dominant than the dusty phase. The momentum of the ternary nanofluid phase and dust phase is decreased. Only one solution is obtained. As shown in Figure 9, for variation in the magnetic field M = 1, 5, the magnetic field encourages the resistive Lorentz force which is present in an electrically conducting fluid. This force resists the fluid particle’s momentum, which lowers the fluid’s velocity in the stretching sheet. When increasing the magnetic field, both the fluid- and dusty-phase velocity profiles decrease, and the fluid phase is more dominant than the dusty phase; it reduces the momentum of TNF and the dust phase. The Brinkman parameter is the relation between drag force and density. Therefore, the drag force increases when increasing the values of the Brinkman number, which slows down the fluid velocity. A rising Brinkman parameter reduces the ternary fluid velocity and decreases the dusty-phase velocity.

Figure 11, Figure 12 and Figure 13 show the axial velocity profiles for the inverse Darcy number 1, 5 values that resist the fluid flow. The flow paths for the fluid in both phases are restricted due to improvement in the permeable factor, which exhibits frictional and drag forces on the liquid. The results include mass suction and injection values and a shrinking boundary while keeping the magnetic field at 0.5, mass transpiration values of 2, −2, and inverse Darcy number of 0.1. The momentum profile in both the fluid and dusty phases decreases with upsurges in the inverse Darcy number compared to the graph in Figure 8, which shows almost similar phenomena for stretching and shrinking boundaries. Figure 8 shows nearly similar phenomena for both stretching and shrinking boundaries. Figure 13 shows the Brinkman parameter for the shrinking boundary and mass suction values. The drag force increases with increasing Brinkman number values, slowing the fluid velocity. Increasing the Brinkman parameter decreases the velocity of the ternary nanofluid phase, and the dusty phase slowly decays compared to the liquid phase.

Figure 14, Figure 15, Figure 16 show the temperatures for the fluid and dusty phases for different values of S = −2, 0 and 2, respectively. Increasing S value increases the thermal boundary layer thickness of the fluid phase. The dusty phase exhibits an increase in the thermal boundary layer when S increases from −2 to 0, while decreases for S = 2.

Figure 17 and Figure 18 show the temperature and velocity graphs for the dusty phase concerning the similarity variable. Figure 17 shows the temperature of the dusty phase for a shrinking boundary for the inverse Darcy number of 1, magnetic field of 0.1, and heat sink of −2. The fluid-phase temperature increases dramatically, and the dusty fluid phase decreases the thermal boundary layer. Compared with the results of Figure 14, the dusty-phase temperature drops for a shrinking boundary. Figure 16 shows the velocity of the dusty phase for the shrinking boundary with varying inverse Darcy number = 1, 5. It will resist the fluid flow (Figure 11). The porous media decreases the velocity profile. Furthermore, in the dusty fluid phase, the flow paths are restricted due to the improvement in the permeable factor. There is frictional and drag forces on the liquid for a Brinkman number of 2.1, magnetic field of 0.1, and heat sink of −2. The shrinking boundary fluid phase increases with decreasing the dusty phase, which reduces the velocity of the fluid flow by creating resistance for the flow by varying the porous media.

Figure 17. Temperature profile versus similarity variable for a shrinking boundary.

Figure 17. Temperature profile versus similarity variable for a shrinking boundary.

Figure 18. Velocity profile versus similarity variable variation in $D{a}^{-1}$.

Figure 18. Velocity profile versus similarity variable variation in $D{a}^{-1}$.

Table 1. Comparison of the present study and related works by other authors [2,6,47,48,49].

Previous Related Works	Fluids	Value of Momentum Solution
Turkyilmazoglu [2]	Newtonian	$f\left(\eta \right)=s-D\frac{1-e^{-\lambda \eta }}{\lambda }$
Crane, 1970 [6]	Newtonian	$\beta =1$
Pavlov, 1974 [47]	Newtonian	$\beta =\sqrt{1+M}$
Umair Khan [48]	Non-Newtonian	$f\left(\eta \right)=f_w+\frac{\lambda }{{\beta }_a}\left(1-exp[-{\beta }_a\eta ]\right),$
Hamid [49]	Newtonian	$f\left(\eta \right)=s+a\frac{1-e^{-C\eta }}{C+b{C}^2}$
Present work	Newtonian	$f\left(\eta \right)=s-d\frac{1-e^{-\lambda \eta }}{\lambda }$

Table 1. Comparison of the present study and related works by other authors [2,6,47,48,49].

Previous Related Works	Fluids	Value of Momentum Solution
Turkyilmazoglu [2]	Newtonian	$f\left(\eta \right)=s-D\frac{1-e^{-\lambda \eta }}{\lambda }$
Crane, 1970 [6]	Newtonian	$\beta =1$
Pavlov, 1974 [47]	Newtonian	$\beta =\sqrt{1+M}$
Umair Khan [48]	Non-Newtonian	$f\left(\eta \right)=f_w+\frac{\lambda }{{\beta }_a}\left(1-exp[-{\beta }_a\eta ]\right),$
Hamid [49]	Newtonian	$f\left(\eta \right)=s+a\frac{1-e^{-C\eta }}{C+b{C}^2}$
Present work	Newtonian	$f\left(\eta \right)=s-d\frac{1-e^{-\lambda \eta }}{\lambda }$

6. Concluding Remarks

This analytical study examines the MHD’s influence across a ternary dusty nanofluid with permeable media, radiation, and a heat source/sink also considered. Using suitable transformations, velocity and temperature equations are converted to a set of feasible ODEs and solved using an analytical method. Physical significance parameters like the solution domain, inverse Darcy number, and Brinkman parameter have been examined. Table 1 is the analytical validation,

Table 2. Comparison values of $-f^{\prime \prime }\left(0\right)$ with the results of Turkyilmazoglu [2] for some specified M and $\beta$ for taking Da${-}^1$ = 0, $\mathrm{\varphi }=0$, $\tau$ = 90, and $\mathrm{\Lambda }=1$.

M and $\mathit{\beta }=0$	Turkyilmazoglu [2]	Present Results
0.0	1.0000	1.0000
0.5	1.2247	1.22451
1.0	1.4142	1.4142
1.5	1.5811	1.5812
2.0	1.7320	1.7322

and

Table 3. Comparison values of $-f^{\prime \prime }\left(0\right)$ with the results of Turkyilmazoglu [2] for some specified M and $\beta =0.5$ for taking Da${-}^1$ = 0, $\mathrm{\varphi }=0$, $\tau$ = 90, and $\mathrm{\Lambda }=1$.

M and $\mathit{\beta }=0.5$	Turkyilmazoglu [2]	Present Results
0.0	1.0380	1.03772
0.5	1.251167	1.25118
1.0	1.43759	1.43728
1.5	1.60208	1.59902
2.0	1.75119	1.75121

gives the numerical comparision with previous studies. The findings of this study are:

• An analytical approach can be used to solve the magnetic field with the Darcy–Brinkman model.
• The fluid- and dusty-phase velocity profiles decrease when increasing the inverse Darcy number.
• The momentum boundary layer becomes thicker as the Brinkman number rises.
• When increasing the solution domain thickness, the particle interaction parameters strength also increases.
• The analysis yields a unique solution when considering mass flow suction.
• Increasing the magnetic field decreases the velocity profile due to Lorentz’s force.
• The fluid-phase temperature in the boundary layer significantly increases compared to the dusty-phase temperature in the boundary layer.

Future work using the particle-phase velocity slip mechanism will expand beyond the existing exact solutions to more specific problems, such as non-Newtonian fluids. The proposed mathematical approach can be extended to include buoyancy effects, activation energy, and viscoelastic fluids over various geometries, like stretching/shrinking sheets, rotating disks, cylinders, cones, wedges, convergent/divergent channels, Riga plates, and micro-channels, among others.