Optimal Control Applied to Oenological Management of Red Wine Fermentative Macerations
Abstract
1. Introduction
- Optimal control for managing industrial bulk red winemaking;
- Weighting approach for solving MOO problems with oenological requirements;
- MCDM algorithms for helping the decision-making process.
2. Materials and Methods
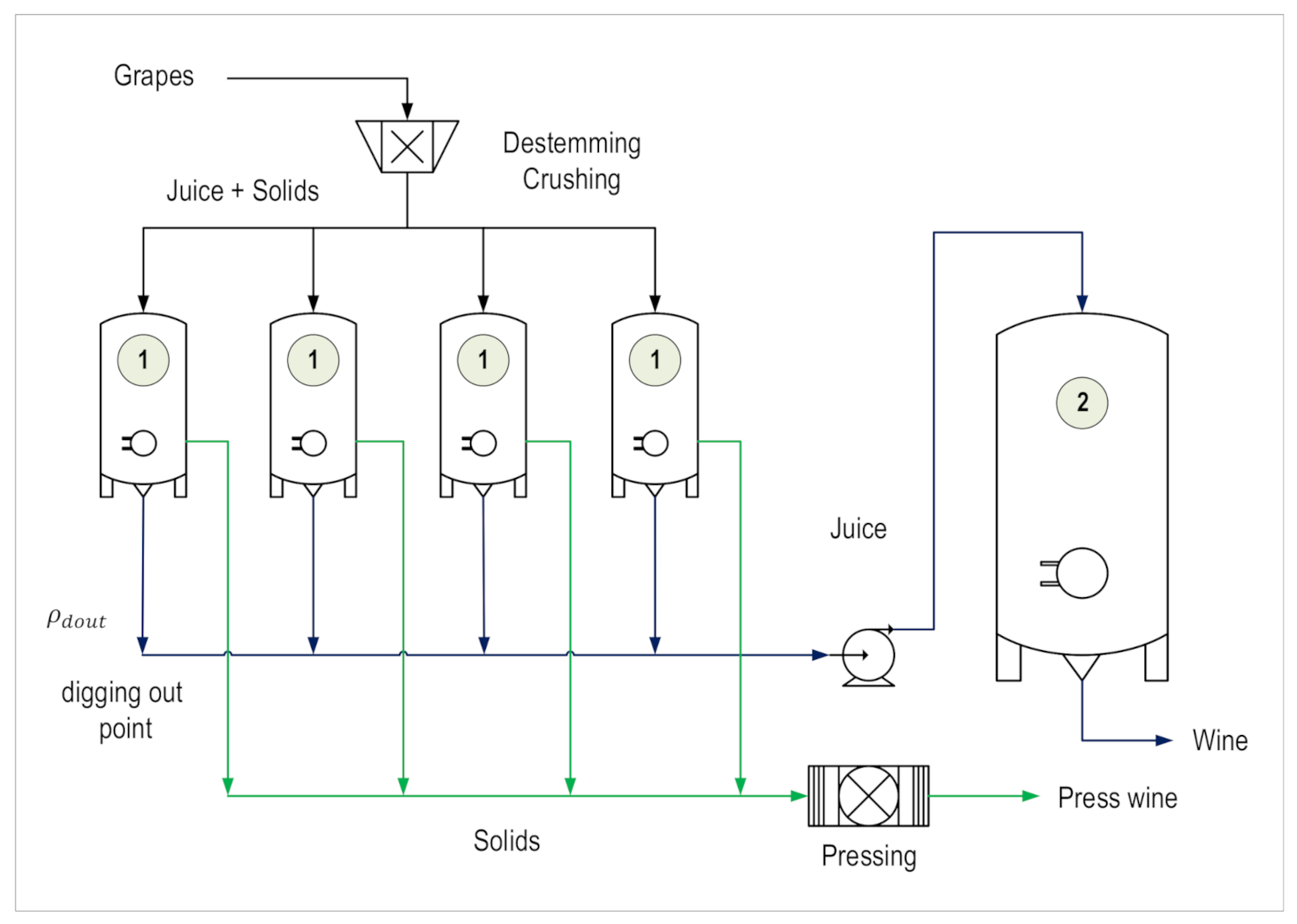
2.1. Process Description
2.2. Fermentation Model
2.3. Multi-Objective Cost Function
2.4. Optimal Control Problem Formulation
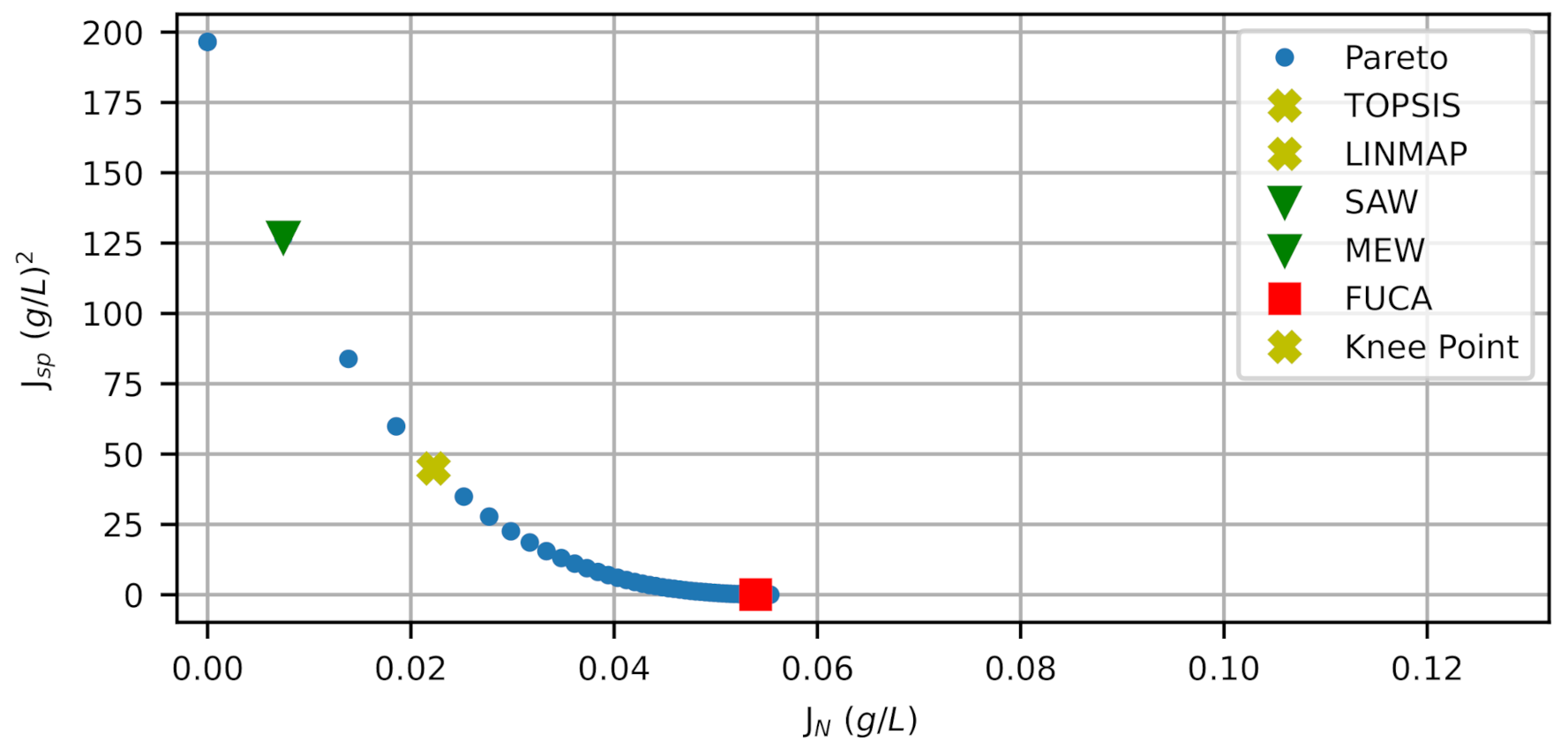
2.5. Selection of Optimal Control Strategy by MCDM
3. Results
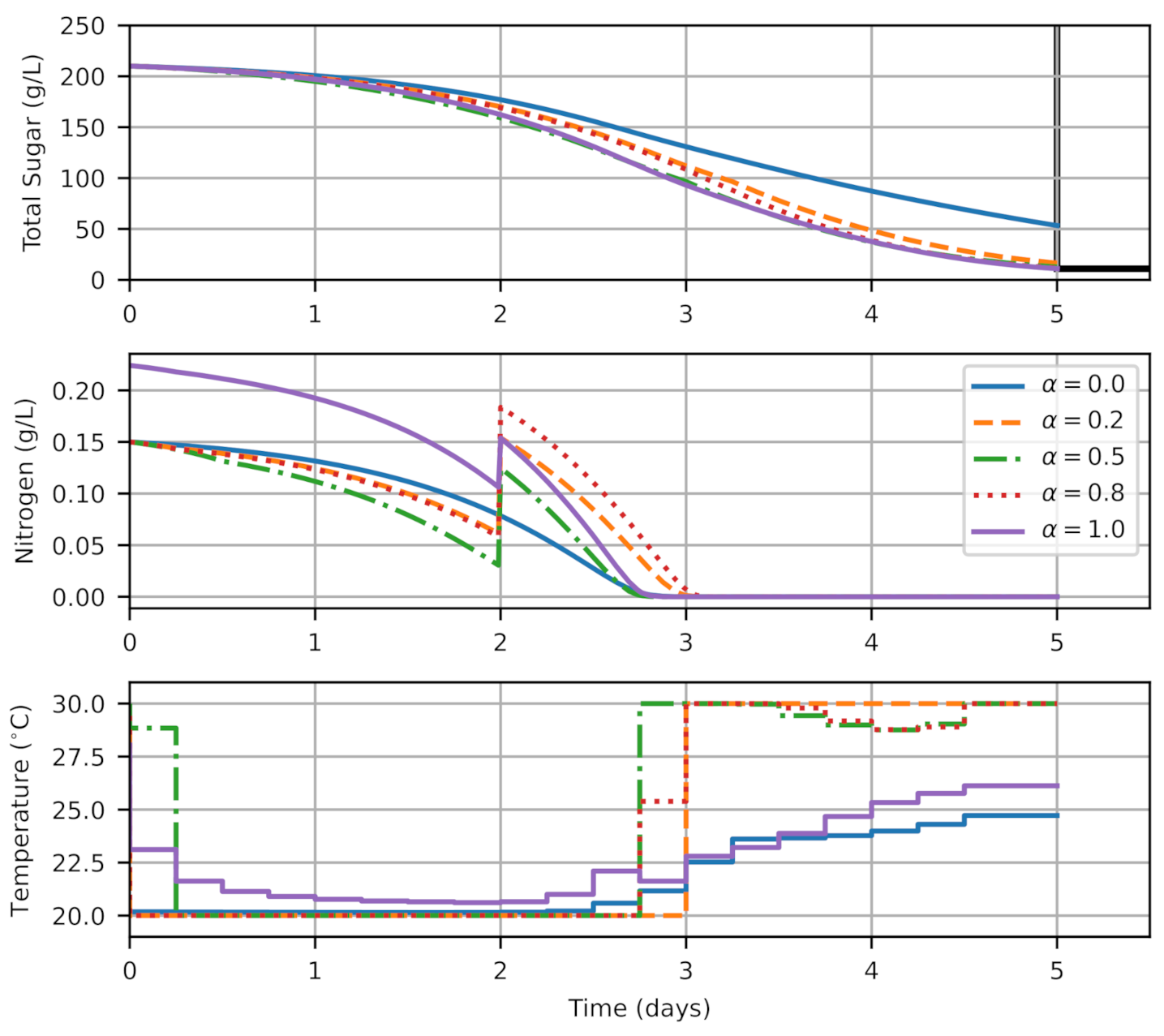
3.1. Free Nutrition Strategies
3.2. Traditional Nutrition Strategies
3.3. Comparison of the Most Suitable Strategies
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Fermentation Model Equations
References
- Cheynier, V.; Salas, E.; Souquet, J.M.; Sarni-manchado, P.; Fulcrand, H. Structure and Properties of Wine Pigments and Tannins. Am. J. Enol. Vitic. 2006, 57, 298–305. [Google Scholar]
- Setford, P.C.; Jeffery, D.W.; Grbin, P.R.; Muhlack, R.A. Modelling the Mass Transfer Process of Malvidin-3-Glucoside during Simulated Extraction from Fresh Grape Solids under Wine-Like Conditions. Molecules 2018, 23, 2159. [Google Scholar] [CrossRef] [PubMed]
- Setford, P.C.; Jeffery, D.W.; Grbin, P.R.; Muhlack, R.A. Factors affecting extraction and evolution of phenolic compounds during red wine maceration and the role of process modelling. Trends Food Sci. Technol. 2017, 69, 106–117. [Google Scholar] [CrossRef]
- Webb, L.B.; Whetton, P.H.; Barlow, E.W. Modelled impact of future climate change on the phenology of winegrapes in Australia. Aust. J. Grape Wine Res. 2007, 13, 165–175. [Google Scholar] [CrossRef]
- Luna, R.; Matias-Guiu, P.; López, F.; Pérez-Correa, J.R. Quality aroma improvement of Muscat wine spirits: A new approach using first-principles model-based design and multi-objective dynamic optimisation through multi-variable analysis techniques. Food Bioprod. Process. 2019, 115, 208–222. [Google Scholar] [CrossRef]
- Miller, K.V.; Block, D.E. A review of wine fermentation process modeling. J. Food Eng. 2020, 273, 109783. [Google Scholar] [CrossRef]
- Coleman, M.C.; Fish, R.; Block, D.E. Temperature-Dependent Kinetic Model for Nitrogen-Limited Wine Fermentations. Appl. Environ. Microbiol. 2007, 73, 5875–5884. [Google Scholar] [CrossRef] [PubMed]
- Cerda-Drago, T.G.; Agosin, E.; Pérez-Correa, J.R. Modelling the oxygen dissolution rate during oenological fermentation. Biochem. Eng. J. 2016, 106, 97–106. [Google Scholar] [CrossRef]
- Zenteno, M.I.; Pérez-Correa, J.R.; Gelmi, C.A.; Agosin, E. Modeling temperature gradients in wine fermentation tanks. J. Food Eng. 2010, 99, 40–48. [Google Scholar] [CrossRef]
- Miller, K.V.; Oberholster, A.; Block, D.E. Creation and validation of a reactor engineering model for multiphase red wine fermentations. Biotechnol. Bioeng. 2019, 116, 781–792. [Google Scholar] [CrossRef]
- Miller, K.V.; Noguera, R.; Beaver, J.; Oberholster, A.; Block, D.E. A combined phenolic extraction and fermentation reactor engineering model for multiphase red wine fermentation. Biotechnol. Bioeng. 2020, 117, 109–116. [Google Scholar] [CrossRef]
- Ashoori, A.; Moshiri, B.; Khaki-Sedigh, A.; Bakhtiari, M.R. Optimal control of a nonlinear fed-batch fermentation process using model predictive approach. J. Process Control 2009, 19, 1162–1173. [Google Scholar] [CrossRef]
- Santos, L.; Dewasme, L.; Coutinho, D.; Wouwer, A.V. Nonlinear model predictive control of fed-batch cultures of micro-organisms exhibiting overflow metabolism: Assessment and robustness. Comput. Chem. Eng. 2012, 39, 143–151. [Google Scholar] [CrossRef]
- Craven, S.; Whelan, J.; Glennon, B. Glucose concentration control of a fed-batch mammalian cell bioprocess using a nonlinear model predictive controller. J. Process Control 2014, 24, 344–357. [Google Scholar] [CrossRef]
- Chang, L.; Liu, X.; Henson, M.A. Nonlinear model predictive control of fed-batch fermentations using dynamic flux balance models. J. Process Control 2016, 42, 137–149. [Google Scholar] [CrossRef]
- Schenk, C.; Schulz, V.; Rosch, A.; von Wallbrunn, C. Less cooling energy in wine fermentation—A case study in mathematical modeling, simulation and optimization. Food Bioprod. Process. 2017, 103, 131–138. [Google Scholar] [CrossRef]
- Vaccari, M.; Bacci di Capaci, R.; Brunazzi, E.; Tognotti, L.; Pierno, P.; Vagheggi, R.; Pannocchia, G. Optimally Managing Chemical Plant Operations: An Example Oriented by Industry 4.0 Paradigms. Ind. Eng. Chem. Res. 2021. [Google Scholar] [CrossRef]
- Narayanan, H.; Luna, M.F.; von Stosch, M.; Cruz Bournazou, M.N.; Polotti, G.; Morbidelli, M.; Butté, A.; Sokolov, M. Bioprocessing in the Digital Age: The Role of Process Models. Biotechnol. J. 2020, 15, 1900172. [Google Scholar] [CrossRef]
- The Association for Packaging and Processing Technologies, Inc. How to Utilize Big Data to Enhance Manufacturing Processes; Technical Report; The Association for Packaging and Processing Technologies, Inc.: Herndon, VA, USA, 2018. [Google Scholar]
- Rodman, A.D.; Gerogiorgis, D.I. Multi-objective process optimisation of beer fermentation via dynamic simulation. Food Bioprod. Process. 2016, 100, 255–274. [Google Scholar] [CrossRef]
- Luna, R.; López, F.; Pérez-Correa, J.R. Design of optimal wine distillation recipes using multi-criteria decision-making techniques. Comput. Chem. Eng. 2021, 145, 107194. [Google Scholar] [CrossRef]
- Torrealba, C.; Luna, R.; Cuevas-Valenzuela, J.; Pérez-Correa, J.R. A multi-criteria decision making guided parametric robustness assessment workflow: Enhancing wine fermentation models in the presence of limited data structures. 2021, submitted.
- Casassa, L.F.; Larsen, R.C.; Beaver, C.W.; Mireles, M.S.; Keller, M.; Riley, W.R.; Smithyman, R.; Harbertson, J.F. Impact of Extended Maceration and Regulated Deficit Irrigation (RDI) in Cabernet Sauvignon Wines: Characterization of Proanthocyanidin Distribution, Anthocyanin Extraction, and Chromatic Properties. J. Agric. Food Chem. 2013, 61, 6446–6457. [Google Scholar] [CrossRef]
- Bhaskar, V.; Gupta, S.K.; Ray, A.K. Applications of multiobjective optimization in chemical engineering. Rev. Chem. Eng. 2000, 16, 1–54. [Google Scholar] [CrossRef]
- Miettinen, K.; Hakanen, J. Why Use Interactive Multi-Objective Optimization in Chemical Process Design. In MULTI-OBJECTIVE OPTIMIZATION: Techniques and Application in Chemical Engineering; World Scientific: Singapore, 2008; pp. 153–188. [Google Scholar] [CrossRef]
- Ministerio de Agricultura, Biblioteca del Congreso Nacional de Chile. Reglamenta Ley N° 18455 que fija normas sobre producción, elaboración y comercialización de alcoholes etilicos, bebidas alcoholicas y vinagres. 1986. Available online: https://www.bcn.cl/leychile/navegar?idNorma=8815 (accessed on 3 June 2021).
- Kameswaran, S.; Biegler, L.T. Simultaneous dynamic optimization strategies: Recent advances and challenges. Comput. Chem. Eng. 2006, 30, 1560–1575. [Google Scholar] [CrossRef]
- Biegler, L.T. 10. Simultaneous Methods for Dynamic Optimization. In Nonlinear Programming; SIAM: Philadelphia, PA, USA, 2010; Chapter 10; pp. 287–324. [Google Scholar] [CrossRef]
- Biegler, L.T. An overview of simultaneous strategies for dynamic optimization. Chem. Eng. Process. Process Intensif. 2007, 46, 1043–1053. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Pérez, D.; Assof, M.; Bolcato, E.; Sari, S.; Fanzone, M. Combined effect of temperature and ammonium addition on fermentation profile and volatile aroma composition of Torrontés Riojano wines. LWT 2018, 87, 488–497. [Google Scholar] [CrossRef]
- Mouret, J.; Farines, V.; Sablayrolles, J.; Trelea, I. Prediction of the production kinetics of the main fermentative aromas in winemaking fermentations. Biochem. Eng. J. 2015, 103, 211–218. [Google Scholar] [CrossRef]
- Wang, Z.; Rangaiah, G.P. Application and Analysis of Methods for Selecting an Optimal Solution from the Pareto-Optimal Front obtained by Multiobjective Optimization. Ind. Eng. Chem. Res. 2017, 56, 560–574. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Yen, G.G.; Juan, T.K. Minimum Manhattan Distance Approach to Multiple Criteria Decision Making in Multiobjective Optimization Problems. IEEE Trans. Evol. Comput. 2016, 20, 972–985. [Google Scholar] [CrossRef]
- Branke, J.; Deb, K.; Dierolf, H.; Osswald, M. Finding Knees in Multi-objective Optimization. In Parallel Problem Solving from Nature—PPSN VIII; Yao, X., Burke, E.K., Lozano, J.A., Smith, J., Merelo-Guervós, J.J., Bullinaria, J.A., Rowe, J.E., Tiňo, P., Kabán, A., Schwefel, H.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 722–731. [Google Scholar]
- Weise, T. Global Optimization Algorithms—Theory and Application. 2nd ed.; Self-Published. 2009. Available online: http://www.it-weise.de/ (accessed on 2 June 2021).



| State Variables | Nomenclature | Values |
|---|---|---|
| Biomass | 0.200 g/L | |
| Nitrogen | 0.150 g/L | |
| Glucose | 105 g/L | |
| Fructose | 105 g/L | |
| Ethanol | 0 g/L |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luna, R.; Lima, B.M.; Cuevas-Valenzuela, J.; Normey-Rico, J.E.; Pérez-Correa, J.R. Optimal Control Applied to Oenological Management of Red Wine Fermentative Macerations. Fermentation 2021, 7, 94. https://doi.org/10.3390/fermentation7020094
Luna R, Lima BM, Cuevas-Valenzuela J, Normey-Rico JE, Pérez-Correa JR. Optimal Control Applied to Oenological Management of Red Wine Fermentative Macerations. Fermentation. 2021; 7(2):94. https://doi.org/10.3390/fermentation7020094
Chicago/Turabian StyleLuna, Ricardo, Bruno M. Lima, José Cuevas-Valenzuela, Julio E. Normey-Rico, and José R. Pérez-Correa. 2021. "Optimal Control Applied to Oenological Management of Red Wine Fermentative Macerations" Fermentation 7, no. 2: 94. https://doi.org/10.3390/fermentation7020094
APA StyleLuna, R., Lima, B. M., Cuevas-Valenzuela, J., Normey-Rico, J. E., & Pérez-Correa, J. R. (2021). Optimal Control Applied to Oenological Management of Red Wine Fermentative Macerations. Fermentation, 7(2), 94. https://doi.org/10.3390/fermentation7020094







