Selection of Spectral Parameters and Optimization of Estimation Models for Soil Total Nitrogen Content during Fertilization Period in Apple Orchards
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Acquisition
2.1.1. Overview of Experimental Orchard
2.1.2. Soil Sample Collection and Analysis
2.1.3. Soil Spectral Collection
2.1.4. Spectral Data Preprocessing
2.2. Modeling Parameter Screening
2.2.1. Characteristic Band Screening
- Correlation coefficient method
- 2.
- Stepwise multiple linear regression (SMLR)
2.2.2. Spectral Characteristic Index (SCI) Screening
2.3. Modeling Methods
2.3.1. Regression Analysis
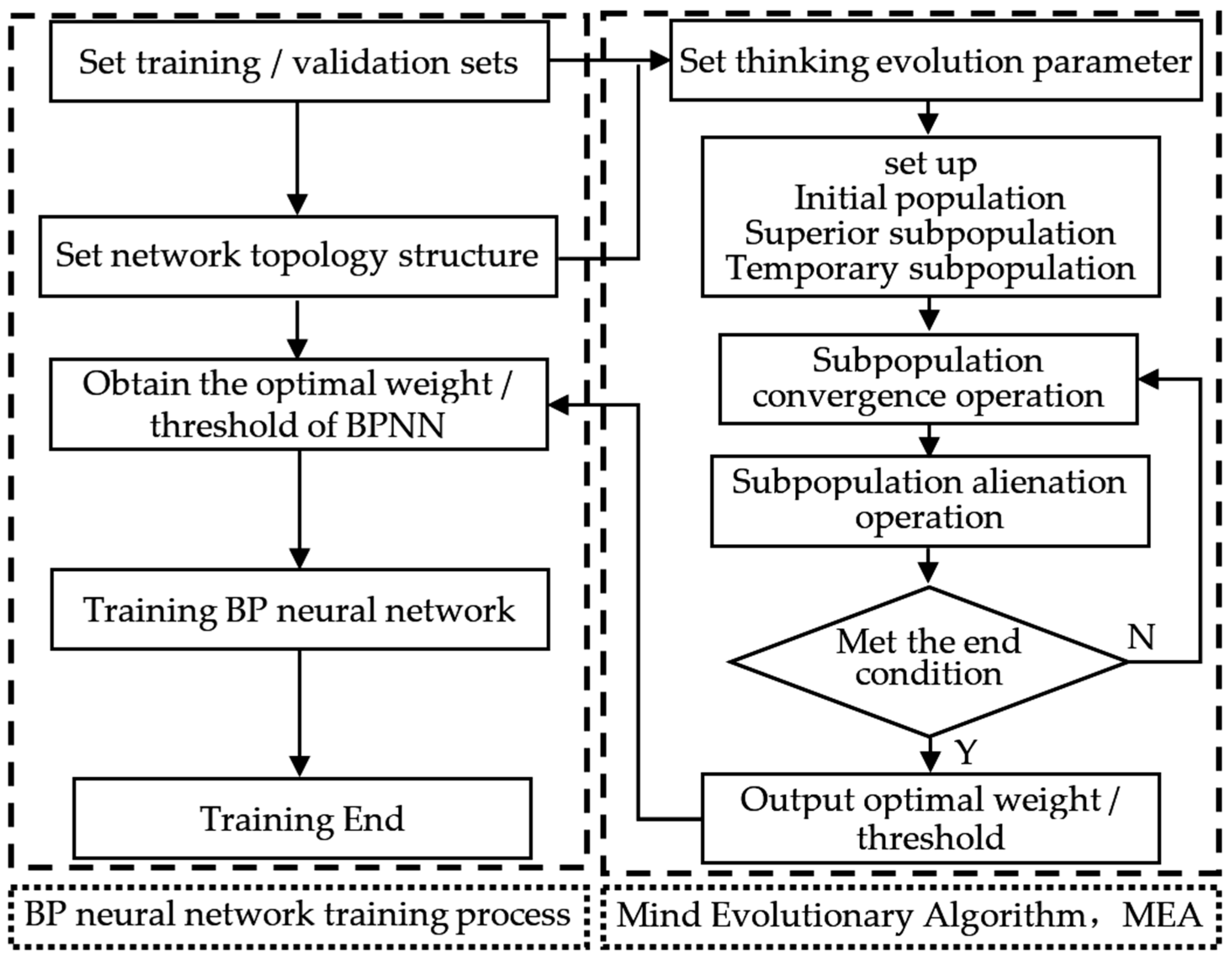
2.3.2. Optimization of BP (Back Propagation) Neural Network Based on Mind Evolution Algorithm (MEA-BPNN)
3. Results
3.1. Selected Soil TN Characteristic Bands and Their Modeling Effects
3.1.1. Modeling Analysis Based on Univariate Regression
3.1.2. Modeling Analysis Based on Multiple Regression
- Modeling effect of characteristic bands based on correlation analysis screening
- 2.
- Modeling effect of characteristic bands based on SMLR screening
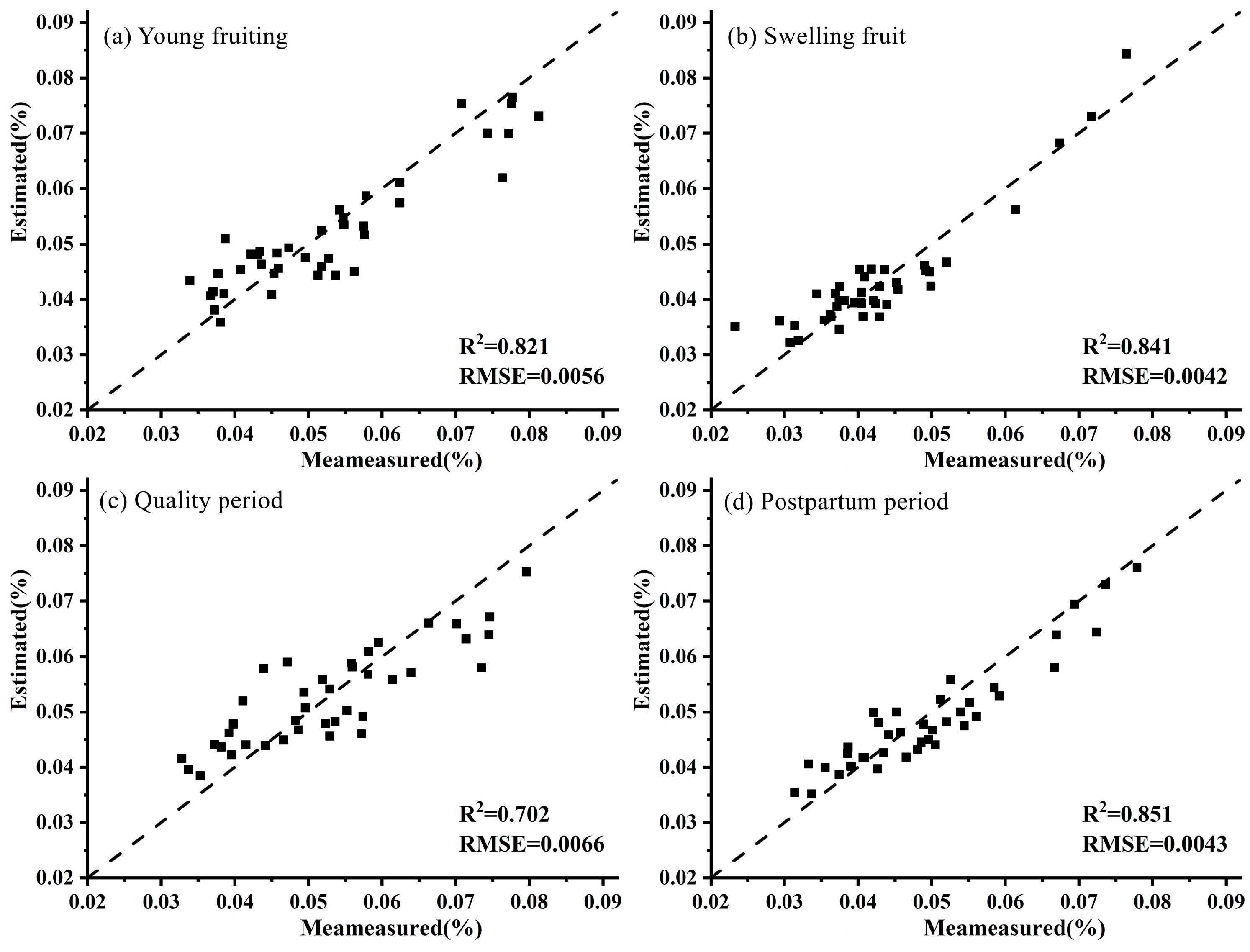
3.1.3. Modeling and Analysis Based on MEA-BPNN
3.2. SCI Screening Results
3.2.1. Independent Soil SCIs for Each Fertilization Period
3.2.2. Comprehensive Soil SCI during the Entire Fertilization Period
3.3. Estimation Model Based on SCI and Characteristic Band Combination
3.3.1. Independent Estimation Models for Each Fertilization Period
3.3.2. Comprehensive Estimation Model for the Entire Fertilization Period
4. Discussion
4.1. Collection and Preprocessing of Hyperspectral Data on TN in Orchard Soil
4.2. Extraction of Characteristic Bands and Selection of SCI
4.3. About Modeling Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y. China’s apple production steadily ranks first in the world. Farmers Daily, 18 November 2023. [Google Scholar]
- Peng, F.T.; Jiang, Y.M.; Gu, M.R.; Shu, H.R. Advances in research on nitrogen nutrition of deciduous fruit crops. J. Fruit Sci. 2003, 20, 54–58. [Google Scholar]
- Gao, Y.M.; Tong, Y.A.; Lu, Y.L.; Wang, X.Y. Effects of soil available nutrients and long-term fertilization on yield of Fuji apple orchard of Weibei area in Shaanxi, China. Acta Hortic. Sin. 2013, 40, 613–622. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Cheng, C.G.; Zhao, D.Y.; Zhou, J.T.; Chen, Y.H.; Zhang, H.T.; Xie, B. Effects of nitrogen application levels on fruit Ca forms and quality of ‘Fuji’ apples. J. Plant Nutr. Fert. 2021, 27, 87–96. [Google Scholar]
- Li, Y.; Xiao, J.; Yan, Y.; Liu, W.; Cui, P.; Xu, C.; Nan, L.; Liu, X. Multivariate analysis and optimization of the relationship between soil nutrients and berry quality of vitis vinifera cv. cabernet franc vineyards in the eastern foothills of the Helan mountains, China. Horticulturae 2024, 10, 61. [Google Scholar] [CrossRef]
- Raese, J.T.; Drake, S.R.; Curry, E.A. Nitrogen fertilizer influences fruit quality, soil nutrients and cover crops, leaf color and nitrogen content, biennial bearing and cold hardiness of ‘Golden Delicious’. J. Plant Nutr. 2007, 30, 1585–1604. [Google Scholar] [CrossRef]
- Deng, J.; Feng, X.Q.; Wang, D.Y.; Lu, J.; Chong, H.T.; Shang, C.; Liu, K.; Huang, L.Y.; Tian, X.H.; Zhang, Y.B. Root morphological traits and distribution in direct-seeded rice under dense planting with reduced nitrogen. PLoS ONE 2020, 15, e0238362. [Google Scholar] [CrossRef]
- Zhang, J.H. Nitrgen imbalance in apple trees and its application in science and technology. Hortic. Seed. 2016, 35, 56–59. [Google Scholar] [CrossRef]
- Bai, Z.J.; Peng, J.; Luo, D.F.; Cai, H.H.; Ji, W.J.; Shi, Z.; Liu, W.Y.; Yin, C.Y. A mid-infrared spectral inversion model for total nitrogen content of farmland soil in southern Xinjiang. Spectrosc. Spect. Anal. 2022, 42, 2768–2773. [Google Scholar]
- Zhang, G.B.; Li, X.C.; Qi, F.Y.; Wu, B.; Cheng, S.H. Grey cluster estimating model of soil organic matter content based on hyperspectral data. J. Grey Syst. UK 2014, 26, 28–37. [Google Scholar]
- Peng, J.; Zhang, Y.Z.; Zhou, Q.; Pang, X.A.; Wu, W.M. The progress on the relationship physics-chemistry properties with spectrum characteristic of the soil. Chin. J. Soil. Sci. 2009, 40, 1204–1208. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, Z.X.; Liu, J.; Yuan, Y.Z.; Sun, H.; Chai, M.; Bi, R.T. Hyperspectral inversion of paddy soil iron oxide in typical subtropical area with Pearl River Delta, China as illustration. J. Appl. Ecol. 2017, 28, 3675–3683. [Google Scholar]
- Vasques, G.M.; Grunwald, S.; Harris, W.G. Spectroscopic models of soil organic carbon in Florida. USA. J. Environ. Qual. 2010, 9, 23–934. [Google Scholar] [CrossRef]
- Liu, J.B.; Han, J.C.; Zhang, Y.; Wang, H.Y.; Kong, H.; Shi, L. Prediction of soil organic carbon with different parent materials development using visible-near infrared spectroscopy. Spectrochim. Acta A 2018, 204, 33–39. [Google Scholar] [CrossRef]
- Liao, Q.H.; Gu, X.H.; Li, C.J.; Chen, L.P.; Huang, W.J.; Du, S.Z.; Fu, Y.Y.; Wang, J.H. Estimation of fluvo-aquic soil organic matter content from hyperspectral reflectance based on continuous wavelet transformation. Trans. CSAE 2012, 28, 132–139. [Google Scholar]
- Lin, L.X.; Wang, Y.J.; Teng, J.Y.; Wang, X.C. Hyperspectral analysis of soil organic matter in coal mining regions using wavelets, correlations, and partial least squares regression. Environ. Monit. Assess 2016, 188, 1–11. [Google Scholar] [CrossRef]
- Divya, Y.; Gopinathan, P. Soil water content measurement using hyper-spectral remote sensing techniques—A case study from north-western part of Tamil Nadu, India. Remote Sens. Appl. Soc. Environ. 2019, 14, 1–7. [Google Scholar] [CrossRef]
- Yang, H.; Kuang, B.; Mouazen, A.M. Quantitative analysis of soil nitrogen and carbon at a farm scale using visible and Near Infrared spectroscopy coupled with wavelength reduction. Eur. J. Soil. Sci. 2012, 63, 410–420. [Google Scholar] [CrossRef]
- Xie, H.T.; Yang, X.M.; Drury, C.F.; Yang, J.Y.; Zhang, X.D. Predicting soil organic carbon and total nitrogen using Mid-and Near-infrared spectra for brookston clay loam soil in sourth-western Ontario, Canada. Can. J. Soil. Sci. 2011, 91, 53–63. [Google Scholar] [CrossRef]
- Zhang, J.J.; Tian, Y.C.; Yao, X.; Cao, W.X.; Ma, X.M.; Zhu, Y. Estimating model of soil total nitrogen content based on near-infrared spectroscopy analysis. Trans. CSAE 2012, 28, 183–188. [Google Scholar]
- Liu, X.Y.; Wang, L.; Chang, Q.R.; Wang, X.X.; Shang, Y. Prediction of total nitrogen and alkali hydrolysable nitrogen content in loess using hyperspectral data based on correlation analysis and partial least squares regression. Chin. J. Appl. Ecol. 2015, 26, 2107–2114. [Google Scholar]
- Li, Y.; Wang, R.H.; Guan, Y.L.; Jiang, H.L.; Wu, X.Q.; Peng, Q. Prediction analysis of soil total nitrogen content based on hyperspectral. Remote Sens. Technol. Appl. 2017, 32, 173–179. [Google Scholar]
- Jia, S.Y.; Li, H.Y.; Wang, Y.J.; Tong, R.Y.; Li, Q. Hyperspectral Imaging Analysis for the classification of soil types and the determination of soil total nitrogen. Sensors 2017, 17, 2252. [Google Scholar] [CrossRef]
- Niu, Z.; Shi, L.; Qiao, H.; Xu, X.; Wang, W.; Ma, X.; Zhang, J. Construction of a hyperspectral estimation model for total nitrogen content in Shajiang black soil. J. Plant Nutr. Soil. Sci. 2023, 186, 196–208. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, G.C.; An, X.H.; Li, M.; Li, E.M.; Cheng, G.G. Estimation for available nitrogen content of apple orchard soil by near infrared spectroscopy and partial least squares regression. North. Hortic. 2018, 3, 113–119. [Google Scholar]
- Yu, X.; Liu, Q.; Wang, Y.B.; Liu, X.Y.; Liu, X. Evaluation of MLSR and PLSR for estimating soil element contents using visible/near-infrared spectroscopy in apple orchards on the Jiaodong peninsula. Catena 2016, 137, 340–349. [Google Scholar] [CrossRef]
- Liu, Y.D.; Xiong, S.S.; Chen, D.B. Estimation of the TN and SOM contents in soil from GAN NAN navel orange plant area by NIR diffuse spectroscopy. Spectrosc. Spect. Anal. 2013, 33, 2679–2682. [Google Scholar]
- Tang, R.N.; Li, X.W.; Li, C.; Jiang, K.X.; Hu, W.F.; Wu, J.J. Estimation of total nitrogen content in rubber plantation soil based on hyperspectral and fractional order derivative. Electronics 2022, 11, 1956. [Google Scholar] [CrossRef]
- Liu, T.L.; Zhu, X.C.; Bai, X.Y.; Peng, Y.F.; Li, M.X.; Tian, Z.Y.; Jiang, Y.M.; Yang, G.J. Hyperspectral estimation model construction and accuracy comparison of soil organic matter content. Smart Agric. 2020, 2, 129–138. [Google Scholar]
- Liu, Z.M.; Li, X.Q.; Chen, G.L.; Ding, H.P.; Xu, M.G.; Yang, C.X. Inversion of soil total nitrogen content in Yunnan Rubber plantation based on hyperspectral. Trop. Agric. Sci. Technol. 2023, 46, 35–41. [Google Scholar]
- Wang, W.Q.; Gao, M.X.; Lang, K.; Wang, J.F. Hyperspectral estimation of total nitrogen in apple orchard soil based on wavelet transform. J. Shandong Agric. Univ. 2021, 52, 845–852. [Google Scholar] [CrossRef]
- Chen, H.Y.; Zhao, G.X.; Li, X.C.; Zhu, X.C.; Sui, L.; Wang, Y.J. Hyper-spectral estimation of soil organic matter content based on wavelet transformation. Chin. J. Appl. Ecol. 2011, 22, 2935–2942. [Google Scholar]
- Wang, L.W.; Wei, Y.X. Estimating the total nitrogen and total phosphorus content of wetland soils using hyperspectral models. Acta Ecol. Sin. 2016, 36, 5116–5125. [Google Scholar]
- Qiu, H.; Chen, H.Y.; Xing, S.H.; Zhang, L.M.; Dong, X.Y. Soil organic matter estimation models based on Hyperion data. J. Fujian Agric. For. Univ. 2017, 46, 460–467. [Google Scholar]
- Li, X.J.; Wang, M.L.; Zhao, M.; Shi, Y.H.; Gao, Q. Vineyard drought monitoring model based on multiple stepwise regression analysis. Agric. Res. Arid. Areas 2022, 40, 249–254. [Google Scholar]
- Nie, X.J.; Zhao, X.H.; Ammara, G.; Hong, W.W.; Zhang, H.B. Inversion of coal-derived carbon content in mine soils based on hyperspectral index and machine learning. J. Chin. Coal Soc. 2023, 48, 2869–2880. [Google Scholar]
- Li, C.; Zhang, G.W.; Zhou, Z.G.; Zhao, W.Q.; Meng, Y.L.; Chen, B.L.; Wang, Y.H. Hyperspectral parameters and prediction model of soil moisture in coastal saline. Chin. J. Appl. Ecol. 2016, 27, 525–531. [Google Scholar]
- Liu, J.F.; Zhao, Z.Y.; Li, C.Y.; Gao, Y.; Zhao, X.; Jiang, W.G.; Gong, Z. Estimation of apple tree canopy SPAD based on UAV multispectral remote sensing. J. Drain. Irrig. Mach. Eng. 2024. Available online: https://link.cnki.net/urlid/32.1814.TH.20240115.1641.004 (accessed on 16 February 2024).
- Leng, J.F.; Gao, X.; Zhu, J.P. The application of multiple linear regression statistical prediction models Statistics and decision-making. Stat. Decis. 2016, 7, 82–85. [Google Scholar]
- Wen, X. Applying MATLAB to Implement Neural Networks; National Defense Industry Press: Beijing, China, 2015; p. 95. [Google Scholar]
- Liu, B.Y.; Zhang, J.H.; Geng, S.C.; Tao, J.J.; Feng, Y. Estimation of N2o emission flus from heterotrophic nitrification process in global forest soils based on BP neural network model. Chin. J. Ecol. 2022, 41, 209–217. [Google Scholar] [CrossRef]
- Sun, C.Y.; Xie, K.M.; Cheng, M.Q. Mind-evolution-based machine learning framework and new development. J. Taiyuan Univ. Technol. 1999, 43, 3–7. [Google Scholar]
- Liu, H.J.; Zhang, X.L.; Zheng, S.F.; Tang, N.; Hu, Y.L. Black soil organic matter prediction model based on field hyperspectral reflectance. Spectrosc. Spect. Anal. 2010, 30, 3355–3358. [Google Scholar]
- Bai, G.S.; Zou, C.Y.; Du, S.N. Effects of self-sown grass on soil moisture and tree growth in apple orchard on Weibei dry plateau. Trans. CSAE 2018, 34, 151–158. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, X.P.; Yang, X.M.; Liang, A.Z.; Shi, X.H.; Fan, R.Q. Effects of data pretreatment and spectrum bands on near infrared spectroscopy model of soil organic carbon in black soil. ACTA Pedol. Sin. 2010, 47, 1005–1012. [Google Scholar]
- Philippe, L.; Baret, F.; Feret, J.B.; José, M.N.; Jean, M. R-M. Estimation of soil clay and calcium carbonate using laboratory, field and airborne hyperspectral measurements. Remote Sens. Environ. 2007, 112, 825–835. [Google Scholar]
- Peng, J.; Chi, C.M.; Xiang, H.Y.; Teng, H.F.; Shi, Z. Inversion of soil salt content based on continuum-removal method. ACTA Pedo Sin. 2014, 51, 459–469. [Google Scholar]
- Xiang, H.Y.; Liu, W.Y.; Peng, J.; Wang, J.Q.; Chi, C.M.; Niu, J.L. Predicting organic matter content in paddy soil using method of continuum removal in southern Xinjiang, China. Soils 2016, 48, 389–394. [Google Scholar]
- Yang, D.H.; Li, Y.Q.; Dao, J.; Wang, J.X. Estimation of soil main nutrient content based on unmanned aerial vehicle multispectral and ground hyperspectral remote sensing. Jiangsu Agri. Sci. 2022, 50, 178–186. [Google Scholar] [CrossRef]
- Wei, L.S. Mathematical Statistics; Science Press: Beijing, China, 2024; p. 1. [Google Scholar]
- Xu, Y.; Shao, G.C.; Ding, M.M.; Zhang, E.Z.; He, J. Inversion model of soil total nitrogen content based on ridge regression. J. Drain. Irrig. Mach. Eng. 2022, 40, 1159–1166. [Google Scholar]
- Ren, H.; Guo, C.L.; Zhao, Z.P.; He, Q.M.; Chen, D.M. Current status of vision and its influencing factors among primary students in Meilan district of Haikou city. Pract. Prev. Med. 2020, 27, 54–56. [Google Scholar]
- Xu, Y.M.; Lin, Q.Z.; Huang, X.H.; Shen, Y.; Wang, L. Experimental study on total nitrogen concentration in soil by VNIR reflectance spectrum. Geogr. Geo. Inform. Sci. 2005, 21, 19–22. [Google Scholar]
- Lu, Z.H.; Liu, X.Y.; Chang, S.J.; Yang, S.L.; Zhao, W.W.; Yang, Y.; Liu, A.J. Hyperspectral inversion of the surface soil N/P ratio in a grassland mining area based on the BP neural network. Pratac. Sci. 2018, 35, 2127–2136. [Google Scholar]
- Zhao, J.H.; Zhang, C.Y.; Min, L.; Li, N.; Wang, Y. Retrieval for soil moisture in farmland using multi-source remote sensing data and feature selection with GA-BP neural network. Trans. CSAE 2021, 37, 112–120. [Google Scholar]
- Wang, S.D.; Shi, P.J.; Zhang, H.B.; Wang, X.C. Retrieval of soil total nitrogen content in reclaimed farmland of mining area based on hyperspectral imaging. Chin. J. Ecol. 2019, 38, 294–301. [Google Scholar]



| Study Area | Sample Size | Index | Soil TN Content (%) | |||
|---|---|---|---|---|---|---|
| Young Fruit | Swelling | Quality | Postpartum | |||
| Modeling area | 100 | Max | 0.0840 | 0.0726 | 0.0882 | 0.0812 |
| Min | 0.0353 | 0.0254 | 0.0406 | 0.0307 | ||
| Mean | 0.0512 | 0.0427 | 0.0523 | 0.0482 | ||
| Validation area | 40 | Max | 0.0813 | 0.0764 | 0.0796 | 0.0779 |
| Min | 0.0339 | 0.0233 | 0.0328 | 0.0290 | ||
| Mean | 0.0526 | 0.0428 | 0.0528 | 0.0491 | ||
| Sampling Period | Input Spectrum | Regression Equation | R2 | RMSE |
|---|---|---|---|---|
| Young fruiting | x = R663 | y = −0.2146x + 0.0954 | 0.101 | 0.0087 |
| y = −349.8x3 + 228.8x2 − 49.818x + 3.6604 | 0.183 | 0.0083 | ||
| y = 0.1095e3.755x | 0.094 | 0.0091 | ||
| x = 1/R663 | y = 0.0098x + 0.0033 | 0.137 | 0.0086 | |
| y = 0.0251x3 − 0.3515x2 + 1.6407x − 2.5031 | 0.186 | 0.0083 | ||
| y = 0.022e0.171x | 0.104 | 0.0090 | ||
| x = LogR663 | y = −0.0461x − 0.0217 | 0.107 | 0.0087 | |
| y = −3.0554x3 − 14.048x2 − 21.523x − 10.938 | 0.189 | 0.0083 | ||
| y = 0.0142e0.804x | 0.099 | 0.0089 | ||
| x = | y = −0.1991x + 0.1416 | 0.104 | 0.0087 | |
| y = −263.37x3 + 368.04x2 − 171.39x + 26.646 | 0.190 | 0.0083 | ||
| y = 0.2445e3.477x | 0.097 | 0.0092 | ||
| Swelling fruit | x = R666 | y = −0.2376x + 0.0982 | 0.238 | 0.0081 |
| y = −34.815x3 + 28.138x2 − 7.6531x + 0.7374 | 0.264 | 0.0080 | ||
| y = 0.1394e5.166x | 0.227 | 0.0082 | ||
| x = 1/R666 | y = 0.013x − 0.0134 | 0.251 | 0.0081 | |
| y = −0.0004x3 + 0.013x2 − 0.0782x + 0.1682 | 0.264 | 0.0080 | ||
| y = 0.0124e0.282x | 0.2376 | 0.0084 | ||
| x = LogR666 | y = −0.0558x − 0.0387 | 0.245 | 0.0081 | |
| y = −0.1746x3 − 0.5915x2 − 0.6622x − 0.2077 | 0.264 | 0.0082 | ||
| y = 0.0071e1.212x | 0.233 | 0.0083 | ||
| x = | y = −0.2306x + 0.154 | 0.241 | 0.0081 | |
| y = −21.463x3 + 34.296x2 − 18.313x + 3.304 | 0.264 | 0.0082 | ||
| y = 0.4688e5.01x | 0.230 | 0.0084 | ||
| Quality period | x = R666 | y = −0.3209x + 0.1203 | 0.215 | 0.0081 |
| y = 24.822x3 − 9.6462x2 + 0.4149x + 0.1602 | 0.246 | 0.0080 | ||
| y = 0.1721e5.679x | 0.220 | 0.0081 | ||
| x = 1/R666 | y = 0.0145x − 0.0166 | 0.228 | 0.0081 | |
| y = −0.0054x3 + 0.0873x2 − 0.4458x + 0.7828 | 0.245 | 0.0081 | ||
| y = 0.0153e0.2568x | 0.233 | 0.0081 | ||
| x = LogR666 | y = −0.0686x − 0.0543 | 0.222 | 0.0082 | |
| y = 0.438x3 + 2.2879x2 + 3.8672x + 2.1798 | 0.246 | 0.0080 | ||
| y = 0.0078e1.213x | 0.227 | 0.0081 | ||
| x = | y = −0.2971x + 0.189 | 0.219 | 0.0081 | |
| y = 28.267x3 − 34.101x2 + 13.124x − 1.5215 | 0.246 | 0.0080 | ||
| y = 0.5798e5.255x | 0.224 | 0.0082 | ||
| Postpartum period | x = R664 | y = −0.4319x + 0.1418 | 0.371 | 0.0074 |
| y = −621.75x3 + 418.04x2 − 93.809x + 7.0712 | 0.478 | 0.0071 | ||
| y = 0.3988e9.803x | 0.4287 | 0.0072 | ||
| x = 1/R664 | y = 0.0206x − 0.0471 | 0.393 | 0.0074 | |
| y = 0.0473x3 − 0.635x2 + 2.8474x − 4.2225 | 0.477 | 0.0071 | ||
| y = 0.0056e0.4627x | 0.4432 | 0.0072 | ||
| x = LogR664 | y = −0.0945x − 0.0964 | 0.382 | 0.0074 | |
| y = −5.5455x3 − 24.909x2 − 37.326x − 18.615 | 0.478 | 0.0071 | ||
| y = 0.0018e2.135x | 0.436 | 0.0073 | ||
| x = | y = −0.4043x + 0.2364 | 0.377 | 0.0075 | |
| y = −417.18x3 + 670.28x2 − 317.29x + 50.13 | 0.479 | 0.0071 | ||
| y = 3.377e9.156x | 0.433 | 0.0072 |
| Sampling Period | Input Spectrum | Regression Equation | R2 | RMSE |
|---|---|---|---|---|
| Young fruiting | x = (R)′ | y = 0.1049 − 46.70x571 + 116.09x849 − 40.17x1425 − 6.29x1925 | 0.71 | 0.0049 |
| x = (1/R)′ | y = 0.0409 − 9.17x809 − 3.46x849 + 5.57x1427 + 0.71x1914 | 0.73 | 0.0047 | |
| x = (LogR)′ | y = 0.0663 − 5.49x559 + 47.46x809 − 10.96x1426 + 0.27x1927 | 0.70 | 0.0050 | |
| x = ()′ | y = 0.0915 − 38.39x559 + 150.86x809 − 45.39x1425 − 2.49x1926 | 0.74 | 0.0047 | |
| x = CR | y = −0.0424 − 0.49x664 − 2.39x694 + 2.77x878 + 0.22x2222 | 0.73 | 0.0048 | |
| Swelling fruit | x = (R)′ | y = 0.0758 − 22.29x567 + 110.10x836 − 41.68x1430 − 8.42x1923 | 0.71 | 0.0043 |
| x = (1/R)′ | y = 0.0274 − 6.50x803 − 8.53x837 + 5.07x1430 + 0.87x1916 | 0.71 | 0.0051 | |
| x = (LogR)′ | y = 0.0986 − 9.46x561 + 37.68x836 − 4.75x1430 + 0.33x1923 | 0.72 | 0.0049 | |
| x = ()′ | y = 0.0979 − 32.91x548 + 103.57x836 − 52.49x1429 − 8.73x1922 | 0.75 | 0.0047 | |
| x = CR | y = 0.9725 + 0.07x499 − 5.77x692 + 4.57x840 + 0.29x2215 | 0.74 | 0.0047 | |
| Quality period | x = (R)′ | y = 0.0847 − 28.52x563 + 101.52x836 − 28.97x1428 − 15.3x1915 | 0.73 | 0.0042 |
| x = (1/R)′ | y = 0.0451 − 4.82x800 − 2.84x827 + 4.87x1415 + 1.15x1915 | 0.72 | 0.0043 | |
| x = (LogR)′ | y = 0.0751 − 3.94x561 + 31.18x827 − 5.83x1428 − 5.42x1915 | 0.72 | 0.0043 | |
| x = ()′ | y = 0.1007 − 40.73x533 + 93.54x827 − 38.18x1428 − 17.50x1915 | 0.76 | 0.0040 | |
| x = CR | y = 1.5867 − 1.2x640 − 3.63x699 + 2.77x849 + 0.57x2219 | 0.78 | 0.0038 | |
| Postpartum period | x = (R)′ | y = 0.0799 − 36.67x585 + 151.09x836 − 33.74x1428 − 13.57x1924 | 0.73 | 0.0044 |
| x = (1/R)′ | y = 0.0345 − 6.06x817 − 7.12x837 + 6.76x1415 + 2.09x1914 | 0.74 | 0.0043 | |
| x = (LogR)′ | y = 0.0951 − 9.69x562 + 39.75x817 − 3.77x1428 − 7.73x1914 | 0.77 | 0.0039 | |
| x = ()′ | y = 0.1074 − 47.69x548 + 137.48x837 − 37.11x1428 − 13.51x1915 | 0.76 | 0.0040 | |
| x = CR | y = 0.9601 + 2.73x662 − 0.81x678 + 1.89x863 + 0.79x2223 | 0.75 | 0.0041 |
| Sampling Period | Input Spectrum | Variables Number | Regression Equation | R2 | RMSE | Max VIF |
|---|---|---|---|---|---|---|
| Young fruiting | x = (R)′ | 8 | y = 0.0848 − 66.35x570 + 82.79x679 + 79.45x808 + 1.66x845 + 10.11x1297 − 41.49x1423 − 14.43x1967 + 1.21x2375 | 0.77 | 0.0043 | 4.69 |
| x = (1/R)′ | 10 | y = 0.0396 + 0.83x541 + 0.72x574 − 2.75x678 − 3.90x706 − 6.14x808 + 3.34x1462 + 2.28x1589 + 3.37x1661 + 0.19x1780 − 0.30x2339 | 0.81 | 0.004 | 8.29 | |
| x = (LogR)′ | 11 | y = 0.0817 − 9.73x541 + 26.18x808 + 31.94x848 − 3.99x1462 − 8.08x1561 − 11.64x1696 − 1.36x1804 − 4.08x2046 − 0.46x2138 − 0.70x2366 − 0.34x2423 | 0.81 | 0.004 | 7.55 | |
| x = ()′ | 12 | y = 0.0874 − 36.52x541 + 164.14x808 − 13.20x975 + 21.72x1001 + 28.58x1281 − 58.75x1422 + 14.54x1588 + 1.73x2138 + 9.52x2236 + 3.41x2311 + 3.76x2342 − 1.04x2423 | 0.76 | 0.0044 | 6.85 | |
| x = CR | 10 | y = 1.5527 − 5.71x693 + 4.95x712 − 9.21x806 + 1.90x876 − 0.08x972 + 2.10x1092 + 3.72x1695 + 1.16x1830 − 0.52x2287 + 0.20x2351 | 0.82 | 0.0039 | 8.57 | |
| Swelling fruit | x = (R)′ | 8 | y = 0.0761 − 46.65x580 + 55.23x691 + 70.7x813 − 9.69x1009 + 23.2x1141 + 3.28x1374 − 65.84x1428 + 3.66x2153 | 0.73 | 0.0049 | 5.01 |
| x = (1/R)′ | 10 | y = 0.0373 + 0.75x554 + 2.18x583 − 3.45x680 − 2.6x691 − 4.5x701 − 4.78x812 − 1.88x1099 + 7.73x1185 − 1.59x2097 − 0.08x2301 | 0.79 | 0.0043 | 9.58 | |
| x = (LogR)′ | 11 | y = 0.0852 − 5.08x554 − 9.97x560 + 14.49x703 + 27.24x777 + 3.26x1062 + 24.78x1192 − 2.8x1367 + 0.61x1627 − 4.98x1931 + 0.39x2301 − 0.19x2438 | 0.81 | 0.0040 | 7.17 | |
| x = ()′ | 12 | y = 0.0837 − 27.62x565 − 37.51x580 + 105.86x719 + 27.28x775 + 26.34x901 + 7.42x1130 + 16.83x1292 − 18x1375 − 53.69x1418 + 17.26x1740 − 15.78x1931 + 0.06x2296 | 0.78 | 0.0044 | 6.57 | |
| x = CR | 10 | y = 3.3908 − 2.85x675 + 4.72x837 − 1.9x983 − 1.81x1008 + 2.58x1087 − 3.77x1352 + 0.5x1841 − 1.36x2092 + 1.17x2188 − 0.57x2293 | 0.84 | 0.0037 | 7.11 | |
| Quality period | x = (R)′ | 8 | y = 0.0992 + 7.34x402 − 27.67x556 − 42.26x562 + 126.85x893 + 16.7x1000 + 23.34x1020 + 9.85x1330 + 4.28x2147 | 0.66 | 0.0047 | 5.75 |
| x = (1/R)′ | 10 | y = 0.0519 + 0.05x428 − 0.05x435 + 0.53x511 − 7.06x816 − 6.96x826 + 0.37x864 + 0.37x2041 + 0.33x2184 − 0.47x2313 + 0.06x2450 | 0.74 | 0.0041 | 6.28 | |
| x = (LogR)′ | 11 | y = 0.0836 − 7.04x555 − 6.22x590 + 15.12x677 + 20.32x826 + 10.25x864 + 15.25x1328 + 0.27x1752 − 1.6x2041 + 3.15x2179 − 1.08x2292 − 0.21x2450 | 0.80 | 0.0036 | 5.59 | |
| x = ()′ | 12 | y = 0.1187 − 48.73x543 − 33.76x549 + 109.16x802 + 4.64x865 − 21.4x1547 + 61.57x1572 + 41.88x1579 − 8.63x1862 + 17.39x2130 − 3.69x2192 + 0.32x2240 − 1.43x2213 | 0.79 | 0.0037 | 8.31 | |
| x = CR | 10 | y = −20.7013 + 0.11x490 − 4.88x698 − 6.61x752 − 5.02x777 + 75.52x779 − 37.54x780 + 4.01x844 − 5.66x1322 + 1.39x1332 − 0.54x2066 | 0.85 | 0.0031 | 9.21 | |
| Postpartum period | x = (R)′ | 8 | y = 0.0765 − 24.13x562 − 86.39x660 + 33.61x679 + 91.15x809 + 83.75x815 − 22.64x1922 − 3.92x2255 + 4.53x2347 | 0.79 | 0.0038 | 7.04 |
| x = (1/R)′ | 10 | y = 0.0351 + 0.15x476 + 1.41x551 − 6.48x679 − 7.35x837 − 7.37x1541 − 9.32x1575 + 3.78x1666 + 0.85x1676 + 1.24x1771 − 0.53x2269 | 0.81 | 0.0034 | 8.81 | |
| x = (LogR)′ | 11 | y = 0.0994 − 11.48x541 + 28.76x829 + 23.56x836 + 6.79x1542 + 5.84x1772 − 0.71x2135 + 2.55x2198 + 1.42x2269 − 0.42x2316 + 0.84x2391 + 0.4x2401 | 0.80 | 0.0036 | 5.42 | |
| x = ()′ | 12 | y = 0.1133 − 65.15x562 + 76.01x809 + 12.11x858 + 26.67x1044 + 30.36x1227 + 1.04x1550 − 14.9x1602 + 15.07x1676 − 27.51x1912 − 15.56x2070 + 7.35x2199 + 8.81x2269 | 0.79 | 0.0037 | 7.57 | |
| x = CR | 10 | y = 39.6808 − 3.47x676 − 41.67x773 + 2.92x858 − 1.78x974 + 4.26x1120 − 2.69x1732 + 2.71x1746 − 0.66x1841 + 0.85x1874 − 0.08x2437 | 0.82 | 0.0034 | 6.91 |
| Sensitive Band Screening | Correlation Analysis | Stepwise Multiple Linear Regression | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sampling Period | Input Spectrum | Variables Number | Modeling | Validation | Variables Number | Modeling | Validation | ||||
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | ||||
| Young fruiting | (R)′ | 5 | 0.75 | 0.0045 | 0.73 | 0.0068 | 8 | 0.78 | 0.0048 | 0.76 | 0.0065 |
| (1/R)′ | 5 | 0.75 | 0.0046 | 0.72 | 0.0070 | 10 | 0.83 | 0.0045 | 0.82 | 0.0056 | |
| (LogR)′ | 5 | 0.73 | 0.0048 | 0.75 | 0.0066 | 11 | 0.86 | 0.0043 | 0.85 | 0.0052 | |
| ()′ | 5 | 0.77 | 0.0044 | 0.76 | 0.0065 | 12 | 0.83 | 0.0045 | 0.81 | 0.0058 | |
| CR | 5 | 0.74 | 0.0048 | 0.71 | 0.0072 | 10 | 0.87 | 0.0043 | 0.87 | 0.0047 | |
| Swelling fruit | (R)′ | 5 | 0.74 | 0.0042 | 0.68 | 0.0060 | 8 | 0.85 | 0.0042 | 0.84 | 0.0043 |
| (1/R)′ | 5 | 0.72 | 0.0045 | 0.66 | 0.0063 | 10 | 0.85 | 0.0041 | 0.84 | 0.0042 | |
| (LogR)′ | 5 | 0.73 | 0.0042 | 0.71 | 0.0058 | 11 | 0.85 | 0.0037 | 0.87 | 0.0038 | |
| ()′ | 5 | 0.75 | 0.0041 | 0.76 | 0.0053 | 12 | 0.84 | 0.0037 | 0.87 | 0.0038 | |
| CR | 5 | 0.81 | 0.0040 | 0.79 | 0.0041 | 10 | 0.86 | 0.0033 | 0.89 | 0.0035 | |
| Quality period | (R)′ | 5 | 0.75 | 0.0041 | 0.68 | 0.0069 | 8 | 0.82 | 0.0048 | 0.69 | 0.0068 |
| (1/R)′ | 5 | 0.73 | 0.0042 | 0.66 | 0.0070 | 10 | 0.84 | 0.0046 | 0.81 | 0.0053 | |
| (LogR)′ | 5 | 0.72 | 0.0043 | 0.60 | 0.0077 | 11 | 0.85 | 0.0046 | 0.82 | 0.0052 | |
| ()′ | 5 | 0.76 | 0.0040 | 0.65 | 0.0072 | 12 | 0.78 | 0.0051 | 0.74 | 0.0062 | |
| CR | 5 | 0.78 | 0.0038 | 0.66 | 0.0071 | 10 | 0.86 | 0.0043 | 0.84 | 0.0049 | |
| Postpartum period | (R)′ | 5 | 0.75 | 0.0042 | 0.70 | 0.0063 | 8 | 0.87 | 0.0043 | 0.85 | 0.0045 |
| (1/R)′ | 5 | 0.77 | 0.0055 | 0.69 | 0.0064 | 10 | 0.87 | 0.0043 | 0.86 | 0.0044 | |
| (LogR)′ | 5 | 0.77 | 0.0056 | 0.70 | 0.0063 | 11 | 0.84 | 0.0046 | 0.83 | 0.0047 | |
| ()′ | 5 | 0.77 | 0.0055 | 0.71 | 0.0062 | 12 | 0.85 | 0.0050 | 0.80 | 0.0051 | |
| CR | 5 | 0.79 | 0.0053 | 0.75 | 0.0057 | 10 | 0.88 | 0.0038 | 0.87 | 0.0042 | |
| Spectral Characteristic Index | Fertilization Period | |||||||
|---|---|---|---|---|---|---|---|---|
| Young Fruiting | Swelling Fruit | Quality Period | Postpartum Period | |||||
| Band Combination | R | Band Combination | R | Band Combination | R | Band Combination | R | |
| RSI | (R860, R870) | 0.84 | (R835, R844) | 0.80 | (R829, R814) | 0.78 | (R826, R842) | 0.89 |
| (R1907, R1941) | −0.80 | (R1905, R1936) | −0.84 | (R1902, R1949) | −0.80 | (R1909, R1926) | −0.91 | |
| (R2203, R2283) | −0.77 | (R2210, R2292) | −0.82 | (R2203, R2216) | −0.78 | (R2213, R2300) | −0.89 | |
| DI | (R1907, R1940) | −0.80 | (R1906, R1935) | −0.86 | (R1903, R1949) | −0.81 | (R1909, R1926) | −0.91 |
| (R2208, R2285) | −0.77 | (R2210, R2291) | −0.82 | (R2215, R2303) | −0.79 | (R2230, R2267) | −0.91 | |
| NDSI | (R1907, R1943) | 0.83 | (R1907, R1937) | 0.82 | (R1909, R1948) | 0.77 | (R1910, R1934) | 0.92 |
| (R2202, R2283) | 0.80 | (R2209, R2286) | 0.83 | (R2163, R2218) | 0.78 | (R2211, R2285) | 0.89 | |
| Spectral Characteristic Index | Band Combination | R |
|---|---|---|
| RSI | (R808, R810) | 0.62 |
| (R1904, R1949) | −0.83 | |
| (R2221, R2300) | −0.72 | |
| DI | (R1904, R1949) | −0.85 |
| (R2210, R2286) | 0.79 | |
| NDSI | (R1908, R1954) | 0.79 |
| (R2210, R2286) | 0.68 |
| Model | Multiple Linear Regression | Mind Evolutionary Algorithm-BPNN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sampling Period | Input Spectrum | Variables Number | Modeling | Validation | Variables Number | Modeling | Validation | ||||
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | ||||
| Young fruiting | (R)′ | 15 | 0.83 | 0.0037 | 0.77 | 0.0064 | 15 | 0.89 | 0.0044 | 0.88 | 0.0047 |
| (1/R)′ | 17 | 0.85 | 0.0036 | 0.80 | 0.0058 | 17 | 0.88 | 0.0045 | 0.85 | 0.0045 | |
| (LogR)′ | 18 | 0.86 | 0.0035 | 0.78 | 0.0062 | 18 | 0.91 | 0.0040 | 0.88 | 0.0047 | |
| ()′ | 19 | 0.83 | 0.0038 | 0.74 | 0.0068 | 19 | 0.92 | 0.0038 | 0.90 | 0.0040 | |
| CR | 17 | 0.87 | 0.0032 | 0.81 | 0.0058 | 17 | 0.94 | 0.0032 | 0.92 | 0.0033 | |
| Swelling fruit | (R)′ | 15 | 0.81 | 0.0041 | 0.73 | 0.0056 | 15 | 0.93 | 0.0290 | 0.92 | 0.0031 |
| (1/R)′ | 17 | 0.86 | 0.0035 | 0.79 | 0.0050 | 17 | 0.92 | 0.0030 | 0.91 | 0.0032 | |
| (LogR)′ | 18 | 0.83 | 0.0038 | 0.84 | 0.0043 | 18 | 0.93 | 0.0027 | 0.91 | 0.0031 | |
| ()′ | 19 | 0.82 | 0.0039 | 0.78 | 0.0050 | 19 | 0.92 | 0.0031 | 0.91 | 0.0031 | |
| CR | 17 | 0.86 | 0.0035 | 0.85 | 0.0042 | 17 | 0.95 | 0.0024 | 0.93 | 0.0029 | |
| Quality period | (R)′ | 15 | 0.85 | 0.0031 | 0.68 | 0.0069 | 15 | 0.87 | 0.0043 | 0.85 | 0.0045 |
| (1/R)′ | 17 | 0.85 | 0.0031 | 0.66 | 0.0071 | 17 | 0.90 | 0.0039 | 0.88 | 0.0041 | |
| (LogR)′ | 18 | 0.85 | 0.0030 | 0.68 | 0.0068 | 18 | 0.88 | 0.0042 | 0.85 | 0.0045 | |
| ()′ | 19 | 0.86 | 0.0030 | 0.69 | 0.0068 | 19 | 0.89 | 0.0040 | 0.88 | 0.0040 | |
| CR | 17 | 0.88 | 0.0028 | 0.71 | 0.0065 | 17 | 0.92 | 0.0035 | 0.91 | 0.0037 | |
| Postpartum period | (R)′ | 15 | 0.82 | 0.0033 | 0.82 | 0.0048 | 15 | 0.92 | 0.0033 | 0.89 | 0.0035 |
| (1/R)′ | 17 | 0.83 | 0.0032 | 0.81 | 0.0051 | 17 | 0.92 | 0.0032 | 0.90 | 0.0034 | |
| (LogR)′ | 18 | 0.83 | 0.0032 | 0.82 | 0.0049 | 18 | 0.91 | 0.0035 | 0.87 | 0.0040 | |
| ()′ | 19 | 0.82 | 0.0034 | 0.79 | 0.0052 | 19 | 0.90 | 0.0036 | 0.87 | 0.0041 | |
| CR | 17 | 0.87 | 0.0032 | 0.86 | 0.0043 | 17 | 0.94 | 0.0027 | 0.93 | 0.0033 | |
| Model | Input Spectrum | Variables Number | Modeling | Validation | Input Spectrum | Variables Number | Modeling | Validation | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |||||
| MLR | R | 1 | 0.35 | 0.0081 | 0.23 | 0.012 | R + SCI | 8 | 0.788 | 0.0045 | 0.611 | 0.0079 |
| (R)′ | 15 | 0.814 | 0.0042 | 0.793 | 0.0057 | (R)′ + SCI | 22 | 0.829 | 0.0040 | 0.798 | 0.0057 | |
| (1/R)′ | 7 | 0.838 | 0.0039 | 0.797 | 0.0057 | (1/R)′ + SCI | 14 | 0.853 | 0.0038 | 0.804 | 0.0056 | |
| (LogR)′ | 12 | 0.835 | 0.004 | 0.796 | 0.0057 | (LogR)′ + SCI | 19 | 0.854 | 0.0037 | 0.813 | 0.0055 | |
| ()′ | 14 | 0.841 | 0.0039 | 0.826 | 0.0053 | ()′ + SCI | 21 | 0.859 | 0.0035 | 0.831 | 0.0049 | |
| CR | 10 | 0.823 | 0.0041 | 0.812 | 0.0055 | CR + SCI | 17 | 0.838 | 0.0039 | 0.828 | 0.0051 | |
| MEA-BP | (R)′ | 15 | 0.826 | 0.0052 | 0.814 | 0.0054 | (R)′ + SCI | 22 | 0.865 | 0.0044 | 0.857 | 0.0045 |
| (1/R)′ | 7 | 0.844 | 0.0051 | 0.826 | 0.0052 | (1/R)′ + SCI | 14 | 0.869 | 0.0042 | 0.861 | 0.0045 | |
| (LogR)′ | 12 | 0.845 | 0.004 | 0.822 | 0.004 | (LogR)′ + SCI | 19 | 0.863 | 0.0045 | 0.855 | 0.0046 | |
| ()′ | 14 | 0.855 | 0.0039 | 0.837 | 0.0051 | ()′ + SCI | 21 | 0.872 | 0.004 | 0.867 | 0.0046 | |
| CR | 10 | 0.861 | 0.0038 | 0.841 | 0.0041 | (CR)′ + SCI | 17 | 0.899 | 0.0038 | 0.890 | 0.0041 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Wang, W.; Wang, H.; Li, R. Selection of Spectral Parameters and Optimization of Estimation Models for Soil Total Nitrogen Content during Fertilization Period in Apple Orchards. Horticulturae 2024, 10, 358. https://doi.org/10.3390/horticulturae10040358
Gao Z, Wang W, Wang H, Li R. Selection of Spectral Parameters and Optimization of Estimation Models for Soil Total Nitrogen Content during Fertilization Period in Apple Orchards. Horticulturae. 2024; 10(4):358. https://doi.org/10.3390/horticulturae10040358
Chicago/Turabian StyleGao, Zhilin, Wenqian Wang, Hongjia Wang, and Ruiyan Li. 2024. "Selection of Spectral Parameters and Optimization of Estimation Models for Soil Total Nitrogen Content during Fertilization Period in Apple Orchards" Horticulturae 10, no. 4: 358. https://doi.org/10.3390/horticulturae10040358
APA StyleGao, Z., Wang, W., Wang, H., & Li, R. (2024). Selection of Spectral Parameters and Optimization of Estimation Models for Soil Total Nitrogen Content during Fertilization Period in Apple Orchards. Horticulturae, 10(4), 358. https://doi.org/10.3390/horticulturae10040358





