Cobalt(II) and Nickel(II) Cubane {M4O4} Complexes Derived from Di-2-pyridyl Ketone and Benzoate: Syntheses, Structure and Magnetic Properties †
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Characterization
2.2. Synthesis of [Co4{(py)2C(O)(OH)}4(O2CPh)4] (1) and [Ni4{(py)2C(O)(OH)}4(O2CPh)4] (2)
2.3. X-Ray Data Collection and Structure Refinement
2.4. Computational Methodology
3. Results
3.1. Structure Description
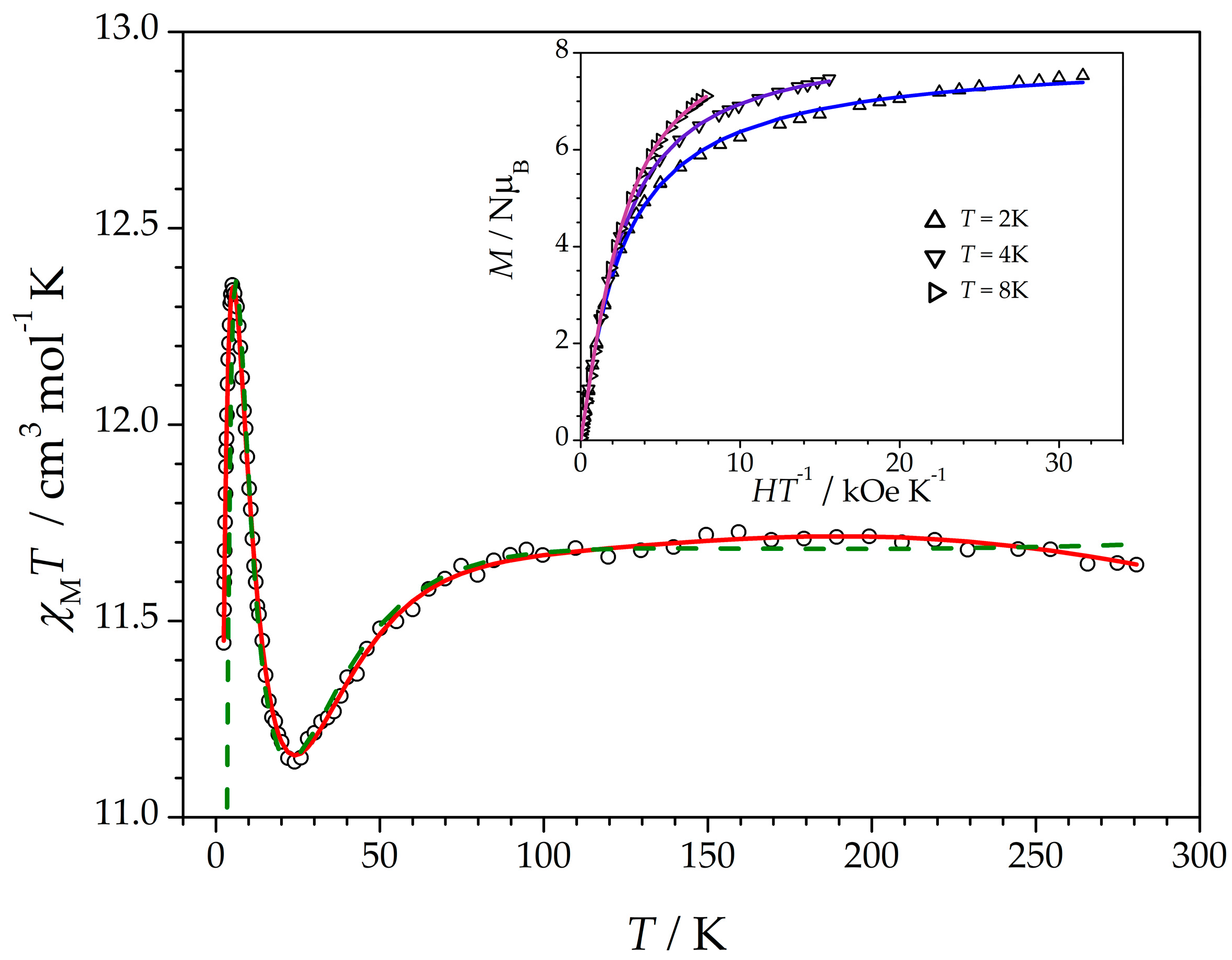
3.2. Magnetic Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Aromí, G.; Brechin, E.K. Synthesis of 3d Metallic Single-Molecule Magnets. In Single-Molecule Magnets and Related Phenomena; Winpenny, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; Volume 122, pp. 1–67. [Google Scholar]
- Sessoli, R.; Powell, A.K. Strategies towards single molecule magnets based on lanthanide ions. Coord. Chem. Rev. 2009, 253, 2328–2341. [Google Scholar] [CrossRef]
- Christou, G. Single-molecule magnets: A molecular approach to nanoscale magnetic materials. Polyhedron 2005, 24, 2065–2075. [Google Scholar] [CrossRef]
- Tasiopoulos, A.J.; Vinslava, A.; Wernsdorfer, W.; Abboud, K.A.; Christou, G. Giant Single-Molecule Magnets: A {Mn84} Torus and Its Supramolecular Nanotubes. Angew. Chem. Int. Ed. 2004, 43, 2117–2121. [Google Scholar] [CrossRef]
- Manoli, M.; Inglis, R.; Manos, M.J.; Nastopoulos, V.; Wernsdorfer, W.; Brechin, E.K.; Tasiopoulos, A.J. A [Mn32] Double-Decker Wheel. Angew. Chem. Int. Ed. 2011, 50, 4441–4444. [Google Scholar] [CrossRef] [PubMed]
- Powell, G.W.; Lancashire, H.N.; Brechin, E.K.; Collison, D.; Heath, S.L.; Mallah, T.; Wernsdorfer, W. Building Molecular Minerals: All Ferric Pieces of Molecular Magnetite. Angew. Chem. Int. Ed. 2004, 43, 5772–5775. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.J.; Wu, Y.; Long, L.S.; Zheng, L.S.; Zheng, Z. A Chiral 60-Metal Sodalite Cage Featuring 24 Vertex-Sharing [Er4(μ3-OH)4] Cubanes. J. Am. Chem. Soc. 2009, 131, 6918–6919. [Google Scholar] [CrossRef]
- Wang, W.G.; Zhou, A.J.; Zhang, W.X.; Tong, M.L.; Chen, X.M.; Nakano, M.; Beedle, C.C.; Hendrickson, D.N. Giant Heterometallic Cu17Mn28 Cluster with Td Symmetry and High-Spin Ground State. J. Am. Chem. Soc. 2007, 129, 1014–1015. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, Y.J.; Wang, Z.M.; Gao, S. A 64-Nuclear Cubic Cage Incorporating Propeller-like FeIII8 Apices and HCOO− Edges. J. Am. Chem. Soc. 2008, 130, 10500–10501. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Yao, S.; Li, Y.G.; Clerac, R.; Lu, Y.; Su, Z.M.; Wang, E.B. Protein-Sized Chiral Fe168 Cages with NbO− Type Topology. J. Am. Chem. Soc. 2009, 131, 14600–14601. [Google Scholar] [CrossRef]
- Müller, A.; Krickemeyer, E.; Das, S.K.; Kögerler, P.; Sarkar, S.; Bögge, H.; Schmidtmann, M.; Sarkar, S. Linking Icosahedral, Strong Molecular Magnets {Mo} to Layers—A Solid-State Reaction at Room Temperature. Angew. Chem. Int. Ed. 2000, 39, 1612–1614. [Google Scholar] [CrossRef]
- Moushi, E.E.; Lampropoulos, C.; Wernsdorfer, W.; Nastopoulos, V.; Christou, G.; Tasiopoulos, A.J. Inducing Single-Molecule Magnetism in a Family of Loop-of-Loops Aggregates: Heterometallic Mn40Na4 Clusters and the Homometallic Mn44 Analogue. J. Am. Chem. Soc. 2010, 132, 16146–16155. [Google Scholar] [CrossRef] [PubMed]
- Kong, J.; Ren, Y.P.; Chen, W.X.; Long, L.S.; Zheng, Z.; Huang, R.B.; Zheng, L.S. A Four-Shell, Nesting Doll-like 3d–4f Cluster Containing 108 Metal Ions. Angew. Chem. Int. Ed. 2008, 47, 2398–2401. [Google Scholar] [CrossRef] [PubMed]
- Moushi, E.E.; Lampropoulos, C.; Wernsdorfer, W.; Nastopoulos, V.; Christou, G.; Tasiopoulos, A. A Large [Mn10Na]4 Loop of Four Linked Mn10 Loops. J. Inorg. Chem. 2007, 46, 3795–3797. [Google Scholar] [CrossRef] [PubMed]
- Stamatatos, T.C.; Abboud, K.A.; Wernsdorfer, W.; Christou, G. “Spin Tweaking” of a High-Spin Molecule: An Mn25 Single-Molecule Magnet with an S=61/2 Ground State. Angew. Chem. Int. Ed. 2007, 46, 884–888. [Google Scholar] [CrossRef]
- Ponomaryov, A.N.; Kim, N.; Hwang, J.; Nojiri, H.; Van Tol, J.; Ozarowski, A.; Park, J.; Jang, Z.; Suh, B.; Yoon, S.; et al. Structural Tailoring Effects on the Magnetic Behavior of Symmetric and Asymmetric Cubane-Type Ni Complexes. Chem. Asian J. 2013, 8, 1152–1159. [Google Scholar] [CrossRef]
- Aromí, G.; Bouwman, E.; Burzurí, E.; Carbonera, C.; Krzystek, J.; Luis, F.; Schlegel, C.; Van Slageren, J.; Tanase, S.; Teat, S.J. A Novel Ni4 Complex Exhibiting Microsecond Quantum Tunneling of the Magnetization. Chem. Eur. J. 2008, 14, 11158–11166. [Google Scholar] [CrossRef]
- Herchel, R.; Nemec, I.; Machata, M.; Trávníček, Z. Solvent- Induced Structural Diversity in Tetranuclear Ni (II) Schiff-Base Complexes: The First Ni4 Single-Molecule Magnet with a Defective Dicubane-like Topology. Dalton Trans. 2016, 45, 18622–18634. [Google Scholar] [CrossRef]
- Ferguson, A.; Lawrence, J.; Parkin, A.; Sanchez-Benitez, J.; Kamenev, K.V.; Brechin, E.K.; Wernsdorfer, W.; Hill, S.; Murrie, M. Synthesis and Characterisation of a Ni4 Single-Molecule Magnet with S4 Symmetry. Dalton Trans. 2008, 45, 6409–6414. [Google Scholar] [CrossRef]
- Escobar, L.B.L.; Guedes, G.P.; Soriano, S.; Marbey, J.; Hill, S.; Novak, M.A.; Vaz, M.G.F. Synthesis, Magnetic and High-Field EPR Investigation of Two Tetranuclear NiII-Based Complexes. Inorg. Chem. 2019, 58, 14420–14428. [Google Scholar] [CrossRef]
- Yang, E.-C.; Wernsdorfer, W.; Hill, S.; Edwards, R.S.; Nakano, M.; Maccagnano, S.; Zakharov, L.N.; Rheingold, A.L.; Christou, G.; Hendrickson, D.N. Exchange bias in Ni4 single-molecule magnets. Polyhedron 2003, 22, 1727–1733. [Google Scholar] [CrossRef]
- Yang, E.-C.; Wernsdorfer, W.; Zakharov, L.N.; Karaki, Y.; Yamaguchi, A.; Isidro, R.M.; Lu, G.D.; Wilson, S.A.; Rheingold, A.L.; Ishimoto, H.; et al. Fast Magnetization Tunneling in Tetranickel (II) Single-Molecule Magnets. Inorg. Chem. 2006, 45, 529–546. [Google Scholar] [CrossRef]
- Moragues-Canovas, M.; Helliwell, M.; Ricard, L.; Riviere, E.; Wernsdorfer, W.; Brechin, E.; Mallah, T. An Ni4 Single-Molecule Magnet: Synthesis, Structure and Low-Temperature Magnetic Behavior. Eur. J. Inorg. Chem. 2004, 2004, 2219–2222. [Google Scholar] [CrossRef]
- Guedes, G.P.; Soriano, S.; Comerlato, N.M.; Speziali, N.L.; Lahti, P.M.; Novak, M.A.; Vaz, M.G.F. Two cobalt (II) cubane compounds: The key role of small ligand changes on the crystal packing and magnetic properties. Eur. J. Inorg. 2012, 2012, 5642–5648. [Google Scholar] [CrossRef]
- Yang, E.-C.; Hendrickson, D.N.; Wernsdorfer, W.; Nakano, M.; Zakharov, L.N.; Sommer, R.D.; Rheingold, A.L.; Ledezma-Gairaud, M.; Christou, G. Cobalt single-molecule magnet. J. Appl. Phys. 2002, 91, 7382–7384. [Google Scholar] [CrossRef]
- Zhang, S.-H.; Zhang, Y.D.; Zou, H.H.; Guo, J.J.; Li, H.P.; Song, Y.; Liang, H. A family of cubane cobalt and nickel clusters: Syntheses, structures and magnetic properties. Inorg. Chim. Acta 2013, 396, 119–125. [Google Scholar] [CrossRef]
- Ma, X.-F.; Wang, Z.; Chen, X.-L.; Kurmoo, M.; Zeng, M.-H. Ligand effect on the single-molecule magnetism of tetranuclear Co (II) cubane. Inorg. Chem. 2017, 56, 15178–15186. [Google Scholar] [CrossRef]
- Wu, Y.; Xi, J.; Xiao, T.; Ferrando-Soria, J.; Ouyang, Z.; Wang, Z.; Luo, S.; Liu, X.; Pardo, E. Switching of easy-axis to easy-plane anisotropy in cobalt (II) complexes. Inorg. Chem. Front. 2021, 8, 5158–5168. [Google Scholar] [CrossRef]
- Galloway, K.W.; Whyte, A.M.; Wernsdorfer, W.; Sanchez-Benitez, J.; Kamenev, K.V.; Parkin, A.; Peacock, R.D.; Murrie, M. Cobalt (II) Citrate Cubane Single-Molecule Magnet. Inorg. Chem. 2008, 47, 7438–7442. [Google Scholar] [CrossRef]
- Palacios, M.A.; Mota, A.J.; Perea-Buceta, J.E.; White, F.J.; Brechin, E.K.; Colacio, E. Antiferromagnetic versus Ferromagnetic Exchange Interactions in Bis(μ-Ooximate) dinickel (II) Units for a Series of Closely Related Cube Shaped Carboxamideoximate-Bridged Ni4 Complexes. A Combined Experimental and Theoretical Magneto-Structural Study. Inorg. Chem. 2010, 49, 10156–10165. [Google Scholar] [CrossRef]
- Das, A.; Klinke, F.J.; Demeshko, S.; Meyer, S.; Dechert, S.; Meyer, F. Reversible Solvatomagnetic Effect in Novel Tetranuclear Cubane-Type Ni4 Complexes and Magnetostructural Correlations for the [Ni4(μ3-O)4] Core. Inorg. Chem. 2012, 51, 8141–8149. [Google Scholar] [CrossRef] [PubMed]
- Aryaeifar, M.; Rudbari, H.A.; Moreno-Pineda, E.; Cuevas-Vicario, J.V.; Paul, S.; Schulze, M.; Wernsdorfer, W.; Lloret, F.; Moinii, N.; Blacque, O. Synthesis, characterization and magnetic properties of halogenated tetranuclear cubane-like nickel(II) complexes. New J. Chem. 2024, 48, 3603–3613. [Google Scholar] [CrossRef]
- Zaleski, C.M.; Depperman, E.C.; Dendrinou-Samara, C.; Alexiou, M.; Kampf, J.W.; Kessissoglou, D.; Kirk, M.L.; Pecoraro, V.L. Metallacryptate Single-Molecule Magnets: Effect of Lower Molecular Symmetry on Blocking Temperature. J. Am. Chem. Soc. 2005, 127, 12862–12872. [Google Scholar] [CrossRef] [PubMed]
- Papaefstathiou, G.S.; Perlepes, S.P. Families of Polynuclear Manganese, Cobalt, Nickel and Copper Complexes Stabilized by Various Forms of Di-2-pyridyl Ketone. Comments Inorg. Chem. 2002, 23, 249–274. [Google Scholar] [CrossRef]
- Efthymiou, C.G.; Mylonas-Margaritis, I.; Raptopoulou, C.P.; Psycharis, V.; Escuer, A.; Papatriantafyllopoulou, C.; Perlepes, S.P. A Ni11 Coordination Cluster from the Use of the Di-2-Pyridyl Ketone/Acetate Ligand Combination: Synthetic, Structural and Magnetic Studies. Magnetochemistry 2016, 2, 30. [Google Scholar] [CrossRef]
- Tsohos, A.; Dionyssopoulou, S.; Raptopoulou, C.P.; Terzis, A.; Bakalbassis, E.G.; Perlepes, S.P. The gem-Diol Form of (py)2 CO as a Ligand in Cobalt(II) Carboxylate Clusters: A Cubane Complex and a Novel Nonanuclear Species with a Vertex-Sharing Double Square Pyramidal Structure. Angew. Chem. Int. Ed. 1999, 38, 983–985. [Google Scholar] [CrossRef]
- Efthymiou, C.G.; Raptopoulou, C.P.; Terzis, A.; Boča, R.; Korabic, M.; Mrozinski, J.; Perlepes, S.P.; Bakalbassis, E.G. A Systematic Exploration of Nickel(II)/Acetate/Di-2-pyridyl Ketone Chemistry: Neutral and Cationic Clusters, and a Novel Mononuclear Complex. Eur. J. Inorg. Chem. 2006, 2016, 2236–2252. [Google Scholar] [CrossRef]
- Tong, M.-L.; Zheng, S.-L.; Shi, J.-X.; Tong, Y.-X.; Lee, H.K.; Chen, X.-M. Synthesis, crystal structures and properties of six cubane-like transition metal complexes of di-2-pyridyl ketone in gem-diol form. J. Chem. Soc. Dalton Trans. 2002, 2002, 1727–1734. [Google Scholar] [CrossRef]
- Papaefstathiou, G.S.; Escuer, A.; Mautner, F.A.; Raptopoulou, C.; Terzis, A.; Perlepes, S.P.; Vicente, R. Use of the Di-2-pyridyl Ketone/Acetate/Dicyanamide “Blend” in Manganese (II), Cobalt (II) and Nickel (II) Chemistry: Neutral Cubane Complexes. Eur. J. Inorg. Chem. 2005, 2005, 879–893. [Google Scholar] [CrossRef]
- Papatriantafyllopoulou, C.; Efthymiou, C.G.; Raptopoulou, C.P.; Vicente, R.; Manessi-Zoupa, E.; Psycharis, V.; Escuer, A.; Perlepes, S.P. Initial use of the di-2-pyridyl ketone/sulfate ‘‘blend’’ in 3d-metal cluster chemistry: Preparation, X-ray structures and physical studies of zinc (II) and nickel (II) cubanes. J. Mol. Struct. 2007, 829, 176–188. [Google Scholar] [CrossRef]
- Wang, H.-S.; Song, Y. Conversion of tetranuclear Ni complexes from a defect dicubane core to a [Ni4O4] cubane-like core via addition of 2-hydroxymethylpyridine: Synthesis, crystal structures, and magnetic properties. Inorg. Chem. Commun. 2013, 35, 86–88. [Google Scholar] [CrossRef]
- Katsenis, A.D.; Inglis, R.; Slawin, A.M.Z.; Kessler, V.G.; Brechin, E.K.; Papaefstathiou, G.S. Transforming the cube: A tetranuclear cobalt(II) cubane cluster and its transformation to a dimer of dimers. Cryst. Eng. Comm. 2009, 11, 2117–2120. [Google Scholar] [CrossRef]
- Padhi, S.K.; Sahu, R. Co (II/III) coordinated pyridine alcoholate ligand generated through metal assisted nucleophilic addition to a C=O function: Temperature dependent synthesis of a mononuclear complex and a neutral cubane cluster. Polyhedron 2008, 27, 2662–2666. [Google Scholar] [CrossRef]
- CRYSALISPRO; Version 1.171.33.55, release 5 January 2010; CrysAlis171.NET; Oxford Diffraction Ltd.: Abingdon, UK, 2010.
- Sheldrick, G.M. A short history of SHELX. Acta Cryst. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SADABS, Program for Empirical Absorption Correction of Area Detector Data; University of Göttingen: Göttingen, Germany, 1996. [Google Scholar]
- Duisenberg, A.J.M. Indexing in single-crystal diffractometry with an obstinate list of reflections. J. Appl. Crystallogr. 1992, 25, 92–96. [Google Scholar] [CrossRef]
- Duisenberg, A.J.M.; Kroon-Batenburg, L.M.J.; Schreurs, A.M.M. An intensity evaluation method: EVAL-14. J. Appl. Crystallogr. 2003, 36, 220–229. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Izsák, R.; Hansen, A.; Neese, F. The resolution of identity and chain of spheres approximations for the LPNO-CCSD singles Fock term. J. Chem. Phys. 2012, 110, 2413–2417. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Ruiz, E.; Rodríguez-Fortea, A.; Cano, J.; Alvarez, S.; Alemany, P. About the calculation of exchange coupling constants in polynuclear transition metal complexes. J. Comput. Chem. 2003, 24, 982–989. [Google Scholar] [CrossRef]
- Ruiz, E.; Cano, J.; Alvarez, S.; Alemany, P. Magnetic Coupling in End-On Azido-Bridged Transition Metal Complexes: A Density Functional Study. J. Am. Chem. Soc. 1998, 120, 11122–11129. [Google Scholar] [CrossRef]
- Ruiz, E.; Alemany, P.; Alvarez, S.; Cano, J. Toward the Prediction of Magnetic Coupling in Molecular Systems: Hydroxo- and Alkoxo-Bridged Cu(II) Binuclear Complexes. J. Am. Chem. Soc. 1997, 119, 1297–1303. [Google Scholar] [CrossRef]
- Ruiz, E.; Alvarez, S.; Cano, J.; Polo, V. About the calculation of exchange coupling constants using density-functional theory: The role of the self-interaction error. J. Chem. Phys. 2005, 123, 164110. [Google Scholar] [CrossRef]
- Segger, R.; People, J.A. Self-consistent molecular orbital methods. XVIII. Constraints and stability in Hartree–Fock theory. J. Chem. Phys. 1977, 66, 3045–3050. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. N-electron valence state perturbation theory: A fast implementation of the strongly contracted variant. Chem. Phys. Lett. 2001, 350, 297–305. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.P. n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Stoychev, G.L.; Auer, A.A.; Neese, F. Automatic Generation of Auxiliary Basis Sets. J. Chem. Theory Comput. 2017, 13, 554–562. [Google Scholar] [CrossRef]
- Neese, F.; Wenmohs, A.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Izsák, R.; Neese, F. An overlap fitted chain of spheres exchange method. J. Chem. Phys. 2011, 135, 144105. [Google Scholar] [CrossRef]
- Cano, J. XVPMag: X-Virtual Package for Magnetism; Universidad de Valencia: Valencia, Spain, 2010. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, W.D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Thomson, J.J. On the structure of the atom: An investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the circumference of a circle; with application of the results to the theory of atomic structure. Lond. Edinb. Dubl. Phil. Mag. 1904, 39, 237–265. [Google Scholar] [CrossRef]
- Moscato, P.; Haque, N.M.; Moscato, A. Continued fractions and the Thomson problem. Sci. Rep. 2023, 13, 7272. [Google Scholar] [CrossRef]
- König, E.; Kremer, S. Irreducible tensor operator methods in intermediate-field coupling. Int. J. Quantum Chem. 1974, 8, 347–362. [Google Scholar] [CrossRef]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d-and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
- Isele, K.; Gigon, F.; Williams, A.F.; Bernardinelli, G.; Franz, P.; Decurtins, S. Synthesis, structure and properties of {M4O4} cubanes containing nickel (ii) and cobalt (ii). Dalton Trans. 2007, 3, 332–341. [Google Scholar] [CrossRef] [PubMed]
- Lloret, F.; Julve, M.; Cano, J.; Ruiz-García, R.; Pardo, R. Magnetic properties of six-coordinated high-spin cobalt (II) complexes: Theoretical background and its application. Inorg. Chim. Acta 2008, 361, 3432–3445. [Google Scholar] [CrossRef]
- Ruiz, E.; Alemany, P.; Alvarez, S.; Cano, J. Structural Modeling and Magneto-Structural Correlations for Hydroxo-Bridged Copper (II) Binuclear Complexes. Inorg. Chem. 1997, 36, 3683–3688. [Google Scholar] [CrossRef]
- Song, X.; Xue, X. Study on the Magneto-Structural Correlation of a New Dinuclear Cobalt (II) Complex with Double μ-Phenoxo Bridges. ACS Omega 2020, 5, 8347–8354. [Google Scholar] [CrossRef]
- Kant, S.; Saha, S.; Lloret, F.; Cano, J.; Mukherjee, R. A tetracobalt (II) cluster with a two vertex truncated dicubane topology endogenously supported by carboxylate-based (2-pyridyl) methylamine ligands: Magneto-structural and DFT studies. Dalton Trans. 2023, 52, 11922–11933. [Google Scholar] [CrossRef] [PubMed]
- Sen, R.; Mondal, K.; dos Santos, M.; Escobar, L.B.L.; Brandão, P.; Reis, M.S.; Lin, Z. A chiral alkali metal capped Ni 4 cubane complex: Synthesis, structure, magnetic and catalytic bromination studies. J. Mol. Struct. 2023, 1274, 13441. [Google Scholar] [CrossRef]
- Scheurer, A.; Ako, A.M.; Saalfrank, R.W.; Heinemann, F.; Hampel, F.; Petukhov, K.; Gieb, K.; Stocker, M.; Müller, P. Synthesis, Magnetic Properties, and STM Spectroscopy of Cobalt (II) Cubanes [CoII4(Cl)4(HL)4]. Chem. Eur. J. 2010, 16, 4784–4792. [Google Scholar] [CrossRef]




| Compound | 1 | 2 |
|---|---|---|
| Empirical formula | C72H56Co4N8O16 | C72H56N8Ni4O16 |
| Formula weight | 1524.97 | 1524.01 |
| Temperature/K | 293(2) | 293(2) |
| Crystal system | Tetragonal | Tetragonal |
| Space group | I-42d | I-42d |
| a/Å | 14.322(1) | 14.172(3) |
| b/Å | 14.322(1) | 14.172(3) |
| c/Å | 38.300(1) | 37.900(8) |
| Volume/Å3 | 7856.1(11) | 7612.1(3) |
| Z | 4 | 4 |
| ρcalc/g cm−3 | 1.289 | 1.330 |
| μ/mm−1 | 0.895 | 1.041 |
| F(000) | 3120.0 | 3136.0 |
| Radiation | Mo Kα (λ = 0.71073) | Mo Kα (λ = 0.71073) |
| 2θ range for data collection/° | 6.45 to 59.15 | 10.064 to 50.054 |
| Index ranges | −18 ≤ h ≤ 18 −19 ≤ k ≤ 15 −51 ≤ l ≤ 51 | −16 ≤ h ≤ 16 −16 ≤ k ≤ 16 −42 ≤ l ≤ 45 |
| Reflections collected | 38328 | 39546 |
| Independent reflections | 5178 | 3340 |
| Rint | 0.058 | 0.081 |
| Data/restraints/parameters | 5178/0/215 | 3340/0/227 |
| Goodness-of-fit on F2 | 0.998 | 1.095 |
| Final R indexes [I ≥ 2σ(I)] | R1 = 0.0401, wR2 = 0.1048 | R1 = 0.0437 wR2 = 0.1215 |
| Final R indexes [all data] | R1 = 0.0557, wR2 = 0.1085 | R1 = 0.0530, wR2 = 0.1290 |
| Largest diff. peak/hole / e Å−3 | 0.72/−0.32 | 0.81/−0.34 |
| Flack parameter | −0.011(8) | 0.06(4) |
| CCDC identification | 2417038 | 2417037 |
| (1) | (2) | ||
|---|---|---|---|
| Co1–O1i | 2.111(2) | Ni1–O1i | 2.005(4) |
| Co1–O1 | 2.032(2) | Ni1–O1 | 2.079(3) |
| Co1–O1iii | 2.233(3) | Ni1–O1ii | 2.166(4) |
| Co1–O3 | 2.028(3) | Ni1–O3 | 2.003(5) |
| Co1–N1 | 2.166(3) | Ni1–N1 | 2.032(6) |
| Co1–N2iii | 2.101(4) | Ni1–N2i | 2.088(5) |
| O1–Co1ii | 2.111(2) | O1–Ni1i | 2.166(4) |
| O1–Co1iii | 2.233(2) | O1–Ni1ii | 2.005(4) |
| O1–C1 | 1.395(4) | O1–C1 | 1.380(7) |
| C1–O2 | 1.390(5) | O2–C1 | 1.389(8) |
| O4–C12 | 1.233(6) | O4–C12 | 1.225(9) |
| C12–O3 | 1.258(5) | O3–C12 | 1.258(9) |
| Co1···Co1i | 3.2175(6) | Ni1···Ni1i | 3.089(1) |
| Co1···Co1ii | 3.2337(9) | Ni1···Ni1ii | 3.191(1) |
| Co1···Co1iii | 3.2337(9) | Ni1···Ni1iii | 3.089(1) |
| Co1–O1–Co1i | 102.61(10) | Ni1–O1–Ni1ii | 97.48(16) |
| Co1i–O1–Co1iii | 96.17(9) | Ni1i–O1–Ni1ii | 95.47(16) |
| Co1–O1–Co1iii | 97.83(9) | Ni1i–O1–Ni1 | 102.78(17) |
| 1 | 2 | |||
|---|---|---|---|---|
| J1 | J2 | J1 | J2 | |
| dM…M a | 3.217 | 3.234 | 3.089 | 3.191 |
| dM…O a | 2.032; 2.233 | 2.032; 2.111 | 2.006; 2.166 | 2.166; 2.079 |
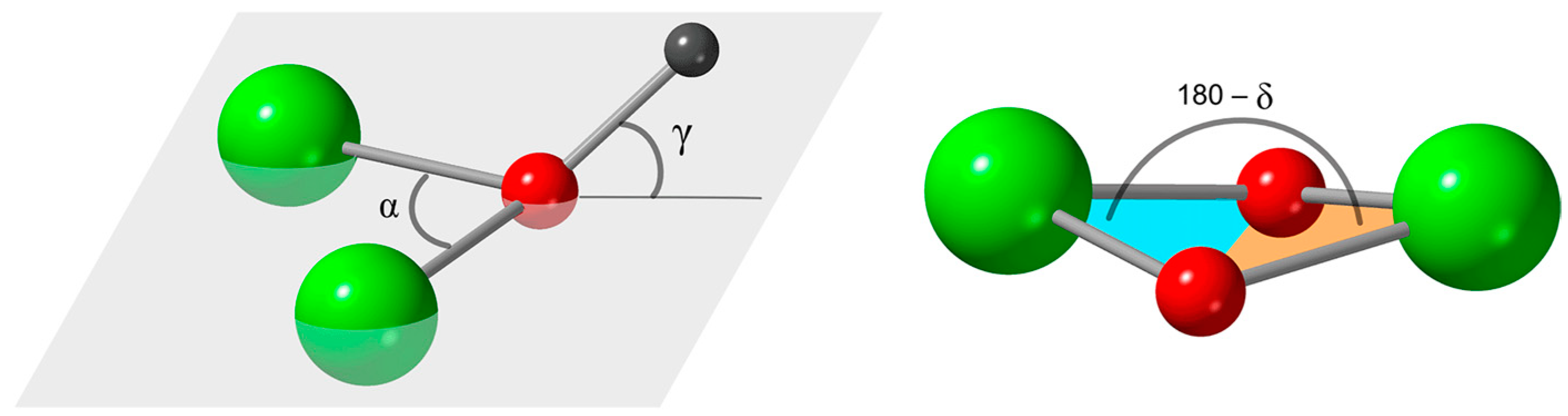
| α b | 97.8; 97.8 | 102.6; 96.2 | 95.5; 95.5 | 102.8; 97.5 |
| δ b | 14.5 | 11.0 | 19.0 | 8.3 |
| γ b | 39.1; 39.1 | 57.7; 46.8 | 35.3; 35.3 | 48.6; 60.8 |
| JDFT c | +0.3 | +2.6 | +14.6 | +3.2 |
| JFit c | +0.12/–0.6 | +3.4/+4.8 | +14.5/+15.1 | +2.3/+2.4 |
| CoZn3 | Co1 | Trimmed Co1 | NiZn3 | Ni1 | Trimmed Ni1 | |
|---|---|---|---|---|---|---|
| D a | +44.3 | +46.5 | +44.8 (+34.1) | +7.6 | +9.3 | +9.3 (+6.8) |
| E/D | 0.216 | 0.250 | 0.255 (0.253) | 0.080 | 0.098 | 0.089 (0.080) |
| g|| | 2.170 | 2.175 | 2.178 (2.089) | 2.300 | 2.291 | 2.290 (2.206) |
| g⊥ | 2.666 | 2.706 | 2.690 (2.449) | 2.358 | 2.358 | 2.357 (2.253) |
| gavg | 2.512 | 2.541 | 2.531 (2.336) | 2.339 | 2.336 | 2.335 (2.238) |
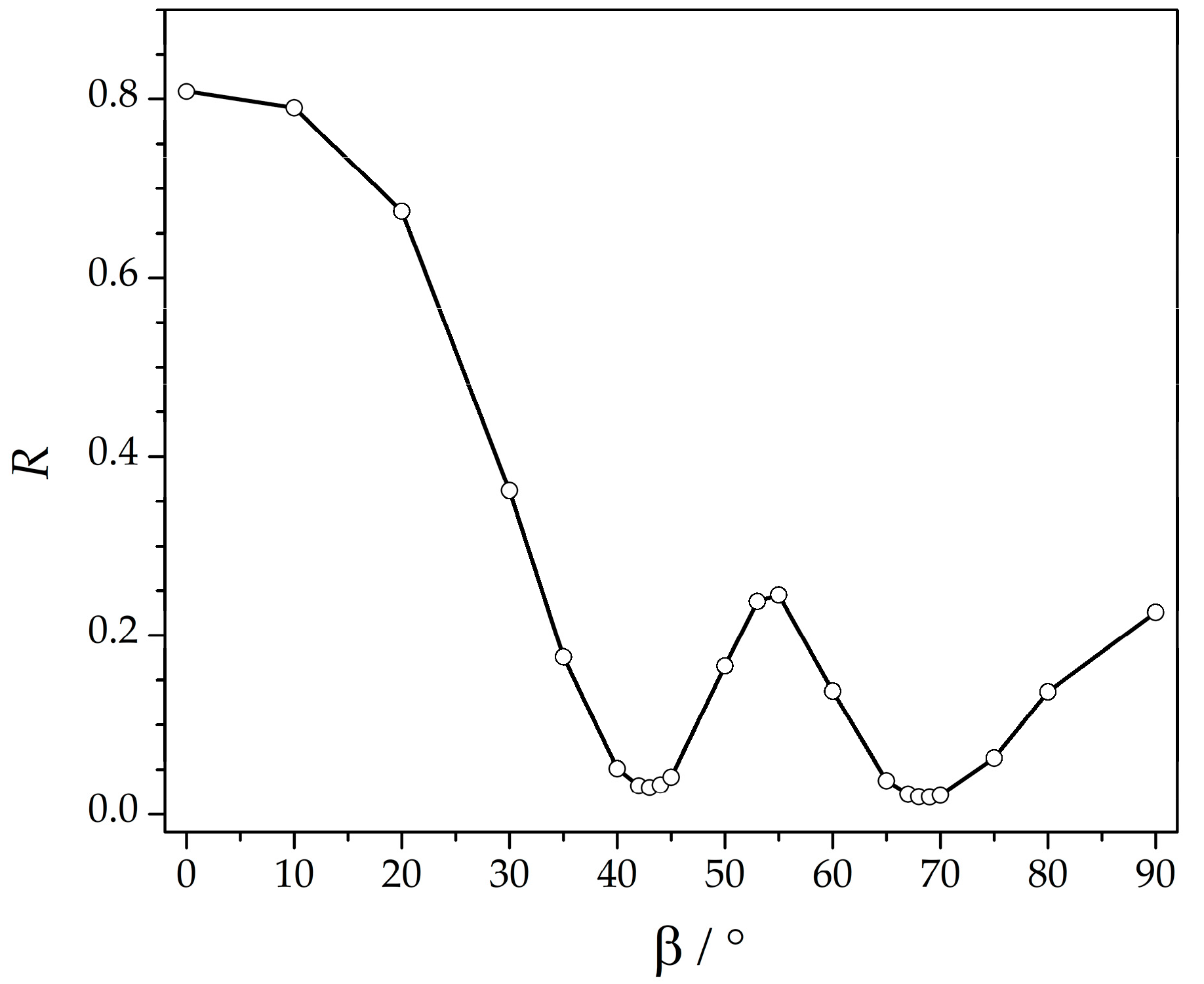
| Parameters | Fit | |
|---|---|---|
| β a | 43 | 69 |
| J1 b | 15.1(2) | 14.5(2) |
| J2 b | 2.42(2) | 2.34(2) |
| D b | 11.76(3) | 10.44(3) |
| g | 2.050(1) | 2.056(1) |
| R | 0.02966 | 0.01952 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pejo, C.; Valiero, S.; Rojas-Dotti, C.; Guedes, G.P.; Cano, J.; Novak, M.A.; Chiozzone, R.; Vaz, M.G.F.; González, R. Cobalt(II) and Nickel(II) Cubane {M4O4} Complexes Derived from Di-2-pyridyl Ketone and Benzoate: Syntheses, Structure and Magnetic Properties. Magnetochemistry 2025, 11, 34. https://doi.org/10.3390/magnetochemistry11040034
Pejo C, Valiero S, Rojas-Dotti C, Guedes GP, Cano J, Novak MA, Chiozzone R, Vaz MGF, González R. Cobalt(II) and Nickel(II) Cubane {M4O4} Complexes Derived from Di-2-pyridyl Ketone and Benzoate: Syntheses, Structure and Magnetic Properties. Magnetochemistry. 2025; 11(4):34. https://doi.org/10.3390/magnetochemistry11040034
Chicago/Turabian StylePejo, Carolina, Santiago Valiero, Carlos Rojas-Dotti, Guilherme P. Guedes, Joan Cano, Miguel A. Novak, Raúl Chiozzone, Maria G. F. Vaz, and Ricardo González. 2025. "Cobalt(II) and Nickel(II) Cubane {M4O4} Complexes Derived from Di-2-pyridyl Ketone and Benzoate: Syntheses, Structure and Magnetic Properties" Magnetochemistry 11, no. 4: 34. https://doi.org/10.3390/magnetochemistry11040034
APA StylePejo, C., Valiero, S., Rojas-Dotti, C., Guedes, G. P., Cano, J., Novak, M. A., Chiozzone, R., Vaz, M. G. F., & González, R. (2025). Cobalt(II) and Nickel(II) Cubane {M4O4} Complexes Derived from Di-2-pyridyl Ketone and Benzoate: Syntheses, Structure and Magnetic Properties. Magnetochemistry, 11(4), 34. https://doi.org/10.3390/magnetochemistry11040034








