High-Coordinate Mononuclear Ln(III) Complexes: Synthetic Strategies and Magnetic Properties
Abstract
:1. Introduction
2. High-Coordinate Ln(III) Complexes
2.1. Ten-Coordinate Ln(III) Complexes
2.1.1. Multi-Dentate Ligand Approach
2.1.2. Mixed Ligand Approach
Crown Ether Ligands
Bidentate N,N-Donor Ligands
Terpyridyl Ligand
Schiff Base and Semicarbazone Ligands
Tripodal Ligands
Glycol Ligand
Radical Ligand
2.1.3. Penta-Nitrate Ln(III) Complexes
3. Twelve-Coordinate Ln(III) Complexes
Mixed Ligand Approach
4. Magneto-Structural Correlation
5. Summary
6. Future Direction
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Clérac, R.; Winpenny, R.E.P. Single-Molecule Magnets and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2016; Volume 172. [Google Scholar]
- Gao, S. Molecular Nanomagnets and Related Phenomena; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Spaldin, N.A. Magnetic Materials: Fundamentals and Applications, 2nd. ed.; Cambridge Uiniversity Press: Cambridge, UK, 1969. [Google Scholar]
- Winpenny, R.E.P. Molecular Cluster Magnets; Worlad Scientific Series in Nanoscience and Nanotechnology; World Scientific: Singapore, 2011. [Google Scholar]
- Gaita-Ariño, A.; Luis, F.; Hill, S.; Coronado, E. Molecular spins for quantum computation. Nat. Chem. 2019, 11, 301–309. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.-S.; Leng, J.-D.; Liu, J.-L.; Meng, Z.-S.; Tong, M.-L. Polynuclear and Polymeric Gadolinium Acetate Derivatives with Large Magnetocaloric Effect. Inorg. Chem. 2012, 51, 405–413. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.N.; Winpenny, R.E.P.; Layfield, R.A. Lanthanide Single-Molecule Magnets. Chem. Rev. 2013, 113, 5110–5148. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Guo, M.; Tang, J. Recent Developments in Lanthanide Single-Molecule Magnets. Chem. Asian J. 2017, 12, 2772–2779. [Google Scholar] [CrossRef] [PubMed]
- Feltham, H.L.C.; Brooker, S. Review of purely 4f and mixed-metal nd-4f single-molecule magnets containing only one lanthanide ion. Coord. Chem. Rev. 2014, 276, 1–33. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Ishikawa, T.; Koshihara, S.Y.; Kaizu, Y. Lanthanide double-decker complexes functioning as magnets at the single-molecular level. J. Am. Chem. Soc. 2003, 125, 8694–8695. [Google Scholar] [CrossRef] [PubMed]
- Spree, L.; Schlesier, C.; Kostanyan, A.; Westerström, R.; Greber, T.; Büchner, B.; Avdoshenko, S.M.; Popov, A.A. Single-Molecule Magnets DyM2N@C80 and Dy2MN@C80 (M = Sc, Lu): The Impact of Diamagnetic Metals on Dy3+ Magnetic Anisotropy, Dy⋅⋅⋅Dy Coupling, and Mixing of Molecular and Lattice Vibrations. Chem. -Eur. J. 2020, 26, 2436–2449. [Google Scholar] [CrossRef] [Green Version]
- Kalita, P.; Acharya, J.; Chandrasekhar, V. Mononuclear pentagonal bipyramidal Ln(III) complexes: Syntheses and magnetic properties. J. Magn. Magn. Mater 2020, 498, 166098. [Google Scholar] [CrossRef]
- He, M.; Guo, F.-S.; Tang, J.; Mansikkamäki, A.; Layfield, R.A. Fulvalene as a platform for the synthesis of a dimetallic dysprosocenium single-molecule magnet. Chem. Sci. 2020, 11, 5745–5752. [Google Scholar] [CrossRef]
- Canaj, A.B.; Dey, S.; Marti, E.R.; Wilson, C.; Rajaraman, G.; Murrie, M. Insight into D6h Symmetry: Targeting Strong Axiality in Stable Dysprosium(III) Hexagonal Bipyramidal Single-Ion Magnets. Angew. Chem. Int. Ed. 2019, 58, 14146–14151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet. Science 2018, 362, 1400–1403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; VCH: Vancouver, BC, Canada, 1993. [Google Scholar]
- Layfield, R.A.; Murugesu, M. Lanthanides and Actinides in Molecular Magnetism; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015. [Google Scholar] [CrossRef]
- Wybourne, B.G. Spectroscopic Properties of Rare Earths; John Wiley & Sons: New York, NY, USA, 1965. [Google Scholar]
- Ishikawa, N.; Sugita, M.; Okubo, T.; Tanaka, N.; Iino, T.; Kaizu, Y. Determination of Ligand-Field Parameters and f-Electronic Structures of Double-Decker Bis(phthalocyaninato)lanthanide Complexes. Inorg. Chem. 2003, 42, 2440–2446. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Jiang, S.-D.; Qin, S.-X. Prediction of the quantized axis of rare-earth ions: The electrostatic model with displaced point charges. Inorg. Chem. Front. 2015, 2, 613–619. [Google Scholar] [CrossRef]
- Bar, A.K.; Kalita, P.; Singh, M.K.; Rajaraman, G.; Chandrasekhar, V. Low-coordinate mononuclear lanthanide complexes as molecular nanomagnets. Coord. Chem. Rev. 2018, 367, 163–216. [Google Scholar] [CrossRef]
- Huang, C.-H. Rare Earth Coordination Chemistry: Fundamentals and Applications; John, Wiley & Sons (Asia) Pte Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Ungur, L.; Chibotaru, L.F. Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets. Inorg. Chem. 2016, 55, 10043–10056. [Google Scholar] [CrossRef]
- Ruiz-Martínez, A.; Alvarez, S. Stereochemistry of Compounds with Coordination Number Ten. Chem. Eur. J. 2009, 15, 7470–7480. [Google Scholar] [CrossRef]
- Cotton, S.; Raithby, P. Systematics and surprises in lanthanide coordination chemistry. Coord. Chem. Rev. 2017, 340, 220–231. [Google Scholar] [CrossRef]
- Daly, S.R.; Kim, D.Y.; Girolami, G.S. Lanthanide N,N-Dimethylaminodiboranates as a new class of highly volatile chemical vapor deposition precursors. Inorg. Chem. 2012, 51, 7050–7065. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Zhang, X.; Meng, X.; Shi, W.; Cheng, P.; Powell, A.K. Constraining the coordination geometries of lanthanide centers and magnetic building blocks in frameworks: A new strategy for molecular nanomagnets. Chem. Soc. Rev. 2016, 45, 2423–2439. [Google Scholar] [CrossRef] [PubMed]
- Pointillart, F.; Cador, O.; Le Guennic, B.; Ouahab, L. Uncommon lanthanide ions in purely 4f Single Molecule Magnets. Coord. Chem. Rev. 2017, 346, 150–175. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Tong, M.-L. Symmetry strategies for high performance lanthanide-based single-molecule magnets. Chem. Soc. Rev. 2018, 47, 2431–2453. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.-S.; Bar, A.K.; Layfield, R.A. Main Group Chemistry at the Interface with Molecular Magnetism. Chem. Rev. 2019, 119, 8479–8505. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.-Y.; Xie, J.; Kong, X.-J.; Long, L.-S.; Zheng, L.-S. Recent advances in the assembly of high-nuclearity lanthanide clusters. Coord. Chem. Rev. 2019, 378, 222–236. [Google Scholar] [CrossRef]
- Thomas, J.E.; Palenik, G.J. A novel decacoordinate cerium complex: The synthesis and characterization of bis(2,6-diacetylpyridine bis(semicarbazone)) cerium(III) perchlorate trihydrate. Inorg. Chim. Acta 1980, 44, 303–304. [Google Scholar]
- Benson, M.T.; Cundari, T.R.; Saunders, L.C.; Sommerer, S.O. Synthesis, structure, computational studies and magnetic properties of a ten-coordinate gadolinium(III) complex. Inorg. Chim. Acta 1997, 258, 127–130. [Google Scholar] [CrossRef]
- Favas, M.C.; Kepert, D.L. Aspects of the Stereochemistry of Nine-Coordination, Ten-Coordination, and Twelve-Coordination. Prog. Inorg. Chem. 2007, 28, 309–367. [Google Scholar]
- Batchelor, L.J.; Cimatti, I.; Guillot, R.; Tuna, F.; Wernsdorfer, W.; Ungur, L.; Chibotaru, L.F.; Campbell, V.E.; Mallah, T. Chemical tuning of the magnetic relaxation in dysprosium(iii) mononuclear complexes. Dalton Trans. 2014, 43, 12146–12149. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Bazhenova, T.A.; Yakushev, I.A.; Lyssenko, K.A.; Maximova, O.V.; Mironov, V.S.; Manakin, Y.V.; Kornev, A.B.; Vasiliev, A.N.; Yagubskii, E.B. Ten-Coordinate Lanthanide [Ln(HL)(L)] Complexes (Ln = Dy, Ho, Er, Tb) with Pentadentate N3O2-Type Schiff-Base Ligands: Synthesis, Structure and Magnetism. Magnetochemistry 2020, 6, 60. [Google Scholar] [CrossRef]
- Jiang, Z.-X.; Liu, J.-L.; Chen, Y.-C.; Liu, J.; Jia, J.-H.; Tong, M.-L. Lanthanoid single-ion magnets with the LnN10 coordination geometry. Chem. Commun. 2016, 52, 6261–6264. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Yang, F.-L.; Feng, X.; Xu, H.; Sun, W.; Liu, H.; Li, X.-L. Half-sandwich lanthanide crown ether complexes with the slow relaxation of magnetization and photoluminescence behaviors. Dalton Trans. 2017, 46, 1317–1323. [Google Scholar] [CrossRef]
- Ding, Y.-S.; Han, T.; Hu, Y.-Q.; Xu, M.; Yang, S.; Zheng, Y.-Z. Syntheses, structures and magnetic properties of a series of mono- and di-nuclear dysprosium(III)-crown-ether complexes: Effects of a weak ligand-field and flexible cyclic coordination modes. Inorg. Chem. Front. 2016, 3, 798–807. [Google Scholar] [CrossRef]
- Wang, H.-L.; Ma, X.-F.; Zou, H.-H.; Wang, K.; Li, B.; Chen, Z.-L.; Liang, F.-P. Mixed chelating ligands used to regulate the luminescence of Ln(iii) complexes and single-ion magnet behavior in Dy-based analogues. Dalton Trans. 2018, 47, 15929–15940. [Google Scholar] [CrossRef]
- Larionov, S.V.; Bryleva, Y.A.; Glinskaya, L.A.; Plyusnin, V.F.; Kupryakov, A.S.; Agafontsev, A.M.; Tkachev, A.V.; Bogomyakov, A.S.; Piryazev, D.A.; Korolkov, I.V. Ln(iii) complexes (Ln = Eu, Gd, Tb, Dy) with a chiral ligand containing 1,10-phenanthroline and (–)-menthol fragments: Synthesis, structure, magnetic properties and photoluminescence. Dalton Trans. 2017, 46, 11440–11450. [Google Scholar] [CrossRef]
- Wei, D.-Y.; Lin, J.-L.; Zheng, Y.-Q. Note: The crystal structure of Tris(nitrato-O,O’)bis(1,10-phenanthroline-N,N’)terbium(III). J. Coord. Chem. 2002, 55, 1259–1262. [Google Scholar] [CrossRef]
- Cotton, S. Lanthanide and Actinide Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Su, Q.-Q.; Fan, K.; Jin, X.-X.; Huang, X.-D.; Cheng, S.-C.; Luo, L.-J.; Li, Y.-J.; Xiang, J.; Ko, C.-C.; Zheng, L.-M.; et al. Syntheses, crystal structures and magnetic properties of a series of luminescent lanthanide complexes containing neutral tetradentate phenanthroline-amide ligands. Inorg. Chem. Front. 2019, 6, 1442–1452. [Google Scholar] [CrossRef]
- Shi, T.; Xu, Y.; Li, M.-X.; Liu, C.-M.; Nfor, E.N.; Wang, Z.-X. A 10-coordinate cerium(III) complex with a ferrocene-based terpyridine ligand exhibiting field-induced slow magnetic relaxation. Polyhedron 2020, 188, 114695. [Google Scholar] [CrossRef]
- Kahwa, I.A.; Selbin, J.; O’Connor, C.J.; Foise, J.W.; McPherson, G.L. Magnetic and luminescence characteristics of dinuclear complexes of lanthanides and a phenolic schiff base macrocyclic ligand. Inorg. Chim. Acta 1988, 148, 265–272. [Google Scholar] [CrossRef]
- Biswas, S.; Das, S.; van Leusen, J.; Kögerler, P.; Chandrasekhar, V. Tetranuclear [2×2] Square-Grid Lanthanide(III) Complexes: Syntheses, Structures, and Magnetic Properties. Eur. J. Inorg. Chem. 2014, 2014, 4159–4167. [Google Scholar] [CrossRef]
- Biswas, S.; Das, S.; Rogez, G.; Chandrasekhar, V. Hydrazone-Ligand-Based Homodinuclear Lanthanide Complexes: Synthesis, Structure, and Magnetism. Eur. J. Inorg. Chem. 2016, 2016, 3322–3329. [Google Scholar] [CrossRef]
- Acharya, J.; Biswas, S.; van Leusen, J.; Kumar, P.; Kumar, V.; Narayanan, R.S.; Kögerler, P.; Chandrasekhar, V. Exploring Tuning of Structural and Magnetic Properties by Modification of Ancillary β-Diketonate Co-ligands in a Family of Near-Linear Tetranuclear DyIII Complexes. Cryst. Growth Des. 2018, 18, 4004–4016. [Google Scholar] [CrossRef]
- Upadhyay, A.; Das, C.; Vaidya, S.; Singh, S.K.; Gupta, T.; Mondol, R.; Langley, S.K.; Murray, K.S.; Rajaraman, G.; Shanmugam, M. Role of the Diamagnetic Zinc(II) Ion in Determining the Electronic Structure of Lanthanide Single-Ion Magnets. Chem. Eur. J. 2017, 23, 4903–4916. [Google Scholar] [CrossRef] [PubMed]
- Campbell, V.E.; Guillot, R.; Riviere, E.; Brun, P.-T.; Wernsdorfer, W.; Mallah, T. Subcomponent Self-Assembly of Rare-Earth Single-Molecule Magnets. Inorg. Chem. 2013, 52, 5194–5200. [Google Scholar] [CrossRef]
- Soek, R.N.; Ferreira, C.M.; Santana, F.S.; Hughes, D.L.; Poneti, G.; Ribeiro, R.R.; Nunes, F.S. Structure and magnetic properties of two new lanthanide complexes with the 1-((E)-2-pyridinylmethylidene)semicarbazone ligand. J. Mol. Struct. 2019, 1184, 254–261. [Google Scholar] [CrossRef] [Green Version]
- Goswami, S.; Biswas, S.; Tomar, K.; Konar, S. Tuning the Magnetoluminescence Behavior of Lanthanide Complexes Having Sphenocorona and Cubic Coordination Geometries. Eur. J. Inorg. Chem. 2016, 2016, 2774–2782. [Google Scholar] [CrossRef]
- Peng, G.; Zhang, Y.-Y.; Li, Z.-Y. Effect of coordination environment on the magnetic relaxation of mononuclear DyIII field-induced single molecule magnets. Inorg. Chem. Commun. 2017, 77, 40–43. [Google Scholar] [CrossRef]
- Li, D.-J.; Gao, D.-Z.; Liao, D.-Z.; Jiang, Z.-H.; Yan, S.-P. Synthesis, structure and magnetic properties of a Pr(III) complex with chelating nitronyl nitroxide radicals. J. Coord. Chem. 2004, 57, 1571–1576. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, J.; Yuan, A.; Song, Y. Slow magnetic relaxation in luminescent mononuclear dysprosium(iii) and erbium(III) pentanitrate complexes with the same LnO10 coordination geometry. Dalton Trans. 2017, 46, 15812–15818. [Google Scholar] [CrossRef] [PubMed]
- Cui, H.; Otsuka, T.; Kobayashi, A.; Takeda, N.; Ishikawa, M.; Misaki, Y.; Kobayashi, H. Structural, Electrical, and Magnetic Properties of a Series of Molecular Conductors Based on BDT-TTP and Lanthanoid Nitrate Complex Anions (BDT-TTP = 2,5-Bis(1,3-dithiol-2-ylidene)-1,3,4,6-tetrathiapentalene). Inorg. Chem. 2003, 42, 6114–6122. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, T.; Cui, H.; Kobayashi, A.; Misaki, Y.; Kobayashi, H. Magnetism of Metallic Molecular Crystals with Rare-Earth Complex Anions. J. Solid State Chem. 2002, 168, 444–449. [Google Scholar] [CrossRef]
- Wada, H.; Ooka, S.; Yamamura, T.; Kajiwara, T. Light Lanthanide Complexes with Crown Ether and Its Aza Derivative Which Show Slow Magnetic Relaxation Behaviors. Inorg. Chem. 2017, 56, 147–155. [Google Scholar] [CrossRef] [PubMed]
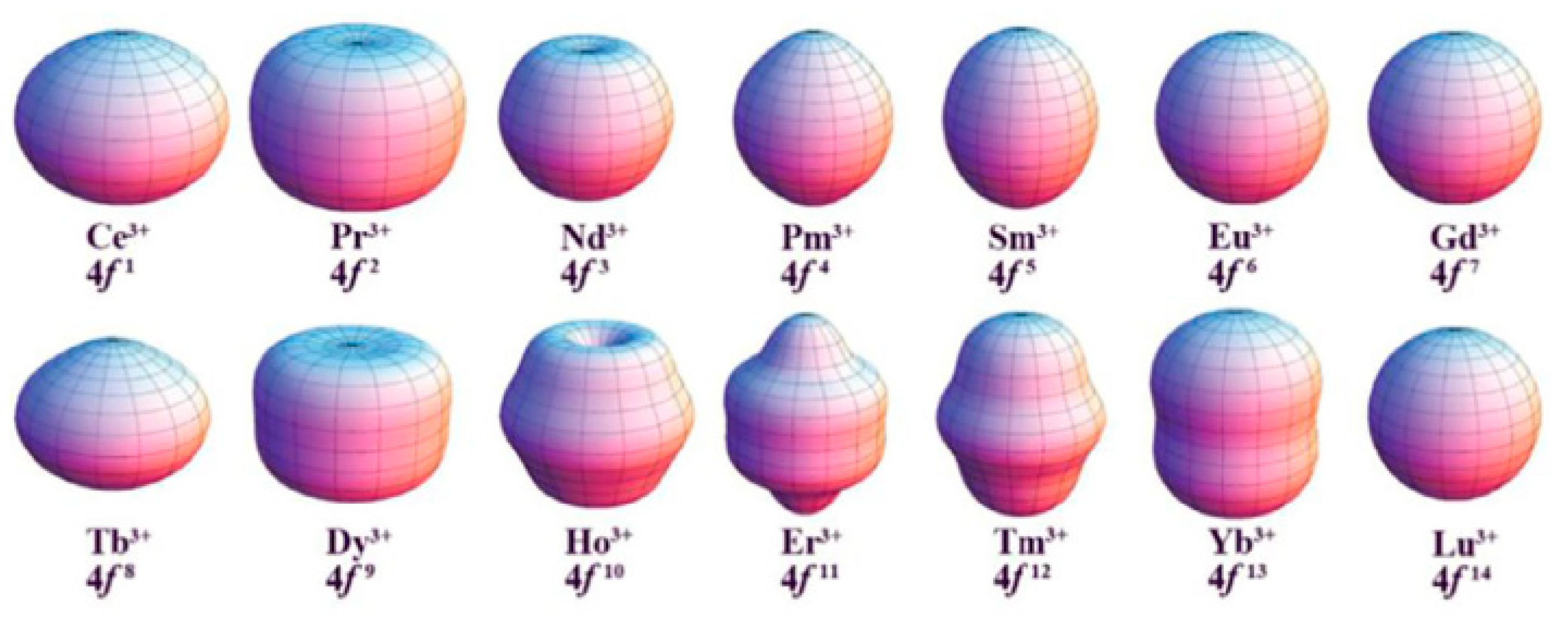
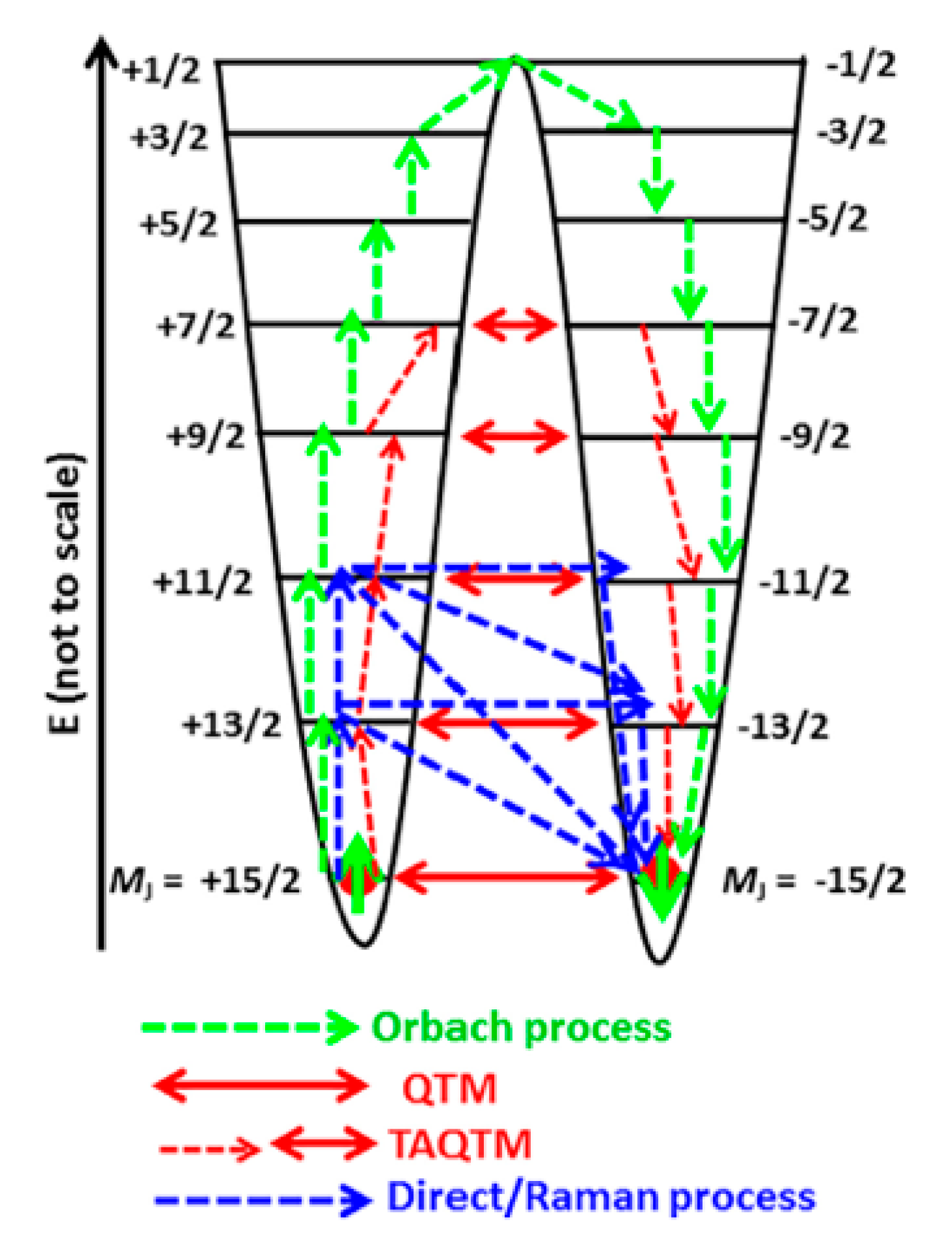
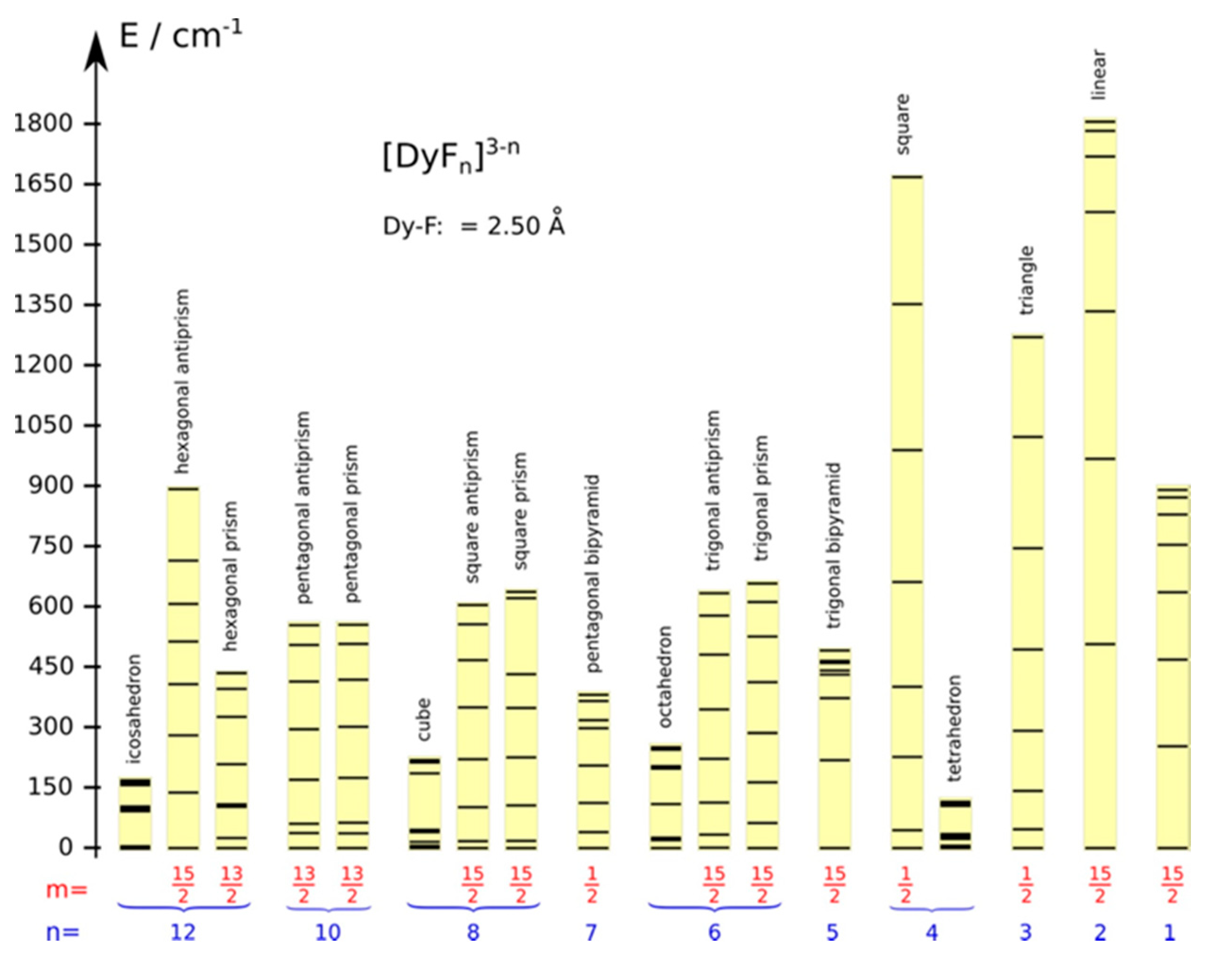
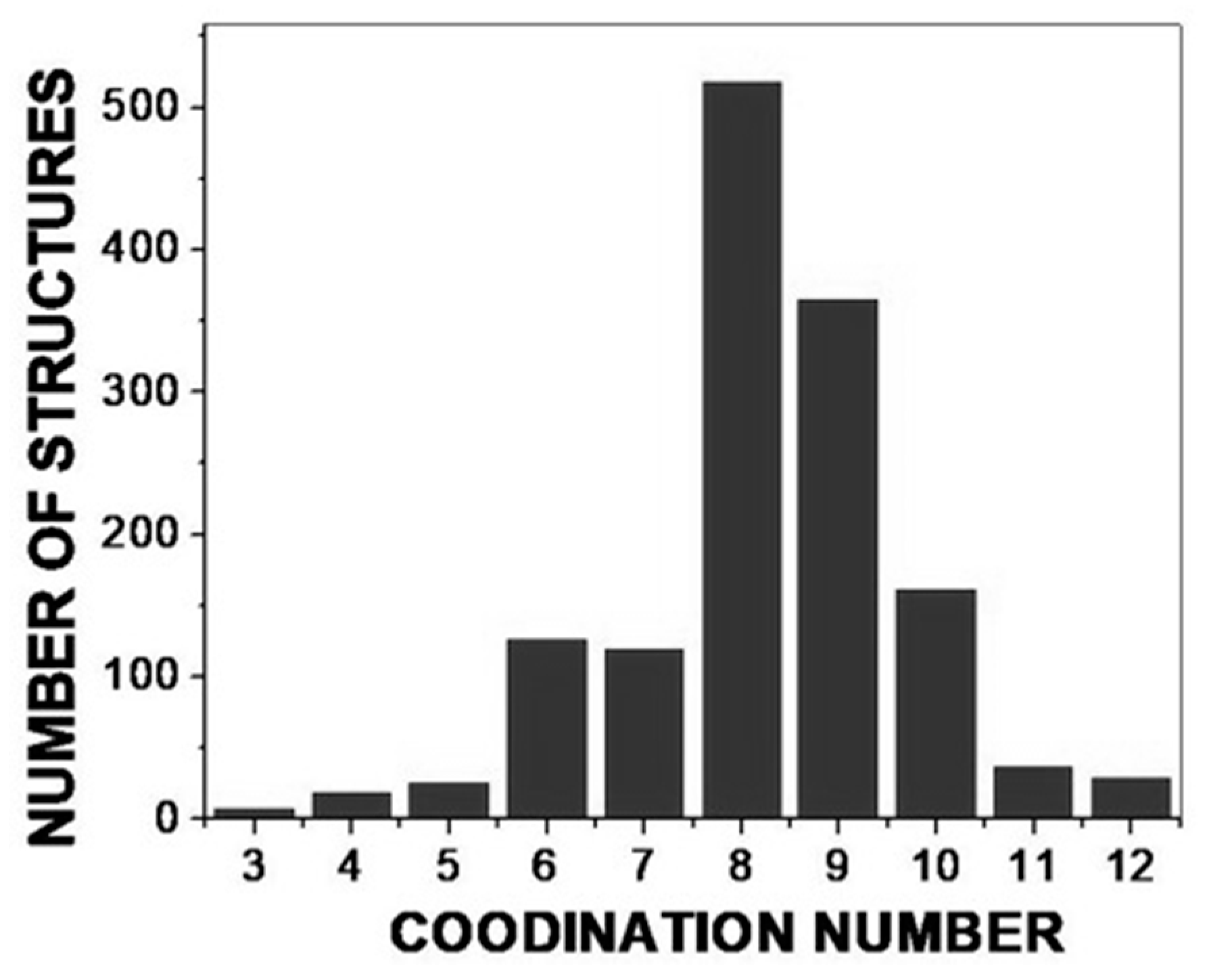

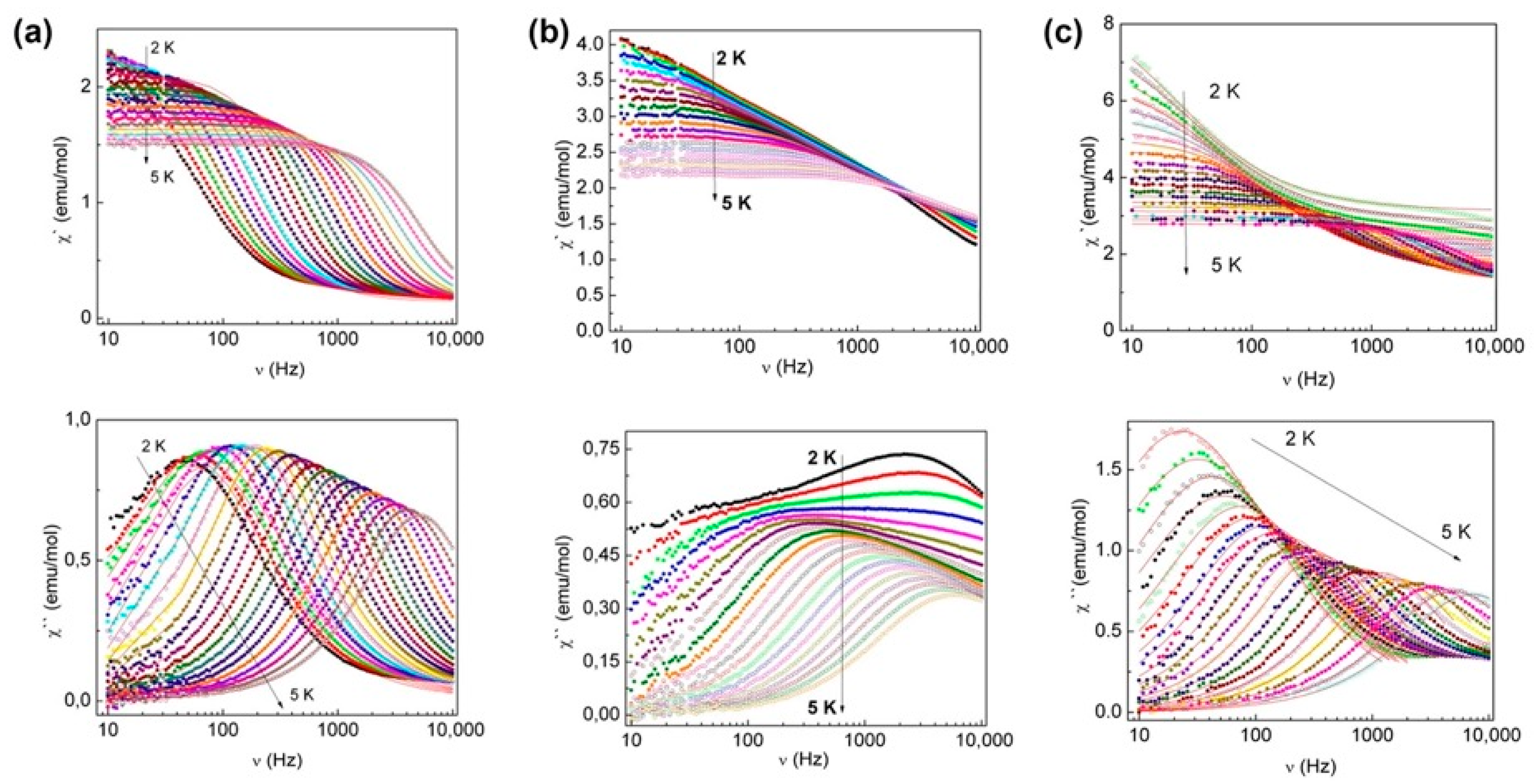

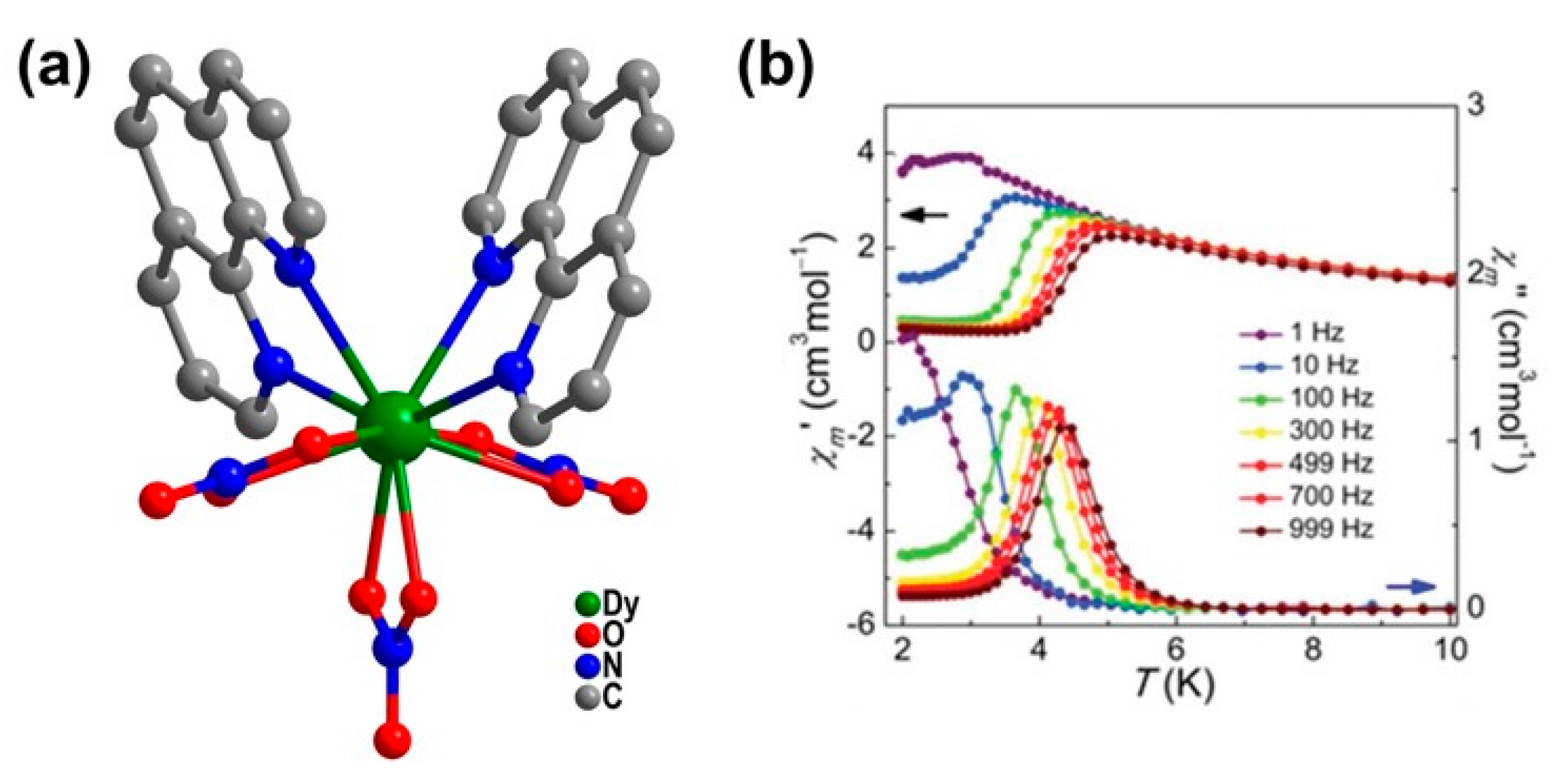
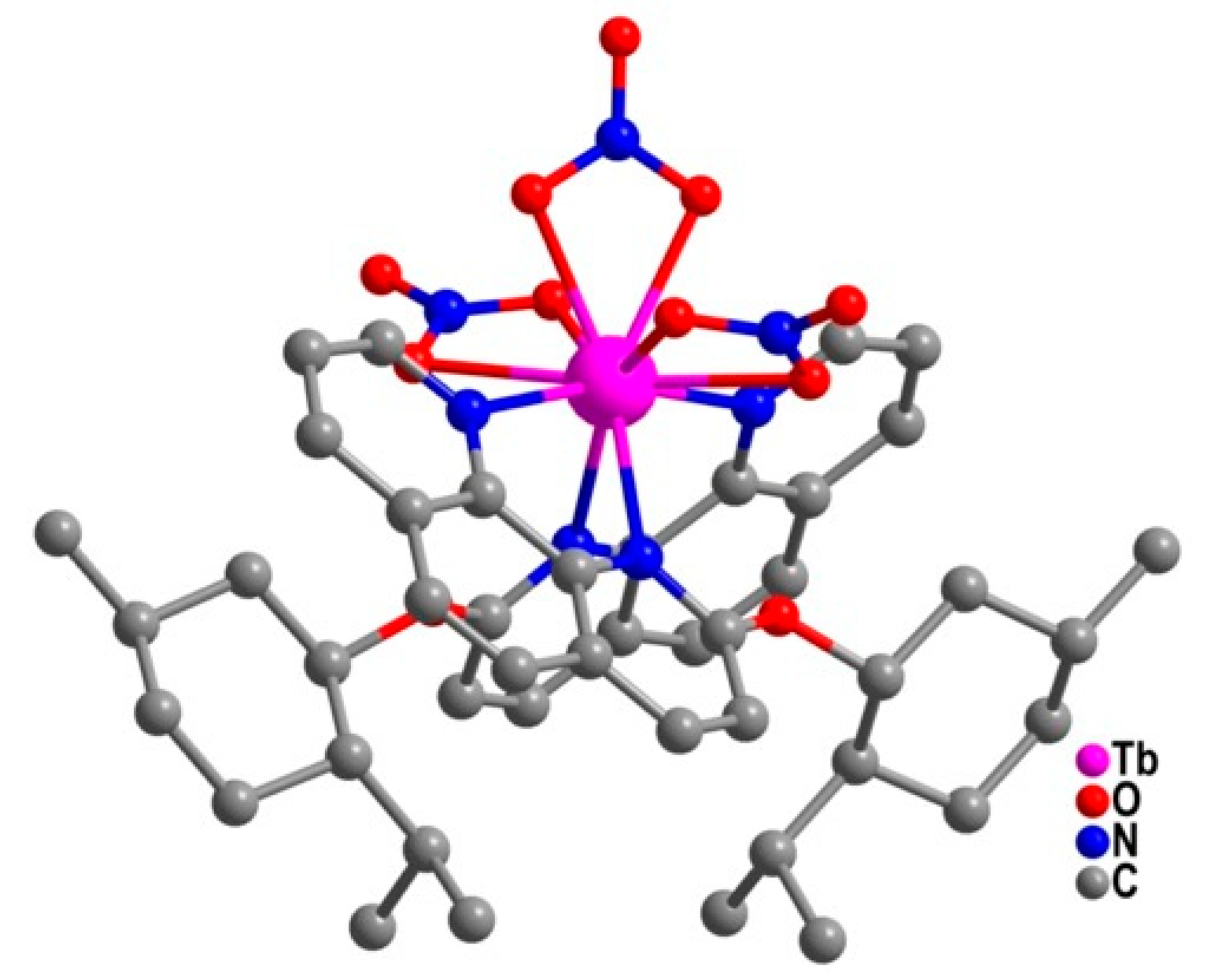

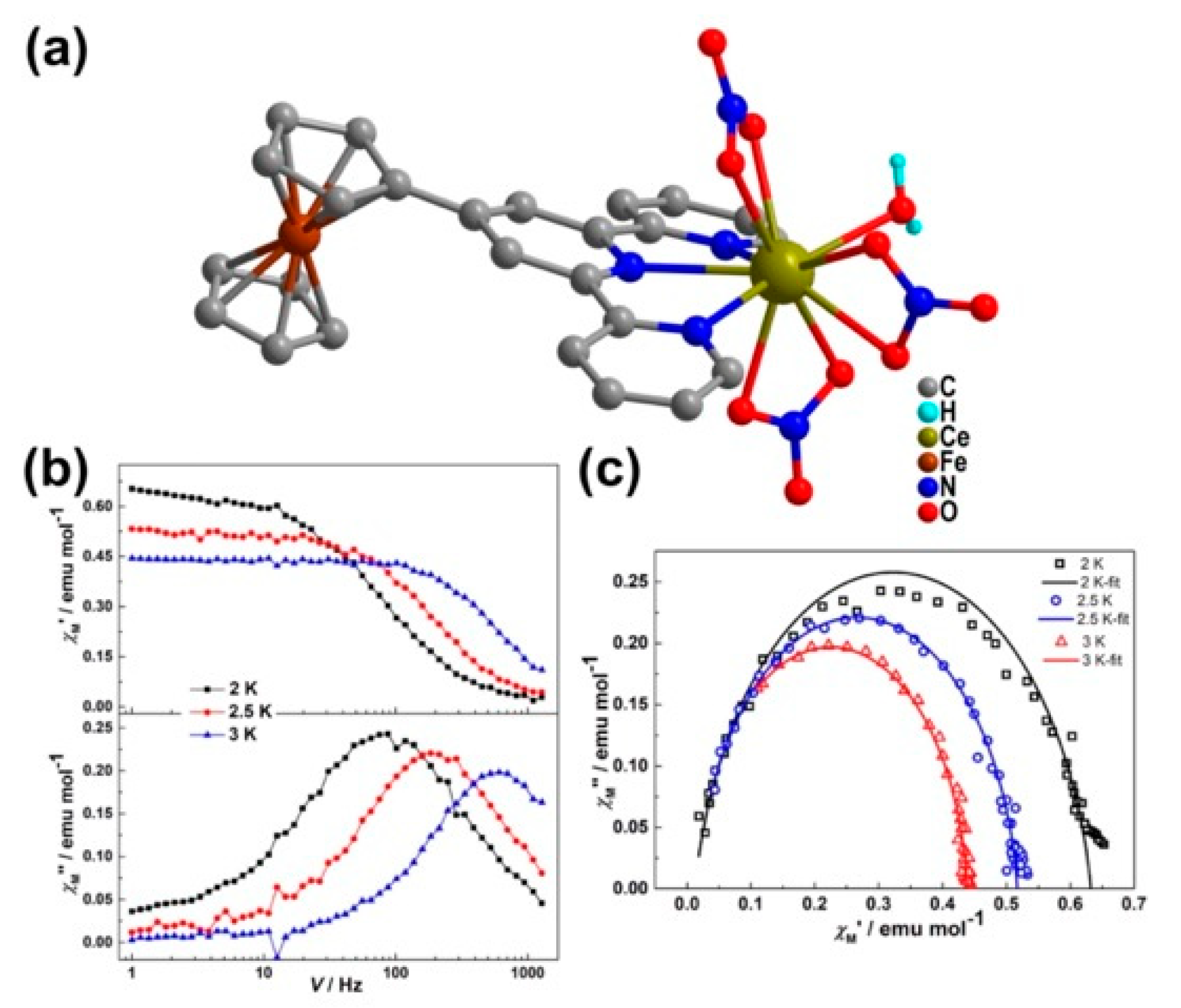
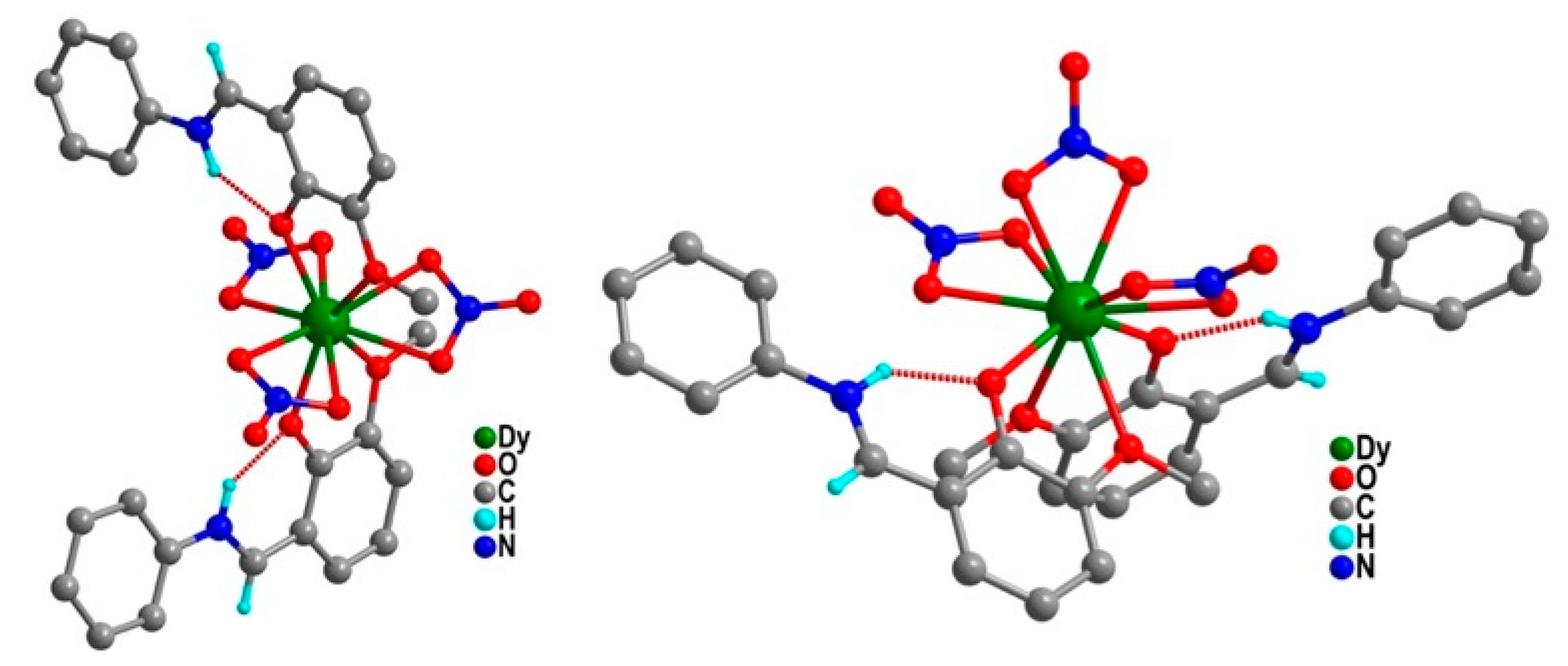
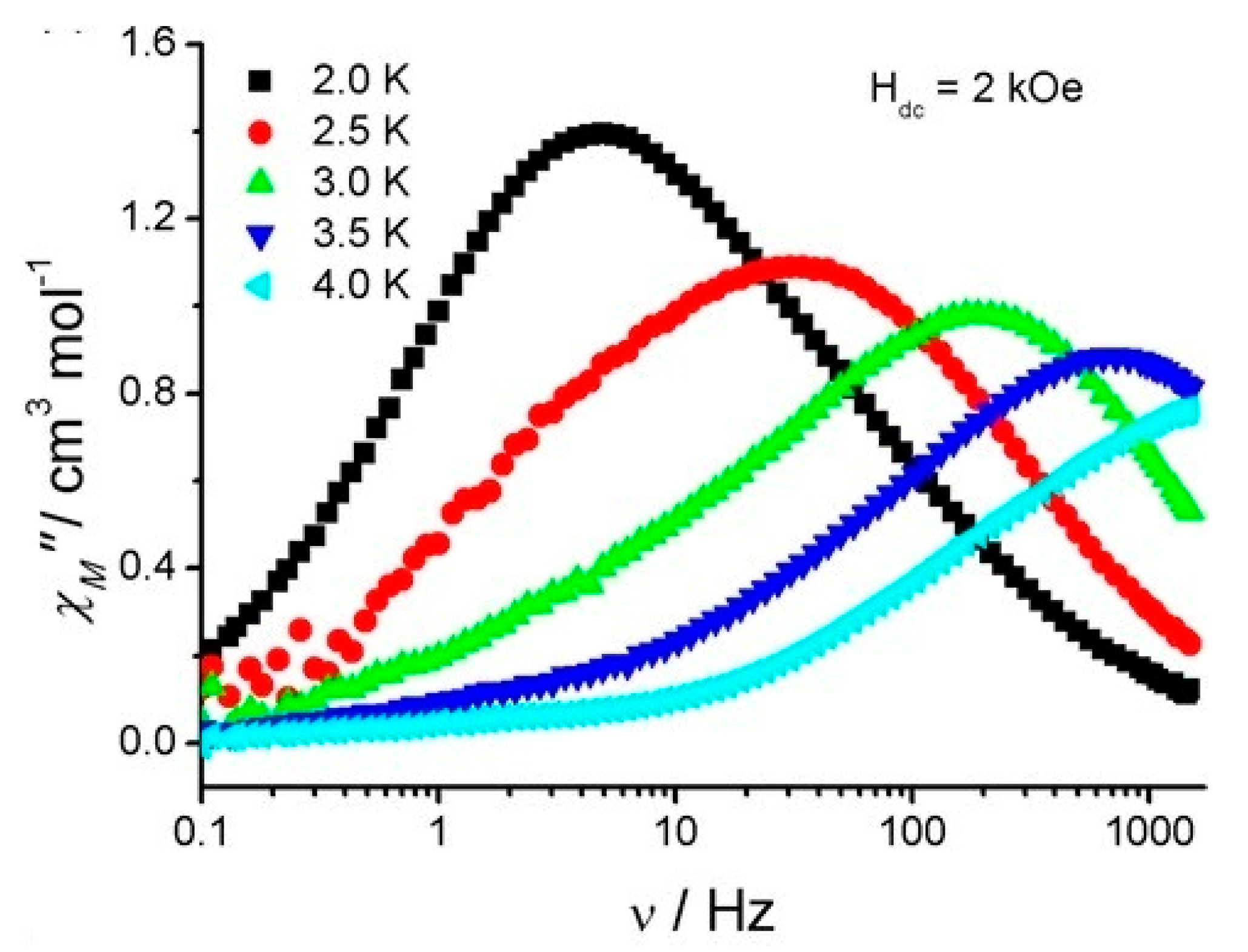
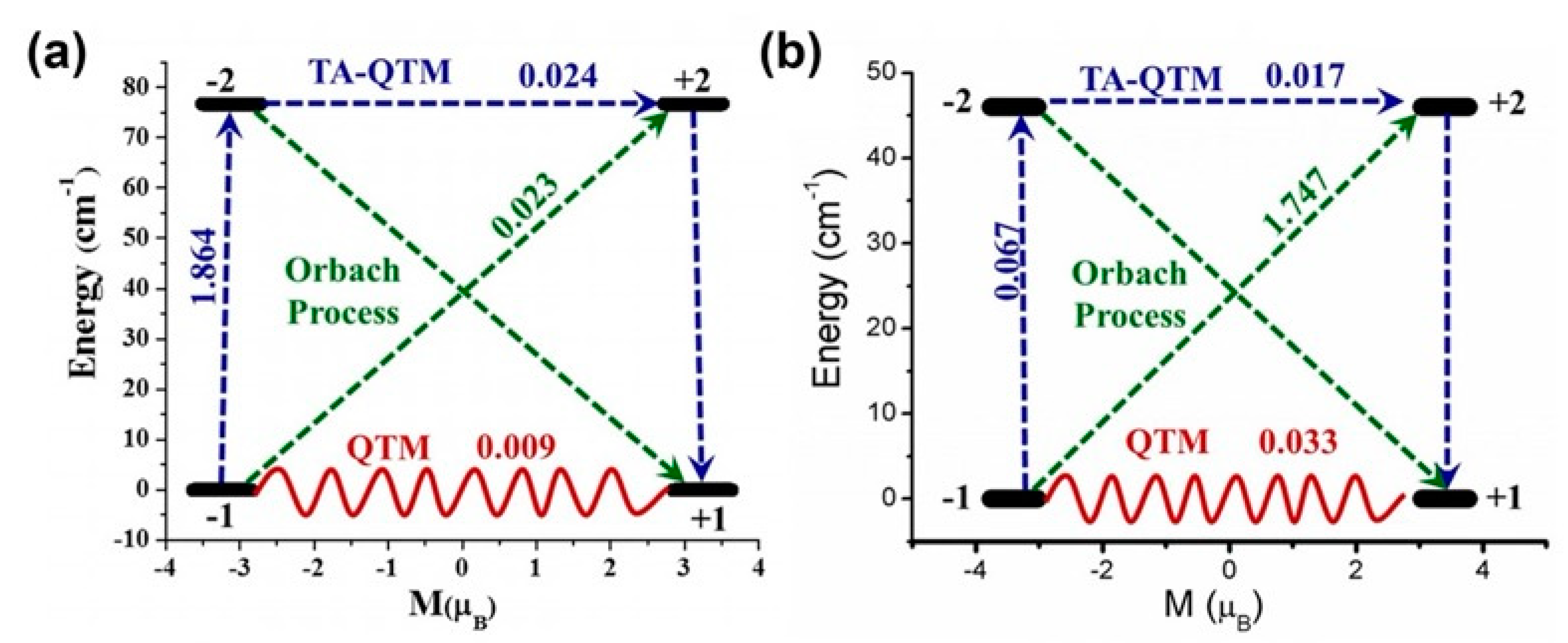
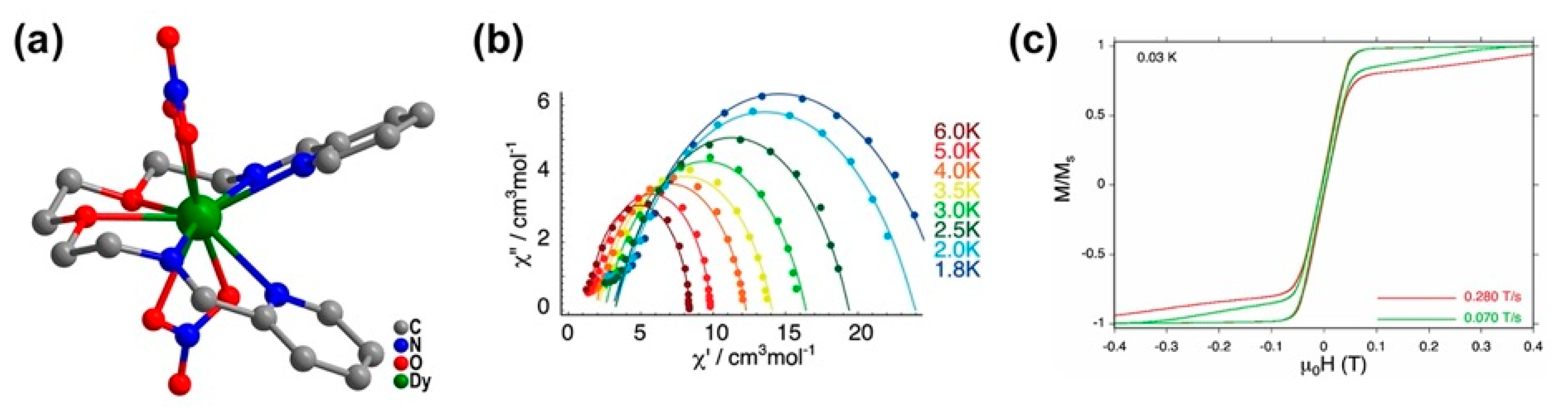
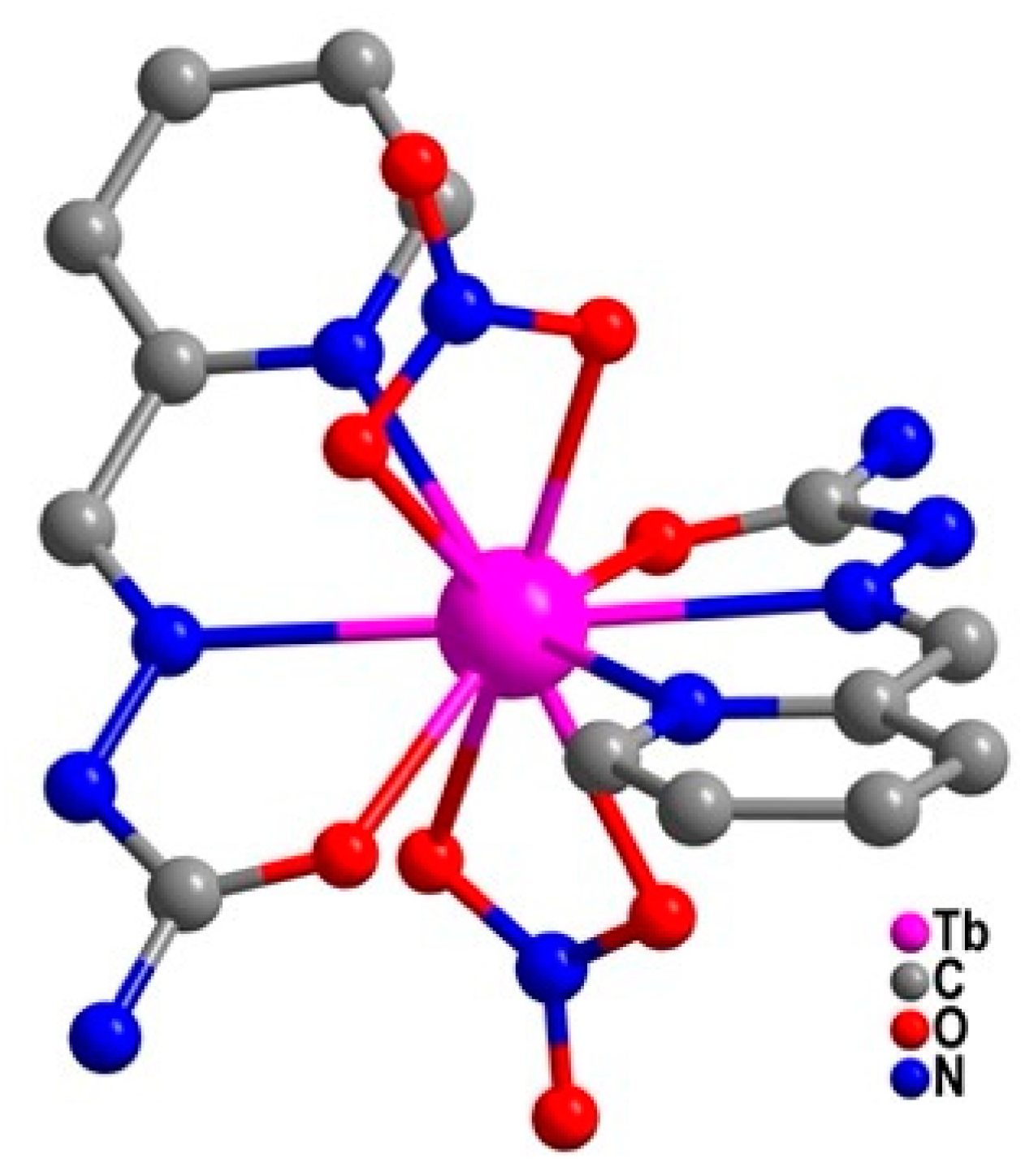
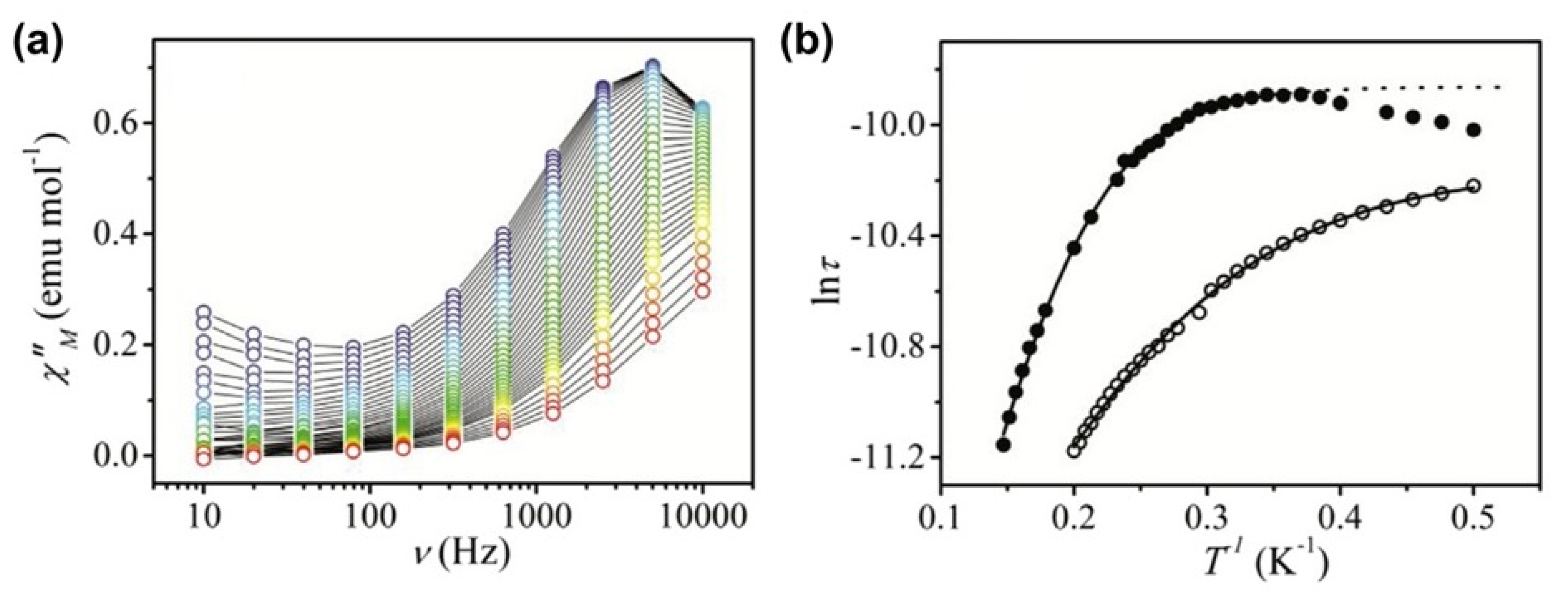
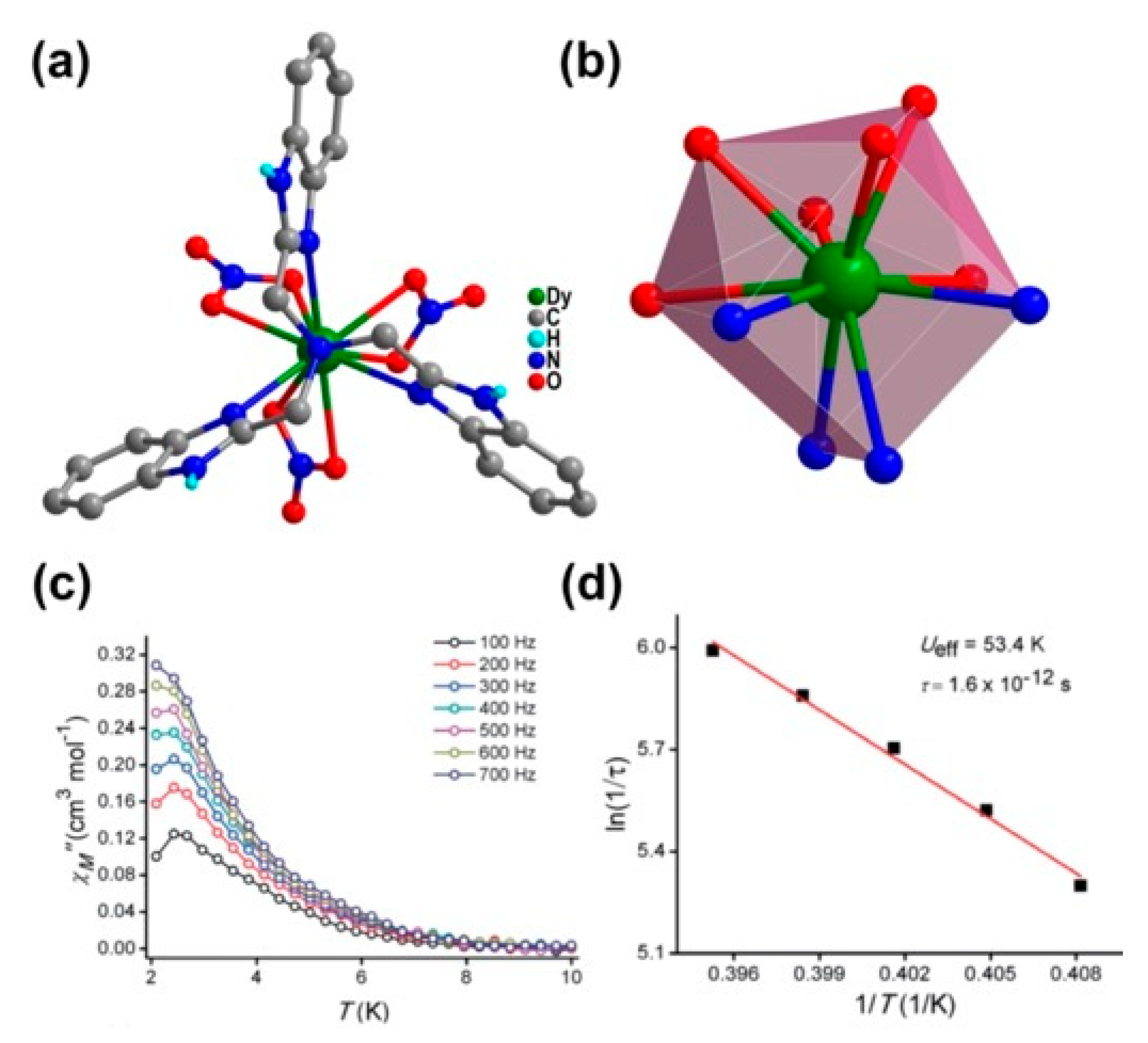
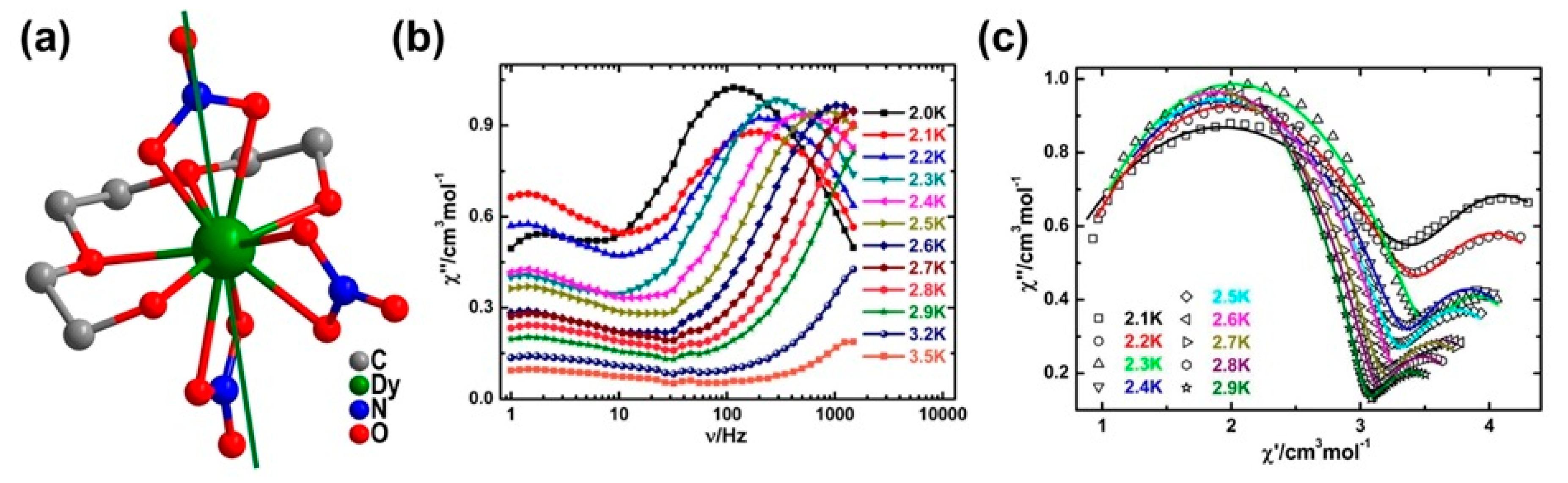
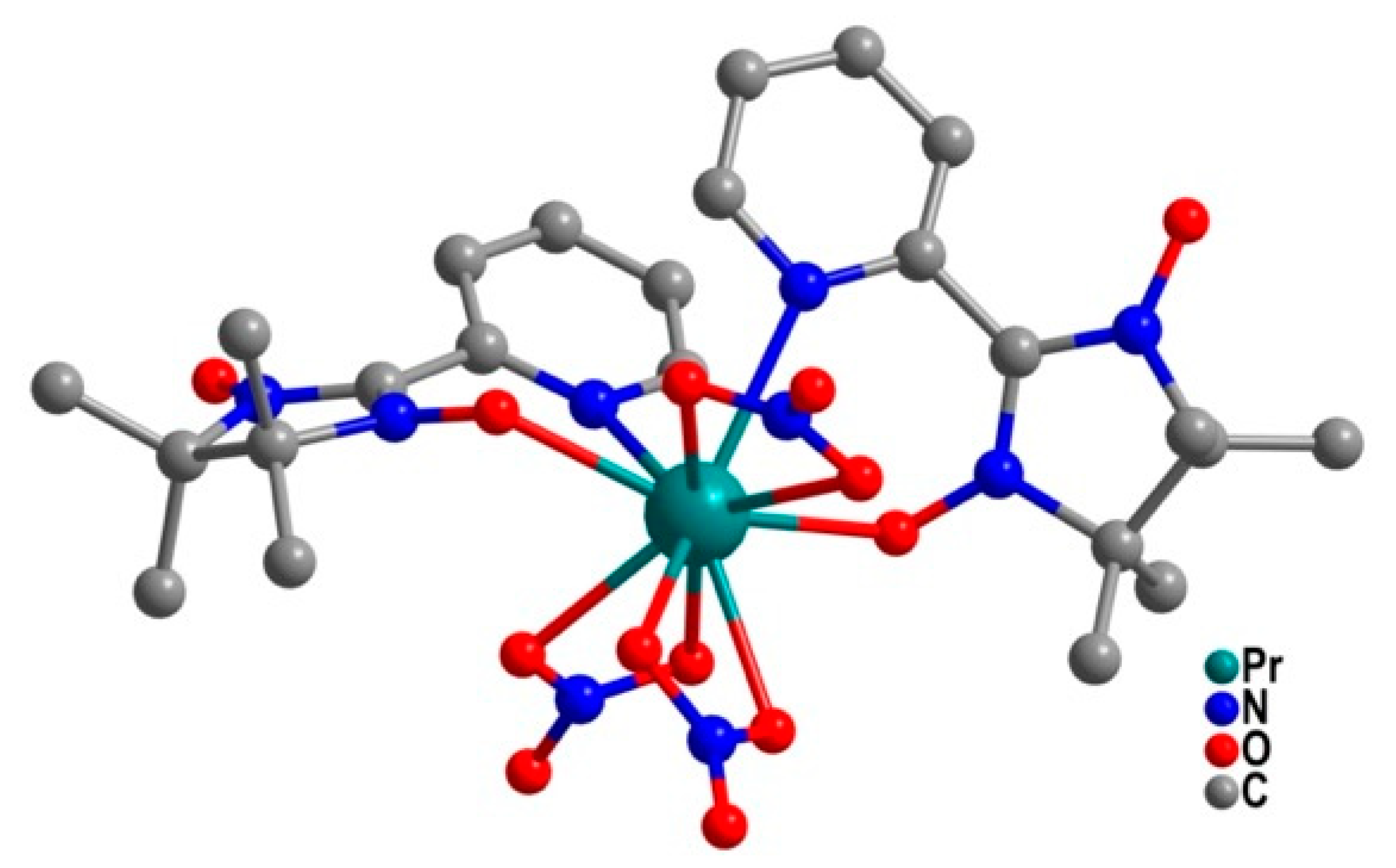
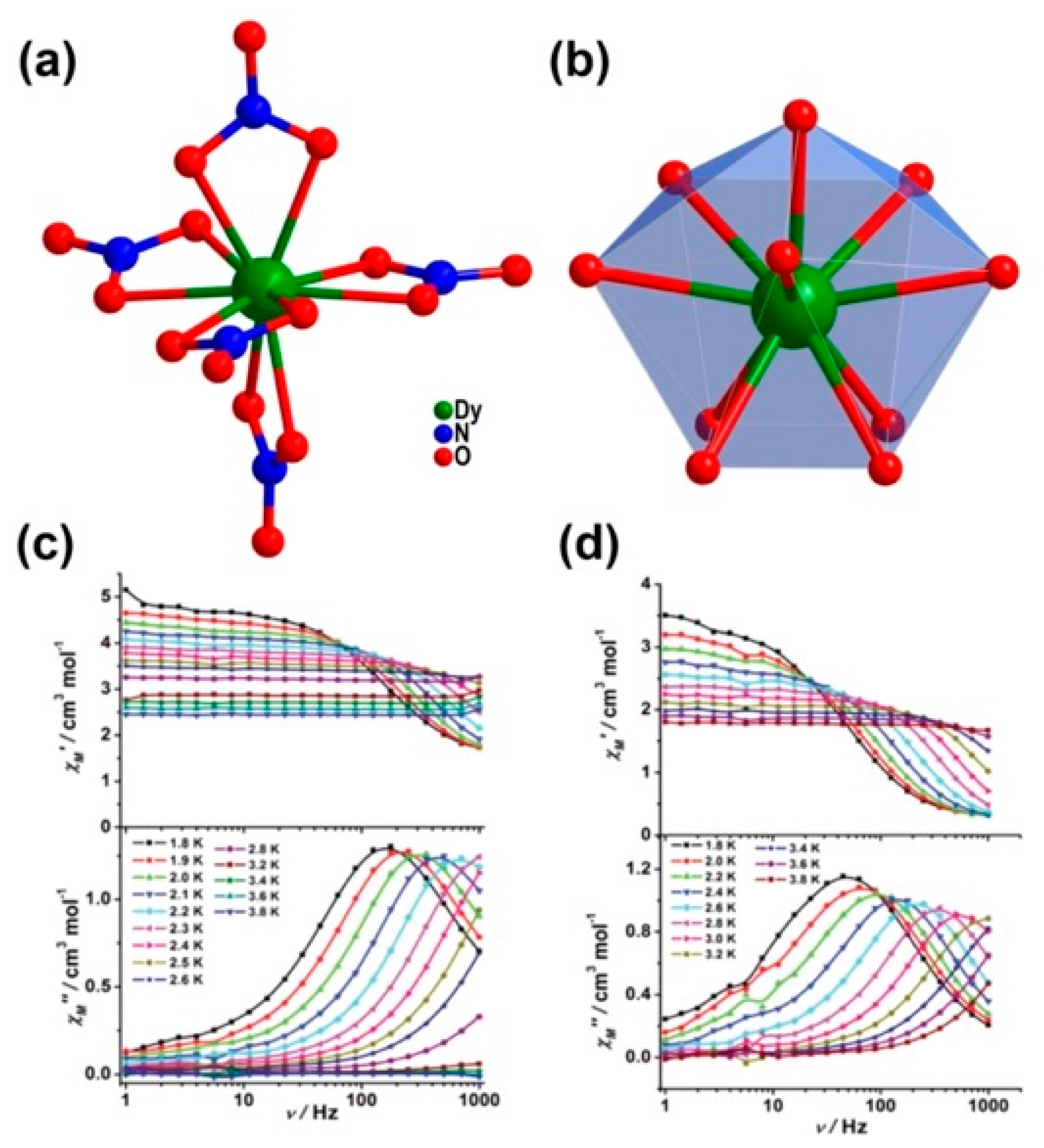
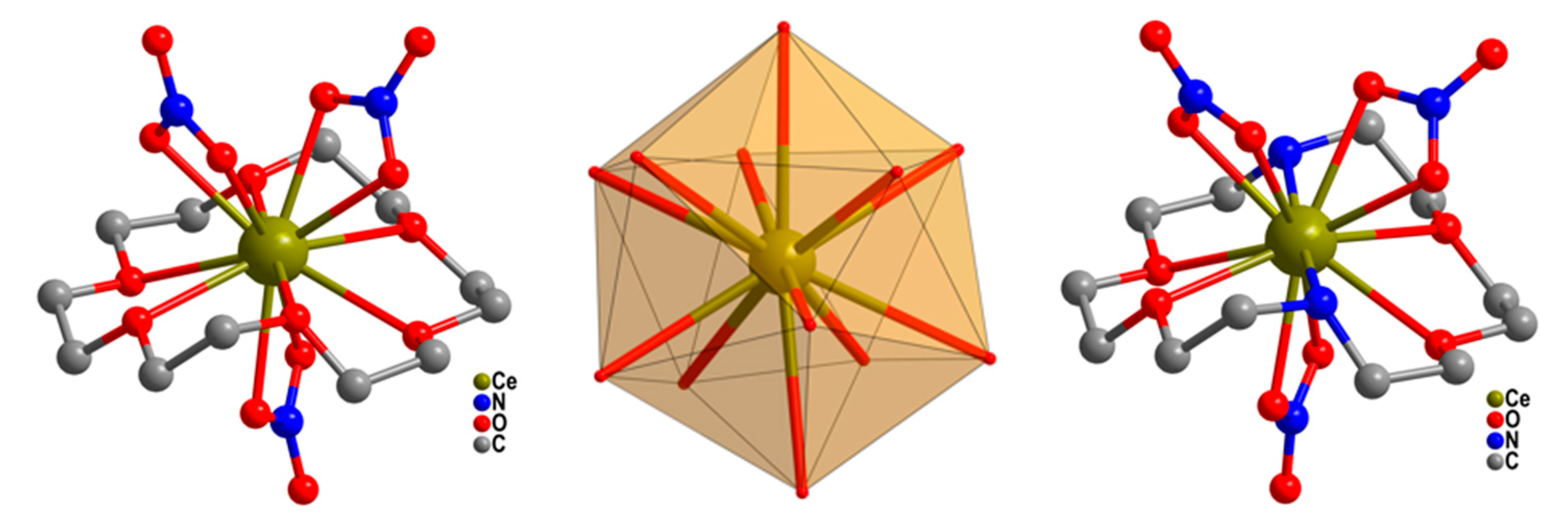
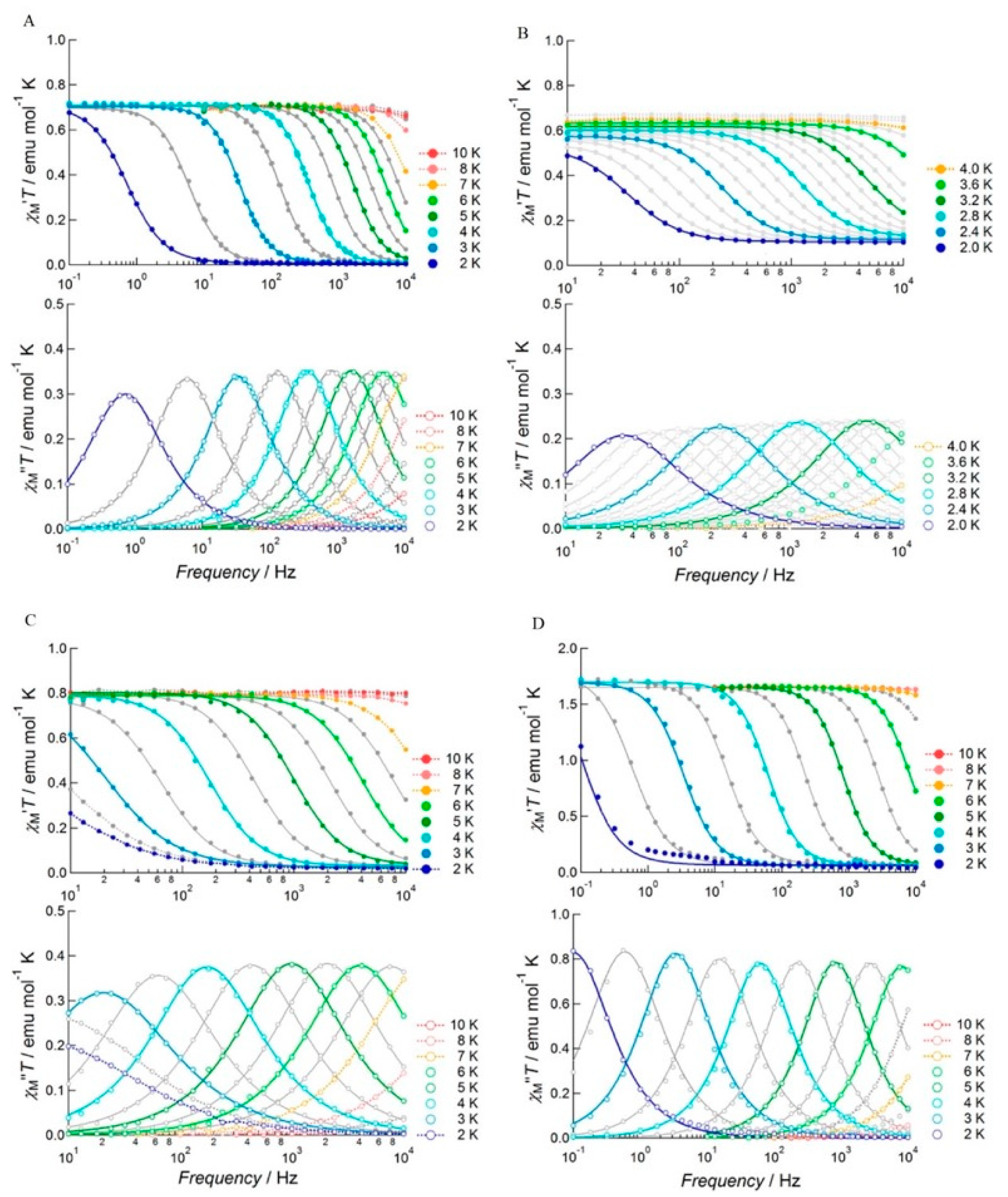

| Relaxation Parameters | 41 | 43 | 44 | 46 |
|---|---|---|---|---|
| n is fixed at 5 | ||||
| ΔE kB−1/K | 30.3(3) | 30.9(4) | 45(2) | 55(4) |
| τ0/ns | 220(17) | 2.2(3) | 26(7) | 2.6(1.9) |
| C/s−1 K−5 | 0.108(10) | 4.1(3) | 0.52(4) | 0.050(12) |
| n is fixed at 9 | ||||
| ΔE kB−1/K | 25.6(7) | 33.4(5) | 23(1) | 73(2) |
| τ0/ns | 9(2) × 102 | 1.6(2) | 6(2) × 103 | 0.14(6) |
| C/s−1 K−5 | 16(4) | 0.350(11) | 22(9) | 10.7(4) |
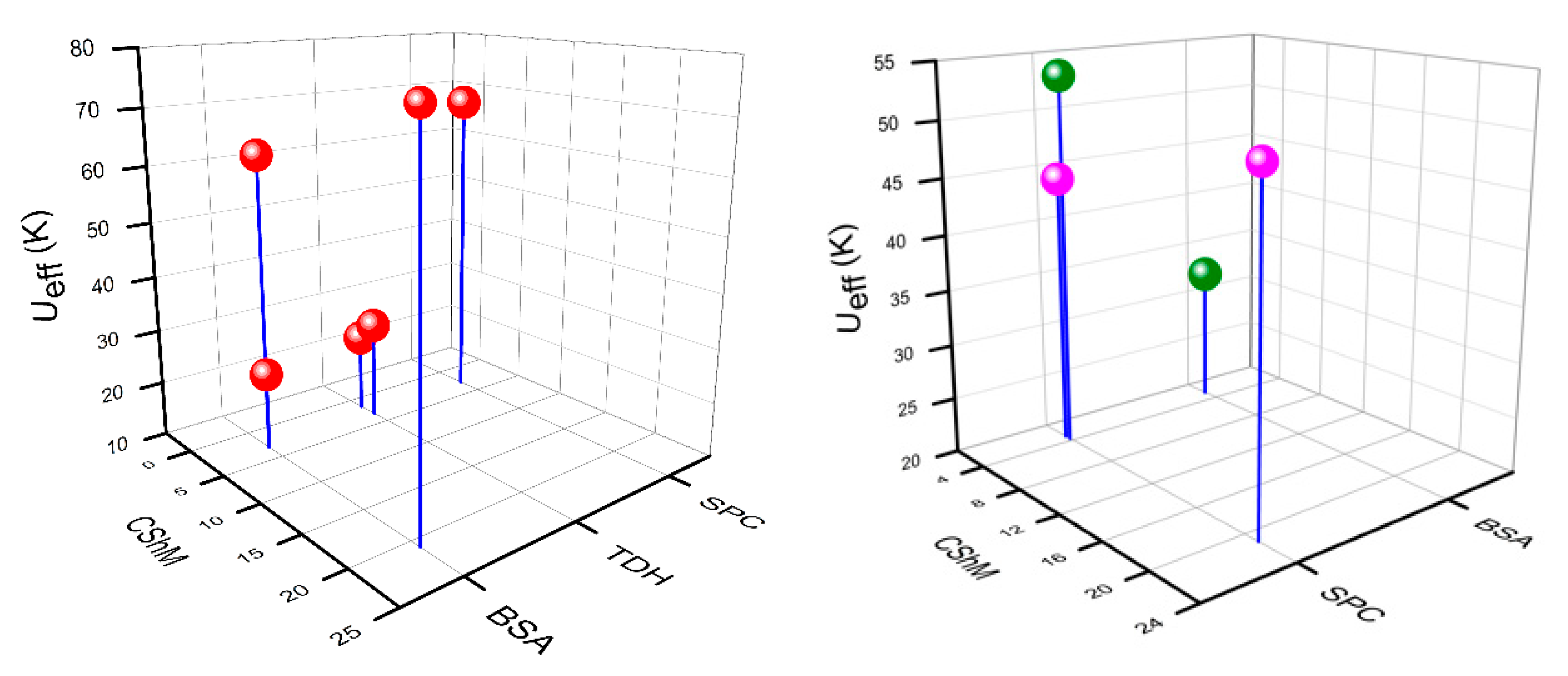
| Sl. No. | Formula (Complex Number) | Co-Ordination Environment | Geometry Around Metal * | ChSM Value | Ueff, τ0 (Hdc) | Ref |
|---|---|---|---|---|---|---|
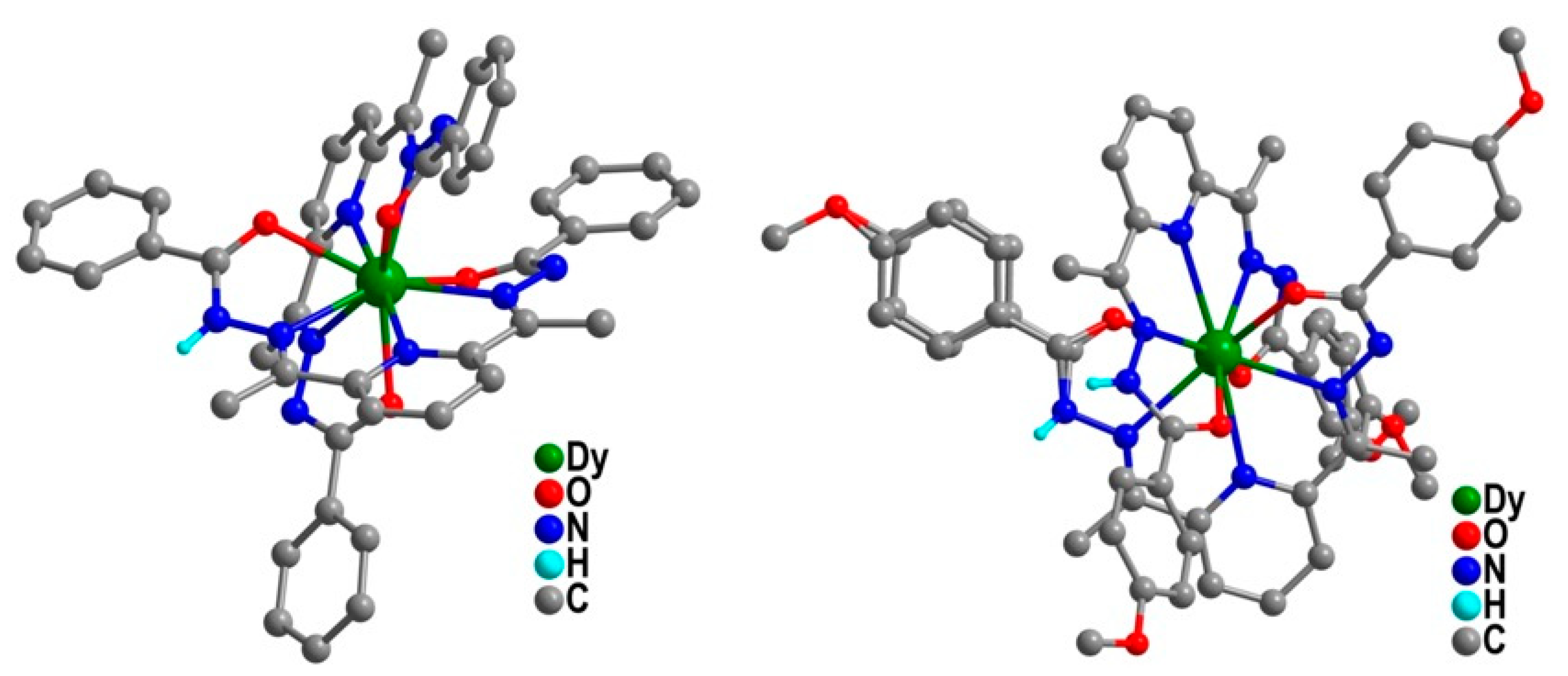
| 1 | [Dy(H2dapbh)2](NO3)3 (1) | 4O6N | BSA | 2.840 | 32.4 K (1000 Oe) | [38] |
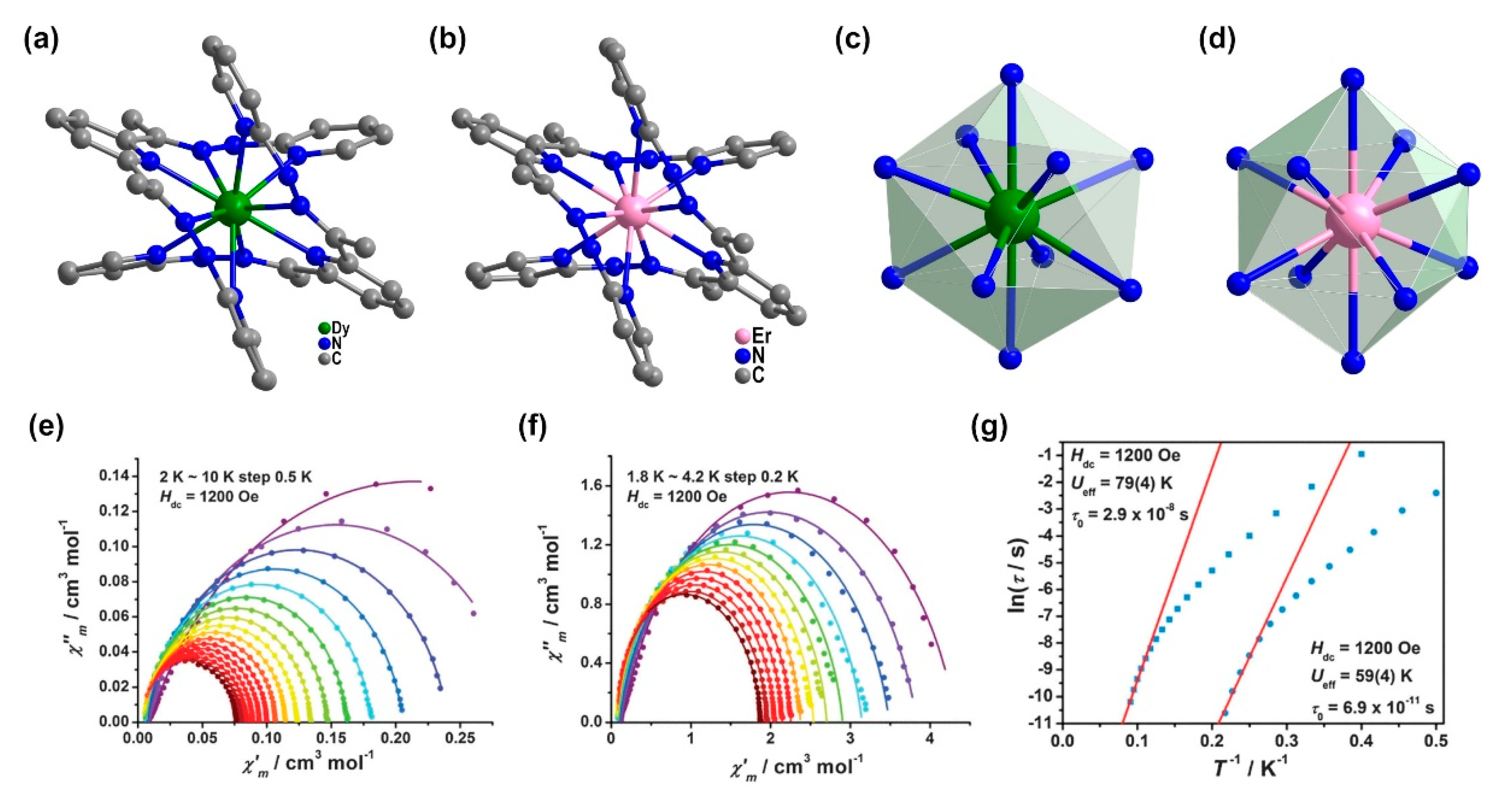
| 2 | [Dy(N5)2](CF3SO3)3 (8) | 10N | BSA | 3.335 | 79 K, 2.9 × 10−8 s, 1200 Oe | [36] |
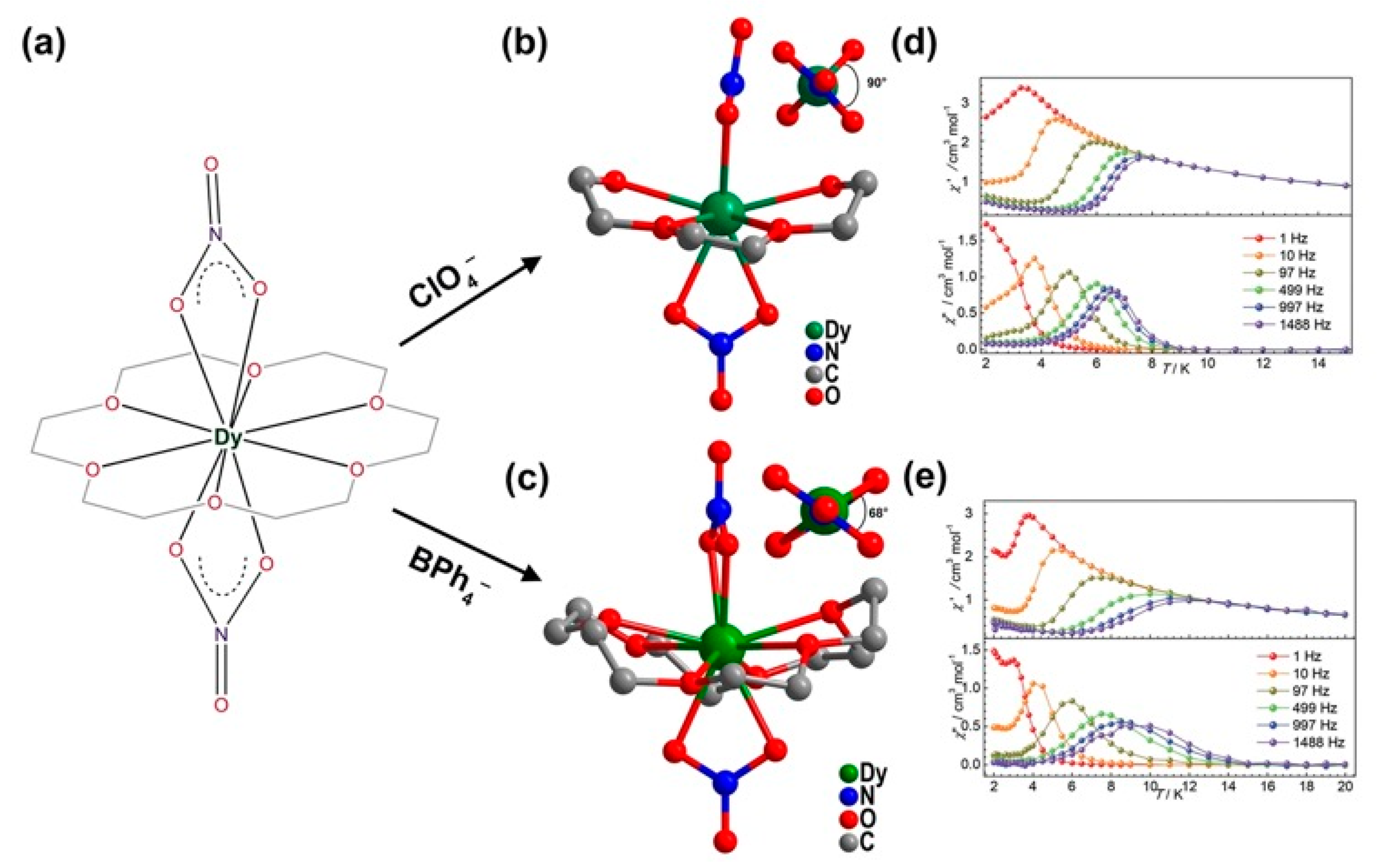
| 3 | [Dy(12-crown-4)(NO3)3] (10) | 10O | SPC | 2.837 | 68 K, 2.07 × 10−10 s (1000 Oe) 75.92 K, 6.8 × 10−11 s (500 Oe) | [37] |
| BSA | 20.899 | |||||
| 4 | [Dy(18-crown-6)(NO3)2]ClO4 (14) | 10O | BSA | 3.101 | 63 K, 1.02 × 10−8 s (1000 Oe) | [38] |
| 5 | [Dy(L2)2(NO3)](ClO4)2 (25) | 6O4N | SPC | 3.223 | 44.3 K, 5.17 × 10−7 s (1000 Oe) | [42] |
| 6 | [Dy(HL3)2(NO3)3] (27) | 10O | BSA | 3.148 | 23.9 K, 2.47 × 10−6 s (2000 Oe) | [48] |
| 7 | [Dy(L4)(NO3)2](NO3) (29) | 6O4N | SPC | 21.104 | 50 K, 6.80 × 10−7 s, (1000 Oe) | [49] |
| 8 | [Dy(ntbi)(NO3)3] (36) | 4O6N | SPC | 3.655 | 53.4 K, 1.6 × 10−12 s (1200 Oe) | [51] |
| 9 | [Dy(H2TEG)(NO3)3]·[18-crown-6] (37) | 10O | TDH | 3.292 | 28 K, 2.49 × 10−9 s (1000 Oe) | [52] |
| 10 | (nBu4N)2[Dy(NO3)5] (39) | 10O | TDH | 1.513 | 24.3 K, 3.40 × 10−9 s, (500 Oe) | [54] |
| 11 | [CeNO3)3(18-crown-6)] (41) | 12O | IC | 1.862 | 30.3 K, 2.20 × 10−7 s (1000 Oe) | [57] |
| 12 | [Ce(NO3)3(1,10-diaza-18-crown-6)] (44) | 10O2N | IC | 1.765 | 44 K, 2.3 × 10−8 s (1000 Oe) | [57] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acharya, J.; Kalita, P.; Chandrasekhar, V. High-Coordinate Mononuclear Ln(III) Complexes: Synthetic Strategies and Magnetic Properties. Magnetochemistry 2021, 7, 1. https://doi.org/10.3390/magnetochemistry7010001
Acharya J, Kalita P, Chandrasekhar V. High-Coordinate Mononuclear Ln(III) Complexes: Synthetic Strategies and Magnetic Properties. Magnetochemistry. 2021; 7(1):1. https://doi.org/10.3390/magnetochemistry7010001
Chicago/Turabian StyleAcharya, Joydev, Pankaj Kalita, and Vadapalli Chandrasekhar. 2021. "High-Coordinate Mononuclear Ln(III) Complexes: Synthetic Strategies and Magnetic Properties" Magnetochemistry 7, no. 1: 1. https://doi.org/10.3390/magnetochemistry7010001
APA StyleAcharya, J., Kalita, P., & Chandrasekhar, V. (2021). High-Coordinate Mononuclear Ln(III) Complexes: Synthetic Strategies and Magnetic Properties. Magnetochemistry, 7(1), 1. https://doi.org/10.3390/magnetochemistry7010001







