A Novel Computational Method to Identify/Analyze Hysteresis Loops of Hard Magnetic Materials

Abstract

In this study, a novel computational method capable of reproducing hysteresis loops of hard magnetic materials is proposed. It is conceptually based on the classical Preisach model but has a completely different approach in the modeling of the hysteron effect. Indeed, the change in magnetization caused by a single hysteron is compared here to the change in velocity of two disk-shaped solids elastically colliding with each other rather than the effect of ideal geometrical entities giving rise to so-called Barkhausen jumps. This allowed us to obtain a simple differential formulation for the global magnetization equation with a significant improvement in terms of computational performance. A sensitivity analysis on the parameters of the proposed method has indeed shown the capability to model a large class of hysteresis loops. Moreover, the proposed method permits modeling of the temperature effect on magnetization of neodymium magnets, which is a key point for the design of electrical machines. Therefore, application of the proposed method to the hysteresis loop of a real NdFeB magnet has been proven to be very accurate and efficient for a large temperature range.

1. Introduction

Increasing needs in the electromechanical industry are pushing the boundaries of research in magnetochemistry towards the development of innovative hard ferromagnetic materials. In fact, permanent magnets (PMs) are crucial for many applications spanning from brushless electric motors to hard disk drives and magnetic fasteners [1]. Among these, neodymium magnets (also known as NdFeB) are nowadays the most widely used for industrial purposes [2,3].

When designing a PM, knowledge and characterization of its hysteretic behavior is of paramount importance and having a good mathematical model capable of reproducing this behavior is important as well. Such mathematical models are intended to provide the functional relationship linking magnetization M (or magnetic flux density B) to the applied magnetic field H.

To date, a large number of hysteresis models have been proposed and applied in computational electromagnetics. A wide bibliography on the identification procedures and on the experimental-numerical results is reported in [4], while Ivànyi has made comparisons and evaluations of several models [5]. Among these, the Preisach model is the most common in electromagnetic analysis due to its accuracy, efficiency, and ability to fit a large class of hysteresis loops [6]. It was first published by Preisach in 1935 [7], and during the next decades, it attracted great research interest [8]. Starting from the original idea of connecting independent relay hysterons, Mayergoyz then provided an in-depth analysis of this model in [9] and proposed the discrete formulation of the Preisach model to make it suitable in numerical computation [10].

The classical Preisach model was born as a static scalar model; however, many extensions and modification attempts have been made in the past years [11,12,13,14,15,16]. For instance, Della Torre included the dynamic effect and proposed a moving Preisach model [11], while an extension to a vector model was provided in [12,13,14,15,16]. An important application of the latter class of models is their usage in magnetic design tools for optimization of PM-based components [17,18,19,20].

The Preisach model is usually considered a phenomenological method, unlike the also known Jiles–Atherton (JA) model that is considered to be based more closely on the physics of magnetism [21]. However, from a computational point of view, the Preisach model provides great advantages compared to JA, as reported by Philips in [22]. Other important models, such as the Stoner and Wohlfarth one [23] and the Hodgdon method [24], are not as popular as the Preisach or JA models. This may be due to their limitations of generality or computation speed.

In this study, a novel computational method, which allows a simple ordinary differential equation (ODE) to be obtained for the global magnetization as a response to the input magnetic field, is presented. It is still based on the Preisach model but conceptually has a completely different approach in the modeling of the hysteron effect. More specifically, the change in magnetization caused by a single hysteron is compared here to the change in velocity of two disk-shaped solids elastically colliding with each other [25,26], while in the classical Preisach model, the hysterons are mainly modelled as ideal geometrical entities giving rise to so-called Barkhausen jumps under certain conditions [13,14]. Since the arrival and collision directions of the moving disk-shaped solids are statistically sampled from a suitable ODE distribution, the global effect of the whole hysterons population is linked to the average change in magnetization. After some manipulations, it is possible to analytically derive the average change in magnetization for some particular probability distribution functions (e.g., normal) [27,28]. This allows a simple ODE for the global magnetization equation rather than a complicated integrodifferential one to be obtained, with a significant improvement in terms of computational performance. In fact, Preisach-based models generally require the numerical solution of integrodifferential equations describing the hysterons distribution and their effect on magnetization.

The main advantage of the proposed computational method is in the analytical simplicity of the ODE describing global magnetization, still allowing a precise estimation of hysteresis loops by the fitting parameters needed to analyze the hysteretic behavior of real materials, such as NdFeB. Furthermore, the proposed method permits modeling of the temperature effect on the magnetization of NdFeB, which is a key aspect in the design of PM-based components subjected to temperature variations, such as electrical machines or particle accelerators [29,30].

2. Materials and Models

2.1. Hard Ferromagnetic Materials

Ferromagnetism is the basic mechanism for which certain materials, such as iron, form or are attracted by magnets [31]. Commercial magnets are made of hard ferromagnetic or ferrimagnetic materials with very large magnetic anisotropy, such as alnico and ferrites, which have a very strong tendency for the magnetization to be pointed along one axis of the crystal, the “easy axis” [32].

PMs are very important components for electric motors and power generators. Key properties of PMs, especially coercivity and remanent magnetization, are strongly dependent on their microstructure. Understanding metallurgical processing, phase stability, and microstructural changes are essential for designing and improving PMs. Widely used PM-based components for the traction motor in electric vehicles and for the power generator in wind turbines contain rare earth elements (REE), such as neodymium and dysprosium, due to their high maximum energy product. Dysprosium is usually employed to sustain NdFeB coercivity at higher temperature. Due to the high supply risk of REE, these elements are listed as critical materials by the U.S. Department of Energy and other international or European institutes.

Compared to rare earth PMs, non-rare earth (non-RE) PMs typically have lower maximum energy products. However, given their small supply risks and low costs, they are largely investigated for less-demanding applications. The main goal for the development of non-RE PMs is to fill in the gap between the more cost-effective but lower performing hard ferrite magnets and the more expensive but higher performing RE PMs. In the past few years, great progress has been made toward improving the microstructure and physical properties of non-RE PMs. Several new candidate-material systems have been investigated, and some have shown realistic potential for replacing RE PMs for some applications [33].

Neodymium Magnets

Neodymium magnets were independently developed in 1984 by General Motors and Sumitomo Special Metals [34,35]. They are made of an alloy containing neodymium, iron, and boron to form the Nd₂Fe₁₄B tetragonal crystalline structure, which makes them the strongest type of PM commercially available [2]. Because of different manufacturing processes, they are divided into two subcategories, namely sintered NdFeB magnets and bonded NdFeB magnets [36].

Sintered NdFeB magnets are prepared by raw materials melted in a furnace, cast into a mold, and cooled to form ingots. The ingots are pulverized and milled; the powder is then sintered into dense blocks. The blocks are then heat-treated, cut to shape, surface treated, and magnetized.

Bonded NdFeB magnets are instead prepared by melt spinning a thin ribbon of the NdFeB alloy. The ribbon contains randomly oriented Nd₂Fe₁₄B nano-scale grains. Then, it is pulverized into particles, mixed with a polymer, and either compression- or injection-molded into bonded magnets.

The neodymium magnet data hereby considered are taken from [30]. In fact, a characterization of the hysteresis cycles for this alloy was performed there for temperatures ranging between 27 °C and 200 °C. Therefore, the effects of temperature on PM performance and, thus, on the hysteresis fitting have been investigated.

2.2. Hysteresis Models

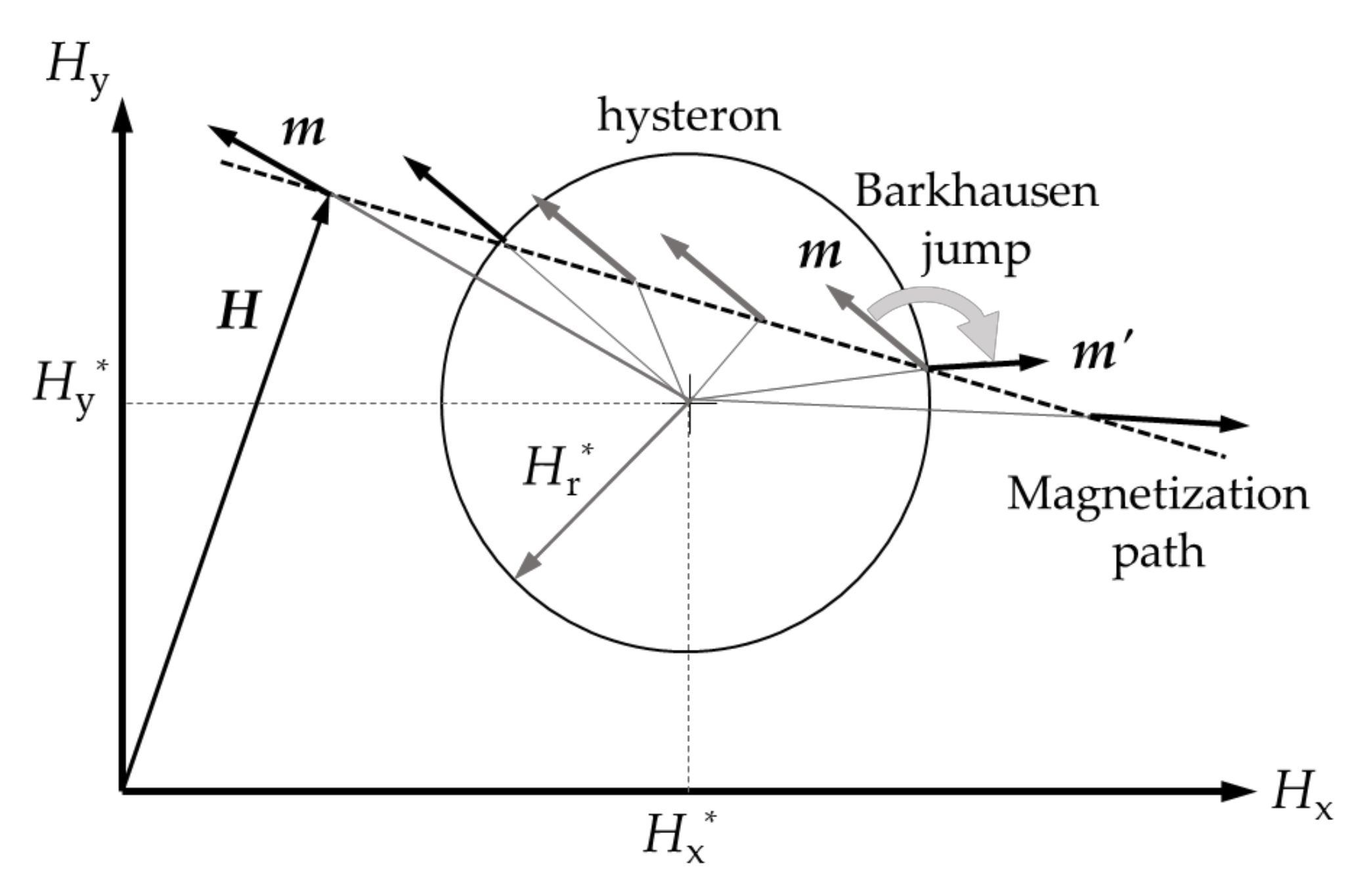
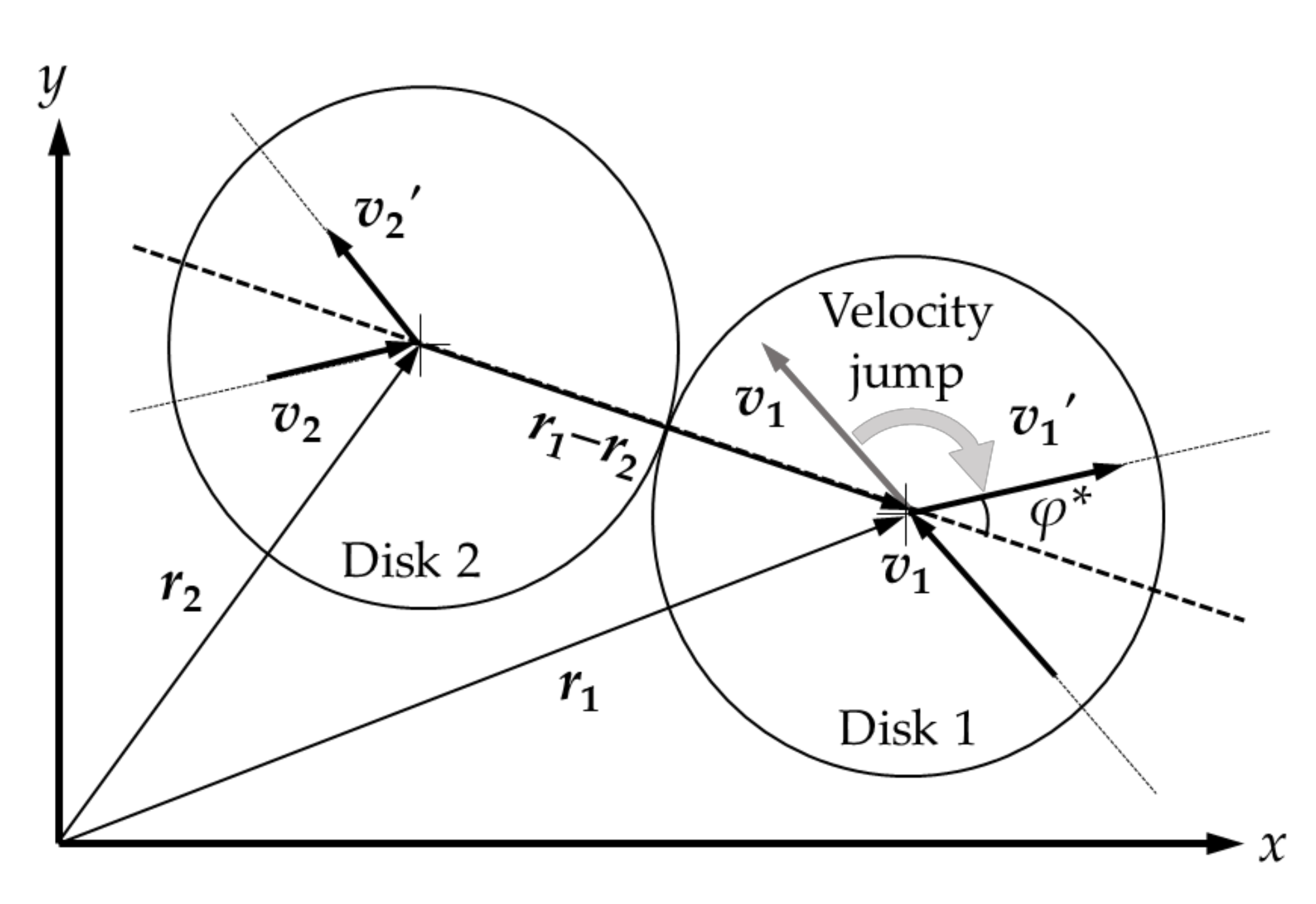
2.2.1. Vector Preisach Hysteresis Model

The Vector Preisach hysteresis model (VPHM) is based on decomposition of the system into several elementary hysteretic entities called hysterons. Each of them is defined by a closed critical surface in the magnetic field plane and its magnetization state is defined by the unitary and dimensionless vector m, as schematically illustrated in Figure 1.

When a generic magnetic field H is applied, the magnetic state m assumes the direction given by the vertex of H and the center of the considered hysteron [13,14,15,16]. If the H vertex moves following a generic trajectory, usually called an applied magnetic field path (dotted line in Figure 1), the state m changes its orientation as described above. However, when the H vertex enters the hysteron surface, m is in a frozen state and remains unchanged until the applied field gets out. In such a case, as soon as H exits the hysteron, m suffers a Barkhausen jump by rotating instantaneously from the magnetization state that it had inside the hysteron to the radial one. For the sake of clarity, the new magnetization state is indicated by m’ in Figure 1.

When an assembly of hysterons is considered, the resulting relative magnetization is computed as the vectorial sum of the magnetization states of all the hysterons. Therefore, in order to model magnetic processes of real materials, proper hysteron distribution functions in the magnetic field plane have to be considered. For instance, assuming circular hysterons, the hysteron distribution function is represented by the so-called Preisach function P(H_x,H_y,H_r), which indicates the probability of existence of hysterons centered in the generic rectangular coordinates H_x, H_y of the applied magnetic field plane and with radius H_r [13]. Hence, given an applied magnetic field H, the magnetization M of a generic material is computed as follows:

$$\mathit{M}\left(\mathit{H}\right)=M_s{{\displaystyle \int }}_{\mathsf{\Omega }}P\left(\Omega \right)\mathit{m}\left(\Omega , \mathit{H}\right)d\Omega$$

(1)

where M_S is the material magnetic saturation and $\Omega =\left\{H_{\mathrm{x}},H_{\mathrm{y}},H_{\mathrm{r}}\right\}$ is the space represented by the coordinates of the centers and by the radii of all the hysterons [13].

Finally, it is worth noticing that the VPHM can be extended also to a three dimensional applied field space and that it is independent on the shape of the critical surface constituting the hysterons.

2.2.2. Modified Magnetization Model for Linear Magnetization Path

The proposed method is based on an analogy between the change in magnetization state m caused by a hysteron and the change in velocity of disk-shaped solids elastically colliding with each other. In particular, two solids (named disk 1 and disk 2) are considered, as schematically sketched in Figure 2. They have velocities v₁ and v₂ before and v₁′ and v₂′ after the collision, respectively.

From classical mechanics [25,26], the velocity after collision ${\mathit{v}}_{\mathbf{1}}\prime$ is linked to the one before ${\mathit{v}}_{\mathbf{1}}$ by the following formula:

$${\mathit{v}}_{\mathbf{1}}\prime -{\mathit{v}}_{\mathbf{1}}=-2\frac{w_2}{w_1+w_2}\frac{\left({\mathit{v}}_{\mathbf{1}}-{\mathit{v}}_{\mathbf{2}}\right)·\left({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right)}{{\left|{\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right|}^2}\left({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}\right)$$

(2)

where $w_1$ and $w_2$ are the masses of disk 1 and disk 2, respectively, and ${\mathit{r}}_{\mathbf{1}}$ and ${\mathit{r}}_{\mathbf{2}}$ are their position vectors. Notice that the vectors resulting by the differences $\left({\mathit{v}}_{\mathbf{1}}-{\mathit{v}}_{\mathbf{2}}\right)$ and $({\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}$) are scalar multiplied with each other.

The change in velocity of disk 1 $\Delta {\mathit{v}}_{\mathbf{1}}$ = ${\mathit{v}}_{\mathbf{1}}\prime -{\mathit{v}}_{\mathbf{1}}$ can be expressed as follows:

$$\Delta {\mathit{v}}_{\mathbf{1}}=a \left|{\mathit{v}}_{\mathbf{1}}-{\mathit{v}}_{\mathbf{2}}\right| cos\phi \widehat{\mathit{r}}$$

(3)

in which a is a constant obtained by grouping the term $-2w_2/\left(w_1+w_2\right)$, φ is the angle between the vectors ${\mathit{v}}_{\mathbf{1}}-{\mathit{v}}_{\mathbf{2}}$ and ${\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}$, and $\widehat{\mathit{r}}$ is the unit vector defining the direction of ${\mathit{r}}_{\mathbf{1}}-{\mathit{r}}_{\mathbf{2}}$. Equation (3) is further simplified by assuming|${\mathit{v}}_{\mathbf{2}}$| = 0 m/s and |${\mathit{v}}_{\mathbf{1}}$| = 1 m/s. In this case, the angle φ corresponds to the angle φ* shown in Figure 2.

Establishing the analogy between the change in magnetization (Barkhausen jump) caused by a hysteron $\Delta \mathit{m}={\mathit{m}}^{\prime }-\mathit{m}$ and the change in velocity of disk 1 (velocity jump) yields the following:

$$\Delta \mathit{m}=b cos\phi \widehat{\mathit{r}}$$

(4)

where b is a suitable constant. Then, by assigning a proper statistical distribution to the angle φ, it is possible to evaluate the expected change in magnetization state $\mathrm{E}\left[\Delta \mathit{m}\right]$. Thus, according to statistical considerations, it can be stated that the material magnetization change is directly proportional to $\mathrm{E}\left[\Delta \mathit{m}\right]$.

In case of linear magnetization, i.e., considering an applied magnetic field H laying along the x-axis and considering the angle φ to be normally distributed with zero mean and variance σ², the expected change in magnetization state $\mathrm{E}\left[\Delta \mathit{m}\right]$ is given by the following:

$$\mathrm{E}\left[\Delta \mathit{m}\right]=b e^{-\frac{{\sigma }^2}{2}} {\widehat{\mathit{r}}}_x$$

(5)

in which ${\widehat{\mathit{r}}}_x$ is the unit vector along the x-axis. Being the instantaneous change in magnetization proportional to $\mathrm{E}\left[\Delta \mathit{m}\right]$ via a constant c, it can be written as follows:

$$\frac{d\mathit{M}}{dt}=\Gamma e^{-\frac{{\sigma }^2}{2}} {\widehat{\mathit{r}}}_x$$

(6)

where $\Gamma$ = bc is a proportionality constant.

It is now assumed that the instantaneous change in magnetization is caused by an applied time-varying magnetic field H(t) with a time-harmonic behavior:

$$\mathit{H}\left(t\right)=H cos \left(\omega t\right) {\widehat{\mathit{r}}}_x$$

(7)

where H is the applied field amplitude and ω is its angular frequency. Therefore, it appears reasonable to hypothesize that the variance σ² and the coefficient $\Gamma$ appearing in Equation (6) have similar time-harmonic behaviors. In particular, we assume time-dependent values of σ²(t) and $\Gamma \left(t\right)$ given by the following expressions:

$${\sigma }^2\left(t\right)/2=\alpha co{s}^2\left(\omega t+\beta \right)$$

(8)

$$\Gamma \left(t\right)=\gamma sin\left(\omega t+\beta \right)$$

(9)

in which α, β, and γ are three parameters and their values depend on the ability of the material of instantaneously change its magnetization.

Combining Equation (6) with Equations (8) and (9) yields the following:

$$\frac{d\mathit{M}\left(t\right)}{dt}=\gamma sin\left(\omega t+\beta \right) e^{-\alpha co{s}^2\left(\omega t+\beta \right)}{\widehat{\mathit{r}}}_x$$

(10)

The amplitude of magnetization M can be computed as follows:

$$M\left(t\right)=M_0+{{\displaystyle \int }}_0^{t}f\left(s\right)ds$$

(11)

where s is the local integration variable, $M_0$ is the initial magnetization, and the function $f\left(t\right)$ is given below:

$$f\left(t\right)= \gamma sin\left(\omega t+\beta \right)e^{-\alpha co{s}^2\left(\omega t+\beta \right)}$$

(12)

Finally, it should be emphasized that the shape of the hysteresis loop curve at generic time t (H($t$), M($t$)) is affected by the choice of the three parameters α, β, and γ. In particular, the latter affects the amplitude of the magnetization time derivative dM/d$t$, resulting in a steeper and more extended curve along the vertical axis of the H−M plane for increasing values of γ. Instead, the parameter β quantifies the phase shift of the function $f\left(t\right)$ with respect to the input field H($t$), while α influences the slope of the time derivative of M(t) and thus of the obtained hysteresis loop.

3. Results and Discussion

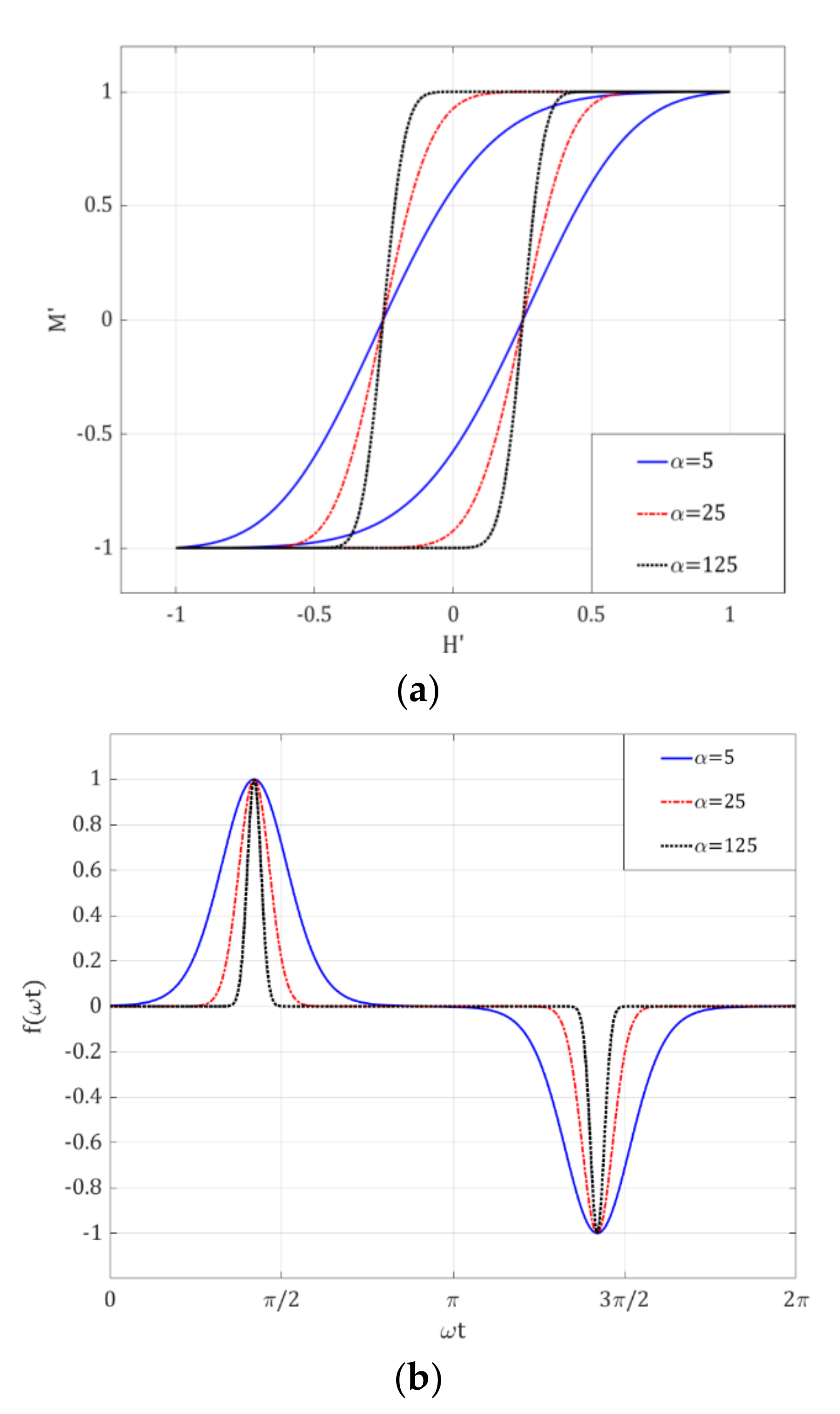
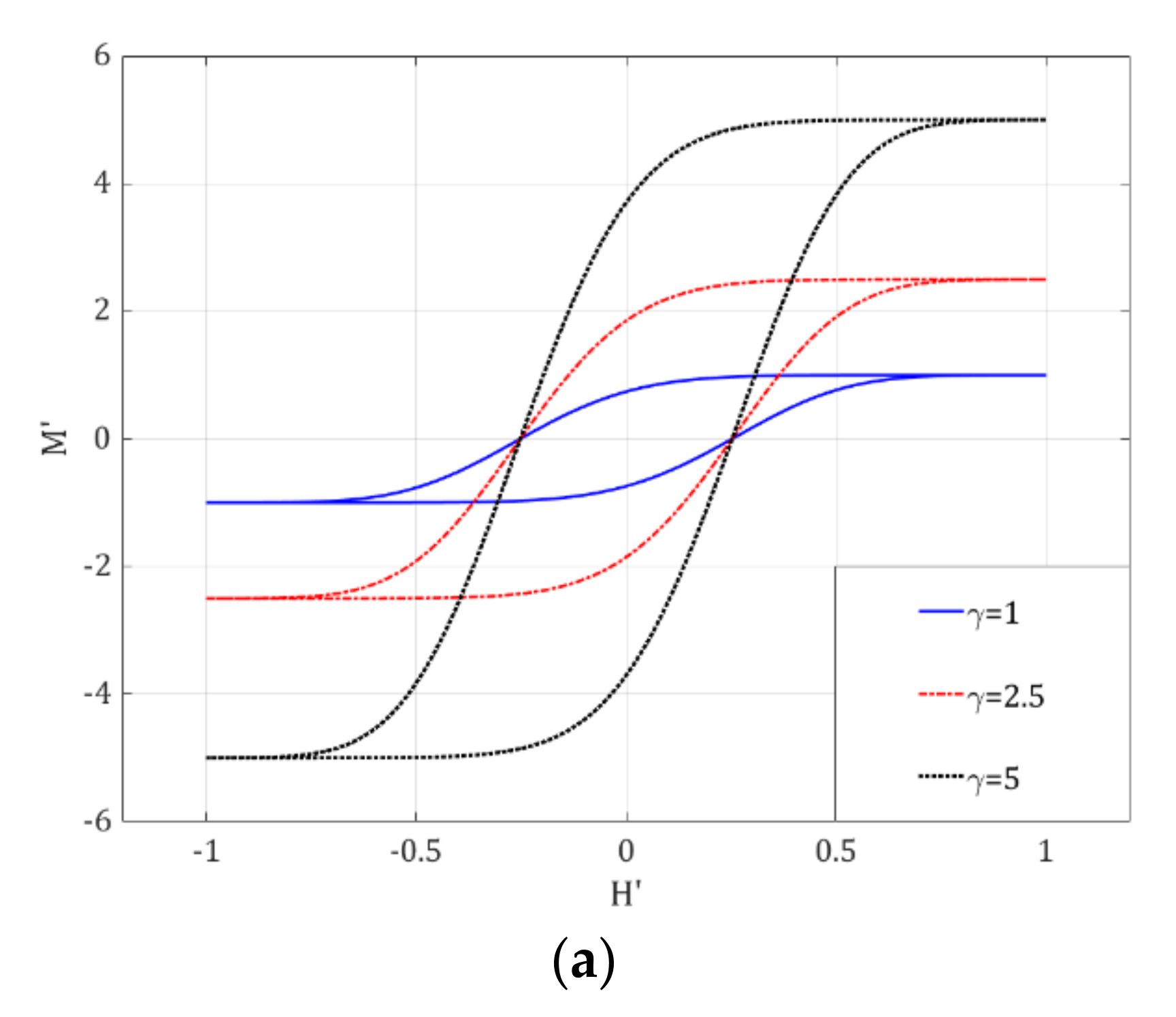
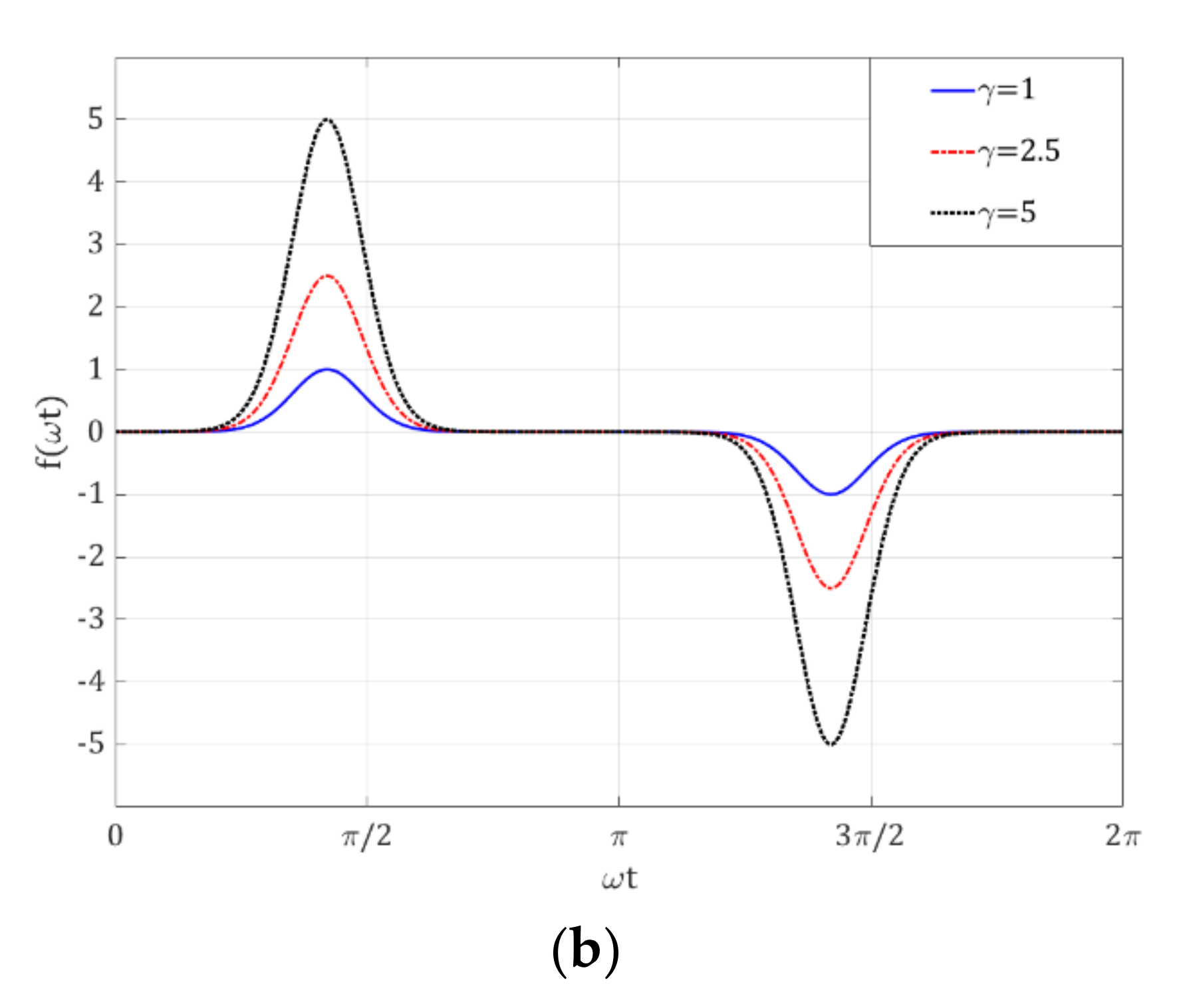
3.1. Sensitivity Analysis

The analytical method defined in the previous section can be applied to model a large class of hysteresis loops. In order to demonstrate its accuracy and generality, a sensitivity analysis is carried out, focusing on the effect of parameters α, β, and γ appearing in Equation (12). With this purpose, different normalized hysteresis loops have been computed in the H′ − M′ plane.

At first, the effect of α is investigated for fixed values of β = 0.25 and γ = 1. In particular, Figure 3a shows different normalized loops for α values ranging between 5 and 125, while Figure 3b reports the corresponding functions $f\left(\omega t\right)$. It is worth noticing that α affects neither the coercivity nor the saturation of the hysteresis loops but that it has a strong influence on the saturation remanence.

Secondly, the influence of β is assessed while keeping α and γ fixed to the values of α = 10 and γ = 1. Specifically, Figure 4a,b shows different normalized loops and the considering functions $f\left(\omega t\right)$, respectively. Unlike α, it can be seen that β has a strong influence on the coercivity and on the magnetic energy while it has no effect on the magnetic saturation of the material. Instead, functions $f\left(\omega t\right)$ are horizontally shifted when β increases, as expected from the role of β as the phase shift of the periodic functions in (12).

Finally, a totally different influence is exercised by the third parameter γ. In fact, small variations in γ correspond to big variations in the magnetic saturation of the resulting normalized hysteresis loops, as can be observed in Figure 5a, comparing the cycles obtained with γ = 1, γ = 2.5, and γ = 5 and fixing α = 10 and β = 0.25. The corresponding functions $f\left(\omega t\right)$, reported in Figure 5b, are affected only in their maximum amplitudes.

Hence, it can be concluded that a proper selection of parameters α, β, and γ allows for modeling a large class of hysteresis loops, characterized by a variety of magnetic energy, coercivity, and saturation remanence levels.

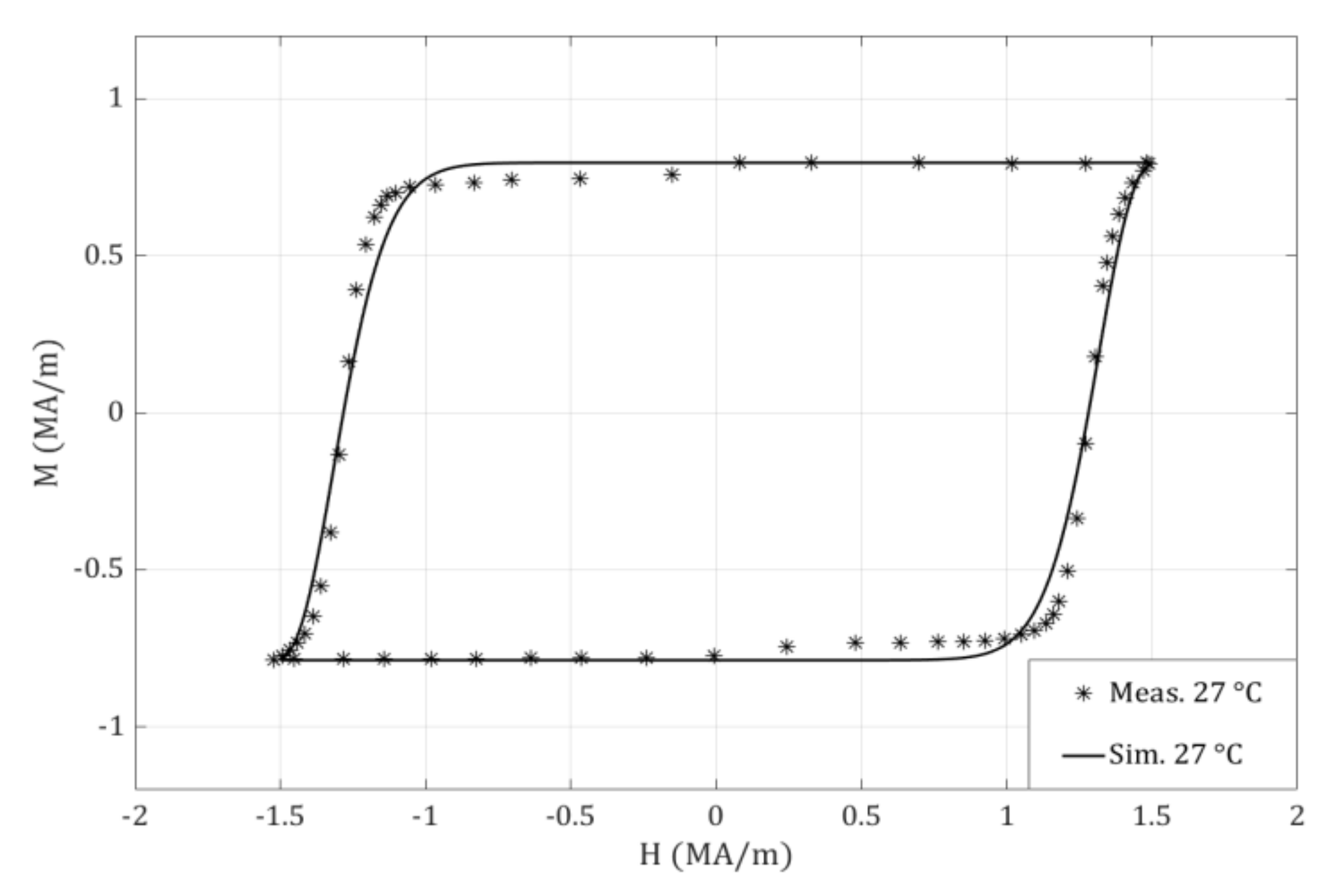
3.2. Hysteresis Loop Modeling

The computational method described in the previous section was applied to model the hysteresis loop of real NdFeB alloy samples at an environmental temperature. With this purpose, experimental data taken from [30] were considered. Through an iterative procedure, it has been found that the best numerical fitting was obtained, imposing α = 20 and β = 1.02, while γ was set equal to the measured magnetic saturation value M_S.

Figure 6 shows the hysteresis loop measured by Ghezelbash et al. in [30] and the one computed by means of Equation (11). As can be noted, the computed and experimental loops almost overlap, meaning that the derived model is very suitable for modeling permanent magnets like NdFeB alloys.

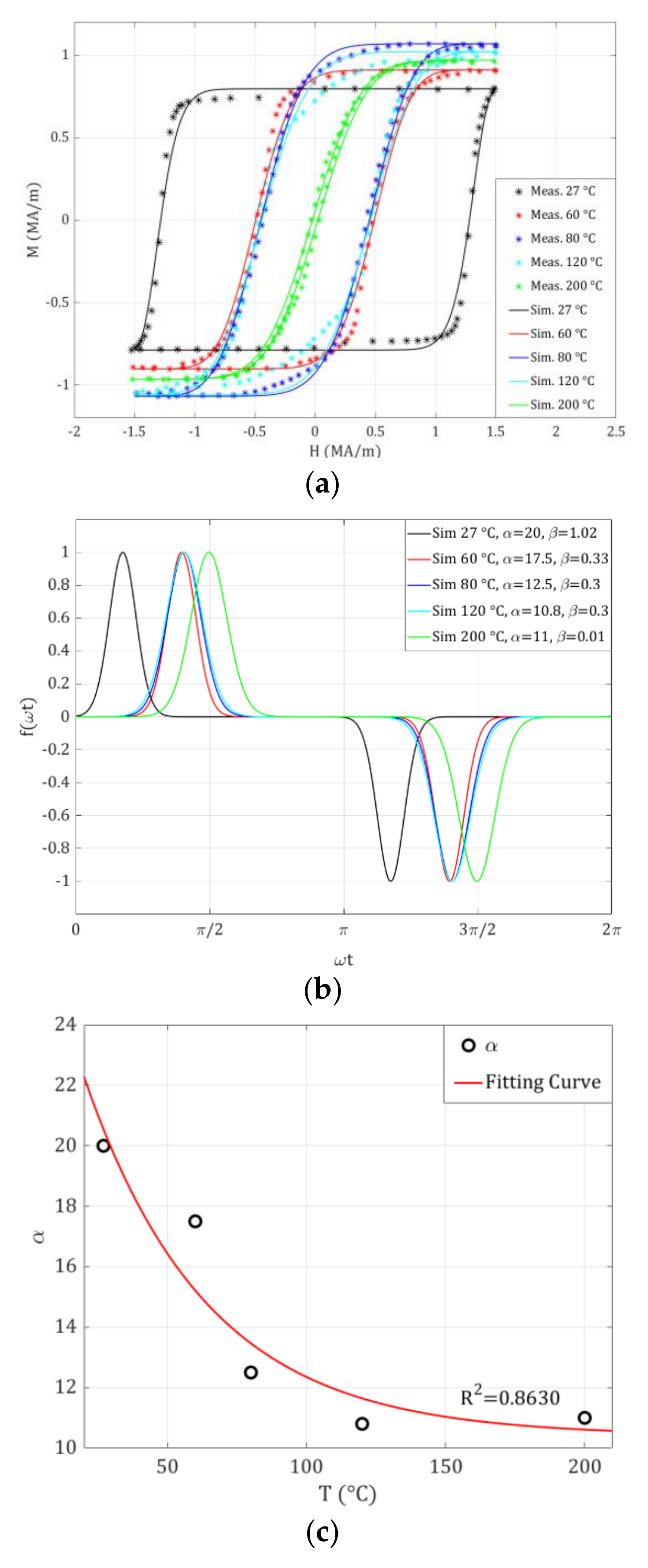
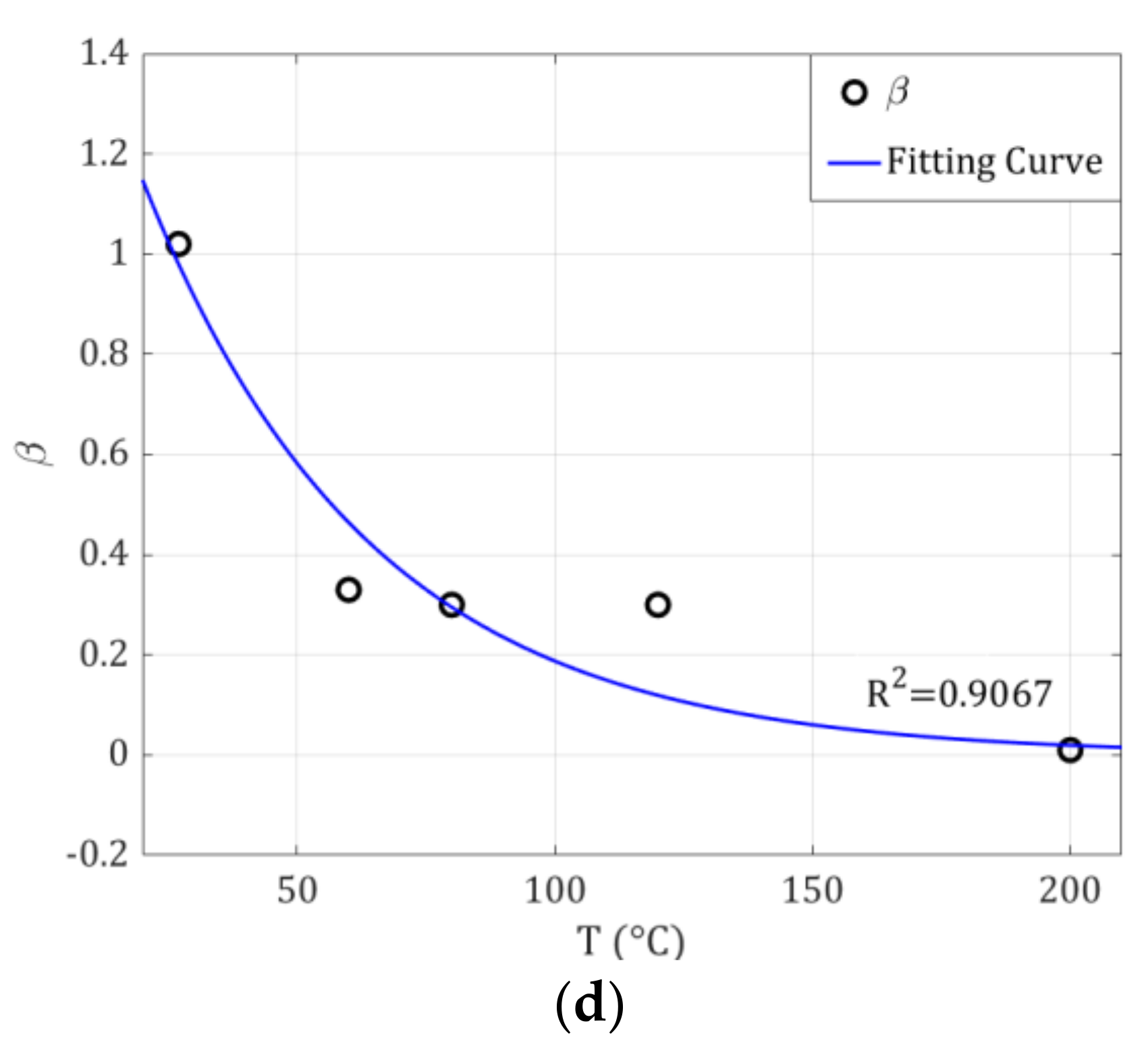
3.3. Temperature Influence on Hysteresis Loop

It has been observed in [29,30] that the variations of sample temperature strongly affect the magnetic properties. Therefore, an in-depth understanding of the temperature effect on magnetization is crucial, especially when such materials are required to operate at different external conditions or overheating, as usually happens for common electric engines.

The hysteresis loops of a real NdFeB employed in [30] and measured at different temperature ranging from 27 °C up to 200 °C was hereby extrapolated as a good exercise for the fitting parameters. In the following, the temperature variations were assumed to not affect hysteron shape but only functions $f\left(\omega t\right)$, specifically the values of parameters α and β while γ was set equal to the measured magnetic saturation value at the considered temperature. Therefore, each hysteresis loop was modeled through a proper choice of parameters α and β and identified through an iterative procedure. In particular, Figure 7a shows the comparison of experimental and computed data, Figure 7b shows the corresponding functions $f\left(\omega t\right)$, while Figure 7c,d shows the values of α and β as functions of the temperature, respectively.

From Figure 7a, it is evident that all the experimental loops can be nicely simulated through the use of the proposed model with a very good accuracy since, for all the considered temperatures, there is an almost perfect agreement between the experimental and measured data. Furthermore, observing Figure 7c,d, it is also evident that α and β depend on temperature as two decreasing exponential functions, as confirmed by the computed correlation coefficient R² greater than 0.86. This behavior is quite common in thermodynamics and confirms the validity of the proposed approach.

In particular, the coefficients α and β were fitted with the following functions:

$$\alpha \left(T\right)=18.77 e^{-T/44.17}+10.46$$

(13)

$$\beta \left(T\right)=1.806 e^{-T/44.17}$$

(14)

It is worth noticing that the two exponential terms have the same characteristic exponent.

4. Conclusions

In this paper, a novel computational method capable of reproducing hysteresis loops of hard magnetic materials was proposed. This method is conceptually based on the Preisach model but has a completely different and innovative approach in modeling the hysteron effect. While in the classical Preisach model the hysterons were modelled as ideal geometrical entities giving rise to so-called Barkhausen jumps, i.e., changes in the magnetization states caused by hysterons, in this study, the Barkhausen jumps are compared to the velocity jumps of rigid disk-shaped solids elastically colliding with each other. This allowed us to obtain a simple differential formulation for the global magnetization equation rather than a complicated integrodifferential one, with a significant improvement in terms of computational performance.

The proposed computational method was tested first for a wide range of ideal hysteretic materials and then for a real NdFeB magnet. A sensitivity analysis on the model parameters showed the capability to model a large class of hysteresis loops, while application of the proposed method to the hysteresis loop of a real NdFeB magnet proved the high accuracy and efficiency for a large temperature range.

Finally, the identification procedure for temperature-dependent hysteresis loops showed a specific dependence on the temperature of the model parameters. More precisely, it has been shown that they follow an exponential decay with an increase in temperature. Therefore, the proposed method permits modeling of the temperature effect on magnetization of hard magnets, which is a key aspect in the design of electrical components and machines usually subjected to temperature variations.