Some Magnetic Properties and Magnetocaloric Effects in the High-Temperature Antiferromagnet YbCoC2
Abstract
1. Introduction
2. Materials and Methods
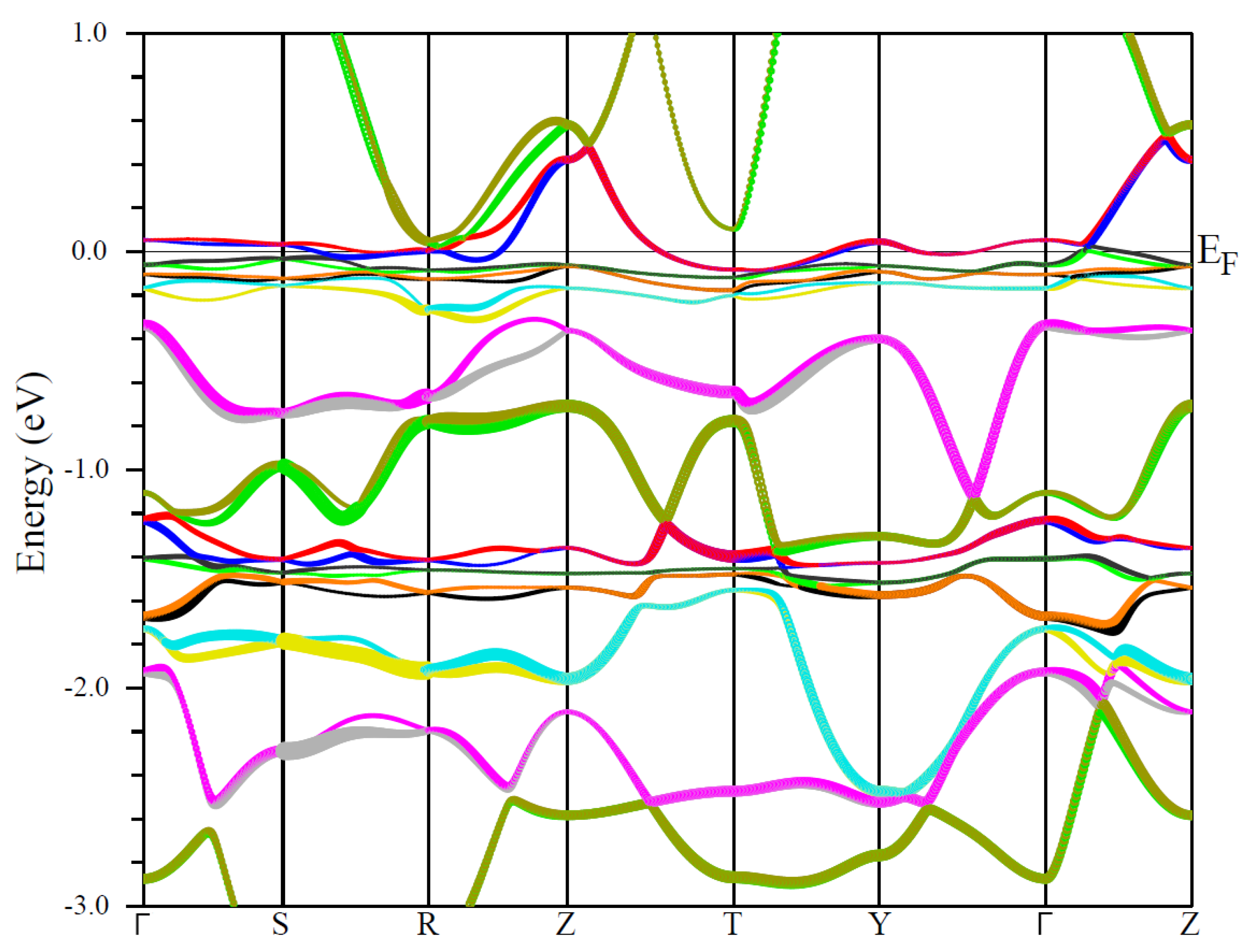
3. Results and Discussion
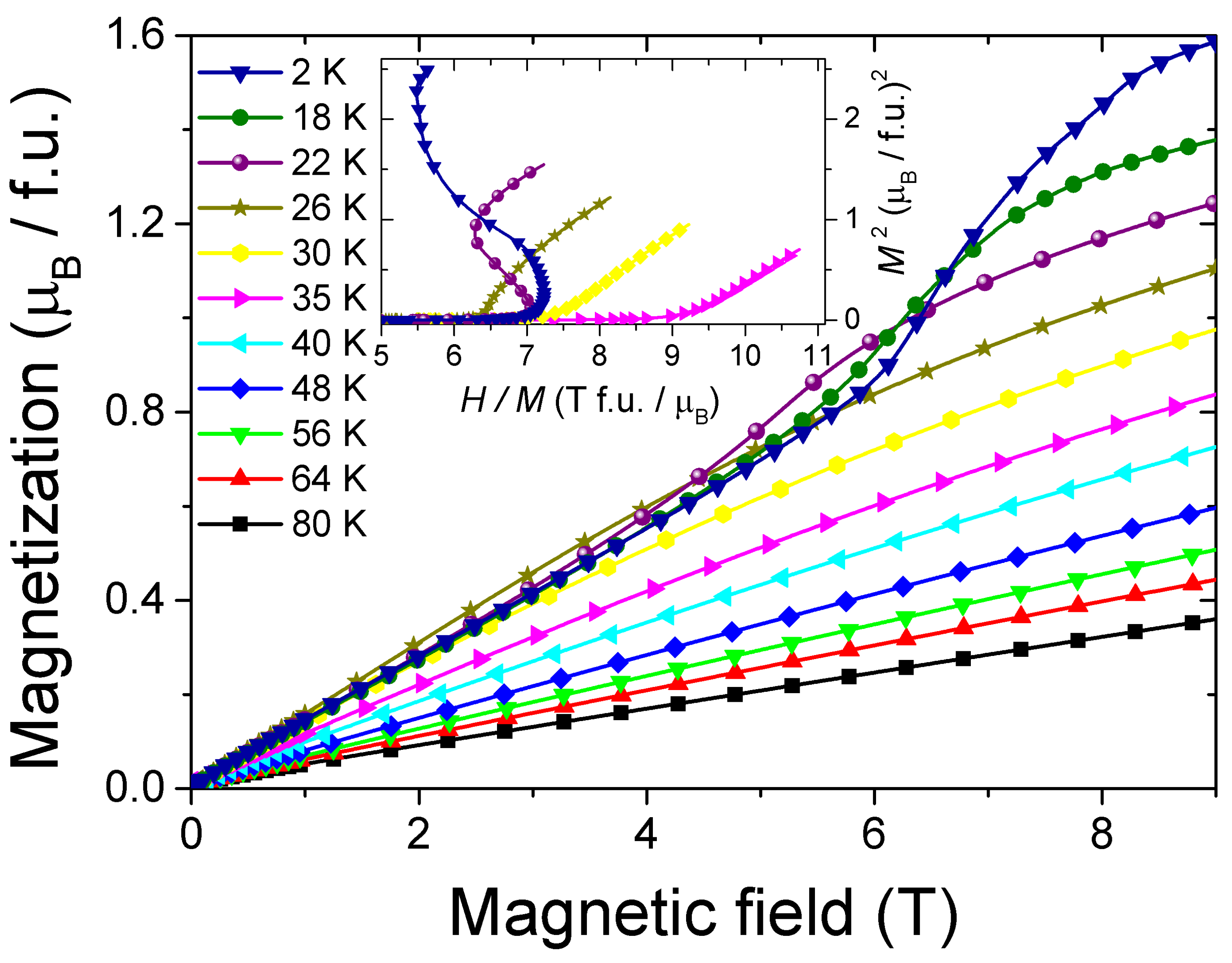
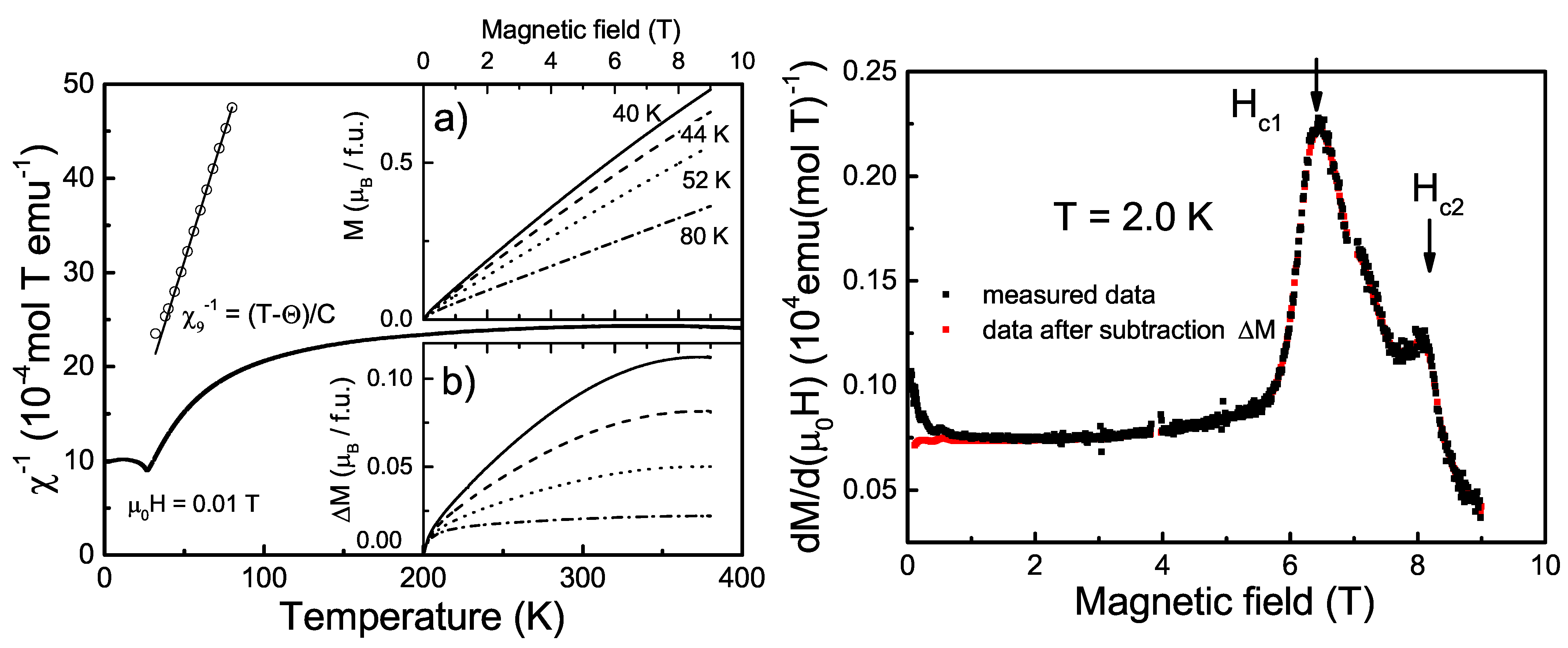
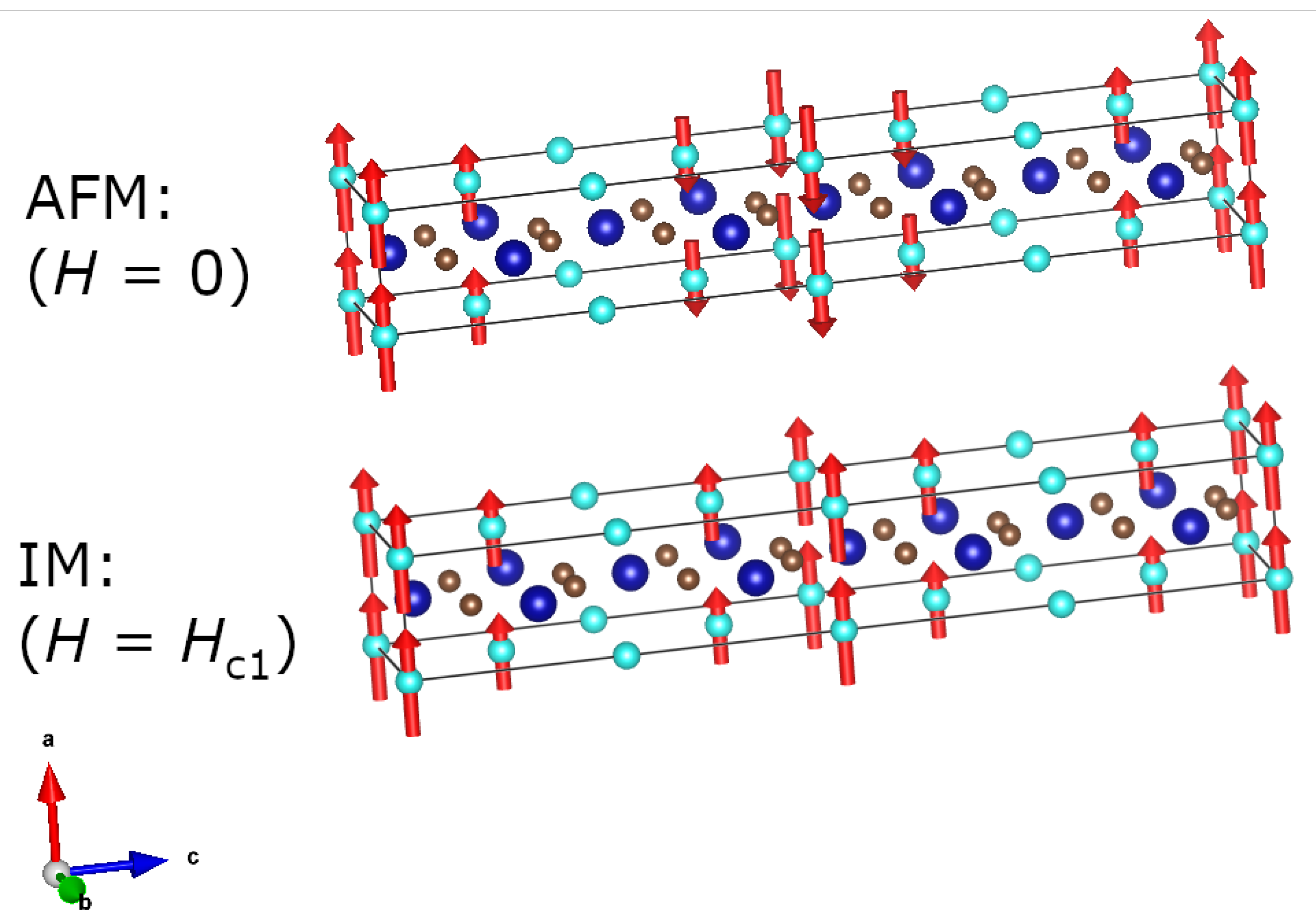
3.1. Magnetic Properties
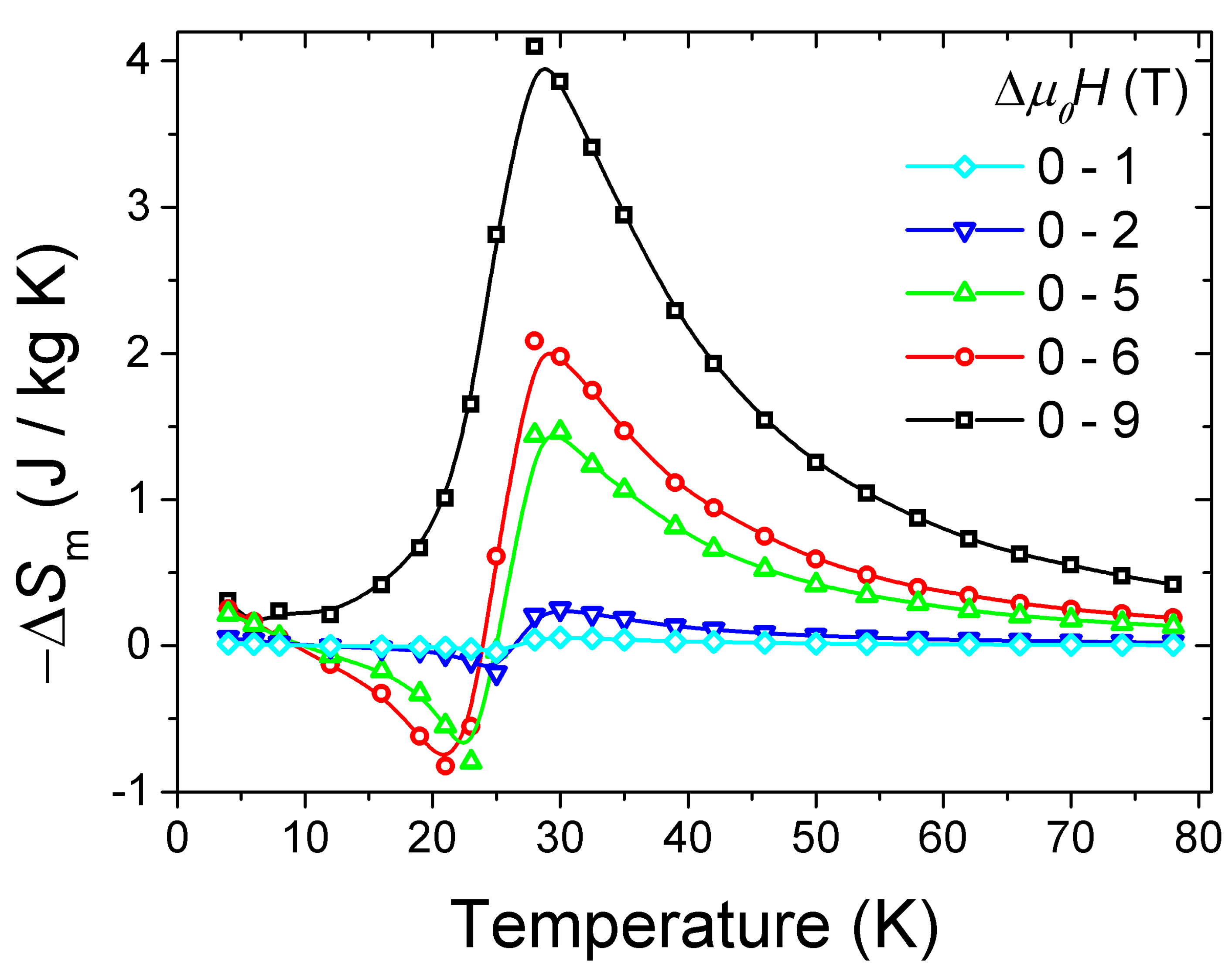
3.2. Magnetocaloric Effect
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TWS | topological Weyl semimetals |
| FM | ferromagnetic |
| MCE | magnetocaloric effect |
| AFM | antiferromagnetic |
| VSM | vibrating sample magnetometer |
| PPMS | physical properties measurement system |
| PM | paramagnetic |
| IM | intermediate magnetic phase |
| DFT | density functional theory |
| DOS | density of states |
| DMFT | dynamical mean field theory |
References
- Ray, R.; Sadhukhan, B.; Richter, M.; Facio, J.I.; van den Brink, J. Tunable chirality of noncentrosymmetric magnetic Weyl semimetals in rare-earth carbides. Npj Quantum Mater. 2022, 7, 19. [Google Scholar] [CrossRef]
- Kurebayashi, D.; Nomura, K. Theory for spin torque in Weyl semimetal with magnetic texture. Sci. Rep. 2019, 9, 5365. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.Z.; Nie, S.M.; Yi, C.J.; Jandke, J.; Shang, T.; Yao, M.Y.; Naamneh, M.; Yan, L.Q.; Sun, Y.; Chikina, A.; et al. Spin fluctuation induced Weyl semimetal state in the paramagnetic phase of EuCd2As2. Sci. Adv. 2019, 5, eaaw4718. [Google Scholar] [CrossRef] [PubMed]
- Borisenko, S.; Evtushinsky, D.; Gibson, Q.; Yaresko, A.; Koepernik, K.; Kim, T.; Ali, M.; van den Brink, J.; Hoesch, M.; Fedorov, A.; et al. Time-reversal symmetry breaking type-II Weyl state in YbMnBi2. Nat. Commun. 2019, 10, 3424. [Google Scholar] [CrossRef] [PubMed]
- Salamatin, D.A.; Martin, N.; Sidorov, V.A.; Chtchelkatchev, N.M.; Magnitskaya, M.V.; Petrova, A.E.; Zibrov, I.P.; Fomicheva, L.N.; Guo, J.; Huang, C.; et al. Dualism of the 4f electrons and its relation to high-temperature antiferromagnetism in the heavy-fermion compound YbCoC2. Phys. Rev. B 2020, 101, 100406. [Google Scholar] [CrossRef]
- Schäfer, W.; Will, G.; Kotsanidis, P.; Yakinthos, J. Magnetic properties of RCoC2 (R = Y, Gd, Tb) compounds. J. Magn. Magn. Mater. 1990, 88, 13–17. [Google Scholar] [CrossRef]
- Amanai, H.; Onodera, H.; Ohashi, M.; Matsuo, S.; Yamauchi, H.; Yamaguchi, Y.; Sato, N. Magnetic properties of the ternary carbide DyCoC2 studied by magnetization measurements, neutron diffraction and 161Dy Mössbauer spectroscopy. J. Magn. Magn. Mater. 1995, 148, 413–418. [Google Scholar] [CrossRef]
- Michor, H.; Steiner, S.; Schumer, A.; Hembara, M.; Levytskyy, V.; Babizhetskyy, V.; Kotur, B. Magnetic properties of HoCoC2, HoNiC2 and their solid solutions. J. Magn. Magn. Mater. 2017, 441, 69–75. [Google Scholar] [CrossRef]
- Kotsanidis, P.A.; Yakinthos, J.K.; Schäfer, W. Crystal and magnetic structures of RCoC2 (R = Nd, Er, Tm). J. Alloy. Compd. 1996, 242, 90–94. [Google Scholar] [CrossRef]
- Schäfer, W.; Kockelmann, W.; Will, G.; Yakinthos, J.K.; Kotsanidis, P.A. Magnetic structures of rare earths R in RCoC2 and RNiC2 compounds. J. Alloy. Compd. 1997, 250, 565–568. [Google Scholar] [CrossRef]
- Lingjian, M.; Youshun, J.; Lingwei, L. Large reversible magnetocaloric effect in the RECoC2 (RE = Ho and Er) compounds. Intermetallics 2017, 85, 69–73. [Google Scholar] [CrossRef]
- Li, B.; Hu, W.J.; Liu, X.G.; Yang, F.; Ren, W.J.; Zhao, X.G.; Zhang, Z.D. Large reversible magnetocaloric effect in TbCoC2 in low magnetic field. Appl. Phys. Lett. 2008, 92, 242508. [Google Scholar] [CrossRef][Green Version]
- Meng, L.; Xu, C.; Yuan, Y.; Qi, Y.; Zhou, S.; Li, L. Magnetic properties and giant reversible magnetocaloric effect in GdCoC2. RSC Adv. 2016, 6, 74765–74768. [Google Scholar] [CrossRef]
- Izyumov, Y.A. Modulated, or long-periodic, magnetic structures of crystals. Sov. Phys. Uspekhi 1984, 27, 845. [Google Scholar] [CrossRef]
- Andreani, L.; Pavarini, E.; Liviotti, E.; Santini, P.; Amoretti, G. Competition between Kondo effect and magnetic interaction in Kondo systems. Phys. B Condens. Matter 1997, 230, 523–528. [Google Scholar] [CrossRef]
- Streltsov, S.V.; Khomskii, D.I. Covalent bonds against magnetism in transition metal compounds. Proc. Natl. Acad. Sci. USA 2016, 113, 10491–10496. [Google Scholar] [CrossRef]
- Terada, N.; Mamiya, H. High-efficiency magnetic refrigeration using holmium. Nat. Commun. 2021, 12, 1212. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, J.; Li, S.; Zhang, Z.; Wang, J.; Ren, Z. Magnetic properties and promising magnetocaloric performances in the antiferromagnetic GdFe2Si2 compound. Sci. China Mater. 2022, 65, 1345–1352. [Google Scholar] [CrossRef]
- Luo, S.; Sun, Y.; Song, J.; Liu, J. Performance analysis of a hybrid pulse detonation engine using liquid hydrogen as fuel. Int. J. Hydrog. Energy 2022, 47, 21537–21551. [Google Scholar] [CrossRef]
- Peschka, W. Liquid Hydrogen: Fuel of the Future; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef]
- Banerjee, B. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964, 12, 16–17. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Anisimov, M.A.; Krasnorussky, V.N.; Bogach, A.V.; Demishev, S.V.; Semeno, A.V.; Salamatin, D.A.; Sidorov, V.A.; Bokov, A.V.; Tsvyashchenko, A.V. Prokhorov General Physics Institute of the Russian Academy of Sciences, Moscow, Russia. 2023; manuscript in preparation. [Google Scholar]
- Pecharsky, V.K.; Gschneidner, K.A. Magnetocaloric effect from indirect measurements: Magnetization and heat capacity. J. Appl. Phys. 1999, 86, 565–575. [Google Scholar] [CrossRef]
- Gschneidner, K.A.; Pecharsky, V.K. Magnetocaloric Materials. Annu. Rev. Mater. Sci. 2000, 30, 387–429. [Google Scholar] [CrossRef]
- Shimura, Y.; Watanabe, K.; Taniguchi, T.; Osato, K.; Yamamoto, R.; Kusanose, Y.; Umeo, K.; Fujita, M.; Onimaru, T.; Takabatake, T. Magnetic refrigeration down to 0.2 K by heavy fermion metal YbCu4Ni. J. Appl. Phys. 2022, 131, 013903. [Google Scholar] [CrossRef]
- Gruner, T.; Jang, D.; Steppke, A.; Brando, M.; Ritter, F.; Krellner, C.; Geibel, C. Unusual weak magnetic exchange in two different structure types: YbPt2Sn and YbPt2In. J. Phys. Condens. Matter 2014, 26, 485002. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salamatin, D.A.; Krasnorussky, V.N.; Magnitskaya, M.V.; Semeno, A.V.; Bokov, A.V.; Velichkov, A.; Surowiec, Z.; Tsvyashchenko, A.V. Some Magnetic Properties and Magnetocaloric Effects in the High-Temperature Antiferromagnet YbCoC2. Magnetochemistry 2023, 9, 152. https://doi.org/10.3390/magnetochemistry9060152
Salamatin DA, Krasnorussky VN, Magnitskaya MV, Semeno AV, Bokov AV, Velichkov A, Surowiec Z, Tsvyashchenko AV. Some Magnetic Properties and Magnetocaloric Effects in the High-Temperature Antiferromagnet YbCoC2. Magnetochemistry. 2023; 9(6):152. https://doi.org/10.3390/magnetochemistry9060152
Chicago/Turabian StyleSalamatin, Denis Alexandrovich, Vladimir Nikolaevich Krasnorussky, Mariya Viktorovna Magnitskaya, Alexei Valeryevich Semeno, Alexander Vladimirovich Bokov, Atanas Velichkov, Zbigniew Surowiec, and Anatoly Vasilyevich Tsvyashchenko. 2023. "Some Magnetic Properties and Magnetocaloric Effects in the High-Temperature Antiferromagnet YbCoC2" Magnetochemistry 9, no. 6: 152. https://doi.org/10.3390/magnetochemistry9060152
APA StyleSalamatin, D. A., Krasnorussky, V. N., Magnitskaya, M. V., Semeno, A. V., Bokov, A. V., Velichkov, A., Surowiec, Z., & Tsvyashchenko, A. V. (2023). Some Magnetic Properties and Magnetocaloric Effects in the High-Temperature Antiferromagnet YbCoC2. Magnetochemistry, 9(6), 152. https://doi.org/10.3390/magnetochemistry9060152






